取引におけるニューラルネットワーク：相対エンコーディング対応Transformer

はじめに

価格予測や市場トレンドの予測は、成功する取引やリスク管理において中心的なタスクです。高精度な価格変動予測により、トレーダーはタイムリーな意思決定ができ、損失を回避できます。しかし、ボラティリティの高い市場では、従来の機械学習モデルはその能力に限界があるかもしれません。

モデルをゼロから学習させるのではなく、まずラベルなしの大規模データで事前学習をおこない、その後に特定のタスク向けにファインチューニングするというアプローチに移行することで、新たに大量のデータを収集することなく、高精度な予測が実現可能となります。たとえば、金融データに適応されたTransformerアーキテクチャをベースとしたモデルは、資産間の相関性や時間的依存性などの情報を活用することで、より正確な予測が可能になります。代替的なAttention機構を導入することで、重要な市場の相関関係を考慮でき、モデルの性能が大幅に向上します。これにより、手動調整や複雑なルールベースモデルへの依存を減らしつつ、新たな取引戦略の開発が可能になります。

そのような代替的Attentionアルゴリズムの一つが、論文「Relative Molecule Self-Attention Transformer」で紹介されました。著者らは、分子グラフに対する新しいSelf-Attention（自己注意）式を提案しており、さまざまな入力特徴量を精密に処理することで、多くの化学領域において高精度かつ高信頼性を実現しています。Relative Molecule Attention Transformer (R-MAT)は、Transformerアーキテクチャに基づく事前学習済みモデルであり、距離や近傍情報を効果的に統合するRelative Self-Attentionの新しいバリエーションを表しています。R-MATは、さまざまなタスクにおいて最先端の競争力ある性能を発揮しています。

1. R-MATアルゴリズム

自然言語処理において、従来のSelf-Attention層は、入力トークンの位置情報を考慮しません。つまり、入力データの順番を入れ替えても、出力結果は変わりません。この位置情報を入力に取り込むため、従来のTransformerでは絶対位置エンコーディングが用いられてきました。これに対して、相対位置エンコーディングは、各トークン対の相対的な距離を導入し、特定のタスクにおいて大きな性能向上をもたらします。R-MATアルゴリズムは、まさにこの相対トークン位置エンコーディングを採用しています。

このアルゴリズムの核心的なアイデアは、グラフ構造や距離情報の柔軟な処理を可能にすることです。R-MATの著者らは、Self-Attentionブロックを拡張し、入力系列中の要素間の相対位置を効率的に表現できるよう、相対位置エンコーディングを応用しました。

分子中の2つの原子の相対的な配置は、以下の3つの相互に関連する要素によって特徴付けられます。

• 相対距離
• 分子グラフ上の距離
• 物理化学的な関係性

2つの原子は次元Dのベクトル𝒙iと𝒙jで表されます。著者らは、これらの関係を、次元D′のペア埋め込みベクトル𝒃ijによって符号化することを提案しています。この埋め込みは、Self-Attentionモジュールの射影層(projection layer)の後に使用されます。

このプロセスはまず、分子グラフにおいてノードiとjの間にいくつのノードが存在するかという情報を用いて、2つの原子間のグラフ上の距離を符号化することから始まります。次に、動径基底関数(radial basis)による距離エンコーディングがおこなわれます。最後に、各結合に対して、原子ペアの物理化学的関係を反映した重み付けが施されます。

著者らは、このような特徴は事前学習を通じて容易に学習される可能性がある一方で、小規模データセットでR-MATを訓練する場合、非常に有効であると述べています。

得られた各原子ペアに対するトークン𝒃ijは、新たなSelf-Attention層の構築に利用されます。これを著者らはRelative Molecule Self-Attentionと名付けました。

この新しいアーキテクチャにおいて、著者らは従来のSelf-AttentionにおけるQuery-Key-Value構造を踏襲しています。トークン𝒃ijは、2つのニューラルネットワークφVとφKを用いて、それぞれKeyおよびValueに特化したベクトル𝒃ijVおよび𝒃ijKに変換されます。各ニューラルネットワークは2層から構成されており、すべてのAttentionヘッドに共通の隠れ層と、ヘッドごとに異なる出力層を備えて、異なる相対埋め込みを生成します。このようにして構成されるRelative Self-Attentionは、以下のように数式で表すことができます。

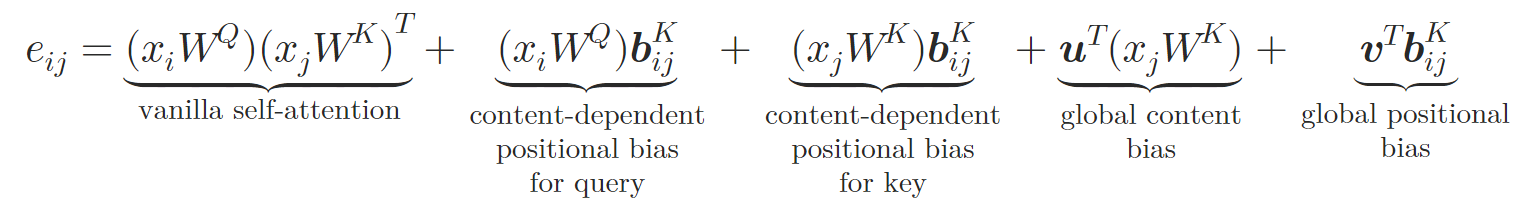
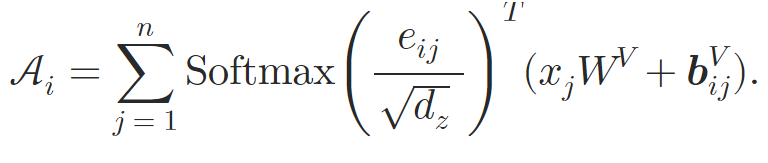
ここで𝒖と𝒗は学習可能なベクトルです。

このようにして、著者らは原子間の関係性を埋め込むことでSelf-Attentionブロックを拡張しています。Attention重みの計算時には、𝒃ijKに基づいて計算される内容依存の位置バイアス、グローバルコンテキストバイアス、およびグローバル位置バイアスを導入します。さらに、加重平均Attentionの計算時には、代替埋め込みである𝒃ijVの情報も組み込まれます。

このRelative Self-Attentionブロックは、Relative Molecule Attention Transformer (R-MAT)の構築に用いられます。

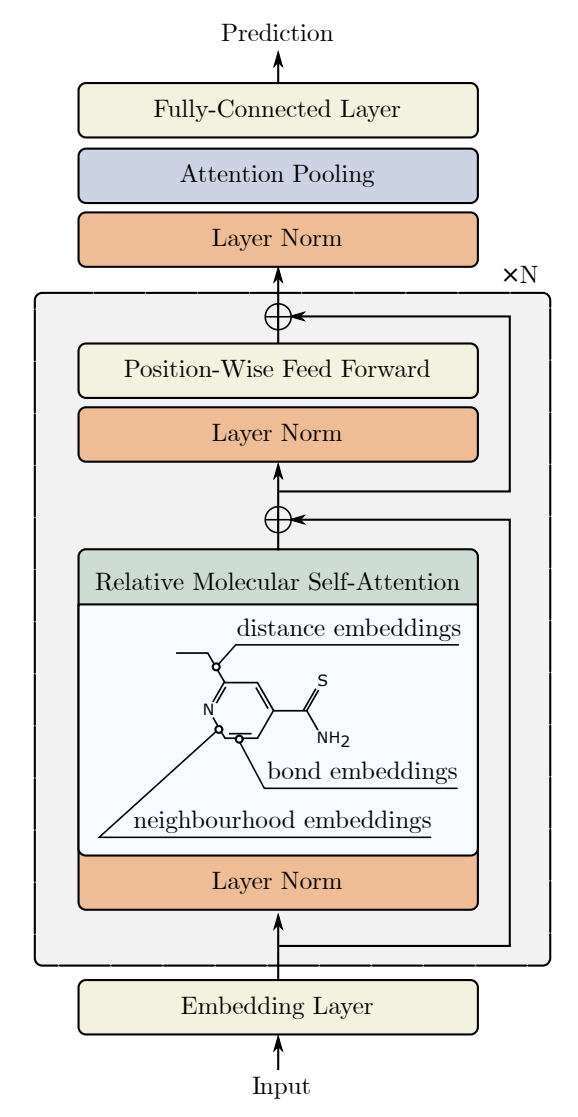
入力データはNatoms×36の行列として表され、N層のRelative Molecule Self-Attentionの積み重ねによって処理されます。各Attention層の後には、従来のTransformerモデルと同様に残差接続付きのMLPが続きます。

Attention層を通じて入力データを処理した後、著者らは表現を固定サイズのベクトルに集約します。このためにSelf-Attentionプーリングが用いられます。

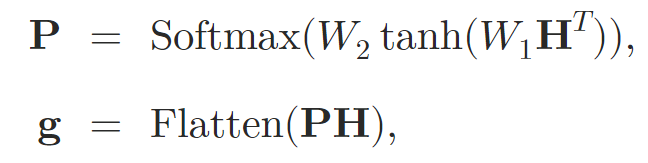
ここで、𝐇はSelf-Attention層から得られた隠れ状態を表し、W1とW2はAttentionプーリングの重みです。

次に、グラフ埋め込み𝐠は、leaky-ReLU活性化関数を持つ2レベルMLPに入力され、最終的な予測が出力されます。

以下に、著者による本手法の可視化図を示します。

2.MQL5での実装

提案されたRelative Molecule Attention Transformer (R-MAT)手法の理論的側面を検討した後、MQL5を使用して提案されたアプローチの独自の解釈を展開していきます。最初に述べておくと、本アルゴリズムの構築は複数のモジュールに分割して進めることにしました。まず、Relative Self-Attentionアルゴリズムを実装する専用オブジェクトを作成し、その後、R-MATモデル全体をまとめる高レベルクラスとして実装します。

2.1 Relative Self-Attentionモジュール

ご存じのとおり、大部分の計算処理はOpenCLコンテキストにオフロードされています。したがって、新しいアルゴリズムの実装を始めるにあたっては、OpenCLプログラムに必要なカーネルを追加する必要があります。まず作成するカーネルは、フィードフォワード処理用のMHRelativeAttentionOutカーネルです。このカーネルは、以前に解説したSelf-Attentionアルゴリズムの実装に基づいていますが、ここではグローバルバッファの数が大幅に増加しています。その目的については、アルゴリズムの構築を進めながら詳しく見ていきます。

__kernel void MHRelativeAttentionOut(__global const float *q,         ///<[in] Matrix of Querys
                                     __global const float *k,         ///<[in] Matrix of Keys
                                     __global const float *v,         ///<[in] Matrix of Values
                                     __global const float *bk,        ///<[in] Matrix of Positional Bias Keys
                                     __global const float *bv,        ///<[in] Matrix of Positional Bias Values
                                     __global const float *gc,        ///<[in] Global content bias vector
                                     __global const float *gp,        ///<[in] Global positional bias vector
                                     __global float *score,           ///<[out] Matrix of Scores
                                     __global float *out,             ///<[out] Matrix of attention
                                     const int dimension              ///< Dimension of Key
                                    )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k_id = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

このカーネルは、3次元のタスク空間内で動作するように設計されています。各次元はそれぞれQuery、Key、Headに対応しています。第2次元では、ワークグループ（並列実行の単位）を生成します。

カーネル本体の中では、まず最初にタスク空間の各次元における現在のスレッド位置（インデックス）を取得し、その範囲（境界）も確認します。その後、必要な要素にアクセスするために、データバッファに対する定数のオフセット値を定義します。

   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads * k_id + h);
   const int shift_gc = dimension * h;
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

次に、ワークグループ内で情報を共有・交換するためのローカルメモリ上の配列を作成します。

   __local float temp[LOCAL_ARRAY_SIZE];

次に、Relative Self-Attentionアルゴリズムに従い、Attention係数を計算します。この処理では、複数のベクトルの内積を計算し、その結果を加算していきます。ここでは、掛け合わせるすべてのベクトルの次元が同じであるという事実を利用します。そのため、必要なすべての乗算を実行するには、単一のループで十分です。

//--- score
   float sc = 0;
   for(int d = 0; d < dimension; d++)
     {
      float val_q = q[shift_q + d];
      float val_k = k[shift_kv + d];
      float val_bk = bk[shift_kv + d];
      sc += val_q * val_k + 
	    val_q * val_bk + 
            val_k * val_bk + 
            gc[shift_q + d] * val_k + 
            gp[shift_q + d] * val_bk;
     }

次のステップでは、計算されたAttention係数を個々のQuery単位で正規化します。正規化には、従来のアルゴリズムと同様にSoftmax関数を使用します。したがって、この正規化手順は既存の実装からそのまま流用され、特別な変更は必要ありません。この段階では、まず係数の指数関数（exp）値を計算します。

   sc = exp(sc / koef);
   if(isnan(sc) || isinf(sc))
      sc = 0;

次に、先ほどローカルメモリに作成した配列を使って、ワークグループ内で得られた係数を合計します。

//--- sum of exp
   for(int cur_k = 0; cur_k < kunits; cur_k += ls)
     {
      if(k_id >= cur_k && k_id < (cur_k + ls))
        {
         int shift_local = k_id % ls;
         temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   uint count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < ls)
         temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

次に、先ほど得た係数を合計値で割り、正規化された値を対応するグローバルバッファに保存します。

//--- score
   float sum = temp[0];
   if(isnan(sum) || isinf(sum) || sum <= 1e-6f)
      sum = 1;
   sc /= sum;
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

正規化された依存係数を計算した後、Attention演算の結果を求めることができます。ここでのアルゴリズムは従来のものに非常に近く、Attention係数を掛ける前に、ValueベクトルとbijVベクトルの和を加えるだけです。

//--- out
   for(int d = 0; d < dimension; d++)
     {
      float val_v = v[shift_kv + d];
      float val_bv = bv[shift_kv + d];
      float val = sc * (val_v + val_bv);
      if(isnan(val) || isinf(val))
         val = 0;
      //--- sum of value
      for(int cur_v = 0; cur_v < kunits; cur_v += ls)
        {
         if(k_id >= cur_v && k_id < (cur_v + ls))
           {
            int shift_local = k_id % ls;
            temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < count && (k_id + count) < kunits)
            temp[k_id] += temp[k_id + count];
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      if(k_id == 0)
         out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]);
     }
  }

スレッド間の同期をおこなうバリアの配置は非常に重要であることを改めて強調したいと思います。バリアは、ワークグループ内の各スレッドが同じ回数だけ到達するように配置しなければなりません。バリアを迂回したり、すべての同期ポイントに達する前に早期に抜けたりするコードは避ける必要があります。そうしないと、あるスレッドがすでに処理を終えたにもかかわらず、他のスレッドがバリアで待機し続ける状態、すなわちカーネルの停滞が発生するリスクがあります。

逆伝播アルゴリズムはMHRelativeAttentionInsideGradientsカーネルで実装されています。この実装は先述のフォワードパスカーネルの処理を完全に逆転させたもので、過去の実装から大きく流用されています。よって、この部分についてはご自身で詳細を確認されることをお勧めします。OpenCLプログラム全体のコードは添付ファイルにて提供されています。

さて、メインプログラムの実装に進みます。ここではRelative Self-Attentionアルゴリズムを実装するためのCNeuronRelativeSelfAttentionクラスを作成します。ただし、実装に入る前に、相対位置符号化(positional encoding)についていくつかのポイントを解説します。

R-MATフレームワークの著者らは、このアルゴリズムを化学産業の課題解決のために提案しました。彼らは分子中の原子の位置関係を、タスクの特性に合わせて記述しています。私たちにとっては、ローソク足間の距離や特徴も重要ですが、それに加えてもう一つの要素があります。それは「方向性」です。トレンドは、単なる距離だけでなく、一方向の価格変動が連続して初めて形成され、市場の傾向として現れます。

次に分析対象のシーケンスの長さの問題があります。分子内の原子数は比較的少数であることが多く、原子ペアごとに偏差ベクトルを計算しても負荷が許容範囲内です。しかし私たちの場合、分析対象となる過去のデータ量は非常に大きくなり得ます。そのため、分析対象となるローソク足の各ペアごとに偏差ベクトルを計算・保持するのは非常にリソースを消費する処理となってしまいます。

このため、著者らが提案した「各シーケンス要素間の偏差を計算する方法」は使わず、代替の方法を検討しました。そこで比較的シンプルな解決策として、入力データの行列とその転置行列との積を取る方法を採用しました。数学的に見ると、二つのベクトルのドット積は、それぞれの大きさの積と、それらのなす角のコサインの積に等しいです。したがって、直交するベクトルの積はゼロとなり、同じ方向を向くベクトルは正の値を、逆方向のベクトルは負の値を返します。つまり、あるベクトルと複数のベクトルを比較すると、ベクトル間の角度が小さくなり、かつ比較対象のベクトルの大きさが大きいほど、その積の値は大きくなります。    

以上の方針が定まったところで、次は新しいオブジェクトの構築に進みます。以下にその構造を示します。

class CNeuronRelativeSelfAttention   :  public CNeuronBaseOCL
  {
protected:
   uint                    iWindow;
   uint                    iWindowKey;
   uint                    iHeads;
   uint                    iUnits;
   int                     iScore;
   //---
   CNeuronConvOCL          cQuery;
   CNeuronConvOCL          cKey;
   CNeuronConvOCL          cValue;
   CNeuronTransposeOCL     cTranspose;
   CNeuronBaseOCL          cDistance;
   CLayer                  cBKey;
   CLayer                  cBValue;
   CLayer                  cGlobalContentBias;
   CLayer                  cGlobalPositionalBias;
   CLayer                  cMHAttentionPooling;
   CLayer                  cScale;
   CBufferFloat            cTemp;
   //---
   virtual bool      AttentionOut(void);
   virtual bool      AttentionGraadient(void);

   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronRelativeSelfAttention(void) : iScore(-1) {};
                    ~CNeuronRelativeSelfAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRelativeSelfAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

ご覧の通り、新しいクラスの構造にはかなり多くの内部オブジェクトが含まれています。これらの機能については、クラスのメソッドを実装しながら徐々に理解していくことになります。現時点で重要なのは、すべてのオブジェクトがstaticとして宣言されているという点です。これにより、クラスのコンストラクタおよびデストラクタは空のままにしておくことができます。これらの宣言済みおよび継承されたオブジェクトの初期化は、Initメソッド内でおこなわれます。このInitメソッドのパラメータには、作成されるオブジェクトのアーキテクチャを正確に定義するための定数が含まれています。メソッドのパラメータは、従来のMulti-Head Self-Attention実装から直接引き継がれており、特に変更は加えられていません。ただし、「内部層の数」を指定するパラメータだけは省かれています。これは意図的な設計であり、この実装では内部オブジェクトを必要な数だけ作成することで、上位のオブジェクト側が層の数を管理する形になっているためです。

bool CNeuronRelativeSelfAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                        uint window, uint window_key, uint units_count, uint heads, 
                                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

メソッド本体では、受け取ったパラメータの一部を渡して、親クラスの同名メソッドを直ちに呼び出します。ご存知の通り、親クラスのメソッドはすでに受け取ったパラメータの最低限の検証と継承オブジェクトの初期化のアルゴリズムを実装しているため、私たちはその処理結果の論理的な成否を確認するだけです。

続いて、受け取った定数をクラスの内部変数に格納し、後続の処理で使用できるようにします。

   iWindow = window;
   iWindowKey = window_key;
   iUnits = units_count;
   iHeads = heads;

次に、宣言された内部オブジェクトの初期化に進みます。まず、Query、Key、Valueの各ベクトルを生成する内部層を、それぞれ対応する内部オブジェクトで初期化します。これらの3層には同一のパラメータを使用します。

   int idx = 0;
   if(!cQuery.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cKey.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cValue.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;

次に、距離行列を計算するためのオブジェクトを準備する必要があります。まずは入力データの転置用オブジェクトを作成します。

   idx++;
   if(!cTranspose.Init(0, idx, OpenCL, iUnits, iWindow, optimization, iBatch))
      return false;

そして、出力を記録するためのオブジェクトを作成します。行列乗算演算は親クラスにすでに実装されています。

   idx++;
   if(!cDistance.Init(0, idx, OpenCL, iUnits * iUnits, optimization, iBatch))
      return false;

次に、BKテンソルとBVテンソルの生成プロセスを構築する必要があります。理論セクションで説明したように、これらの生成は2層からなるMLPによっておこなわれます。第一層はすべてのAttentionヘッドで共有され、第二層は各Attentionヘッドごとに個別のトークンを生成します。今回の実装では、それぞれの要素に対して2つの連続した畳み込み層を使用します。層間には双曲線正接関数(tanh)を適用して非線形性を導入します。

   idx++;
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;

加えて、グローバルなコンテンツバイアスおよび位置バイアスのための学習可能なベクトルも必要です。これらを作成するために、以前の実装で用いた方法を採用します。つまり、2層からなるMLPを構築します。そのうちの1層は定数「1」を持つ静的な層で、もう1層は必要なテンソルを生成する学習可能な層です。これらのオブジェクトへのポインタは、配列cGlobalContentBiasとcGlobalPositionalBiasに格納します。

   idx++;
   CNeuronBaseOCL *neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;
   idx++;
   CBufferFloat *buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;
   idx++;
   buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;

この時点で、Relative Attentionモジュールに正しく入力データを設定するために必要なオブジェクトはすべて準備できました。次の段階では、Attentionの出力を処理するコンポーネントに進みます。まずは、Multi-head Attentionの結果を格納するためのオブジェクトを作成し、そのポインタを cMHAttentionPooling配列に追加します。

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(neuron)
     )
      return false;

次に、MLPプーリング操作を追加します。

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, 
                                                                       optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iHeads, iUnits, 1, optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;

出力にSoftmax層を追加します。

   idx++;
   conv.SetActivationFunction(None);
   CNeuronSoftMaxOCL *softmax = new CNeuronSoftMaxOCL();
   if(!softmax ||
      !softmax.Init(0, idx, OpenCL, iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(conv)
     )
      return false;
   softmax.SetHeads(iUnits);

プーリングMLPの出力では、シーケンス内のすべての要素について、各Attentionヘッドの正規化された重み係数が取得されることに注意してください。ここで、最終的な結果を取得するには、結果のベクトルをMulti-head Attentionブロックからの対応する出力で乗算するだけです。ただし、シーケンスの各要素の表現ベクトルのサイズは、内部の次元と同じになります。したがって、結果を元の入力データのレベルに調整するためのスケーリングオブジェクトも追加します。

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iUnits, optimization, iBatch) ||
      !cScale.Add(neuron)
     )
      return false;
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey, iWindowKey, 4 * iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(LReLU);
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(None);

不要なコピー操作を排除するために、ここでデータバッファを差し替える必要があります。そして、メソッドの処理結果（論理値）を呼び出し元のプログラムに返します。

//---
   if(!SetGradient(conv.getGradient(), true))
      return false;
//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

この場合、置き換えているのは勾配バッファのポインタだけであることに注意してください。これは、Attentionブロック内で残差接続が生成されることによるものです。ただし、この部分については、feedForwardメソッドの実装時に説明します。

フィードフォワードメソッドのパラメータとして受け取るのは、ソースデータオブジェクトへのポインタです。これを、そのまま内部オブジェクトの同名メソッドに渡し、Query・Key・Valueエンティティを生成します。

bool CNeuronRelativeSelfAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cQuery.FeedForward(NeuronOCL) ||
      !cKey.FeedForward(NeuronOCL) ||
      !cValue.FeedForward(NeuronOCL)
     )
      return false;

外部プログラムから受け取ったソースデータオブジェクトのポインタについて、その妥当性はチェックしていません。この操作は内部オブジェクトのメソッというのも、この操作はすでに内部オブジェクトのメソッド内で実装されているため、この段階でのチェックポイントは不要だからです。

次に、解析対象オブジェクト間の距離を求めるためのエンティティの生成に進みます。元のデータテンソルを転置します。

   if(!cTranspose.FeedForward(NeuronOCL) ||
      !MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), iUnits, iWindow, iUnits, 1)
     )
      return false;

次に、元のデータテンソルとその転置コピーとの行列積を直ちに実行します。この演算結果を用いて、BKおよびBVエンティティを生成します。そのために、対応する内部モデルの層をループ処理で順番に通過させていきます。

   if(!((CNeuronBaseOCL*)cBKey[0]).FeedForward(cDistance.AsObject()) ||
      !((CNeuronBaseOCL*)cBValue[0]).FeedForward(cDistance.AsObject())
     )
      return false;
   for(int i = 1; i < cBKey.Total(); i++)
      if(!((CNeuronBaseOCL*)cBKey[i]).FeedForward(cBKey[i - 1]))
         return false;
   for(int i = 1; i < cBValue.Total(); i++)
      if(!((CNeuronBaseOCL*)cBValue[i]).FeedForward(cBValue[i - 1]))
         return false;

次に、グローバルバイアスのエンティティを生成するためのループを実行します。

   for(int i = 1; i < cGlobalContentBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).FeedForward(cGlobalContentBias[i - 1]))
         return false;
   for(int i = 1; i < cGlobalPositionalBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).FeedForward(cGlobalPositionalBias[i - 1]))
         return false;

これで作業の準備段階は完了です。上記のRelative Attentionのフィードフォワードカーネルに対するラッパーメソッドを呼び出します。

   if(!AttentionOut())
      return false;

その後、結果の処理に進みます。まず、プーリングMLPを使用して、Attentioni headの影響テンソルを生成します。

   for(int i = 1; i < cMHAttentionPooling.Total(); i++)
      if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).FeedForward(cMHAttentionPooling[i - 1]))
         return false;

次に、結果のベクトルをMulti-head Attentionの結果として乗算します。

   if(!MatMul(((CNeuronBaseOCL*)cMHAttentionPooling[cMHAttentionPooling.Total() - 1]).getOutput(),
              ((CNeuronBaseOCL*)cMHAttentionPooling[0]).getOutput(),
              ((CNeuronBaseOCL*)cScale[0]).getOutput(),
              1, iHeads, iWindowKey, iUnits)
     )
      return false;

次に、スケーリングMLPを使用して取得した値をスケーリングする必要があります。

   for(int i = 1; i < cScale.Total(); i++)
      if(!((CNeuronBaseOCL*)cScale[i]).FeedForward(cScale[i - 1]))
         return false;

得られた結果に元のデータを加算し、親クラスから継承された最上位の結果バッファに書き込みます。この操作をおこなうために、結果バッファのポインタは差し替えずにそのまま残しておく必要がありました。

   if(!SumAndNormilize(NeuronOCL.getOutput(), 
                       ((CNeuronBaseOCL*)cScale[cScale.Total() - 1]).getOutput(), 
                       Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

順伝播メソッドの実装が完了したら、通常は逆伝播アルゴリズムの構築に進みます。これらはcalcInputGradientsメソッドおよびupdateInputWeightsメソッド内で構成されます。最初のメソッドは、最終的な結果に対する各モデル要素の影響度に応じて、誤差勾配を分配します。2つ目のメソッドは、全体の誤差を減少させるようにモデルのパラメータを調整します。詳細については、添付のコードを参照してください。このクラスとそのすべてのメソッドの完全なコードがそこにあります。では次の作業フェーズに進みましょう。R-MATフレームワークを実装する最上位オブジェクトの構築です。

2.2 R-MATフレームワークの実装

R-MATフレームワークの高レベルアルゴリズムを整理するため、新しいクラスCNeuronRMATを作成します。その構造体を以下に示します。

class CNeuronRMAT :  public CNeuronBaseOCL
  {
protected:
   CLayer               cLayers;
   //---
   virtual bool         feedForward(CNeuronBaseOCL *NeuronOCL)
   override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronRMAT(void) {};
                    ~CNeuronRMAT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRMAT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

前のクラスとは異なり、今回のクラスにはネストされた動的配列オブジェクトが1つしか含まれていません。一見すると、これだけではこのような複雑なアーキテクチャを実装するには不十分に思えるかもしれません。しかし実際には、アルゴリズムを構築するために必要なオブジェクトへのポインタを格納するための動的配列が宣言されています。

この動的配列はstaticとして宣言されているため、クラスのコンストラクタおよびデストラクタは空のままにしておくことができます。内部オブジェクトと継承オブジェクトの初期化は、Initメソッド内で処理されます。

bool CNeuronRMAT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                       uint window, uint window_key, uint units_count, uint heads, 
                       uint layers, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

初期化メソッドのパラメータには、作成されるオブジェクトに対するユーザーの要件を明確に解釈するための定数が含まれています。ここでは、内部層の数を含む、Attentionブロックに関するおなじみのパラメータ群が登場します。

最初におこなう操作は、親クラスの同名メソッドを呼び出すという、もはや標準的ともいえる処理です。次に、ローカル変数を用意します。

   cLayers.SetOpenCL(OpenCL);
   CNeuronRelativeSelfAttention *attention = NULL;
   CResidualConv *conv = NULL;

次に、内部層の数と同じ回数だけ繰り返すループを追加します。

   for(uint i = 0; i < layers; i++)
     {
      attention = new CNeuronRelativeSelfAttention();
      if(!attention ||
         !attention.Init(0, i * 2, OpenCL, window, window_key, units_count, heads, optimization, iBatch) ||
         !cLayers.Add(attention)
        )
        {
         delete attention;
         return false;
        }

ループの中では、まず先に実装したRelative Attentionオブジェクトの新しいインスタンスを作成し、外部プログラムから受け取った定数を渡して初期化します。

ご存知の通り、Relative Attentionクラスのフォワードパスメソッドは残差接続のストリームを管理しているため、このレベルではその処理を省略して先に進むことができます。

次に、従来のTransformerに似たFeedForwardブロックを作成します。ただし、よりシンプルな見た目の高レベルオブジェクトを作るために、このブロックのアーキテクチャを少し変更することにしました。代わりに、残差接続を含む畳み込みブロックであるCResidualConvを初期化します。その名前の通り、このブロックには残差接続も含まれているため、上位クラスでの実装は不要です。

      conv = new CResidualConv();
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window, window, units_count, optimization, iBatch) ||
         !cLayers.Add(conv)
        )
        {
         delete conv;
         return false;
        }
     }

したがって、Relative Attentionの1層を構築するために作成するオブジェクトは2つだけで済みます。作成したオブジェクトのポインタは、それらが呼び出される順番に従って動的配列に追加し、内部Attention層生成ループの次の繰り返しに進みます。

すべてのループを無事に完了した後、最後の内部層のデータバッファポインタを対応する上位バッファに置き換えます。

   SetOutput(conv.getOutput(), true);
   SetGradient(conv.getGradient(), true);
//---
   return true;
  }

その後、処理の論理結果を呼び出し元プログラムに返し、メソッドを終了します。

ご覧の通り、R-MATフレームワークのアルゴリズムを複数のブロックに分割することで、かなり簡潔なハイレベルオブジェクトを構築することができました。

なお、この簡潔さはクラスの他のメソッドにも反映されています。たとえば、feedForwardメソッドを見てみましょう。このメソッドは入力データオブジェクトへのポインタをパラメータとして受け取ります。

bool CNeuronRMAT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *neuron = cLayers[0];
   if(!neuron.FeedForward(NeuronOCL))
      return false;

メソッド本体では、まず最初のネストされたオブジェクトの同名メソッドを呼び出します。その後、すべてのネストされたオブジェクトに対して順番にループを組み、それぞれのメソッドを呼び出します。各呼び出し時には、前のオブジェクトの出力ポインタを入力として渡します。

   for(int i = 1; i < cLayers.Total(); i++)
     {
      neuron = cLayers[i];
      if(!neuron.FeedForward(cLayers[i - 1]))
         return false;
     }
//---
   return true;
  }

すべてのループ処理を終えた後は、あらかじめバッファポインタの差し替えをおこなっているため、データのコピーすら必要ありません。したがって、処理結果の論理値を呼び出し元のプログラムに返してメソッドを終了します。

同様の手法は逆伝播（バックワードパス）メソッドにも適用されており、そちらはご自身でのご確認をお勧めします。これにて、MQL5を用いたR-MATフレームワークの実装アルゴリズムの検討を終了します。本記事のクラスおよびすべてのメソッドの完全なコードは添付ファイルにてご覧いただけます。

また、環境とのインタラクションやモデルの学習プログラムの完全なコードも同様に添付しており、これらは以前のプロジェクトから変更なしで移植したものです。モデル構造に関しては、環境状態エンコーダの一部の層を入れ替えた程度の軽微な調整のみがおこなわれています。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRMAT;
   descr.window=BarDescr;
   descr.count=HistoryBars;
   descr.window_out = EmbeddingSize/2;                // Key Dimension
   descr.layers = 5;                                  // Layers
   descr.step = 4;                                    // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

学習済みモデルのアーキテクチャの詳細な説明は、添付ファイルにてご覧いただけます。

3.テスト

私たちはMQL5を用いてR-MATフレームワークの実装において大きな進展を遂げました。次に、最終段階であるモデルの学習と得られた方策のテストに進みます。本プロジェクトでは、先述のモデル学習アルゴリズムに従い、口座状態のエンコーダ、Actor、Criticの3つのモデルを同時に学習させます。口座状態エンコーダは市場状況の解釈を担当し、Actorは学習した方策に基づいて取引判断をおこない、CriticはActorの行動を評価して方策調整の方向性を示します。

学習には2023年のEURUSD、H1（1時間足）の実際の過去データを用い、すべてのインジケーターのパラメータはデフォルト値のままとしています。

モデルは逐次的に学習され、学習データセットも定期的に更新されます。

学習済み方策の有効性は2024年1月の過去データを用いて検証されました。以下にそのテスト結果を示します。

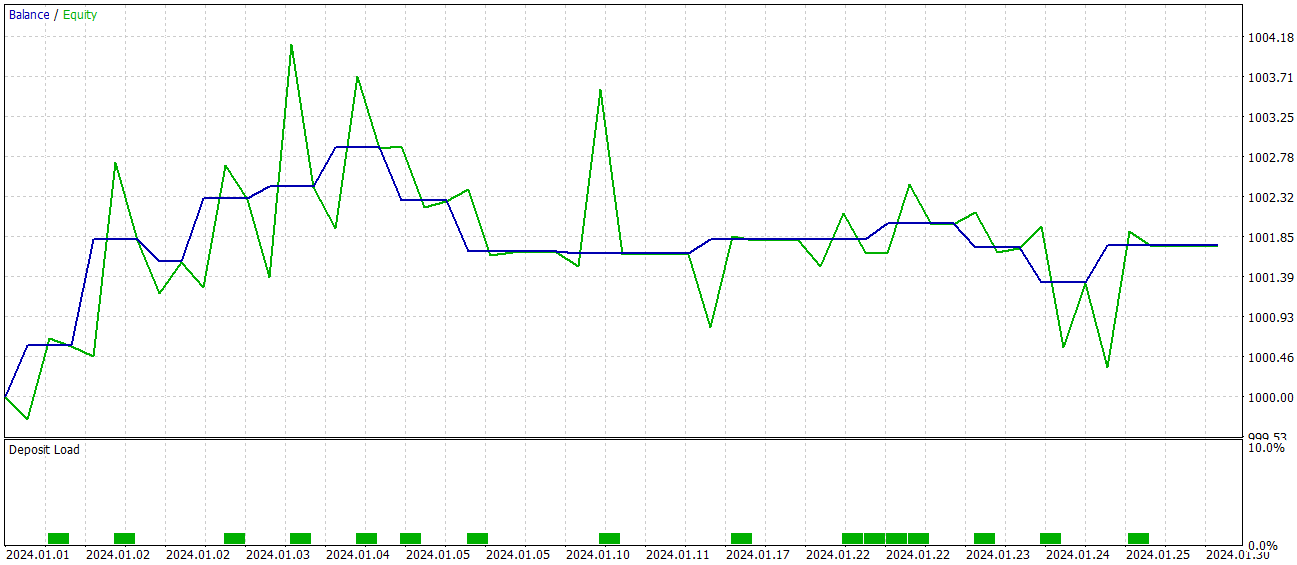
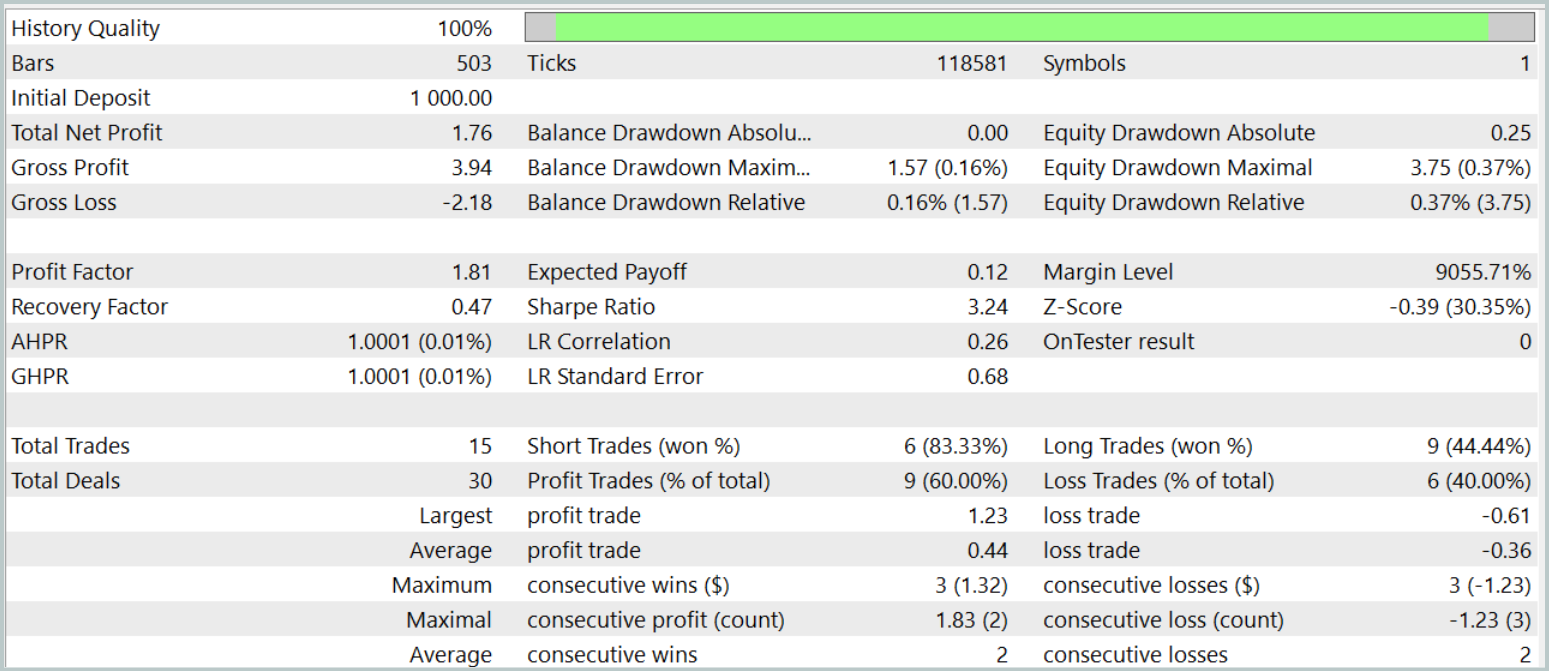
テスト段階において、モデルは60％の勝率を達成しました。さらに、ポジションあたりの平均利益および最大利益はいずれも対応する損失指標を上回りました。

しかしながら、試験期間中にモデルが実行した取引はわずか15回にとどまったという「落とし穴」があります。収支グラフを見ると、主な利益は月初に得られており、その後は横ばいの推移が続いています。したがって、現時点ではモデルの潜在能力について語ることはできても、長期的な取引で実用化するにはさらなる改良が必要です。

結論

Relative Molecule Attention Transformer (R-MAT)は、複雑な特性の予測分野における重要な進歩を示しています。取引の文脈では、R-MATは市場のさまざまな要因間の複雑な関係を、相対的な距離や時間的依存性を考慮して分析する強力なツールと位置付けられます。

実践面では、MQL5を用いて提案手法の独自実装をおこない、実際のデータでモデルを学習させました。テスト結果は提案手法の可能性を示していますが、実運用に向けてはさらなる改良が必要です。

参照文献

• Relative Molecule Self-Attention Transformer
• 本連載の他の記事

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	事例収集のためのEA
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	Test.mq5	EA	モデルテストEA
5	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	ライブラリ	OpenCLプログラムコードライブラリ