MQL5における相関分析の要素：ピアソンのカイ二乗検定による独立性と相関比

はじめに

この記事では、ランダム変数間の依存関係の検出と評価を含む、相関分析を中心とした数理統計の重要なトピックを取り上げます。相関分析で最も広く利用されるツールの1つが相関比です。しかし、たとえば株価の上昇など、データ間の依存関係を評価する際に、相関比の計算だけでは不十分な場合があります。その理由は次の通りです。第一に、相関比は主に線形的な依存関係を評価するための指標です。第二に、相関比の値がゼロであったとしても、それが計算に使用されたデータサンプルが正規分布とは異なる分布を持つ場合、必ずしも依存関係が存在しないことを意味するわけではありません。データが依存関係を持つかどうかを判断するには、独立性を評価する基準を定義する必要があります。本稿では、最も有名な独立性の基準であるピアソンのカイ二乗独立性検定について詳しく説明します。また、調査対象の依存関係が非線形であるかを判断する際に役立つ相関比などの数値特性についても解説します。

独立仮説

データは未知の分布関数F(X, Y)を持つ2次元ランダム変数(X, Y)の観測値であると仮定します。このデータに対して、独立性仮説H0を検定する必要があると仮定します。F(X, Y) = F(X)*F(Y)を検定する必要があります。ここで、F(X)およびF(Y)は、それぞれ1次元分布関数を表します。

この記事におけるランダム変数XおよびYとは、さまざまな金融商品の価格の対数の増分、または1つの金融商品の価格の1の遅れによる増分のいずれかを意味します。

ピアソンのカイ二乗独立性検定

ピアソンのカイ二乗独立性検定は、有限の結果を持つ離散型ランダム変数だけでなく、連続型ランダム変数にも適用可能な手法です。ただし、連続型変数の場合には事前にグループ化を行うことが必須です。この検定では、まずランダム変数Xの領域をA1、A2、...Aiという互いに重ならないi個の区間に分割し、同時にランダム変数Yの領域をB1、B2、...Bjという互いに重ならないj個の区間に分割します。これにより、2次元ランダム変数(X、Y)の値域は、ixj個の長方形（セル）に分けられます。わかりやすくするために、この分割に基づいて、データを「特徴分割表」（または相関表、2次元ランダム変数の確率分布表）と呼ばれる形式に整理します。

                              

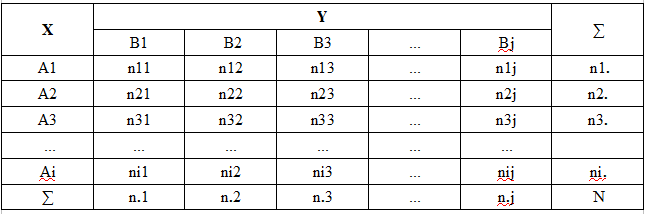
表の内容

• Ai = (Xi-1, Xi)：ランダムなX値のグループのi番目の間隔

• Bj = (Yj-1, Yj)：ランダムなY値のグループのj番目の間隔

• nij：セルの実際のグループ頻度（値がAiとBjの間隔内に入る観測値のペア(X, Y)の数）

• ni.：i行目の観測値の数

• n.j：j列目の観測値の数

• N：サンプル量

独立性のカイ二乗検定として次の統計が使用されます。

CHI2 = (Actual – Expected) ^2 / Expected

ここで

• Actual：nijセルの実際のグループ頻度

• Expected：nijセルの期待グループ頻度

これらの統計は、自由度がv = (j-1)(i-1)のカイ二乗分布です。

推定されたCHI2統計量が、ある「アルファ」有意水準で自由度vのカイ二乗分布の臨界値を超える場合、独立性の帰無仮説は棄却されます。

サンプルデータに基づいて実際の頻度を計算します。期待頻度を構築するための原則は次のとおりです。ランダム変数XとYが独立している場合、次の式が有効です。

P {Ai, Bj} = P {Ai}*P{Bj}

つまり、事象Aiと事象Bjが同時に起こる確率は、事象Aiが起こる確率と事象Bjが起こる確率の積に等しいということです。

事象{Ai、Bj}、事象{Ai}、事象{Bj}の数学的期待値を求めるには、この等式の両方の部分にN*N、つまり観測数の2乗を掛けます。

N*N * P {Ai, Bj} = N *P{Ai} * N* P{Bj}

すると次のようになります。

• N *P{Ai}：i行目の観測値の数の数学的期待値

• N* P{Bj}：j列目の観測値の数の数学的期待値

• N * P {Ai, Bj} = (N *P{Ai} * N* P{Bj})/N：i行目とj列目の交点のセルヒット数の数学的期待値

次に、N *P{Ai}とN* P{Bj}の数学的期待値（相関表からの実際の頻度）の代わりにniとnjの推定値を代入すると、期待される頻度の望ましい推定値が得られます。

Expected = (ni. * n.j)/N

したがって、独立性仮説によれば、i行目とj列目の交点にあるセルにヒットする期待頻度は、i行目とj列目の観測値の合計をサンプルサイズで割った積に等しくなります。

そのため、基準を計算する際には、実際の頻度が期待頻度から大きく外れるほど、データが独立していない可能性が高いと考えるのが自然です。

Chi2Test指標

ピアソンのカイ二乗独立性検定の計算は、Chi2Test指標に実装されています。この指標は、単一の金融商品の隣接する価格増分間の各バーの独立性仮説をテストします。

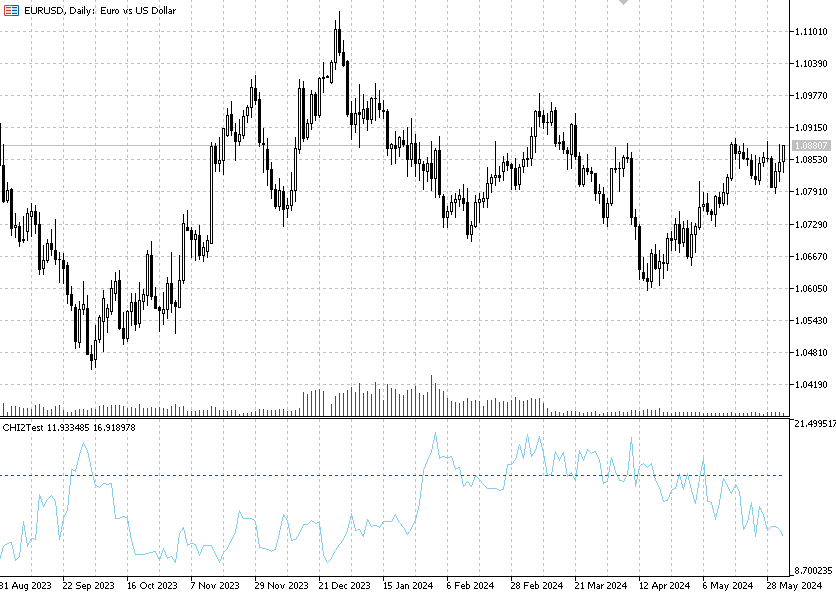
指標には4つの入力があります。

• alpha：有意水準

• Data：計算用のデータウィンドウ

• Tails：標準偏差の数

• 偶発係数

カイ二乗統計量を計算するには、まず特徴分割表の実際の頻度を計算する必要があります。これは関数Crosstabによっておこなわれます。

//+------------------------------------------------------------------+
//|  Calculate the table of contingency of two random values (X,Y)   |
//+------------------------------------------------------------------+
bool Crosstab(const double &dataX[],const double &dataY[],const double &bins[],matrix &freq)
  {

   int datasizeX=ArraySize(dataX);
   int datasizeY=ArraySize(dataY);
   int binssize=ArraySize(bins);
   if(datasizeX==0 || datasizeY==0 || binssize==0)
      return(false);
   if(datasizeX != datasizeY)
      return(false);

   for(int i=0; i<datasizeX; i++)
     {
      if(!MathIsValidNumber(dataX[i]) || !MathIsValidNumber(dataY[i]))
         return(false);
     }

   matrix m_freq=matrix::Zeros(binssize, binssize);
   
   for(int x=0; x<binssize; x++)
     {
      for(int i=0; i<datasizeX; i++)
        {
         for(int y=0; y<binssize; y++)
           {
            if(dataX[i]<=bins[x] && dataY[i]<=bins[y]) 
              {
               m_freq[x,y]=m_freq[x,y]+1;
               break;
              }
           }
        }
     }
     
   matrix Actual = m_freq;
   vector p1,p2,diffp;
   for (int j=1; j<binssize; j++)
   {
   p1 = m_freq.Row(j-1);
   p2 = m_freq.Row(j);
   diffp = p2-p1;
   Actual.Row(diffp,j);   
   }
   freq = Actual; 
   
   return(true);
  }

扱うデータは連続データであるため、まずはデータを適切にグループ化する必要があります。この際、以下の点に留意することが推奨されています。期待度数の最小値は1以上であることが望ましく、また期待度数が5未満のセルの数も少ない方がよいです（たとえば、セルの総数が10未満の場合、期待度数が5未満のセルは最大でも2つまでが推奨されます）。しかし、株式データの分布は裾が重いため、これらの要件を満たすようなグループ化間隔を設定するのは容易ではありません。

そこで、まずデータを標準化し、その後グループ化することを提案します。また、データ量に応じて、分布の裾を2シグマから4シグマの範囲でトリミングする方法が有効です。このプロセスは指標内のTailsパラメータで制御されます。たとえば、データ量が少ない場合（200～300個の値）、Tailsパラメータを2シグマに設定すると良いでしょう。この設定により、グループ化間隔として (-2, -1)、(-1, 0)、(0, 1)、(1, 2)を得ることができ、結果として4×4の特徴分割表を構築できます。さらに、カイ二乗統計を正しく計算するためには、期待度数が小さい隣接するグループを統合して調整をおこなう必要があります。

クラメールの連関係数

残念ながら、カイ二乗統計(CHI2)は確率的依存性の数値的尺度としては適していません。そのため、この目的にはクラメールの連関係数が使用されます。この係数は0から1の範囲で値を取り、0はデータ間に依存関係がないこと、1は完全な（機能的な）依存関係があることを意味します。

クラメールの偶発係数はカイ二乗統計に基づいて次の式で計算されます。

偶発係数 = sqrt (CHI2 / N*(Bins_count-1))、

ここで、Bins_countは特徴分割表内の行数（または列数）です。

したがって、実際には、主要なカイ二乗統計とそれに基づいて計算された偶発係数の2つの統計が1つの指標に実装されています。

金融商品の独立性をテストしたい場合には、Crosstabスクリプトを使用します。この際、「X vs Y」パラメータをtrueに設定します。それ以外の場合、スクリプトは現在の銘柄データに基づいて統計を計算します。計算に使用するサンプルデータは、チャートの最後から2番目のバー以降のデータが対象となります。

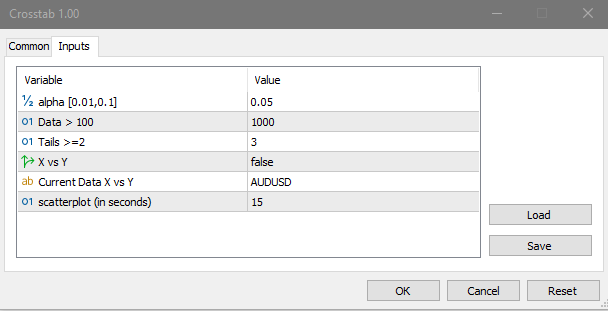
Crosstabスクリプトは次の情報を計算して記録します。

• 実際の頻度(Actual)と期待される頻度(Expected)の行列

• グループ化されたデータから計算されたr相関比

• グループ化されていないデータから計算されたピアソン相関比（グループ化されたデータから計算された統計は精度が低いため、計算の精度を比較するため）

• Nxy、Nyx相関比

• 相関依存性がないという仮説を検定した結果（f統計量相関独立性）

• 相関依存性線形性（f統計量線形/非線形）の仮説を検定した結果、

• CHI2カイ二乗統計

• クラメールの連関係数

ペアの依存関係を視覚的に評価するための散布図（相関フィールド）も画面に表示されます。

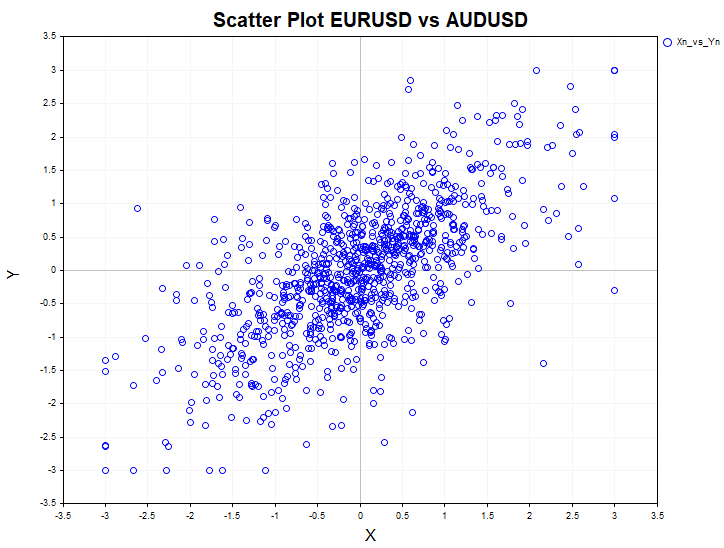
Crosstab_Modelsスクリプトを使用して、モデルデータの独立性をテストします。使用されるモデルは、均一分布、一次自己回帰、ARCH自己回帰条件付き異分散、およびロジスティックマッピングです。

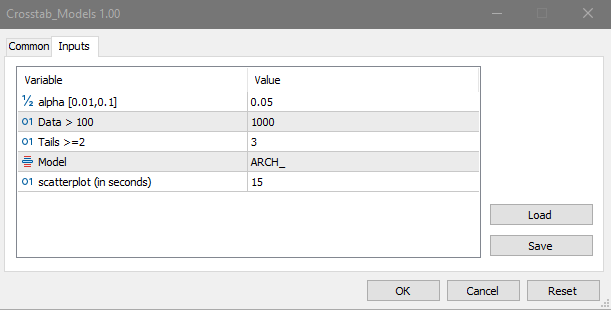
モデルデータは、実際のデータから得られた結果を比較するために使用される一種のテンプレートとして機能します。たとえば、1次元の非線形動的システムにおける非線形依存関係（ロジスティックマッピング）は次のようになります。

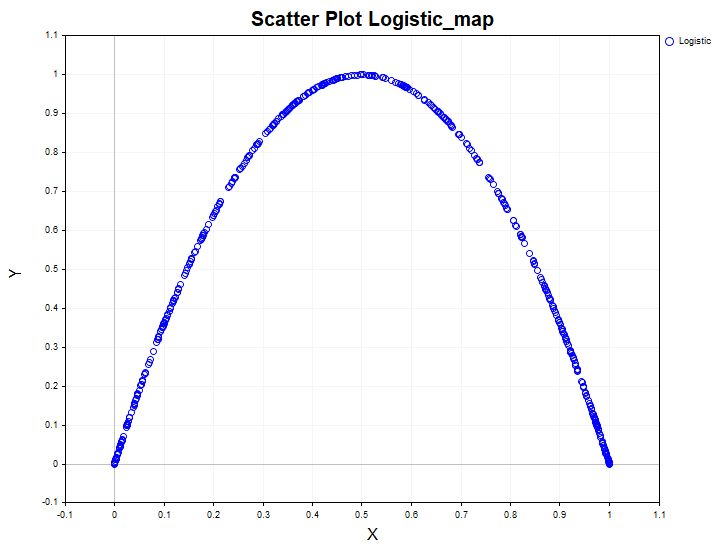
このようなシステムのデータを線形相関比のみで分析すると、このプロセスがホワイトノイズであると誤って結論付けてしまう可能性があります。一方で、カイ二乗独立性検定はデータが依存関係にあることを容易に明らかにし、相関比はその依存関係が非線形であることを確認します。

相関比

相関比は相関依存性の非線形性を評価するために使用されます。

Nyx = sqrt (D[E(Y|X)]/Sy)

Nxy = sqrt (D[E(X|Y)])/Sx)

ここで

• E(Y|X)：Yランダム値の条件付き数学的期待値

• E(X|Y)：Xランダム値の条件付き数学的期待値

• D[E(Y|X)]：Yランダム値の条件付き数学的期待分散

• D[E(X|Y)]：Xランダム値の条件付き数学的期待分散

• Sy、Sx：YとXのランダム値の無条件分散

次のことを覚えておきましょう。

• E(Y|X)条件付き数学的期待値はランダムな値です。

• E[E(Y|X)] = E[Y]（Yランダム値の無条件数学的期待値は、Y無条件数学的期待値に等しい）。

• Y分散は、E[Y]の数学的期待値からのYランダム値の偏差の二乗の数学的期待値、D[Y] = E[(Y – E(Y) )^2)]です。

• したがって、D[E(Y|X)] = E{[ E(Y|X) – E[Y] ] ^ 2}となります。言い換えると、E(Y|X) 無条件数学的期待値の分散は、E(Y|X) 無条件数学的期待値のE[Y] 無条件数学的期待値からの偏差の二乗の数学的期待値に等しくなります。

言い換えれば、相関比率は2つの分散—条件付き分散と無条件分散—の比率の平方根です。相関率は相関表、つまりグループ化されたデータに基づいてのみ計算できます。その特性をリストしてみましょう。

• 相関比はXとYに関して非対称です。つまり、Nxy != Nyxです。

• 0 ≤ | r | ≤ Nxy ≤ 1、0 ≤ | r | ≤ Nyx ≤ 1の場合、指標の値は[0,1]の範囲内にあり、常にr相関線形比以上であり、これを法としてとられます。

• データが独立している場合、Nxy=Nyx=0となります。逆は真ではありません。つまり、相関がないことは独立性を意味するわけではありません。

• | r | = Nyx =Nyx <1の場合、XとYの相関は線形です。つまり、回帰方程式に対して直線よりも良い曲線は見つかりません。

• XとYの相関が非線形の場合、| r | < min (Nxy, Nyx)となります。相関比と相関関係の差が小さいほど、XとYの関係は線形関係に近くなります。

サンプル相関関係を計算することで、2つのランダム変数の間に相関関係がないという仮説（H0：Nyx = 0）を確認できます。

これをおこなうには、次の統計が計算されます。

F = Nyx^2 * (N-Bins_count) / (1- Nyx^2) *(Bins_count-1)

検定された仮説が正しい場合、F統計量は、自由度v1 = Bins_count-1およびv2 = N-Bins_countのフィッシャーの法則に従って分布します。

F統計量の計算値がこの統計量の臨界値を超える場合、帰無仮説はアルファ有意水準で棄却されます（対立仮説H1：Nyx >0が受け入れられます）。

相関依存性が存在すると確信しているとしましょう。この依存関係が線形であるか非線形であるかという疑問が生じます。2つのランダム変数間の相関依存性の線形性に関する仮説がこの質問に答えます。

YとXの相関関係の依存性の線形性に関する仮説（H0：Nyx^2 = r^2)を検定する場合、次の統計が使用されます。

F = (Nyx^2 - r^2) * (N-Bins_count) / (1- Nyx^2) *(Bins_count-2)

検定された仮説が正しい場合、F統計量は、自由度v1 = Bins_count-2およびv2 = N-Bins_countのフィッシャーの法則に従って分布します。

相関の線形性に関する帰無仮説は、F統計量の計算値がこの統計量の臨界値を超える場合、アルファ有意水準で棄却されます（対立仮説H1：Nyx^2 != r^2が受け入れられます）。

結論

この記事では、ピアソンのカイ二乗独立性検定や相関比など、相関分析における重要なツールについて検討しました。これらのツールを活用することで、データ内に潜む関係性をより正確に評価することが可能です。CHI2Test指標は、独立性の仮説を検証し、データ内の関係性の有無について統計的に有効な結論を導き出します。

カイ二乗統計に加え、CrosstabおよびCrosstab_Modelsスクリプトは相関比を計算し、相関の依存性やその線形性に関する仮説を、モデルデータも含めて検証します。さらに、相関フィールドグラフが画面に表示されるため、ペア間の依存性を視覚的に評価することもできます。また、ユーザーは必要なアルファ有意水準を設定することで、統計テストの精度を調整可能です。有意水準を低く設定するほど、誤った結論を得るリスクを抑えることができます。