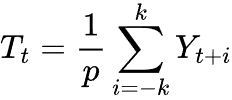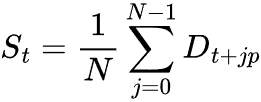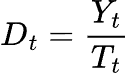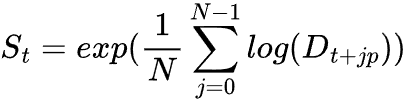
データサイエンスとML（第34回）：時系列分解、株式市場を核心にまで分解

はじめに

時系列データの予測は容易ではありません。パターンは隠れていることが多く、ノイズや不確実性に満ちています。また、チャートは市場パフォーマンスの概要を示すものに過ぎず、具体的に何が起こっているかを深く理解することを目的としていないため、実態を正しく捉えにくいこともあります。

統計的予測や機械学習の分野では、市場の価格データ（始値、高値、安値、終値）という時系列データを、単一の時系列配列よりも洞察に富んだ複数の成分に分解することを目指しています。

この記事では、季節的分解（英語）と呼ばれる統計手法について説明します。これを用いて株式市場のトレンドや季節パターンを分析・検出することを目指します。

季節分解とは

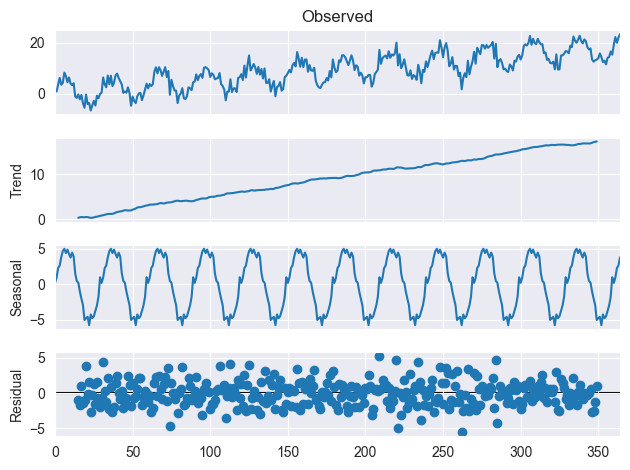
季節分解は、時系列データをトレンド、季節性、残差といった複数の成分に分解するための統計的手法です。これらの成分は次のように説明できます。

トレンド

時系列データのトレンド成分は、時間の経過に伴う長期的な変化やパターンを指します。

データの大まかな動きの方向性を示します。たとえば、データが時間とともに増加している場合はトレンド成分が上向きに傾き、減少している場合は下向きに傾きます。

トレンドはほとんどのトレーダーにとって馴染み深いものであり、チャートを見るだけで市場のトレンドを簡単に把握できます。

季節性

時系列データの季節性成分は、一定期間ごとに繰り返し現れる周期的なパターンを指します。たとえば、装飾品やギフトを専門に扱う小売業者の月別売上データを分析すると、クリスマス商戦で12月に売上がピークを迎え、その後の1月や2月は売上が落ち着く傾向があることが季節性成分として捉えられます。

残差

残差成分は、トレンド成分や季節成分を取り除いた後に残るランダムな変動を示します。つまり、トレンドや季節パターンでは説明できないデータのノイズや誤差を指します。

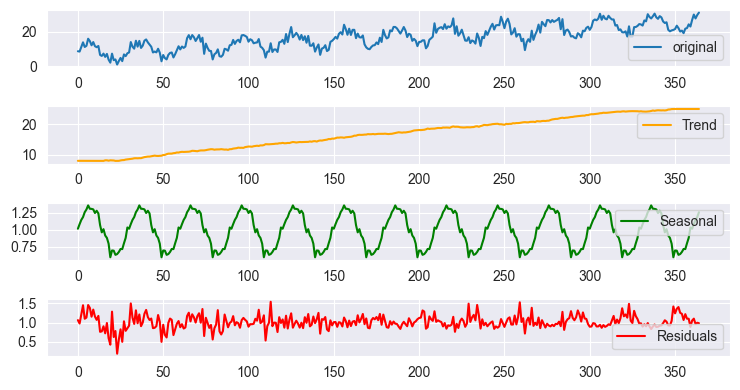
これをさらに理解するには、下の画像をご覧ください。

季節分解をおこなう理由

数学的な詳細に入り、MQL5で季節分解を実装する前に、まず時系列データで季節分解をおこなう理由を理解しましょう。

1. データの根本的なパターンや傾向を検出する
   
   季節分解は、生データを見ただけではすぐには分かりにくいデータの傾向やパターンを識別するのに役立ちます。データを構成要素（トレンド、季節性、残差）に分解することで、これらの成分がデータ全体の動きにどのように寄与しているかをより深く理解できます。
   
   
2. 季節性の影響を取り除く
   
   季節分解を使うことで、データから季節性の影響を除去し、根本的なトレンドに注目したり、逆に季節パターンだけを扱いたい場合にも対応できます。たとえば、強い季節パターンを持つ気象データの分析などが該当します。
   
   
3. 正確な予測をおこなうには
   
   データを複数の成分に分けることで、問題に応じて不要な情報を除外しやすくなります。たとえばトレンドの予測をおこなう際には、季節性の影響を除いたトレンド成分だけに着目する方が効果的です。
   
   
4. 異なる期間や地域におけるトレンドを比較する
   
   季節分解は、異なる期間や地域ごとのトレンドを比較するのにも役立ちます。これにより、さまざまな要因がデータに与える影響を洞察できます。たとえば、複数の地域の小売売上データを比較する際に、季節パターンの地域差を特定し、それに応じて分析を調整できます。

MQL5で季節分解を実装する

この分析アルゴリズムを実装するために、まずトレンド特性、季節パターン、ノイズを含む単純なランダムデータを生成します。これは、特にデータが単純でクリーンではない外国為替市場や株式市場のような、実際のデータシナリオでよく見られる特徴です。

このタスクにはPythonプログラミング言語を使用します。

ファイル：season_decomposition_visualization.ipynb

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import os

sns.set_style("darkgrid")

# Create synthetic time-series data
np.random.seed(42)
time = np.arange(0, 365)  # 1 year (daily data)
trend = 0.05 * time  # Linear upward trend
seasonality = 5 * np.sin(2 * np.pi * time / 30)  # 30-day periodic seasonality
noise = np.random.normal(scale=2, size=len(time))  # Random noise

# Combine components to form the time-series
time_series = trend + seasonality + noise

# Plot the original time-series
plt.figure(figsize=(10, 4))
plt.plot(time, time_series, label="Original Time-Series", color="blue")
plt.xlabel("Time (Days)")
plt.ylabel("Value")
plt.title("Synthetic Time-Series with Trend and Seasonality")
plt.legend()
plt.show()

結果

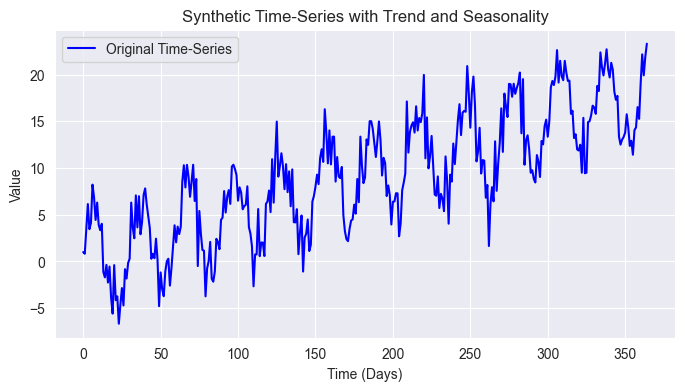
株式市場はもっと複雑であることは承知していますが、この単純なデータを用いて、時系列に加えた30日間の季節パターン、全体的なトレンドを抽出し、データからノイズをある程度除去してみましょう。

トレンド抽出

トレンドの特徴を抽出するには、移動平均(MA)を使います。移動平均は一定期間の値の平均をとることで時系列データを平滑化し、短期的な変動を除去して基礎的なトレンドを浮き彫りにします。

加法モデルの季節分解では、トレンドは季節周期pと同じ期間の移動平均を用いて推定されます。

ここで

 = 時刻tにおけるトレンド成分

 = ウィンドウのサイズまたは季節期間

 = 季節期間の半分

 = 観測された時系列値

乗法モデルの季節分解では、代わりに幾何平均を用いてトレンドを推定します。

ここで

 =積演算子。和を取る代わりにウィンドウ内のすべての値を掛け合わせる操作のことです。乗法分解では、季節効果がデータに加算されるのではなく乗算されると仮定しています。

複雑な数学に思えるかもしれませんが、MQL5の数行のコードで実装可能です。

vector moving_average(const vector &v, uint k, ENUM_VECTOR_CONVOLVE mode=VECTOR_CONVOLVE_VALID)
 {
   vector kernel = vector::Ones(k) /  k;
   vector ma = v.Convolve(kernel, mode);
    
   return ma;  
 }

移動平均は、ローリングウィンドウ方式とは異なり、畳み込み法を用いて計算します。畳み込み法は柔軟で効率的であり、配列の端にある欠損値も適切に処理できるためです。

これにより、移動平均の計算式は以下のようにまとめられます。

//--- compute the trend

   int n = (int)timeseries.Size();  
   res.trend = moving_average(timeseries, period);
   
   // We align trend array with the original series length
   
   int pad = (int)MathFloor((n - res.trend.Size()) / 2.0);
   int pad_array[] = {pad, n-(int)res.trend.Size()-pad};
   
   res.trend = Pad(res.trend, pad_array, edge);

季節成分の抽出

季節成分の抽出とは、時系列データの中で一定の間隔（例：日次、月次、年次など）で繰り返されるパターンを取り出すことを指します。

この成分は、元の時系列データからトレンドを取り除いた後に算出されます。抽出方法は加法モデルか乗法モデルかによって異なります。

加法モデル

トレンドを推定した後、トレンドを除去した系列（デトレンド系列）は以下のように計算されます。

ここで

 = 時刻tにおけるトレンド除去値

 = 時刻tにおける時系列値

 = 時刻tにおけるトレンド成分

季節成分を算出するには、デトレンドされた値を季節周期pのすべての完全なサイクルにわたって平均化します。

ここで

 = データセット内の完全な季節サイクルの数

 = 季節期間（例：月周期の日次データの場合は30）

 = 抽出された季節成分

乗法モデル

乗法モデルの場合、時系列のデトレンドは引き算の代わりに割り算でおこないます。

季節成分は、算術平均の代わりに幾何平均を用いて抽出されます。

これは、モデルの乗法的性質による偏りを防ぐのに役立ちます。

この関数はMQL5で次のように実装できます。

//--- compute the seasonal component
   
   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }
   
   vector detrended = {};
   vector seasonal = {};
   
   switch(model)
     {
      case  additive:
        {
          detrended = timeseries - res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = SliceStep(detrended, i, period).Mean(); //Arithmetic mean over cycles
        }    
        break;
      case  multiplicative:
        {
          detrended = timeseries / res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = MathExp(MathLog(SliceStep(detrended, i, period)).Mean()); //Geometric mean
        }    
        break;
      default:
        printf("Unknown model for seasonal component calculations");
        break;
     }

    
    vector seasonal_repeated = Tile(seasonal, (int)MathFloor(n/period)+1);
    res.seasonal = Slice(seasonal_repeated, 0, n);

Pad関数は、ベクトルの周囲にパディングを追加します。これはNumpy.padに似ており、本例では移動平均の値を中央に寄せるのに役立ちます。

また、対数変換関数MathLogはゼロや負の値には使用できないため、乗法モデルは正の値のみの時系列に限定すべきです。この条件をチェックし、厳密に適用する必要があります。

   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }

Tile関数は、季節成分のベクトルを複数回繰り返して大きなベクトルを作成します。この処理は、時系列データにおける繰り返される季節パターンを捉えるために重要です。

残差計算

最後に、残差はトレンド成分と季節成分を差し引くことで計算します。

加法モデルの場合

乗法モデルの場合

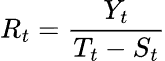
ここで

 = 時刻tにおける元の時系列値

 = 時刻tにおけるトレンド値

 = 時刻tにおける季節値

すべてを1つの関数にまとめる

参考にしたseasonal_decompose関数と同様に、すべての計算を1つの関数seasonal_decomposeにまとめ、この関数はトレンド、季節成分、残差の各ベクトルを含む構造体を返すようにしました。

enum seasonal_model
 {
   additive,
   multiplicative
 };

struct seasonal_decompose_results
 {
   vector trend;
   vector seasonal;
   vector residuals;
 };
 
seasonal_decompose_results seasonal_decompose(const vector &timeseries, uint period, seasonal_model model=additive)
 {
   seasonal_decompose_results res;
   
   if (timeseries.Size() < period)
    {
      printf("%s Error: Time series length is smaller than the period. Cannot compute seasonal decomposition.",__FUNCTION__);
      return res;
    }
   
//--- compute the trend

   int n = (int)timeseries.Size();  
   res.trend = moving_average(timeseries, period);
   
   // We align trend array with the original series length
   
   int pad = (int)MathFloor((n - res.trend.Size()) / 2.0);
   int pad_array[] = {pad, n-(int)res.trend.Size()-pad};
   
   res.trend = Pad(res.trend, pad_array, edge);

//--- compute the seasonal component
   
   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }
   
   vector detrended = {};
   vector seasonal = {};
   
   switch(model)
     {
      case  additive:
        {
          detrended = timeseries - res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = SliceStep(detrended, i, period).Mean(); //Arithmetic mean over cycles
        }    
        break;
      case  multiplicative:
        {
          detrended = timeseries / res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = MathExp(MathLog(SliceStep(detrended, i, period)).Mean()); //Geometric mean
        }    
        break;
      default:
        printf("Unknown model for seasonal component calculations");
        break;
     }


    
    vector seasonal_repeated = Tile(seasonal, (int)MathFloor(n/period)+1);
    res.seasonal = Slice(seasonal_repeated, 0, n);

//--- Compute Residuals

    if (model == additive)
        res.residuals = timeseries - res.trend - res.seasonal;
    else  // Multiplicative
        res.residuals = timeseries / (res.trend * res.seasonal);
        
   return res;
 }

いよいよこの関数をテストできます。

乗法モデルで季節分解をテストするために、正の値も生成し、それらをCSVファイルに保存しました。

ファイル：season_decomposition_visualization.ipynb

# Create synthetic time-series data
np.random.seed(42)
time = np.arange(0, 365)  # 1 year (daily data)
trend = 0.05 * time  # Linear upward trend
seasonality = 5 * np.sin(2 * np.pi * time / 30)  # 30-day periodic seasonality
noise = np.random.normal(scale=2, size=len(time))  # Random noise

# Combine components to form the time-series
time_series = trend + seasonality + noise

# Fix for multiplicative decomposition: Shift the series to make all values positive
min_value = np.min(time_series)
if min_value <= 0:
    shift_value = abs(min_value) + 1  # Ensure strictly positive values
    time_series_shifted = time_series + shift_value
else:
    time_series_shifted = time_series

ts_pos_df = pd.DataFrame({
    "timeseries": time_series_shifted
})

ts_pos_df.to_csv(os.path.join(files_path,"pos_ts_df.csv"), index=False)

MQL5スクリプト内で、本記事で紹介したdataframeライブラリを使って、両方の時系列データセットを読み込みます。データを読み込んだ後、季節分解アルゴリズムを実行します。

ファイル：season_decompose test.mq5

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Additive model
   
   CDataFrame df;
   df.FromCSV("ts_df.csv");
   
   vector time_series = df["timeseries"];
   
//---
    
    seasonal_decompose_results res_ad = seasonal_decompose(time_series, 30, additive);
    
    df.Insert("original", time_series);
    df.Insert("trend",res_ad.trend);
    df.Insert("seasonal",res_ad.seasonal);
    df.Insert("residuals",res_ad.residuals);
    
    df.ToCSV("seasonal_decomposed_additive.csv");

//--- Multiplicative model

   CDataFrame pos_df;
   pos_df.FromCSV("pos_ts_df.csv");
   
   time_series = pos_df["timeseries"];
   
//---
    
    seasonal_decompose_results res_mp = seasonal_decompose(time_series, 30, multiplicative);
    
    pos_df.Insert("original", time_series);
    pos_df.Insert("trend",res_mp.trend);
    pos_df.Insert("seasonal",res_mp.seasonal);
    pos_df.Insert("residuals",res_mp.residuals);
    
    pos_df.ToCSV("seasonal_decomposed_multiplicative.csv");
  }

結果をPythonで可視化するために、新しいCSVファイルに保存しました。

加法モデルを用いた季節分解の結果プロット

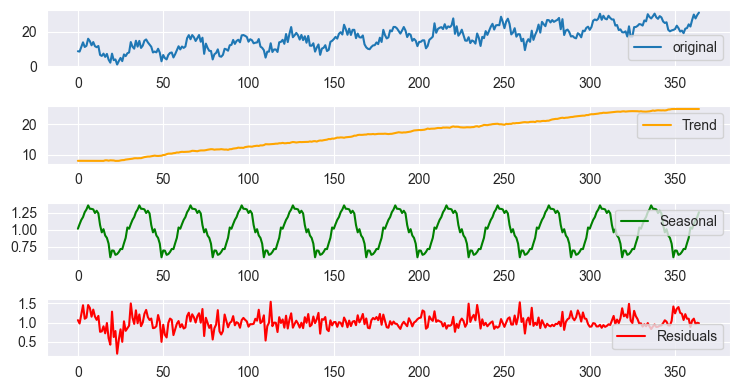
乗法モデルを用いた季節分解の結果プロット

プロットはスケールの関係でほぼ同じに見えますが、実際のデータを詳しく見ると結果は異なります。これは、Pythonのstats modelsライブラリにあるtsa.seasonal.seasonal_decompose関数と同様の結果です。

季節分解関数が完成したので、これを使って株式市場の分析を進めていきましょう。

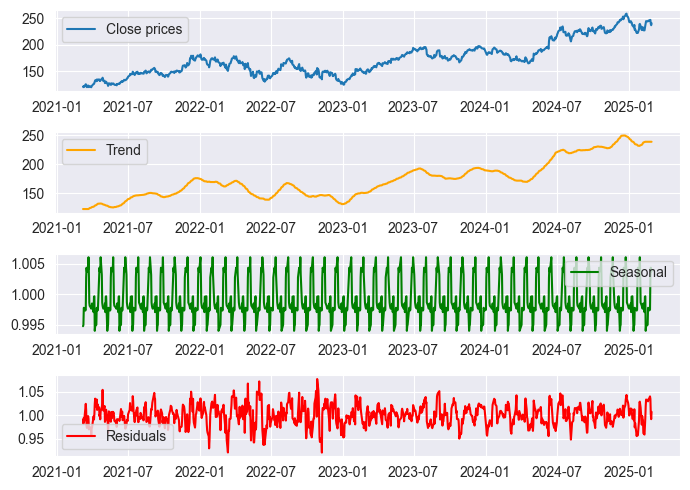
株式市場のパターンを観察する

株式市場を分析する際、特に確立された基盤が強い企業の場合、トレンドを特定することは比較的簡単です。多くの大手で財政的に安定した企業は、一貫した成長や革新、市場の需要により、時間の経過とともに上昇傾向を示します。

しかし、株価の季節パターンを検出するのははるかに難しいことがあります。トレンドとは異なり、季節性は一定の間隔で繰り返される価格変動を指し、必ずしも明確ではなく、異なる時間軸で発生する場合があります。

日中の季節性

取引日の特定の時間帯に、価格の動きが繰り返されることがあります（例：市場の開場や閉場時にボラティリティが増加する）。

月次または四半期ごとの季節性

株価は、決算報告や経済状況、投資家の心理に基づいた周期をたどることがあります。

長期的な季節性

一部の銘柄は、経済サイクルや企業固有の要因により、長期間にわたって繰り返される傾向を示します。

ケーススタディ：Apple (AAPL)の株価

Apple株を例に、季節パターンは22営業日ごとに現れると仮定できます。これは年間の取引日数から、おおよそ1か月に相当します。この仮定は、1か月あたり約22営業日（週末と祝日を除く）あることに基づいています。

季節分解を用いて、Appleの株価が22日ごとに繰り返される価格変動を示すか分析できます。強い季節性があれば、価格変動は予測可能なサイクルに従っている可能性があり、トレーダーやアナリストにとって有用です。逆に明確な季節性が見られない場合は、価格変動は主に外部要因やノイズ、支配的なトレンドによるものと考えられます。

ここでは、1000本のバーの日次終値データを収集し、22日周期の乗法モデルによる季節分解を実施します。

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>

input uint bars_total = 1000;
input uint period_ = 22;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   
    vector close, time;
    close.CopyRates(Symbol(), PERIOD_D1, COPY_RATES_CLOSE, 1, bars_total); //closing prices
    time.CopyRates(Symbol(), PERIOD_D1, COPY_RATES_TIME, 1, bars_total); //time
   
    seasonal_decompose_results res_ad = seasonal_decompose(close, period_, multiplicative);
    
    CDataFrame df; //A dataframe object for storing the seasonal decomposition outcome
    
    df.Insert("time", time);
    df.Insert("close", close);
    df.Insert("trend",res_ad.trend);
    df.Insert("seasonal",res_ad.seasonal);
    df.Insert("residuals",res_ad.residuals);
    
    df.ToCSV(StringFormat("%s.%s.period=%d.seasonal_dec.csv",Symbol(), EnumToString(PERIOD_D1), period_));
  }

結果は、Jupyter Notebook「stock_market seasonal dec.ipynb」で可視化しました。以下がその結果です。

上記のグラフでは季節パターンがいくつか見られますが、常に何らかの誤差が伴うため、季節パターンを100%確信することはできません。課題は誤差値を解釈し、それに応じて分析をおこなうことです。

残差プロットを見ると、2020年から2022年にかけて残差値が急上昇していることがわかります。これは世界的なパンデミックが発生した期間であることは周知の事実です。そのため、季節パターンが乱れて一貫性がなかった可能性があり、その期間に見られる季節パターンを信頼できないことを示しています。

経験則

良好な分解：  残差はランダムノイズ（ホワイトノイズ）のように見えること

不良な分解：残差に依然として明確な構造（除去されなかったトレンドや季節性の影響）が見られること

残差の可視化には、以下のようなさまざまな数学的手法を用いることができます。

分布図

正規分布に近い形状の残差プロットが得られていることから、Apple株には月ごとのパターンが存在している可能性が示唆されます。これは良い兆候と言えるでしょう。

平均と標準偏差

加法モデルでは、残差の平均値が0に近い場合、トレンドと季節性によって大部分の変動が説明されていることを意味します。

乗法モデルでは、残差の平均値が1に近い場合、元の時系列データがトレンドと季節性によってうまく説明されていることを示します。

標準偏差値は小さい必要がある

print("Residual Mean:", residuals.mean())  # Should be close to 0
print("Residual Std Dev:", residuals.std())  # Should be small

出力

Residual Mean: 1.0002367590572043
Residual Std Dev: 0.021749969975933727

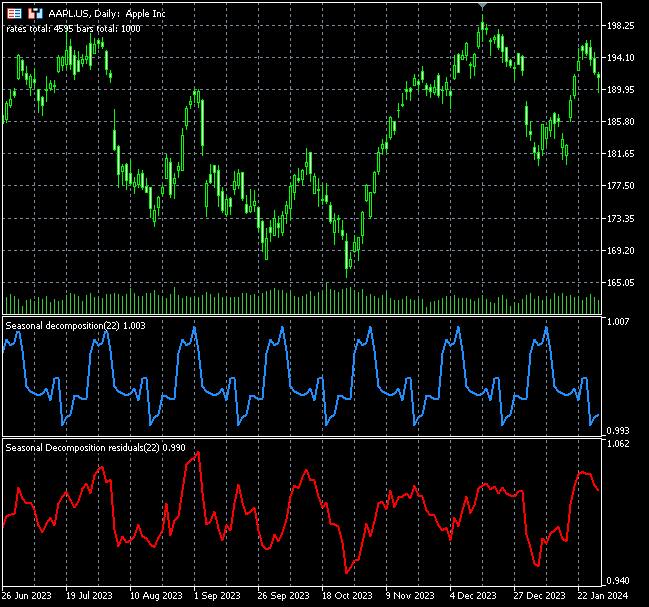
最後に、すべてをインジケーター内に配置できます。

#property indicator_separate_window
#property indicator_buffers 2
#property indicator_plots 1

#property indicator_color1 clrDodgerBlue
#property indicator_style1 STYLE_SOLID
#property indicator_type1 DRAW_LINE
#property indicator_width1 2

//+------------------------------------------------------------------+

double trend_buff[];
double seasonal_buff[];

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>

input uint bars_total = 10000;
input uint period_ = 22;
input ENUM_COPY_RATES price = COPY_RATES_CLOSE;

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   
   SetIndexBuffer(0, seasonal_buff, INDICATOR_DATA);
   SetIndexBuffer(1, trend_buff, INDICATOR_CALCULATIONS);
   
//---
   
   IndicatorSetString(INDICATOR_SHORTNAME, "Seasonal decomposition("+string(period_)+")");
   PlotIndexSetString(1, PLOT_LABEL, "seasonal ("+string(period_)+")");
   
   PlotIndexSetDouble(0, PLOT_EMPTY_VALUE, 0.0);
   
   ArrayInitialize(seasonal_buff, EMPTY_VALUE);
   ArrayInitialize(trend_buff, EMPTY_VALUE);
    
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
    
    if (prev_calculated==rates_total) //not on a new bar, calculate the indicator on the opening of a new bar  
      return rates_total;
    
    ArrayInitialize(seasonal_buff, EMPTY_VALUE);
    ArrayInitialize(trend_buff, EMPTY_VALUE);

//---

    Comment("rates total: ",rates_total," bars total: ",bars_total);
    
    //if (rates_total<(int)bars_total)
    //  return rates_total;
          
    vector close_v;
    close_v.CopyRates(Symbol(), Period(), price, 0, bars_total); //closing prices
      
    seasonal_decompose_results res = seasonal_decompose(close_v, period_, multiplicative);
    
    for (int i=MathAbs(rates_total-(int)bars_total), count=0; i<rates_total; i++, count++) //calculate only the chosen number of bars
      {
         trend_buff[i] = res.trend[count];
         seasonal_buff[i] = res.seasonal[count];
      }
    
//--- return value of prev_calculated for next call
   return(rates_total);
  }

季節分解の計算は、その性質上、すべてのレートを使用して毎回リアルタイムで新しいデータが到着するたびに再計算するとなると計算コストが非常に高くなってしまいます。そのため、計算および描画に使用するバーの数を制限する必要があります。

この制約を踏まえ、季節パターンと残差をそれぞれ視覚化する目的で、ロジックは共通のまま、描画処理を分けた2つのインジケーターを作成しました。

以下は、Apple銘柄に適用した際のインジケーター描画結果です。 

このインジケーターに表示される季節パターンは、チャート上に見られるように、取引シグナルとして、あるいは買われ過ぎ・売られ過ぎの状態として解釈することも可能です。ただし現時点では、取引面での活用についてはまだ検証していないため、判断は保留せざるを得ません。ぜひ宿題としてご自身で検証してみてください。

最後に

季節分解は、アルゴリズム取引において有用な分析手法のひとつです。データサイエンティストの中には、手元の時系列データから新たな特徴量を作成するために季節分解を活用する人もいれば、データの構造をより深く理解した上で、その後に用いる機械学習手法を適切に選ぶために使用する人もいます。こうした背景から、季節分解をいつ使うべきかという問いは重要な検討ポイントとなります。 

多くの場合、まず時系列データを傾向（トレンド）、季節性、残差の3つに分けることから始めます。データに明確な季節性が確認できれば、季節指数平滑法（Holt-Winters法）などの手法で予測を試みることが一般的です。一方で、季節性がはっきりしない、あるいは周期が不規則な場合には、ARIMAモデルやその他の機械学習モデル（ランダムフォレスト、勾配ブースティング、LSTMなど）を用いて、隠れたパターンを抽出・予測するアプローチが選ばれます。

添付ファイルの表

ファイル名とパス	説明と使用法
Include\pandas.mqh	Pandasのような形式でデータを保存および操作するための Dataframeクラス
Include\Seasonal Decompose.mqh	MQL5で季節分解を可能にするすべての関数とコード行
Indicators\Seasonal Decomposition.mq5	季節成分をプロットするインジケーター
Indicators\Seasonal Decomposition residuals.mq5	残差成分をプロットするインジケーター
Scripts\seasonal_decompose test.mq5	季節分解関数とその構成要素を実装およびデバッグするために使用される簡単なスクリプト
Scripts\stock market seasonal dec.mq5	銘柄の終値を分析し、分析目的で結果をCSVファイルに保存するためのスクリプト
Python\seasonal_decomposition_visualization.ipynb	CSVファイルで季節分解結果を視覚化するためのJupyter Notebook
Python\stock_market seasonal dec.ipynb	株式の季節分解結果を視覚化するためのJupyter Notebook
Files\*.csv	PythonコードとMQL5の両方からの季節分解結果とデータを含むCSVファイル