Neuroredes profundas (Parte VIII). Aumentando la calidad de la clasificación de los conjuntos bagging
1 080
2
Contenido
- Introducción
- Preparando los datos fuente
- Procesando los ejemplos de ruido en el subconjunto pretrain
- Entrenamiento de conjuntos de clasificadores de redes neuronales en datos fuente libres de ruido y cálculo de predicciones continuas de redes neuronales en subconjuntos de prueba
- Definición de los umbrales para las predicciones continuas obtenidas, transformación de las mismas en etiquetas de clase y cálculo de las métricas de las redes neuronales
- Simulando los conjuntos
- Optimizando los hiperparámetros de las redes neuronales de los clasificadores de los conjuntos
- Optimizando los hiperparámetros de post-procesado
- Combinando varios de los mejores conjuntos en un superconjunto, además de sus salidas
- Analizando el resultado de los experimentos
- Conclusión
- Anexos
Introducción
En las dos partes anteriores (1, 2) hemos creado un conjunto general (ensemble) de clasificadores de redes neuronales ELM. Entonces hablamos sobre cómo mejorar la calidad de clasifición. Entre las muchas posibilidades disponibles, hemos elegido dos: reducir la influencia de los ejemplos de ruido y seleccionar el umbral óptimo con el cual las predicciones continuas de las redes neuronales del conjunto se convierten en etiquetas de clase. En este artículo, nos proponemos probar de manera experimental cómo influyen en la calidad de la clasificación:
- los métodos de eliminación de ruidos,
- los tipos de umbral,
- la optimización de los hiperparámetros de las redes neuronales del conjunto general y el post-procesado
Luego compararemos la calidad de la clasificación, que se obtiene al promediar y al realizar la votación por mayoría simple de un superconjunto compuesto por los mejores conjuntos según los resultados de la optimización. Todos los cálculos see realizarán en el entorno R 3.4.4.
1. Preparando los datos fuente
Para preparar los datos fuente, utilizaremos los scripts descritos anteriormente.
En el primer bloque (Library), cargamos las funciones y bibliotecas necesarias.
En el segundo bloque (prepare), usando las cotizaciones transmitidas desde el terminal con etiquetas temporales, calculamos los valores de los indicadores (en nuestro caso, se trata de los filtros digitales) y las variables adicionales basadas en OHLC. Combinamos este conjunto de datos en dataframe dt. Luego determinamos los parámetros de los valores atípicos en estos datos y los imputamos. A continuación, definimos los parámetros de normalización y normalizamos los datos. Obtenemos el conjunto resultante de datos fuente DTcap.n.
En el tercer bloque (Data X1) formamos dos conjuntos:
- data1 — contiene los 13 indicadores con las etiquetas temporales Data y la variable objetivo Class;
- X1 — es el mismo conjunto de predictores, pero sin etiqueta temporal. La variable objeto se convierte en valor numérico (0, 1).
En el cuarto bloque (Data X2), también formamos dos conjuntos:
- data2 — contiene 7 predictores y una etiqueta temporal (Data, CO, HO, LO, HL, dC, dH, dL);
- Х2 — los mismos predictoes pero sin etiqueta temporal.
#--1--Library------------- patch <- "C:/Users/Vladimir/Documents/Market/Statya_DARCH2/PartVIII/PartVIII/" source(file = paste0(patch,"importar.R")) source(file = paste0(patch,"Library.R")) source(file = paste0(patch,"FunPrepareData_VII.R")) source(file = paste0(patch,"FUN_Stacking_VIII.R")) import_fun(NoiseFiltersR, GE, noise) #--2-prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt$features, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) meth <- qc(expoTrans, range)# "spatialSign" "expoTrans" "range" "spatialSign", preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) DTcap.n <- NormData(DTcap, preproc = preproc) }, env) #--3-Data X1------------- evalq({ subset <- qc(pretrain, train, test, test1) foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 names(data1) <- subset X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 names(X1) <- subset }, env) #--4-Data-X2------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 names(data2) <- subset X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 names(X2) <- subset rm(dt, DT, pre.outl, DTcap, meth, preproc) }, env)
En el quinto bloque (bestF), ordenamos los predictores del conjunto Х1 en orden creciente, según la importancia de su información (orderX1). Entre ellos, seleccionamos aquellos cuyo coeficiente es superior a 0.5 (featureX1). Imprimimos los coeficientes y los nombres de los predictores representados.
#--5--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") -> rx1 rx1$stopri[ ,1] -> orderX1 featureX1 <- dp$filter(rx1$stopri %>% as.data.frame(), rx1$stopri[ ,2] > 0.5) %>% dp$select(V1) %>% unlist() %>% unname() }, env) print(env$rx1$stopri) [,1] [,2] [1,] 6 1.0423206 [2,] 12 1.0229287 [3,] 7 0.9614459 [4,] 10 0.9526798 [5,] 5 0.8884596 [6,] 1 0.8055126 [7,] 3 0.7959655 [8,] 11 0.7594309 [9,] 8 0.6960105 [10,] 2 0.6626440 [11,] 4 0.4905196 [12,] 9 0.3554887 [13,] 13 0.2269289 colnames(env$X1$pretrain$x)[env$featureX1] [1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl" [10] "stlm"
Realizamos los mismos cálculos para el segundo conjunto de datos Х2. Obtenemos orderX2 y featureX2.
evalq({
orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx2
rx2$stopri[ ,1] -> orderX2
featureX2 <- dp$filter(rx2$stopri %>% as.data.frame(), rx2$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx2$stopri)
[,1] [,2]
[1,] 1 1.6650259
[2,] 5 1.6636689
[3,] 3 0.7751799
[4,] 2 0.7751351
[5,] 6 0.5692846
[6,] 7 0.5496889
[7,] 4 0.4970882
colnames(env$X2$pretrain$x)[env$featureX2]
[1] "CO" "dC" "LO" "HO" "dH" "dL"
Con ello, podemos considerar finalizada la preparación de los datos fuente para los experimentos. Hemos preparado dos conjuntos de datos X1/data1, X2/data2, así como los predictores clasificados por importancia orderX1, orderX2. Todos los scripts mostrados más arriba se encuentran en el archivo Prepare_VIII.R.
2. Procesando los ejemplos de ruido en el subconjunto pretrain
Muchos autores, entre ellos el que escribe, han dedicado sus publicaciones a la criba de los predictores de ruido. Aquí proponemos investigar otra posibilidad igualmente importante, pero menos utilizada: la definición y el procesamiento de ejemplos de ruido en conjuntos de datos. Entonces, ¿por qué algunos ejemplos en los conjuntos de datos se consideran ruido y con qué métodos se pueden procesar? Vamos a intentar explicarlo.
Bien, nos enfrentamos a una tarea de clasificación, y tenemos un conjunto de predictores de entrenamiento y una variable objetivo. Consideramos que la variable objetivo se corresponde adecuadamente con la estructura interna del conjunto de entrenamiento. Pero en realidad, la estructura de datos del conjunto de predictores es mucho más complicada que la estructura de la variable objetivo propuesta. Resulta que en el conjunto hay ejemplos que se corresponden bien con el objetivo, y también los hay que no se corresponden en absoluto, distorsionando fuertemente el modelo durante el entrenamiento. Como resultado, disminuye la calidad de la clasificación del modelo. Ya hemos analizado con detalle los enfoques de determinación y procesamiento de los ejemplos de ruido. Aquí vamos a ver cómo los tres métodos de procesamiento afectan a la calidad de la clasificación del conjunto.
- corrección de ejemplos etiquetados erróneamente;
- eliminación de los mismos del conjunto;
- asignación de estos a una clase aparte
Determinaremos y procesaremos los ejemplos de ruido usando la función NoiseFiltersR::GE(). Esta buscará los ejemplos de ruido y cambiará sus etiquetas (corrigiendo la etiqueta errórea). Los ejemplos que no puedan ser etiquetados de nuevo, serán eliminados. Los ejemplos de ruido detectados también se pueden eliminar del conjunto por sí solos o ser seleccionados como una clase separada asignándoles una nueva etiqueta. Todos los cálculos los realizaremos con el subconjunto pretrain, puesto que los conjuntos generales se van a entrenar con este. Echemos un vistazo al resultado del trabajo de la función:
#---------------------------
import_fun(NoiseFiltersR, GE, noise)
#-----------------------
evalq({
out <- noise(x = data1[[1]] %>% dp$select(-Data))
summary(out, explicit = TRUE)
}, env)
Filter GE applied to dataset
Call:
GE(x = data1[[1]] %>% dp$select(-Data))
Parameters:
k: 5
kk: 3
Results:
Number of removed instances: 0 (0 %)
Number of repaired instances: 819 (20.46988 %)
Explicit indexes for removed instances:
.......
Estructura de salida de la función out:
> str(env$out) List of 7 $ cleanData :'data.frame': 4001 obs. of 14 variables: ..$ ftlm : num [1:4001] 0.293 0.492 0.47 0.518 0.395 ... ..$ stlm : num [1:4001] 0.204 0.185 0.161 0.153 0.142 ... ..$ rbci : num [1:4001] -0.0434 0.1156 0.1501 0.25 0.248 ... ..$ pcci : num [1:4001] -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... ..$ fars : num [1:4001] 0.208 0.255 0.246 0.279 0.267 ... ..$ v.fatl: num [1:4001] 0.4963 0.4635 0.0842 0.3707 0.0542 ... ..$ v.satl: num [1:4001] -0.0146 0.0248 -0.0353 0.1797 0.1205 ... ..$ v.rftl: num [1:4001] -0.2695 -0.0809 0.1752 0.3637 0.5305 ... ..$ v.rstl: num [1:4001] 0.398 0.362 0.386 0.374 0.357 ... ..$ v.ftlm: num [1:4001] 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... ..$ v.stlm: num [1:4001] -0.275 -0.226 -0.285 -0.11 -0.148 ... ..$ v.rbci: num [1:4001] 0.5374 0.4811 0.0978 0.2992 -0.0141 ... ..$ v.pcci: num [1:4001] -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ... $ remIdx : int(0) $ repIdx : int [1:819] 16 27 30 31 32 34 36 38 46 58 ... $ repLab : Factor w/ 2 levels "-1","1": 2 2 2 1 1 2 2 2 1 1 ... $ parameters:List of 2 ..$ k : num 5 ..$ kk: num 3 $ call : language GE(x = data1[[1]] %>% dp$select(-Data)) $ extraInf : NULL - attr(*, "class")= chr "filter"
Aquí:
- out$cleanData — es el conjunto de datos tras corregir la etiqueta de los ejemplos de ruido,
- out$remIdx — son los índices de los ejemplos eliminados (en nuestro ejemplo no hay),
- out$repIdx — son los índices de los ejemplos cuya variable objetivo ha sido reetiquetada,
- out$repLab — son las nuevas etiquetas de dichos ejemplos de ruido. De esta forma, usando out$repIdx, podemos eliminarlos del conjunto o asignarles una nueva etiqueta.
Tras determinar los índices de los ejemplos de ruido, preparamos cuatro conjuntos para el entrenamiento de los conjuntos generales combinados en la estructura denoiseX1pretrain.
- denoiseX1pretrain$origin — es el conjunto original de reentrenamiento;
- denoiseX1pretrain$repaired — es el conjunto de datos en el que se ha corregido la etiqueta de los ejemplos de ruido;
- denoiseX1pretrain$removed — es el conjunto de datos en el que se han eliminado los ejemplos de ruido;
- denoiseX1pretrain$relabeled — es el conjunto de datos en el que se les ha asignado la etiqueta a los ejemplos de ruido (es decir, nuestra variable objetivo ahora tiene tres clases).
#--2-Data Xrepair-------------
#library(NoiseFiltersR)
evalq({
out <- noise(x = data1$pretrain %>% dp$select(-Data))
Yrelab <- X1$pretrain$y
Yrelab[out$repIdx] <- 2L
X1rem <- data1$pretrain[-out$repIdx, ] %>% dp$select(-Data)
denoiseX1pretrain <- list(origin = list(x = X1$pretrain$x, y = X1$pretrain$y),
repaired = list(x = X1$pretrain$x, y = out$cleanData$Class %>%
as.numeric() %>% subtract(1)),
removed = list(x = X1rem %>% dp$select(-Class),
y = X1rem$Class %>% as.numeric() %>% subtract(1)),
relabeled = list(x = X1$pretrain$x, y = Yrelab))
rm(out, Yrelab, X1rem)
}, env)
En los subconjuntos denoiseX1pretrain$origin|repaired|relabeled los predictores х son idénticos, mientras que la variable objetivo у es diferente en todos. Echemos un vistazo a su estructura:
#------------------------- env$denoiseX1pretrain$repaired$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$relabeled$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$repaired$y %>% table() . 0 1 1888 2113 env$denoiseX1pretrain$removed$y %>% table() . 0 1 1509 1673 env$denoiseX1pretrain$relabeled$y %>% table() . 0 1 2 1509 1673 819
Puesto que en el conjunto denoiseX1pretrain$removed ha cambiado el número de ejemplos, vamos a comprobar cómo ha cambiado la importancia de los predictores:
evalq({
orderF(x = denoiseX1pretrain$removed$x %>% as.matrix(),
type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx1rem
rx1rem$stopri[ ,1] -> orderX1rem
featureX1rem <- dp$filter(rx1rem$stopri %>% as.data.frame(),
rx1rem$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx1rem$stopri)
[,1] [,2]
[1,] 6 1.0790642
[2,] 12 1.0320772
[3,] 7 0.9629750
[4,] 10 0.9515987
[5,] 5 0.8426669
[6,] 1 0.8138830
[7,] 3 0.7934568
[8,] 11 0.7682185
[9,] 8 0.6720211
[10,] 2 0.6355753
[11,] 4 0.5159589
[12,] 9 0.3670544
[13,] 13 0.2170575
colnames(env$X1$pretrain$x)[env$featureX1rem]
[1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl"
[10] "stlm" "pcci"
Ha cambiado el orden y la composición de los mejores predictores. Tendremos que tenerlo en cuenta al entrenar los conjuntos generales.
Bien, ya tenemos listos los 4 subconjuntos: denoiseX1pretrain$origin, repaired, removed, relabeled. Con ellos vamos a entrenar los conjuntos generales ELM. Los scripts de eliminación de ruido se encuentran en el archivo Denoise.R. La estructura de los datos fuente Х1 y denoiseX1pretrain tiene el aspecto siguiente:
Fig. 1. Estructura de los datos fuente.
3. Entrenamiento de conjuntos de clasificadores de redes neuronales en datos fuente libres de ruido y cálculo de predicciones continuas de redes neuronales en subconjuntos de prueba
Vamos a escribir la función de entrenamiento del conjunto general y de obtención de las predicciones que en lo sucesivo será los datos de entrada para el combinador de entrenamiento en el conjunto stacking.
Ya hemos hablado de estos cálculos en el artículo anterior, por eso no vamos a detenernos en sus detalles. Brevemente, podemos decir que:
- en el bloque 1 (Input) se definen las constantes,
- en el bloque 2 (createEns) se define la función CreateEns(), que crea el conjunto general de los clasificadores individuales de redes neuronales con parámetros constantes e inicialización reproducible,
- en el bloque 3 (GetInputData) la función GetInputData() calcula las predicciones de todos los subconjuntos Х1$ train/test/test1 con el conjunto general Ens.
#--1--Input------------- evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear n <- 500 r = 7L SEED <- 12345 #--2-createENS---------------------- createEns <- function(r = 7L, nh = 5L, fact = 7L, X, Y){ Xtrain <- X[ , featureX1] k <- 1 rng <- RNGseq(n, SEED) #---creste Ensemble--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Y[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #--3-GetInputData -FUN----------- GetInputData <- function(Ens, X, Y){ #---predict-InputPretrain-------------- Xtrain <- X[ ,featureX1] k <- 1 rng <- RNGseq(n, SEED) #---create Ensemble--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 predict(Ens[[i]], newdata = Xtrain[-idx, ]) } %>% unname() -> InputPretrain #---predict-InputTrain-- Xtest <- X1$train$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> InputTrain #[ ,n] #---predict--InputTest---- Xtest1 <- X1$test$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---predict--InputTest1---- Xtest2 <- X1$test1$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---res------------------------- return(list(InputPretrain = InputPretrain, InputTrain = InputTrain, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
Ya tenemos el conjunto denoiseX1pretrain, con cuatro grupos de datos para entrenar los conjuntos generales: el original (origin), con la etiqueta corregida (repaired), con los datos eliminados (removed) y con ejemplos de ruido reetiquetados (relabeled). Entrenando el conjunto general con cada uno de estos grupos de datos, obtendremos cuatro conjuntos. Usando estos conjuntos generales con la función GetInputData(), obtendremos cuatro grupos de predicciones en tres subgrupos: train, test y test1. Más abajo se muestran los scripts para cada grupo general de forma desplegada (solo para que la depuración y comprensión resulten más simples).
#---4--createEns--origin-------------- evalq({ Ens.origin <- vector(mode = "list", n) res.origin <- vector("list", 4) x <- denoiseX1pretrain$origin$x %>% as.matrix() y <- denoiseX1pretrain$origin$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.origin GetInputData(Ens = Ens.origin, X = x, Y = y) -> res.origin }, env) #---4--createEns--repaired-------------- evalq({ Ens.repaired <- vector(mode = "list", n) res.repaired <- vector("list", 4) x <- denoiseX1pretrain$repaired$x %>% as.matrix() y <- denoiseX1pretrain$repaired$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.repaired GetInputData(Ens = Ens.repaired, X = x, Y = y) -> res.repaired }, env) #---4--createEns--removed-------------- evalq({ Ens.removed <- vector(mode = "list", n) res.removed <- vector("list", 4) x <- denoiseX1pretrain$removed$x %>% as.matrix() y <- denoiseX1pretrain$removed$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.removed GetInputData(Ens = Ens.removed, X = x, Y = y) -> res.removed }, env) #---4--createEns--relabeled-------------- evalq({ Ens.relab <- vector(mode = "list", n) .res.relab <- vector("list", 4) x <- denoiseX1pretrain$relabeled$x %>% as.matrix() y <- denoiseX1pretrain$relabeled$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.relab GetInputData(Ens = Ens.relab, X = x, Y = y) -> res.relab }, env)
La estructura de los resultados de predicción de los conjuntos generales se muestra abajo:
> env$res.origin %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.747 0.774 0.733 0.642 0.28 ... $ InputTrain : num [1:1001, 1:500] 0.742 0.727 0.731 0.66 0.642 ... $ InputTest : num [1:501, 1:500] 0.466 0.446 0.493 0.594 0.501 ... $ InputTest1 : num [1:251, 1:500] 0.093 0.101 0.391 0.547 0.416 ... > env$res.repaired %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.815 0.869 0.856 0.719 0.296 ... $ InputTrain : num [1:1001, 1:500] 0.871 0.932 0.889 0.75 0.737 ... $ InputTest : num [1:501, 1:500] 0.551 0.488 0.516 0.629 0.455 ... $ InputTest1 : num [1:251, 1:500] -0.00444 0.00877 0.35583 0.54344 0.40121 ... > env$res.removed %>% str() List of 4 $ InputPretrain: num [1:955, 1:500] 0.68 0.424 0.846 0.153 0.242 ... $ InputTrain : num [1:1001, 1:500] 0.864 0.981 0.784 0.624 0.713 ... $ InputTest : num [1:501, 1:500] 0.755 0.514 0.439 0.515 0.156 ... $ InputTest1 : num [1:251, 1:500] 0.105 0.108 0.511 0.622 0.339 ... > env$res.relab %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 1.11 1.148 1.12 1.07 0.551 ... $ InputTrain : num [1:1001, 1:500] 1.043 0.954 1.088 1.117 1.094 ... $ InputTest : num [1:501, 1:500] 0.76 0.744 0.809 0.933 0.891 ... $ InputTest1 : num [1:251, 1:500] 0.176 0.19 0.615 0.851 0.66 ...
Vamos a ver qué aspecto tiene la distribución de estas entradas/salidas. Miramos las 10 primeras salidas de los conjuntos InputTrain[ ,1:10]:
#------Ris InputTrain------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTrain[ ,1:10], horizontal = T, main = "res.origin$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTrain[ ,1:10], horizontal = T, main = "res.repaired$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTrain[ ,1:10], horizontal = T, main = "res.removed$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTrain[ ,1:10], horizontal = T, main = "res.relab$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
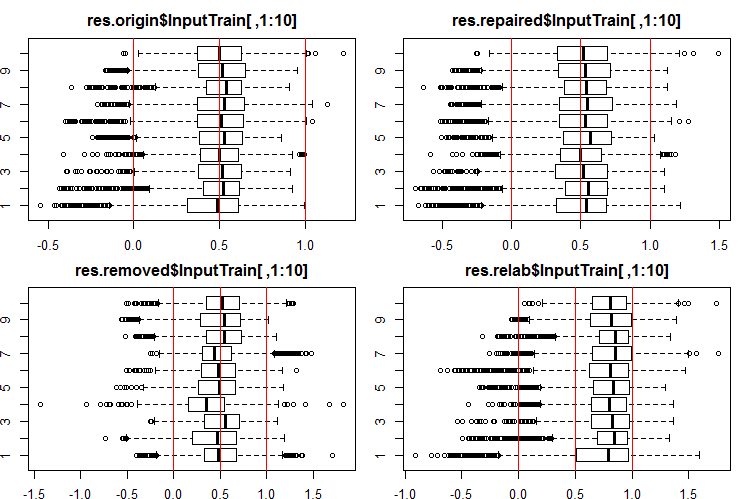
Fig. 2. Distribución de las predicciones de las salidas de InputTrain con cuatro conjuntos generales distintos.
Miramos las 10 primeras salidas de los conjuntos InputTest[ ,1:10]:
#------Ris InputTest------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2), las = 1) boxplot(env$res.origin$InputTest[ ,1:10], horizontal = T, main = "res.origin$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest[ ,1:10], horizontal = T, main = "res.repaired$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest[ ,1:10], horizontal = T, main = "res.removed$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest[ ,1:10], horizontal = T, main = "res.relab$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
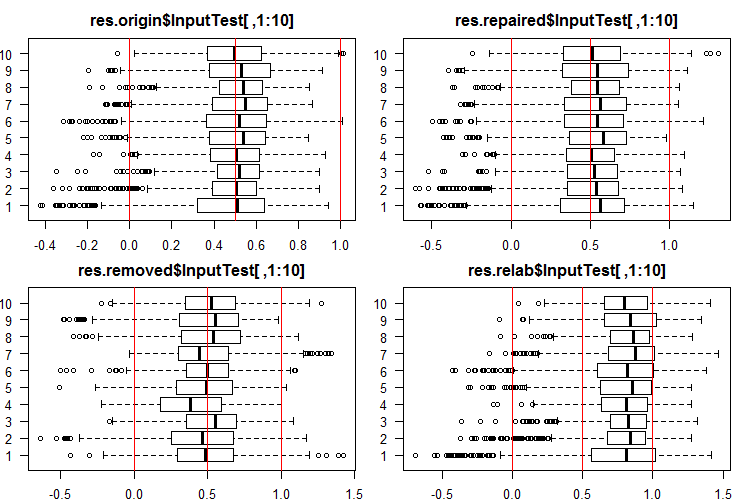
Fig. 3. Distribución de las predicciones de las salidas de InputTest con cuatro conjuntos generales distintos.
Miramos las 10 primeras salidas de los conjuntos InputTest1[ ,1:10]:
#------Ris InputTest1------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTest1[ ,1:10], horizontal = T, main = "res.origin$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest1[ ,1:10], horizontal = T, main = "res.repaired$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest1[ ,1:10], horizontal = T, main = "res.removed$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest1[ ,1:10], horizontal = T, main = "res.relab$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
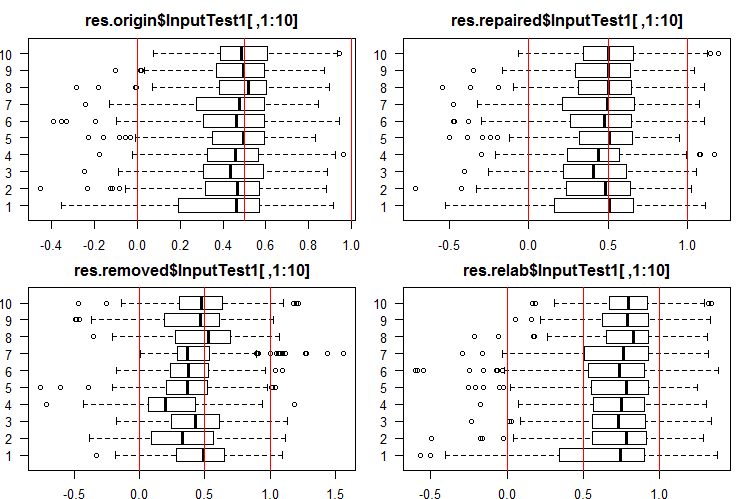
Fig. 4. Distribución de las predicciones de las salidas de InputTest1 con cuatro conjuntos generales distintos.
La distribución de todas las predicciones se diferencia mucho de las predicciones obtenidas con los datos normalizados con el método SpatialSign en nuestros anteriores experimentos. Puede experimentar con diferentes métodos de normalización de forma inpendiente.
Caculando la predicción de los subconjuntos X1$train/test/test1 con cada conjunto general, obtendremos cuatro grupos de datos: res.origin, res.repaired, res.removed y res.relab, cuya distribución podemos ver en las figuras 2 — 4.
Definimos la calidad de la clasificación de cada conjunto general, convirtiendo las predicciones continuas en etiquetas de clase.
4. Definición de los umbrales para las predicciones continuas obtenidas, transformación de las mismas en etiquetas de clase y cálculo de las métricas de las redes neuronales
Para convertir las predicciones continuas en etiquetas de clase, se usan uno o varios umbrales de división en estas clases. Las predicciones continuas de los conjuntos InputTrain, que se obtuvieron de la quinta red neuronal de todos los grupos generales, tienen el aspecto siguiente:
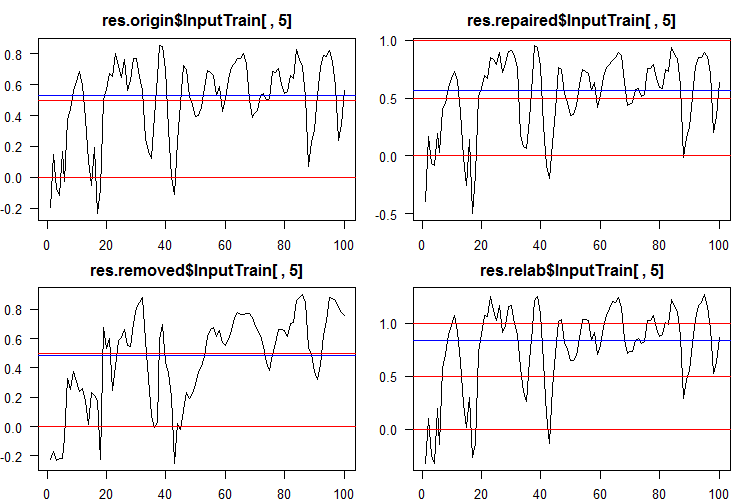
Fig. 5 Predicciones continuas de la quinta red neuronal de diferentes conjuntos generales.
Como vemos, los gráficos de la predicción continua de los modelos origin, repaired, relabeled se parecen en su forma, pero tienen un rango diferente. Se distingue especialmente por su forma la línea de predicción del modelo removed.
Para simplificar los cálculos posteriores, reuniremos en una estructura predX1 todos los modelos y sus predicciones. Para ello, escribiremos una función compacta que repetirá todos los cálculos en un ciclo. Aquí tenemos el script y la figura de la estructura de predX1:
library("doFuture")
#---predX1------------------
evalq({
group <- qc(origin, repaired, removed, relabeled)
predX1 <- vector("list", 4)
foreach(i = 1:4, .packages = "elmNN") %do% {
x <- denoiseX1pretrain[[i]]$x %>% as.matrix()
y <- denoiseX1pretrain[[i]]$y
SEED = 12345
createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> ens
GetInputData(Ens = ens, X = x, Y = y) -> pred
return(list(ensemble = ens, pred = pred))
} -> predX1
names(predX1) <- group
}, env)
Fig. 6. Estructura del conjunto predX1
Recordemos: para obtener las métricas de la calidad de la predicción del conjunto, debemos ejecutar dos operaciones: la poda y la promediación (o votación por mayoría simple). Para podar, necesitamos convertir las salidas de todas las redes neuronales del conjunto general de su forma convencional a etiquetas de clase. A continuación, definimos las métricas de la red neuronal y elegimos su cantidad con los mejores valores. Después promediamos las predicciones continuas de estas mejores redes neuronales y obtenemos la predicción continua promediada del conjunto general. Determinamos de nuevo el umbral, convertimos la predicción promediada en etiquetas de clase y calculamos los valores finales de calidad de la clasificación del conjunto general.
De esta forma, debemos transformar dos veces la predicción continua en etiquetas de clase. Los umbrales de transformación en estas dos etapas pueden ser tanto iguales, como distintos. ¿Qué variantes de umbral podemos utilizar?
- El umbral adoptado por defecto. En nuestro caso, es igual a 0.5.
- Un umbral igual a la mediana. Podemos considerarlo más fiable. Pero la mediana se puede definir solo en el subconjunto de validación, y puede usarse solo en la simulación de los subconjuntos posteriores. Por ejemplo, en el subconjunto InputTrain, nosotros determinamos los umbrales que vamos a usar en los subconjuntos InputTest y InputTest1.
- Un umbral optimizado según diversos criterios. Por ejemplo, puede tratarse del error de clasificación mínimo, la precisión máxima "1", o "0", etc. Los umbrales óptimos los vamos a determinar con el subconjunto InputTrain, y los usaremos en los subconjuntos InputTest y InputTest1.
- Al promediar las salidas de las mejores redes neuronales del conjunto general, podemos usar la calibración. Algunos autores escriben que solo se pueden promediar salidas bien calibradas. Pero entre nuestras tareas no se incluye la comprobación de esta afirmación.
Para determinar el umbral óptimo, usaremos la función InformationValue::optimalCutoff(). Esta se describe con detalle en el paquete.
Para determinar los umbrales según los puntos 1 y 2, no necesitaremos cálculos adicionales. Para calcular los umbrales óptimos según el punto 3, escribiremos la función GetThreshold().
#--function------------------------- evalq({ import_fun("InformationValue", optimalCutoff, CutOff) import_fun("InformationValue", youdensIndex, th_youdens) GetThreshold <- function(X, Y, type){ switch(type, half = 0.5, med = median(X), mce = CutOff(Y, X, "misclasserror"), both = CutOff(Y, X,"Both"), ones = CutOff(Y, X, "Ones"), zeros = CutOff(Y, X, "Zeros") ) } }, env)
Calcularemos solo los cuatro tipos de umbral descritos en esta función (half, med, mce, both). Los dos primeros son los umbrales de mitad y de mediana. El umbral mce ofrece un error de clasificación mínimo, el umbral both es el error máximo del coeficiente youdensIndex = (sensitivity + specificity —1). El orden de cálculo será el siguiente:
1. En el conjunto predX1 calculamos por separado en cada grupo de datos (origin, repaired, removed y relabeled) los cuatro tipos de umbral para cada una de las 500 redes neuronales del conjunto general en el subconjunto InputTrain.
2. A continuación, usando estos umbrales, convertimos las predicciones continuas de todas las redes neuronales de los conjuntos generales en todos los subconjuntos (train|test|test1) en clases y determinamos la magnitud media F1. Obtenemos cuatro grupos de métricas, con tres subconjuntos en cada uno. Más abajo se muestra un script descrito paso a paso para el grupo origin.
Determinamos los 4 tipos de pasadas en el conjunto predX1$origin$pred$InputTrain:
#--threshold--train--origin--------
evalq({
Ytest = X1$train$y
Ytest1 = X1$test$y
Ytest2 = X1$test1$y
testX1 <- vector("list", 4)
names(testX1) <- group
type <- qc(half, med, mce, both)
registerDoFuture()
cl <- makeCluster(4)
plan(cluster, workers = cl)
foreach(i = 1:4, .combine = "cbind") %dopar% {# type
foreach(j = 1:500, .combine = "c") %do% {
GetThreshold(predX1$origin$pred$InputTrain[ ,j], Ytest, type[i])
}
} -> testX1$origin$Threshold
stopCluster(cl)
dimnames(testX1$origin$Threshold) <- list(NULL,type)
}, env)
Usamos los dos ciclos incorporados en cada cálculo. En el ciclo externo elegimos el tipo de umbral, creamos un clúster y paralelizamos los cálculos en 4 núcleos. En el ciclo interno, iteramos por las predicciones de InputTrain de cada una de las 500 redes neuronales incluidas en el conjunto general. Determinamos los 4 tipos de pasadas para cada una. La estructura de los datos obtenidos será la siguiente:
> env$testX1$origin$Threshold %>% str() num [1:500, 1:4] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "half" "med" "mce" "both" > env$testX1$origin$Threshold %>% head() half med mce both [1,] 0.5 0.5033552 0.3725180 0.5125180 [2,] 0.5 0.4918041 0.5118821 0.5118821 [3,] 0.5 0.5005034 0.5394191 0.5394191 [4,] 0.5 0.5138439 0.4764055 0.5164055 [5,] 0.5 0.5241393 0.5165478 0.5165478 [6,] 0.5 0.4673319 0.4508287 0.4608287
Usando los umbrales obtenidos, convertimos las predicciones continuas del grupo origin de los subconjuntos train, test y test1 en etiquetas de clase y calculamos las métricas (mean(F1)).
#--train--------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTrain[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTrainScore
dimnames(testX1$origin$InputTrainScore)[[2]] <- type
}, env)
#--test-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTestScore
dimnames(testX1$origin$InputTestScore)[[2]] <- type
}, env)
#--test1-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest1[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTest1Score
dimnames(testX1$origin$InputTest1Score)[[2]] <- type
}, env)
Echemos un vistazo a la distribución de las métricas en el grupo origin y sus tres subconjuntos. El script de abajo es para el grupo origin:
k <- 1L #origin # k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
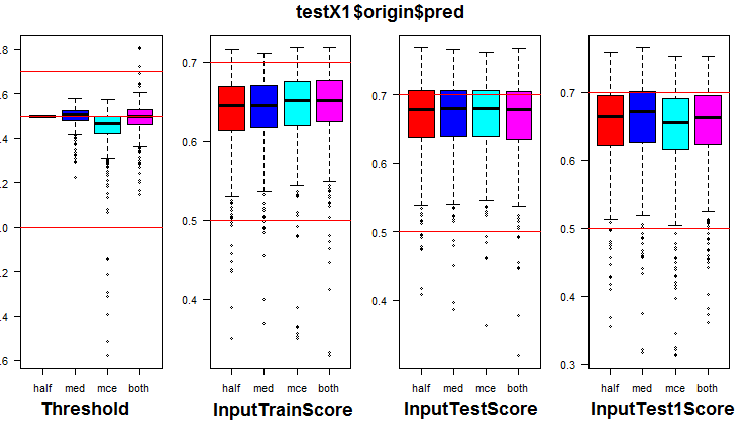
Fig. 7. Distribución de los umbrales y métricas en el grupo origin
La visualización ha mostrado que usar "med" como umbral para los datos del grupo origin no ofrece una mejoría notoria de la calidad en comparación con "half".
Calculamos los 4 tipos de umbrales en todos los grupos (ármese de paciencia, porque ocupará bastante tiempo y memoria).
library("doFuture") #--threshold--train--------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y registerDoFuture() cl <- makeCluster(4) plan(cluster, workers = cl) while (k <= 4) { # group foreach(i = 1:4, .combine = "cbind") %dopar% {# type foreach(j = 1:500, .combine = "c") %do% { GetThreshold(predX1[[k]]$pred$InputTrain[ ,j], Ytest, type[i]) } } -> testX1[[k]]$Threshold dimnames(testX1[[k]]$Threshold) <- list(NULL,type) k <- k + 1 } stopCluster(cl) }, env)
Utilizando los umbrales obtenidos, calculamos las métricas en todos los grupos y subconjuntos:
#--train-------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTrain[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTrainScore dimnames(testX1[[k]]$InputTrainScore)[[2]] <- type k <- k + 1 } }, env) #--test----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTestScore dimnames(testX1[[k]]$InputTestScore)[[2]] <- type k <- k + 1 } }, env) #--test1----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest1[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTest1Score dimnames(testX1[[k]]$InputTest1Score)[[2]] <- type k <- k + 1 } }, env)
En cada grupo de datos, hemos añadido las métricas de cada una de las 500 redes neuronales del conjunto general con los cuatro umbrales diferentes en los tres subconjuntos.
Vamos a ver cómo están distribuidas las métricas en cada grupo y subconjunto. Aquí mostramos el script para el subconjunto repaired. Para los demás grupos es análogo, solo cambia el número del grupo. Reuniremos los gráficos de todos los grupos en uno para que se vea mejor.
# k <- 1L #origin k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
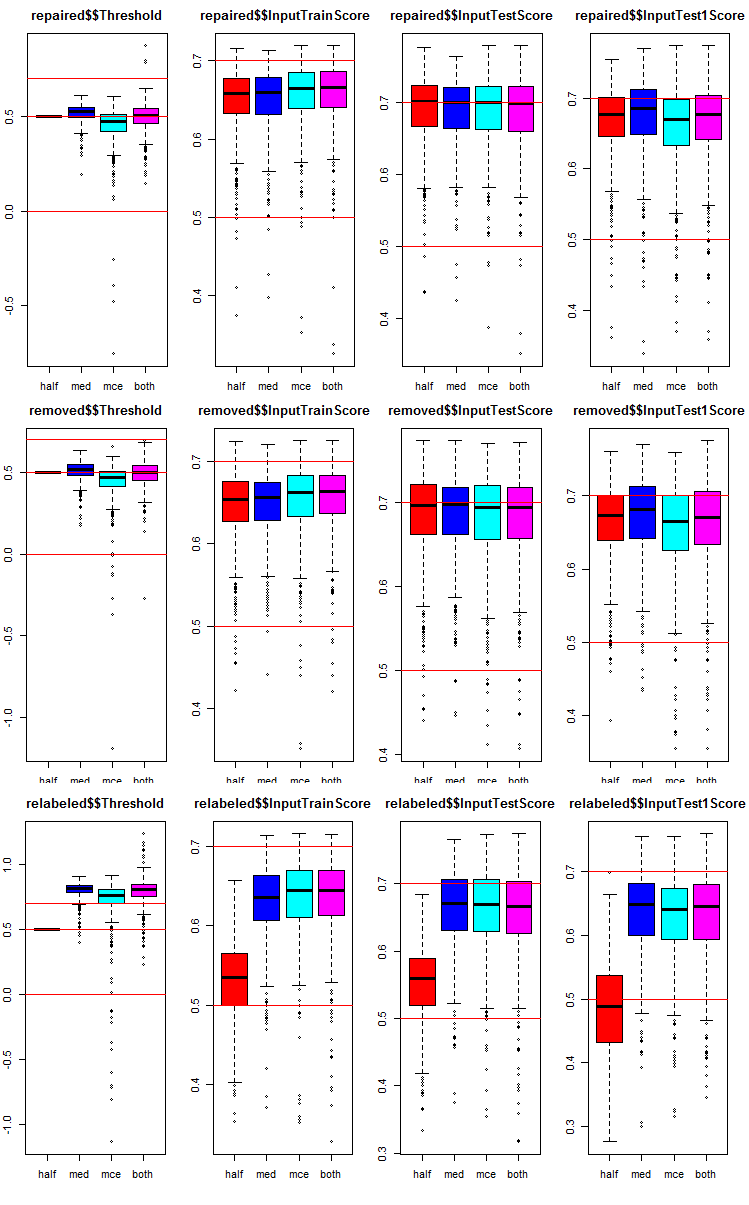
Fig. 8. Gráficos de distribución de las métricas de cada red neuronal del conjunto general en los tres grupos de datos con los tres subconjuntos y cuatro pasadas distintas.
Qué tienen en común los tres grupos:
- las métricas del primer subconjunto de prueba (InputTestScore) son bastante mejores que las métricas del subconjunto de validación (InputTrainScore);
- las métricas del segundo subconjunto de prueba (InputTest1Score) son notoriamente peores que las del primero;
- el umbral del tipo "half" en todos los subconjuntos, con excepción de relabeled, muestra resultados que no son peores que los demás.
5. Simulando los conjuntos
5.1.Determinamos las 7 redes neuronales con mejores métricas en cada grupo general y en cada grupo de datos en el subconjunto InputTrain
Realizamos la poda. En cada grupo de datos del conjunto testX1 necesitamos elegir los 7 valores de InputTrainScore con mayores magnitudes de F1 medio. Precisamente sus índices serán los mejores índices de las redes neuronales en el conjunto general. El script se muestra más abajo, podrá encontrar este en el archivo Test.R.
#--bestNN---------------------------------------- evalq({ nb <- 3L k <- 1L while (k <= 4) { foreach(j = 1:4, .combine = "cbind") %do% { testX1[[k]]$InputTrainScore[ ,j] %>% order(decreasing = TRUE) %>% head(2*nb + 1) } -> testX1[[k]]$bestNN dimnames(testX1[[k]]$bestNN) <- list(NULL, type) k <- k + 1 } }, env)
Hemos obtenido los índices de las redes neuronales con los mejores valores en los cuatro grupos de datos (origin, repaired, removed, relabeled). Vamos a echarles un vistazo y comparar cuánto se diferencian entre sí estas mejores redes neuronales, dependiendo del grupo de datos y el tipo de umbral.
> env$testX1$origin$bestNN half med mce both [1,] 415 75 415 415 [2,] 191 190 220 220 [3,] 469 220 191 191 [4,] 220 469 469 469 [5,] 265 287 57 444 [6,] 393 227 393 57 [7,] 75 322 444 393 > env$testX1$repaired$bestNN half med mce both [1,] 393 393 154 154 [2,] 415 92 205 205 [3,] 205 154 220 220 [4,] 462 190 393 393 [5,] 435 392 287 287 [6,] 392 220 90 90 [7,] 265 287 415 415 > env$testX1$removed$bestNN half med mce both [1,] 283 130 283 283 [2,] 207 110 300 300 [3,] 308 308 110 110 [4,] 159 134 192 130 [5,] 382 207 207 192 [6,] 192 283 130 308 [7,] 130 114 134 207 env$testX1$relabeled$bestNN half med mce both [1,] 234 205 205 205 [2,] 69 287 469 469 [3,] 137 191 287 287 [4,] 269 57 191 191 [5,] 344 469 415 415 [6,] 164 75 444 444 [7,] 184 220 57 57
Podemos notar que los índices de las redes neuronales con los tipos de umbral "mce" y "both" coinciden con mucha frecuencia.
5.2. Promediamos las predicciones continuas de estas 7 mejores redes neuronales.
Tras elegir las predicciones de las 7 mejores redes neuronales, las promediamos en cada grupo de datos, en los subconjuntos InputTrain, InputTest, InputTest1 y según cada tipo de umbral. Script para procesar el subconjunto InputTrain en los 4 grupos:
#--Averaging--train------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTrain[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TrainYpred dimnames(testX1[[k]]$TrainYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Vamos a echar un vistazo a la estructura y los valores estadísticos de las predicciones continuas promediadas obtenidas con el grupo de datos repaired:
> env$testX1$repaired$TrainYpred %>% str() num [1:1001, 1:4] 0.849 0.978 0.918 0.785 0.814 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "Y.aver_half" "Y.aver_med" "Y.aver_mce" "Y.aver_both" > env$testX1$repaired$TrainYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.2202 Min. :-0.4021 Min. :-0.4106 Min. :-0.4106 1st Qu.: 0.3348 1st Qu.: 0.3530 1st Qu.: 0.3512 1st Qu.: 0.3512 Median : 0.5323 Median : 0.5462 Median : 0.5462 Median : 0.5462 Mean : 0.5172 Mean : 0.5010 Mean : 0.5012 Mean : 0.5012 3rd Qu.: 0.7227 3rd Qu.: 0.7153 3rd Qu.: 0.7111 3rd Qu.: 0.7111 Max. : 1.1874 Max. : 1.0813 Max. : 1.1039 Max. : 1.1039
Vemos que aquí la estadística de los dos últimos tipos de umbral también es idéntica. Veamos los scripts para los dos subconjuntos restantes InputTest, InputTest1:
#--Averaging--test------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TestYpred dimnames(testX1[[k]]$TestYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env) #--Averaging--test1------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest1[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$Test1Ypred dimnames(testX1[[k]]$Test1Ypred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Y ahora echemos un vistazo a las estadísticas del subconjunto InputTest del grupo de datos repaired:
> env$testX1$repaired$TestYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.1524 Min. :-0.5055 Min. :-0.5044 Min. :-0.5044 1st Qu.: 0.2888 1st Qu.: 0.3276 1st Qu.: 0.3122 1st Qu.: 0.3122 Median : 0.5177 Median : 0.5231 Median : 0.5134 Median : 0.5134 Mean : 0.5114 Mean : 0.4976 Mean : 0.4946 Mean : 0.4946 3rd Qu.: 0.7466 3rd Qu.: 0.7116 3rd Qu.: 0.7149 3rd Qu.: 0.7149 Max. : 1.1978 Max. : 1.0428 Max. : 1.0722 Max. : 1.0722
Aquí la estadística de los dos últimos tipos de umbral también es idéntica.
5.3. Determinamos los umbrales para la promediación de las predicciones continuas
Ahora tenemos las predicciones promediadas de cada conjunto general. Las tenemos que convertir en etiquetas de clase y determinar las métricas definitivas para todos los grupos de datos y todos los tipos de umbral. Para ello, por analogía con los cálculos anteriores, definiremos los mejores umbrales, usando solo los subconjuntos InputTrain. El script que mostramos más abajo calcula los umbrales en cada grupo y en cada subconjunto:
#-th_aver------------------------------ evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold GetThreshold(testX1[[k]]$TrainYpred[ ,j], Ytest, type[i]) } } -> testX1[[k]]$th_aver dimnames(testX1[[k]]$th_aver) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env)
5.4. Convertimos las predicciones continuas promediadas de los conjuntos generales en etiquetas de clase, y luego calculamos las métricas de los conjuntos generales en los subconjuntos InputTrain, InputTest y InputTest1 de todos los grupos de datos.
Disponiendo de los umbrales calculados arriba th_aver, definimos las métricas:
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TrainScore dimnames(testX1[[k]]$TrainScore) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest1, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TestScore dimnames(testX1[[k]]$TestScore) <- list(type, colnames(testX1[[k]]$TestYpred)) k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest2, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$Test1Score dimnames(testX1[[k]]$Test1Score) <- list(type, colnames(testX1[[k]]$Test1Ypred)) k <- k + 1 } }, env)
Vamos a componer un recuadro de resumen y analizar las métricas obtenidas. Comenzaremos con el grupo origin (en él los ejemplos de ruido no se procesan de ninguna forma). A nosotros nos importan los valores TestScore y Test1Score. Los valores del subconjunto TestTrain son indicativos, los necesitamos para compararlos con los de prueba:
> env$testX1$origin$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.711 0.708 0.712 0.712 med 0.711 0.713 0.707 0.707 mce 0.712 0.704 0.717 0.717 both 0.711 0.706 0.717 0.717 > env$testX1$origin$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.750 0.738 0.745 0.745 med 0.748 0.742 0.746 0.746 mce 0.742 0.720 0.747 0.747 both 0.748 0.730 0.747 0.747 > env$testX1$origin$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.735 0.732 0.716 0.716 med 0.733 0.753 0.745 0.745 mce 0.735 0.717 0.716 0.716 both 0.733 0.750 0.716 0.716
¿Qué podemos ver en el recuadro adjunto?
El mejor resultado, 0.750 en TestScore, lo ha mostrado la opción con el umbral "half" en ambas transformaciones (tanto en la poda, como en la promediación). Sin embargo, en el subconjunto Test1Score, la calidad desciende hasta 0.735.
Las variantes de los umbrales con la poda (med, mce, both) y med con la promediación muestran un resultado más estable en ambos subconjuntos ~0.745.
Veamos el siguiente grupo de datos repaired (con la etiqueta de los ejemplos de ruido corregida):
> env$testX1$repaired$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.711 0.717 0.717 med 0.709 0.709 0.713 0.713 mce 0.728 0.714 0.709 0.709 both 0.728 0.711 0.717 0.717 > env$testX1$repaired$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.759 0.761 0.756 0.756 med 0.754 0.748 0.747 0.747 mce 0.758 0.755 0.743 0.743 both 0.758 0.732 0.754 0.754 > env$testX1$repaired$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.744 0.724 0.724 med 0.738 0.748 0.744 0.744 mce 0.697 0.720 0.677 0.677 both 0.697 0.743 0.731 0.731
El mejor resultado que vemos en el recuadro es 0.759 en la combinación half/half. Las variantes de los umbrales con la poda (med, mce, both) y med con la promediación muestran un resultado más estable en ambos subconjuntos ~0.750.
Veamos el siguiente grupo de datos removed (con los ejemplos de ruido eliminados del conjunto):
> env$testX1$removed$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.720 0.724 0.718 med 0.715 0.717 0.715 0.717 mce 0.721 0.722 0.725 0.723 both 0.721 0.720 0.725 0.723 > env$testX1$removed$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.761 0.769 0.761 0.751 med 0.752 0.749 0.760 0.752 mce 0.749 0.755 0.753 0.737 both 0.749 0.736 0.753 0.760 > env$testX1$removed$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.712 0.732 0.716 0.720 med 0.729 0.748 0.740 0.736 mce 0.685 0.724 0.721 0.685 both 0.685 0.755 0.721 0.733
Analizamos el recuadro. El mejor resultado, 0.769 en TestScore, lo muestra la variante con los umbrales med/half. Sin embargo, en el subconjunto Test1Score, la calidad desciende hasta 0.732. Para el subconjunto TestScore, la mejor combinación de umbrales con la poda (half, med, mce, both) y half con la promediación, da los mejores valores de todos los grupos.
Echemos un vistazo al último grupo de datos relabeled (con los ejemplos de ruido aislados en una clase aparte):
> env$testX1$relabeled$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.672 0.559 0.529 0.529 med 0.715 0.715 0.711 0.711 mce 0.712 0.715 0.717 0.717 both 0.710 0.718 0.720 0.720 > env$testX1$relabeled$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.572 0.555 0.555 med 0.736 0.748 0.746 0.746 mce 0.739 0.747 0.745 0.745 both 0.710 0.756 0.754 0.754 > env$testX1$relabeled$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.664 0.498 0.466 0.466 med 0.721 0.748 0.740 0.740 mce 0.739 0.732 0.716 0.716 both 0.734 0.737 0.735 0.735
El mejor resultado de este grupo lo da la combinación de umbrales: con la poda (med, mce, both) y both o med con la promediación.
Tenga en cuenta que usted puede obtener resultados distintos a los nuestros.
En la figura de abajo se muestra la estructura de los datos de testX1 después de los cálculos mencionados anteriormente:
Fig. 9. Estructura de los datos de testX1.
6. Optimizando los hiperparámetros de las redes neuronales de los clasificadores de los conjuntos
Todos los cálculos anteriores los hemos realizado con conjuntos generales con idénticos hiperparámetros para las redes neuronales, establecidos por experiencia personal. Como ya sabemos, los hiperparámetros de las redes neuronales, como los de otros modelos, deben optimizarse según un conjunto de datos concreto para obtener mejores resultados. Para el entrenamiento, usaremos los datos con el ruido eliminado, divididos en 4 grupos (origin, repaired, removed y relabeled). Por eso debemos obtener los hiperparámetros óptimos de las redes neuronales del conjunto general precisamente para estos conjuntos. En el artículo anterior describimos pormenorizadamente todas las cuestiones relacionadas con la optimización bayesiana, por eso no vamos a detenernos en los detalles de esta.
Vamos a optimizar los 4 hiperparámetros de las redes neuronales:
- número de predictores — numFeature = c(3L, 13L) en el rango de 3 a 13;
- la proporción de ejemplos usados en el entrenamiento — r = c(1L, 10L) en el rango de 10 % a 100%;
- número de neuronas en la capa oculta — nh = c(1L, 51L) en el rango de 1 a 51;
- tipo de función de activación — fact = c(1L, 10L) índice en la lista de funciones de activación Fact.
Establecemos las constantes:
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L) ) }, env)
Escribimos la función de adecuación, que retornará el valor de calidad de Score = meаn(F1) y la predicción del conjunto general en las etiquetas de las clases. Realizaremos la poda (elección de las mejores redes neuronales en el conjunto general) y la promediación de las predicciones continuas usando el mismo umbral = 0.5. Más arriba hemos comprobado que se trata de una variante bastante buena, por lo menos, para la primera aproximación. Este es el aspecto del script:
#---Fitnes -FUN----------- evalq({ n <- 500 numEns <- 3 # SEED <- c(12345, 1235809) fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) k <- 1 rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
La variable SEED comentada tiene dos valores. Esto es necesario para comprobar de forma experimental la influencia de este parámetro en el resultado. Hemos realizado la optimización con los mismos datos fuente y parámetros, pero con dos valores de SEED distintos. El mejor resultado lo ha mostrado SEED = 1235809. En los scripts de abajo usaremos precisamente este valor. Pero mostraremos los hiperparámetros e índices de calidad de la clasificación obtenidos para ambos valores de SEED. Usted podrá experimentar tabién con otros valores.
Comprobamos si funciona la función de adecuación, cuánto tiempo ocupa una pasada de su cálculo y cuál es el resultado:
evalq({
Ytrain <- X1$pretrain$y
Ytest <- X1$train$y
Ytest1 <- X1$test$y
Xtrain <- X1$pretrain$x
Xtest <- X1$train$x
Xtest1 <- X1$test$x
orderX <- orderX1
SEED <- 1235809
system.time(
res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
)
}, env)
user system elapsed
5.89 0.00 5.99
env$res$Score
[1] 0.741
Más abajo mostramos el script de optimización de los hiperparámetros de la red neuronal, secuencialmente para cada grupo de datos cuyo ruido ha sido eliminado. Usamos 20 puntos de la inicialización aleatoria inicial y 20 de las posteriores iteraciones.
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100, control = c(100, 50, 8)) } -> OPT_Res1 group <- qc(origin, repaired, removed, relabeled) names(OPT_Res1) <- group }, env)
Tras iniciar el script para su ejecución, ármese de paciencia para aproximadamente media hora (esto depende de su hardware). Ordenamos los valores Score obtenidos en orden descendente y seleccionamos los tres mejores. Le asignamos los valores de estos índices a la variable best.res (para SEED = 12345) y best.res1 (para SEED = 1235809 ).
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res
names(best.res) <- group
}, env)
evalq({
foreach(i = 1:4) %do% {
OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res1
names(best.res1) <- group
}, env)
Echamos un vistazo a los índices best.res:
env$best.res # $origin # Round numFeature r nh fact Value # 1 39 10 7 20 2 0.769 # 2 12 6 4 38 2 0.766 # 3 38 4 3 15 2 0.766 # # $repaired # Round numFeature r nh fact Value # 1 5 10 5 20 7 0.767 # 2 7 5 2 36 9 0.766 # 3 28 5 10 6 8 0.766 # # $removed # Round numFeature r nh fact Value # 1 1 11 6 44 9 0.764 # 2 8 8 6 26 7 0.764 # 3 19 12 1 40 5 0.763 # # $relabeled # Round numFeature r nh fact Value # 1 24 9 10 1 10 0.746 # 2 7 9 9 2 8 0.745 # 3 32 4 1 1 10 0.738
Lo mismo para los índices best.res1:
> env$best.res1 $origin Round numFeature r nh fact Value 1 19 8 3 41 2 0.777 2 32 8 1 33 2 0.777 3 23 6 1 35 1 0.770 $repaired Round numFeature r nh fact Value 1 26 9 4 17 3 0.772 2 33 11 9 30 9 0.771 3 38 5 4 17 2 0.770 $removed Round numFeature r nh fact Value 1 30 5 4 17 2 0.770 2 8 8 2 13 6 0.769 3 32 5 3 22 7 0.766 $relabeled Round numFeature r nh fact Value 1 34 12 5 8 9 0.777 2 33 9 5 4 9 0.763 3 36 12 7 4 9 0.760
Como podemos ver, los resultados ya tienen un aspecto mejor. Usted podrá mostrar para la comparación, no los tres mejores resultados, sino diez de ellos: las diferencias serán aún más notorias.
Cada inicio de la optimización dará valores de hiperparámetros y resultados distintos. Podemos optimizar los hiperparámetros con diferentes valores de instalación inicial del GNA, además de usar una inicialización inicial concreta.
Reunimos los mejores hiperparámetros de las redes neuronales de los conjuntos generales para los 4 grupos de datos. Los necesitaremos para crear los grupos generales con hiperparámetros óptimos.
#---best.param-------------------
evalq({
foreach(i = 1:4, .combine = "rbind") %do% {
OPT_Res1[[i]]$Best_Par %>% unname()
} -> best.par1
dimnames(best.par1) <- list(group, qc(numFeature, r, nh, fact))
}, env)
Los propios hiperparámetros:
> env$best.par1 numFeature r nh fact origin 8 3 41 2 repaired 9 4 17 3 removed 5 4 17 2 relabeled 12 5 8 9
Podrá encontrar todos los scripts de este apartado en el archivo Optim_VIII.R.
7. Optimización de los hiperparámetros de post-procesado (umbrales de poda y promediación)
La optimización de los hiperparámetros de las redes neuronales da una pequeña mejora de la calidad de clasificación. Más arriba ya nos hemos comprobado que la combinación de los tipos de umbral en la poda y la promediación influyen con mayor intensidad en la calidad de la clasificación.
Ya hemos optimizado los hiperparámetros en la combinación continua de los umbrales half/half. Es posible que la combinación no sea la ideal. Vamos a repetir la optimización con dos parámetros optimizables adicionales th1 = с(1L, 2L)), el tipo de umbral en la poda del conjunto general (elección de las mejores redes neuronales) y th2 = c(1L, 4L), el tipo de umbral al convertir la predicción promediada del conjunto general en etiquetas de clase. Definimos las constantes y el rango de los valores de los hiperparámetros optimizados.
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds_m <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L), th1 = c(1L, 2L), th2 = c(1L, 4L) ) }, env)
Vamos a pasar a la función de adecuación. La hemos modificado un poco: hemos añadido los dos parámetros formales th1, th2. En el cuerpo de la función, en el bloque test calculamos el umbral, dependiendo de th1. En el bloque test-average determinamos el umbral con la ayuda de la función GetThreshold(), dependiendo del tipo de umbral th2.
#---Fitnes -FUN----------- evalq({ n <- 500L numEns <- 3L # SEED <- c(12345, 1235809) fitnes_m <- function(numFeature, r, nh, fact, th1, th2){ bestF <- orderX %>% head(numFeature) k <- 1L rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- ifelse(th1 == 1L, 0.5, median(y.pr)) -> th foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > th, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred th <- GetThreshold(ensPred, Yts$Ytest1, type[th2]) ifelse(ensPred > th, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Comprobamos cuánto tiempo ocupa una iteración de esta función de adecuación, y si esta funciona:
#---res fitnes------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Xtrain <- X1$pretrain$x Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 th1 <- 1 th2 <- 4 system.time( res_m <- fitnes_m(numFeature = 10, r = 7, nh = 5, fact = 2, th1, th2) ) }, env) user system elapsed 6.13 0.04 6.32 > env$res_m$Score [1] 0.748
El tiempo de ejecución de la función ha cambiado de forma poco significativa. Después de ello, iniciamos la optimización y esperamos el resultado:
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res1 <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes_m, bounds = bonds_m, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100) #, control = c(100, 50, 8)) } -> OPT_Res_m group <- qc(origin, repaired, removed, relabeled) names(OPT_Res_m) <- group }, env)
Seleccionamos los 10 mejores hiperparámetros obtenidos para cada grupo de datos:
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res_m[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(10)
} -> best.res_m
names(best.res_m) <- group
}, env)
$origin
Round numFeature r nh fact th1 th2 Value
1 19 8 3 41 2 2 4 0.778
2 25 6 8 51 8 2 4 0.778
3 39 9 1 22 1 2 4 0.777
4 32 8 1 21 2 2 4 0.772
5 10 6 5 32 3 1 3 0.769
6 22 7 2 30 9 1 4 0.769
7 28 6 10 25 5 1 4 0.769
8 30 7 9 33 2 2 4 0.768
9 40 9 2 48 10 2 4 0.768
10 23 9 1 2 10 2 4 0.767
$repaired
Round numFeature r nh fact th1 th2 Value
1 39 7 8 39 8 1 4 0.782
2 2 5 8 50 3 2 3 0.775
3 3 12 6 7 8 1 1 0.769
4 24 5 10 45 5 2 3 0.769
5 10 7 8 40 2 1 4 0.768
6 13 5 8 40 2 2 4 0.768
7 9 6 9 13 2 2 3 0.766
8 19 5 7 46 6 2 1 0.765
9 40 9 8 50 6 1 4 0.764
10 20 9 3 28 9 1 3 0.763
$removed
Round numFeature r nh fact th1 th2 Value
1 40 7 2 39 8 1 3 0.786
2 13 5 3 48 3 2 3 0.776
3 8 5 6 18 1 1 1 0.772
4 5 5 10 24 3 1 3 0.771
5 29 13 7 1 1 1 4 0.771
6 9 7 3 25 7 1 4 0.770
7 17 9 2 17 1 1 4 0.770
8 19 7 7 25 2 1 3 0.768
9 4 10 6 19 7 1 3 0.765
10 2 4 4 47 7 2 3 0.764
$relabeled
Round numFeature r nh fact th1 th2 Value
1 7 8 1 13 1 2 4 0.778
2 26 8 1 19 6 2 4 0.768
3 3 6 3 45 4 2 2 0.766
4 20 6 2 40 10 2 2 0.766
5 13 4 3 18 2 2 3 0.762
6 10 10 6 4 8 1 3 0.761
7 31 11 10 16 1 2 4 0.760
8 15 13 7 7 1 2 3 0.759
9 5 7 3 20 2 1 4 0.758
10 9 9 3 22 8 2 3 0.758
Vemos una mejora poco significativa de la calidad. Los mejores hiperparámetros para cada grupo de datos se diferencian mucho de los hiperparámetros obtenidos en la anterior optimización sin tener en cuenta la diferente combinación de umbrales. Los mejores índices de calidad los observamos para los grupos de datos reetiquetados (repaired ) y con ejemplos de ruido eliminados (removed).
#---best.param------------------- evalq({ foreach(i = 1:4, .combine = "rbind") %do% { OPT_Res_m[[i]]$Best_Par %>% unname() } -> best.par_m dimnames(best.par_m) <- list(group, qc(numFeature, r, nh, fact, th1, th2)) }, env) # > env$best.par_m------------------------ # numFeature r nh fact th1 th2 # origin 8 3 41 2 2 4 # repaired 7 8 39 8 1 4 # removed 7 2 39 8 1 3 # relabeled 8 1 13 1 2 4
Podrá encontrar los scripts de este apartado en el archivo Optim_mVIII.R
8. Combinando varios de los mejores conjuntos en un superconjunto, además de sus salidas
Combinamos varios de los mejores conjuntos generales en un superconjunto, y sus salidas en forma de cascada, mediante votación por mayoría simple.
Para comenzar, combinamos los resultados de varios de los mejores conjuntos generales obtenidos al optimizar. Después de optimizar, la función retorna no solo los mejores hiperparámetros, sino también las predicciones en las etiquetas de las clases en todas las iteraciones. Formamos un superconjunto de los 5 mejores conjuntos generales en cada grupo de datos, y mediante votación por mayoría simple, comprobamos si en esta variante mejoran los índices de calidad de la clasificación.
La secuencia de cálculos es la siguiente:
- en el ciclo buscamos consecutivamente en los 4 grupos de datos;
- determinamos los índices de las 5 mejores predicciones en cada grupo de datos;
- combinamos las predicciones con estos índices en un frame de datos;
- cambiamos en todas las predicciones la etiqueta de clase de "0" a "-1";
- sumamos por líneas estas predicciones;
- convertimos estos valores sumados en etiquetas de clase (-1, 0, 1) con la condición: si el valor es superior a 3, la clase = 1; si es menor a -3, la clase = -1; de lo contrario, el valor de la clase = 0
Este es el aspecto del script que ejecuta estos cálculos:
#--Index-best-------------------
evalq({
prVot <- vector("list", 4)
foreach(i = 1:4) %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(.) ifelse(. == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x)) ->.;
ifelse(. > 3, 1, ifelse(. < -3, -1, 0))
} -> prVot
names(prVot) <- group
}, env)
Ha aparecido una tercera clase, adicional, la clase "0". Si "-1" es "Sell", y "1" es "Buy", entonces "0" es "no estoy seguro". El usuario debe decidir cómo reacciona el experto a esta señal. Puede estar fuera del mercado, y puede estar en el mercado y no hacer nada, esperando una nueva señal para actuar. Los modelos de comportamiento deberán ser construidos y comprobados al simular el experto.
Para obtener las métricas, debemos:
- pasar sucesivamente en el ciclo por cada grupo de datos;
- cambiar en el valor actual de la variable objetivo Ytest1 la etiqueta de clase "0" a la etiqueta "-1";
- combinar en un frame de datos la variable actual y la prVot predicha, obtenida más arriba;
- eliminar del frame de datos las líneas donde el valor prVot = 0;
- calcular las métricas.
Calculamos y miramos el resultado.
evalq({
foreach(i = 1:4) %do% { #group
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = prVot[[i]]) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred)
} -> Score
names(Score) <- group
}, env)
env$Score
$origin
$origin$metrics
Accuracy Precision Recall F1
-1 0.806 0.809 0.762 0.785
1 0.806 0.804 0.845 0.824
$origin$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 49
1 37 201
Accuracy : 0.8063
95% CI : (0.7664, 0.842)
No Information Rate : 0.5631
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6091
Mcnemar's Test P-Value : 0.2356
Sensitivity : 0.8093
Specificity : 0.8040
Pos Pred Value : 0.7621
Neg Pred Value : 0.8445
Prevalence : 0.4369
Detection Rate : 0.3536
Detection Prevalence : 0.4640
Balanced Accuracy : 0.8066
'Positive' Class : -1
$repaired
$repaired$metrics
Accuracy Precision Recall F1
-1 0.82 0.826 0.770 0.797
1 0.82 0.816 0.863 0.839
$repaired$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 147 44
1 31 195
Accuracy : 0.8201
95% CI : (0.7798, 0.8558)
No Information Rate : 0.5731
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6358
Mcnemar's Test P-Value : 0.1659
Sensitivity : 0.8258
Specificity : 0.8159
Pos Pred Value : 0.7696
Neg Pred Value : 0.8628
Prevalence : 0.4269
Detection Rate : 0.3525
Detection Prevalence : 0.4580
Balanced Accuracy : 0.8209
'Positive' Class : -1
$removed
$removed$metrics
Accuracy Precision Recall F1
-1 0.819 0.843 0.740 0.788
1 0.819 0.802 0.885 0.841
$removed$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 145 51
1 27 207
Accuracy : 0.8186
95% CI : (0.7789, 0.8539)
No Information Rate : 0.6
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.6307
Mcnemar's Test P-Value : 0.009208
Sensitivity : 0.8430
Specificity : 0.8023
Pos Pred Value : 0.7398
Neg Pred Value : 0.8846
Prevalence : 0.4000
Detection Rate : 0.3372
Detection Prevalence : 0.4558
Balanced Accuracy : 0.8227
'Positive' Class : -1
$relabeled
$relabeled$metrics
Accuracy Precision Recall F1
-1 0.815 0.809 0.801 0.805
1 0.815 0.820 0.828 0.824
$relabeled$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 39
1 37 178
Accuracy : 0.8151
95% CI : (0.7741, 0.8515)
No Information Rate : 0.528
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6292
Mcnemar's Test P-Value : 0.9087
Sensitivity : 0.8093
Specificity : 0.8203
Pos Pred Value : 0.8010
Neg Pred Value : 0.8279
Prevalence : 0.4720
Detection Rate : 0.3820
Detection Prevalence : 0.4769
Balanced Accuracy : 0.8148
'Positive' Class : -1
#---------------------------------------
La calidad ha mejorado notablemente en todos los grupos. Los mejores índices de Balanced Accuracy se han obtenido en los grupos removed (0.8227) y repaired (0.8209)
Vamos a combinar también las predicciones grupales mediante votación por mayoría simple. Combinamos en forma de cascada:
- iteramos en el ciclo por todos los grupos de datos;
- determinamos los índices de las pasadas con los mejores resultados;
- elegimos las predicciones de estas mejores pasadas;
- sustituimos en cada columna la etiqueta de la clase "0" por la etiqueta "-1";
- sumamos línea a línea las predicciones en el grupo.
Veamos el resultado obtenido:
#--Index-best-------------------
evalq({
foreach(i = 1:4, .combine = "+") %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(x) ifelse(x == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x))
} -> prVotSum
}, env)
> env$prVotSum %>% table()
.
-20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 14 16 18 20
166 12 4 6 7 6 5 3 6 1 4 4 5 6 5 10 7 3 8 24 209
Dejamos solo los mayores valores de la votación y calculamos las métricas:
evalq({
pred <- {prVotSum ->.;
ifelse(. > 18, 1, ifelse(. < -18, -1, 0))}
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = pred) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred) -> ScoreSum
}, env)
env$ScoreSum
> env$ScoreSum
$metrics
Accuracy Precision Recall F1
-1 0.835 0.849 0.792 0.820
1 0.835 0.823 0.873 0.847
$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 141 37
1 25 172
Accuracy : 0.8347
95% CI : (0.7931, 0.8708)
No Information Rate : 0.5573
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6674
Mcnemar's Test P-Value : 0.1624
Sensitivity : 0.8494
Specificity : 0.8230
Pos Pred Value : 0.7921
Neg Pred Value : 0.8731
Prevalence : 0.4427
Detection Rate : 0.3760
Detection Prevalence : 0.4747
Balanced Accuracy : 0.8362
'Positive' Class : -1
Hemos obtenido un muy buen índice de Balanced Accuracy = 0.8362.
podrá encontrar el script descrito en este apartado en el archivo Voting.R
Pero no debemos olvidar un detalle. Al optimizar los hiperparámetros, hemos implicado el conjunto de prueba InputTest. Esto signifcia que podemos comenzar a trabajar desde el próximo conjunto de prueba InputTest1. Lo más probable es que la combinación en cascada de los conjuntos generales genere el mismo efecto positivo sin la optimización de los hiperparámetros. Lo comprobamos con los resultados de promediación que hemos obtenido antes.
Combinamos las salidas promediadas de los conjuntos generales obtenidos en el punto 5.2.
Repetimos los cálculos descritos en el punto 5.4, con un cambio. Al convertir la predicción promediada continua en etiquetas de clase, estas etiquetas serán [-1, 0, 1]. La secuencia de cálculo en cada subconjunto será train/test/test1:
- iteramos sucesivamente en el ciclo por los 4 grupos de datos;
- según los 4 tipos de umbrales de poda;
- según los 4 tipos de umbrales de promediación;
- convertimos la predicción promediada continua del conjunto general en etiquetas de clases [-1, 1];
- los sumamos según los 4 tipos de umbrales de promediación;
- reetiquetamos la suma con las nuevas etiquetas [-1, 0, 1];
- añadimos a la estructura VotAver el resultado obtenido.
#---train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) VotAver <- vector("list", 4) names(VotAver) <- group while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Train.clVoting dimnames(VotAver[[k]]$Train.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test------------------------------ evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test.clVoting dimnames(VotAver[[k]]$Test.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test1------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test1.clVoting dimnames(VotAver[[k]]$Test1.clVoting) <- list(NULL, type) k <- k + 1 } }, env)
Tras determinar las promediaciones promediadas reetiquetadas en los subconjuntos y grupos, calculamos sus métricas. Secuencia de los cálculos:
- en el ciclo, iteramos por los grupos;
- en el ciclo, pasamos por los 4 tipos de umbrales de promediación;
- cambiamos en la predicción actual la etiqueta de clase "0" a "-1";
- combinamos en un frame de datos la predicción actual y la reetiquetada;
- eliminamos del frame de datos las líneas en las que la predicción es igual a 0;
- calculamos las métricas y las añadimos a la estructura VotAver.
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TrainScoreVot names(VotAver[[k]]$TrainScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest1 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TestScoreVot names(VotAver[[k]]$TestScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest2 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$Test1ScoreVot names(VotAver[[k]]$Test1ScoreVot) <- type k <- k + 1 } }, env)
Reunimos los datos de una forma legible y les echamos un vistazo:
#----TrainScoreVot-------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TrainScoreVot %>% unlist() %>% unname()
} -> TrainScoreVot
dimnames(TrainScoreVot) <- list(group, type)
}, env)
> env$TrainScoreVot
half med mce both
origin 0.738 0.750 0.742 0.752
repaired 0.741 0.743 0.741 0.741
removed 0.748 0.755 0.755 0.755
relabeled 0.717 0.741 0.740 0.758
#-----TestScoreVot----------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TestScoreVot %>% unlist() %>% unname()
} -> TestScoreVot
dimnames(TestScoreVot) <- list(group, type)
}, env)
> env$TestScoreVot
half med mce both
origin 0.774 0.789 0.797 0.804
repaired 0.777 0.788 0.778 0.778
removed 0.801 0.808 0.809 0.809
relabeled 0.773 0.789 0.802 0.816
#----Test1ScoreVot--------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$Test1ScoreVot %>% unlist() %>% unname()
} -> Test1ScoreVot
dimnames(Test1ScoreVot) <- list(group, type)
}, env)
> env$Test1ScoreVot
half med mce both
origin 0.737 0.757 0.757 0.755
repaired 0.756 0.743 0.754 0.754
removed 0.759 0.757 0.745 0.745
relabeled 0.734 0.705 0.697 0.713
Los mejores resultados se han mostrado en el subconjunto de prueba en el grupo de datos removed, con la variante de procesamiento de los ejemplos de ruido.
Reunimos de nuevo los resultados en cada subconjunto de cada grupo de datos, según los tipos de promediación.
#==Variant-2========================================== #--TrainScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Train.clVoting ->.; apply(., 1, function(x) sum(x)) ->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Train.clVotingSum ifelse(Ytest == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TrainScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--TestScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test.clVotingSum ifelse(Ytest1 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TestScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--Test1ScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test1.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test1.clVotingSum ifelse(Ytest2 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$Test1ScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env)
Reunimos los resultados de una forma legible.
evalq({
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TrainScoreVotSum %>% unlist() %>% unname()
} -> TrainScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TestScoreVotSum %>% unlist() %>% unname()
} -> TestScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$Test1ScoreVotSum %>% unlist() %>% unname()
} -> Test1ScoreVotSum
ScoreVotSum <- cbind(TrainScoreVotSum, TestScoreVotSum, Test1ScoreVotSum)
dimnames(ScoreVotSum ) <- list(group, qc(TrainScoreVotSum, TestScoreVotSum,
Test1ScoreVotSum))
}, env)
> env$ScoreVotSum
TrainScoreVotSum TestScoreVotSum Test1ScoreVotSum
origin 0.763 0.807 0.762
repaired 0.752 0.802 0.748
removed 0.761 0.810 0.765
relabeled 0.766 0.825 (!!) 0.711
Analizamos los resultados del subconjunto de prueba. El mejor resultado, inesperadamente, ha sido el de relabeled. Los resultados en todos los grupos son mucho mejores que los obtenidos en el punto 5.4. El método de cascada para la combinación de salidas de los conjuntos generales mediante votación por mayoría simple da una mejora en la calidad de la clasificación (Accuracy) del 5% al 7%.
Los scripts de este apartado se encuentran en el archivo Voting_aver.R. La estructura de los datos obtenidos se muestra en la figura de abajo:
Fig. 10. Estructura de datos VotAver.
En la figura de abajo se muestra el esquema simplificado de los cálculos al completo: se indican las etapas, los scripts usados y las estructuras de datos.
Fig. 11. Estructura y orden de los cálculos principales en el artículo.
8. Analizando el resultado de los experimentos
Hemos procesado los ejemplos de ruido en los conjuntos de datos originales en los subconjuntos pretrain (!) de tres formas:
- hemos reetiquetado "erróneamente" los datos etiquetados sin cambiar el número de clases (repaired);
- hemos quitado del subconjunto los ejemplos de "ruido" (removed);
- hemos aislado los ejemplos de "ruido" en una clase aparte (relabeled).
Hemos obtenido 4 grupos de datos (origin, repaired, removed, relabeled) en la estructura denoiseX1pretrain. Entrenamos con ellos el conjunto general de 500 redes neuronales de clasificadores ELM, obteniendo cuatro conjuntos generales. Calculamos las prediciones continuas de los tres subconjuntos Х1$train/test/test1 con estos 4 conjuntos generales y los reunimos en la estructura predX1.
A continuación, calculamos los 4 tipos de pasada para las predicciones continuas de cada una de las 500 redes neuronales de cada conjunto general en el subconjunto InputTrain (!). Usando estos umbrales, convertimos las predicciones continuas en etiquetas de clases (0, 1). Calculamos las métricas (mean(F1)) para cada red neuronal de los conjuntos generales y las reunimos en la estructura testX1$$(InputTrainScore|InputTestScore|InputTest1Score). La visualización de esta distribución de métricas en 4 grupos de datos y 3 subconjuntos muestra que:
- En primer lugar, las métricas en el primer subconjunto de prueba son superiores a las de InputTrainScore en todos los grupos;
- En segundo lugar, en los grupos repaired y removed , las métricas son visualmente superiores a las de los otros dos.
Ahora elegimos las 7 mejores redes neuronales con los mayores valores mean(F1) en cada conjunto general, y luego promediamos sus predicciones continuas. Añadimos sus valores a la estructura testX1$$(TrainYpred|TestYpred|Test1Ypred). Tras calcular los umbrales th_aver en el subconjunto TrainYpred, determinamos las métricas de todas las predicciones y las añadimos a la estructura testX1$$(TrainScore|TestScore|Test1Score). Ahora podemos analizarlas.
Al combinar diferentes umbrales de poda y promediación en distintos grupos de datos, obtenemos las métricas en el rango de 0.75 — 0.77. El mejor resultado se ha obtenido en el grupo removed con ejemplos de "ruido" eliminados.
La optimización de los hiperparámetros de las redes neuronales de los conjuntos generales nos da un aumento estable de las métricas en todos los grupos de hasta 0.77+.
La optimización de los hiperparámetros de las redes neuronales y los umbrales de post-procesado (poda y promediación) da un resultado elevado y estable en todos los grupos con ejemplos procesados de "ruido" en la zona de 0.78+.
Vamos a crear un superconjunto a partir de varios conjuntos generales con hiperparámetros óptimos; después tomaremos las predicciones de estos conjuntos generales y las combinaremos mediante votación por mayoría simple en cada grupo de datos. Como resultado, obtendremos las métricas en los grupos repaired y removed en el rango 0.82+. Combinando estas predicciones de superconjuntos mediante votacion por mayoría simple, obtendremos un valor final de la métrica de 0.836. De esta forma, la combinación en cascada de predicciones mediante votación por mayoría simple da una calidad aumentada en un 6-7%.
Vamos a comprobar la afirmación con las predicciones promediadas de los superconjuntos que hemos obtenido anteriormente. Tras repetir los cálculos y transformaciones en los grupos, obtendremos métricas de 0.8+ en el grupo removed del subconjunto Test. Una vez continuada la combinación en cascada, obtendremos las métricas con los valores 0,8+ en el subconjunto Test en todos los grupos de datos.
Podemos sacar la conclusión de que la combinación en cascada de los conjuntos generales mediante votación por mayoría simple en verdad mejora significativamente la calidad de clasificación.
Conclusión
En el artículo hemos analizado tres métodos para aumentar la calidad de los conjuntos bagging, además de la optimización de los hiperparámetros de las redes neuronales de los conjuntos generales y de post-procesado. Según los resultados de los experimentos, podemos sacar las siguientes conclusiones:
- el procesamiento de los ejemplos de ruido con los métodos repaired y removed mejora la calidad de clasificación de los conjuntos generales;
- la elección del tipo de poda y promediación, así como su combinación, influyen significativamente en su calidad de clasificación;
- la combinación de varios conjuntos generales en un superconjunto con combinación en cascada de su predicciones mediante votación por mayoría simple da el mayor aumento de calidad de la clasificación;
- la optimización de los hiperparámetros de las redes neuronales de los conjuntos generales mejora de forma poco significativa los índices de calidad de la clasificación. Sería oportuno realizar la primera optimización con datos nuevos, y después repetirla periódicamente cuando disminuya la calidad. La periodicidad se define de forma experimental.
Anexos
En GitHub/PartVIII se encuentran los siguientes archivos:
- Importar.R — funciones de importación de paquetes.
- Library.R — biblioteceas necesarias.
- FunPrepareData_VII.R — funciones de preparación de los datos fuente.
- FunStacking_VIII.R — funciones de creación y simulación del conjunto.
- Prepare_VIII.R — funciones y scripts de preparación de los datos fuente para los combinadores entrenables.
- Denoise.R — scripts de procesamiento de los ejemplos de ruido
- Ensemles.R — scripts de creación de conjuntos
- Threshold.R — scripts para determinar los umbrales
- Test.R - scripts de comprobación de conjuntos
- Averaging.R - scripts de promediación de la salidas continuas de los conjuntos
- Voting_aver.R - combinación de las salidas promediadas en cascada mediante votación por mayoría simple
- Optim_VIII.R - scripts de optimización de los hiperparámetros de las redes neuronales
- Optim_mVIII.R - scripts de optimización de los hiperparámetros de las redes neuronales y el post-procesado
- Voting.R - combinación en cascada de las salidas del superconjunto mediante votación por mayoría simple
- SessionInfo_VII.txt — lista de paquetes usados en los scripts del artículo.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/4722
Indicador universal RSI para operar simultáneamente en dos direcciones
50 000 trabajos ejecutados en la bolsa Freelance de MQL5.com
Integración de un experto en MQL y bases de datos (SQL Server, .NET y C#)
Representación personalizada de la historia comercial y creación de gráficos para los informes
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Вопросы по коду и обсуждение можно вести в ветке
Удачи