Tercera generación de neuroredes: "Neuroredes profundas"
4 834
0
Contenido
- Neuroredes de segunda generación
- 1.1. Arquitectura de conexiones
- 1.2. Tipos principales de neuroredes
- 1.2.1. Redes multicapa de conexión completa y extension directa MLP (multilayer perceptron)
- 1.2.2. Red de Jordan
- 1.2.3. Red de Elman
- 1.2.4. Red de función de base radial (RBF)
- 1.2.5. Redes dinámicas de aprendizaje de cuantización vectorial (Dynamic learning vector quantization, DLVQ networks)
- 1.2.6. Red neuronal de Hopfield
- 1.3. Métodos de entrenamiento
- 1.4. Desventajas
- Aprendizaje profundo
- 2.1. Un poco de historia
- 2.2. Auto-asociadores. Auto-codificadores y Máquina de Boltzmann restringida. Diferencias y peculiaridades
- 2.3. Redes auto-asociadoras acumulativas (stacked autoassociators network). Auto-codificadores acumulativos (Stackеd Autoencoder SAE), Redes Acumulativas de Boltzmann (Stacked RBM)
- 2.4. Entrenamiento de las redes profundas (DN). Etapas del aprendizaje. Peculiaridades
- Experimentos prácticos
- 3.1. Lenguaje R
- 3.2. Variantes de implementación y tareas solubles
- 3.3. Preparación de los datos para el experimento
- 3.3.1. Datos de origen
- 3.3.2. Variables (predictores) de entrada
- 3.3.2.1. Welles Wilder's Directional Movement Index - ADX(HLC, n)
- 3.3.2.2. aroon(HL, n)
- 3.3.2.3. Commodity Channel Index - CCI(HLC, n)
- 3.3.2.4. chaikinVolatility (HLC, n)
- 3.3.2.5. Chande Momentum Oscillator - CMO(Med, n)
- 3.3.2.6. MACD oscillator
- 3.3.2.7. OsMA(Med,nFast, nSlow, nSig)
- 3.3.2.8. Relative Strength Index - RSI(Med,n)
- 3.3.2.9. Stochastic Oscillator - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
- 3.3.2.10. Stochastic Momentum Index - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
- 3.3.2.11. Volatility (Yang and Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)
- 3.3.3. Datos de salida (meta)
- 3.3.4. Despejar datos
- 3.3.5. Formación de muestras de entrenamiento y prueba
- 3.3.6. Balance de clases
- 3.3.7. Preprocesado
- 3.4. Construcción, entrenamiento y testado de modelos
- Implementación del programa (indicador y experto)
Introducción
En el artículo se estudiarán los conceptos básicos del tema "Aprendizaje profundo" (Deep Learning), "Red profunda" (Deep Network) sin exposiciones matemáticas complejas, como se dice, "de forma que lo entienda un niño".
Se realizarán experimentos con datos reales, que confirmarán (o no) las ventajas teóricas de las "redes profundas" con respecto a las "superficiales", mediante la determinación y comparación de métricas. La tarea a resolver es la clasificación. Crearemos un indicador y un experto que usen el modelo de red profunda y que funcionen conectados conforme al esquema cliente-servidor, además, los pondremos a prueba.
Se presupone que los lectores están familiarizados con los conceptos básicos del tema de las "Neuroredes". Dado que no se ha establecido aún una terminología en el tema del aprendizaje profundo, se recurrirá al inglés en los casos imprescindibles.
1. Neuroredes de segunda generación
Las neuroredes se adaptan a la resolución de un amplio espectro de tareas relacionadas de una u otra forma con el procesamiento de imágenes.
En la lista de tareas típicas para las neuredes se encuentran:
- La aproximación de las funciones según un conjunto de puntos (regresión);
- La clasificación de datos conforme a un conjunto de clases establecido;
- La categorización de datos con revelación de clases-prototipos desconocidas de antemano;
- La compresión de la información;
- El restablecimiento de los datos perdidos;
- La memoria asociativa;
- La optimización, gestión óptima y otros.
De todo lo enumerado, en el artículo estudiaremos solo la "Clasificación".
1.1. Arquitectura de conexiones
La presencia o ausencia de bucles de conexiones de retorno influye de una forma decisiva en el método de procesamiento de la información. Si las conexiones de retorno entre neuronas no existen (es decir, la red no tiene estructura de capas consecutivas, donde cada neurona recibe información solo de la capa precedente), el procesamiento de la información en la red será unidireccional. La señal de entrada se procesa mediante la secuencia de las capas, y la respuesta se obtiene de manera garantizada tras una cantidad de tactos igual a la cantidad de capas.
La presencia de conexiones de retorno puede hacer la dinámica de la neurored (llamada en este caso recurrente) impredecible. En principio, la red puede "atascarse" y no proporcionar nunca una respuesta. Además, de acuerdo con Turing, no existe un algoritmo que permita determinar para una red recurrente aleatoria si llegarán alguna vez sus elementos a un estado de equilibrio (el así llamado problema de la parada).
Hablando de manera general, el hecho de que las neuronas en las redes recurrentes participen muchas veces en el procesamiento de la información, permite a tales redes realizar un procesamiento de la información más diverso y profundo. En este caso, es recomendable aplicar medidas especiales para que la red no entre en un bucle permanente (por ejemplo, usar conexiones simétricas, como en la red de Hopfield, o limitar de manera forzosa la cantidad de iteraciones).
| Tipo de entrenamiento Tipo de conexiones | Con "supervisor" | Sin "supervisor" |
|---|---|---|
| Sin conexiones de retorno | Perceptrones de capa múltiple (aproximación de funciones, clasificación) | Redes competitivas, mapas de Kohonen (compresión de datos, separación de rasgos) |
| Con conexiones de retorno | Aproximadores recurrentes (predicción de series temporales, entrenamiento en modo on-line) | Red de Hopfield (memoria asociativa, agrupamiento de datos, optimización) |
Recuadro 1. Clasificación de las neuroredes según el tipo de conexión y el tipo de aprendizaje
1.2. Tipos principales de neuroredes
Historicamente, tras su comienzo con el perceptrón, las neuroredes han andado un largo camino en su desarrollo. A día de hoy, se conocen y aplican con utilidad un buen número de neuroredes, diferentes en cuanto a su estructura y métodos de aprendizaje.
Entre las más célebres, podemos mencionar:
1.2.1. Redes multicapa de conexión completa y extension directa MLP (multilayer perceptron)
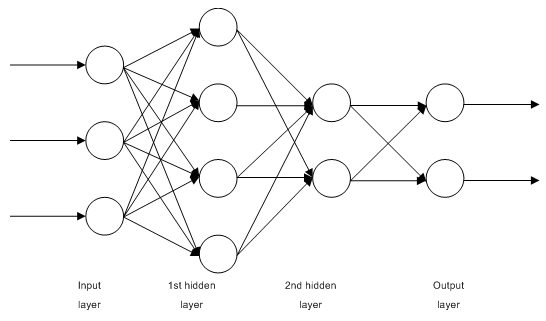
Fig. 1. Esquema estructural de la neurored de capa múltiple
1.2.2. La red de Jordan, es una red parcialmente recurrente, semejante a las redes de Elman (Jordan networks are partially recurrent networks and similar to Elman networks).
Se la puede estudiar como una red de propagación directa con neuronas adicionales de contexto en la capa de entrada.
Esta neuronas de contexto toman la entrada a partir de sí mismas (conexión de retorno directa, direct feedback) y de las neuronas de salida. Las neuronas de contexto preservan el estado actual de la red. En la red de Jordan, la cantidad de neuronas de contexto y de salida debe ser la misma.
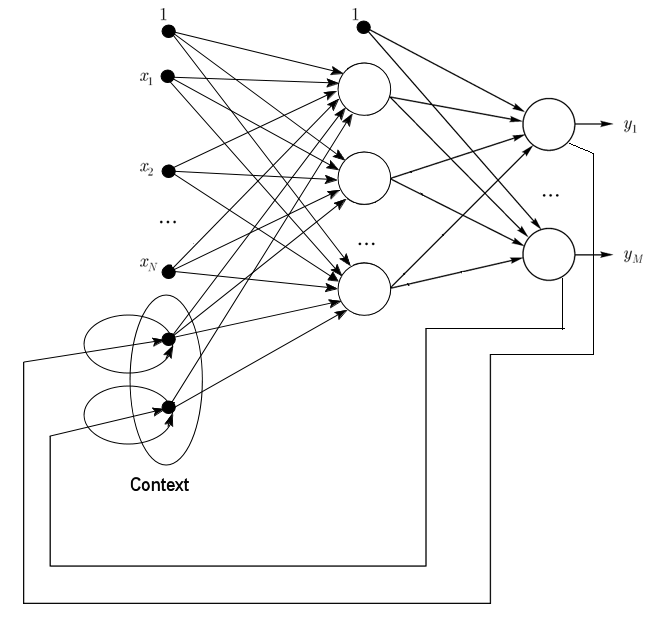
Fig. 2. Esquema estructural de la red de jordan
1.2.3. La red de Elman es una red parcialmente recurrente, similar a las redes de Jordan (Elman networks are partially recurrent networks and similar to Jordan networks). La diferencia entre las redes de Elman y Jordan se concreta en que en las redes de Elman las neuronas de contexto toman la entrada, no a partir de las neuronas de salida, sino de a partir de las ocultas. Además, en las neuronas de contexto no existe ninguna conexión de retorno directa.
En la red de Elman, el número de neuronas de contexto y ocultas deber ser el mismo. La principal ventaja de la red de Elman reside en que la cantidad de neuronas de contexto se determina, no por la dimensión de la salida (como sucede igualmente en la red de Jordan), sino por la cantidad de neuronas ocultas, lo que la hace más flexible. Se pueden añadir o quitar fácilemte nueronas ocultas, a diferencia de la cantidad de salidas.
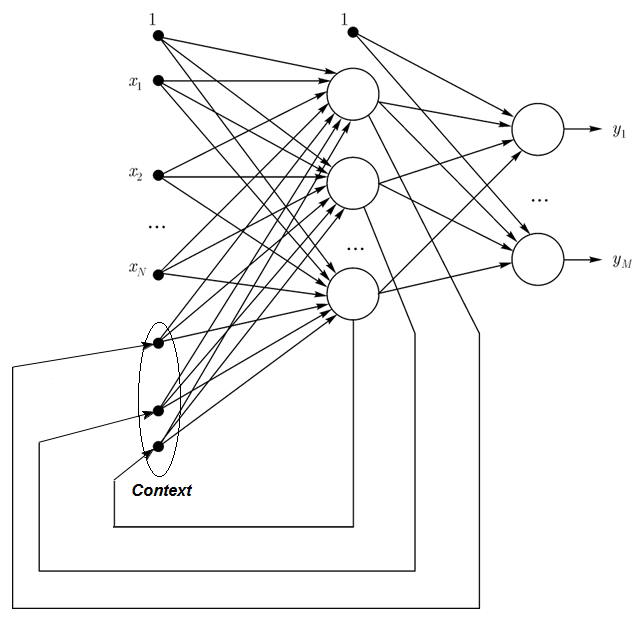
Fig. 3. Esquema estructural de la red de Elman
1.2.4. La red de funciones de base radial (RBF) , es una red de neuronas de propagación directa, que contiene una capa intermedia (oculta) de neuronas con simetría radial. Esta neurona transforma la distancia desde un vector de entrada dado hasta el "centro" que le corresponda según una cierta ley lineal (normalmente una función gaussiana).
Las redes RBF tienen una serie de ventajas con respecto a las redes de capa múltiple de propagación directa. En primer lugar, modelan una función lineal aleatoria con ayuda de solo una capa intermedia, logrando con ello también liberar al desarrollador de la necesidad de resolver la cuestión de la cantidad de capas. En segundo lugar, los parámetros de combinación lineal en la capa de salida se pueden optimizar por completo con ayuda de métodos bien conocidos de optimización lineal, que funcionan a gran velocidad y no sufren dificultades con los mínimos locales, que tanto estorban en el aprendizaje con el uso del algoritmo de propagación inversa del error. Por eso, la red RBF aprende de forma muy simple, mucho más rápido que usando el algoritmo DI (distribución inversa).
Desventajas de las redes RBF: estas redes disponen de propiedades de extrapolación deficientes y son demasiado engorrosas en el caso de que el vector de entrada tenga grandes dimensiones.
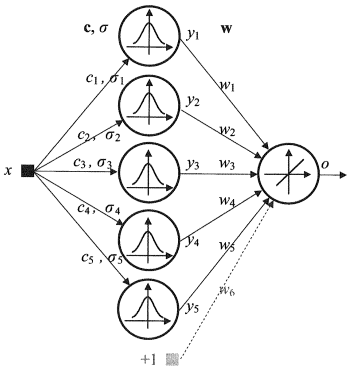
Fig. 4. Esquema estructural de la RBF
1.2.5. Las redes dinámicas de aprendizaje de cuantización vectorial (Dynamic learning vector quantization, DLVQ networks) son parecidas a los mapas auto-organizables de Kohonen (SOM). A diferencia de los SOM, aprende con un supervisor, y carece de relaciones vecinales entre prototipos (But they perform supervised learning and lack a neighborhood relationship between the prototypes). La cuantización vectorial es una operación mucho más general que el agrupamiento.
1.2.6. La red neuronal de Hopfield es una una red neuronal de conexión completa con una matriz simétrica de conexiones. En el proceso de trabajo, la dinámica de tales redes converge (convierte) en una de las posiciones de equilibrio. Estas posiciones de equilibrio son los mínimos locales del funcional, llamado energía de la red. Una red así puede ser utilizada como memoria auto-asociativa, como filtro, y también para resolver ciertas tareas de optimización.
A diferencia de muchas redes neuronales que trabajan hasta obtener la respuesta determinando la cantidad de tactos, las redes de Hopfield trabajan hasta conseguir el equilibrio cuando el siguiente estado de la red es exactamente igual al anterior: el estado incial es la imagen de entrada, y al alcanzar el equilibrio, reciben la imagen de salida. El aprendizaje de las redes de Hopfield exige que el patrón de entrenamiento sea suministrado en las capas de entrada y salida de forma simultánea.
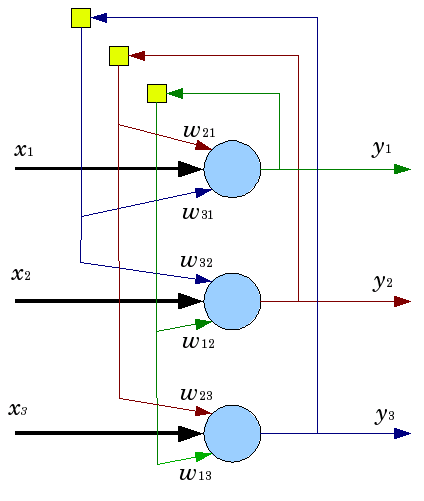
Fig. 5. Esquema de la red de Hopfield con tres neuronas
A pesar de las cualidades interesantes que posee, una red neuronal en el modelo clásico de Hopfield está lejos de la perfección. Posee un volumen de memoria relativamente modesto, aproximadamente un 15% de la cantidad de neuronas de una red N, al tiempo que los sistemas de modos de redireccionamiento pueden guardar hasta 2N de imágenes diferentes, usando N bits.
Además, las redes neuronales de Hopfield no pueden resolver la tarea de reconocimiento, si la imagen se encuentra desplazada o girada con respecto a su estado recordado inicial. Estas y otras desventajas determinan a día de hoy la opinión general con respecto al modelo de Hopfield, se lo concibe más bien como una construcción teórica cómoda a la hora de investigar, que como un medio práctico de utilización diaria.
Hay otras muchas que no hemos mencionado aquí (Hamming, Grossberg, las redes de teoría de la resonancia adaptativa (ART-1, ART-2), etcétera), ya que no han logrado ser aplicadas ampliamente en nuestra esfera de intereses.
1.3. Métodos de entrenamiento
La capacidad de aprendizaje es la principal propiedad del cerebro. Para las redes neuronales artificiales, entenderemos como aprendizaje el proceso de configuración de la arquitectura de la red (estructuras de las conexiones entre neuronas) y de los pesos de las conexiones sinápticas (que influyen en las señales de los coeficientes), para una resolución efectiva de la tarea establecida. Normalmente, el aprendizaje de una neurored tiene lugar sobre la base de una cierta muestra. Conforme se da el proceso de aprendizaje, que tiene lugar según un cierto algoritmo, la red deberá reaccionar cada vez mejor (de forma más adecuada) a las señales de entrada.
Se suelen nombrar tres paradigamas del aprendizaje: supervisado, no supervisado y mixto. En el primer método, se conocen las respuestas correctas a cada parámetro de entrada, y los pesos se adecuan de tal forma que se minimice el error. El aprendizaje no supervisado permite distribuir las imágenes por categorías mediante la explicación de la estructura interna y la naturaleza de los datos. En el aprendizaje mixto se combinan los dos enfoques expuestos más arriba.
1.3.1. Reglas básicas del aprendizaje de las redes neuronales
Se conocen cuatro normas elementales en el aprendizaje, determinadas por las arquitecturas de las redes relacionadas con ellas: la corrección de errores, la regla de Boltzmann, la regla de Hebb y el método competitivo.
1.3.1.1. Corrección de errores
Para cada ejemplo de entrada se ha establecido una salida necesaria (meta), que puede no coincidir con el valor real (predicho). La regla de aprendizaje al corregir un error, consiste en usar la diferencia entre la variable meta y la predicha para el cambio de pesos, con el objetivo de reducir el error de divergencia. El entrenamiento se lleva a cabo solo en caso de que se dé un resultado erróneo. Se conoce una gran cantidad de modificaciones de esta regla de entrenamiento.
1.3.1.2. Regla de Boltzmann
La regla de Boltzmann es una regla estocástica de aprendizaje, determinada por la analogía con principios termodinámicos. Como resultado de su ejecución, se realiza el ajuste de los coeficientes de peso de las neuronas, de acuerdo con las distribuciones de probabilidad necesarias. El aprendizaje de la regla de Boltzmann puede ser estudiado como un caso determinado de corrección de errores, en el que entendemos por error la divergencia de las correlaciones de los estados en los dos modos.
1.3.1.3. Regla de Hebb
La regla de Hebb es el algoritmo más conocido de aprendizaje de las redes neuronales, cuya esencia consiste en lo siguiente: si las neuronas de ambas partes de la sinápsis se excitan simultáneamente y de manera regular, entonces la intensidad de la conexión sináptica crecerá. una peculiaridad importante es que el cambio del peso sináptico depende solo de la actividad de las neuronas unidas por esta sinápsis. Se ha propuesto una gran cantidad de variedades de esta regla, que se distinguen por las peculiaridades de modificación de los pesos sinápticos.
1.3.1.4. Método competitivo
A diferencia de la regla de Hebb, en la que multitud de neuronas de salida pueden excitarse simultáneamente, aquí las neuronas de salida compiten entre sí. Y la neurona de salida con el valor máximo de suma ponderada, se convierte en la "ganadora" ("el ganador se lo lleva todo"). Las salidas del resto de neuronas de salida quedan establecidas en estado inactivo. En el aprendizaje se modifican solo los pesos de la neurona "ganadora" hacia el lado del aumento de la cercanía con el parámetro de entrada dado.
Existe una gran cantidad de algoritmos de aprendizaje, orientados a la solución de diferentes tareas. Entre ellos, destacan los algoritmos de propagación inversa del error, que es uno de los algoritmos actuales más exitosos. Su idea principal consiste en que el cambio de pesos de las sinápsis sucede teniendo en cuenta el gradiente local de la función del error.
La diferencia entre la respuesta real y la correcta de la red neuronal, determinada en la capa de entrada, se propaga en dirección opuesta (fig.5), contra el flujo de señales. Así, cada neurona es capaz de determinar la contribución de cada uno de sus pesos en el error total de la red. La regla más sencilla de aprendizaje corresponde al método del descenso más pronunciado, es decir, los pesos sinápticos cambian de forma proporcional a su contribución al error general.
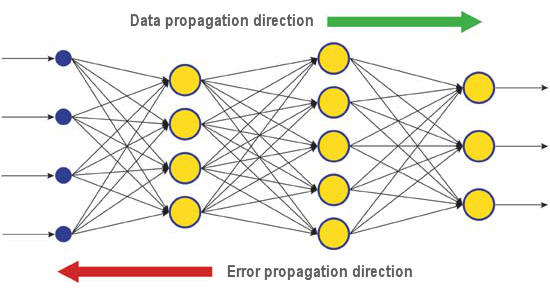
Fig. 6. Esquema de propagación de datos y error en la neurored durante el aprendizaje con el método de propagación inversa del error
Por supuesto que en este tipo de aprendizaje de la red neuronal no existe la certeza de que ella haya aprendido de la mejor forma, dado que siempre cabe la posibilidad de que el algoritmo entre en el mínimo local. Para ello se usan métodos especiales que permitan "sacar" la solución encontrada del extremo local. Si después de varias acciones así la red neuronal converge en la misma decisión, entonces podemos llegar a la conclusión de que la solución encontrada seguramente será la óptima.
1.4. Desventajas
- La principal dificultad a la hora de usar neuroredes, es la llamada "maldición de la dimensión". Al aumentar la dimensión de las entradas y la cantidad de capas, la complejidad de la red y el tiempo de aprendizaje crecen exponencialmente, no siendo al mismo tiempo el resultado obtenido óptimo.
- Otra dificultad que entraña el uso de las redes neuronales, consiste en que la las redes de neuronas tradicionales no son capaces de explicar de qué forma resuelven una tarea. Para muchas esferas del saber, esta excplicación es más importante que el propio resultado (por ejemplo, en medicina). La representación interna de los resultados del aprendizaje es con frecuencia tan compleja, que resulta imposible analizarla, a excepción de ciertos casos muy simples, que normalmente no son interesantes.
2. Aprendizaje profundo
En la actualidad, la teoría y práctica del aprendizaje de máquinas están experiementando un auténtica "revolución profunda", auspiciada por la aplicación exitosa de los métodos del Deep Learning (aprendizaje profundo), que representan la tercera generación de redes neuronales. A diferencia de las redes neuronales clásicas de los años 80-90 del siglo pasado (segunda generación), los nuevos paradigmas de aprendizaje permiten librarse de una serie de problemas que retenían la difusión y aplicación exitosas de las redes neuronales tradicionales.
Las redes entrenadas con ayuda de algoritmos de aprendizaje profundo, no solo superaron en precisión a los mejores métodos alternativos, sino también en una serie de tareas en las que mostraron rudimentos de comprensión del sentido de la información suministrada (por ejemplo, a la hora de reconocer imágenes, en el análisis de información de texto, etcétera).
En la actualidad, los métodos industriales de más éxito en el campo del reconocimiento visual y de voz están construidos sobre la utilización de redes profundas, y gigantes de la industria de IT, como Apple, Google, Facebook, emplean a grupos de investigadores que se dedican a las neuroredes profundas.
2.1. Un poco de historia
Un equipo de doctorandos de la universidad de Toronto (Canadá), a cargo del profesor Geoffrey E. Hinton ganó un concurso organizado por la compañía farmacéutica Merck. Con una cantidad de datos limitada a su disposición, que describía la estructura química de 15 moléculas, el grupo de Hinton logró crear y usar un sistema informático especial que determinaba cuál de estas moléculas funcionaría de forma más efectiva como medicina.
La peculiaridad de este trabajo consiste en que los desarrolladores del sistema utilizaron una red neuronal artificial, usando como base el llamado "aprendizaje profundo" (Deep Learning). En definitiva, su sistema logró realizar los cálculos e investigaciones necesarias en base a una cantidad de datos de origen extremadamente pequeña: normalmente, para el entrenamiento de las redes neronales, antes de comenzar a usarlas se necesita cargar en el sistema una matriz de información enorme.
El logro del equipo de Hinton parece tanto más impresionante si tenemos en cuenta que la solicitud de participación se realizó literalmente en el último momento. Lo que es más, el sistema de "aprendizaje profundo" se creó en condiciones en las que se carecía de datos concretos sobre la interacción de las moléculas propuestas con objetos meta. El uso exitoso de la metodología del "aprendizaje profundo" se convirtió en un nuevo avance en el desarrollo de la inteligencia artificial, una esfera rica en logros en la segunda mitad del 2012.
Así, este verano, Jeff Dean y Andrew Y. Ng, de Google, mostraron un nuevo sistema de reconocimiento de imágenes con una precisión de identificación de un gato en una fotografía del 15,8%. Para entrenar el sistema de agrupamiento, de 16 mil nódulos, se usó la red ImageNet, que contiene 14 millones de imágenes de 20 mil objetos diferentes. El año pasado, científicos suizos mostraron un sistema que reconocía mejor que una persona las señales de tráfico en fotografías (la precisión fue del 99,46% en un conjunto de 50 000 imágenes, mientras que las personas tuvieron una precisión máxima del 99,22%, y la precisión media del grupo de 32 personas fue "solo" del 98,84%). En octubre de este año, Richard F. Rashid, coordinador de los programas científicos de Microsoft, mostró en una conferencia en Tianjin (República Popular China) tecnología de traducción en vivo del inglés al chino mandarín, conservando la voz original.
Todas esta tecnologías, que demuestran un avance en la esfera de la inteligencia artificial, de una u otra forma se apoyan en la metodología del "aprendizaje profundo". El principal aporte en la teoría del aprendizaje profundo la está llevando a cabo en la actualidad precisamente el profesor Hinton que, a propósito, es tataranieto de George Boole, el científico inglés que inventó el álgebra booleana, que constituye la base de las máquinas calculadoras modernas.
La teoría del aprendizaje profundo completa las tecnologías habituales de aprendizaje de máquinas, mediante algoritmos especiales para el análisis de la información de entrada conforme a varios niveles de representación. La peculiaridad del nuevo enfoque reside en que el "aprendizaje profundo" estudia el objeto mientras no encuentre niveles de representación lo suficientemente informativos para tener en cuenta todos los factores capaces de influir en las características del objeto estudiado.
De esta forma, una red neuronal en base a semejante enfoque necesita menos información de entrada para el aprendizaje, y la red entrenada es capaz de analizar la información con una precisión bastante mayor que las redes neuronales habituales. El propio Hinton y sus colegas anuncian que su tecnología es especialemnete conveniente para la búsqueda de peculiaridades en las matrices de información multidimensionales, bien estructuradas.
La tecnología de inteligencia artificial (IA) en general, y el aprendizaje profundo en particular, se aplican ahora ampliamente en diferentes sistemas, incluyendo el ayudante por voz Apple Siri en base a la tecnología Nuance Communications y el reconocimiento de direcciones en el servicio de Visionado de calles de Google. Así y con todo, los científicos valoran con mucha precaución los éxitos en esta esfera, dado que la historia de la creación de una IA es rica en grandes promesas y fracasos no menos grandes.
Así, en los años 60 del siglo XX, los científicos consideraban que para la creación de una IA plena y completa solo quedaban 10 años. Después, en los años 80, surgió una ola de compañías jóvenes que propusieron una "IA preparada", tras lo cual hubo en esta esfera una auténtica "edad de hielo", hasta la época actual, cuando las grandes posibilidades de cálculo disponibles en los servicios en la nube, han abierto un nuevo nivel para la implementación de potentes redes neuronales que usan una nueva base teórica y algorítmica.
Merece la pena hacer mención aparte al hecho de que las redes neuronales (incluso de tercera generación, tales como las redes convolucionales, los auto-codificadores, las máquinas de Boltzmann) no tienen nada en común con las neuronas biológicas, excepto el nombre.
El nuevo paradigma de aprendizaje implementa la idea de aprendizaje en dos etapas. En la primera etapa, se extrae la infomación sobre la estructura interna de los datos de entrada a partir de una gran matriz de datos no marcados con ayuda de auto-asociadores (mediante el aprendizaje por capas no supervisado). A continuación, usando esta información en una red multicapa, se la entrena de forma supervisada (con datos marcados) con los métodos conocidos. Al mismo tiempo, sería deseable tener la mayor cantidad posible de datos no marcados. La cantidad de datos marcados puede ser mucho menor. Para nuestro caso, no es algo demasiado importante.
2.2. Auto-asociadores. Auto-codificadores y Máquina de Boltzmann restringida. Diferencias y peculiaridades
2.2.1. Auto-codificador
El primer asociador (АА) fue el neocognitrón Fukushima.
Se muestra el esquema en la fig.7.
Fig. 7. Neocognitrón Fukushima
La tarea del Auto-Asociador (АА) es obtener una imagen lo más precisa posible de la entrada.
Se utilizan dos tipos de АА: el generador y el sintetizador. En calidad del primer tipo, se usan las máquinas de Boltzmann restringidas (Restricted Boltzmann Machine, RBM) y en calidad del segundo, los auto-codificadores (АE).
Un auto-codificador es una neurored con una capa abierta, que adoptando un algoritmo de aprendizaje no supervisado y un método de propagación inversa del error, establece un valor meta igual al vector de entrada, es decir, y = x.
Tenemos un ejemplo de auto-codificador en la fig.8.
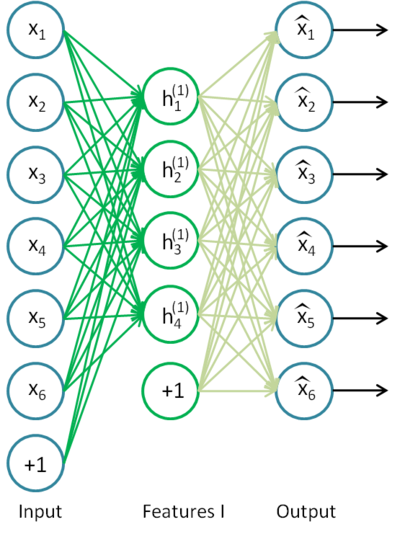
Fig. 8. Esquema estructural de un auto-codificador
El auto-codificador intenta construir la función h(x)=x. En otras palabras, intenta encontrar una aproximación de una función tal, que la respuesta de la red neuronal sea aproximadamente igual al valor de los rasgos de entrada. Para que la solución a esta tarea no sea trivial, la cantidad de neuronas de la capa oculta debe ser menor a la dimensión de los datos de entrada (como en la figura).
Esto permite obtener datos comprimidos al transmitir la señal de entrada a la salida de la red. Por ejemplo, si el vector de entrada constituye un conjunto de niveles de brillo de una imagen de 10х10 píxeles (un total de 100 rasgos), y la cantidad de neuronas de la capa oculta es de 50, la red se verá obligada a aprender la compresión de la imagen. Y es que la exigencia h(x)=x, significa que a partir de los niveles de activación de cincuenta neuronas de la capa oculta, la capa de salida debe restablecer 100 píxeles de la imagen de origen. Una compresión así es posible , si en los datos hay interconexiones ocultas, correlación de rasgos y alguna estructura en general. En esta forma, el funcionamiento del auto-codificador recuerda mucho al método de análisis de los componentes principales (PCA), en el sentido de que se reduce la dimensión de los datos de entrada.
Resulta sorprendente que los experimentos que anunciaron Bengio y otros (2007), demostrasen que al entrenar con un descenso gradiente estocástico, los dispositivos auto-codificadores no lineales con una cantidad de neuronas ocultas superior a las entradas (llamadas super-plenas), tenían representaciones útiles (en el sentido del error de clasificación, medido en la red, que tomó esta representación en la entrada).
Más tarde, con la aprición de idea de la dispersión (sparsity) se hizo más extendido el Auto-codificador disperso (sparse Autoencoder).
Un Auto-codificador Disperso, es un auto-codificador cuya cantidad de neuronas ocultas es bastante superior a la dimensión de la entrada, pero estas tienen una activación dispersa. La activación dispersa es cuando la cantidad de neuronas inactivas en la capa oculta supera significativamente la cantidad de activas. Si describimos la dispersión de manera no formal, podemos considerar que una neurona está activa cuando el valor de su función de transmisión está cercano a 1. Si se usa una función sigmoide de transmisión, entonces para una neurona inactiva su valor deberá ser cercano a 0 (para una función de tangente hiperbólica, a -1).
Existe una variante de dispositivo auto-codificador, llamada Auto-codificador denoising (Vincent y otros, 2008). Se trata del mismo Auto-codificador, pero su entrenamiento es específico. Durante el entrenamiento, en la entrada se dan de forma casual datos "corrompidos" (sustituyen ciertos valores por 0). Además, para comparar con la salida, presentan "no corrompidos". De esta forma, se puede obligar al auto-codificador a restablecer los datos de entrada perjudicados.
2.2.2. Máquina de Boltzmann restringida (Restricted Boltzmann Machine, RBM).
No voy a acentuar la atención sobre la historia de la procedencia de la máquina de Boltzmann restringida (RBM), solo voy a recordar al lector que todo comenzó con las neuroredes recurrentes, que son redes de conexión de retorno, y algunas de las cuales son extramadamente difíciles de entrenar. A causa de esta pequeña dificultad en el entrenamiento, la gente comenzó a inventar modelos recurrentes más limitados, para los que se pudiesen adoptar algoritmos de aprendizaje más sencillos. Uno de estos modelos fue la red neuronal de Hopfield, y él fue quien introdujo el concepto de energía de la red, comparando la dinámica de las neuroredes con la termodinámica.
El siguiente paso hacia la RBM fueron las máquinas de Bolztmann simples, que se distinguen de la red de Hopfield por el hecho de tener una naturaleza estocástica, y las neuronas están divididas en dos grupos, que describen los estados visibles y ocultos (por analogía con los modelos ocultos de Markov). Una máquina de Boltzmann restringida se distingue de la común por la ausencia de conexiones entre las neuronas de una capa.
En la fig. 9 mostramos el esquema estructural de la RBM.
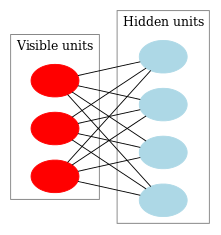
Fig. 9. Esquema estructural de la RBM
La peculiridad de este modelo reside en que con un estado dado de las neuronas de un grupo, los estados de las neuronas de otro grupo serán independientes el uno del otro. Ahora podemos pasar a ver un poquito de teoría, donde precisamente esta propiedad juega un papel clave.
Interpretaciones y objetivo
Las RBM se integran de manera análoga a los modelos ocultos de Markov. Tenemos una serie de estados que podemos observar (neuronas visibles) y una serie de estados que se encuentran ocultos y cuyos estados no podemos ver directamente (neuronas ocultas). Pero podemos hacer una conclusión basada en la probabilidad con respecto a los estados ocultos, basándonos en los estados que podemos observar. Tras entrenar ese modelo, obtenemos también la posibilidad de extraer conclusiones con respecto a los estados visibles, conociendo los ocultos (que siguen el teorema de Bayes). Esto permite genarar datos a partir de esa distribución de probabilidad sobre la que hemos entrenado al modelo.
De esta forma, podemos formular el objetivo del entrenamiento del modelo: es imprescindible configurar los parámetros del modelo de tal forma, que el vector restablecido desde el estado original sea el más cercano al original. Entendemos por restablecido, al vector obtenido mediante una conclusión de probabilidad a partir de los estados ocultos, que a su vez se ha obtenido mediante una conclusión de probabilidad a partir de los estados visibles, es decir, del vector original.
El algoritmo de aprendizaje es la desviación comparativa (divergencia contrastiva) (Contrastive Divergence CD-k)
Este algoritmo fue creado por el profesor Hinton en 2002, y se distingue por su sencillez. La idea principal es que las esperanzas matemáticas son sustituidas por valores totalmente determinados. Se introduce el concepto del proceso de muestreo de Gibbs (Gibbs sampling).
El proceso CD-k tiene el siguiente aspecto:
- El estado de las neuronas visibles se iguala a la imagen de entrada;
- Se infieren las probabilidades de los estados de la capa oculta;
- A cada neurona de la capa oculta se le pone como correspondencia el estado "1", con una probabilidad igual a su estado actual;
- Se infieren las probabilidades de la capa visible en base a la capa oculta;
- Si la iteración actual es menor a k, entonces se retorna al paso 2;
- Se infieren las probabilidades de los estados de la capa oculta;
En las lecciones de Hinton, tiene el aspecto que sigue:
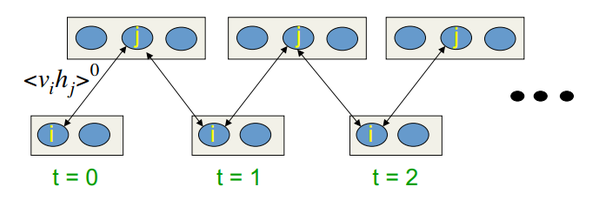
Fig. 10. Algoritmo de aprendizaje CD-k
Es decir, cuanto más tiempo hagamos el muestreo, mayor será la precisión de nuestro gradiente. Al mismo tiempo, el profesor afirma que incluso para CD-1 (solo una iteración del muestreo), el resultado obtenido ya es bueno.
2.3. Redes auto-asociadoras acumulativas (stacked autoassociators network). Auto-codificadores acumulativos (Stackеd Autoencoder SAE), Redes Acumulativas de Boltzmann (Stacked RBM)
Para extraer abstracciones de alto nivel del conjunto de datos de entrada, los auto-asociadores se combinan en una red.
En la fig. 11 se representa el esquema estructural del auto-codificador apilado y de una neurored, que juntos constituyen una neurored Profunda con pesos inicializados mediante un Auto-codificador Apilado ("Deep neural network with weights initialized by Stacked AutoEncoder")
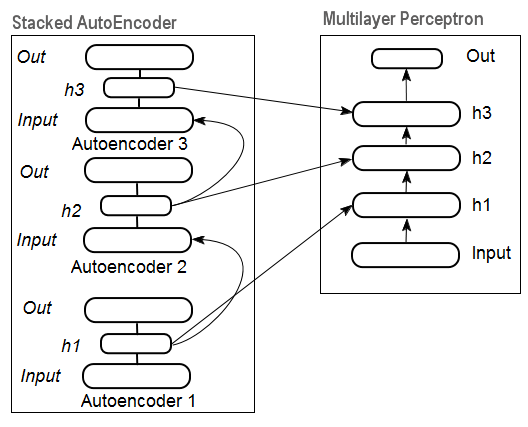
Fig. 11. Esquema estructural de una DN SAE
En la fig.12 se muestra el esquema de una RBM apilada (SRBM) y de una neurored, que juntos constituyen una neurored Profunda con pesos inicializados mediante una SRBM ("Deep neural network with weights initialized by SRBM").
Los esquemas de las redes profundas se representan precisamente de esa forma, subrayando que la información se extrae desde abajo hacia arriba.
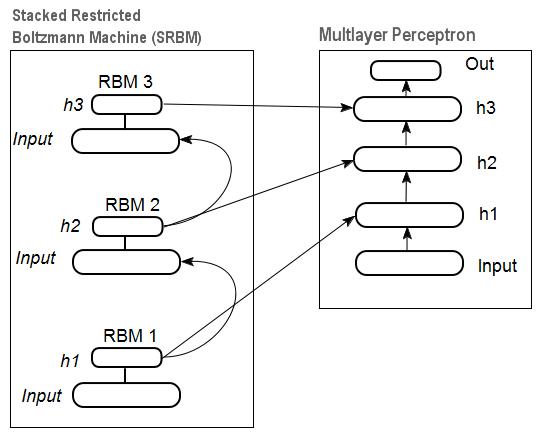
Fig. 12. Esquema estructural de una DN SRBM
2.4. Entrenamiento de las redes profundas (DN). Etapas del aprendizaje. Peculiaridades
El entrenamiento de las redes profundas pasa por dos etapas. En la primera etapa, se entrena por capas sin supervisión en la matriz de datos no marcados a la red auto-asociativa (SAE o SRBM, dependiendo del tipo de DN), después de lo cual, las neuronas de las capas ocultas del MLP ordinario son inicializadas por los pesos de las capas ocultas de la red auto-asociativa obtenidos después del entrenamiento. En la fig. 11 y la fig. 12 se muestra de forma esquemática este proceso de entrenamiento y traspaso. Después de entrenar el primer АЕ/RBM del peso de las neuronas de la capa oculta se convierten en entradas de la segunda, y así sucesivamente. De esta forma, de los datos se extrae información cada vez más generalizada sobre la estructura (línea, contorno, patrón, etcétera).
En la segunda etapa, tiene lugar el ajuste preciso de MLP (aprendizaje supervisado) en el conjunto marcado de datos, mediante métodos bien conocidos. Está prácticamente demostrado que tal inicialización establece los pesos de las neuronas de las capas ocultas de MLP en la zon del mínimo global, y el ulterior ajuste preciso tiene lugar en un breve periodo de tiempo.
Además, para las redes profundas con una cantidad de capas superior a tres, D.Hinton propuso realizar el ajuste preciso también en dos etapas. En la primera, se entrenan solo las dos capas superiores, y solo después se entrena toda la red.
Es imprescindible hacer notar que al entrenar sin supervisión la SRBM da menos resultados estables que el SAE.
Observación. En la literatura ocurre con frecuencia cierta confusión con los términos. Las SRBM son identificadas con las redes de creencia profunda (Deep belief network DBN). A pesar de que las RBM han superados a las DBN, se trata de estructuras cardinalmente distintas. La DBN es una neurored multicapa cuyo peso de las neuronas de las capas ocultas es inicializado de manera casual por patrones binarios.
3. Experimentos prácticos
La implementación de las redes profundas será representada en el lenguaje R.
3.1. Lenguaje R
Un poco de historia. El lenguaje R es un lenguaje de programación (así como un medio para cálculo estadístico y construcción de gráficos), que fue desarrollado en 1996 por los científicos neozelandeses Ross lhaka y Robert Gentleman en la universidad de Auckland.
R es un proyecto GNU, es decir, un software libre cuya filosofía de uso se resume en los siguientes principios, o para ser más exacto, libertades:
- libertad de iniciar el programa con cualquier cometido (libertad 0);
- libertad para estudiar cómo funciona el programa y adaptarlo a las propias necesidades (libertad 1);
- libertad para distribuir copias para ayudar al prójimo (libertad 2);
- libertad para mejorar el programa y hacer de su mejora algo accesible a todos, para beneficio de la comunidad.
Bajo una perspectiva histórica, representa una implementación alternativa al lenguaje de programación S. El último fue desarrollado en la compañía Bell Labs por John Chambers y sus colegas en el año 1976. En la actualidad, R continúa su mejora, gracias a los esfuerzos del "R Development Core Team", del cual es igualmente miembro J.Chambers.
Para repetir los experimentos, será necesario que instale el lenguaje R y Rstudio. Hay información suficiente sobre la instalación y cómo conseguirlo en la red y en las aplicaciones. Si surge alguna pregunta, lo discutiremos de manera adicional en el debate del artículo.
Ventajas del lenguaje R:
- A día de hoy, el lenguaje R, de facto, es el estándar en el cálculo estadístico.
- Continúa su desarrollo y es apoyado por la comunidad científica internacional de las universidades de todo el mundo.
- Dispone de un amplio abanico de paquetes para todos los campos avanzados de análisis de datos (Data mining). Además, desde la aparición de una nueva idea en las publicaciones científicas hasta su implementación en el paquete R transcurren no más de dos semanas.
- Y en último lugar, pero no menos importante, es absolutamente gratuito. Como dijo un famoso desarrollador de sistemas operativos libres: "Los programas con como el sexo: es mejor cuando es gratis".
3.2. Variantes de implementación y tareas solubles
Son posibles dos variantes de implementación práctica.
La primera es el uso de los programas únicos de J.Hinton para Matlab. Para lo que hay que usar el paquete "R.matlab". El paquete proporciona los métodos writeMat() y readMapara la lectura de archivos MAT. Esto da la posibilidad de comunicarse (ejecutar el código, enviar y recibir objetos, etcétera) con Matlab v6 o superior iniciado de manera local o un host remoto en el enclace cliente-servidor. Es posible conocer información más detallada en la descripción del paquete. Este es el camino para aquellos que disponen de Matlab y saben manejarlo bien. Yo no he seguido este camino, pero puedo hablar sobre la posibilidad de unir Matlab y MQL de esa forma.
La segunda, es usar los paquetes del lenguaje R sobre este tema. Este precisamente es el camino que vamos a usar.
Sobre el tema del artículo "neuroredes profundas" conozco tres paquetes:
-
"deepnet" es un paquete sencillo, capaz de implementar el modelo DN SAE y DN SRBM. La longitud del conjunto de datos de entrada en el aprendizaje sin supervisión y con supervisión es la misma. No hay posibilidad de realizar un ajuste preciso en las dos etapas. Se usa para aprender a explorar y poner a prueba los modelos en la etapa inicial.
-
"darh" es un paquete muy amplio y desarrollado de modelado para DN SRBM. Para las DN SAE hay un modelo, pero no he logrado iniciarlo. Este paquete es para aquellos que saben del tema, y permite crear y configurar un modelo de cualquier complejidad. Se ha construido en base a los programas originales de Hinton, en el lenguaje m para Matlab.
-
"H2O" es un paquete muy serio, diseñado para el aprendizaje de modelos de redes profundas (y no solo) en "grandes conjuntos de datos" (>1 Gb) grabados en archivos csv.
En los experimentos sucesivos vamos a usar el paquete "deepnet".
3.3. Preparación de datos para los experimentos (de entrada y meta)
Hoy, en el "Análisis intelectual de datos" (Data mining) ya se ha establecido un determinado orden de trabajo:
- Elección de los datos de origen (estudio, análisis, preparación, valoración). División en conjuntos (muestras) de entrenamiento, de validación y de prueba;
- Entrenamiento de los modelos en la muestra de aprendizaje y elección del modelo o los modelos para la validación;
- Valoración de la calidad del modelo o los modelos sobre la muestra de prueba, y determinación de los parámetros óptimos del modelo o del mejor modelo del paquete, según medidas concretas;
- Puesta en funcionamiento del modelo o los modelos.
El primer punto es el más laborioso, pero también el más importante para el resultado final. Para ser justo, diré que este punto no ha sido aún formalizado, y que, en gran parte, se trata de una forma de arte. Depende mucho de la experiencia del investigador. ¡Pero! Es sencillamente imprescindible obtener valoraciones cuantitavivas del conjunto de entrada para elegir las más importantes. Seleccionar automáticamente las mejores variables para el modelo concreto sería todavía mejor. Así que R nos proporciona un funcional amplio para resolver las tareas en todas estas etapas.
El tema "Datos de origen" no es solo extremadamente importante, sino también muy amplio. Merece un artículo aparte. Dado que la tarea del presente artículo es hablar de la manera más sencilla sobre lo complicado, no vamos a cavar muy hondo, pero prestaremos atención a los momentos importantes.
3.3.1. Datos de origen
Para nuestra tarea de "Clasificación", necesitamos un paquete de variables (de entrada) independientes y una variable meta. Dado que la ventaja básica declarada de las redes profundas es su capacidad de aprender rápidamente en las muestras de entrada de grandes dimensiones, crearemos un conjunto de datos de entrada de 17 predictores (11 indicadores). ZigZag actuará como variable meta. Cargamos en el entorno R los vectores de las cotizaciones Open, High, Low, Close con una profundidad de 4000 barras. Cómo se hace esto lo discutiremos más tarde, durante la escritura del indicador. Ahora mismo no importa. Todos los cálculos siguientes se realizarán en R.
Reunimos en una matriz estos 4 vectores, más el precio medio y la amplitud del cuerpo de la barra. Lo transformamos en una función:
pr.OHLC <- function (o, h, l, c)
{
#Unimos los vectores de las cotizaciones en una matriz, desplegándolos de manera preliminar
#La indexación de los vectores de las series temporales en R comienza a partir de 1.
#La dirección de la indexación comienza desde los antiguos hacia los nuevos.
price <- cbind(Open = rev(o), High = rev(h), Low = rev(l), Close = rev(c))
Med <- (price[, 2] + price[, 3])/2
CO <- price[, 4] - price[, 1]
#añadimos a la matriz Med y CO
price <- cbind(price, Med, CO)
}
Veamos lo que hemos obtenido (estado en el momento 08.10. 14 12:00)
> head(price)
Open High Low Close Med CO
[1,] 1.33848 1.33851 1.33824 1.33844 1.338375 -4e-05
[2,] 1.33843 1.33868 1.33842 1.33851 1.338550 8e-05
[3,] 1.33849 1.33862 1.33846 1.33859 1.338540 1e-04
[4,] 1.33858 1.33861 1.33856 1.33859 1.338585 1e-05
[5,] 1.33862 1.33868 1.33855 1.33855 1.338615 -7e-05
[6,] 1.33853 1.33856 1.33846 1.33855 1.338510 2e-05
3.3.2. Variables (predictores) de entrada
Enumeramos los indicadores. Los indicadores son elegidos sin preferencia alguna, de manera casual, con el objeto de obtener la máxima dimensión de entradas.
El cálculo de todos los indicadores se realiza con el paquete "TTR", en el que se adjuntan numerosos indicadores.
3.3.2.1. Welles Wilder's Directional Movement Index - ADX(HLC, n) - 4 out (Dip, Din,DX, ADX)
Calculamos y vemos qué aspecto tienen en las primeras 200 barras:
> library(TTR)
> adx<-ADX(price, n = 16)
> plot.ts(head(adx, 200))
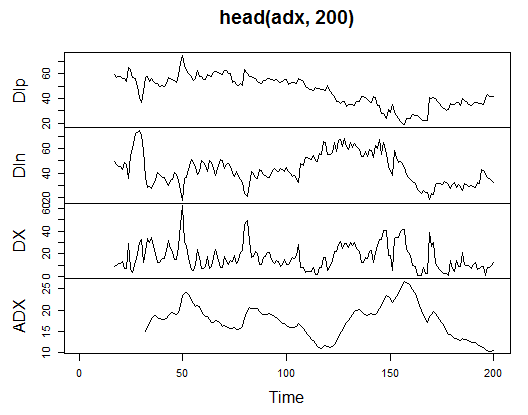
Fig. 13. Indicador Welles Wilder's Directional Movement Index - ADX(HLC, n)
> summary(adx) DIp DIn DX ADX Min. :15.90 Min. : 5.468 Min. : 0.00831 Min. : 5.482 1st Qu.:41.21 1st Qu.: 33.599 1st Qu.: 8.05849 1st Qu.:14.046 Median :47.36 Median : 43.216 Median :16.95423 Median :18.099 Mean :47.14 Mean : 46.170 Mean :19.73032 Mean :19.609 3rd Qu.:53.31 3rd Qu.: 55.315 3rd Qu.:27.97471 3rd Qu.:23.961 Max. :80.12 Max. :199.251 Max. :81.08751 Max. :52.413 NA's :16 NA's :16 NA's :16 NA's :31
Como se puede ver, al incio de la matriz hay 31 valores indeterminados (NA). A continuación, realizaremos los mismos cálculos con todos los indicadores, sin aclaraciones detalladas.
3.3.2.2. aroon(HL, n) - 1 out (oscillator)
Calculamos y miramos las primeras 200 barras de solo una variable - 'oscillator'
> ar<-aroon(price[ , c('High', 'Low')], n = 16)[ ,'oscillator']
> plot(head(ar, 200), t = "l")
> abline(h = 0)
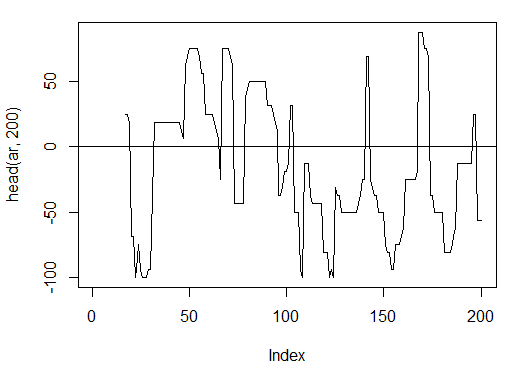
Fig. 14. Indicador aroon(HL, n)
> summary(ar) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -100.00 -56.25 -18.75 -7.67 43.75 100.00 16
3.3.2.3. Commodity Channel Index - CCI(HLC, n) - 1 out
> cci<-CCI(price[ ,2:4], n = 16)
> plot.ts(head(cci, 200))
> abline(h = 0)
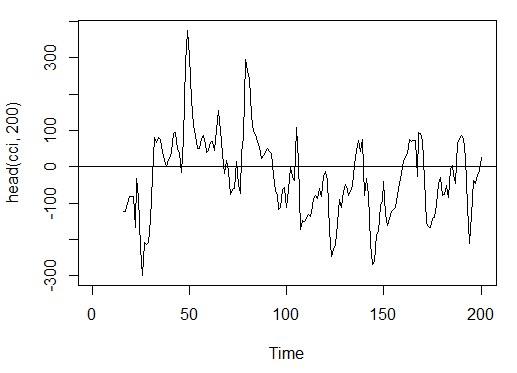
Fig. 15. Indicador Commodity Channel Index - CCI(HLC, n)
> summary(cci) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -469.10 -90.95 -18.74 -14.03 66.91 388.20 15
3.3.2.4. Chaikin Volatility - chaikinVolatility (HLC, n) - 1 out
> chv<-chaikinVolatility(price[ , 2:4], n = 16)
> summary(chv)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-0.67570 -0.29940 0.02085 0.12890 0.41580 5.15700 31
> plot(head(chv, 200), t = "l")
> abline(h = 0)
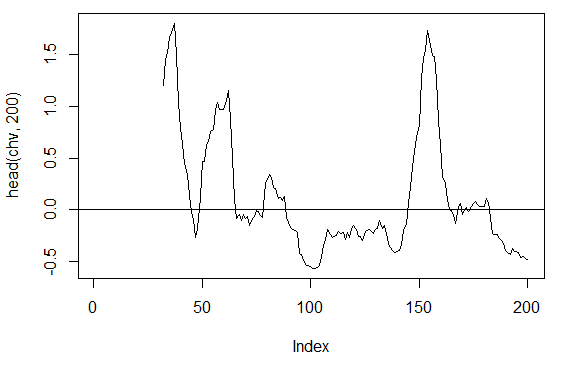
Fig. 16. Indicador chaikinVolatility (HLC, n)
3.3.2.5. Chande Momentum Oscillator - CMO(Med, n) - 1 out
> cmo<-CMO(price[ ,'Med'], n = 16)
> plot(head(cmo, 200), t = "l")
> abline(h = 0)
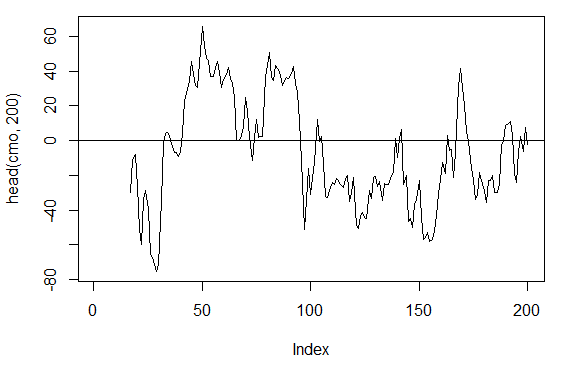
Fig. 17. Indicador Chande Momentum Oscillator - CMO(Med, n)
> summary(cmo) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -97.670 -32.650 -5.400 -6.075 19.530 93.080 16
3.3.2.6. MACD oscillator - MACD(Med, nFast, nSlow, nSig) usaremos solo 1 out (macd)
> macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'] > plot(head(macd, 200), t = "l") > abline(h = 0)
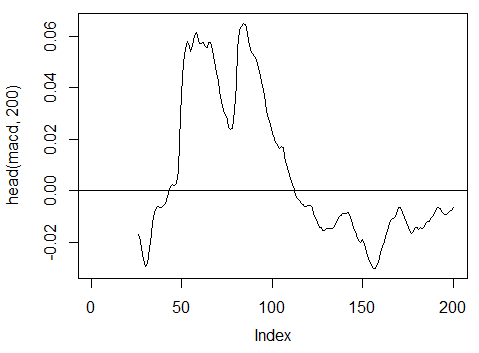
Fig. 18. Indicador MACD oscillator
> summary(macd) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.346900 -0.025150 -0.005716 -0.011370 0.013790 0.088880 25
3.3.2.7. OsMA(Med,nFast, nSlow, nSig) – 1 out
> osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'] > plot(head(osma, 200), t = "l") > abline(h = 0)
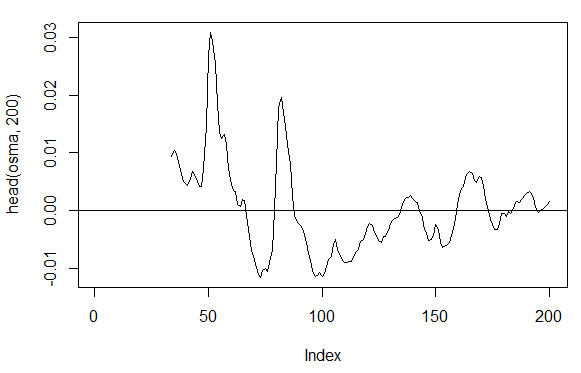
Fig. 19. Indicador OsMA(Med,nFast, nSlow, nSig)
> summary(osma) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.10560 -0.00526 0.00034 0.00007 0.00646 0.05922 33
3.3.2.8. Relative Strength Index - RSI(Med,n) – 1 out
> rsi<-RSI(price[ ,'Med'], n = 16)
> plot(head(rsi, 200), t = "l")
> abline(h = 50)
Fig. 20. Indicador Relative Strength Index - RSI(Med,n)
> summary(rsi) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 5.32 37.33 47.15 46.53 55.71 84.82 16
3.3.2.9. Stochastic Oscillator - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3) - 3 out
> stoh<-stoch(price[ ,2:4], 14, 3, 3) > plot.ts(head(stoh, 200))
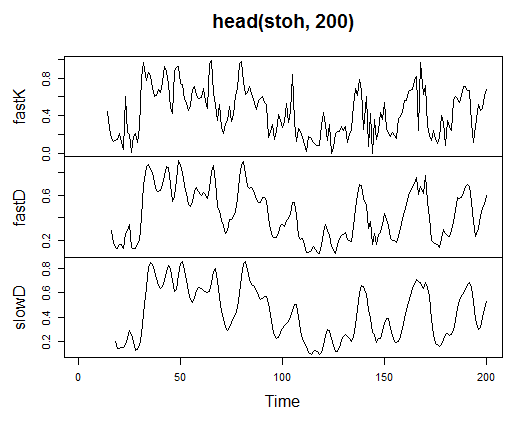
Fig. 21. Indicador Stochastic Oscillator - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
> summary(stoh) fastK fastD slowD Min. :0.0000 Min. :0.01782 Min. :0.02388 1st Qu.:0.2250 1st Qu.:0.23948 1st Qu.:0.24873 Median :0.4450 Median :0.44205 Median :0.44113 Mean :0.4622 Mean :0.46212 Mean :0.46207 3rd Qu.:0.6842 3rd Qu.:0.67088 3rd Qu.:0.66709 Max. :1.0000 Max. :0.99074 Max. :0.97626 NA's :13 NA's :15 NA's :17
3.3.2.10. Stochastic Momentum Index - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9) — 2 out
> smi<-SMI(price[ ,2:4],n = 13, nFast = 2, nSlow = 25, nSig = 9) > plot.ts(head(smi, 200))
Fig. 22. Indicador Stochastic Momentum Index - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
> summary(smi) SMI signal Min. :-82.185 Min. :-78.470 1st Qu.:-33.392 1st Qu.:-31.307 Median : -9.320 Median : -8.839 Mean : -8.942 Mean : -8.985 3rd Qu.: 15.664 3rd Qu.: 14.069 Max. : 71.878 Max. : 63.865 NA's :25 NA's :33
3.3.2.11. Volatility (по Yang and Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)- 1 out
> vol<-volatility(price[ ,1:4],n = 16,calc = "yang.zhang", N =96) > plot.ts(head(vol, 200))
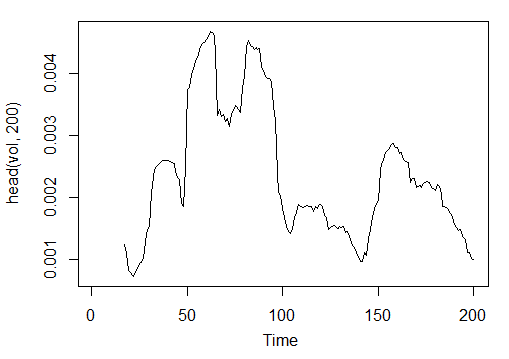
Fig. 23. Indicador Volatility (Yang and Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)
> summary(vol) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 0.000599 0.001858 0.002638 0.003127 0.004015 0.012840 16
Y bien, tenemos 17 variables de 11 indicadores en el símbolo EURUSD, con el marco temporal М15, en la muestra OHLC, con una profundidad de 4000 barras.
Los reunimos en una matriz y grabamos todos los cálculos mostrados más arriba con una función con un parámetro formal р, que necesitaremos al efectuar la optimización.
Calculamos la matriz de las variables de entrada con la ayuda de la fórmula:
In<-function(p = 16){
adx<-ADX(price, n = p);
ar<-aroon(price[ ,c('High', 'Low')], n=p)[ ,'oscillator'];
cci<-CCI(price[ ,2:4], n = p);
chv<-chaikinVolatility(price[ ,2:4], n = p);
cmo<-CMO(price[ ,'Med'], n = p);
macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'];
osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'];
rsi<-RSI(price[ ,'Med'], n = p);
stoh<-stoch(price[ ,2:4],14, 3, 3);
smi<-SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9);
vol<-volatility(price[ ,1:4],n = p,calc="yang.zhang", N=96);
In<-cbind(adx, ar, cci, chv, cmo, macd, osma, rsi, stoh, smi, vol);
return(In)
}
> X<-In()
> tail(X)
DIp DIn DX ADX ar cci chv
[3995,] 46.49620 36.32411 12.28212 18.17544 25.0 168.0407 0.1835102
[3996,] 52.99009 31.61164 25.26952 18.61882 37.5 227.7030 0.3189822
[3997,] 58.11948 28.16241 34.72000 19.62515 37.5 145.2337 0.3448520
[3998,] 56.00323 30.48687 29.50206 20.24245 37.5 118.5831 0.3068059
[3999,] 55.96197 28.78737 32.06467 20.98134 37.5 116.5376 0.3517668
[4000,] 54.97777 26.85440 34.36713 21.81795 62.5 160.0767 0.6169701
cmo macd osma rsi fastK
[3995,] 29.71342 -0.020870825 0.01666593 52.91932 0.8832685
[3996,] 41.89526 -0.009654368 0.02230591 61.49793 0.8833819
[3997,] 30.98237 -0.002051532 0.02392699 58.94513 0.7259475
[3998,] 33.84813 0.003454534 0.02354645 58.00549 0.7930029
[3999,] 38.84892 0.009590136 0.02374564 60.63806 0.8367347
[4000,] 54.71698 0.019303110 0.02676689 66.64815 0.9354120
fastD slowD SMI signal vol
[3995,] 0.7773581 0.7735064 -35.095406 -47.27712 0.003643196
[3996,] 0.7691688 0.7761507 -26.482951 -43.11828 0.003858942
[3997,] 0.8308660 0.7924643 -19.699762 -38.43458 0.003920541
[3998,] 0.8007775 0.8002707 -13.141932 -33.37605 0.003916109
[3999,] 0.7852284 0.8056239 -6.569699 -28.01478 0.003999789
[4000,] 0.8550499 0.8136852 2.197810 -21.97226 0.004293766
Ya tenemos los datos de entrada sin procesar.
3.3.3. Datos de salida (meta)
Vamos a pasar a la formación de los (datos meta) de salida. Como ya hemos dicho más arriba, vamos a aplicar ZigZag.
Tomamos ZigZag con una amplitud de canal de 37 puntos grandes. ZigZag lo calcularemos según el precio medio. También se puede calcular el indicador según los precios HL, pero según el precio medio es menos "inestable". A continuación, extraemos la señal (0 - Buy, 1 -Sell) y la convertimos en una matriz de entrada, que adopta el modelo de la red.
Escribimos la función:
Out<-function(ch=0.0037){ # Zigzag tiene un valor (determinado) en cada barra, y no solo en los picos zz<-ZigZag(price[ ,'Med'], change = ch, percent = F, retrace = F, lastExtreme = T); n<-1:length(zz); # En las últimas barras, sustituimos los valores no determinados por los últimos conocidos for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1];} #Determinamos la velocidad de cambio de Zigzag y desplazamos una barra hacia el futuro dz<-c(diff(zz), NA); #Si la velocidad >0 - la señal = 0(Buy), si <0, la señal = 1 (Sell) de otra forma NA sig<-ifelse(dz>0, 0, ifelse(dz<0, 1, NA)); return(sig); }
Calculamos las señales.
> Y<-Out() > table(Y) Y 0 1 1567 2423
La correlación de clases está desequilibrada. La cantidad de ejemplos de una clase es bastante superior a la cantidad de ejemplos de la otra. Todos los modelos de clasificación se comportan con este tipo de paquetes de manera poco amistosa.
Al separar en muestras de entrenamiento y de prueba, adoptaremos medidas para solucionar esta situación.
3.3.4. Despejar datos
Despejamos nuestros conjuntos de datos de aquellos datos que no estén determinados. En nuestro caso, entendemos despejar como un grupo de tareas bastante más amplio. Se trata tanto de eliminar "variables virtualmente iguales a cero", como de eliminar otras fuertemente correlacionadas, así como otras tareas que en nuestro caso no realizaremos.
Escribimos nuestra función y limpiamos nuestros datos
Clearing<-function(x, y){
dt<-cbind(x,y);
n<-ncol(dt)
dt<-na.omit(dt)
return(dt);
}
> dt<-Clearing(X,Y); nrow(dt)
[1] 3957
La matriz se ha hecho 43 barras más corta.
3.3.5. Formación de muestras de entrenamiento y prueba
Existen varios métodos de división de los datos de origen en muestras de entrenamiento y de prueba. Aplicaremos la división casual común de datos de origen en train y test, con una correlación de 8/10. No olvidemos que las muestras deben estar estratificadas, es decir, la correlación de la cantidad de ejemplos de las clases en train y test deberá corresponder a la correlación de las clases en el conjunto de origen. Además, no estaría mal corregir la desigualdad de las clases en el conjunto de origen. Esto se puede hacer de dos formas, igualando o bien hacia la clase mayor, o bien hacia la clase menor. Dado que es mejor tener más ejemplos, igualamos hacia la clase mayor "1". Vamos a necesitar el paquete "caret".
Formulamos un nuevo conjunto de datos equilibrado, en el que las cantidades de ejemplos de las clases serán las mismas y serán iguales al mayor.
3.3.6. Balance de clases
Escribiremos una función que iguale la cantidad de clases en la muestra hacia el lado mayor (si la desviación es superior al 15%) y que retornará una matriz equilibrada
Balancing<-function(DT){
#Calculamos un recuadro con la cantidad de clases
cl<-table(DT[ ,ncol(DT)]);
#Si el desequilirio es menor al 15%, retornamos la matriz de origen
if(max(cl)/min(cl)<= 1.15) return(DT)
#De otra forma, equilibramos hacia el lado mayor
DT<-if(max(cl)/min(cl)> 1.15){
upSample(x = DT[ ,-ncol(DT)],y = as.factor(DT[ , ncol(DT)]), yname = "Y")
}
#Transformamos y (el factor) en un número
DT$Y<-as.numeric(DT$Y)
#Recodificamos y de 1,2 a 0,1
DT$Y<-ifelse(DT$Y == 1, 0, 1)
#Transformamos la trama de datos en una matriz
DT<-as.matrix(DT)
return(DT);
}
Aclaración breve. En la primera línea, calculamos la cantidad de ejemplos de cada clase (el vector, cuya dimensión es igual a la cantidad de clases).
Encontramos la relación del mayor con respecto al menor, y si es menor al umbral establecido, salimos. Si es superior, calculamos la función, dando por separado la x y la y, que hemos transformado previamente en un factor.
Estas son las exigencias para los parámetros formales de la función upSample(). Dado que no necesitamos la variable meta en forma de factor, la transformamos de nuevo a una cifra con los valores 0 y 1. ¡Preste atención! Al transformar la variable numérica (0,1) en un factor, obtemos una variable de texto de "0" y "1". Pero al realizar el proceso inverso a variable numérica, obtenemos 1 y 2 (!). Así que las sustituimos por 0 y 1. Con la última línea transformamos nuestro conjunto de datos de la clase "trama de datos" a la clase "matriz". La calculamos:
dt.b<-Balancing(dt) x<-dt.b[ ,-ncol(dt.b)] y<-dt.b[ , ncol(dt.b)]
De esta forma, ya tenemos listo el conjunto de datos de origen dt (de entrada y salida) y el conjunto dt.b equilibrado.
Dividimos en muestras train/test
Con ayuda de la función holdout() del paquete "rminer" obtemos los índices de las muestras de entrenamiento y prueba
> library('rminer')
> t<-holdout(y, ratio = 8/10, mode = "random")
El objeto t, es una lista que contiene los índices de los conjuntos de entrenamiento (t$tr) y prueba (t$ts). Los conjuntos obtenidos están estratificados.
3.3.7. Preprocesado
En nuestro conjunto de datos de entrada se encuentran variables con los diapasones de amplitudes más diversos. Hay que recordar que las redes profundas, en esencia, son simplemente neuroredes con un método especial de inicialización de pesos.
Las neuroredes, en la entrada, pueden adoptar variables en el diapasón (-1; 1) o (0, 1). Normalizamos las variables de entrada en el diapasón [-1, 1].
Usamos la función preProcess() del paquete "caret". Hay que prestar atención a que los parámetros del preprocesado deben ser calculados sobre el conjunto de entrenamiento, y además hay que guardarlos para el posterior preprocesado del conjunto de prueba y de los datos que lleguen de nuevo.
> spSign<-preProcess(x[t$tr, ], method = "spatialSign") > x.tr<-predict(spSign, x[t$tr, ]) > x.ts<-predict(spSign, x[t$ts, ])
Ya tenemos todo listo para la construcción, entrenamiento y testado del modelo de la red profunda.
3.4. Construcción, entrenamiento y testado de modelos
Vamos a construir y entrenar un modelo DN SAE. Fórmula del modelo y descripción de las variables:
sae.dnn.train(x, y, hidden = c(10), activationfun = "sigm", learningrate = 0.8, momentum = 0.5, learningrate_scale = 1, output = "sigm", sae_output = "linear", numepochs = 3, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)
donde:
- х es la matriz de datos de entrada;
- y es el vector o matriz de variables meta;
- hidden es el vector con el número de neuronas en cada capa oculta. Por defecto c(10);
- activationfun es la función de activación de las nueronas ocultas. Puede ser "sigm", "linear", "tanh". Por defecto "sigm";
- learningrate es el nivel de entrenamiento para el descenso de gradiente. Por defecto = 0.8;
- momentum es el momento para el descenso de gradiente. Por defecto = 0.5;
- learningrate_scale el nivel de entrenamiento puede ser multiplicado por esta magnitud después de cada iteración. Por defecto =1.0;
- numepochs es el número de iteraciones para el entrenamiento. Por defecto =3;
- batchsize es el tamaño de las pequeñas porciones con las que se realiza el entrenamiento. Por defecto =100;
- output es la función de activación para las neuronas de salida, puede ser "sigm", "linear", "softmax". Por defecto "sigm";
- sae_output es la función de activación para las neuronas de salida de SAE, puede ser "sigm", "linear", "softmax". Por defecto "linear";
- hidden_dropout es la parte eliminable para las capas ocultas. Por defecto =0;
- visible_dropout es la parte eliminable de la capa visible (de entrada). Por defecto =0.
Creamos un modelo con un tamaño (17, 100, 100, 100, 1), lo entrenamos, midiendo el tiempo de entrenamiento, y observamos la medida de las previsiones.
> system.time(SAE<-sae.dnn.train(x= x.tr, y= y[t$tr], hidden=c(100,100,100), activationfun = "tanh", learningrate = 0.6, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 10, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. user system elapsed 12.92 0.00 13.09
Como podemos ver, el entrenamiento pasa por dos etapas. Al principio se entrenan los AE por capas, después de lo cual, se entrena la neurored propiamente dicha.
Tanto la gran cantidad de periodos de entrenamiento, como el enorme número de neuronas ocultas en las tres capas han sido establecidos ha propósito. ¡El proceso completo ha ocupado algo más de 13 segundos!
Miremos en las previsiones del conjunto de prueba de predictores.
> pr.sae<-nn.predict(SAE, x.ts); > summary(pr.sae) V1 Min. :0.2649 1st Qu.:0.2649 Median :0.5881 Mean :0.5116 3rd Qu.:0.7410 Max. :0.7410
Transformamos en los niveles 0,1 y calculamos las medidas
> pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) > confusionMatrix(y[t$ts], pr) Confusion Matrix and Statistics Reference Prediction 0 1 0 316 128 1 134 378 Accuracy : 0.7259 95% CI : (0.6965, 0.754) No Information Rate : 0.5293 P-Value [Acc > NIR] : <2e-16 Kappa : 0.4496 Mcnemar's Test P-Value : 0.7574 Sensitivity : 0.7022 Specificity : 0.7470 Pos Pred Value : 0.7117 Neg Pred Value : 0.7383 Prevalence : 0.4707 Detection Rate : 0.3305 Detection Prevalence : 0.4644 Balanced Accuracy : 0.7246 'Positive' Class : 0
El coeficiente no es espectacular. Pero para nosotros es importante, no el coeficiente, sino el beneficio que obtenemos con estas señales. Comprobamos esto en las últimas 500 barras (una semana, aproximadamente). Obtemos las señales de las últimas 500 barras secuenciales de nuestra red entrenada.
Normalizamos los últimos 500 datos de entrada, obtenemos las previsiones de la nuerored entrenada y las convertimos en señales -1= (Sell) y 1 = (Buy)
> new.x<-predict(spSign,tail(dt[ ,-ncol(dt)], 500)) > pr.sae1<-nn.predict(SAE, new.x) > pr.sig<-ifelse(pr.sae1>mean(pr.sae1), -1, 1) > table(pr.sig) pr.sig -1 1 235 265 > new.y<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) > table(new.y) new.y -1 1 201 299 > cm1<-confusionMatrix(new.y, pr.sig) > cm1 Confusion Matrix and Statistics Reference Prediction -1 1 -1 160 41 1 75 224 Accuracy : 0.768 95% CI : (0.7285, 0.8043) No Information Rate : 0.53 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.5305 Mcnemar's Test P-Value : 0.002184 Sensitivity : 0.6809 Specificity : 0.8453 Pos Pred Value : 0.7960 Neg Pred Value : 0.7492 Prevalence : 0.4700 Detection Rate : 0.3200 Detection Prevalence : 0.4020 Balanced Accuracy : 0.7631 'Positive' Class : -1
¡El coeficiente Accuracy no está mal! Pero, una vez más, lo que a nosotros nos interesa no es el coeficiente, sino el beneficio.
Ponemos a prueba el beneficio paras las últimas 500 barras con nuestras señales pronosticadas y obtenemos la curva de balance:
> bal<-cumsum(tail(price[ , 'CO'], 500) * pr.sig) > plot(bal, t = "l") > abline(h = 0)
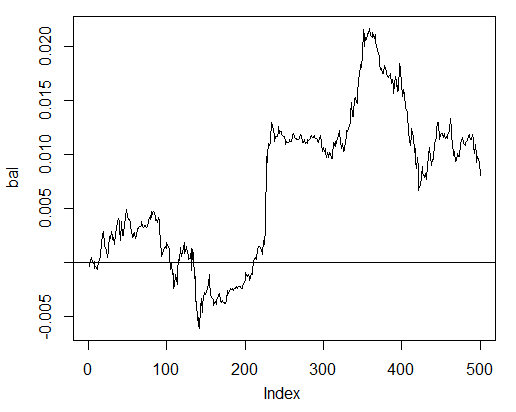
Fig. 24. Balance para las últimas 500 barras según las señales de la neurored
El balance ha sido calculado sin tener en cuenta el spread, el deslizamiento y demás encantos del mercado real.
Lo comparamos con el balance que se obtendría según las señales ideales de ZZ. La línea roja es el balance según las señales de la neurored:
> bal.zz<-cumsum(tail(price[ , 'CO'], 500) * new.y) > plot(bal.zz, t = "l") > lines(bal, col = 2)
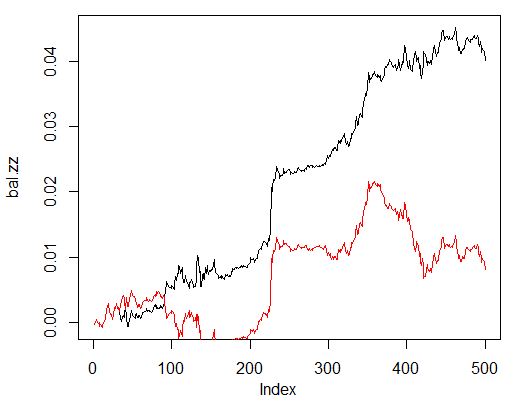
Fig. 25. Balance para las últimas 500 barras según las señales de la neurored y las señales de Zigzag
Hay potencial para mejorar.
Para facilitar el testado, escribiremos dos funciones auxiliares, Estimation() y Testing(). La primera proporcionará los coeficientes (Accuracy/Err), y la segunda, el balance (Bal/BalZZ).
Esto permitirá (cambiando algunos parámetros de la red) obtener directamente un resultado, y ver qué parámetros y cómo influyen en la calidad de la red obtenida.
En lo sucesivo, tras escribir una función fitness, se podrán encontrar los parámetros óptimos de la red con la ayuda de algoritmos evolutivos (genéticos), sin interrumpir el proceso de comercio. En este artículo no vamos a ocuparnos de ello, puede ser que lo hagamos en el siguiente.
Aquí tenemos la función Estimation(), que calcula los coeficientes (Err/Accuracy):
Estimation<-function(X, Y, r = 8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs = 50, CM=F){ #Índices de los conjuntos de entrenamiento y prueba t<-holdout(Y, ratio = r, mode = m) #Parámetros de preprocesado prepr<-preProcess(X[t$tr, ], method = norm) #Dividimos en conjuntos train y test con preprocesado x.tr<-predict(prepr, X[t$tr, ]) x.ts<-predict(prepr, X[t$ts, ]) y.tr<- Y[t$tr]; y.ts<- Y[t$ts] #Entrenamos el modelo SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) #Obtenemos la previsión para el conjunto de prueba pr.sae<-nn.predict(SAE, x.ts) #La recodificamos en señales 1,0 pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) #Calculamos el coeficiente Accuracy o el error de clasificación if(CM) err<-unname(confusionMatrix(y.ts, pr)$overall[1]) if(!CM) err<-nn.test(SAE, x.ts, y.ts, mean(pr.sae)) return(err) }
Parámetros formales:
- X – matriz de predictores de entrada crudos;
- Y – vector de la variable meta;
- r – correlación train/test;
- m – régimen de formación de muestras (casual o consecutivo);
- norm – régimen de normalización de las variables de entrada ([ -1, 1]= "spatialSign";[0, 1]="range");
- h – vector con la cantidad de neuronas en las capas ocultas;
- act – función de activación de las neuronas ocultas;
- LR – nivel de entrenamiento;
- Мом — momento;
- out – función de activación de la capa de salida;
- sae – función de activación del auto-codificador;
- Ep – cantidad de épocas de entrenamiento;
- Bs – tamaño de las mini muestras;
- СM– booleana , si TRUE se genera Accuracy. de otra forma Err.
Por ejemplo, calculamos el error de clasificación sobre el conjunto desequilibrado dt con una red con tres capas ocultas y 30 neuronas en cada una de ellas:
> Err<-Estimation(X = dt[ ,-ncol(dt)], Y = dt[ ,ncol(dt)], h=c(30, 30, 30), LR= 0.7) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > Err [1] 0.1376263
La siguiente función Testing() calcula el balance según las señales pronosticadas o según las ideales (ZigZag):
Testing<-function(dt1, dt2, r=8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs=50, pr = T, bar = 500){ X<-dt1[ ,-ncol(dt1)] Y<-dt1[ ,ncol(dt1)] t<-holdout(Y, ratio = r, mode = m) prepr<-preProcess(X[t$tr, ], method = norm) x.tr<-predict(prepr, X[t$tr, ]) y.tr<- Y[t$tr]; SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) X<-dt2[ ,-ncol(dt2)] Y<-dt2[ ,ncol(dt2)] x.ts<-predict(prepr, tail(X, bar)) y.ts<-tail(Y, bar) pr.sae<-nn.predict(SAE, x.ts) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1) sig.zz<-ifelse(y.ts == 0, 1,-1 ) bal<-cumsum(tail(price[ ,'CO'], bar) * sig) bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz) if(pr) return(bal) if(!pr) return(bal.zz) }
Parámetros formales:
- dt1 – matriz de variables de entrada y meta sobre la que se realiza el entrenamiento de la red;
- dt2 - matriz de variables de entrada y meta sobre la que se realiza el testado de la red entrenada;
- pr – booleana, si TRUE generamos el balance según las señalas predichas, de otra forma, según ZigZag;
- bar -número de últimas barras a usar para el cálculo del balance.
Por ejemplo, calculamos el balance sobre las últimas 500 barras de nuestro conjunto dt al entrenar sobre el conjunto equilibrado dt.b con la neurored, con los mismos parámetros que más arriba:
> Bal<-Testing(dt.b, dt, h=c(30, 30, 30), LR= 0.7) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > plot(Bal, t = "l") > abline(h = 0)
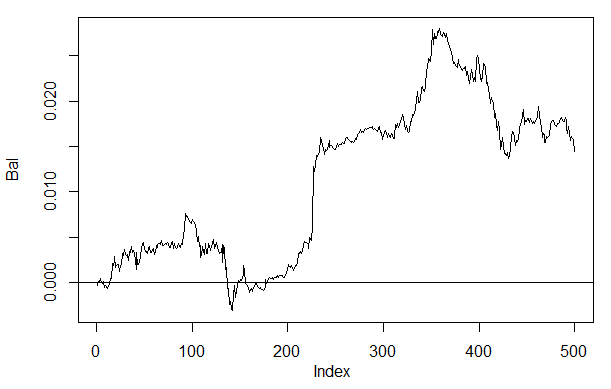
Fig. 26. Balance en las últimas 500 barras según las señales de la neurored h(30,30,30)
Si lo comparamos con el balance obtenido, entonces notaremos mejoras significativas. No obstante, es interesante otra cosa.
Si miramos el gráfico de precios en estas últimas 500 barras, entonces veremos qué segmentos han gustado más a nuestra neurored (150-350 barras).
> plot(tail(price[ ,'Close'], 500), t = "l") > abline(v = c(150,350), col=2)
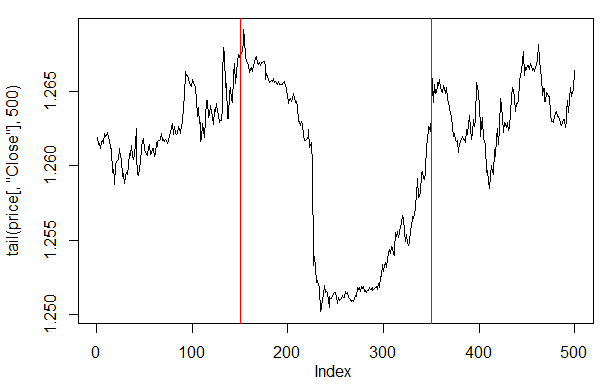
Fig. 27. Gráfico del precio Close en las últimas 500 barras
Observación: Al descodificar las salidas pronosticadas, hemos adoptado una variante simplificada mayor/menor que la media. Aunque se pueden adoptar otras variantes.
Por ejemplo, mayor a 0.6 o menor a 0.4 (se corta el segmento inestable 0.4-0.6). Se pueden obtener límites aún más precisos de las clases al realizar el calibrado. Sobre esto hablaremos más tarde.
Vamos a cambiar un poco nuestra función Testing(), introduciendo el parámetro adicional dec, que permite elegir la variante de descodificación ("mean" o "60/40"), y comprobaremos en aquellos mismos valores predichos cómo va a influir esto en el balance.
Testing.1<-function(dt1, dt2, r = 8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs = 50, pr = T, bar = 500, dec=1){ X<-dt1[ ,-ncol(dt1)] Y<-dt1[ ,ncol(dt1)] t<-holdout(Y, ratio = r, mode = m) prepr<-preProcess(X[t$tr, ], method = norm) x.tr<-predict(prepr, X[t$tr, ]) y.tr<- Y[t$tr]; SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) X<-dt2[ ,-ncol(dt2)] Y<-dt2[ ,ncol(dt2)] x.ts<-predict(prepr, tail(X, bar)) y.ts<-tail(Y, bar) pr.sae<-nn.predict(SAE, x.ts) #Variante +/- mean if(dec == 1) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1) #Variante 60/40 if(dec == 2) sig<-ifelse(pr.sae>0.6, -1, ifelse(pr.sae<0.4, 1, 0)) sig.zz<-ifelse(y.ts == 0, 1,-1 ) bal<-cumsum(tail(price[ ,'CO'], bar) * sig) bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz) if(pr) return(bal) if(!pr) return(bal.zz) }
Calculamos y miramos el balance con la primera y la segunda variante de descodificación.
Para repetir los resultados, antes de cada inicio de la función, establecemos el generador de números pseudoaleatorios en el mismo valor.
> set.seed<-1245 > Bal1<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 1) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > set.seed<-1245 > Bal2<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > plot(Bal2, t = "l") > lines(Bal1, col = 2)
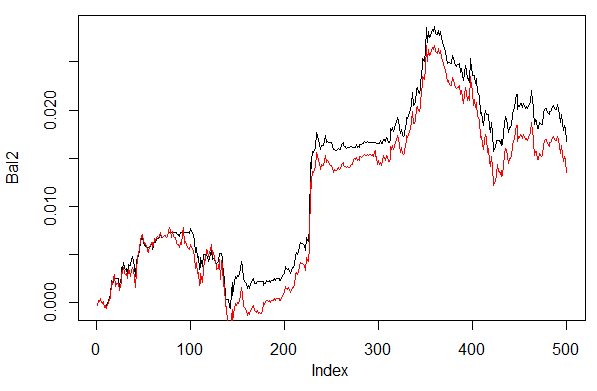
Fig. 28. Balance en las últimas 500 barras según las señales de la neurored con diferentes métodos de descodificación de las predicciones
Como podemos ver, el balance según la segunda variante 60/40 tiene mejor aspecto. Así que tiene sentido buscar caminos para mejorar los resultados también en esta dirección.
Y en último lugar. La teoría dice que un conjunto de varias neuroredes da resultados mejores y más estables. Vamos a poner a prueba un conjunto de varias neuroredes, que serán entrenadas con las mismas muestras (aunque nada nos impide entrenarlas con muestras independientes). El resultado de las predicciones del conjunto lo determinaremos como la media simple de las predicciones de todas las redes. Existen también otros métodos de promediación más refinados.
Vamos a mejorar nuestra función Testing(), añadiéndole otro parámetro más — ans=1, que indica la cantidad de redes en el grupo.
3.4.1. Cálculos paralelos
Teniendo en cuenta que los cálculos de varios modelos independientes pueden ir bien en paralelo, aprovecharemos la posibilidad proporcionada por el lenguaje R, y crearemos para el cálculo un agrupamiento de varios núcleos de nuestro procesador, o de computadoras de la red local (si dispone de varias computadoras), independientemente de qué sistema operativo tengan dichas computadoras.
Para ello, necesitaremos el magnífico paquete "foreach" y el paquete "doParallel". Escribiremos una función sencilla, que se encargará de iniciar el agrupamiento en todos los núcleos de nuestro procesador.
library(doParallel) library(foreach) puskCluster<-function(){ cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) clusterSetRNGStream(cl) return(cl) }
Unas cuantas aclaraciones. En las dos primeras líneas cargamos las bibliotecas imprescindibles (deberán ser previamente instaladas en su computadora). Después determinamos cuántos núcleos tiene el procesador, creamos un agrupamiento, registramos el paquete para los cálculos paralelos, establecemos en cada flujo de cálculos un generador independiente de números aleatorios (GPAN) y retornamos el handle del agrupamiento. En general, el tema de la calidad del GPAN en los cálculos de los diferentes modelos es extremadamente importante. Pero se trata de un tema aparte.
Y bien, después de iniciar el agrupamiento y de haber realizado los cáluclos necesarios, no debemos olvidarnos de detenerlo:
cl<-puskCluster() stopCluster(cl)
Los cálculos paralelos los realizaremos según la siguiente fórmula del paquete "foreach":
SAE<-foreach(times(ans), .packages = "deepnet") %dopar% sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs)
donde times(ans) es la cantidad de redes que queremos obtener, y .packages indica de qué paquete tomar la función calculada.
El resultado, en forma de lista, contendrá la cantidad que necesitamos de redes entrenadas.
Acto seguido, necesitamos obtener las previsiones de cada neurored, y calcular la media.
pr.sae<-(foreach(i = 1:ans, .combine = "+") %do% nn.predict(SAE[[i]], x.ts))/ans
Unas cuantas aclaraciones, el vector i es el de los índices de las neuroredes entrenadas,.combine="+" muestra en qué forma retornar las predicciones calculadas sobre todas las reuroredes. En nuestro caso, hemos pedido retornar la suma y realizamos estos cálculos de forma secuencial, y no paralela (operador %do%). Después de esto, hemos dividido la suma por la cantidad de neuroredes, obteniendo el resultado final. Sencillo y elegante.
Calculamos el balance obtenido con el uso de los grupos de 3 y 4 neuroredes, con los mismos parámetros que en los cálculos anteriores y con la descodificación 60/40. Comparamos con los resultados en una neurored. Para determinar la efectividad de los cálculos paralelos, aumentamos la cantidad de épocas hasta 300, y medimos el tiempo de ejecución del pronóstico.
1. Una neurored:
> system.time(Bal21<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000057 ####loss on step 20000 is : 0.000043 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000081 ####loss on step 20000 is : 0.000086 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000072 ####loss on step 20000 is : 0.000066 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.069451 ####loss on step 20000 is : 0.079629 deep nn has been trained. user system elapsed 115.78 0.00 116.96 > plot(Bal21, t = "l") > abline(h = 0)
2. Grupo de 3 neuroredes:
> system.time(Bal41<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=3)) user system elapsed 0.22 0.06 233.64 > lines(Bal41, col=4)
3. Grupo de 4 neuroredes:
> system.time(Bal44<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=4)) user system elapsed 0.13 0.03 247.86 > lines(Bal44, col=2)
Como podemos ver, el tiempo de ejecución con los cálculos paralelos es óptimo, si la cantidad de flujos es un múltiplo de la cantidad de núcleos. Yo he implicado 2 núcleos.
Y en lo que respecta al balance, pues no hay prácticamente ninguna ventaja. En el gráfico de abajo, el azul denota 3 redes, el rojo, 4 redes, y el negro, una red.
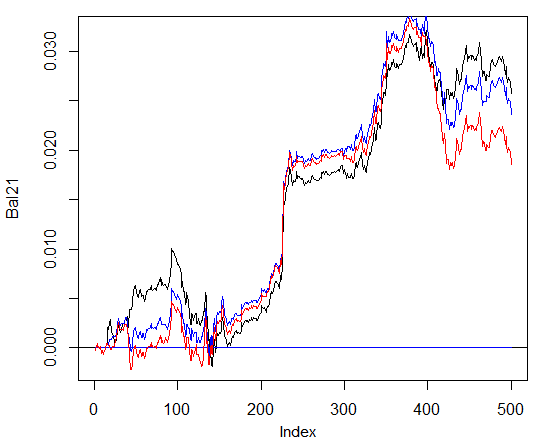
Fig. 29. Balance para las últimas 500 barras según las señales de un agrupamiento que consta de 3 y 4 neuroredes y una neurored
En general, el resultado depende de muchos parámetros, comenzando por los datos de entrada y salida, su método de normalización, la cantidad de capas ocultas y la cantidad de neuronas en estas capas, del nivel de entrenamiento, la cantidad de épocas de entrenamiento y muchos, muchos otros factores.
Los últimos tres ejemplos. Calculamos el balance en las últimas 1000 barras con tres neuroredes con diferente cantidad de neuronas ocultas en tres capas ocultas.
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000054 ####loss on step 20000 is : 0.000044 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000078 ####loss on step 20000 is : 0.000079 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000090 ####loss on step 20000 is : 0.000072 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.072633 ####loss on step 20000 is : 0.057917 deep nn has been trained. user system elapsed 116.09 0.02 116.26 > max(Bal0) [1] 0.04725 > plot(Bal0, t="l") > tail(Bal0,1) [1] 0.03514
Beneficio máximo 472 puntos, en la última barra 351 p. En el gráfico se muestra en color negro.
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(13, 8, 5), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.005217 ####loss on step 20000 is : 0.004846 training layer 2 autoencoder ... ####loss on step 10000 is : 0.051324 ####loss on step 20000 is : 0.046230 training layer 3 autoencoder ... ####loss on step 10000 is : 0.023292 ####loss on step 20000 is : 0.026113 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.057788 ####loss on step 20000 is : 0.056932 deep nn has been trained. user system elapsed 64.04 0.01 64.24 Warning message: In sae$encoder[[i - 1]]$W[[1]] %*% t(train_x) + sae$encoder[[i - : longer object length is not a multiple of shorter object length > lines(Bal0, col="blue")
Una variante claramente poco efectiva.
Y la tercera variante:
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000018 ####loss on step 20000 is : 0.000013 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000062 ####loss on step 20000 is : 0.000048 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000053 ####loss on step 20000 is : 0.000055 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.096490 ####loss on step 20000 is : 0.084860 deep nn has been trained. user system elapsed 186.18 0.00 186.39 > lines(Bal0, col="red") > max(Bal0) [1] 0.0543
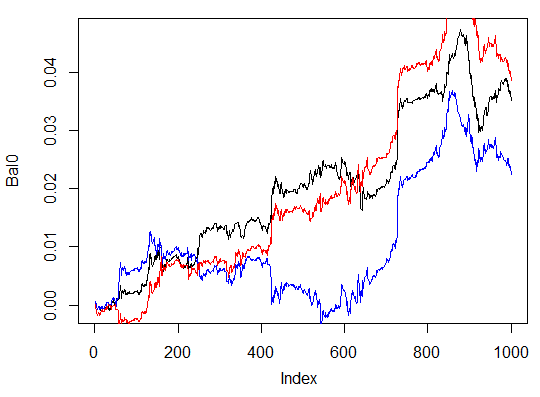
Fig. 30. Balance para las últimas 1000 barras según las señales de tres neuroredes con diferente cantidad de neuronas ocultas
Como podemos ver, la última variante es la mejor de las tres, el beneficio máximo es de 543 puntos(!). Hemos cambiado (del techo) solo la cantidad de neuronas ocultas, y ya tenemos una mejora significativa. Por eso, la búsqueda de parámetros óptimos se debe realizar con la ayuda de algoritmos evolutivos. Queda a la discreción del lector estudiar estas variantes por sí mismo.
Además, no debemos olvidar que en este paquete no ha sido implementado por completo el algoritmo del autor.
4. Implementación del programa (indicador y experto)
Vamos a pasar a la implementación de programa de un indicador y un experto que usan una red profunda para obtener señales comerciales.
Es posible la implementación en dos variantes:
- Primera. Todo el trabajo de entrenamiento de la neurored lo realizamos en Rstudio manualmente. Después de obtener resultados aceptables, guardamos la neurored en el catálogo correspondiente. Después iniciamos el experto y el indicador en el gráfico. El experto carga la red habitual. El indicador prepara el vector de nuevos datos de entrada en cada nueva barra y los transmite al experto. El experto presenta los datos de la neurored, recibe la señal y a continuación la ejecuta. El experto se ocupa de sus obligaciones habituales (abrir, cerrar órdenes, trailing, etcétera). La tarea del indicador es preparar y transmitir al experto los nuevos datos de entrada en cada barra nueva y, lo que es más importante, presentar en el gráfico las señales obtenidas de la neurored durante el pronóstico. El control visual, como ha demostrado la práctica, es el método más efectivo de valoración del funcionamiento de la red.
- Segunda. Iniciamos en el gráfico el experto y el indicador. En el primer inicio, el indicador transmite al experto un gran conjunto de datos de entrada y salida ya preparados. El experto inicia el entrenamiento, el testado y la elección de la mejor neurored. Después, el funcionamiento continúa según la primera variante.
Construimos la conexión indicador-experto según la primara variante. Un experto con el mínimo de "florituras".
¿Por qué de una forma tan complicada? Esta variante de ejecución da la posibilidad de conectar a un experto varios indicadores ubicados en varios símbolos/marcos temporales y trabajar con ellos de manera consecuente. Para ello, es necesario efectuar una pequeña modernización del experto. Pero sobre esto hablaremos más tarde.
Abajo presentamos el esquema de interacción del indicador y el experto:
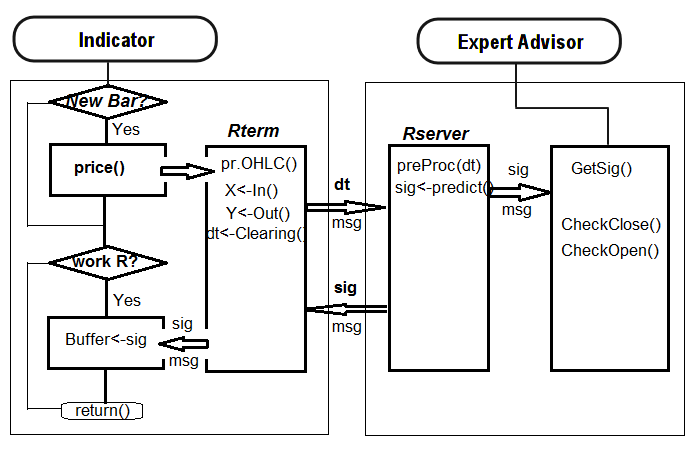
Fig. 31. Esquema estructural de la interacción entre el indicador y el experto
4.1. Entrenar y guardar el modelo
Con ayuda del indicador establecido en el gráfico que necesitemos, obtendremos todos los datos de origen necesarios. Para ello, hay que ubicar el indicador en la gráfica, indicando la variable de entrada send=false, es decir, la "imagen" se escribe, pero no se envía al servidor. Con el primer inicio en este símbolo o marco temporal, el indicador creará en la carpeta de datos del terminal (/MQL4/Files) los siguientes directorios: /Symbol/TF/Test_Data/.
Esta organización de directorios da la posibilidad de no amontonar los resultados de los experimentos en el entrenamiento preliminar de modelos y no escribir con nuevos datos sobre los antiguos. En el directorio /Symbol/TF/Test_Data/ se encontrarán todos nuestros resultados intermedios del trabajo diario, y en el directorio /Symbol/TF/ se ubicará el modelo según el cual funcionará el experto (habrá que trasladarlo allí manualmente). El mismo resultado se obtendrá con el primer inicio en el nuevo símbolo o marco temporal del experto.
Bien. En el símbolo EURUSD MT(М30) hay 4000 barras según el estado del día 14.10.14. Necesitamos la trama de datos dt[].
Balanceamos las clases:
> dt.b<-Balancing(dt) > table(dt.b[ ,ncol(dt.b)]) 0 1 2288 2288
Ahora, con la ayuda de la función Testing.1(), escrita con anterioridad, entrenamos la neurored profunda con las cantidades de épocas (500 y 300) y nos fijamos en el balance obtenido en las últimas 500 barras según las señales predichas por la neurored.
> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=500, bar=500)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000017 ####loss on step 20000 is : 0.000015 ####loss on step 30000 is : 0.000015 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000044 ####loss on step 20000 is : 0.000041 ####loss on step 30000 is : 0.000039 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000042 ####loss on step 20000 is : 0.000042 ####loss on step 30000 is : 0.000036 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.089417 ####loss on step 20000 is : 0.043276 ####loss on step 30000 is : 0.069399 deep nn has been trained. user system elapsed 267.59 0.08 269.37 > plot(bal, t="l")
Guardamos la neurored con otro nombre y entrenamos la segunda
> SAE1<-SAE > system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=500)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000020 ####loss on step 20000 is : 0.000016 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000050 ####loss on step 20000 is : 0.000050 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000051 ####loss on step 20000 is : 0.000043 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.083888 ####loss on step 20000 is : 0.083941 deep nn has been trained. user system elapsed 155.32 0.02 156.25 > lines(bal, col=2)
Miremos a los gráficos de balance (el último resultado en rojo).
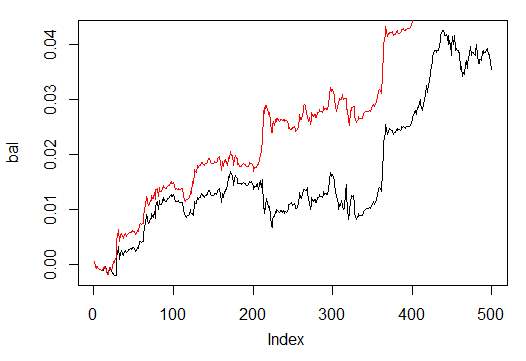
Fig. 32. Balance para las últimas 500 barras según las señales de las neuroredes entrenadas con un número de periodos de 500 y 300
Como podemos ver, la neurored entrenada durante 300 épocas, ha mostrado un mejor resultado que la entrenada con 500.
El tiempo de entrenamiento de la última red es totalmente asumible en un entrenamiento que funcione de forma operativa durante el comercio en este marco temporal.
Para el funcionamiento sucesivo en un gráfico real, necesitamos dos objetos: el modelo entrenado "SAE" y los parámetros de normalización de los datos de entrada - "prepr". Lo guardamos en el directorio correspondiente, en mi caso "D:/Alpari Limited MT4/MQL4/Files/EURUSD/M30/Test_2014-10-14" (ya estará determinado y establecido como directorio de trabajo, si usted ha abierto en Rstudio el área de trabajo "i_SAE_EURUSD_30.Rdata", guardada por el indicador.
save(SAE, prepr, file="SAE.model") En el archivo "SAE.model" hemos guardado el modelo propiamente dicho y los parámetros de normalización, sin los cuales no tiene sentido la aplicación del modelo. Usted puede experimentar y guardar los modelos que le gusten cada día, se irán guardando en la carpeta "/File/Symbol/TF/Test_Data". Para que el modelo use el experto, hay que colocar el archivo "SAE.model" en la carpeta "File/Symbol/TF/" manualmente. En esta carpeta puede estar solo un modelo, según el cual precisamente trabajará el experto.
Ahora, tras cargar el archivo (load("SAE.model")), el experto cargará en el área de trabajo estos objetos para usarlos durante el funcionamiento. Con esto hemos terminado la parte manual del trabajo, podemos colocar el indicador-experto en el gráfico y ponerlo a prueba en tiempo real.
Para determinar la efectividad del funcionamiento del experto son necesarios criterios cuantitativos. Como muestra la experiencia, el coeficiente Accuracy no conviene mucho para este papel.
Podemos usar la media de la relación del balance de las predicciones con respecto al balance de ZigZag, o la relación del balance en la última barra con respecto a la cantidad de barras. Por ejemplo, en nuestro caso, el balance de ZigZag:
sig.zz<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) bal.zz<-cumsum(tail(price[ , 'CO'], 500) * sig.zz) Kzz<-mean(bal.zz / bal) > Kzz [1] 0.9173312
Se trata de un índice muy elevado, pero es relativo.
Si miramos qué aspecto tiene a lo largo del tiempo, podremos ver que en las primeras 50-100 barras es un índice poco estable, aunque después se haga casi continuo. Las estadísticas se muestran más abajo:
> plot(bal/bal.zz, t="l") > summary(bal/bal.zz) Min. 1st Qu. Median Mean 3rd Qu. Max. -15.2500 0.7341 0.7844 0.9173 0.8833 55.0000
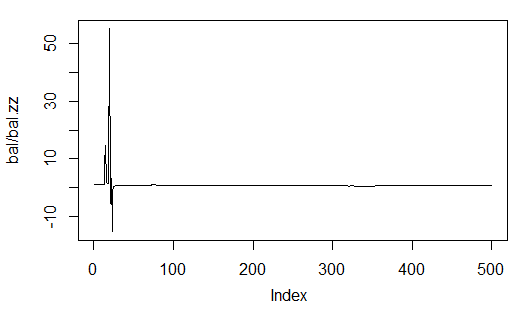
Fig. 33. Relación del balance según las predicciones con respecto al balance según ZigZag
El segundo es más concreto, muestra cuántos puntos de beneficio corresponden a una barra en un segmento con una longitud de N barras.
Por ejemplo, para el balance según las predicciones de la neurored en un segmento de 500 barras:
> Kb<-tail(bal,1)/length(bal)*10^Dig > Kb [1] 11.508
y según las señales de Zigzag:
> Kbz<-tail(bal.zz,1)/length(bal)*10^Dig > Kbz [1] 13.784
Tras determinar el límite inferior de la efectividad de uno de estos índices, podemos saber el momento cuando hay que entrenar de nuevo la neurored u optimizar sus parámetros.
El experto mostrará en el gráfico los siguientes índices OP – operación ejecutada, Acc – Accuracy, K – se trata del Kb determinado con anterioridad, Kmax – es lo mismo que Kb, pero determinado en el pico del balance (da una impresión de cuánto se distingue este índice en la última barra con respecto al máximo).
4.2. Orden de instalación e iniciación
En el archivo SAE.zip adjunto se encuentran:
- El indicador i_SAE.mq4, hay que ponerlo en la carpeta ~/MQL4/Indicators/
- El experto e_SAE.mq4, hay que ponerlo en la carpeta ~/MQL4/Experts/
- La biblioteca mt4Rb7.dll, hay que ponerla en la carpeta ~/MQL4/Libraries/.
- El archivo de encabezamiento mt4Rb7.mqh, hay que ponerlo en la carpeta v ~/MQL4/Include/. La biblioteca y el archivo de encabezamiento han sido desarrollados y amablemente proporcionados por Bernd Kreuss. En la denominación he añadido el índice del último cambio (b7). En caso de tener muchas versiones con nombre iguales (como sucede conmigo), a veces se dan casos cuya rectificación requiere muchísimo tiempo.
- Scripts en R: i_SAE.r (el script principal del indicador), i_SAE_fun.r (función del script del indicador), e_SAE.r (script del experto), e_SAE_init.r(script de inicialización del experto), SAE_SetDir.r (script de comprobación y creación de los directorios necesarios). Dado que los scripts no dependen del símbolo, ni del marco temporal, ni del terminal, se los puede ubicar en un directorio aparte (en mi caso, se trata de "C:Rdata/SAE/"). En el directorio "C:Rdata/"se encuentran diferentes scripts que no están relacionados con un proyecto concreto. Si ha colocado un script en una carpeta diferente a la mía, introduzca los cambios correspondientes en el indicador y el experto (corrija el camino hacia los scripts).
- SAE.model - es el archivo con el modelo "SAE" y los parámetros de normalización - "prepr". El modelo ha sido entrenado con los datos EURUSD (M30), cuya última fecha es el 14.10.14. El proceso de entrenamiento se encuentra más arriba en el artículo.
Asimismo, no olvide corregir el camino hacia el directorio en el que se encuentra instalado el lenguaje R en su computadora.
El inicio para comenzar a trabajar es mejor realizarlo en la secuencia que tenemos a continuación: colocamos el experto en el gráfico. Si ha decidido usted colocar un experto más en otro símbolo, es necesario indicar un puerto diferente a los servidores inciados anteriormente, por ejemplo, port = 8886 (por defecto port = 8888).
Observación. Se trata de una variante totalmente irracional. Cada servidor ocupa cerca de 120-130 Mb. Por ahora es así.
Después de una inicialización normal del experto, aparecerá la alerta ¡"No hay resultados de cálculo! Symbol". Después de esto, establezca el indicador con la variable externa send = true e indicando el puerto del servidor al que debe conectarse el indicador (ver más arriba). Si todo funciona correctamente, en la línea generada aparecerán los datos reales - "operación", Accuracy, K y Kmax y comenzará el comercio.
Lo mejor para controlar el estado del funcionamiento de un proceso R, es abrir la ventana del administrador de tareas de Windows. Si después de iniciar el experto o el indicador en la lista no aparece Rterm, significa que el proceso R se ha interrumpido. El motivo principal por el que puede haberse interrumpido el proceso es un error sintáctico en los scripts, una discordancia de las longitudes del vector receptor en MQL y del vector extraído de Rterm-а.
Se pueden depurar los scripts en Rstudio, iniciando el script línea por línea de principio a fin.
Por desgracia, no he logrado iniciar el experto en el simulador, por eso hay que ponerlo a prueba en la cuenta demo.
4.3. Modos y métodos de mejora de los indicadores de calidad
- Cambiar el conjunto de indicadores usado en la entrada.
- Cambiar el método de normalización de los datos de entrada.
- Optimizar los parámetros del "supervisor" y los indicadores en la entrada.
- Cambiar la codificación de la variable de entrada por una matriz con dos columnas. Calibrar la señal pronosticada.
- Optimizar los parámetros de la neurored (cantidad de neuronas en las capas ocultas, su número, nivel de entrenamiento, cantidad de épocas).
Conclusión
Hemos creado, entrenado y puesto a prueba modelos de redes profundas con inicialización de los pesos de las neuronas de las capas ocultas de los SAE Las redes se entrenan realmente rápido, lo que permite entrenarlas de nuevo sin detener el proceso de comercio.
Los resultados mostrados por las neuroredes son medios (me refiero a la métrica). Nuestra tarea no era conseguir un resultado ideal.
Usando un modelo así y determinando continuamente el coeficiente de efectividad, podemos entrenar y optimizar de nuevo el modelo de manera operativa, sin interrumpir el proceso de comercio.
Anejos:
- SAE.zip - indicador, experto y archivos acompañantes (por texto).
- R_intro.zip - literatura sobre el lenguaje R y Rstudio en ruso.
- DeepLearning.zip - literatura sobre el tema "aprendizaje profundo".
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1103
Revisión de la gestión del dinero
¡Protegerse, los desarrolladores!
Trabajamos con archivos ZIP con los medios de MQL5, sin usar bibliotecas ajenas
Aplicación de los contenedores para componer la interfaz gráfica: clase CBox
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso