
Red neuronal profunda con Stacked RBM. Auto-aprendizaje, auto-control
El artículo es la continuación de artículos anteriores sobre neuroredes profundas y elección de predictores. En este veremos las particularidades de una neurored iniciada con Stacked RBM, así como su implementación en el paquete "darch". Asimismo, se mostrará la posibilidad de usar modelos ocultos de Márkov para mejorar los resultados de predicción de la neurored. Al final, implementaremos de forma programática un ejemplar del experto.
Contenido
- 1. Esquema estructural de DBN
- 2. Preparación y elección de datos
- 2.1. Variables de entrada
- 2.2. Variables de salida
- 2.3. Trama de datos original
- 2.3.1. Eliminando las variables de alta correlación
- 2.4. Eligiendo las variables importantes
- 3. Parte experimental.
- 3.1. Construcción de modelos
- 3.1.1. Breve descripción del paquete "darch"
- 3.1.2. Construcción del modelo DBN. Parámetros.
- 3.2. Formación de los extractos de entrenamiento y prueba
- 3.2.1. Equilibrado de clases y pre-procesado.
- 3.2.2. Codificación de la variable meta
- 3.3. Entrenando el modelo
- 3.3.1. Pre-entrenamiento
- 3.3.2. Entrenamiento preciso
- 3.4. Poniendo el modelo a prueba. Métricas.
- 3.4.1. Decodificación de la predicción.
- 3.4.2. Mejorando el resultado de la predicción
- Calibrado
- Suavizado con la ayuda del modelo de la cadena de Márkov
- Corrección de las señales predichas según la curva de equilibro teórico
- 3.4.3. Métricas
- 4. Esquema estructural del experto
- 4.1. Describiendo el funcionamiento del experto
- 4.2. Auto-control Auto-aprendizaje
- Orden de instalación e iniciación
- Rutas y métodos de mejora de los índices de calidad.
- Conclusión
Introducción
Al preparar los datos para realizar nuestros experimientos, utilizaremos las variables del artículo anterior sobre la valoración y elección de los predictores. Conformaremos un conjunto original, lo limpiaremos y elegiremos las variables.
Analizaremos las formas de dividir el extracto original en conjuntos de entrenamiento, de prueba y de validación.
Con la ayuda del paquete "darch" construiremos un modelo de red DBN y la entrenaremos con nuestros conjuntos de datos. Después de la simulación, obtendremos las métricas con las que valorar la calidad del modelo. Veremos las amplias posibilidades que proporciona el paquete para el ajuste de parámetros de la neurored.
Veremos cómo pueden ayudarnos los modelos ocultos de Márkov en la mejora de las predicciones de la neurored.
Desarrollaremos un experto en el que el modelo se entrenará periódicamente sobre la marcha, sin interrumpir el comercio, según los resultados de control constante. En el experto usaremos el modelo DBN del paquete "darch". También mostraremos una variante del experto construida con el uso de SAE DBN del artículo anterior.
Indicaremos las rutas y métodos de mejora de los índices de calidad del modelo.
1. Esquema estructural de una neurored profunda inicializada con Stacked RBM (DN_SRBM)
Recordemos que DN_SRBM consta de una cantidad n de RBM igual al número de capas ocultas de la neurored y, propiamente, de la misma red. El entrenamiento se realiza en dos etapas.
La primera etapa es el PRE-ENTRENAMIENTO. En ella, cada RBM se entrena consecutivamente con el conjunto de entrada (sin meta), sin supervisión. Después de esto, el peso de las capas ocultas RBM se traslada a las capas ocultas existentes de la neurored.
La segunda etapa es el AJUSTE PRECISO, en esta etapa, la neurored se entrena de forma supervisada. Hemos analizado esto al detalle en el artículo anterior, así que no lo repetiremos. Haremos notar solo que, a diferencia del paquete "deepnet", que hemos usado en el artículo anterior, el paquete "darch" da la posibilidad de implementar capacidades más amplias al construir y ajustar modelos. Hablaremos de ello más en profundidad cuando construyamos el modelo. En la fig.1 se muestra el esquema estructural de DN_SRBM y su proceso de entrenamiento
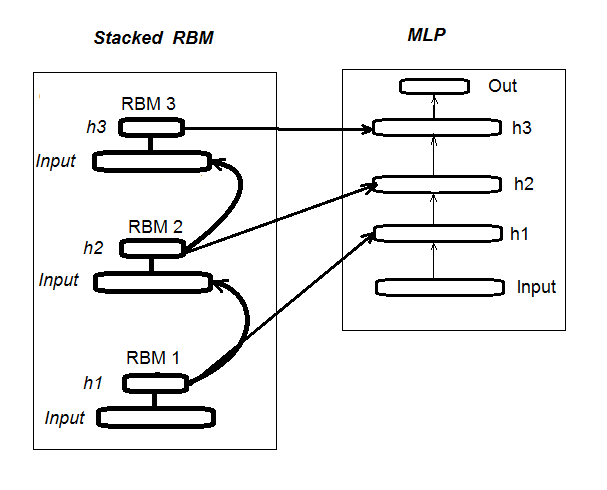
Fig. 1. Esquema estructural de DN SRBM
2. Preparación y elección de datos
2.1. Variables de entrada (signos, predictores)
En el artículo anterior hemos discutido la evaluación y selección de los predictores, así que no detallaremos este proceso. Solo recordaremos que tomamos 11 indicadores (todos ellos osciladores: ADX, aroon, ATR, CCI, chaikinVolatility, CMO, MACD, RSI, stoch, SMI, volatility). De varios de estos se eligieron algunas variables. Así, formamos un conjunto de entrada de 17 variables. Tomaremos las cotizaciones de las últimas 6000 barras en EURUSD, М30 a estado de 14.02.16 y calcularemos los valores de los indicadores con la ayuda de la función In().
#---2--------------------------------------------- In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp - DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p) %>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA") %>% as.data.frame() %>% mutate(., oscK = fastK - fastD) %>% transmute(.,slowD, oscK) %>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) kst <- KST(price[ ,4])%>% as.data.frame() %>% mutate(., oscKST = kst - signal) %>% select(.,oscKST) %>% as.matrix() In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, kst) return(In) }
En la salida, obtenemos la matriz de datos de entrada.
2.2 Datos de salida (variable meta)
Como variable meta tomaremos las señales recibidas de ZZ. La función que calcula el zigzag y una señal:
#----3------------------------------------------------ ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) require(magrittr) if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) if (mode == "m") {pr <- pr[ ,'Med']} if (mode == "hl") {pr <- pr[ ,c("High", "Low")]} if (mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) dz <- zz %>% diff %>% c(., NA) sig <- sign(dz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(cbind(zz, sig)) }
Parámetros de la función:
pr = price – matriz de la cotizaciones OHLCMed;
ch – longitud mínima de la curva del zigzag en puntos (4 dígitos) o en magnitudes reales (por ejemplo ch = 0.0035);
mode – precio aplicado ( "m" - medio, "hl" - High y Low. "cl" - Close), el medio se usa por defecto.
La función retorna la matriz con dos variables: el zigzag propiamente dicho y la señal recibida en base a la inclinación del zigzag en el diapasón [-1;1]. Desplazamos la señal una barra a la izquiera (hacia el futuro). Precisamente conforme a esta señal vamos a entrenar a la neurored.
Calculamos las señales para ZZ con una longitud de curva no inferior a 37 puntos (4 dígitos).
> out <- ZZ(ch = 37, mode = "m") Loading required package: TTR Loading required package: magrittr > table(out[ ,2]) -1 1 2828 3162
Como podemos ver, las clases están ligeramente desequilibradas. Al formar los conjuntos para el entrenamiento, tomaremos medidas para igualarlas.
2.3. Trama de datos original
Escribiremos una función que creará una trama de datos original, la limpiará de datos indeterminados (NA) y transformará la variable meta en un factor con dos clases, «-1» y «+1». Esta función une las funciones In() y ZZ() descritas anteriormente. Cortaremos directamente las últimas 500 barras, conforme a las que determinaremos la calidad de predicción del modelo.
#-----4--------------------------------- form.data <- function(n = 16, z = 37, len = 500){ require(magrittr) x <- In(p = n) out <- ZZ(ch = z, mode = "m") data <- cbind(x, y = out[ ,2]) %>% as.data.frame %>% head(., (nrow(x)-len))%>% na.omit data$y <- as.factor(data$y) return(data) }
2.3.1. Eliminando las variables de alta correlación
Eliminaremos de nuestro conjunto original las variables con un coeficiente de correlación por encima de 0.9. Escribiremos una función que formará la trama de datos original, eliminaremos de ella las variables con correlación alta y retornaremos los datos limpios.
Podemos mirar de forma preliminar qué variables tienen una correlación por encima de 0.9.
> data <- form.data(n = 16, z = 37) # preparamos la trama de datos > descCor <- cor(data[ ,-ncol(data)])# quitamos de ella la variable meta > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.1887 0.0532 0.2077 0.3040 0.5716 0.9588 > highCor <- caret::findCorrelation(descCor, cutoff = 0.9) > highCor [1] 12 9 15 > colnames(data[ ,highCor]) [1] "rsi" "cmo" "SMI"
De esta forma, deberán ser eliminadas las variables mostradas más arriba. Limpiamos de ellas la trama de datos.
> data.f <- data[ ,-highCor] > colnames(data.f) [1] "DX" "ADX" "oscDX" "ar" "tr" [6] "atr" "cci" "chv" "sign" "vsig" [11] "slowD" "oscK" "signal" "vol" "Class"
Lo anotamos de forma compacta, con una función:
#---5----------------------------------------------- cleaning <- function(n = 16, z = 37, cut = 0.9){ data <- form.data(n, z) descCor <- cor(data[ ,-ncol(data)]) highCor <- caret::findCorrelation(descCor, cutoff = cut) data.f <- data[ ,-highCor] return(data.f) } > data.f <- cleaning()
No todos los autores de paquetes e investigadores están de acuerdo con que haya que eliminar los datos de alta correlación de los conjuntos. Sin embargo, hay que comparar los resultados con el uso de ambas variantes. En nuestro caso, elegiremos la variante con eliminación.
2.4. Eligiendo las variables importantes
La elección de variables importantes la realizaremos según tres índices: la importancia global, la importancia local (en la interacción) y la importancia parcial por clases. Usaremos las posibilidades del paquete "randomUniformForest", descritas con detalle en el artículo anterior. Reuniremos todas las acciones anteriores y posteriores en una función para para que todo resulte más compacto. Es decir, tras implementarla, obtendremos como resultado tres conjuntos:
- uno con las mejores variables en contribución e interacción;
- otro con las variables para la clase «-1»;
- y un tercero con las variables para la clase «+1».
#-----6------------------------------------------------ prepareBest <- function(n, z, cut, method){ require(randomUniformForest) require(magrittr) data.f <<- cleaning(n = n, z = z, cut = cut) idx <- rminer::holdout(y = data.f$Class) prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)], method = method) x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)]) x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)]) y.train <- data.f[idx$tr, ncol(data.f)] y.test <- data.f[idx$ts, ncol(data.f)] #--------- ruf <- randomUniformForest( X = x.train, Y = y.train, xtest = x.test, ytest = y.test, mtry = 1, ntree = 300, threads = 2, nodesize = 1 ) imp.ruf <- importance(ruf, Xtest = x.test) best <- imp.ruf$localVariableImportance$classVariableImportance %>% head(., 10) %>% rownames() #-----partImport best.sell <- partialImportance(X = x.test, imp.ruf, whichClass = "-1", nLocalFeatures = 7) %>% row.names() %>% as.numeric() %>% colnames(x.test)[.] best.buy <- partialImportance(X = x.test, imp.ruf, whichClass = "1", nLocalFeatures = 7) %>% row.names() %>% as.numeric() %>% colnames(x.test)[.] dt <- list(best = best, buy = best.buy, sell = best.sell) return(dt) }
Vamos a explicar el orden de los cálculos de la función. Parámetros formales:
n – parámetro de datos de entrada;
z – parámetro de datos de salida;
cut – umbral de correlación de las variables;
method – método de pre-procesado de los datos de entrada.
Cálculos por orden:
- creamos el conjunto original de datos data.f , del que se han eliminado las variables de alta correlación, y lo guardamos para utilizarlo posteriormente;
- determinamos los índices del conjunto de entrenamiento y de prueba idx ;
- definimos los parámetros de pre-procesado prep ;
- dividimos el conjunto original en entrenamiento y prueba, normalizamos los datos de entrada;
- entrenamos y ponemos a prueba con los conjuntos obtenidos el modelo ruf;
- calculamos la importancia de las variables imp.ruf ;
- elegimos las 10 variables más importantes en cuanto a contribución e interacción best ;
- seleccionamos las 7 variables más importantes para la clase «-1» y «+1» best.buy, best.sell ;
- formamos una hoja con tres conjuntos de predictores best, best.buy, best.sell.
Calculamos estos conjuntos y evaluamos los valores de la importancia global, local y parcial de las variables seleccionadas.
> dt <- prepareBest(16, 37, 0.9, c("center", "scale","spatialSign")) Loading required package: randomUniformForest Labels -1 1 have been converted to 1 2 for ease of computation and will be used internally as a replacement. 1 - Global Variable Importance (14 most important based on information gain) : Note: most predictive features are ordered by 'score' and plotted. Most discriminant ones should also be taken into account by looking 'class' and 'class.frequency'. variables score class class.frequency percent 1 cci 4406 -1 0.51 100.00 2 signal 4344 -1 0.51 98.59 3 ADX 4337 -1 0.51 98.43 4 sign 4327 -1 0.51 98.21 5 slowD 4326 -1 0.51 98.18 6 chv 4296 -1 0.52 97.51 7 oscK 4294 -1 0.52 97.46 8 vol 4282 -1 0.51 97.19 9 ar 4271 -1 0.52 96.95 10 atr 4237 -1 0.51 96.16 11 oscDX 4200 -1 0.52 95.34 12 DX 4174 -1 0.51 94.73 13 vsig 4170 -1 0.52 94.65 14 tr 4075 -1 0.50 92.49 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 7 14 7 2 - Local Variable importance Variables interactions (10 most important variables at first (columns) and second (rows) order) : For each variable (at each order), its interaction with others is computed. cci slowD atr tr DX atr 0.1804 0.1546 0.1523 0.1147 0.1127 cci 0.1779 0.1521 0.1498 0.1122 0.1102 slowD 0.1633 0.1375 0.1352 0.0976 0.0956 DX 0.1578 0.1319 0.1297 0.0921 0.0901 vsig 0.1467 0.1209 0.1186 0.0810 0.0790 oscDX 0.1452 0.1194 0.1171 0.0795 0.0775 tr 0.1427 0.1168 0.1146 0.0770 0.0750 oscK 0.1381 0.1123 0.1101 0.0725 0.0705 sign 0.1361 0.1103 0.1081 0.0704 0.0685 signal 0.1326 0.1068 0.1045 0.0669 0.0650 avg1rstOrder 0.1452 0.1194 0.1171 0.0795 0.0775 vsig oscDX oscK signal ar atr 0.1111 0.1040 0.1015 0.0951 0.0897 cci 0.1085 0.1015 0.0990 0.0925 0.0872 slowD 0.0940 0.0869 0.0844 0.0780 0.0726 DX 0.0884 0.0814 0.0789 0.0724 0.0671 vsig 0.0774 0.0703 0.0678 0.0614 0.0560 oscDX 0.0759 0.0688 0.0663 0.0599 0.0545 tr 0.0733 0.0663 0.0638 0.0573 0.0520 oscK 0.0688 0.0618 0.0593 0.0528 0.0475 sign 0.0668 0.0598 0.0573 0.0508 0.0455 signal 0.0633 0.0563 0.0537 0.0473 0.0419 avg1rstOrder 0.0759 0.0688 0.0663 0.0599 0.0545 chv vol sign ADX avg2ndOrder atr 0.0850 0.0850 0.0847 0.0802 0.1108 cci 0.0824 0.0824 0.0822 0.0777 0.1083 slowD 0.0679 0.0679 0.0676 0.0631 0.0937 DX 0.0623 0.0623 0.0620 0.0576 0.0881 vsig 0.0513 0.0513 0.0510 0.0465 0.0771 oscDX 0.0497 0.0497 0.0495 0.0450 0.0756 tr 0.0472 0.0472 0.0470 0.0425 0.0731 oscK 0.0427 0.0427 0.0424 0.0379 0.0685 sign 0.0407 0.0407 0.0404 0.0359 0.0665 signal 0.0372 0.0372 0.0369 0.0324 0.0630 avg1rstOrder 0.0497 0.0497 0.0495 0.0450 0.0000 Variable Importance based on interactions (10 most important) : cci atr slowD DX tr vsig oscDX 0.1384 0.1284 0.1182 0.0796 0.0735 0.0727 0.0677 oscK signal sign 0.0599 0.0509 0.0464 Variable importance over labels (10 most important variables conditionally to each label) : Class -1 Class 1 cci 0.17 0.23 slowD 0.20 0.09 atr 0.14 0.15 tr 0.04 0.12 oscK 0.08 0.03 vsig 0.06 0.08 oscDX 0.04 0.08 DX 0.07 0.08 signal 0.05 0.04 ar 0.04 0.02
Resultados
- En cuanto a importancia global, las 14 variables de entrada están a la par.
- Las 10 mejores se definen por su valor sumario de contribución (importancia global) y a su interacción (importancia local).
- Las siete mejores variables en cuanto a importancia parcial para cada clase se muestran más abajo en los gráficos.
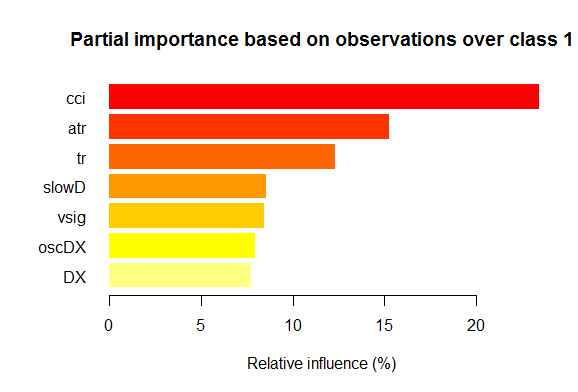
Fig. 2. Importancia parcial de las variables para la clase "1"
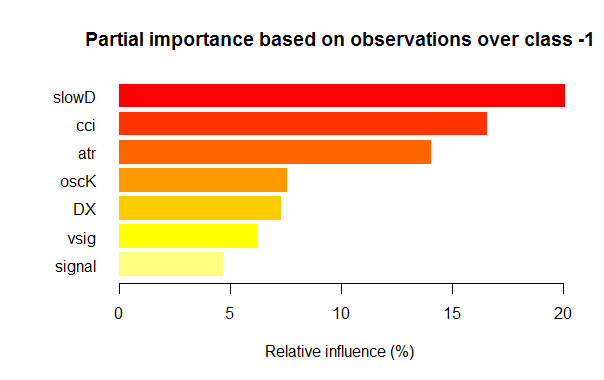
Fig. 3. Importancia parcial de las variables para la clase "-1"
Como podemos ver, para clases diferentes las variables más importantes se diferencian tanto por su composición, como por su ranking. Así, mientras que para la clase «-1» es más importante la variable slowD, para la clase «+1» esta se halla solo en el 4 puesto.
Bien, los conjuntos de datos ya está listos. Ahora podemos proceder a los experimentos.
3. Parte experimental.
Realizaremos los experimentos en el entorno R, para ser más exactos, en Revolution R Open, version 3.2.2, distribución de la empresa Revolution Analytics. http://www.revolutionanalytics.com/revolution-r-open
Esta distribución tiene una serie de ventajas con respecto a la R 3.2.2 habitual:
- cálculos más rápidos y de mayor calidad gracias al uso de multi-threaded processing with Intel® Math Kernel Library ;
- capacidades ampliadas con Reproducible R Toolkit . Una pequeña aclaración: el lenguaje R se desarrolla activamente, mejorando de forma constante los paquetes existentes y añadiendo nuevos. El aspecto negativo de este progreso es la périda de reproducibilidad. Es decir, sus productos escritos varios meses atrás, que funcionan bien, de repente dejan de funcionar después de la habitaul actualización de los paquetes. Tendremos que perder un montón de tiempo para detectar y liquidar algún error provocado por un cambio en uno de los paquetes. Por ejemplo, en el primer artículo sobre neuroredes profundas, se propuso un experto que en el momento de la escritura funcionaba estupendamente. Sin embargo, unos meses después de la publicación, varios usuarios comunicaron que no era capaz de funcionar. El análisis mostró que la actualización del paquete "svSocket" provocó que el experto dejara de funcionar. A día de hoy, sigo sin entender el motivo. El experto perfeccionado se adjuntará a este archivo. Este problema se convirtió en algo tremendamente actual, y en Revolution Analytics lo resolvieron de forma muy simple. Ahora, al lanzar una nueva distribución, se registra el estado de todos los paquetes en el repositorio CRAN para la fecha de salida de la distribución, copiándolos en su espejo. Ningún cambio en el repositorio CRAN después de esta fecha podrá influir en los paquetes «congelados» en el espejo de Revolution. Además, a partir de 2014, la empresa hace capturas diarias del repositorio CRAN, fijando el estado actual y las versiones de los paquetes. Con la ayuda de su paquete "checkpoint", ahora podemos cargar los paquetes necesarios que sean actuales para la fecha que deseemos. En otras palabras, disponemos de nuestra propia mini máquina del tiempo.
Y otra noticia más. Hace nueve meses, Microsoft compró Revolution Analytics con la promesa de apoyar sus desarrollos, dejando la distribución Revolution R Open (RRO) accesible de forma gratuita. A esto le siguió una serie de mensajes sobre las novedades en RRO y Revolution R Enterpise (por no hablar de la integración R con SQL Server, PowerBI, Azure y Cortana Analitics). Ahora tenemos un mensaje que anuncia que la siguiente actualización de RRO se llamará Microsoft R Open y que Revolution R Enterprise será Microsoft R Server. Bueno, y literalmente en los últimos días, Microsoft R ha anunciado que R estará disponible en Visual Studio. R Tools for Visual Studio (RTVS) sigue al modelo Python Tools for Visual Studio. Será una adición gratuita a Visual Studio, que proporcionará un IDE completo para R, con la posibilidad de editar y depurar scripts de forma interactiva.
Para cuando se terminó de escribir el artículo, ya había salido Microsoft R Open (R 3.2.3), por eso usaremos en lo sucesivo paquetes para esta versión.
3.1. Construcción de modelos
3.1.1. Breve descripción del paquete "darch"
El paquete "darch" ver. 0.10.0 proporciona un amplio espectro de funciones que permiten no solo crear y entrenar un modelo, sino literalmente construirlo y ajustarlo ladrillo a ladrillo conforme a sus preferencias. Como se ha indicado anteriormente, la red consta de un número n de RBM (n = layers -1) y de la neurored MLP con un número de capas layers. El pre-entrenamiento por capas de RBM se realiza con datos no formateados y sin supervisión. El ajuste de la neurored se realiza con supervisión con datos no formateados. La división de estos estadios de entrenamiento nos da la posibilidad de usar diferentes datos en cuanto a volumen (¡pero no en cuanto a estructura!) u obtener varios modelos diferentes entrenados sobre la base de un pre-entrenamiento. Además, si los datos para el pre-entrenamiento y el ajuste preciso son iguales, es posible realizar el entrenamiento de una sola vez sin dividirlo en dos estadios. Podemos saltarnos el pre-entrenamiento y usar una red multicapa o, al contrario, usar solo RBM sin neurored. Además, tenemos acceso a todos los parámetros internos. El paquete está previsto para los usuarios avanzados. Después analizaremos la división del proceso: pre-entrenamiento y ajuste preciso.
3.1.2. Construcción del modelo DBN. Parámetros.
Vamos a describir el orden de construcción, entrenamiento y puesta a prueba de DBN.
newDArch(layers, batchSize, ff=FALSE, logLevel=INFO, genWeightFunc=generateWeights),
donde:
- layers : es la matriz con la indicación del número de capas y neuronas en cada capa. Por ejemplo : layers = c(5,10,10,2) – capa de entrada con 5 neuronas (visibles), dos capas ocultas con 10 neuronas en cada una, y una capa de salida con 2 salidas.
- BatchSize : tamaño del mini-extracto durante el entrenamiento.
- ff : indica si hay que usar el formato ff para los pesos, el desplazamiento y las salidas. El formato ff se aplica para guardar de forma comprimida datos de grandes dimensiones.
- LogLevel : nivel de logueo y muestra de información al ejecutar una función.
- GenWeightFunction: función para generar la matriz de pesos RBM. Existe la posibilidad de usar la función de usuario para la activación.
El objeto darch creado, contiene (layers - 1) RBM unidas en un red acumulativa, y que además se usarán el pre-entrenamiento de la neurored. Los dos atributos fineTuneFunction y executeFunction contienen las funciones para el ajuste preciso (por defecto backpropagation) y para la ejecución ( por defecto runDarch). El entrenamiento de la red se realiza con la ayuda de dos funciones de entrenemiento, preTrainDArch() y fineTuneDArch(). La primera función entrena a la red RBM sin supervisión con el método de divergencia contrastiva (contrastive divergence). La segunda función usa la función indicada en el atributo fineTuneFunction para el ajuste preciso de la neurored. Después de ejecutar la neurored, las salidas de cada capa se pueden encontrar en el atributo executeOutputs o solo la capa de salida en el atributo executeOutput.
2. Función de pre-entrenamiento del objeto darch
preTrainDArch(darch, dataSet, numEpoch = 1, numCD = 1, ..., trainOutputLayer = F),donde:
- darch: ejemplar de la clase 'Darch';
- dataSet : conjunto de datos para el entrenamiento ;
- numEpoch : número de épocas de entrenamiento;
- numCD : número de iteraciones del muestreo. Como norma general, basta una;
- ... : parámetros adicionales que se pueden transmitir a la función trainRBM;
- trainOutputLayer : magnitud lógica que muestra si la capa de salida RBM debería ser entrenada.
La función ejecuta para cada RBM la función de entrenamiento trainRBM(), copiando después del entrenamiento los pesos y los desplazamientos (biases) a las capas correspondientes de la neurored del objeto darch.
3. Función de ajuste preciso del objeto darchfineTuneDArch(darch, dataSet, dataSetValid = NULL, numEpochs = 1, bootstrap = T,
isBin = FALSE, isClass = TRUE, stopErr = -Inf, stopClassErr = 101,
stopValidErr = -Inf, stopValidClassErr = 101, ...),
donde:
- darch: ejemplar de la clase 'Darch';
- dataSet : conjunto de datos para el entrenamiento (también se pueden usar para la validación) y la puesta a prueba;
- dataSetValid : conjunto de datos usados para la validación;
- numxEpoch : número de épocas de entrenamiento;
- bootstrap : lógica, si es necesario aplicar arranque (bootstrap) al crear datos de validación;
- isBin : indica si los datos de salida se deben interpretar cómo valores lógicos. Por defecto — FALSE. Si TRUE, cada valor superior a 0.5 se interpretará como 1, y cada valor menor, como 0.
- isClass : indica si la red se entrena para la clasificación. Si TRUE, entonces la estadística para la clasificación será determinada. Por defecto, TRUE.
- stopErr : criterios de interrupción del entrenamiento de la neurored debido a un error durante el entrenamiento. Por defecto -Inf;
- stopClassErr : criterios de interrupción del entrenamiento de la neurored debido a un error de clasificación durante el entrenamiento. Por defecto, 101;
- stopValidErr : criterios de interrupción de la neurored debido a un error de validación de datos. Por defecto -Inf;
- stopValidClassErr : criterios de interrupción de la neurored debido a un error de clasificación durante la validación. Por defecto, 101;
- ... : parámetros adicionales que se pueden transmitir a la función de entrenamiento.
La función entrena la red establecida con la función guardada en el atributo fineTuneFunction del objeto darch. Los datos de entrada (trainData, validData, testData) y las clases que les pertenecen (targetData, validTargets, testTargets) pueden ser transmitidos como una matriz dataSet o ff. Los datos y clases para la validación y la puesta a prueba no son obligatorios. Si se presentan entonces la neurored se ejecutará con estos conjuntos de datos y las estadísticas se calcularán. El atributo isBin indica si se deberán integrar los datos de entrada como datos dobles. Si isBin = TRUE, cada valor de salida superior a 0.5 se interpretará como 1, y en el caso contrario, como 0. Asimismo, podemos establecer los criterios de interrupción del entrenamiento basándonos en el error (stopErr, stopValidErr) o la clasificación correcta (stopClassErr, stopValidClassErr) en los conjuntos de entrenamiento o validación.
Todos los parámetros tienen valores por defecto. Sin embargo, hay otros valores disponibles. Por ejemplo:
La función de activación de neuronas: están disponibles sigmoidUnitDerivative, linearUnitDerivative, softmaxUnitDerivative, tanSigmoidUnitDerivative. Por defecto, — sigmoidUnitDerivative.
Funciones de ajuste preciso de la neurored — por defecto, la propagación inversa del error (backpropagation), también está disponible la propagación inversa elástica del error rpropagation (resilient-propagation) en cuatro variantes ("Rprop+", "Rprop-", "iRprop+", "iRprop-") y minimizeClassifier (esta función se entrena con un clasificador de la red Darch mediante el método del gradiente conjugado no lineal). Para los dos últimos algoritmos y para aquellos que saben mucho del tema, existe otra implementación del ajuste preciso de la neurored con la posibilidad de configurar multitud de sus parámetros. Por ejemplo:
rpropagation(darch, trainData, targetData, method="iRprop+",
decFact=0.5, incFact=1.2, weightDecay=0, initDelta=0.0125,
minDelta=0.000001, maxDelta=50, ...),
donde:
- darch – objeto darch para el entrenamiento;
- trainData – conjunto de datos de entrada para el entrenamiento;
- targetData – salida esperada para el conjunto de entrenamiento;
- method – método de entrenamiento. Por defecto, es "iRprop+". Son posibles "Rprop+", "Rprop-", "iRprop-";
- decFact – factor decreciente para el entrenamiento. Por defecto, 0.5;
- incFact - factor creciente para el entrenamiento. Por defecto, 1.2;
- weightDecay – reducción del peso durante el entrenamiento. Por defecto 0;
- initDelta – valor de la inicialización durante la actualización. Por defecto 0.0125;
- minDelta – límite inferior para el tamaño del paso. Por defecto 0.000001;
- maxDelta – límite superior para el tamaño del paso. Por defecto, 50.
La función retorna el objeto darch con la red entrenada.
3.2. Formación de los extractos de entrenamiento y prueba
Ya hemos formado el conjunto de datos original. Ahora hay que dividirlo en conjuntos de entrenamiento, de validación y de prueba. La proporción es por defecto 2/3. En los diferentes paquetes se presenta multitud de funciones que efectúan esta división. Yo uso la función rminer::holdout(), que calcula los índices para la división del conjunto original en conjuntos de entrenamiento y prueba.
holdout(y, ratio = 2/3, internalsplit = FALSE, mode = "stratified", iter = 1,
seed = NULL, window=10, increment=1),
donde:
- y – variable meta deseada, vector o factor numérico, en este caso se aplica una división estratificada (es decir, las proporciones entre clases son iguales para todas las partes);
- ratio – rango de la separación (en tanto por ciento se establece el tamaño del conjunto de entrenamiento; el tamaño del conjuto de prueba se establece en número total de ejemplares);
- internalsplit – si TRUE, entonces los datos de entrenamiento se dividen otra vez en conjunto de entrenamiento y validación. El mismo "ratio" se aplica para la división interna;
- mode – modo de muestreo. Son posibles las opciones:
- stratified – división estratificada aleatoria (si hay factor y; de lo contrario, división aleatoria estándar);
- random – división aleatoria estándar;
- order – modo estático, cuando los primeros ejemplares se usan para el entrenamiento, y el resto, para la puesta a prueba (se usa ampliamente para las series temporales);
- rolling – ventana móvil, más conocida como ventana deslizante (se usa mucho al realizar predicciones en los mercados de fondos y financieros), de forma análoga sucede con order, con la excepción de que window es el tamaño de la ventana, iter es el deslizamiento de la iteración, e increment es el número de ejemplos en el que la ventana se desliza hacia adelante con cada iteración. El tamaño del conjunto de entrenamiento para cada iteración se fija con window, mientras que el conjunto de prueba es igual a ratio, con la excepción de la última iteración (donde puede ser menor).
- incremental – modo de incremento de entrenamiento, también conocido como ventana creciente, es análogo a order, con la exepción de que window es el tamaño inicial de la ventana, iter son las iteraciones incrementadas, e increment el número de ejemplos añadidos a cada iteración. En cada iteración, el tamaño del conjunto de entrenamiento crece (+increment), mientras que el tamaño conjunto de prueba es igual a ratio, con la excepción de la última iteración, donde puede ser menor.
- iter – número de iteraciones del modo de incremento del reentrenamiento (se usa solo cuando mode = "rolling" o "incremental", normalmente iter se establece en el ciclo).
- seed – si NULL, entonces se usa random seed, de lo contrario, seed se fija (en los cálculos posteriores se retornará siempre el mismo resultado);
- window – tamaño de la ventana de entrenamiento ( si mode = "rolling") o tamaño incial de la ventana de entrenamiento (si mode = "incremental");
- increment – número de ejemplos añadidos a la ventana de entrenamiento en cada iteración (si mode="incremental" o mode="rolling").
3.2.1. Equilibrado de clases y pre-procesado.
Escribiremos una función que iguala (en caso necesario) el número de clases en el extracto hacia el lado mayor, divide el extracto en conjuntos de entrenamiento y de prueba, realiza el pre-procesado (normalización, en caso necesario) y retorna la hoja con los conjuntos correspondientes train, test. Para el equilibrado, usaremos la función caret::upSample(), que añade muestras extraídas de forma aleatoria por sustitución, haciendo la distribución de clases idéntica. Hay que decir que no todos los investigadores reconocen la necesidad de equilibrar las clases. Pero como ya sabemos, la práctica es el criterio de la verdad, y como resultado de mis numerosos experimentos, los conjuntos equilibrados siempre muestran los mejores resultados en el entrenamiento. Pero esto no debe impedirle a usted que experimente por su cuenta.
Para el pre-procesado, usaremos la función caret::preProcess(). Los parámetros del pre-procesado los guardaremos en la variable prepr. Puesto que ya los hemos analizado y aplicado en artículos anteriores, no voy a detenerme en su descripción.
#---7---------------------------------------------------- prepareTrain <- function(x , y, rati, mod = "stratified", balance = F, norm, meth) { require(magrittr) require(dplyr) t <- rminer::holdout(y = y, ratio = rati, mode = mod) train <- cbind(x[t$tr, ], y = y[t$tr]) if(balance){ train <- caret::upSample(x = train[ ,best], y = train$y, list = F)%>% tbl_df train <- cbind(train[ ,best], select(train, y = Class)) } test <- cbind(x[t$ts, ], y = y[t$ts]) if (norm) { prepr <<- caret::preProcess(train[ ,best], method = meth) train = predict(prepr, train[ ,best])%>% cbind(., y = train$y) test = predict(prepr, test[ ,best] %>% cbind(., y = test$y)) } DT <- list(train = train, test = test) return(DT) }
Nota para el pre-procesamiento: normalizaremos las variables de entrada en el intervalo (-1, 1).
3.2.2. Codificación de la variable meta
Al resolver la tarea de la clasificación, la variable meta será un factor con varios niveles (clases). En el modelo se establece un vector (columna), que consta de los estados sucesivos de la meta. Por ejemplo, y = с("1", "1", "2", "3", "1"). Para darle la neurored para su entrenamiento, es necesario codificar (transformar) la variable meta en una matriz con una cantidad de columnas igual al número de clases. En cada línea de esta matriz puede haber solo una unidad en cada columna. Esta transformación, junto con el uso de la capa de salida de la función de activación softmax() permite obtener la probabilidad del estado de la variable meta predicha en cada clase. Realizaremos el copiado con la ayuda de la función classvec2classmat(). Hay que decir que no se trata del único método, ni el mejor para copiar una variable meta, pero lo vamos a usar por su sencillez. La transformación inversa (decodificación) de los valores predichos de la variable meta se puede realizar de diversas formas, sobre las que hablaremos más tarde.
3.3. Entrenando el modelo
3.3.1. Pre-entrenamiento
Como ya hemos dicho con aterioridad, primero crearemos el objeto de arquitectura profunda DArch, que contiene dentro de sí el número necesario de RBM con los parámetros por defecto de entrenamiento preliminar y la neurored iniciada con los pesos aleatorios y la función de activación de neuronas establecida por defecto. En la etapa de creación del objeto, si es necesario, se pueden cambiar los parámetros del pre-entrenamiento. Después de ello, realizamos el entrenamiento preliminar de la red RBM sin supervisión, suministrando en la entrada el conjunto de entrenamiento (sin variable meta). Al terminar el pre-entrenamiento, obtenemos DАrch, en la que los pesos y desviaciones obtenidas durante el entrenamiento de RBM se han trasladado a la neurored. De forma preliminar, necesitamos definir la situación de las neuronas ocultas en forma de vector (por ejemplo):
L<- c( 14, 50, 50, 2)
El número de neuronas en la capa de entrada es igual al número de variables de entrada. Las dos capas ocultas contendrán 50 neuronas cada una, la capa de salida, dos neuronas. Voy a explicar esto último. Si la variable (factor) meta tiene dos niveles (clases), en pricipio nos las podemos arreglar con una salida. Pero el paso del vector a matriz con dos columnas, cada una de las cuales corresponde a una clase, nos permite utilizar en la capa de salida la función de activación softmax() que funciona muy bien en tareas de clasificación. Además, las salidas en forma de probabilidad de clases nos dan posibilidades adicionales en el posterior análisis de resultados. Más abajo hablaremos de ello.
El número de épocas de entrenamiento lo estableceremos de forma experimeintal, normalmente entre 10-50.
El número de iteraciones del muestreo lo dejaremos por defecto, pero podemos experimentar un poco, aumentando esta parámetro. Le daremos forma en una función aparte:
#----8-------------------------------------------------------------- pretrainDBN <- function(L, Bs, dS, nE, nCD, InM = 0.5, FinM = 0.9) { require(darch) # crea un objeto DArch dbn <- newDArch(layers = L, batchSize = Bs, logLevel = 5) # establecemos el momento inicial setInitialMomentum(dbn) <- InM # establecemos el momento final setFinalMomentum(dbn) <- FinM # establecemos el tiempo de permutación de momentos del inicial al final setMomentumSwitch(dbn) <- round(0.8 * nE) dbn <- preTrainDArch(dbn, dataSet = dS, numEpoch = nE, numCD = nCD, trainOutputLayer = T) return(dbn) }
3.3.2. Entrenamiento preciso
Como ya hemos dicho más arriba, para el entrenamiento preciso, el paquete propone las funciones backpropagation(), rpropagation(), minimizeClassifier(), minimizeAutoencoder(). Las dos últimas no las vamos a analizar, puesto que no han sido lo suficientemente documentadas en el paquete y no hay disponibles ejemplos con su uso. En mis experimentos, estas características no han mostrado buenos resultados.
Además, quiero hablar una vez más acerca de las actualizaciones de los paquetes. Durante el proceso de escritura del artículo, la versión actual era la 0.9, pero cuando se finalizó, ya había salido la versión 0.10, en la que había cambios sustanciales. Hemos tenido que rehacer todos los cálculos. Según los resultados de una breve simulación, podemos decir que la velocidad de funcionamiento ha aumentado significativamente, lo cual no podemos decir sobre la calidad de los resultados (esto no es culpa del paquete, sino del que lo aplica).
Veamos las dos primeras funciones. La primera (backpropagation) está instalada por defecto en el objeto DАrch y usa los parámetros de entrenamiento de la neurored presentados aquí. La segunda (rpropagation) también tiene los parámetros por defecto y cuatro métodos de entrenamiento (los he descrito más arriba) por defecto "iRprop+" . Por supuesto, los parámetros y el método de entrenamiento se pueden cambiar. Aplicar estas funciones es muy sencillo: sustituya en la función FineTuneDarch() la función de entrenamiento preciso
setFineTuneFunction(dbn) <- rpropagation
Aparte de la función de ajuste preciso, debemos establecer (en caso necesario) las funciones de activación de las neuronas en cada capa. Recordemos que por defecto en todas las capas tenemos sigmoidUnit. En el paquete están disponibles sigmoidUnitDerivative, linearUnitDerivative, tanSigmoidUnitDerivative, softmaxUnitDerivative . Definimos el ajuste preciso mediante una función aparte con la habilidad de elegir la función del ajuste preciso. Reunimos las funciones de activación posibles en una lista aparte :
actFun <- list(sig = sigmoidUnitDerivative, tnh = tanSigmoidUnitDerivative, lin = linearUnitDerivative, soft = softmaxUnitDerivative)
Vamos a escribir una función con el ajuste preciso de la neurored, que entrenará y generará dos neuroredes: una, entrenada con la ayuda de la función backpropagation, y la segunda, con la ayuda de la función rpropagation:
#-----9----------------------------------------- fineMod <- function(variant=1, dbnin, dS, hd = 0.5, id = 0.2, act = c(2,1), nE = 10) { setDropoutOneMaskPerEpoch(dbnin) <- FALSE setDropoutHiddenLayers(dbnin) <- hd setDropoutInputLayer(dbnin) <- id layers <<- getLayers(dbnin) stopifnot(length(layers)==length(act)) if(variant < 0 || variant >2) {variant = 1} for(i in 1:length(layers)){ fun <- actFun %>% extract2(act[i]) layers[[i]][[2]] <- fun } setLayers(dbnin) <- layers if(variant == 1 || variant == 2){ # backpropagation if(variant == 2){# rpropagation #setDropoutHiddenLayers(dbnin) <- 0.0 setFineTuneFunction(dbnin) <- rpropagation } mod = fineTuneDArch(darch = dbnin, dataSet = dS, numEpochs = nE, bootstrap = T) return(mod) } }
Algunas aclaraciones sobre los parámetros formales de la función.
- variant - elección de la función de ajuste preciso (1- backpropagation, 2- rpropagation).
- dbnin - modelo de obtención, resultado del pre-entrenamiento.
- dS - conjunto de datos para el ajuste preciso (dataSet).
- hd - coeficiente de muestreo (hiddenDropout) en las capas ocultas de la neurored.
- id - coeficiente de muestreo (inputDropout) en la capa de entrada de la neurored.
- act - vector con indicación de la función de activación de las neuronas en cada capa de la neurored. La longitud del vector es una unidad menor que el número de capas.
- nE - número de épocas de entrenamiento.
dataSet — nueva esencia aparecida en esta versión. El motivo de su aparición no está totalmente claro. De manera estándar, en el lenguaje se aceptan dos modos de suministro de variables al modelo, con la pareja (x, y) o mediante la fórmula (y~., data). La aparición de esta esencia no añade nada significativo, pero sí que confunde a los usuarios. No obstante, el autor puede tener sus razones, que me son desconocidas.
3.4. Poniendo el modelo a prueba. Métricas.
El entrenamiento del modelo a instruir lo realizaremos con conjuntos de prueba. Hay que tener en cuenta que vamos a calcular dos métricas: Accuracy formal y K cualitativa. Hablaremos sobre ella más abajo. Para esta tarea, necesitaremos dos conjuntos diferentes de datos, y he aquí el motivo. Para calcular Accuracy necesitamos los valores de la variable meta, y ZigZag, como recordamos, no suele estar definido en las últimas barras. Por eso, el conjunto de prueba para definir Accuracy lo definiremos con la función prepareTrain(), y para definir los índices de calidad, usaremos la función
#---10------------------------------------------- prepareTest <- function(n, z, norm, len = 501) { x <- In(p = n ) %>% na.omit %>% extract( ,best) %>% tail(., len) CO <- price[ ,"CO"] %>% tail(., len) if (norm) { x <- predict(prepr,x) } dt <- cbind(x = x, CO = CO) %>% as.data.frame() return(dt) }
Pondremos a prueba el modelo con las últimas 500 barras de la historia.
La propia simulación la realizaremos con las dos funciones testAcc() y testBal().
#---11----- testAcc <- function(obj, typ = "bin"){ x.ts <- DT$test[ ,best] %>% as.matrix() y.ts <- DT$test$y %>% as.integer() %>% subtract(1) out <- predict(obj, newdata = x.ts, type = typ) if (soft){out <- max.col(out)-1} else {out %<>% as.vector()} acc <- length(y.ts[y.ts == out])/length(y.ts) %>% round(., digits = 4) return(list(Acc = acc, y.ts = y.ts, y = out)) } #---12----- testBal <- function(obj, typ = "bin") { require(fTrading) x <- DT.test[ ,best] CO <- DT.test$CO out <- predict(obj, newdata = x, type = typ) if(soft){out <- max.col(out)-1} else {out %<>% as.vector()} sig <- ifelse(out == 0, -1, 1) sig1 <- Hmisc::Lag(sig) %>% na.omit bal <- cumsum(sig1 * tail(CO, length(sig1))) K <- tail(bal, 1)/length(bal) * 10 ^ Dig Kmax <- max(bal)/which.max(bal) * 10 ^ Dig dd <- maxDrawDown(bal) return(list(sig = sig, bal = bal, K = K, Kmax = Kmax, dd = dd)) }
La primera función retorna propiamente Acc y los valores de la variable meta (real y predicho) para un posible análisis posterior. La segunda retorna las señales predichas para el experto sig, el balance obtenido conforme a estas señales bal, el coeficiente de calidad K, el valor máximo de este coeficiente en el segmento testado Kmax y la reducción máxima dd en ese segmento.
A la hora de calcular el balance, es necesario recordar que la última señal predicha se refiere a una barra futura y aún sin formar, por eso hay que eliminarla durante los cálculos. Hemos hecho esto desplazando el vector sig una barra a la derecha.
3.4.1. Decodificación de la predicción.
Es posible decodificar el resultado obtenido (pasarlo de matriz a vector) con la ayuda de "WTA". La clase es igual al número de columna con el máximo valor de probabilidad, además, se puede establecer el umbral del valor de esta probabilidad, por debajo de este la clase no está definida.
out <- classmat2classvec(out, threshold = 0.5) o out <- max.col(out)-1
Si establecemos un umbral de 0.5 y la mayor probabilidad en las columnas es inferior a este umbral, obtendremos la clase adicional "no_definida". Debemos tener esto en cuenta a la hora de calcular métricas como Accuracy.
3.4.2. Mejorando el resultado de la predicción
¿Podemos mejorar el resultado de la predicción depués de obtenerlo? Es posible utilizar los siguientes tres métodos.
- Calibrado
CORElearn::calibrate(correctClass, predictedProb, class1 = 1, method = c("isoReg", "binIsoReg", "binning", "mdlMerge"), weight=NULL, noBins=10, assumeProbabilities=FALSE)
donde:
- correctClass – vector con las etiquetas correctas de las clases para los problemas de clasificación;
- predictedProb – vector con la clase predicha 1 (de probabilidad), de la misma longitud que correctClass;
- method — uno de ("isoReg", "binIsoReg", "binning", "mdlMerge"). Puede ver los detalles en la descripción del paquete;
- weight — el vector (si se indica) debe ser de la misma longitud que correctClass, y representar el peso de cada observación, en el caso contrario, por defecto los pesos de todas las observaciones serán igual a 1;
- noBins — el valor del parámetro depende de method y define el número deseado o inicial de canales;
- assumeProbabilities — lógica, si TRUE, el valor en predictedProb se espera en el diapasón [0, 1], es decir, como una evaluación de la probabilidad, de otra forma el algoritmo puede ser utilizado como una simple regresión isotónica.
Este método se aplica en el caso de una variable meta con dos niveles establecidos por un vector.
- Suavizado de los resultados de la predicción mediante el uso del modelo de cadena de Markov
Este es un tema muy amplio y complejo que merece un artículo aparte, por lo que no voy a ahondar en la teoría, sólo en las definiciones básicas.
El proceso de Márkov es un proceso aleatorio que posee la siguiente propiedad: para cualquier momento temporal t0 la probabilidad de cualquier estado de un sistema depende en el futuro solo de su estado en el presente, y no depende de cuándo y de qué forma ha llegado el sistema a ese estado.
Clasificación de los procesos aleatorios de Márkov:
- con tiempo discreto y estados discretos (cadena de Márkov);
- con estados continuos y tiempo discreto (secuencias de Márkov);
- con estados discretos y tiempo continuo (cadena continua de Márkov);
- con estado continuo y tiempo continuo.
Aquí en lo sucesivo solo se estudiarán los procesos de Márkov con estados discretos S1, S2, ..., Sn.
La cadena de Márkov es un proceso aleatorio de Márkov con estados discretos y tiempo discreto.
Los momentos t1, t2, ..., cuando un sistema S puede cambiar su estado se estudian como ciertos pasos consecutivos de un proceso. Como argumento del que depende el proceso interviene, no el tiempo t, si no el número del paso 1,2,...,k,...
El proceso aleatorio se caracteriza por una secuencia de estados S(0), S(1), S(2), ..., S(k), ..., donde S(0) es el estado incial (antes del primer paso); S(1) es el estado después del primer paso; S(k) es el estado del sistema después del paso k.
Las probabilidades de los estados de la cadena de Márkov son Pi(k) probabilidades de que después del paso k (y antes del paso (k + 1)) el sistema S se encontrará en el estado Si,(i = 1 , 2 , ..., n).
La distribución inicial de las probabilidades de la cadena de Márkov es la distribución de las probabilidades de los estados al inicio del proceso.
La probabilidad de transición en el paso k del estado Si al estado Sj es la probabilidad condicional de que el sistema S después del paso kllegue al estado Sj, con la condición de que justo antes de ello (después del paso k—1) se encuentre en el estado Si.
Las posibilidades de transición de la cadena uniforme de Márkov Рij forman una matriz cuadrada de un tamaño n x n. Sus peculiaridades son:
- Cada línea caracteriza un estado elegido del sistema, y sus elementos, la probabilidad de todas las transiciones posibles en un paso del estado seleccionado (i).
- Los elementos de las columnas son las probabilidades de todas las posibles transiciones en un paso del estado (j) establecido.
- La suma de las probabilidades de cada fila es igual a uno.
- En la diagonal principal, hay Рij probabilidades de que el sistema no salga del estado Si y se quede en él.
El proceso de Márkov puede ser tanto observable, como oculto. El Modelo Oculto de Márkov ( Hidden Markov Model(HMM)) consta de la pareja de procesos discretos estocásticos {St} y {Xt}. El proceso observable {Xt} está relacionado con el proceso de Márkov no observable (oculto) de los estados {St}, con la ayuda de las llamadas distribuciones condicionales.
Estrictamente hablando, el proceso observable de Markov de los estados (clases) de nuestra serie temporal meta no es uniforme. Obviamente, la probabilidad de transición de un estado a otro depende del tiempo de permanencia en el estado actual. Es decir, en los primeros pasos tras el cambio de estado, su probabilidad de cambio es baja y crece conforme aumenta el tiempo de permanencia en el estado. Estos modelos se conocen como semi-Markovianos (HSMM). No vamos a profundizar en su análisis.
La idea es la siguiente: sobre la base de una secuencia discreta de señales ideales (meta) obtenidas a partir de zigzag, definimos los parámetros de HMM. Después, una vez tenemos las señales predichas por la red neuronal, las suavizamos con ayuda de HMM.
¿Que nos da esto? Por regla general, en la predicción de la neurored, existen las llamadas "emisiones", segmentos de cambio en el estado, de una o dos barras de longitud. Sabemos que la variable meta no tiene duraciones tan cortas. Aplicando a una secuencia predicha un modelo resultante de la meta, podemos llevarla a transiciones más probables.
Para estos cálculos vamos a usar el paquete "mhsmm", pensado para calcular los modelos ocultos de Márkov y semi-markovianos. Usaremos la función smooth.discrete(), que realiza un suavizado simple de la serie temporal de los valores discretos.
obj <- smooth.discrete(y)
La secuencia suavizada de estados resultante por defecto, es una secuencia de estados más probable, obtenida con la ayuda del algoritmo Viterbi (la llamada decodificación global). También existe la opción de suavizar con otro método smoothed, donde se identificarán los estados individuales más probables (la llamada decodificación local).
Para suavizar la nueva serie temporal se aplica un método estándar
sm.y <- predict(obj, x = new.y)
- Corrección de las señales predichas según la curva de equilibro teórico
La idea consiste en lo siguiente. Teniendo la línea de balance, podemos calcular su desviación de la media. Según estas desviaciones, calculamos las señales correctivas. En los momentos en los que la desviación se vuelve negativa, o bien desactivan la ejecución de las señales predichas, o bien las hacen inversas. La idea en general es buena, pero hay un "pero". En la barra cero tenemos una señal predicha, pero no hay valores de balance y en consecuencia, tampoco hay señal de corrección. Aquí tenemos dos posibles soluciones: la clasificación, prediciendo la señal correctiva a partir de una señal correctiva existente y las desviaciones; o mediante regresión, usando las desviaciones existentes en las barras formadas, pronosticamos la desviación en la barra que comienza y en base a ello, determinamos la señal correctiva. Podemos optar por un camino más simple y adoptar el valor de la señal correctiva para la nueva barra en base a la ya formada.
Puesto que todos los métodos enumerados arriba ya nos son conocidos y están comprobados, intentaremos usar las posibilidades de las cadenas de Márkov. En el paquete "markovchain", aparecido recientemente, se presenta una serie de funciones que permiten determinar los parámetros del modelo oculto de Márkov y hacer un pronóstico de los futuros estados de varias barras futuras, en función de un proceso discreto observable. La idea ha sido tomada de este artículo.
3.4.3. Métricas
Para valorar la calidad de la predicción del modelo, se usa una serie entera de métricas (Accuracy, AUC, ROC y otras). En un artículo anterior he dicho que las métricas formales en nuestro caso no definen la calidad. El objetivo y la tarea del experto es obtener el máximo beneficio con una reducción permisible. Para estos objetivos se ha introducido el índice de calidad К, que muestra el beneficio medio en puntos en una barra en un segmento fijo de la historia con una longitud N. Se calcula dividiendo el Return(sig, N) acumulativo por la longitud del segmento N. Accuracy lo calcularemos solo de forma indicativa.
Al fin, realizaremos los cálculos y obtendremos los resultados:
- Datos fuente. Tenemos la matriz price[], obtenida como resultado de la ejecución de la función price.OHLC(). En ella se contienen las cotizaciones, el precio medio y el cuerpo de las barras. Todas las fuentes se pueden obtener cargando en Rstudio la "imagen" que se encuentra adjunta.
# Definimos las constantes n = 34; z = 37; cut = 0.9; soft = TRUE. # Definimos el método de pre-procesado method = c("center", "scale","spatialSign") # formamos el conjunto de datos original data.f <- form.data(n = n, z = z) # definimos el conjunto de predictores importantes best <- prepareBest(n = n, z = z, cut = cut, norm = T, method) # Los cálculos ocupan cerca de 3 min en un procesador de 2 núcleos. Usted puede saltarse esta etapa, # y usar de aquí en adelante todo el conjunto de predictores. Para ello, comente la línea anterior y # descomente las dos inferiores. # data.f <- form.data(n = n, z = z) # best <- colnames(data.f) %>% head(., ncol(data.f) - 1) # Preparamos el conjunto para el entrenamiento de la neurored DT <- prepareTrain(x = data.f[ , best], y = data.f$y, balance = TRUE, rati = 501, mod = "stratified", norm = TRUE, meth = method) # Cargamos las bibliotecas necesarias require(darch) require(foreach) # Definimos las funciones de activación disponibles actFun <- list(sig = sigmoidUnitDerivative, tnh = tanSigmoidUnitDerivative, lin = linearUnitDerivative, soft = softmaxUnitDerivative) # Convertimos la variable meta if (soft) { y <- DT$train$y %>% classvec2classmat()} # en una matriz if (!soft) {y = DT$train$y %>% as.integer() %>% subtract(1)} # a un vector con valores [0, 1] # creamos dataSet para el entrenamiento dataSet <- createDataSet( data = DT$train[ ,best] %>% as.matrix(), targets = y , scale = F ) # Definimos las constantes para la neurored # Número de neuronas en la capa de entrada (igual al número de predictores) nIn <- ncol(dataSet@data) # Número de neuronas en la capa de salida nOut <- ncol(dataSet@targets) # Vector con el número de neuronas en cada capa de la neurored # Si usted va usar otra estructura de neurored, hay que reescribir este vector Layers = c(nIn, 2 * nIn , nOut) # Otros datos relacionados con el entrenamiento Bath = 50 nEp = 100 ncd = 1 # Pre-entrenamiento de la neurored preMod <- pretrainDBN(Layers, Bath, dataSet, nEp, ncd) # Parámetros adicionales para el ajuste preciso Hid = 0.5; Ind = 0.2; nEp = 10 # Entrenamos los modelos, uno con backpropagation, y otro con rpropagation # Esto lo hacemos solo para comparar los resultados model <- foreach(i = 1:2, .packages = "darch") %do% { dbn <- preMod if (!soft) {act = c(2, 1)} if (soft) {act = c(2, 4)} fineMod(variant = i, dbnin = dbn, hd = Hid, id = Ind, dS = dataSet, act = act, nE = nEp) } # Simulamos para obtener Accuracy resAcc <- foreach(i = 1:2, .packages = "darch") %do% { testAcc(model[[i]]) } # Preparamos el conjunto de datos para la simulación del coeficiente de calidad DT.test <- prepareTest(n = n, z = z, T) # Simulamos resBal <- foreach(i = 1:2, .packages = "darch") %do% { testBal(model[[i]]) }
Vemos el resultado:
> resAcc[[1]]$Acc [1] 0.5728543 > resAcc[[2]]$Acc [1] 0.5728543
En ambos modelos ha resultado igual de malo.
Pero aquí tenemos el coeficiente de calidad —
> resBal[[1]]$K [1] 5.8 > resBal[[1]]$Kmax [1] 20.33673 > resBal[[2]]$Kmax [1] 20.33673 > resBal[[2]]$K [1] 5.8
muestra resultados exactamente iguales, además de bastante buenos. Eso sí, alarma la elevada reducción:
> resBal[[1]]$dd$maxdrawdown [1] 0.02767
Intentaremos corregir la reducción con la ayuda de una señal correctora obtenida a partir del cálculo realizado más abajo:
bal <- resBal[[1]]$bal # señal en las últimas 500 barras sig <- resBal[[1]]$sig[1:500] # media de la línea del balance ma <- pracma::movavg(bal,16, "t") # momento de la media roc <- TTR::momentum(ma, 3)%>% na.omit # desviación de la línea de balance con respecto a la media dbal <- (bal - ma) %>% tail(., length(roc)) # sumamos los dos vectores dbr <- (roc + dbal) %>% as.matrix() # calculamos la señal correctora sig.cor <- ifelse(dbr > 0, 1, -1) # sign(dbr) da el mismo resultado # señal resultante S <- sig.cor * tail(sig, length(sig.cor)) # balance de la señal resultante Bal <- cumsum(S * (price[ ,"CO"]%>% tail(.,length(S)))) # coeficiente de calidad de la señal corregida Kk <- tail(Bal, 1)/length(Bal) * 10 ^ Dig > Kk [1] 28.30382
El resultado mostrado de la calidad de la señal corregida es muy bueno. Veamos qué aspecto tienen en el gráfico las líneas dbal, roc y dbr, según las cuales calculamos la señal correctora.
matplot(cbind(dbr, dbal, roc), t="l", col=c(1,2,4), lwd=c(2,1,1)) abline(h=0, col=2) grid()
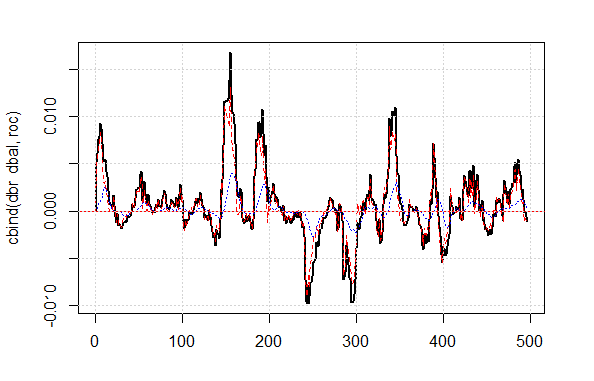
Fig.4 Desviación de la línea de balance con respecto a la media
La línea de balance antes y después de la corrección de las señales se muestra en la fig. 5.
plot(c(NA,NA,NA,Bal), t="l") lines(bal, col= 2) lines(ma, col= 4)
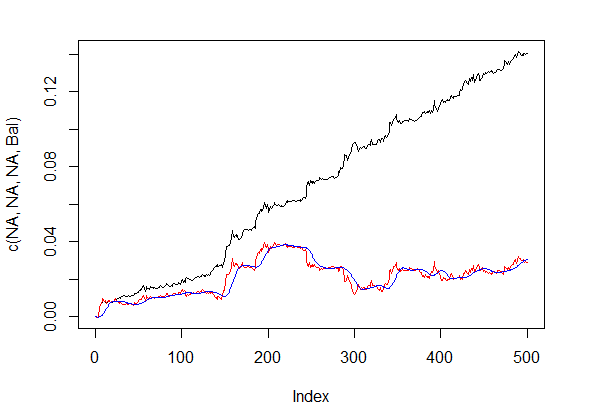
Fig.5 Línea de balance antes y después de la corrección de las señales
Bien, tenemos el valor de la señal predicho por la neurored en la barra cero, pero no tenemos el valor de corrección. Queremos usar el modelo oculto de Márkov para predecir esta señal. Según los estados observados de la señal correctora, determinamos los parámetros del modelo y a continuación, usando los valores de los últimos estados, predeciremos el estado de una barra adelante. Para comenzar, escribiremos la función correct(), que calculará la señal correctora conforme a la predicha, la señal resultante y sus índices de calidad. En otras palabras, escribiremos de forma compacta los cálculos que hemos realizado más arriba.
Quiero aclarar lo siguiente: por "señal" entendemos la secuencia de números enteros -1 y 1. Por "estado" entendemos la secuencia de números enteros 1 y 2, correspondientes a estas señales. Para las transformaciones mutuas usaremos las funciones:
#---13---------------------------------- sig2stat <- function(x) {x %>% as.factor %>% as.numeric} stat2sig <- function(x) ifelse(x==1, -1, 1) #----14--correct----------------------------------- correct <- function(sig){ sig <- Hmisc::Lag(sig) %>% na.omit bal <- cumsum(sig * (price[ ,6] %>% tail(.,length(sig)))) ma <- pracma::movavg(bal, 16, "t") roc <- TTR::momentum(ma, 3)%>% na.omit dbal <- (bal - ma) %>% tail(., length(roc)) dbr <- (roc + dbal) %>% as.matrix() sig.cor <- sign(dbr) S <- sig.cor * tail(sig, length(sig.cor)) bal <- cumsum(S * (price[ ,6]%>% tail(.,length(S)))) K <- tail(bal, 1)/length(bal) * 10 ^ Dig Kmax <- max(bal)/which.max(bal) * 10 ^ Dig dd <- fTrading::maxDrawDown(bal) corr <<- list(sig.c = sig.cor, sig.res = S, bal = bal, Kmax = Kmax, K = K, dd = dd) return(corr) }
Para obtener el vector de señales con una predicción de 1 barra adelante, usaremos el paquete "markovchain" y la función pred.sig().
#---15---markovchain---------------------------------- pred.sig <- function(sig, prev.bar = 10, nahead = 1){ require(markovchain) # Transformamos en estados las señales correctoras observadas stat <- sig2stat(sig) # Calculamos los parámetros del modelo # si el modelo aún no existe en el entorno if(!exists('MCbsp')){ MCbsp <<- markovchainFit(data = stat, method = "bootstrap", nboot = 10L, name="Bootstrap MС") } # Establecemos las constantes necesarias newData <- tail(stat, prev.bar) pr <- predict(object = MCbsp$estimate, newdata = newData, n.ahead = nahead) # fijamos la señal predicha a la señal de entrada sig.pr <- c(sig, stat2sig(pr)) return(sig.pr = sig.pr) }
Ahora anotamos el cálculo de la señal resultante para darle al experto una forma compacta:
sig <- resBal[[1]]$sig sig.cor <- correct(sig) sig.c <- sig.cor$sig.c pr.sig.cor <- pred.sig(sig.c) sig.pr <- pr.sig.cor$sig.pr # Vector de señales resultante para el experto S <- sig.pr * tail(sig, length(sig.pr))
- Suavizado de la señal predicha.
#---16---smooth------------------------------------
smoooth <- function(sig){
# suavizamos la señal predicha
# definimos los parámetros del modelo oculto de Márkov
# si el modelo aún no existe en el entorno
require(mhsmm)
if(!exists('obj.sm')){
obj.sm <<- sig2stat(sig)%>% smooth.discrete()
}
# suavizamos la señal con el modelo obtenido
sig.s <- predict(obj.sm, x = sig2stat(sig))%>%
extract2(1)%>% stat2sig()
# calculamos el balance con la señal suavizada
sig.s1 <- Hmisc::Lag(sig.s) %>% na.omit
bal <- cumsum(sig.s1 * (price[ ,6]%>% tail(.,length(sig.s1))))
K <- tail(bal, 1)/length(bal) * 10 ^ Dig
Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
dd <- fTrading::maxDrawDown(bal)
return(list(sig = sig.s, bal = bal, Kmax = Kmax, K = K, dd = dd))
}
Calculamos y comparamos el balance basado en las señales predicha y suavizada.
sig <- resBal[[1]]$sig sig.sm <- smoooth(sig) plot(sig.sm$bal, t="l") lines(resBal[[1]]$bal, col=2)
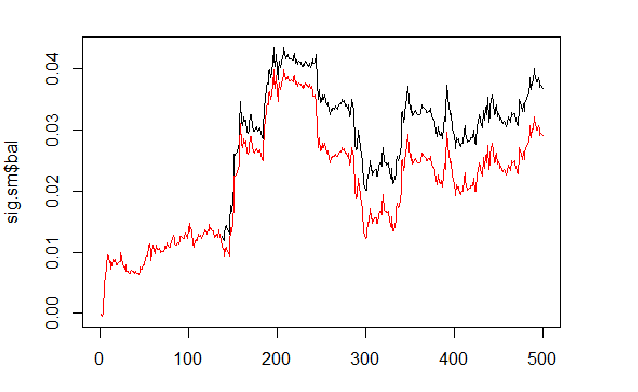
Fig.6 Balance basado en las señales suavizada y predicha
Como podemos ver, la calidad es ahora significativamente mayor, pero la reducción ha permanecido. No vamos a usar este método en nuestro experto.
sig.sm$dd $maxdrawdown [1] 0.02335 $from [1] 208 $to [1] 300
4. Esquema estructural del algoritmo del experto
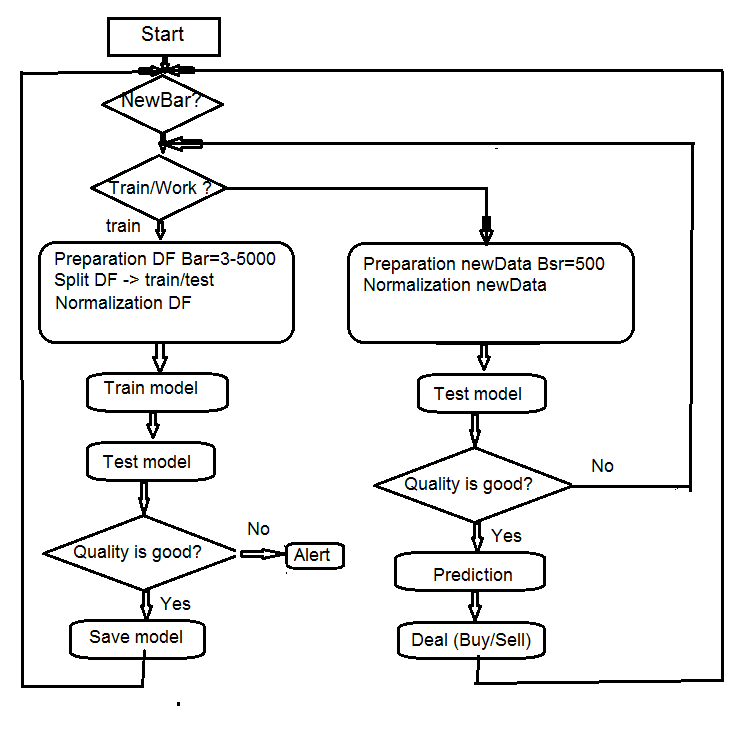
Fig.7 Esquema estructural del algoritmo del experto
4.1. Describiendo el funcionamiento del experto
Dado que el funcionamiento del experto tiene lugar en dos flujos (mql y Rterm), describiremos el proceso de interacción entre ellos. Hablaremos aparte sobre qué operaciones se ejecutan en cada uno de ellos.
4.1.1 MQL
Después de colocar el experto en el gráfico:
en la función init()
- comprobamos los ajustes del terminal (disponibilidad de DLL, permiso para comerciar);
- establecemos el temporizador;
- iniciamos Rterm;
- calculamos y transferimos al entorno del proceso R las constantes necesarias para el funcionamiento;
- comprobamos si funciona Rterm, si no, alerta;
- salimos de init().
En la función deinit()
- detenemos el temporizador;
- eliminamos los objetos gráficos;
- Detenemos Rterm.
En la función onTimer()
- comprobamos si funciona Rterm;
- si Rterm no está ocupado y la nueva barra es (LastTime != Time[0]):
- establecemos la profundidad de la historia dependiendo de si se trata o no del primer inicio del experto;
- formamos cuatro vectores de las cotizaciones (Open, High, Low, Close) y los transmitimos a Rterm;
- iniciamos el script y salimos sin esperar el resultado de su ejecución;
- establecemos la bandera get_sig = true;
- establecemos LastTime= Time[0].
- De lo contrario, si Rterm funciona, no está ocupado y la bandera get_sig = true:
- definimos la longitud del vector sig, que debemos recibir de Rterm;
- adaptamos el tamaño del vector de recepción al tamaño de la fuente. Si falla la compilación, el proceso R caerá;
- obtenemos el orden de las señales (vector);
- según la última señal, determinamos qué operación hay que ejecutar (BUY, SELL, Nothing);
- si hemos recibido una señal real, y no ERR, reseteamos la bandera get_sig=false.
- después procedemos de manera estándar:
- CheckForClose()
- CheckForOpen()
En esta parte, nuestro experto es un "Ejecutor" que efectúa las disposiciones obtenidas de su parte "pensante", envía órdenes, realiza un seguimiento del estado de las posiciones abiertas y los posibles errores durante su apertura, además de otras muchas funciones de un experto normal.
4.1.2 Rterm
El script operativo consta de dos partes. Una de ellas se ejecuta con la primera entrada, la segunda, en las siguientes.
- si first:
- cargamos (en caso imprescindible) las bibliotecas necesarias del repositorio en internet, las instalamos y cargamos en el entorno Rterm;
- definimos las funciones necesarias;
- creamos una matriz de cotizaciones;
- preparamos el conjunto de datos para el entrenamiento y la simulación del modelo;
- creamos y entrenamos el modelo;
- ponemos a prueba el modelo;
- calculamos las señales para la ejecución;
- comprobamos la calidad de la predicción. Si es igual o mayor al mínimo establecido, continuamos. En caso contrario, transmitimos una alerta.
- si !first:
- preparamos el conjunto de datos para la simulación y la predicción;
- probamos el modelo con los nuevos datos;
- calculamos las señales para la ejecución;
- comprobamos la calidad de la predicción. Si es igual o superior al mínimo establecido, continuamos. En caso contario, establecemos first = TRUE, es decir, requerimos que el modelo se entrene de nuevo.
4.2. Auto-control y Auto-aprendizaje
El control de calidad de la predicción de las señales con el modelo lo realizaremos usando el coeficiente K. Son posibles dos variantes para definir los límites de la calidad permisible. La primera es estabecer una caída máxima del coeficiente con respecto a su valor máximo. Es decir, si К < Kmax * 0.8, entonces es mejor entrenarse de nuevo o detener la ejecución de las señales con el experto. La segunda es estabecer un valor K mínimo, alcanzado el cual habrá que ejecutar las mismas acciones. En el experto vamos a realizar el segundo método.
5. Orden de instalación e iniciación
En los archivos adjuntos al artículo presentamos dos expertos: e_DNSAE.mq4 y e_DNRBM.mq4. Estos usan conjuntos de datos idénticos y un conjunto de funciones casi igual. La diferencia consiste en el modelo de red profunda usado. El primero usa DN, SAE inicializada y el paquete "deepnet". Podrá encontrar la descripción del paquete en el artículo anterior sobre las redes neuronales. El segundo usa DN, RBM inicializada y el paquete "darch".
Distribuimos de forma estándar:
- *.mq4 en la carpeta ~/MQL4/Expert
- *.mqh en la carpeta ~/MQL4/Include
- *.dll en la carpeta ~/MQL4/Libraries
- *.r en la carpeta C:/RData
Corregimos la ruta al lenguaje R establecido y hacia los scripts (tanto en mq4: #define, como en *.r: source() ).
Con el primer inicio, el experto carga las bibliotecas necesarias del repositorio y las instala en el entorno Rterm. Usted también podrá instalarlas de forma preliminar de acuerdo con la lista adjunta.
Normalmente, el proceso R "cae" precisamente debido a la ausencia de las bibliotecas necesarias, o porque las rutas hasta los scripts se han indicado de forma inadecuada, solo en último lugar el fallo se debe a los errores de sintaxis.
Se adjunta aparte una captura de la sesión con los datos fuente, podrá abrirla con la ayuda de Rstudio, para comprobar que todas las funciones desempeñen su trabajo correctmente, así como para llevar a cabo experimentos.
6. Rutas y métodos de mejora de los índices de calidad.
Hay varias vertientes en las que se pueden mejorar los índices de calidad.
- valoración y elección de los indicadores: aplicar algoritmo genético de optimización (GA).
- definir los parámetros óptimos de los predictores y de la variable meta - GA.
- definir los parámetros óptimos de la neurored - GA.
Conclusión
Los experimentos realizados con el paquete "darch" han mostrado los siguientes resultados.
- La neurored profunda, la RBM inicializada, se entrenan peor que con SAE. Para nosotros, esto no es una noticia.
- La red aprende deprisa.
- El paquete tiene un gran potencial en cuanto a la mejora de la calidad de la predicción, proporcionando acceso prácticamente a todos los parámetros internos del modelo.
- El paquete permite usar solo una neurored o RBM con un gran surtido de parámetros con respecto a otros, estándar.
- El paquete se desarrolla de forma permanente, y en el siguiente lanzamiento el desarrollador promete que habrá posibilidades adicionales.
- La integración del lenguaje R con el terminal МТ4/МТ5, prometida por los desarrolladores, dará la posibilidad a los tráders de usar los algoritmos más recientes sin utilizar DLL adicionales.
Se adjunta
- La sesión R del proceso Sess_DNRBM_GBPUSD_30
- Un archivo zip con el experto " e_DNRBM "
- Un archivo zip con el experto " e_DNSAE"
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1628
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Cómo desarrollar y depurar rápidamente cualquier estrategia de scalping en MetaTrader 5
Cómo desarrollar y depurar rápidamente cualquier estrategia de scalping en MetaTrader 5
 Interfaces gráficas X: Actualizaciones para la librería Easy And Fast (build 2)
Interfaces gráficas X: Actualizaciones para la librería Easy And Fast (build 2)
 Asesor experto multiplataforma: reutilizando los componentes de la Biblioteca Estándar MQL5
Asesor experto multiplataforma: reutilizando los componentes de la Biblioteca Estándar MQL5
 Interfaces gráficas IX: Elementos "Indicador de progreso" y "Gráfico lineal" (Capítulo 2)
Interfaces gráficas IX: Elementos "Indicador de progreso" y "Gráfico lineal" (Capítulo 2)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso