Evaluación y selección de variables en modelos de aprendizaje de máquinas
4 715
0
Introducción
Este artículo se centra en aspectos específicos relacionados con la elección, los prerrequisitos y la evaluación de las variables de entrada de los modelos de aprendizaje de máquinas. Vamos a describir varios métodos de normalización, y también sus características. Revelaremos los momentos importantes del proceso que influyen de manera decisiva en el resultado final de los modelos de entrenamiento. Echaremos un vistazo exhaustivo a métodos nuevos, poco conocidos, que determinan la naturaleza informativa y la visualización de los datos de entrada.
El paquete "RandomUniformForests" nos ayudará a calcular y analizar el concepto tan importante de variable, a diferentes niveles, combinándolo en varias situaciones distintas. Estudiaremos la correspondencia de los predictores y un objetivo, así como la interacción que existe entre los predictores, y aprenderemos a seleccionar el conjunto óptimo de predictores teniendo en cuenta los aspectos más importantes.
Con el paquete "RoughSets", echaremos un vistazo al problema de elegir los predictores desde una perspectiva diferente, basándonos en otro concepto. Demostraremos que se pueden optimizar tanto los conjuntos de predictores como los ejemplos de entrenamiento.
Ejecutamos nuestros cálculos y experimentos con el lenguaje R, en concreto Revolution R Open 3.2.1 .
1. Variables de entrada (signos, predictores)
Las variables de entrada (independiente, predictores) y salida (destino) pueden ser de estos tipos:
Binario — tiene dos valores: {0,1}, {-1,1}, {"sí", "no"}, {"hombre", "mujer"}.
Nominal (factores) con un número finito de niveles. Por ejemplo, el factor "día de la semana" tiene siete niveles, cada uno de los cuales tiene un nombre (lunes, martes, etc). Los factores se pueden ordenar y desordenar. Por ejemplo, el factor "hora del día" tiene 24 niveles y está ordenado. El factor "distrito de la ciudad" tiene 32 niveles y está desordenado porque todos los niveles tienen la misma importancia. La declaración de un factor ordenado se tiene que especificar de forma explícita.
Cuantitativo continuo (numérico). El rango de variables continuas de infinito a +infinito.
Los datos de las cotizaciones (OHLC) no se utilizan como variables de entrada numéricas. Se aplica el logaritmo de la diferencia o el logaritmo del ratio de la cotización. Sin embargo, se suele utilizar una combinación de varios indicadores. Si todas las variables son uniformes, el conjunto de datos de entrada se configura como una matriz; o, más frecuentemente, como un dataframe en donde cada columna es una variable, y donde cada línea representa el estado de las variables en un momento determinado. En la primera o última columna se coloca una variable destino.
1.1. Limpieza
La limpieza implica lo siguiente:
a) Eliminación o transformación de los datos perdidos (inciertos) "NA".
Muchos modelos no permiten agujeros (gaps) en los datos de entrada. Por lo tanto, tenemos que eliminar las filas que contienen datos perdidos, o bien rellenar los agujeros con datos interpolados. Existen varios paquetes que proporcionan las funciones necesarias para este propósito. La eliminación de los datos inciertos NA viene incorporada de forma predeterminada, pero es mejor que la implemente usted mismo por medio de na.omit(dt) antes del entrenamiento real.
b) Eliminación de las variables "cero-opcionales" (numéricas y nominales).
En algunos casos, sobre todo durante la transformación o conversión de variables, los predictores pueden aparecer con un solo valor único, o con varios valores que ocurren muy raramente. En muchos modelos esto puede llevar a un colapso o derivar en operaciones inestables. Debemos identificar los predictores de varianza cercana a cero y eliminarlos antes de realizar la simulación. Utilice la función caret::nearZeroVar() del paquete "caret" para identificar y eliminar tales predictores. Aunque la necesidad de este punto es un tema de debate.
c) Identificación y eliminación de los predictores correlacionados (numéricos).
Mientras que algunos modelos gestionan los predictores correlacionados excepcionalmente bien (por ejemplo, PLS, LARS y otros parecidos mediante la regularización L1), a otros modelos les puede resultar más conveniente reducir el nivel de correlación entre predictores. Para identificar y eliminar los predictores fuertemente correlacionados (por ejemplo, el umbral del coeficiente de correlación se establece a un valor > 0.9) utilizamos la función caret::findCorrelation() del paquete "caret". Este paquete es muy potente, y recomiendo utilizarlo en las tareas de análisis.
d) Identificación y eliminación de las dependencias lineales (factores).
La función caret::findLinearCombos() utiliza la QR-expansión de transferencias de la matriz para presentar combinaciones lineales, si existen. Analicemos, por ejemplo, esta matriz:
ltfrDesign <- matrix(0, nrow = 6, ncol = 6) ltfrDesign[, 1] <- c(1, 1, 1, 1, 1, 1) ltfrDesign[, 2] <- c(1, 1, 1, 0, 0, 0) ltfrDesign[, 3] <- c(0, 0, 0, 1, 1, 1) ltfrDesign[, 4] <- c(1, 0, 0, 1, 0, 0) ltfrDesign[, 5] <- c(0, 1, 0, 0, 1, 0) ltfrDesign[, 6] <- c(0, 0, 1, 0, 0, 1)
Nótese que las columnas 2 y 3 son adiciones a la primera. De igual modo, las columnas 4, 5 y 6 se forman en la primera columna. La función caret::findLinearCombos() devuelve la lista que enumera estas dependencias junto con el vector de las posiciones de la columna, que pueden borrarse para eliminar las dependencias lineales.
comboInfo <- findLinearCombos(ltfrDesign) comboInfo $linearCombos $linearCombos[[1]] [1] 3 1 2 $linearCombos[[2]] [1] 6 1 4 5 $remove [1] 3 6 ltfrDesign[, -comboInfo$remove] [,1] [,2] [,3] [,4] [1,] 1 1 1 0 [2,] 1 1 0 1 [3,] 1 1 0 0 [4,] 1 0 1 0 [5,] 1 0 0 1 [6,] 1 0 0 0
Este tipo de dependencias puede ocurrir al utilizar un número elevado de predictores binarios, o cuando los predictores de factor se convierten en una "simulación".
1.2. Transformación, preprocesamiento de datos
Muchos modelos requieren que los datos de entrada numéricos estén en un rango determinado (normalización, estandarización), o que se conviertan de alguna manera (factores). Por ejemplo, las redes neuronales y las máquinas de vectores de soporte (SVM) aceptan datos de entrada en el rango [-1, 1] o [0, 1]. Hay muchos paquetes del lenguaje R que ofrecen características especiales para realizar tales transformaciones, o bien ellos mismos ejecutan la conversión. Recuerde que la definición de los parámetros de preprocesamiento se lleva a cabo solo sobre un conjunto entrenamiento de datos de entrada. Los conjuntos de prueba y validación, los datos nuevos y los modelos de predicción entrantes se convierten con los parámetros obtenidos en el conjunto entrenamiento.
Normalización (escalada)
Una fórmula general para convertir una variable en el rango {+ h, -l}. Dependiendo del rango deseado h = +1; l = (-1 o 0). Algunos recursos recomiendan reducir el rango a {-0.9; 0.9} o {0.1; 0.9} para evitar utilizar secciones de saturación de funciones de activación (tanh/sig). Esto se refiere a las redes neuronales, SVM y otros modelos con funciones de activación con nombre.
Xn = (x - min(x)) / (max(x) - min(x)) * (h - l) + l;
La transformación inversa (denormalización) se ejecuta de acuerdo a esta fórmula:
x = (x - l) / (h - l) * (max(x) - min(x)) + min(x);
Estandarización
Sabiendo que una distribución variable es casi normal, podemos normalizar mediante la fórmula siguiente:
x = (x - mean(x)) / sd(x)
Algunos paquetes proporcionan funciones especiales para el preprocesamiento. Así pues, la función preProcess() del paquete "caret" ofrece estos métodos de preprocesamiento: "BoxCox", "YeoJohnson", "expoTrans", "center", "scale", "range", "knnImpute", "bagImpute", "medianImpute", "pca", "ica" y "spatialSign".
"BoxCox", "YeoJohnson", "expoTrans"
La conversión Yeо-Johnson se parece ligeramente al modelo Box-Cox, sin embargo puede aceptar predictores con valores cero o negativos, mientras que los valores del predictor de la transformación Box-Cox tienen que ser estrictamente positivos. La transformación exponencial de Manly (1976) también se puede aplicar en valores positivos y negativos.
la transformación de "rango" escala los datos dentro del rango [0, 1]. ¡Esto es importante! Si los valores de las nuevas muestras son superiores o inferiores a los utilizados en el sistema de entrenamiento, entonces dichos valores estarán fuera del rango y el resultado previsto será incorrecto.
"center" — se descuenta la media, "scale" se divide por la desviación estándar (escala). Normalmente se utilizan juntas, lo que se llama "estandarización".
"knnImpute", "bagImpute", "medianImpute" — cálculo de los datos perdidos o indefinidos, utilizando algoritmos diferentes.
"spatialSign" — transformación, datos del predictor de proyectos del círculo unitario en dimensiones р, donde р es el número de predictores. Fundamentalmente, los datos del vector se dividen por su norma. Los datos se tienen que centrar y escalar antes de la transformación.
"pca" — en algunos casos se utiliza el análisis del componente principal para transformar los datos en un subespacio más pequeño, donde las nuevas variables no se correlacionan entre sí. Este método realiza tanto el centrado como el escalado, y los nombres de la columna se cambian a PC1, PC2, etc.
"isa" — del mismo modo, se puede utilizar el análisis de componente independiente para encontrar nuevas variables que sean combinaciones lineales del conjunto original, donde los componentes son independientes (a diferencia de la no correlación en PCA). Las nuevas variables se marcan como IC1, IC2, etc.
El paquete "clusterSim" es excelente. Sirve para encontrar los procedimientos de agrupación de datos óptimos, y cuenta con la función dataNormalization() para normalizar los datos de 18 maneras diferentes, tanto por columnas como por filas. En esta lista aparecen todos:
n1 — estandarización ((x – mean) / sd);
n2 — estandarización posicional ((x – median) / mad);
n3 — unificación ((x – mean) / range);
n3а — unificación posicional ((x – median) / range);
n4 — unificación con cero mínimo ((x – min) / range);
n5 — normalización en el rango <-1, 1> ((x – mean) / max(abs(x – mean)));
n5a — normalización posicional en el rango <-1,1> ((x – median) / max(abs(x-median)));
n6 — transformación de cociente (x/sd);
n6a — transformación de cociente posicional (x/mad);
n7 — transformación de cociente (x/range);
n8 — transformación de cociente (x/max);
n9 — transformación de cociente (x/mean);
n9a — transformación de cociente posicional (x/median);
n10 — transformación de cociente (x/sum);
n11 — transformación de cociente (x/sqrt(SSQ));
n12 — normalización ((x-mean)/sqrt(sum((x-mean)^2)));
n12a — normalización posicional ((x-median)/sqrt(sum((x-median)^2)));
n13 — normalización, siendo cero el punto central ((x-midrange)/(range/2)).
"Variables ficticias" - muchos modelos tienen que transformar los predictores de factor en "simulaciones". La función dummyVar() del paquete "caret" puede utilizarse con este propósito. La función toma la fórmula y el conjunto de datos, y muestra el objeto que puede utilizarse en la creación de variables ficticias.
2. Datos de salida (variable destino)
Ya que estamos resolviendo el problema de la clasificación, la variable destino es un factor con un número de niveles (clases). La mayoría de modelos obtiene mejores resultados al entrenar con un destino que tiene dos clases. Cuando hay muchas clases especiales se tienen que tomar medidas para gestionar bien estas cuestiones. La variable destino se codifica en el proceso de preparación de los datos de entrenamiento y se descifra después de la predicción.
Las clases se codifican de varias maneras diferentes. El paquete "Simulation of neural networks in the Stuttgart University" (simulación de redes neuronales de la Universidad de Stuttgart) proporciona dos funciones: decodeClassLabels() , que codifica las clases de vectores en la matriz que contiene las columnas correspondientes, y encodeClassLabels(), que hace la transformación inversa después de la predicción del modelo. Por ejemplo:
> data(iris) > labels <- decodeClassLabels(iris[,5]) > class <- encodeClassLabels(labels) > head(labels) setosa versicolor virginica [1,] 1 0 0 [2,] 1 0 0 [3,] 1 0 0 [4,] 1 0 0 [5,] 1 0 0 [6,] 1 0 0 > head(class) [1] 1 1 1 1 1 1
Por lo tanto, el número de salidas del modelo es igual al número de clases objetivo. Este no es el único método de codificación (uno a uno) que se aplica al destino. Si el destino tiene dos clases, se puede gestionar una salida. No cabe duda de que codificar una variable destino en la matriz tiene muchas ventajas.
3. Evaluación y selección de predictores
La experiencia demuestra que el incremento de los datos de entrada (predictor) no siempre implica una mejora en el modelo, sino todo lo contrario. Los predictores 3-5 influyen en el resultado. Muchos paquetes de agregación, tales como "rminer", "caret", "SuperLearner" y "mlr", vienen con funciones integradas que calculan la importancia de las variables. La mayoría de aproximaciones que reducen el número de predictores se pueden dividir en dos categorías (utilizamos la terminología de John, Kohavi y Pfleger, 1994):
- Filtrado. Los métodos de filtrado evalúan la relevancia de los predictores fuera de los modelos de predicción; finalmente, el modelo solo utiliza los predictores que cumplen unos criterios determinados. Por ejemplo, en las tareas de clasificación, los predictores se pueden evaluar de manera individual para comprobar si existe una relación admisible entre el predictor y las clases observadas. Sólo los predictores que tienen dependencias de pronóstico importantes se incluyen el el modelo de clasificación.
Envoltura. Los métodos de envoltura evalúan varios modelos y utilizan procedimientos que añaden o quitan predictores con el objetivo de encontrar la combinación óptima que optimiza la eficiencia del modelo. En esencia, los métodos de envoltura son algoritmos de búsqueda que consideran los predictores como entradas, y la eficiencia del modelo como salidas que se tienen que optimizar. Los predictores se pueden iterar de muchas maneras distintas: eliminación/adición recursiva, algoritmos genéticos y recocido simulado, entre otros.
En este artículo no trataremos las técnicas de envoltura, sino que analizaremos varios métodos de filtrado desde puntos de vista nuevos; en mi opinión, estos enfoques eliminan los inconvenientes mencionados.
3.1. Filtrado
La importancia de los predictores, esto es, su capacidad informativa, se establece mediante métodos y criterios externos. Llamamos importancia a la contribución de las variables en la mejora de la calidad de la predicción del modelo.
Tras lo cual, normalmente tendremos tres opciones:
Tomar un número determinado de predictores que tengan la importancia más alta.
Tomar el porcentaje del total de predictores con la importancia más alta.
- Tomar los predictores cuya importancia supere el umbral.
Todos los casos permiten optimizar la cantidad, el porcentaje o el umbral.
Formemos ahora un conjunto de datos de entrada y salida para analizar los métodos y realicemos algunos experimentos.
Datos de entrada
Incluiremos 11 indicadores (osciladores) sin ninguna preferencia previa en el conjunto de entrada. Vamos a tomar algunas variables de los indicadores. A continuación escribimos una función para formar el conjunto de entrada de 17 variables.
Tomamos las cotizaciones de las últimas 4000 barras de TF = M30 / EURUSD.
In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp -DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p)%>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA")%>% as.data.frame() %>% mutate(., oscK = fastK - fastD)%>% transmute(.,slowD, oscK)%>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) vol <- volatility(price[ ,1:4], n = p, calc = "yang.zhang", N = 144) In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, vol) return(In) }
Estos indicadores se conocen muy bien y suelen aplicarse con frecuencia, así que no explicaremos muchos detalles acerca de los mismos. Simplemente comentaré el método de cálculo "pipe"(%>%) del paquete "magrittr", basado en el ejemplo del indicador MACD. Este es el orden de escritura:
Se calcula el indicador que devuelve dos variables (macd, signal).
La matriz obtenida se convierte al dataframe.
Se añade la nueva variable vsig al dataframe (en orden de escritura):
- Se toma la variable signal;
- Se calcula la primera diferencia;
- Los vectores NA se añaden al principio porque al calcular la primera diferencia el vector es una unidad menor que el original;
- Se multiplica por 10.
Se eligen solamente las variables necesarias (columnas) vsig, signal del dataframe.
El dataframe se convierte a la matriz.
Este método de cálculo es muy conveniente cuando los resultados intermedios no hacen falta. Además, las fórmulas se leen y se entienden mejor.
Así pues obtendremos la matriz de los datos de entrada.
x <- In(p = 16) > summary(x) DX ADX oscDX Min. : 0.02685 Min. : 5.291 Min. :-93.889 1st Qu.: 8.11788 1st Qu.:14.268 1st Qu.: -9.486 Median :16.63550 Median :18.586 Median : 5.889 Mean :20.70162 Mean :20.716 Mean : 4.227 3rd Qu.:29.90428 3rd Qu.:24.885 3rd Qu.: 19.693 Max. :79.80812 Max. :59.488 Max. : 64.764 NA's :16 NA's :31 NA's :16 ar tr atr Min. :-100.0000 Min. :0.0000000 Min. :0.000224 1st Qu.: -50.0000 1st Qu.:0.0002500 1st Qu.:0.000553 Median : -6.2500 Median :0.0005600 Median :0.000724 Mean : -0.8064 Mean :0.0008031 Mean :0.000800 3rd Qu.: 50.0000 3rd Qu.:0.0010400 3rd Qu.:0.000970 Max. : 100.0000 Max. :0.0150300 Max. :0.003104 NA's :16 NA's :1 NA's :16 cci chv cmo Min. :-515.375 Min. :-0.67428 Min. :-88.5697 1st Qu.: -84.417 1st Qu.:-0.33704 1st Qu.:-29.9447 Median : -5.674 Median : 0.03057 Median : -2.4055 Mean : -1.831 Mean : 0.11572 Mean : -0.6737 3rd Qu.: 83.517 3rd Qu.: 0.44393 3rd Qu.: 28.0323 Max. : 387.814 Max. : 3.25326 Max. : 94.0649 NA's :15 NA's :31 NA's :16 sign vsig rsi Min. :-0.38844 Min. :-0.43815 Min. :12.59 1st Qu.:-0.07124 1st Qu.:-0.05054 1st Qu.:39.89 Median :-0.00770 Median : 0.00009 Median :49.40 Mean :-0.00383 Mean :-0.00013 Mean :49.56 3rd Qu.: 0.05075 3rd Qu.: 0.05203 3rd Qu.:58.87 Max. : 0.38630 Max. : 0.34871 Max. :89.42 NA's :33 NA's :34 NA's :16 slowD oscK SMI Min. :0.0499 Min. :-0.415723 Min. :-74.122 1st Qu.:0.2523 1st Qu.:-0.043000 1st Qu.:-33.002 Median :0.4720 Median : 0.000294 Median : -5.238 Mean :0.4859 Mean :-0.000017 Mean : -4.089 3rd Qu.:0.7124 3rd Qu.: 0.045448 3rd Qu.: 22.156 Max. :0.9448 Max. : 0.448486 Max. : 75.079 NA's :19 NA's :17 NA's :25 signal vol Min. :-71.539 Min. :0.003516 1st Qu.:-31.749 1st Qu.:0.008204 Median : -5.319 Median :0.011274 Mean : -4.071 Mean :0.012337 3rd Qu.: 19.128 3rd Qu.:0.015312 Max. : 71.695 Max. :0.048948 NA's :33 NA's :16
Datos de salida (destino)
Utilizaremos las señales recibidas de ZZ como variable destino. Esta es la fórmula de cálculo del zigzag:
ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) if(ch > 1) ch <- ch/(10 ^ (Dig - 1)) if(mode == "m"){pr <- pr[ ,'Med']} if(mode == "hl") {pr <- pr[ ,c("High", "Low")]} if(mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1]} dz <- zz %>% diff %>% c(0,.) sig <- sign(dz) return(cbind(zz, sig)) }
Los parámetros de la función:
- pr = price — matriz de cotizaciones OHLCMed;
- ch — longitud mínima de la curva del zigzag en puntos (4 signos);
- mode — precio aplicado (m — media, hl — máximo y mínimo, cl — cierre). Se utiliza la media de forma predeterminada.
La función devuelve la matriz con dos variables: el zigzag y la señal obtenida, de acuerdo a la inclinación del zigzag en el intervalo [-1; 1].
Calculamos las señales de dos ZZ con una longitud de tramo diferente:
out1 <- ZZ(ch = 25) out2 <- ZZ(ch = 50)
Así es como se muestran en el gráfico:
> matplot(tail(cbind(out1[ ,1], out2[ ,1]), 500), t="l")
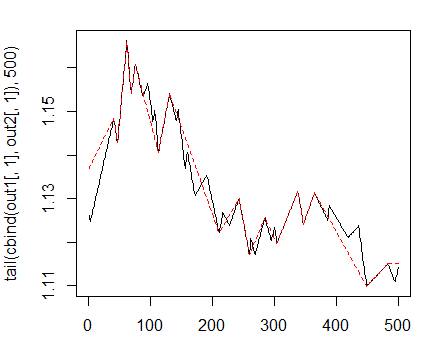
Fig. 1. Longitud mínima de las curvas de los zigzags 25/75 p
A continuación utilizamos el primer ZZ con el tramo más corto. Vamos a combinar en el dataframe general las variables de entrada y el destino, eliminando los datos indefinidos con la condición = "0", y también quitaremos la clase "0" del destino.
> data <- cbind(as.data.frame(x) , Class = factor(out1[ ,2])) %>% + na.omit > data <- data[data$Class != 0, ] > data$Class <- rminer::delevels(data$Class, c("0", "1"), "1")
Esta es la distribución de las clases en el destino:
> table(data$Class) -1 1 1980 1985
Por lo que podemos observar las clases están bien balanceadas. Hemos preparado un conjunto de datos de entrada y salida, por lo tanto estamos en condiciones de valorar la importancia de los predictores.
Primero de todo comprobaremos la correlación de los datos de entrada:
> descCor <- cor(data[ ,-ncol(data)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03803 0.26310 0.31750 0.57240 0.95730
¿Qué variables de entrada tienen una correlación superior al 90%?
> highCor <- caret::findCorrelation(descCor, cutoff = .90) > highCor [1] 12 15
La respuesta es — rsi y SMI. Formamos, pues, un conjunto de datos sin estas dos variables y observamos la correlación de las restantes.
> data.f <- data[ ,-highCor] > descCor <- cor(data.f[ ,-ncol(data.f)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03219 0.21610 0.27060 0.47820 0.89880
Evaluamos la importancia de la variable (VI) con un nuevo paquete, "Random Uniform Forests", que proporciona un amplio abanico de instrumentos de análisis y visualización. En palabras de los mismos desarrolladores, determinar la importancia de las variables sirve para evaluar qué, cuando, dónde y cómo repercuten en el problema a solucionar.
Este paquete proporciona varias medidas de importancia de una variable. Vamos a analizarlas antes de continuar con nuestro estudio exhaustivo.
La importancia de la variable global establece variables que reducen al máximo el error de predicción, pero no nos dice nada sobre la influencia de la variable importante en las respuestas.
Por ejemplo, nos interesa saber qué variables tienen una influencia mayor sobre la clase separada, o cómo es la interacción de las variables.
La importancia de la variable se mide por unidades y árboles, lo que hace que las variables tengan un valor; los puntos de corte son accidentales. En consecuencia, todas las variables tienen la misma probabilidad de ser seleccionadas, pero recibe la importancia la que más reduce la entropía en cada nodo.
Importancia de la variable local
Definición: Un predictor es importante localmente en la primera orden si para la misma observación y todos los árboles, tiene la mayor frecuencia de aparición en un nodo terminal.
Importancia parcial
Definición: Un predictor es importante parcialmente si para la misma observación, clase y todas las órdenes, tiene la mayor frecuencia de aparición en el nodo terminal.
Interacciones
Nos interesa saber cómo los predictores influyen en el problema. Por ejemplo, algunas variables pueden tener un impacto relativamente bajo en el problema, pero pueden impactar más fuertemente en las variables relevantes; o una variable puede interactuar mucho con los demás, lo que la convierte en influyente. Definamos qué se entiende por interacción.
Definición: Un predictor interactúa con otro si en la misma observación, y para todos los árboles, los dos tienen respectivamente las frecuencias más altas de aparición en el nodo terminal.
Dependencias parciales
Estas son las herramientas que permiten determinar cómo una variable determinada, un par de variables, influyen en el valor de la respuesta, conociendo el valor del resto de variables. O dicho de otro modo, una dependencia parcial es la zona donde la variable ejerce un efecto de influencia máximo, en función del valor de la respuesta. El concepto de dependencia parcial se lo debemos a Friedman (2002), quien lo utilizó por primera vez en Gradient Boosting Machines (GBM), aunque se implementa de manera diferente en Random Uniform Forests.
De acuerdo a las ideas aplicadas en el paquete Random Uniform Forests, podemos determinar la importancia de una variable basándonos en el siguiente esquema: Importancia = contribución + interacción, donde contribución es la influencia de una variable sobre los errores de predicción, e interacción es el impacto producido en otras variables.
Realizando experimentos
Dividiremos nuestro conjunto de datos data.f[] en conjuntos de entrenamiento y pruebas con ratio 2/3, normalizaremos en el rango -1;1 y probaremos el modelo. Utilizamos la función rminer::holdout() para dividir el conjunto en dos partes. Para la normalización utilizamos la función caret::preProcess() y el método c("spatialSign"). Durante el entrenamiento del modelo se paralizarán automáticamente los cálculos de los núcleos de procesamiento disponibles mediante el paquete "doParallel". El número de núcleos a utilizar en los cálculos se puede especificar con la opción "threads".> idx <- rminer::holdout(y = data.f$Class)
> prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)],
+ method = c("spatialSign"))
> x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
> x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
> y.train <- data.f[idx$tr, ncol(data.f)]
> y.test <- data.f[idx$ts, ncol(data.f)]
> ruf <- randomUniformForest( X = x.train,
+ Y = y.train,
+ xtest = x.test,
+ ytest = y.test,
+ mtry = 1, ntree = 300,
+ threads = 2,
+ nodesize = 2
+ )
Las etiquetas -1 1 se convierten a 1 2 para facilitar los cálculos, y se utilizarán internamente.
> print(ruf)
Llamada:
randomUniformForest.default(X = x.train, Y = y.train, xtest = x.test,
ytest = y.test, ntree = 300, mtry = 1, nodesize = 2, threads = 2)
Tipo de bosque uniforme aleatorio: Clasificación
paramsObject
ntree 300
mtry 1
nodesize 2
maxnodes Inf
replace TRUE
bagging FALSE
depth Inf
depthcontrol FALSE
OOB TRUE
importance TRUE
subsamplerate 1
classwt FALSE
classcutoff FALSE
oversampling FALSE
outputperturbationsampling FALSE
targetclass -1
rebalancedsampling FALSE
randomcombination FALSE
randomfeature FALSE
categorical variables FALSE
featureselectionrule entropy
Evaluación out-of-bag (OOB)
Estimación OOB de la tasa de error: 20.2%
Tasa de error OOB vinculada (con desviación 1%): 21.26%
Matriz de confusión OOB:
Referencia
Predicción -1 1 class.error
-1 1066 280 0.2080
1 254 1043 0.1958
Estimación OOB de AUC: 0.798
Estimación OOB de AUPR: 0.7191
Estimación OOB de F1-score: 0.7962
Estimación OOB (ajustada) de la media geométrica: 0.7979
Límites de Breiman
Error de predicción esperado (bajo clases aproximadamente equilibradas): 18.42%
Límite superior: 27.76%
Correlación media entre los árboles: 0.0472
Fuerza (margen): 0.4516
Desviación estándar de la fuerza: 0.2379
Conjunto de prueba
Tasa de error: 19.97%
Matriz de confusión:
Referencia
Predicción -1 1 class.error
-1 541 145 0.2114
1 119 517 0.1871
Área bajo la curva ROC: 0.8003
Área bajo la curva precision-recall: 0.7994
Puntuación F1: 0.7966
Media geométrica: 0.8001
Descifremos lo anterior poco a poco:
- Error de entrenamiento (error interno) dado 1% de desviación = 21.26%.
- Límites de Breiman — propiedades teóricas propuestas por Breiman (2001). Como los bosques uniformes aleatorios heredan las propiedades de los bosques aleatorios, también se aplican aquí. Para la clasificación, se dan dos fronteras de error de predicción, la correlación promedio entre los árboles, la fuerza y la desviación estándar de la fuerza.
- Error de predicción esperado = 18.42%. El error del límite superior = 27.76%.
- Error de prueba = 19.97% (error externo). (Si la evaluación externa es menor o igual a la interna, y menor que el límite superior de los límites de Breiman, entonces no es probable que ocurra ningún reentrenamiento.)
Veamos el gráfico de un error de entrenamiento:
> plot(ruf)
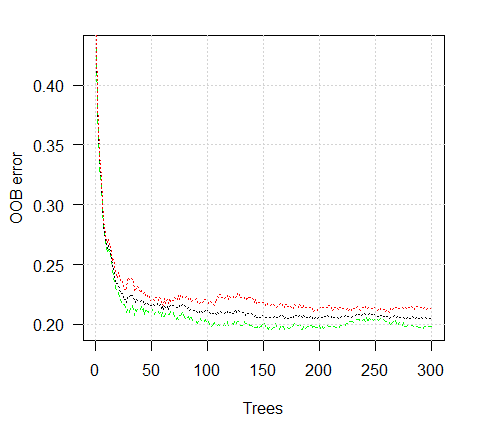
Fig. 2. Error de entrenamiento dependiendo del número de árboles
> summary(ruf) Importancia de la variable global: Nota: la mayoría de características predictivas se imprimen y están ordenadas por 'score' (puntuación). También se deberían tener en cuenta las más discriminantes mediante 'class' y 'class.frequency'. variables score class class.frequency percent 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 Resumen del tamaño del árbol promedio (número de nodos): Min. 1st Qu. Median Mean 3rd Qu. Max. 3 1044 1313 1213 1524 1861 Resumen de los nodos hoja promedio (número de nodos terminales): Min. 1st Qu. Median Mean 3rd Qu. Max. 2 522 657 607 762 931 Resumen del tamaño de los nodos hoja (número de observaciones por nodo hoja): Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 1.000 2.000 4.355 3.000 2632.000 Profundidad del árbol promedio : 10 Profundidad del árbol (balanceado) teórica : 11
Como se observa, todas las variables son importantes. Se indica en qué clases aparecen con más frecuencia las variables.
Otras estadísticas adicionales:
> pr.ruf <- predict(ruf, x.test, type = "response"); > ms.ruf <- model.stats(pr.ruf, y.test) Conjunto de prueba Tasa de error: 19.97% Matriz de confusión: Referencia Predicción -1 1 class.error -1 540 144 0.2105 1 120 518 0.1881 Área bajo la curva ROC: 0.8003 Área bajo la curva precision-recall: 0.7991 F1-score: 0.7969 Media geométrica: 0.8001
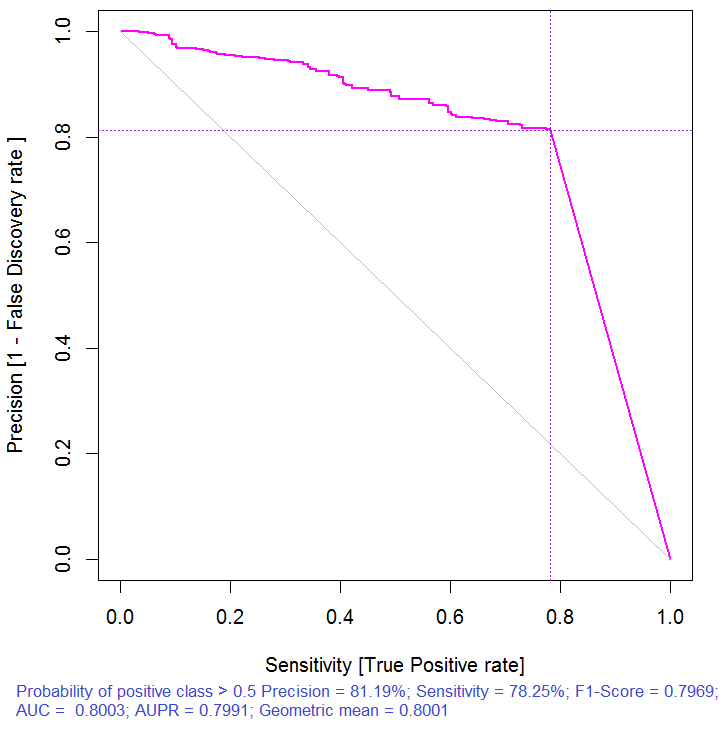
Fig. 3. Curva precision-recall
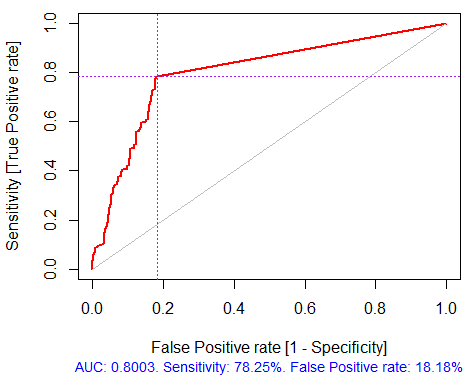
Fig. 4. Curva ROC o curva de error
Si nos detenemos aquí, que es lo que suelen ofrecer muchos paquetes de filtrado, tendríamos que seleccionar los predictores con los mejores indicadores de importancia global. Esta opción no proporciona buenos resultados porque no tiene en cuenta la influencia mutua de los predictores.
> imp.ruf <- importance(ruf, Xtest = x.test, maxInteractions = 3) 1 - Importancia de la variable global (las 15 más importantes según la ganancia de información) : Nota: la mayoría de características predictivas se imprimen y están ordenadas por 'score' (puntuación). También se deberían tener en cuenta las más discriminantes mediante 'class' y 'class.frequency'. variables score class class.frequency percent 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 2 - Importancia de la variable local Interacciones de variables (las 10 variables más importantes) : Se calcula la interacción de cada variable con las demás. cci cmo slowD oscK signal atr chv cmo 0.1933 0.1893 0.1345 0.1261 0.1146 0.1088 0.1062 cci 0.1770 0.1730 0.1182 0.1098 0.0983 0.0925 0.0899 slowD 0.1615 0.1575 0.1027 0.0943 0.0828 0.0770 0.0744 signal 0.1570 0.1530 0.0981 0.0897 0.0782 0.0725 0.0698 atr 0.1490 0.1450 0.0902 0.0818 0.0703 0.0646 0.0619 ADX 0.1468 0.1428 0.0879 0.0795 0.0680 0.0623 0.0596 ar 0.1452 0.1413 0.0864 0.0780 0.0665 0.0608 0.0581 oscK 0.1441 0.1401 0.0853 0.0769 0.0654 0.0596 0.0570 DX 0.1407 0.1367 0.0819 0.0735 0.0620 0.0562 0.0536 oscDX 0.1396 0.1356 0.0807 0.0723 0.0608 0.0551 0.0524 avg1rstOrder 0.1483 0.1443 0.0895 0.0811 0.0696 0.0638 0.0612 ADX tr ar vsig DX oscDX sign cmo 0.1026 0.1022 0.1013 0.1000 0.0977 0.0973 0.0964 cci 0.0864 0.0859 0.0850 0.0837 0.0815 0.0810 0.0802 slowD 0.0708 0.0704 0.0695 0.0682 0.0660 0.0655 0.0647 signal 0.0663 0.0659 0.0650 0.0637 0.0614 0.0610 0.0601 atr 0.0584 0.0579 0.0570 0.0557 0.0535 0.0531 0.0522 ADX 0.0561 0.0557 0.0548 0.0534 0.0512 0.0508 0.0499 ar 0.0546 0.0541 0.0533 0.0519 0.0497 0.0493 0.0484 oscK 0.0534 0.0530 0.0521 0.0508 0.0486 0.0481 0.0473 DX 0.0500 0.0496 0.0487 0.0474 0.0452 0.0447 0.0439 oscDX 0.0489 0.0485 0.0476 0.0463 0.0440 0.0436 0.0427 avg1rstOrder 0.0577 0.0572 0.0563 0.0550 0.0528 0.0524 0.0515 vol avg2ndOrder cmo 0.0889 0.1173 cci 0.0726 0.1010 slowD 0.0571 0.0855 signal 0.0526 0.0810 atr 0.0447 0.0730 ADX 0.0424 0.0707 ar 0.0409 0.0692 oscK 0.0397 0.0681 DX 0.0363 0.0647 oscDX 0.0352 0.0636 avg1rstOrder 0.0439 0.0000 Importancia de la variable basada en las interacciones (10 más importantes) : cmo cci slowD signal oscK atr ADX ar 0.1447 0.1419 0.0877 0.0716 0.0674 0.0621 0.0563 0.0533 chv DX 0.0520 0.0485 Importancia de la variable sobre las etiquetas (las 10 variables más importantes con respecto a cada etiqueta) : Class -1 Class 1 cci 0.16 0.23 cmo 0.20 0.18 slowD 0.09 0.10 oscK 0.09 0.07 signal 0.05 0.07 tr 0.02 0.07 ADX 0.06 0.03 chv 0.06 0.04 atr 0.05 0.06 ar 0.05 0.03
Como podemos ver, la importancia de las variables basándose en su interacción con otras resalta las diez primeras que no coinciden con el orden de importancia global. Y finalmente, la importancia de las variables por clases que tienen en cuenta su contribución y su implicación. Cabe señalar que la variable tr se sitúa en el sexto lugar debido a una fuerte interacción, aunque estaba en el último lugar sobre la base de la importancia global, y, en teoría, se tendría que haber abandonado.
Así pues, las diez variables primeras:
> best <- Cs(cci, cmo, slowD, oscK, signal, tr, ADX. chv, atr, ar)Comprobemos cómo ha mejorado la calidad del modelo con el conjunto de los predictores más importantes.
> x.tr <- x.train[ ,best] > x.tst <- x.test[ ,best] > ruf.opt <- randomUniformForest(X = x.tr, + Y = y.train, + xtest = x.tst, + ytest = y.test, + ntree = 300, + mtry = "random", + nodesize = 1, + threads = 2) Las etiquetas -1 1 se han convertido a 1 2 para facilitar los cálculos, y se utilizarán internamente. > ruf.opt Llamada: randomUniformForest.default(X = x.tr, Y = y.train, xtest = x.tst, ytest = y.test, ntree = 300, mtry = "random", nodesize = 1, threads = 2) Tipo de bosque uniforme aleatorio: Clasificación paramsObject ntree 300 mtry random nodesize 1 maxnodes Inf replace TRUE bagging FALSE depth Inf depthcontrol FALSE OOB TRUE importance TRUE subsamplerate 1 classwt FALSE classcutoff FALSE oversampling FALSE outputperturbationsampling FALSE targetclass -1 rebalancedsampling FALSE randomcombination FALSE randomfeature FALSE categorical variables FALSE featureselectionrule entropy Evaluación out-of-bag (OOB) Estimación OOB de la tasa de error: 18.69% Tasa de error OOB vinculada (con desviación 1%): 19.67% Matriz de confusión OOB: Referencia Predicción -1 1 class.error -1 1079 253 0.1899 1 241 1070 0.1838 Estimación OOB de AUC: 0.8131 Estimación OOB de AUPR: 0.7381 Estimación OOB de F1-score: 0.8125 Estimación OOB (ajustada) de la media geométrica: 0.8131 Límites de Breiman Error de predicción esperado (bajo clases aproximadamente equilibradas): 14.98% Límite superior: 28.18% Correlación media entre los árboles: 0.0666 Fuerza (margen): 0.5548 Desviación estándar de la fuerza: 0.2945 > pr.ruf.opt <- predict(ruf.opt, x.tst, type = "response") > ms.ruf.opt <- model.stats(pr.ruf.opt, y.test) Conjunto de prueba Tasa de error: 17.55% Matriz de confusión: Referencia Predicción -1 1 class.error -1 552 124 0.1834 1 108 538 0.1672 Área bajo la curva ROC: 0.8245 Área bajo la curva precision-recall: 0.8212 F1-score: 0.8226 Media geométrica: 0.8244
Fig. 5. Curva ROC o curva de error
Fig. 6. Curva precision-recall
La calidad ha mejorado claramente. El error de predicción del test establecido a 17.55% es menor que el nivel superior 28.18%, en consecuencia el reentrenamiento es altamente improbable. El modelo tiene otros muchos hiperparámetros cuyo ajuste puede contribuir a mejorar la calidad del modelo, sin embargo, este no es el objetivo del presente artículo.
> imp.ruf.opt <- importance(ruf.opt, Xtest = x.tst) Se han extraído las variables relevantes. 1 - Importancia de la variable global (las 10 más importantes según la ganancia de información) : Nota: la mayoría de características predictivas se imprimen y están ordenadas por 'score' (puntuación). También se deberían tener en cuenta las más discriminantes mediante 'class' y 'class.frequency'. variables score class class.frequency percent 1 atr 3556 -1 0.50 100.00 2 oscK 3487 -1 0.51 98.07 3 chv 3465 1 0.51 97.45 4 signal 3432 1 0.51 96.51 5 cci 3424 1 0.50 96.30 6 slowD 3415 1 0.51 96.04 7 ADX 3397 -1 0.50 95.52 8 ar 3369 -1 0.50 94.76 9 tr 3221 1 0.53 90.59 10 cmo 3177 -1 0.50 89.36 percent.importance 1 10 2 10 3 10 4 10 5 10 6 10 7 10 8 10 9 9 10 9 2 - Importancia de la variable local Interacciones de variables (las 10 variables más importantes) : Se calcula la interacción de cada variable con las demás. atr cci oscK slowD ADX tr chv cci 0.1748 0.1625 0.1620 0.1439 0.1411 0.1373 0.1349 atr 0.1650 0.1526 0.1522 0.1341 0.1312 0.1274 0.1251 oscK 0.1586 0.1462 0.1457 0.1277 0.1248 0.1210 0.1186 chv 0.1499 0.1375 0.1370 0.1190 0.1161 0.1123 0.1099 ar 0.1450 0.1326 0.1321 0.1140 0.1112 0.1074 0.1050 signal 0.1423 0.1300 0.1295 0.1114 0.1085 0.1047 0.1024 ADX 0.1397 0.1273 0.1268 0.1088 0.1059 0.1021 0.0997 slowD 0.1385 0.1262 0.1257 0.1076 0.1048 0.1010 0.0986 cmo 0.1276 0.1152 0.1147 0.0967 0.0938 0.0900 0.0876 tr 0.1242 0.1118 0.1113 0.0932 0.0904 0.0866 0.0842 avg1rstOrder 0.1466 0.1342 0.1337 0.1156 0.1128 0.1090 0.1066 signal ar cmo avg2ndOrder cci 0.1282 0.1182 0.1087 0.1412 atr 0.1184 0.1084 0.0989 0.1313 oscK 0.1120 0.1020 0.0925 0.1249 chv 0.1033 0.0933 0.0838 0.1162 ar 0.0984 0.0884 0.0789 0.1113 signal 0.0957 0.0857 0.0762 0.1086 ADX 0.0931 0.0831 0.0736 0.1060 slowD 0.0919 0.0819 0.0724 0.1049 cmo 0.0810 0.0710 0.0615 0.0939 tr 0.0776 0.0676 0.0581 0.0905 avg1rstOrder 0.0999 0.0900 0.0804 0.0000 Importancia de la variable basada en las interacciones (10 más importantes) : atr cci oscK chv slowD ADX signal ar 0.1341 0.1335 0.1218 0.0978 0.0955 0.0952 0.0898 0.0849 tr cmo 0.0802 0.0672 Importancia de la variable sobre las etiquetas (las 10 variables más importantes con respecto a cada etiqueta) : Class -1 Class 1 atr 0.17 0.14 oscK 0.16 0.11 tr 0.03 0.16 cci 0.14 0.13 slowD 0.12 0.09 ADX 0.10 0.10 chv 0.08 0.10 signal 0.09 0.07 cmo 0.07 0.03 ar 0.06 0.06
Fig. 7. Importancia de las variables según la ganancia de información
Como podemos ver, la importancia global de las variables casi se ha estabilizado, pero la importancia de las variables por clases se clasifica de forma diferente. La variable tr está en el tercer lugar.
Dependencia parcial sobre el predictor
Consideremos la dependencia parcial de las variables más importantes.
> plot(imp.ruf.opt, Xtest = x.tst)
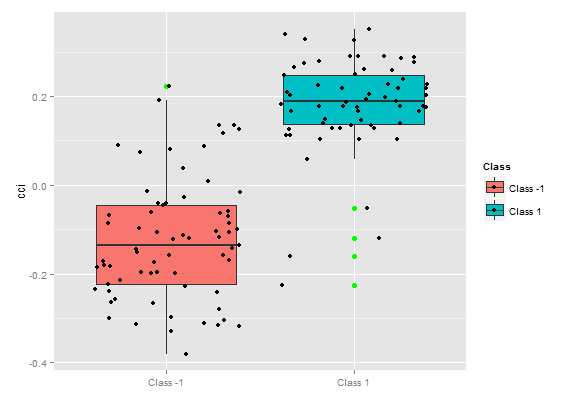
Fig. 8. Dependencia parcial de la variable cci
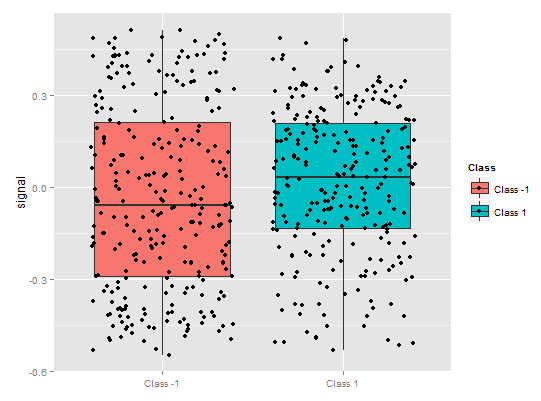
> pd.signal <- partialDependenceOverResponses(x.tst, + imp.ruf.opt, + whichFeature = "signal", + whichOrder = "all" + )
Fig. 9. Dependencia parcial de la variable signal
Las cosas cambian con respecto a la dependencia parcial de la señalal de la figura de arriba. En ambas clases se observa una cobertura de datos casi completa.
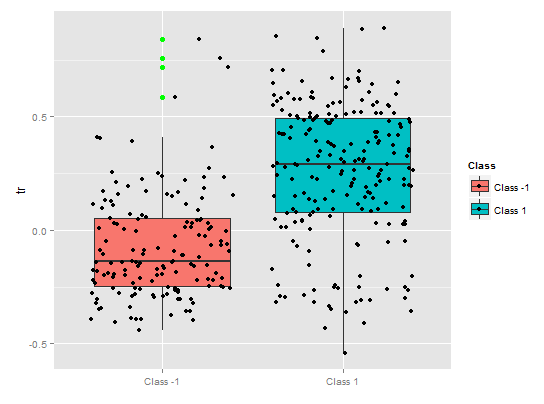
> pd.tr <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "tr",
whichOrder = "all"
)
La dependencia parcial de la variable tr ilustra una separación razonable por clases, aunque todavía hay una cobertura considerable.
Fig. 10. Dependencia parcial de la variable tr
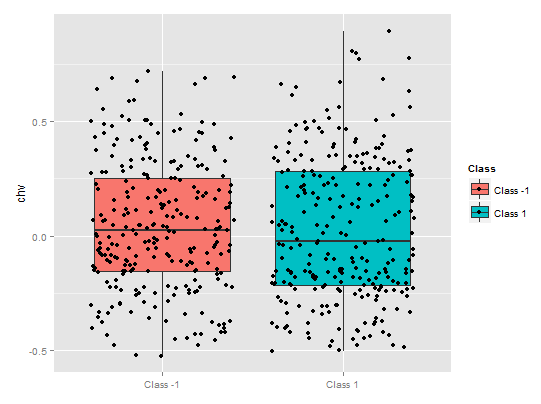
> pd.chv <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "chv",
whichOrder = "all")
La dependencia parcial de la variable chv es despreciable. Se observa una cobertura de información completa por clases.
Fig. 11. Dependencia parcial de la variable chv
De esta manera podemos determinar visualmente cómo se relacionan los datos del predictor con las clases, y qué tan dependientes son.
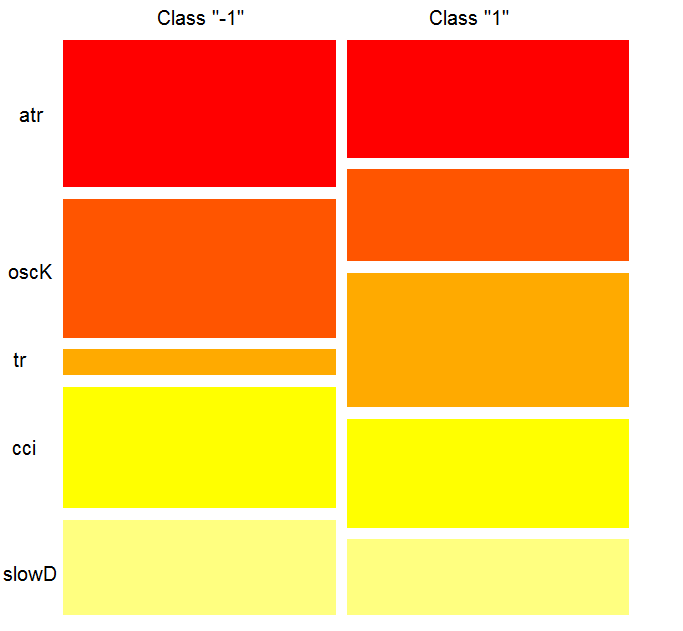
La importancia de la variable sobre las clases
"La importancia de la variable" sobre las clases proporciona una perspectiva local. Primero de todo, hay que fijar la clase teniendo en cuenta las variables que son importantes y actúan como constantes, y, finalmente, se consideran las variables importantes para cada clase. Por lo tanto, cada variable tiene importancia, como si no hubiera otras clases.
Aquí no nos interesan las variables que implican elegir una clase, sino aquellas que serán importantes en la clase cuando esta última se seleccione. El orden de las variables determina su clasificación libre con respecto a su rango en cada clase, sin tener en cuenta la importancia de la clase.
¿Qué vemos en el gráfico? El predictor tr es considerablemente más importante para la classe "1" que para la clase "-1". Y viceversa, el predictor oscK es más importante para la clase "-1" que para la clase "1". La importancia de los predictores es diferente en cada clase.
Fig. 12. Importancia de las variables por clases
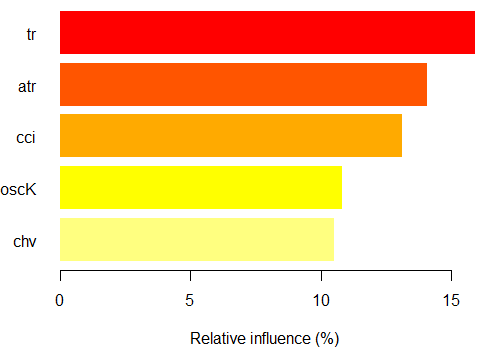
La importancia de las variables según la interacción
El gráfico de abajo ilustra cómo se presentan las variables con respecto a su interacción conjunta con otra variable. Observación importante: la primera variable no es necesariamente el más importante, en cambio, es la que tiene el mayor impacto mutuo con los demás.
Fig. 13. La importancia de las variables según la interacción
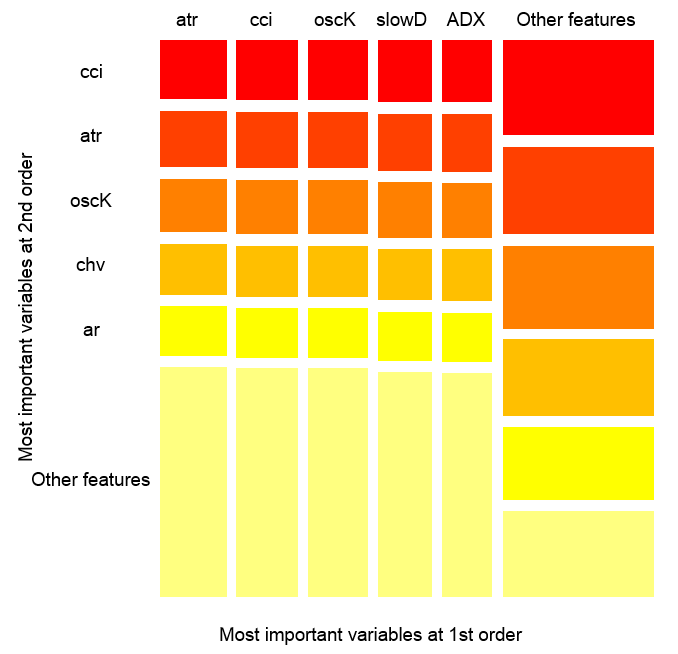
Interacciones de las variables sobre las observaciones
Fig. 14. Importancia de las variables sobre las observaciones
La figura de arriba muestra la interacción de las órdenes primera y segunda para todos los predictores, de acuerdo a nuestra definición de interacción. El área es igual a una unidad. La primera orden indica que las variables (ordenadas de manera descendente por influencia) son más importantes, si la decisión correspondiente se tiene que tomar teniendo cuenta una sola variable. La segunda orden indica que si la variable desconocida ya se ha seleccionado en la primera orden, entonces la segunda variable más importante será una de la segunda orden.
Para más información, la interacción proporciona una tabla con las características ordenadas. La primera orden ofrece oportunidades ordenadas a las variables más importantes. La segunda orden ofrece oportunidades ordenadas a la segunda variable más importante. La intersección de un par de variables proporciona la influencia relativa mutua. Nótese que las medidas dependen tanto del modelo como de los datos. Por lo tanto, la confianza de las mediciones depende directamente de la confianza en las predicciones. También podemos añadir la metavariabe "otros signos" para que el algoritmo muestre la vista predeterminada para ver las variables agrupadas menos relevantes.
Importancia parcial
Echemos un vistazo a la importancia parcial según las observaciones x.tst en la clase "-1".
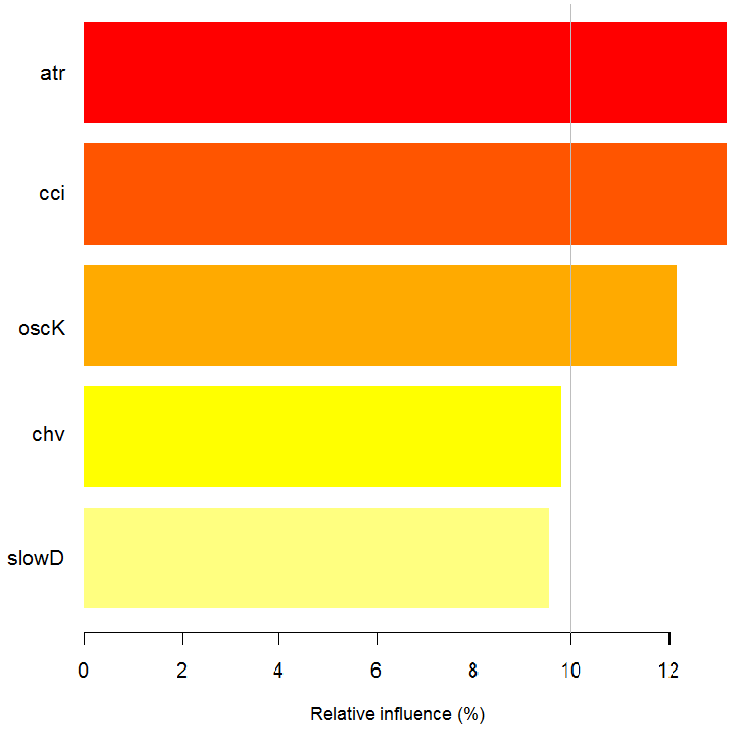
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "-1") Influencia relativa: 67.41% Según x.tst y la clase «-1»
Fig. 15. Importancia parcial de las variables según las observaciones de la case "-1"
Los predictores más importantes de la clase "-1" son los cinco que se ilustran en la figura de arriba.
Ahora es el turno de la clase "+1"
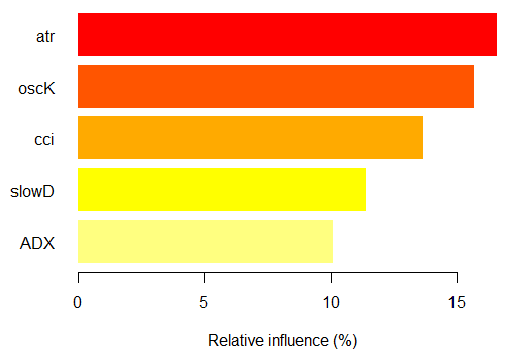
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "1") Influencia relativa: 64.45%
Fig. 16. Importancia parcial de las variables según las observaciones de la clase "+1"
Como vemos, los predictores son diferentes tanto en estructura como en clasificación.
Veamos ahora la dependencia parcial entre los predictores cci y atr, que son los más importantes en la primera y segunda órdenes de la interacción del predictor.
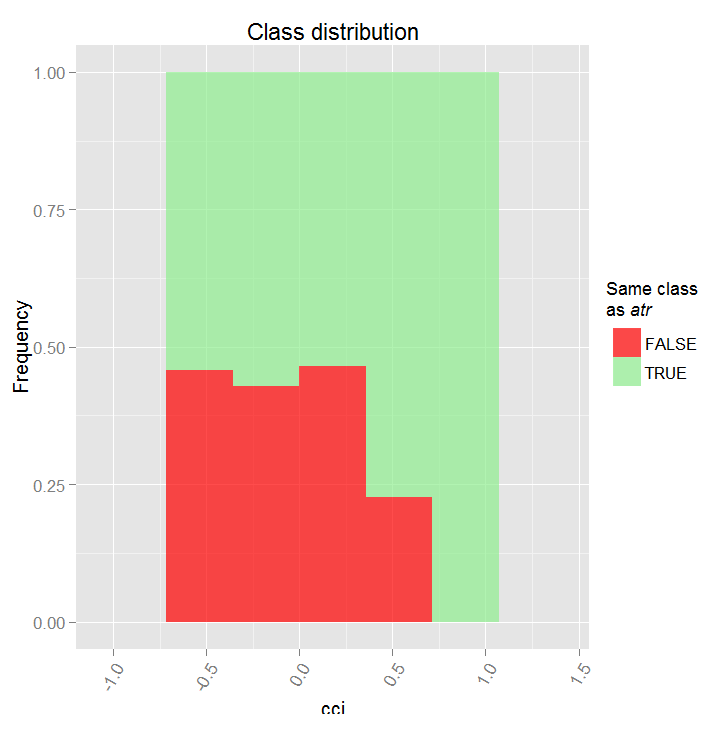
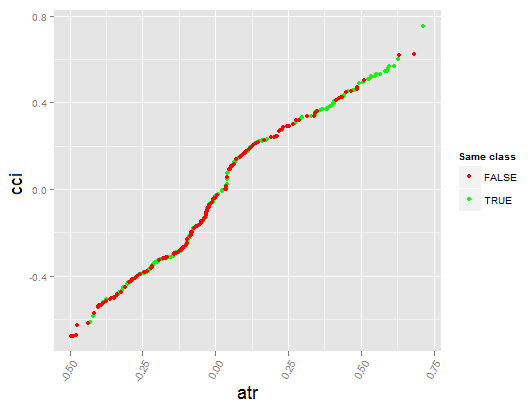
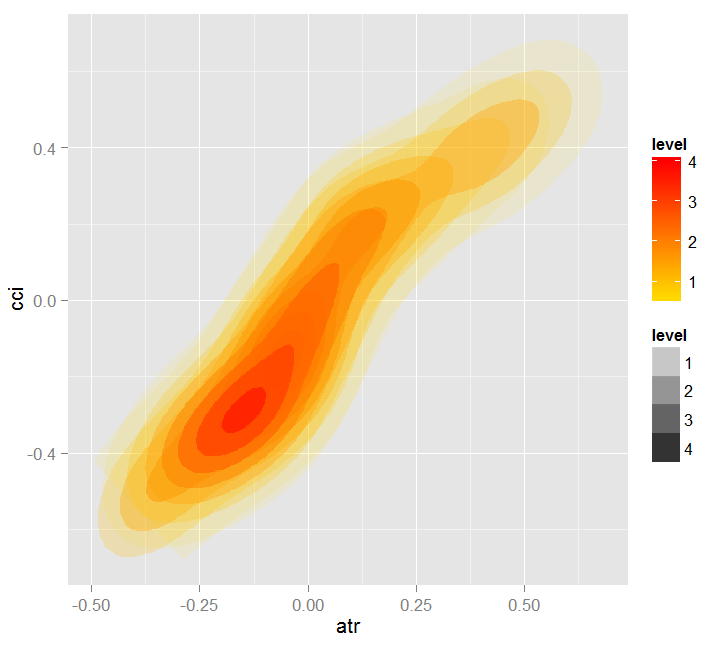
> par.dep.1 <- partialDependenceBetweenPredictors(Xtest = x.tst, + imp.ruf.opt, + features = Cs(atr, cci), + whichOrder = "all", + perspective = T) Nivel de interacciones entre atr y cci en la primera orden: 0.1748 (99.97% de la característica(s) con máximo nivel) Nivel de interacciones entre atr y cci en la segunda orden: 0.1526 (87.28% de la característica(s) con máximo nivel) Distribución de la clase : para una variable del par, se muestra la probabilidad estimada de que la variable considerada tenga la misma clase que la otra. Si la misma clase tiende a ser TRUE entonces la variable posiblemente influencia a la otra (por la categoría o los valores considerados) al predecir una etiqueta. Dependencia : para el par de variables, muestra la forma de su dependencia y el acuerdo estimado en la predicción de la misma clase, para los valores que definen la dependencia. En caso de variables categóricas, se utiliza la tabulación cruzada. Mapa de calor : para el par de variables, muestra el área donde la dependencia es más efectiva. Cuanto más oscuro es el color, tanto más fuerte es la dependencia. La variable dominante del par es, posiblemente, la más discriminante ('Importancia de la variable global') y/o la que tiene el nivel más alto de interacciones ( 'Importancia de la variable basada en interacciones').
Fig. 17. Dependencia parcial entre los predictores cci y atr
Fig. 18. Dependencia entre los predictores atr y cci
Fig. 19. Mapa de calor de la dependencia entre los predictores atr y cci
La importancia de la variable global se determina para describir qué variables globales influyen más en la reducción de los errores de predicción.
La importancia de la variable local describe qué hace que una variable sea influyente de acuerdo a su interacción con otras.
Esto nos lleva a la importancia parcial, que muestra cuándo una variable determinada es más importante. El último paso al analizar la importancia de la variable es la dependencia parcial, que establece cuándo y/o cómo se asocia la variable con una respuesta.
En resumen: la importancia de la variable en los bosques uniformes aleatorios va desde el nivel más alto al más bajo con detalles. Finalmente, averiguamos qué variables son importantes, y aprendemos matices de peso en cada clase. Entonces analizamos por qué son influenciables según su interacción, y seleccionamos una variable considerando todas las clases como una. El siguiente paso consiste en aprender de dónde obtienen su influencia, analizando cada clase. Finalmente, observando la "dependencia parcial", descubrimos cuándo es importante la variable, y cómo. Todas las medidas operan en cualquier conjunto de pruebas o entrenamiento, a excepción de la "variable global de la importancia".
La evaluación multinivel de los predictores permite seleccionar los más importantes y crear conjuntos óptimos, reduciendo significativamente la dimensión de los datos y mejorando la calidad de las predicciones.
No solo es posible evaluar y elegir los predictores, sino también los elementos de observación más informativos.
Echemos ahora un vistazo a otro paquete interesante: "RoughSet".
Descripción breve: este paquete cubre dos secciones principales, la teoría de conjuntos aproximados (RST, Rough Set Theory) y la teoría de conjuntos aproximados difusos (FRST, Fuzzy Rough Set Theory). RST fue propuesta por Z. Pawlak (1982, 1991), y ofrece instrumentos matemáticos sofisticados para modelar y analizar sistemas de información heterogéneos e imprecisos. Las relaciones indistinguibles entre objetos RST no requieren parámetros adicionales para extraer la información.
La teoría FRST, extensión RST, fue propuesta por D. Dubois y H. Prade (1990). Combina los conceptos de incertidumbre e indistinguibilidad y se expresan en los conjuntos difusos propuestos por L.A. Zadeh (1965) y RST. Este concepto permite analizar los atributos continuos (variables) sin tener que discretizar los datos preliminares. Hay muchos métodos que se han utilizado en varias áreas diferentes, basándose en los conceptos descritos anteriormente. Los métodos utilizan la relación de indistinguibilidad y el concepto de aproximación inferior y superior para resolver problemas.
Permítame hacer ahora un pequeño paréntesis.
Generalmente, los métodos utilizados en la representación del conocimiento desempeñan un papel importante en los sistemas de información. Los métodos más conocidos en los sistemas de formación de conceptos inductivos son: reglas de producción, árboles de decisión, cálculo de predicados y redes semánticas.
En el momento de extraer y generalizar el conocimiento almacenado en los arrays de información se presentan estos problemas:
- Los datos son diferentes (cuantitativo, cualitativo, estructural).
- Las bases de datos suelen ser grandes, por lo tanto, no se pueden utilizar algoritmos de complejidad exponencial para recuperar el conocimiento, son inaceptables.
- La información contenida en las matrices de datos puede ser incompleta, excesiva, distorsionada o controvertida; también pueden faltar atributos. En consecuencia, solo se pueden utilizar los atributos existentes para construir las reglas de clasificación.
En la actualidad, cada vez se utiliza más la teoría de conjuntos aproximados como marco teórico para extraer conocimiento de las bases de datos (minería de datos).
Los conjuntos aproximados tienen límites indefinidos, es decir, no se pueden describir con precisión con las características disponibles.
La teoría de conjuntos aproximados fue propuesta por Zdzislaw Pawlak en 1982, y se ha convertido en un nuevo instrumento matemático que sirve para operar con información incompleta. El concepto más importante de esta teoría es la así llamada aproximación superior e inferior de los conjuntos aproximados, que permite evaluar la posibilidad o la necesidad de pertenencia de un elemento a un conjunto con límites "difusos".
La aproximación inferior está formada por elementos que definitivamente pertenecen a X, y la superior contiene elementos que posiblemente pertenecen a X. La región límite del conjunto X es la diferencia entre las aproximaciones mayor y menor; es decir, la región límite tiene elementos del conjunto X que pertenecen a una aproximación superior que no es inferior.
El concepto simple pero potente de los conjuntos aproximados se ha convertido en la base de varios estudios teóricos: lógica, álgebra, topología; y otros estudios aplicados: inteligencia artificial, razonamiento aproximado, análisis de datos intelectual, teoría de la decisión, procesamiento de imágenes y reconocimiento de patrones.
El concepto de "conjunto aproximado" trata la "imperfección de los datos" en relación a la "granularidad" de la información. Este concepto es inherentemente topológico y complementa otros enfoques bien conocidos que se utilizan para gestionar la información incompleta, por ejemplo, conjuntos difusos, razonamiento bayesiano, algoritmos evolutivos, redes neuronales y métodos estadísticos de análisis de datos.
Veámoslo ahora. Por consiguiente, los métodos proporcionados en este paquete se pueden agrupar:
Conceptos básicos de RST y FRST. En esta parte observamos cuatro tareas diferentes: relación de indiscernibilidad, aproximación inferior y superior, región positiva y matriz de discernibilidad.
Discretización. Se utiliza para convertir los datos físicos en nominales. Desde el punto de vista RST, esta tarea intenta mantener la discernibilidad de los objetos.
Selección de características. Se trata de un proceso de búsqueda de subconjuntos de predictores que intentan obtener la misma calidad que el conjunto de predictores. En otras palabras, el objetivo es seleccionar las características esenciales y eliminar la dependencia. Es útil y necesario cuando nos enfrentamos a conjuntos de datos que contienen características múltiples. En términos RST y FRST, la elección se los predictores se refiere a la búsqueda de reductos y superreductos.
Selección de la instancia. Este proceso elimina las copias ruidosas, innecesarias o conflictivas del conjunto de datos de entrenamiento, manteniendo la consistencia. Por lo tanto, la precisión de la clasificación es buena en tanto que se eliminan las muestras que no contribuyen de forma positiva.
Inducción de la regla. Como hemos mencionado antes, la inducción de reglas se utiliza para generar reglas y proporcionar conocimiento a la tabla solución. En el aprendizaje de máquinas, este proceso se llama fase de entrenamiento.
Predicción/clasificación. Esta tarea sirve para predecir los valores de una variable a partir del nuevo conjunto de datos (conjunto de prueba).
Solo vamos a explorar dos categorías de la lista: elección de predictores y selección de ejemplos.
Construyamos pues el conjunto de datos de entrada y salida. Utilizamos los mismos datos que hemos obtenido antes, transformándolos en la clase "DecisionTable" con la que opera el paquete.> library(RoughSets) Cargando el paquete: Rcpp > require(magrittr) > data.tr <- SF.asDecisionTable(data.f[idx$tr, ], + decision.attr = 16, + indx.nominal = 16) > data.tst <- SF.asDecisionTable(data.f[idx$ts, ], + decision.attr = 16, + indx.nominal = 16 + ) > true.class <- data.tst[ ,ncol(data.tst)]Como hemos indicado antes, RST utiliza datos nominales. Como tenemos datos numéricos continuos, vamos a convertirlos en datos nominales con una función de discretización especializada, disponible en el paquete.
> cut.values <- D.global.discernibility.heuristic.RST(data.tr) > data.tr.d <- SF.applyDecTable(data.tr, cut.values)
Veamos qué obtenemos como resultado:
> summary(data.tr.d) DX ADX (12.5,20.7]: 588 (17.6,19.4]: 300 (20.7, Inf]:1106 (19.4,25.4]: 601 [-Inf,12.5]: 948 (25.4,31.9]: 294 (31.9, Inf]: 343 [-Inf,17.6]:1104 oscDX ar (1.81, Inf]:1502 (-40.6,40.6]:999 [-Inf,1.81]:1140 (40.6,71.9] :453 (71.9, Inf] :377 [-Inf,-40.6]:813 tr atr (0.000205,0.000365]:395 (0.00072,0.00123]:1077 (0.000365,0.0005] :292 (0.00123, Inf] : 277 (0.0005,0.00102] :733 [-Inf,0.00072] :1288 (0.00102,0.00196] :489 (0.00196, Inf] :203 [-Inf,0.000205] :530 cci chv (-6.61, Inf]:1356 (-0.398,0.185]:1080 [-Inf,-6.61]:1286 (0.185,0.588] : 544 (0.588, Inf] : 511 [-Inf,-0.398] : 507 cmo sign (5.81,54.1]: 930 [-Inf, Inf]:2642 (54.1, Inf]: 232 [-Inf,5.81]:1480 vsig slowD (0.0252, Inf]:1005 [-Inf, Inf]:2642 [-Inf,0.0252]:1637 oscK signal (-0.0403,0.000545]:633 (-11.4, Inf]:1499 (0.000545,0.033] :493 [-Inf,-11.4]:1143 (0.033, Inf] :824 [-Inf,-0.0403] :692 vol Class (0.0055,0.00779]:394 -1:1319 (0.00779,0.0112]:756 1 :1323 (0.0112,0.0154] :671 (0.0154, Inf] :670 [-Inf,0.0055] :151
Los predictores se discretizan de forma diferente. Las variables como slowD, sign no están separadas en absoluto. Las variables signal, vsig, cci, oscDX simplemente se dividen en dos partes. Las otras variables se dividen entre 3 y 6 clases.
Seleccionamos las variables importantes:
> reduct1 <- FS.quickreduct.RST(data.tr.d, control = list()) > best1 <- reduct1$reduct > best1 DX ADX oscDX ar tr atr cci 1 2 3 4 5 6 7 chv cmo vsig oscK signal vol 8 9 11 13 14 15
Los datos que no se dividieron (slowD, sign) se eliminan del conjunto. Ejecutamos la discretización del conjunto de prueba y lo transformamos de acuerdo a la reducción realizada.
> data.tst.d <- SF.applyDecTable(data.tst, cut.values) > new.data.tr <- SF.applyDecTable(data.tr.d, reduct1) > new.data.tst <- SF.applyDecTable(data.tst.d, reduct1)
Ahora es el momento de utilizar el paquete llamado "reglas de inducción". Vamos a extraer un conjunto de reglas que enlazan los predictores y un objetivo. Se utiliza una de estas opciones:
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9, timesCovered = 3)
Comprobemos en el conjunto de prueba cómo funcionan estas reglas en la predicción:
> pred.vals <- predict(rules, new.data.tst) > table(pred.vals) pred.vals -1 1 655 667
Métricas:
> caret::confusionMatrix(true.class, pred.vals[ ,1]) Matriz de confusión y estadísticas Referencia Predicción -1 1 -1 497 163 1 158 504 Precisión : 0.7572 95% CI : (0.7331, 0.7801) Tasa de información : 0.5045 P-valor [Acc > NIR] : <2e-16 Kappa : 0.5144 P-valor del test de Mcnemar: 0.8233 Sensibilidad : 0.7588 Especificidad : 0.7556 Pos pred valor : 0.7530 Neg pred valor : 0.7613 Prevalencia : 0.4955 Tasa de detección : 0.3759 Prevalencia de la detección : 0.4992 Precisión equilibrada : 0.7572 Clase 'positiva' : -1
Estos son algunos ejemplos:
> ##-----Selección de la instancia----------- > res.1 <- IS.FRIS.FRST(decision.table = data.tr, control = list(threshold.tau = 0.5, alpha = 1, type.aggregation = c("t.tnorm", "lukasiewicz"), t.implicator = "lukasiewicz")) > new.data.tr <- SF.applyDecTable(data.tr, res.1) > nrow(new.data.tr) [1] 2353Aproximadamente 300 ejemplos se han clasificado como menores y se han descartado. Extraemos un conjunto de reglas de este conjunto y comparamos la calidad de la predicción con el conjunto anterior.
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9,
timesCovered = 3)
> pred.vals <- predict(rules, new.data.tst)
> table(pred.vals)
pred.vals
-1 1
638 684
> caret::confusionMatrix(true.class, pred.vals[ ,1])
Matriz de confusión y estadísticas
Referencia
Predicción -1 1
-1 506 154
1 132 530
Precisión : 0.7837
95% CI : (0.7605, 0.8056)
Tasa de información : 0.5174
P-valor [Acc > NIR] : <2e-16
Kappa : 0.5673
P-valor del test de Mcnemar : 0.2143
Sensibilidad : 0.7931
Especificidad : 0.7749
Pos pred valor : 0.7667
Neg pred valor : 0.8006
Prevalencia : 0.4826
Tasa de detección : 0.3828
Prevalencia de la detección : 0.4992
Precisión equilibrada : 0.7840
Clase 'positiva' : -1
La calidad es mayor que en el caso anterior. Cabe señalar que, al igual que sucede con RandomUniformForests, es imposible obtener resultados reproducibles en los experimentos repetidos. Cada lanzamiento nuevo proporciona un resultado ligeramente distinto.
¿Cómo son las reglas? Veámoslo:> head(rules) [[1]] [[1]]$idx [1] 6 4 11 [[1]]$values [1] "(85.1, Inf]" "(0.00137, Inf]" "(0.0374, Inf]" [[1]]$consequent [1] "1" [[1]]$support [1] 1335 1349 1363 1368 1372 1390 1407 1424 1449 1454 [11] 1461 1472 1533 1546 1588 1590 1600 1625 1630 1661 [21] 1667 1704 1720 1742 1771 1777 1816 1835 1851 1877 [31] 1883 1903 1907 1912 1913 1920 1933 1946 1955 1981 [41] 1982 1998 2002 2039 2040 2099 2107 2126 2128 2191 [51] 2195 2254 2272 2298 2301 2326 2355 2356 2369 2396 [61] 2472 2489 2497 2531 2564 2583 2602 2643 [[1]]$laplace 1 0.9857143
La lista contiene estos datos:
- $idx — índice de los predictores que participan en esta regla. En el ejemplo anterior, estos son 6("atr") , 4("ar") y 11("vsig").
- $values — rango de los indicadores donde opera la regla.
- $consequent — solución: class = "1". Para hacerlo más comprensible: si "atr" está en el rango "(85.1, Inf]" Y "ar" está en el rango "(0.00137, Inf]" Y "vsig" está en el rango "(0.0374, Inf]", ENTONCES Class = "1".
- $support — índices de los ejemplos que soportan esta solución.
- $laplace — una evaluación de nivel de confianza para esta regla.
El cálculo de las reglas requiere un tiempo considerable.
Conclusión
Hemos analizado nuevas oportunidades basándonos en la evaluación de predictores y visualizando los resultados obtenidos. Finalmente hemos elegido el más valioso. También hemos examinado los niveles de importancia, así como las dependencias del predictor y su impacto en las respuestas. Los resultados de los experimentos se aplicarán en el siguiente artículo, donde hablaremos de las redes profundas con RBM.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2029
Gestión de errores y logging en MQL5
MQL5 para principiantes, protección antivandálica de los objetos gráficos
Interfaces gráficas I: Funciones para los botones del formulario y eliminación de los elementos de la interfaz (Capítulo 4)
Interfaces gráficas I: "Animar" la interfaz gráfica (Capítulo 3)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso