Neuroredes profundas (Parte II). Desarrollo y selección de predictores
1 257
0
Contenido
- Introducción
- 1 Desarrollo de las características
- 2. Elección de los predictores
- Conclusión
- Anexos
Introducción
En la anterior parte de este artículo analizamos diversos aspectos sobre la obtención y la preparación de los datos de entrada y la variable objeto. Para reproducir los scripts este artículo, necesitamos ejecutar correctamente todos los scripts de la primera parte, o bien descargar el resultado del cálculo de la primera parte del artículo del anexo en RStudio.
1 Desarrollo de las características
La creación de las características es la ciencia (y el arte) de obtener información adicional de los datos en mano. Nuestro objetivo no es añadir nuevos datos, sino hacer uso de los que ya tenemos. Las nuevas capacidades nos permitirán obtener nuevas características a partir de una muestra de datos. Estos signos permiten caracterizar y dividir con mayor precisión los datos de entrenamiento, proporcionando así una mayor precisión al modelo.
Tecnológicamente, el proceso se puede dividir en dos etapas:
- Transformación: dependiendo del escenario, puede darse uno de los cuatro tipos de transformaciones: la normalización de los datos, la eliminación de la asimetría de las variables, la eliminación de los valores atípicos y la discretización de datos.
- Creación de características: la extracción de una nueva variable a partir de otras ya existentes se conoce como creación de una característica. Ayuda a descubrir las conexiones ocultas de un conjunto de datos.
1.1. Transformación de las características
1.1.1. Transformación
¿Qué supone la transformación de una variable?
En el modelado de datos, una transformación constituye el reemplazo de una variable por una función. Por ejemplo, la sustitución de una variable x por una raíz cuadrada o cúbica, o un logaritmo x, sería una transformación. En otras palabras, la transformación es un proceso que cambia la distribución de una variable o la relación de esta variable con otras.
Vamos a enumerar las situaciones en las que resulta útil la transformación de una variable.
- Cuando queremos cambiar la escala de una variable o normalizar sus valores para una mejor comprensión. Esta transformación es necesaria si los datos tienen diferentes escalas. En este caso, la forma de la distribución de la variable no cambia.
- Cuando debemos convertir las relaciones lineales y curvilíneas complejas entre las variables en una relación lineal, puesto que esta resulta más vívida y proporciona una mejor capacidad de pronóstico. En tales casos, se puede utilizar un diagrama de dispersión para encontrar una relación entre dos variables continuas. En tales casos se utiliza generalmente una transformación logarítmica.
- Cuando es necesario cambiar una distribución asimétrica a una simétrica para lograr una interpretación y un análisis más simples. Algunos métodos de modelado requieren una distribución normal de las variables. Por lo tanto, cuando tratamos con una distribución no uniforme, podemos utilizar las transformaciones que reducen la asimetría. Para una distribución con asimetría a la derecha tomaremos una raíz cuadrada o cúbica o un logaritmo de una variable, mientras que para una distribución asimétrica a la izquierda, usaremos el cuadrado/cubo o una función exponencial.
- Cuando una variable continua necesita ser transformada en una discreta. El método utilizado para tal transformación será la discretización.
¿Cuáles son los métodos generales de transformación?
Hay varios métodos utilizados para la transformación de variables. Ya hemos mencionado algunos de ellos: la raíz cuadrada y cúbica, los logaritmos, las funciones trigonométricas y la segmentación. Echemos un vistazo a algunos métodos en detalle para destacar sus ventajas y desventajas.
- Tomar el logaritmo: este es un método de transformación general que se utiliza para cambiar la forma de la distribución de una variable en un segmento de distribución. Por lo general se usa para reducir la asimetría a la derecha. Esta función no es aplicable al cero y otros valores negativos.
- Raíz cuadrada/cúbica: esta función tiene un impacto significativo en la distribución de la variable, aunque no tan poderoso como el logaritmo. La ventaja de la raíz cúbica es que puede ser utilizada para el cero y los valores negativos. La raíz cuadrada puede tomarse solo para los valores positivos y cero.
- Discretización/binning: se utiliza para la categorización de los valores. Se ejecuta para datos originales, percentiles y frecuencias. La elección del método de clasificación se basa en la naturaleza de los datos. Podemos llevar a cabo una segmentación conjunta de variables interdependientes.
Cualquier transformación de los datos conduce al cambio de la distribución de las variables. Para ilustrar esto, usaremos ejemplos de dos métodos de transformación.
Los dos problemas de nuestro conjunto inicial de datos son los valores atípicos y la asimetría a la derecha. Ya hemos analizado varias maneras de eliminar los valores atípicos. Ahora intentaremos en primer lugar eliminar/reducir la asimetría y luego eliminar los valores atípicos.
Método 1.
Para deshacerse de la fuerte asimetría a la derecha del conjunto x, vamos a aplicar un logaritmo de base 2 y luego eliminar los valores atípicos. Puesto que los valores de las variables del conjunto de datos inicial son mucho menores que 1 y hay valores negativos entre ellos, para aumentar la precisión vamos a aplicar los logaritmos a las variables, añadiendo 1 a cada uno de ellas. Veamos cómo cambia la curva.
evalq({x.ln <- apply(x, 2, function(x) log2(x + 1))
sk.ln <- skewness(x.ln)},
env)
> env$sk.ln
ftlm stlm rbci pcci v.fatl
Skewness -0.2715663 -2.660613 -4.484301 0.4267873 1.253008
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 1.83489 2.065224 -0.0343451 -15.62414 0.01529019
v.pcci
Skewness 0.1811206
Tres variables — stlm, rbci y v.ftlm han recibido una fuerte asimetría a la izquierda; tres variables v.fatl, v.satl y v.rftl han permanecido con un fuerte sesgo a la derecha; el resto de las variables han visto su asimetría equilibrada. Vamos a quitar e imputar los valores atípicos de este conjunto de datos y luego comprobaremos la asimetría y la distribución de las variables:
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
remove_outliers(x.ln[ ,i])
} -> x.ln.out
colnames(x.ln.out) <- colnames(x.ln)
},
env)
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
capping_outliers(x.ln[ ,i])
} -> x.ln.cap
colnames(x.ln.cap) <- colnames(x.ln)
},
env)
evalq({
sk.ln.out <- skewness(x.ln.out)
sk.ln.cap <- skewness(x.ln.cap)
},
env)
> env$sk.ln.out
ftlm stlm rbci pcci
Skewness -0.119055 -0.3549119 -0.1099921 -0.01476384
v.fatl v.satl v.rftl v.rstl
Skewness -0.02896319 -0.03634833 -0.06259749 -0.2120127
v.ftlm v.stlm v.pcci
Skewness -0.05819699 -0.01661317 -0.05420077
> env$sk.ln.cap
ftlm stlm rbci pcci
Skewness -0.1814781 -0.4582045 -0.1658855 -0.02849945
v.fatl v.satl v.rftl v.rstl
Skewness -0.04336238 -0.04400781 -0.0692754 -0.2269408
v.ftlm v.stlm v.pcci
Skewness -0.06184128 -0.02856397 -0.06258243
Los datos de los dos conjuntos de datos (x.out y x.cap) son casi simétricos. La distribución se muestra en los siguientes diagramas.
par(mfrow = c(2,2)) boxplot(env$x.ln, main = "x.ln with outliers", xlab = "") boxplot(env$x.ln.out, main = "x.ln.out without outliers", xlab = "") boxplot(env$x.ln.cap, main = "x.ln.cap with imputed outliers", xlab = "") par(mfrow = c(1,1))
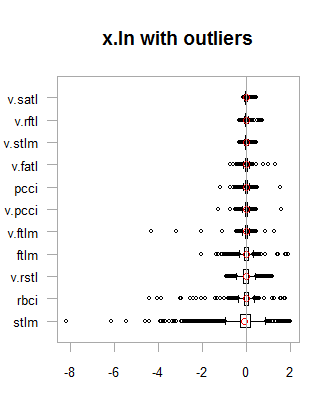
Fig. 1. Datos con transformación logarítmica con y sin datos atípicos
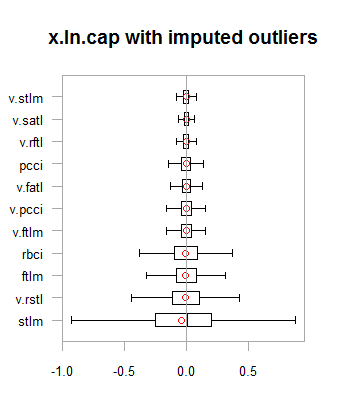
Fig.2. Datos con transformación logarítmica con datos atípicos imputados
Los resultados son muy similares a la transformación anterior, con una excepción, el rango del cambio de variables se ha ampliado.
Vamos a transformar el frame de datos x.ln.cap y ver la variación y la covariación del conjunto:
evalq(x.ln.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetLnCap, env)
Construimos los gráficos
require(GGally) evalq(ggpairs(dataSetLnCap, columns = 2:7, mapping = aes(color = Class), title = "PredLnCap1"), env) evalq(ggpairs(dataSetLnCap, columns = 8:13, mapping = aes(color = Class), title = "PredLnCap2"), env)
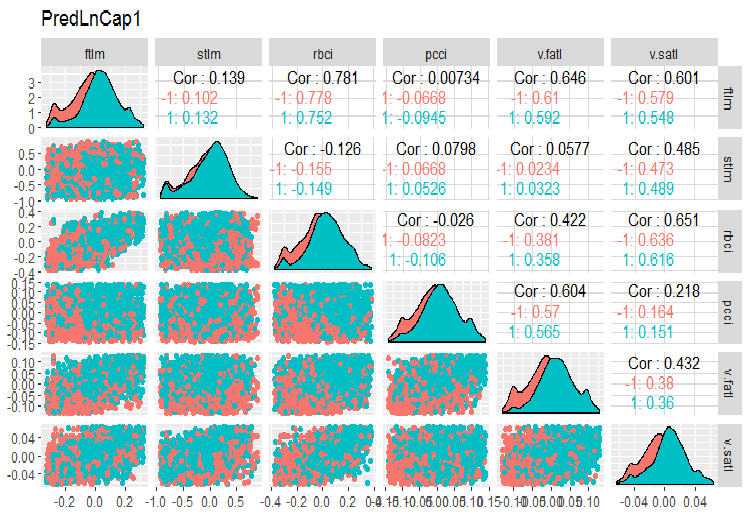
Fig.3. Parámetros de los datos transformados logarítmicamente, parte 1
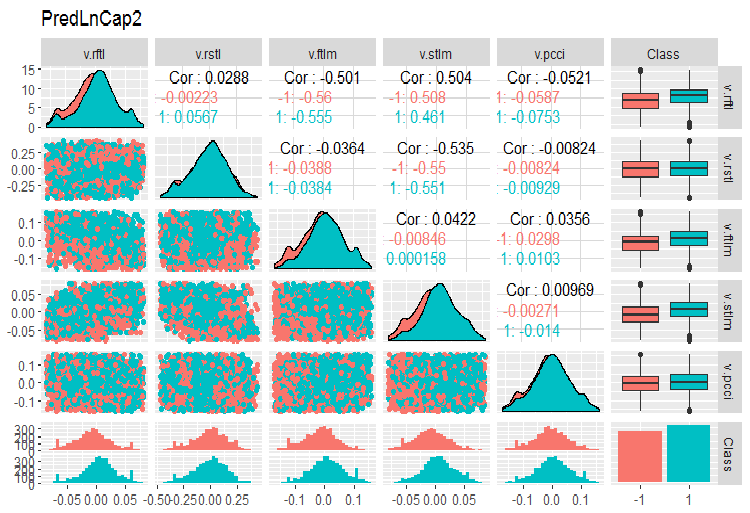
Fig. 4. Parámetros de los datos transformados logarítmicamente, parte 2
Método 2.
Transformamos los datos utilizando la función sin(2*pi*x), quitamos e imputamos los valores atípicos y después evaluamos la asimetría, la distribución de los valores atípicos y la covariación de las variables transformadas en los gráficos.
evalq({x.sin <- apply(x, 2, function(x) sin(2*pi*x))
sk.sin <- skewness(x.sin)
},
env)
#----------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
remove_outliers(x.sin[ ,i])
} -> x.sin.out
colnames(x.sin.out) <- colnames(x.sin)
},
env)
#-----------------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
capping_outliers(x.sin[ ,i])
} -> x.sin.cap
colnames(x.sin.cap) <- colnames(x.sin)
},
env)
#-----------
evalq({
sk.sin.out <- skewness(x.sin.out)
sk.sin.cap <- skewness(x.sin.cap)
},
env)
¿Cómo es la asimetría de estos conjuntos de datos transformados?
env$sk.sin ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.0009679463 v.fatl v.satl v.rftl v.rstl Skewness 0.03280465 0.5217757 0.05611136 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.04923953 -0.2123434 0.01738377 > env$sk.sin.out ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03532892 v.fatl v.satl v.rftl v.rstl Skewness 0.00360966 -0.02380975 -0.05336561 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.0009366441 0.01835948 0.0008843329 > env$sk.sin.cap ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03283132 v.fatl v.satl v.rftl v.rstl Skewness 0.007588308 -0.02424707 -0.04106469 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.007003051 0.009237835 0.002101687
Como se puede ver, con esta transformación todos los conjuntos son simétricos. Veamos el aspecto de estos conjuntos:
par(mfrow = c(2, 2)) boxplot(env$x.sin, main = "x.sin with outlier") abline(h = 0, col = 2) boxplot(env$x.sin.out, main = "x.sin.out without outlier") abline(h = 0, col = 2) boxplot(env$x.sin.cap, main = "x.sin.cap with capping outlier") abline(h = 0, col = 2) par(mfrow = c(1, 1))
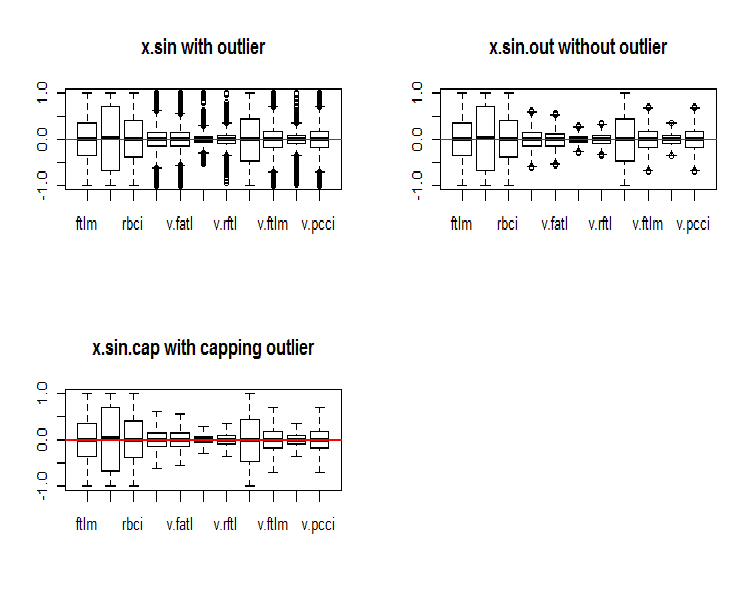
Fig.5. Conjunto de datos transformado por la función sin()
A primera vista, estos conjuntos de datos tienen mejor aspecto que los anteriores (inicial y transformado).
Veamos cómo están distribuidos los NA en las variables después de que los valores atípicos hayan sido eliminados.
require(VIM)
evalq(a <- aggr(x.sin.out), env)
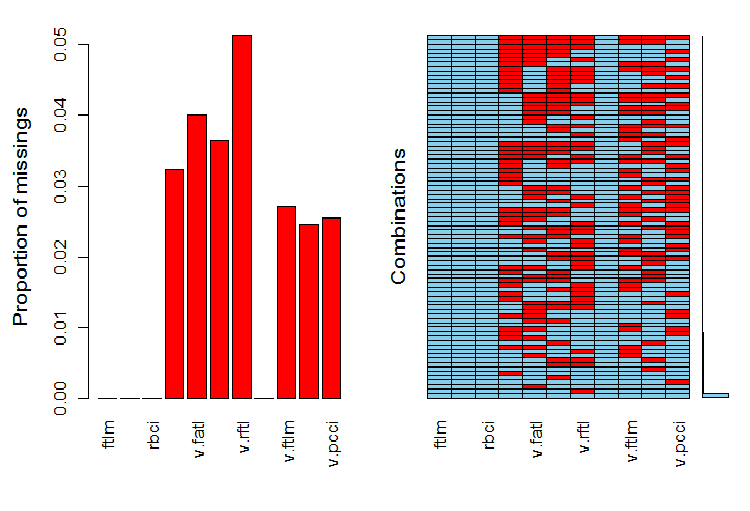
Fig.6. Distribución de NA en el conjunto de datos
En la parte izquierda de la tabla se muestra el número (relativo) de datos no definidos en cada variable. El lado derecho muestra combinaciones de ejemplos con un número diferente de NA (aumentando de forma ascendente). Podemos ver los valores:
> print(env$a) Missings in variables: Variable Count pcci 256 v.fatl 317 v.satl 289 v.rftl 406 v.ftlm 215 v.stlm 194 v.pcci 201
¿Cuál es la distribución de NA en las variables?
par(mfrow = c(3, 4)) evalq( foreach(i = 1:ncol(x.sin.out)) %do% { barMiss(x.sin.out, pos = i, only.miss = TRUE, main = "x.sin.out without outlier") }, env ) par(mfrow = c(1, 1))
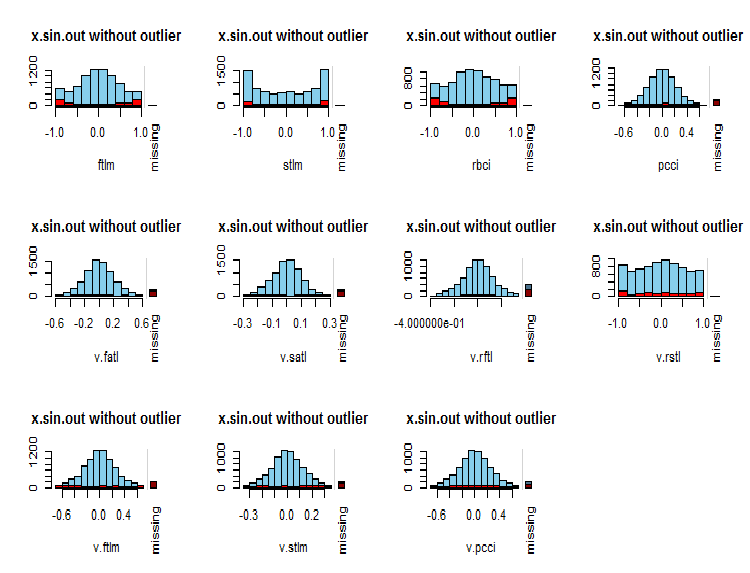
Fig.7. Distribución de NA en las variables
En azul se muestran los valores observados para la variable, y en rojo, el número de NA de otras variables en diferentes rangos de valores de la variable actual. La barra de la derecha representa la contribución de los NA de la variable actual en el número total de NA de todas las variables.
Finalmente, vamos a echar un vistazo a la variación y covariación del conjunto transformado con valores atípicos imputados.
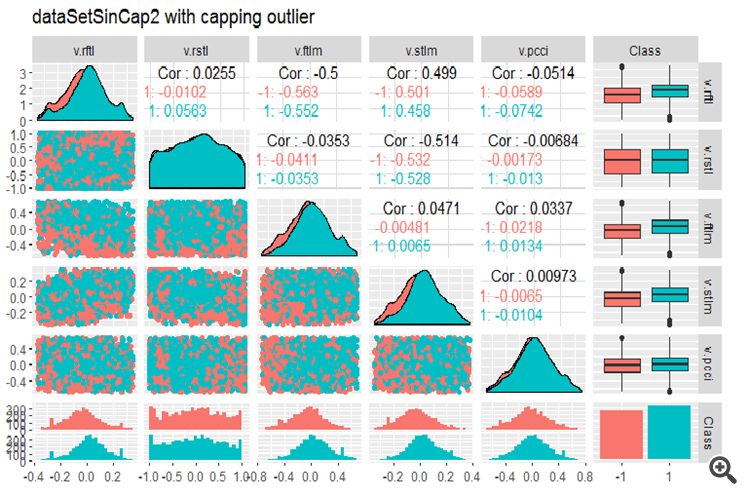
#--------------- evalq(x.sin.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetSinCap, env) require(GGally) evalq(ggpairs(dataSetSinCap, columns = 2:7, mapping = aes(color = Class), title = "dataSetSinCap1 with capping outlier "), env) evalq(ggpairs(dataSetSinCap, columns = 8:13, mapping = aes(color = Class), title = "dataSetSinCap2 with capping outlier"), env) #---------------------------
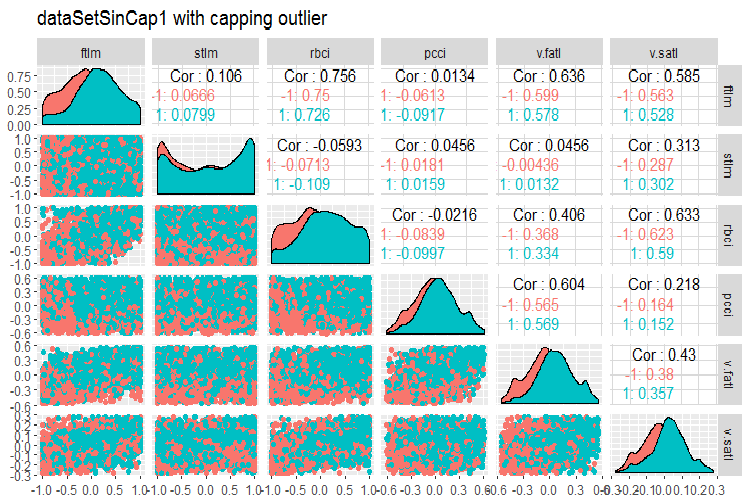
Fig.8. Parámetros de los datos sin() transformados, parte 1
Fig.9. Parámetros de los datos sin() transformados, parte 2
1.1.2. Normalización
Puesto que estamos preparando los datos para una red neural, las variables deben ser traídas dentro del rango de {-1 .. + 1}. Para ello, usaremos la función preProcess()::caret y method = “spatialSign”. Alternativamente, podemos centrar o dimensionar los datos antes de la normalización. Este es un proceso muy simple y no vamos a detenernos en él en este artículo.
Hay algo a tener en cuenta, sin embargo: los parámetros de normalización los obtenemos a partir del conjunto de datos de entrenamiento, y se utilizarán para procesar los conjuntos de prueba y validación.
Para su posterior uso en otros experimentos dividiremos nuestro conjunto, obtenido en los cálculos anteriores, (dataSet sin quitar los valores altamente correlacionados) en train/test/val y lo traeremos dentro del intervalo (-1, + 1) sin estandarización.
Al realizar la normalización con la estandarización, tenga en cuenta que al definir los parámetros de normalización (media/mediana, SD/mad), los parámetros de imputación de los valores atípicos deben ser también definidos. De cara al futuro, se van a utilizar para train/val/test. Anteriormente en este artículo ya escribimos dos funciones: prep.outlier() y treatOutlier(), que están diseñadas para este propósito.
Secuencia de ejecución de las operaciones:
- Definición de parámetros para los valores atípicos en train
- Elimación de los valores atípicos en train
- Definición de los parámetros de estandarización en train
- Imputación de los valores atípicos en train/val/test
- Normalización de train/val/test.
No vamos a considerar esta variante aquí, usted podrá estudiarla por su cuenta.
Dividimos el conjunto en train/val/test:
evalq(
{
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(clean = data.frame(dataSet) %>% na.omit(),
train = clean[train, ],
val = clean[val, ],
test = clean[test, ]) -> DT
}, env)
Definimos los parámetros de normalización para el conjunto train y normalizamos los conjuntos train/test/val:
require(foreach)
evalq(
{
preProcess(DT$train, method = "spatialSign") -> preproc
list(train = predict(preproc, DT$train),
val = predict(preproc, DT$val),
test = predict(preproc, DT$test)
) -> DTn
},
env)
Vamos a echar un vistazo a las estadísticas totales del conjunto train:
> table.Stats(env$DTn$train %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5909 -0.7624 -0.6114 -0.8086 Quartile 1 -0.2054 -0.2157 -0.2203 -0.2110 Median 0.0145 0.0246 0.0147 0.0068 Arithmetic Mean 0.0070 0.0190 0.0085 0.0028 Geometric Mean -0.0316 -0.0396 -0.0332 -0.0438 Quartile 3 0.2139 0.2462 0.2341 0.2277 Maximum 0.6314 0.8047 0.7573 0.7539 SE Mean 0.0060 0.0073 0.0063 0.0065 LCL Mean (0.95) -0.0047 0.0047 -0.0037 -0.0100 UCL Mean (0.95) 0.0188 0.0333 0.0208 0.0155 Variance 0.0719 0.1058 0.0784 0.0848 Stdev 0.2682 0.3252 0.2800 0.2912 Skewness -0.0762 -0.0221 -0.0169 -0.0272 Kurtosis -0.8759 -0.6688 -0.8782 -0.7090 v.fatl v.satl v.rftl v.rstl Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5160 -0.5943 -0.6037 -0.7591 Quartile 1 -0.2134 -0.2195 -0.1988 -0.2321 Median 0.0015 0.0301 0.0230 0.0277 Arithmetic Mean 0.0032 0.0151 0.0118 0.0177 Geometric Mean -0.0323 -0.0267 -0.0289 -0.0429 Quartile 3 0.2210 0.2467 0.2233 0.2657 Maximum 0.5093 0.5893 0.6714 0.7346 SE Mean 0.0058 0.0063 0.0062 0.0074 LCL Mean (0.95) -0.0082 0.0028 -0.0003 0.0033 UCL Mean (0.95) 0.0146 0.0274 0.0238 0.0321 Variance 0.0675 0.0783 0.0757 0.1083 Stdev 0.2599 0.2798 0.2751 0.3291 Skewness -0.0119 -0.0956 -0.0648 -0.0562 Kurtosis -1.0788 -1.0359 -0.7957 -0.7275 v.ftlm v.stlm v.rbci v.pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5627 -0.6279 -0.5925 -0.7860 Quartile 1 -0.2215 -0.2363 -0.2245 -0.2256 Median -0.0018 0.0092 -0.0015 -0.0054 Arithmetic Mean -0.0037 0.0036 -0.0037 0.0013 Geometric Mean -0.0426 -0.0411 -0.0433 -0.0537 Quartile 3 0.2165 0.2372 0.2180 0.2276 Maximum 0.5577 0.6322 0.5740 0.9051 SE Mean 0.0061 0.0065 0.0061 0.0070 LCL Mean (0.95) -0.0155 -0.0091 -0.0157 -0.0124 UCL Mean (0.95) 0.0082 0.0163 0.0082 0.0150 Variance 0.0732 0.0836 0.0742 0.0975 Stdev 0.2706 0.2892 0.2724 0.3123 Skewness 0.0106 -0.0004 -0.0014 0.0232 Kurtosis -1.0040 -1.0083 -1.0043 -0.4159
En el recuadro vemos que las variables son simétricas y tienen unos parámetros muy cercanos.
Veamos la distribución de las variables en los conjuntos train/val/test:
boxplot(env$DTn$train %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Train") abline(v = 0, col = 2) boxplot(env$DTn$test %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Test") abline(v = 0, col = 2) boxplot(env$DTn$val %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Val") abline(v = 0, col = 2)
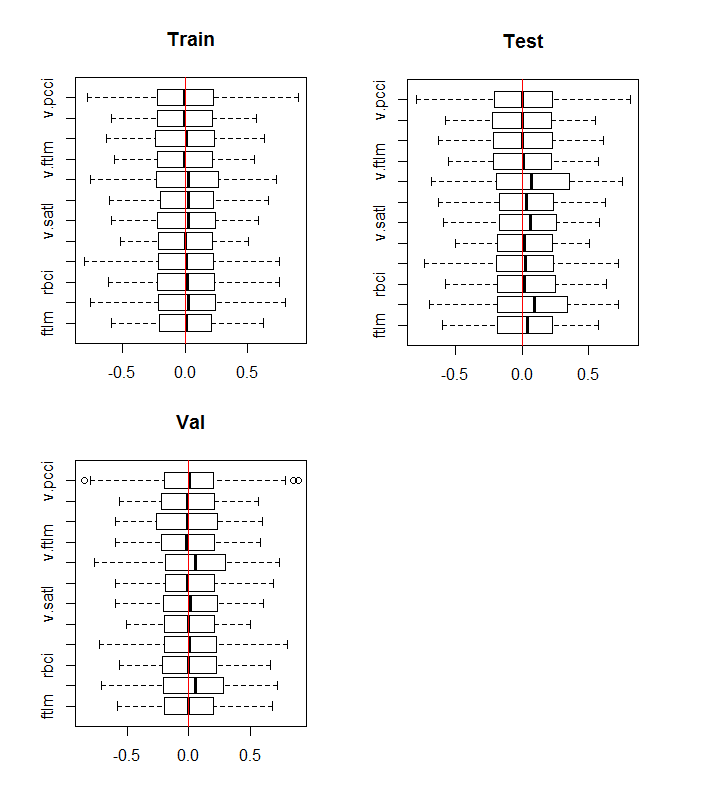
Fig.10. Distribución de las variables en los conjuntos train/val/test después de la normalización
La distribución de las variables es casi la misma en todos los conjuntos. También tenemos que tener en cuenta la correlación y covarianza de las variables en el conjunto train:
require(GGally) evalq(ggpairs(DTn$train, columns = 2:7, mapping = aes(color = Class), title = "DTn$train1 "), env) evalq(ggpairs(DTn$train, columns = 8:14, mapping = aes(color = Class), title = "DTn$train2"), env)
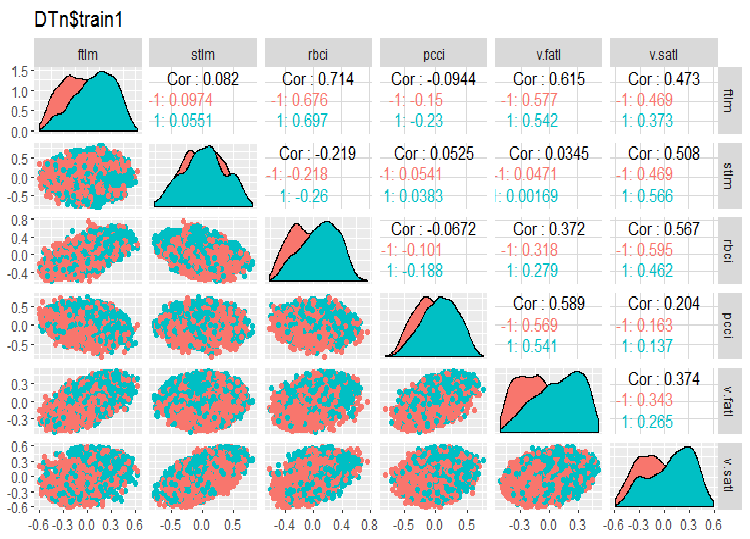
Fig.11. Variación y covariación del conjunto train 1
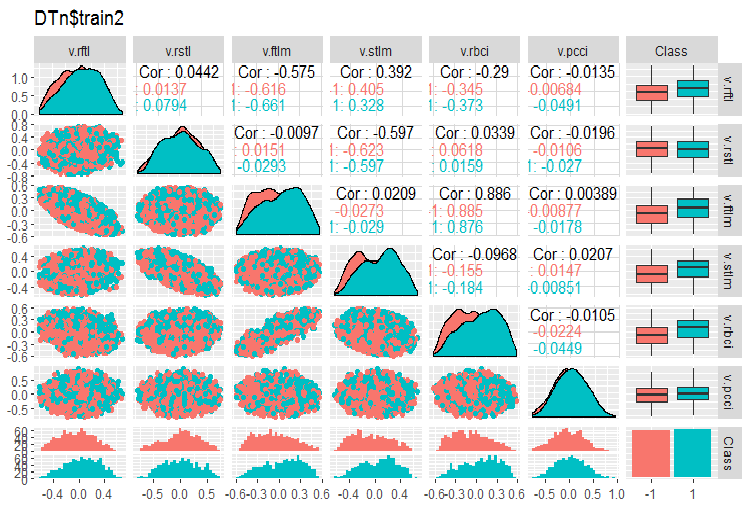
Fig.12. Variación y covariación del conjunto train 2
No hay datos altamente correlacionados, la distribución es compacta y no tiene valores atípicos, los datos están bien divididos. En vista de ello, solo tenemos dos variables problemáticas stlm y v.rstl. Posteriormente, cuando vayamos a evaluar la relevancia de los predictores, concretaremos esta opinión preliminar. Ahora podemos observar la correlación de estos predictores y la variable objetivo:
> funModeling::correlation_table(env$DTn$train %>% tbl_df %>% + select(-Data), str_target = 'Class') Variable Class 1 Class 1.00 2 v.fatl 0.38 3 ftlm 0.34 4 rbci 0.28 5 v.rbci 0.28 6 v.satl 0.27 7 pcci 0.24 8 v.ftlm 0.22 9 v.stlm 0.22 10 v.rftl 0.18 11 v.pcci 0.08 12 stlm 0.03 13 v.rstl -0.01Podemos ver que las variables indicadas se encuentran en el fondo del recuadro, con índices muy pequeños. La relevancia de la variable v.pcci. también es cuestionable. Vamos a ver más de cerca la variable v.fatl en todos los conjuntos train/val/test:
require(ggvis) evalq( DTn$train %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$train$v.fatl"), env) evalq( DTn$val %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$val$v.fatl"), env) evalq( DTn$test %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$test$v.fatl"), env)
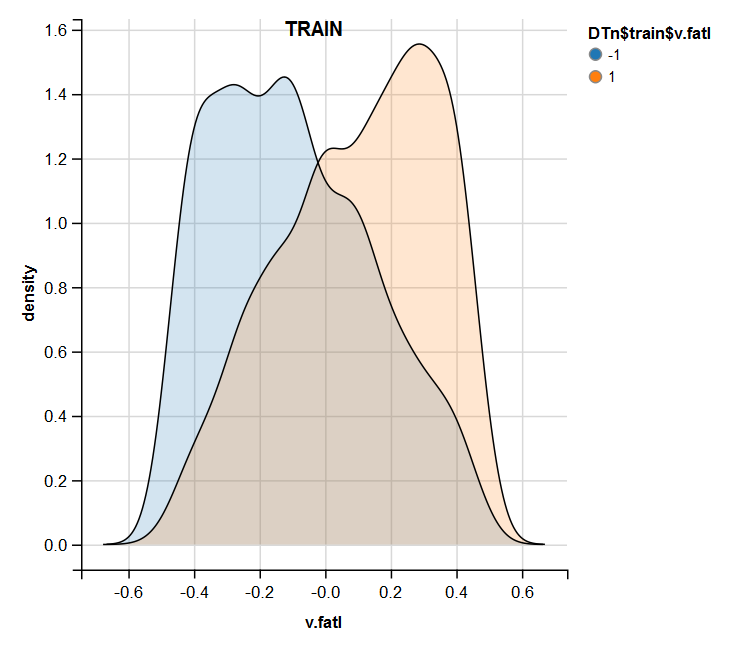
Fig.13. Distribución de la variable v.fatl en el conjunto train después de la normalización
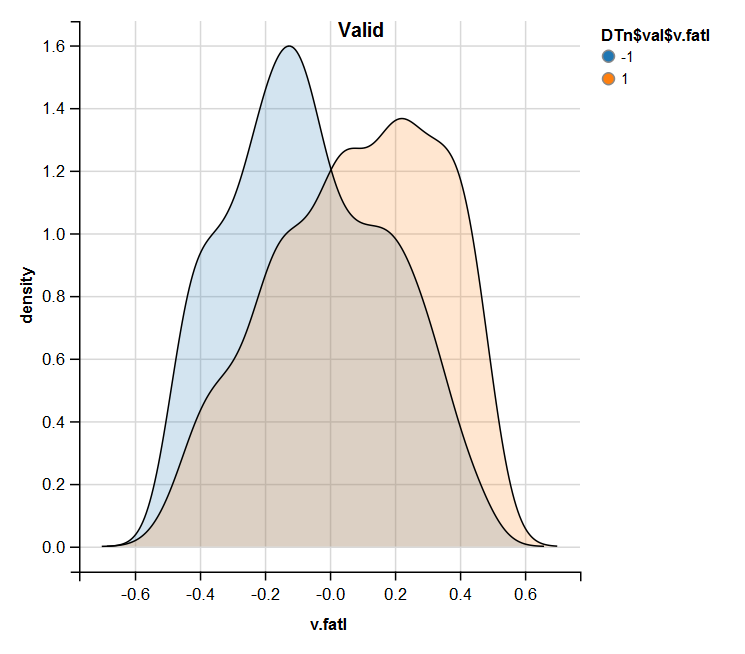
Fig.14. Distribución de la variable v.fatl en el conjunto valid después de la normalización
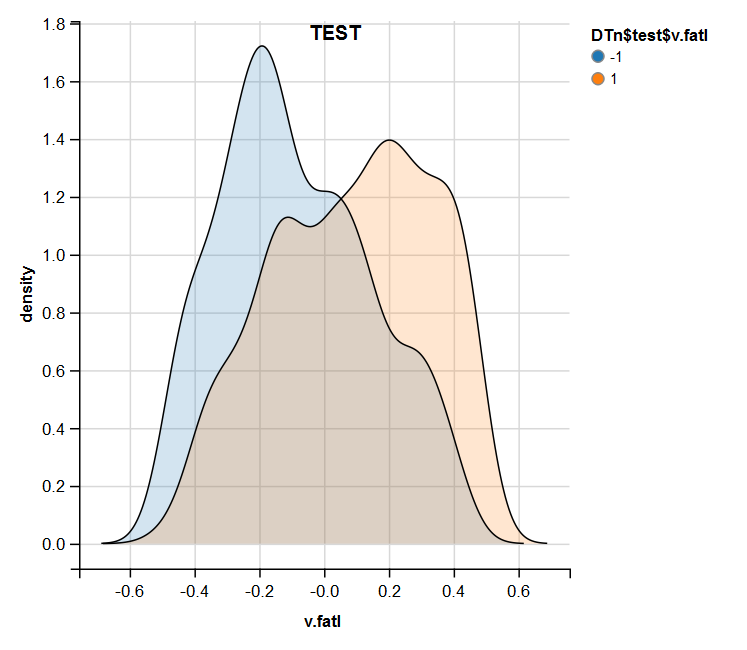
Fig.15. Distribución de la variable v.fatl en el conjunto test después de la normalización
El análisis realizado muestra que la normalización produce a menudo una buena distribución de los predictores, sin valores atípicos y datos altamente correlacionados. En general, esto depende de la naturaleza de los datos en bruto.
1.1.3. Discretización
La discretización es el proceso de transformación de una variable continua en una discreta dividiendo sus valores en áreas usando diferentes métodos para la definición de los límites.
Podemos destacar dos grupos de métodos de división: los métodos cuantitativos, sin relación con la variable objetivo, y los métodos que tengan en cuenta la correspondencia de rangos con la variable objetivo.
El primer grupo de métodos está casi totalmente cubierto por la función cut2()::Hmisc. La muestra se puede dividir en un número predeterminado de áreas con límites especificados, en cuartiles, en áreas con un número mínimo de ejemplos en cada una y en áreas de frecuencia equivalente.
El segundo grupo de métodos es más interesante porque divide la variable en áreas relacionadas con los niveles de la variable objetivo. Vamos a ver varios paquetes que implementan estos métodos.
Discretización. Este paquete supone un conjunto de algoritmos de discretización con entrenador. También se puede agrupar en términos "descendente" y "ascendente", que implementan los algoritmos de discretización. Vamos a analizar algunos de ellos en el ejemplo de nuestro conjunto dataSet.
En primer lugar, vamos a limpiar el conjunto (sin quitar variables altamente correlacionadas), y a dividirlo en train/val/test con una proporción 2000/1000/1000.
require(discretization)
require(caret)
require(pipeR)
evalq(
{
dataSet %>%
preProcess(.,
method = c("zv", "nzv", "conditionalX")) %>%
predict(., dataSet) %>%
na.omit -> dataSetClean
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(train = dataSetClean[train, ],
val = dataSetClean[val, ],
test = dataSetClean[test, ]) -> DT
},
env)
Vamos a utilizar la función mdlp()::discretization, que describe la discretización usando el principio de longitud mínima de descripción. Esta función discretiza los atributos continuos de la matriz de datos usando un criterio de entropía con la longitud mínima de descripción como regla de detención.
evalq(
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()}) -> mdlp.train, envir = env)
La función devuelve una lista con dos espacios: cutp, un frame de datos con puntos de corte para cada variable y Disc.data, un frame de datos con variables marcadas.
> env$mdlp.train%>%str() List of 2 $ cutp :List of 12 ..$ : num [1:2] -0.0534 0.0278 ..$ : chr "All" ..$ : num -0.0166 ..$ : num [1:2] -0.0205 0.0493 ..$ : num [1:3] -0.0519 -0.0055 0.019 ..$ : num 0.000865 ..$ : num -0.00909 ..$ : chr "All" ..$ : num 0.0176 ..$ : num [1:2] -0.011 0.0257 ..$ : num [1:3] -0.03612 0.00385 0.03988 ..$ : chr "All" $ Disc.data:'data.frame': 2000 obs. of 13 variables: ..$ ftlm : int [1:2000] 3 3 3 3 3 2 1 1 1 1 ... ..$ stlm : int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ rbci : int [1:2000] 2 2 2 2 2 2 1 1 1 1 ... ..$ pcci : int [1:2000] 2 2 1 2 2 1 1 2 3 2 ... ..$ v.fatl: int [1:2000] 4 4 3 4 3 1 1 2 3 2 ... ..$ v.satl: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rftl: int [1:2000] 1 2 2 2 2 2 2 2 1 1 ... ..$ v.rstl: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ v.ftlm: int [1:2000] 2 2 1 1 1 1 1 1 2 1 ... ..$ v.stlm: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rbci: int [1:2000] 4 4 3 3 2 1 1 2 3 2 ... ..$ v.pcci: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ...
¿Qué dice nos dice el primer espacio?
Tenemos tres variables no marcadas, cuyos valores no están relacionados en absoluto con la variable objetivo. Son 2,8 y 12 (stlm, v.rstl, v.pcci). Se pueden quitar sin pérdida alguna de calidad en el conjunto de datos. Por cierto, estas variables se definieron como irrelevantes en el apartado anterior.
4 variables son divididas en dos clases, 3 variables son divididas en 3 clases y dos variables son divididas en 4 clases.
Segmentaremos nuestros conjuntos val/test usando los puntos de corte obtenidos en train. Para ello, eliminaremos del conjunto train las variables no marcadas y guardamos el conjunto en el frame de datos train.d. A continuación, usando la función findInterval(), marcamos el conjunto test/val con los puntos de corte obtenidos anteriormente.
evalq(
{
mdlp.train$cutp %>%
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> train.d
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> test.d
colnames(test.d) <- colnames(train.d)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> val.d
colnames(val.d) <- colnames(train.d)
},env
)
¿Qué aspecto tienen estos conjuntos?
> env$train.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 3 2 2 4 1 1 2 1 4 1 2 3 2 2 4 1 2 2 1 4 1 3 3 2 1 3 1 2 1 1 3 1 4 3 2 2 4 2 2 1 2 3 1 5 3 2 2 3 2 2 1 2 2 1 6 2 2 1 1 1 2 1 1 1 -1 > env$test.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 1 1 1 2 1 1 1 1 2 -1 2 1 1 3 3 1 1 2 2 3 -1 3 1 1 2 2 1 1 1 2 2 -1 4 2 1 2 3 1 1 2 2 3 1 5 2 2 2 3 1 1 1 2 3 1 6 2 2 2 4 1 1 2 2 3 1 > env$val.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 2 2 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 1 2 2 1 3 2 2 2 3 2 2 1 2 2 1 4 2 2 2 4 2 2 2 2 3 1 5 2 2 2 3 2 2 1 2 2 1 6 2 2 2 3 2 2 2 2 2 1 > env$train.d$v.fatl %>% table() . 1 2 3 4 211 693 519 577 > env$test.d$v.fatl %>% table() . 1 2 3 4 49 376 313 262 > env$val.d$v.fatl %>% table() . 1 2 3 4 68 379 295 258
El uso posterior de los conjuntos con datos discretos depende del modelo utilizado. Si se trata de una red neuronal, los predictores tendrán que ser transformados en variables dummy-. ¿Cómo de bien están divididas las clases por estas variables? ¿Cómo de bien se correlacionan con la variable objetivo? Vamos a visualizar estas relaciones con la ayuda de cross-plot()::funModeling. Cross_plot muestra cómo la variable de entrada se correlaciona con la variable objetivo, obteniendo los coeficientes de probabilidad para cada rango de cada entrada.
Analicemos ahora las tres variables v.fatl, ftlm y v.satl, divididas en 4, 3 y 2 rangos respectivamente. Construimos los gráficos
evalq(
cross_plot(data = train.d,
str_input = c("v.fatl", "ftlm", "v.satl"),
str_target = "Class",
auto_binning = F,
plot_type = "both"), #'quantity' 'percentual'
env
)
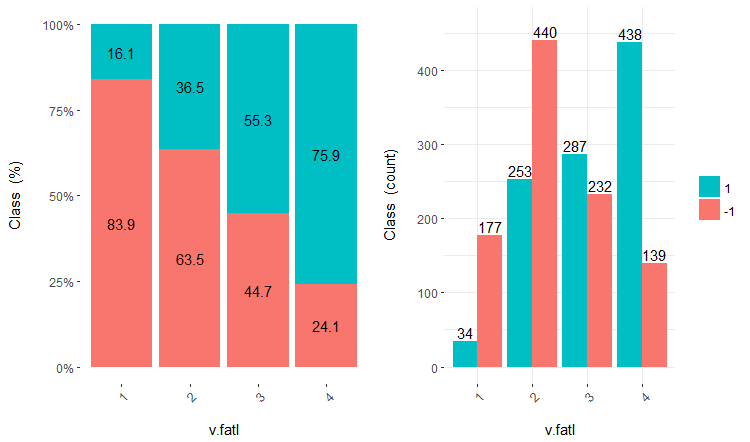
Fig.16. Cross-plot de la variable v.fatl/Class
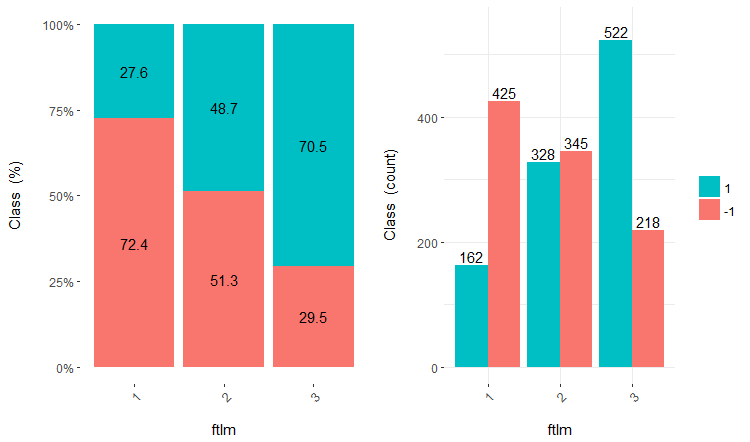
Fig.17. Cross-plot de la variable ftlm/Class
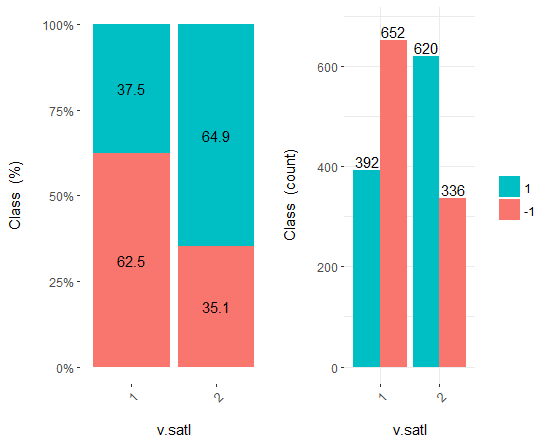
Fig.18. Cross-plot de la variable v.satl/Class
Podemos ver que los predictores están bien correlacionados con los niveles de la variable objetivo y tienen umbrales muy pronunciados que dividen los niveles de la variable objetivo Class.
Podemos simplemente dividir los predictores en áreas iguales (de una manera no óptima) para ver cómo se correlacionan en ese caso con la variable objetivo. Vamos a tomar tres variables anteriores y dos malas (stlm, v.rstl) del conjunto train (no discretizado). Las dividimos en 10 áreas frecuenciales equivalentes y analizamos sus cross-plot con la variable objetivo:
evalq(
cross_plot(
DT$train %>% select(-Data) %>%
select(c(v.satl, ftlm, v.fatl, stlm, v.rstl, Class)) %>%
as.data.frame(),
str_input = Cs(v.satl, ftlm, v.fatl, stlm, v.rstl),
str_target = "Class",
auto_binning = T,
plot_type = "both"), #'quantity' 'percentual'
env
)
Trazamos los cinco gráficos de estas variables:
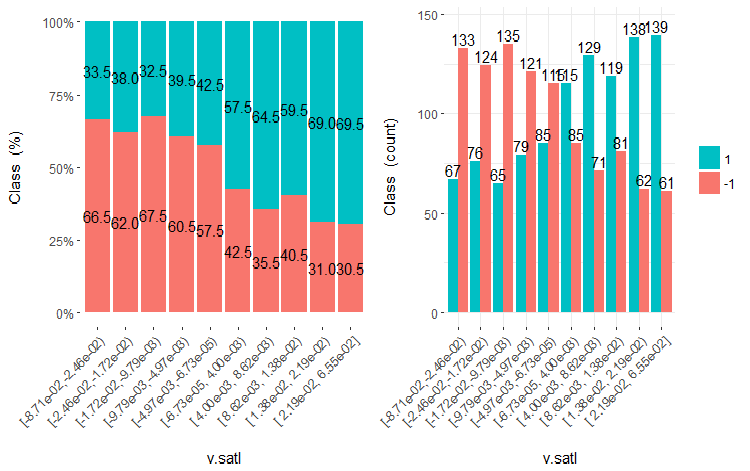
Fig.19. Cross-plot de la variable v.satl (10 áreas) vs Class
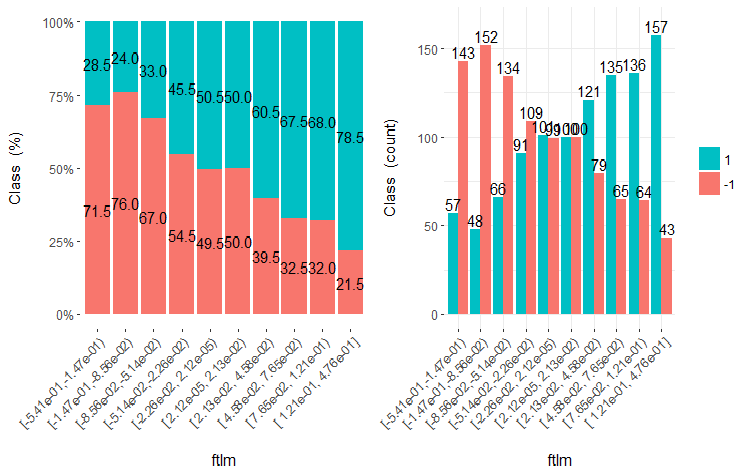
Fig.20. Cross-plot de la variable ftlml (10 áreas) vs Class
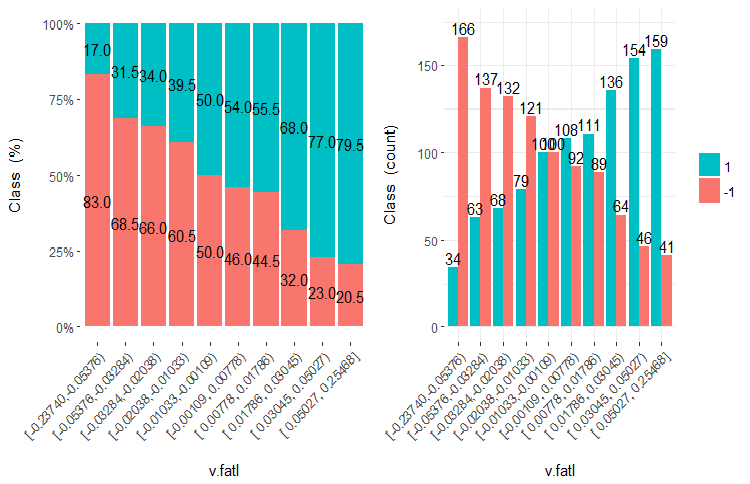
Fig.21. Cross-plot de la variable v.fatl (10 áreas) vs Class
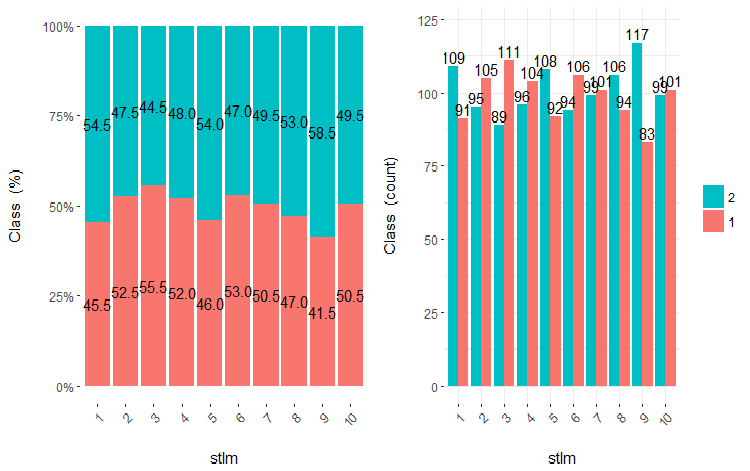
Fig.22. Cross-plot de la variable stlm (10 áreas) vs Class
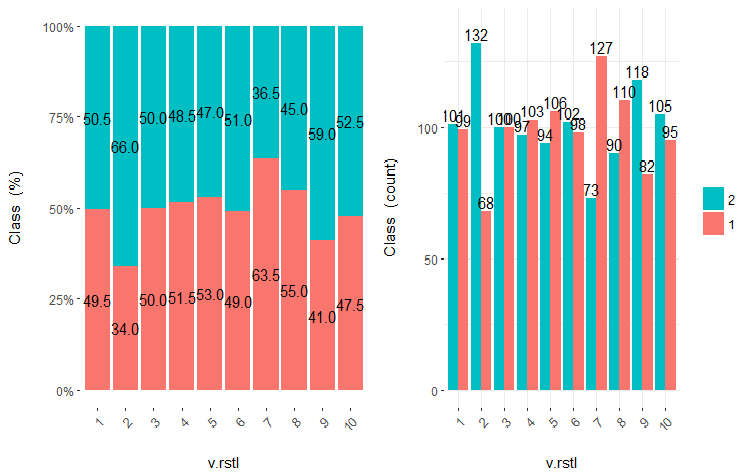
Fig.23. Cross-plot de la variable v.rstl (10 áreas) vs Class
Como se puede ver a partir de los diagramas, incluso al dividir en 10 segmentos discretos de frecuencia equivalente las variables v.fatl, ftlm y v.satl estas tienen un umbral de división de los niveles de la variable bien pronunciado. Ahora está claro por qué las otras dos variables (stlm, v.rstl) son irrelevantes. Por cierto, esta es una manera eficaz de identificar la importancia de los predictores. Vamos a volver a esto más adelante en este artículo.
Ahora, vamos a ver cómo la variable de entrada se correlaciona con la variable objetivo, comparándolas con el método bayesiano posterior conversion rate. Resulta útil para comparar los valores categóricos que no tienen un orden interno. Para ello, vamos a utilizar la función bayes_plot::funModeling. Tomamos las variables v.fatl, ftlm y v.satl de los conjuntos train.d, val.d y test.d.
#------BayesTrain------------------- evalq( { bayesian_plot(train.d, input = "v.fatl", target = "Class", title = "Bayesian comparison train$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "ftlm", target = "Class", title = "Bayesian comparison train$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "v.satl", target = "Class", title = "Bayesian comparison train$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------BayesTest------------------------ evalq( { bayesian_plot(test.d, input = "v.fatl", target = "Class", title = "Bayesian comparison test$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "ftlm", target = "Class", title = "Bayesian comparison test$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "v.satl", target = "Class", title = "Bayesian comparison test$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #-------------BayesVal--------------------------------- evalq( { bayesian_plot(val.d, input = "v.fatl", target = "Class", title = "Bayesian comparison val$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "ftlm", target = "Class", title = "Bayesian comparison val$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "v.satl", target = "Class", title = "Bayesian comparison val$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------------------------------------
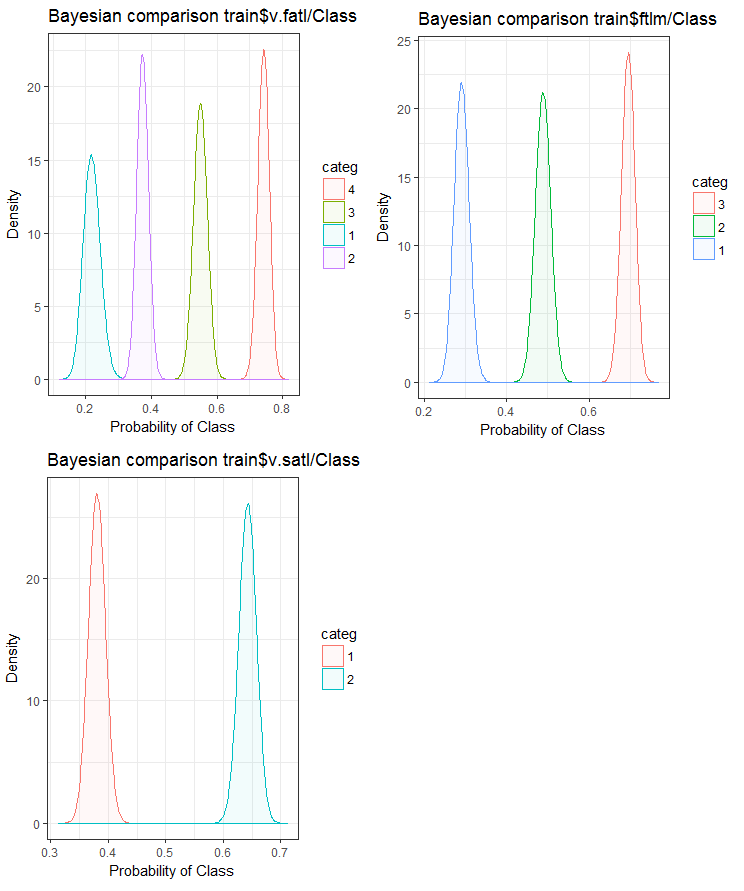
Fig.24. Comparación bayesiana de variables con la variable objetivo en el conjunto train
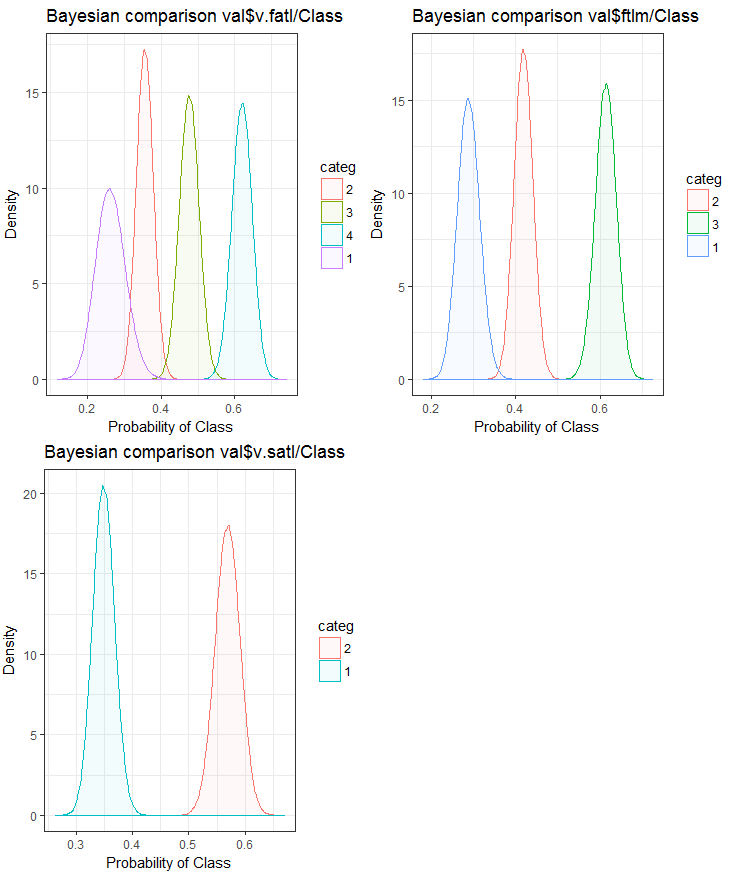
Fig.25. Comparación bayesiana de variables con la variable objetivo en el conjunto val
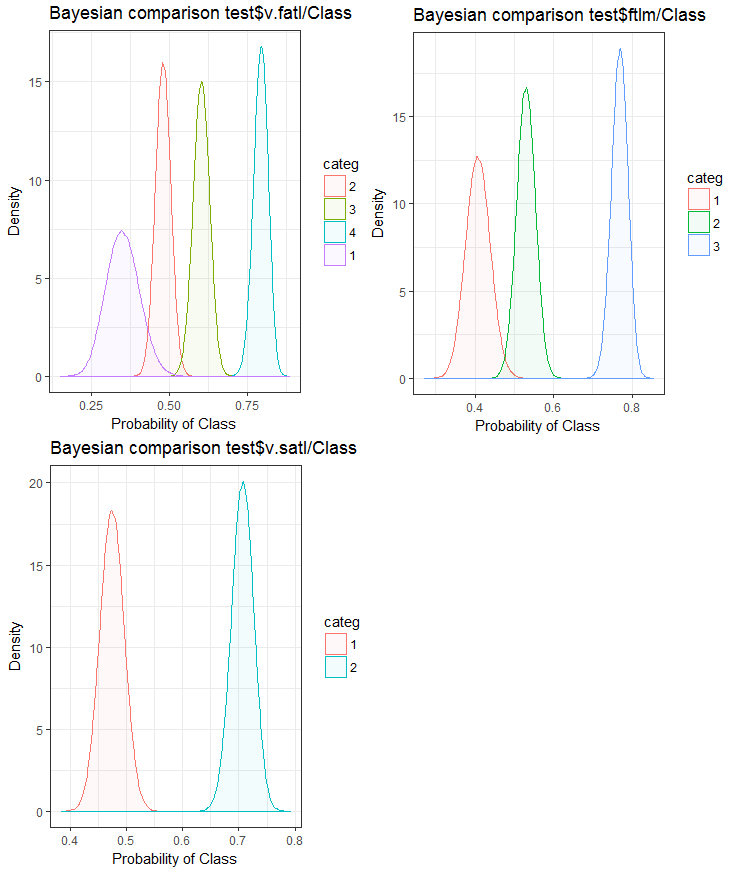
Fig.26. Comparación bayesiana de variables con la variable objetivo en el conjunto test
Podemos ver que la correlación de los predictores con la variable objetivo va más a la deriva en las variables con 4 niveles y más. Ese fenómeno es menos acusado en las variables con dos grupos. Hay que comprobar en el futuro cómo influye el uso de predictores de solo dos rangos en la precisión de los modelos.
Esta misma tarea - la división de la variable en segmentos que se correspondan perfectamente con los niveles de la variable objetivo - se puede resolver de otra forma, con la ayuda del magnífico paquete smbinning. Puede comprobarlo usted mismo. El anterior artículo analiza otro método interesante de discretización, con la ayuda del paquete "RoughSets".
La discretización es un método eficaz para transformar predictores. Por desgracia, no todos los modelos pueden trabajar con los predictores de factores.
1.2. Creación de características
La creación de una variable es un proceso de creación de nuevas variables basadas en las ya existentes. Por ejemplo, tenemos una fecha (dd-mm-aa) como variable de entrada en el conjunto de datos. Podemos crear nuevas variables que estarán mejor relacionadas con la variable objetivo (día, mes, año, día de la semana). Este paso se utiliza para revelar las interrelaciones ocultas en la variable.
La creación de variables derivadas es un proceso en el que se crea una nueva variable usando un conjunto de funciones o utilizando diferentes métodos. El tipo de variable a crear depende de la curiosidad del analista de negocios, de su conjunto de hipótesis y de sus conocimientos teóricos. El surtido de métodos es muy amplio: la aplicación de logaritmos, la segmentación y la elevación a la enésima potencia son solamente algunos ejemplos de métodos de transformación.
La creación de variables ficticias o dummy es otro método popular para trabajar con variables. Por lo general, las variables ficticias se utilizan para transformar las variables categóricas en numéricas. La variable categórica puede tomar valores de 0 y 1. Podemos crear variables ficticias para más de dos clases de variables categóricas con variables N o N-1.
En este artículo se discuten las situaciones que nos encontramos a diario como analistas. ¿Cómo extraer la máxima información de un conjunto de datos? Aquí hay algunas maneras.
- Utilice los valores de fecha y hora como variables. Podemos crear nuevas variables teniendo en cuenta las diferencias de fecha y hora.
- Crear nuevas relaciones y proporciones: en lugar de almacenar las pasadas entradas y salidas en el conjunto de datos, podemos incluir en el conjunto las relaciones con un posible mayor significado.
- Aplicar transformaciones convencionales. En cuanto a las fluctuaciones y las áreas de la variable junto con la salida, podemos ver si la correlación mejora después de las transformaciones básicas. La mayoría de las transformaciones de uso frecuente incluyen log, exp, variaciones cuadradas y trigonométricas.
- Compruebe las variables de estacionalidad y cree un modelo para el periodo necesario (semana, mes, sesión, etc.).
Podemos entender de forma intuitiva que el comportamiento del mercado el lunes es diferente al del miércoles y el jueves. Es decir, el día de la semana es una característica importante. No menos importante es el periodo del día en el que se encuentra el mercado (sesión asiática, europea o americana). ¿Cómo podemos definir estas características?
Vamos a utilizar el paquete timekit. La función central del paquete es tk_augment_timeseries_signature(), que suma a las etiquetas de tiempo del conjunto inicial pr toda una serie de datos de tiempo que pueden ser útiles como características adicionales y como parámetros adicionales de grupo. ¿Qué datos son?
| Index | valor del índice que fue resuelto |
| Index.num | valor numérico del índice en segundos. Base “1970-01-01 00:00:00” |
| diff | diferencia en segundos con el valor numérico del índice anterior |
| Year | año, componente del índice |
| half | mitad del componente del índice |
| quarter | trimestre, componente del índice |
| month | mes, componente del índice con base 1 |
| month.xts | mes, componente del índice con base 0, de la misma forma que se implementa en xts |
| month.lbl | etiqueta de mes como factor ordenado, que se inicia en enero y termina en diciembre |
| day | día, componente del índice |
| hour | hora, componente del índice |
| minute | minuto, componente del índice |
| second | segundo, componente del índice |
| hour12 | componente de la hora en una escala de 12 horas |
| am.pm | mañana (am) = 1, tarde (pm) = 2 |
| wday | día de la semana con base 1. Domingo = 1, sábado = 7 |
| wday.xts | día de la semana con base 0, de la misma forma que se implementa en xts. Domingo = 0, sábado = 6 |
| wday.lbl | marca para el día de la semana como factor ordenado. Comienza el domingo y termina el sábado |
| mday | día del mes |
| qday | día del trimestre |
| yday | día del año. |
| mweek | semana del mes |
| week | número de la semana en un año (comienza con el domingo) |
| week.iso | número de la semana en un año según la norma ISO (comienza con el lunes) |
| week2 | módulo para la frecuencia de dos semanas |
| week3 | módulo para la frecuencia de tres semanas |
| week4 | módulo para la frecuencia de cuatro semanas |
Tomamos el conjunto de datos pr inicial, lo fortalecemos con la función tk_augment_timeseries_signature(), añadimos al conjunto inicial las variables mday, wday.lbl, hour, eliminamos los datos indefinidos (NA) y agrupamos los datos por días de la semana.
evalq(
{
tk_augment_timeseries_signature(pr) %>%
select(c(mday, wday.lbl, hour)) %>%
cbind(pr, .) -> pr.augm
pr.compl <- pr.augm[complete.cases(pr.augm), ]
pr.nest <- pr.compl %>% group_by(wday.lbl) %>% nest()
},
env)
> str(env$pr.augm)
'data.frame': 8000 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..................................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ mday : int 10 10 10 10 10 10 10 10 10 10 ...
$ wday.lbl: Ord.factor w/ 7 levels "Sunday"<"Monday"<..: 3 3 3 3 3 3 3 3 3 3 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ...
El mismo resultado se puede alcanzar si usamos la biblioteca lubridate, eliminando de paso los datos del sábado.
require(lubridate)
evalq({pr %>% mutate(.,
wday = wday(Data), #label = TRUE, abbr = TRUE),
day = day(Data),
hour = hour(Data)) %>%
filter(wday != "Sat") -> pr1
pr1.nest <- pr1 %>% na.omit %>%
group_by(wday) %>% nest()},
env
)
#-------
str(env$pr1)
'data.frame': 7924 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..........................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ wday : int 3 3 3 3 3 3 3 3 3 3 ...
$ day : int 10 10 10 10 10 10 10 10 10 10 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ...
Los datos agrupados por días de la semana tienen el aspecto siguiente (domingo = 1, lunes = 2, etcétera):
> env$pr1.nest # A tibble: 5 × 2 wday data <int> <list> 1 4 <tibble [1,593 Ч 32]> 2 5 <tibble [1,632 Ч 32]> 3 6 <tibble [1,624 Ч 32]> 4 2 <tibble [1,448 Ч 32]> 5 3 <tibble [1,536 Ч 32]>
De los datos en el conjunto pr principal se pueden usar adicionalmente las variables dL, dH en las últimas 3 barras.
2. Elección de los predictores
Hay muchos métodos y criterios para evaluar la importancia de los predictores. Algunos de ellos fueron analizados en los artículos anteriores. Dado que en este artículo hemos hecho énfasis en la visualización, vamos a comparar un método visual y un método analítico para la evaluación de la importancia de los predictores.
2.1. Evaluación visual
Usaremos el paquete smbinning. En los anteriores apartados hemos evaluado los predictores con la ayuda del paquete funModeling, y hemos llegamos a la conclusión de que la visualización de una relación es una manera sencilla y fiable de identificar los predictores relevantes. Vamos a ver cómo trabaja el paquete smbinning con los datos normalizados y transformados, y también vamos a comprobar cómo impacta la transformación de los predictores en su importancia.
Reunimos en un conjunto los datos log-transformados, seno-transformados, añadimos los datos tanh-transformados y los datos normalizados y evaluamos la dependencia de la variable objetivo y de los predictores en estos conjuntos.
La secuencia de procesamiento del conjunto primario (que se muestra en el diagrama de abajo) es la siguiente: limpiamos los datos en bruto de dataSet (sin eliminar los datos altamente correlacionados), y dividiendo el conjunto de datos en los conjuntos train/val/test, obtenemos el conjunto DT. A continuación, para cada tipo de transformación ejecutamos las acciones según el esquema. Reunimos todo en un script:
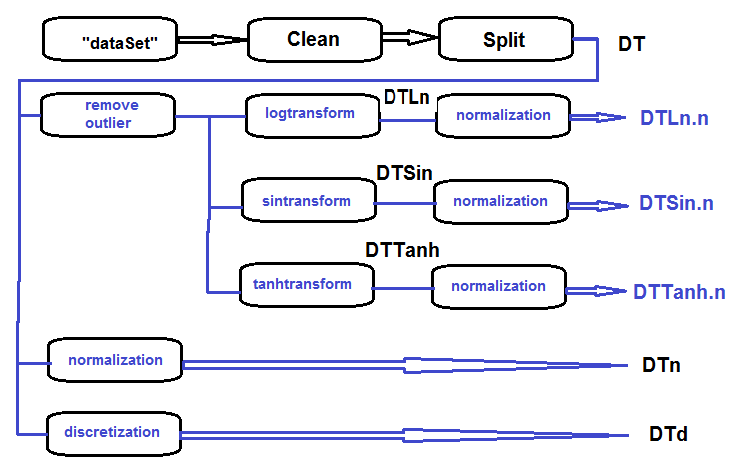
Fig.27. Esquema estructural del procesamiento preliminar
Limpiamos el conjunto, lo dividimos en train/val/test y quitamos los datos innecesarios:
#----Clean--------------------- require(caret) require(pipeR) evalq( { train = 1:2000 val = 2001:3000 test = 3001:4000 DT <- list() dataSet %>% preProcess(., method = c("zv", "nzv", "conditionalX")) %>% predict(., dataSet) %>% na.omit -> dataSetClean list(train = dataSetClean[train, ], val = dataSetClean[val, ], test = dataSetClean[test, ]) -> DT rm(dataSetClean, train, val, test) }, env)
Procesamos todos los valores atípicos en todos los conjuntos:
#------outlier-------------
evalq({
# definimos la nueva lista para el resultado
DTcap <- list()
# pasamos por los tres conjuntos
foreach(i = 1:3) %do% {
DT[[i]] %>%
# retiramos las columnas de(Data, Class)
select(-c(Data, Class)) %>%
# transformamos en data.frame y guardamos en la variable de tiempo x
as.data.frame() -> x
if (i == 1) {
# en la primera entrada, definimos los parámetros de los valores atípicos
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
prep.outlier(x[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
}
# sustitutos los valores atípicos 5/95 % y guardamos el resultado en x.cap
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = x[ ,i], impute = T, fill = T,
lower = lower, upper = upper,
med = med, cap1 = cap1, cap2 = cap2)
} %>% as.data.frame() -> x.cap
colnames(x.cap) <- colnames(x)
return(x.cap)
} -> Dtcap
#quitamos las variables innecesarias
rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
Transformamos las variables en todos los conjuntos Dtcap sin valores atípicos de la función log(x+1). Obtenemos la lista DTLn con tres conjuntos de variables log-transformadas.
#------logtrans------------
evalq({
DTLn <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) log2(x + 1)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTLn
},
env)
Transformamos las variables en todos los conjuntos Dtcap sin valores atípicos con la función sin(2*pi*x). Obtenemos la lista DTSin con tres conjuntos de variables seno-transformadas.
#------sintrans--------------
evalq({
DTSin <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) sin(2*pi*x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTSin
},
env)
Transformamos las variables en todos los conjuntos Dtcap sin valores atípicos con la función tanh(x). Obtenemos la lista DTTanh con tres conjuntos de variables tanh-transformadas.
#------tanhTrans----------
evalq({
DTTanh <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) tanh(x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTTanh
},
env)
Normalizamos los conjuntos DT, DTLn, DTSin, DTTanh.
#------normalize----------- evalq( { # definimos los parámetros de normalización preProcess(DT$train, method = "spatialSign") -> preproc list(train = predict(preproc, DT$train), val = predict(preproc, DT$val), test = predict(preproc, DT$test) ) -> DTn }, env) #--ln--- evalq( { preProcess(DTLn[[1]], method = "spatialSign") -> preprocLn list(train = predict(preprocLn, DTLn[[1]]), val = predict(preprocLn, DTLn[[2]]), test = predict(preprocLn, DTLn[[3]]) ) -> DTLn.n }, env) #---sin--- evalq( { preProcess(DTSin[[1]], method = "spatialSign") -> preprocSin list(train = predict(preprocSin, DTSin[[1]]), val = predict(preprocSin, DTSin[[2]]), test = predict(preprocSin, DTSin[[3]]) ) -> DTSin.n }, env) #-----tanh----------------- evalq( { preProcess(DTTanh[[1]], method = "spatialSign") -> preprocTanh list(train = predict(preprocTanh, DTTanh[[1]]), val = predict(preprocTanh, DTTanh[[2]]), test = predict(preprocTanh, DTTanh[[3]]) ) -> DTTanh.n }, env)
Discretizamos nuestro conjunto DT con la ayuda de la función mdlp::discretization.
##------discretize----------
#--------preCut---------------------
# definimos los parámetros de discretización (cutpoint)
require(pipeR)
require(discretization)
evalq(
#require(pipeR)
# ¡requiere cierto tiempo!
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()
}) -> mdlp.train,
env)
#-------cut_opt----------
evalq(
{
DTd <- list()
mdlp.train$cutp %>%
# definimos las columnas que tienen que ser discretizadas
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> DTd$train
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
# reorganizamos los datos de acuerdo con los rangos calculados
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> DTd$test
colnames(DTd$test) <- colnames(DTd$train)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
# reorganizamos los datos de acuerdo con los rangos calculados
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> DTd$val
colnames(DTd$val) <- colnames(DTd$train)
# arreglamos un poco
rm(test.d, val.d)
},
env
)
Recordamos qué variables tenemos en el conjunto de datos inicial DT$train:
require(funModeling)
plot_num(env$DT$train %>% select(-Data), bins = 20)
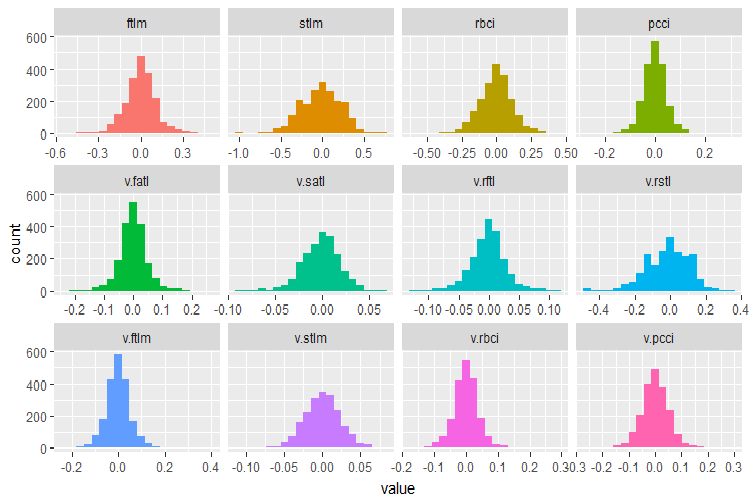
Fig.28. Distribución de las variables en el conjunto de datos DT$train
Utilizamos las capacidades del paquete smbinning para identificar predictores relevantes en los subconjuntos train de todos los conjuntos de datos normalizados obtenidos anteriormente (Dtn, DTLn.n, DTSin.n y DTTanh.n). La variable objetivo en este paquete debe ser numérica, con los valores (0, 1). Vamos a escribir una función para realizar las transformaciones necesarias.
#-------------------------------- require(smbinning) targ.int <- function(x){ x %>% tbl_df() %>% mutate(Cl = (as.numeric(Class) - 1) %>% as.integer()) %>% select(-Class) %>% as.data.frame() }
Además, este paquete no acepta variables que tengan un punto en el nombre. Vamos a escribir una función que renombrará todas las variables con un punto como variables con un guión bajo.
renamepr <- function(X){
X %<>% rename(v_fatl = v.fatl,
v_satl = v.satl,
v_rftl = v.rftl,
v_rstl = v.rstl,
v_ftlm = v.ftlm,
v_stlm = v.stlm,
v_rbci = v.rbci,
v_pcci = v.pcci)
return(X)
}
Calculamos y dibujamos los gráficos de los predictores relevantes.
par(mfrow = c(2,2)) #--Ln-------------- evalq({ df <- renamepr(DTLn.n[[1]]) %>% targ.int sumivt.ln.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.ln.n, cex = 0.7) rm(df) }, env) #---Sin----------------- evalq({ df <- renamepr(DTSin.n[[1]]) %>% targ.int sumivt.sin.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.sin.n, cex = 0.7) rm(df) }, env) #---norm------------- evalq({ df <- renamepr(DTn[[1]]) %>% targ.int sumivt.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.n, cex = 0.7) rm(df) }, env) #-----Tanh---------------- evalq({ df <- renamepr(DTTanh.n[[1]]) %>% targ.int sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.7) rm(df) }, env) par(mfrow = c(1,1))
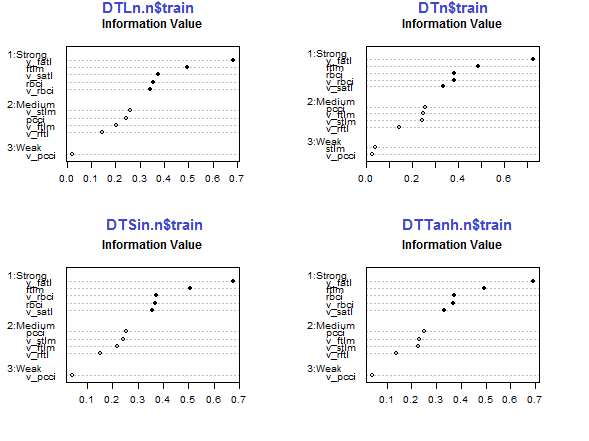
Fig.29. Importancia de los predictores en el subconjunto train de los conjuntos normalizados
Los cinco predictores — v_fatl, ftlm, v_satl, rbci, v_rbci, son fuertes en todos los conjuntos aunque en un orden diferente. Los cuatro predictores pcci, v_ftlm, v_stlm, v_rftl tienen una fuerza media. v_pcci y stlm son débiles. Podemos ver para cada conjunto la distribución de las variables por orden de importancia:
env$sumivt.ln.n Char IV Process 5 v_fatl 0.6823 Numeric binning OK 1 ftlm 0.4926 Numeric binning OK 6 v_satl 0.3737 Numeric binning OK 3 rbci 0.3551 Numeric binning OK 11 v_rbci 0.3424 Numeric binning OK 10 v_stlm 0.2591 Numeric binning OK 4 pcci 0.2440 Numeric binning OK 9 v_ftlm 0.2023 Numeric binning OK 7 v_rftl 0.1442 Numeric binning OK 12 v_pcci 0.0222 Numeric binning OK 2 stlm NA No significant splits 8 v_rstl NA No significant splits
Las tres últimas variables se pueden descartar tranquilamente. Es decir, quedan cinco fuertes y cuatro medias. Vamos a definir los nombres de las mejores variables (IV > 0.1).
evalq(sumivt.sin.n$Char[sumivt.sin.n$IV > 0.1] %>% na.omit %>% as.character() -> best.sin.n, env) > env$best.sin.n [1] "v_fatl" "ftlm" "rbci" "v_rbci" "v_satl" "pcci" [7] "v_ftlm" "v_stlm" "v_rftl"
Analizaremos con más detalle las variables v_fatl y ftlm.
evalq({
df <- renamepr(DTTanh.n[[1]]) %>% targ.int
x = 'v_fatl'
y = 'Cl'
res <- smbinning(df = df,
y = y,
x = x)
#res$ivtable # Tabulation and Information Value
#res$iv # Information value
#res$bands # Bins or bands
#res$ctree # Decision tree from partykit
par(mfrow = c(2,2))
sub = paste0(x, " vs ", y) #rbci vs Cl"
boxplot(df[[x]]~df[[y]],
horizontal = TRUE,
frame = FALSE, col = "lightblue",
main = "Distribution")
mtext(sub,3) #ftlm
smbinning.plot(res, option = "dist",
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "goodrate", #"badrate"
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "WoE",
sub = sub) #"pcci vs Cl")
par(mfrow = c(1, 1))
}, env)
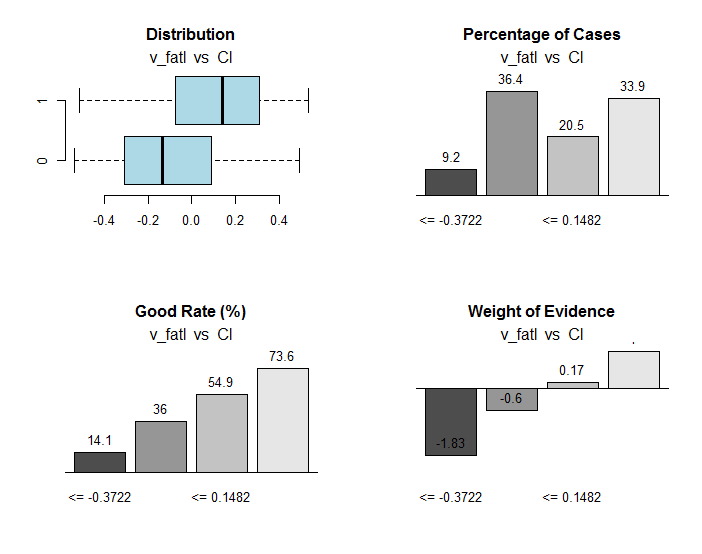
Fig.30. Relación de los rangos de la variable v_fatl con la variable objetivo Cl
En el objeto res, aparte de otra información útil, se contienen los puntos de división de la variable en rangos relacionados de forma óptima con la variable objetivo. En nuestro caso concreto, contamos con 4 rangos.
> env$res$cuts [1] -0.3722 -0.0433 0.1482
Hacemos un cálculo análogo para la variable ftlm y construimos los gráficos:
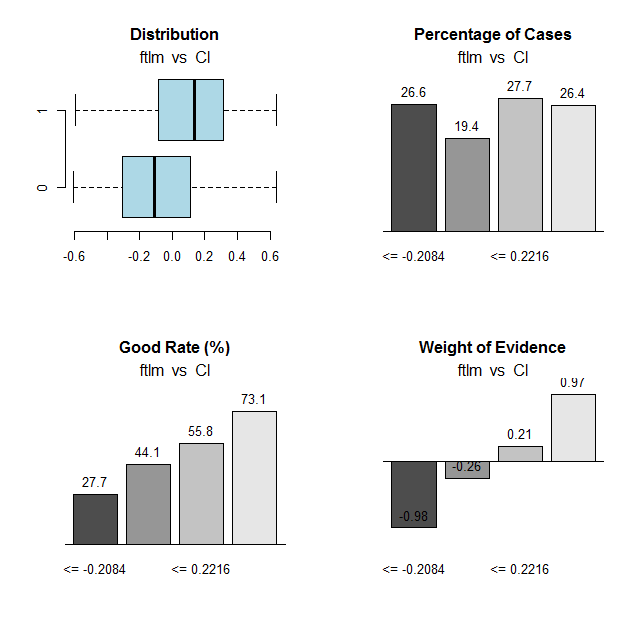
Fig.31. Relación de los rangos de la variable ftlm con la variable objetivo Cl
Puntos de división de los rangos:
> env$res$cuts [1] -0.2084 -0.0150 0.2216
Los puntos de corte nos permitirán discretizar las variables en nuestros conjuntos y ver cuánto difieren:
- las variables importantes definidas anteriormente con la ayuda de la función mdlp::discretization de las variables definidas con la ayuda de la función smbinning::smbinning;
- la división de las variables en rangos.
Ya disponemos de un conjunto de datos discretizados con la función mdlp::discretization DTd. Vamos a hacer lo mismo, pero esta vez con la ayuda de la función smbinning::smbinning y solo con el subconjunto train.
Definimos los parámetros de discretización:
evalq({
res <- list()
DT$train %>% renamepr() %>% targ.int() -> df
x <- colnames(df)
y <- "Cl"
foreach(i = 1:(ncol(df) - 1)) %do% {
smbinning(df, y = y, x = x[i])
} -> res
res %>% lapply(., function(x) x[1] %>% is.list) %>%
unlist -> idx
}, env)
Discretizamos el subconjunto DT$train:
evalq({
DT1.d <- list()
DT$train %>% renamepr() %>%
targ.int() %>% select(-Cl) -> train
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(train[ ,i],
vec = res[[i]]$cuts,
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$train$Class) -> DT1.d$train
colnames(DT1.d$train) <- colnames(train)[idx] %>%
c(., 'Class')
},
env)
Definimos las mejores variables con una importancia de información mayor a 0,1, en orden creciente:
evalq({
DT$train %>% renamepr() %>% targ.int() -> df
sumivt.dt1.d = smbinning.sumiv(df = df, y = 'Cl')
sumivt.dt1.d$Char[sumivt.dt1.d$IV > 0.1] %>%
na.omit %>% as.character() -> best.dt1.d
rm(df)
},
env)
Dibujamos el gráfico de división de las variables en el conjunto DTd$train:
require(funModeling) plot_num(env$DTd$train)
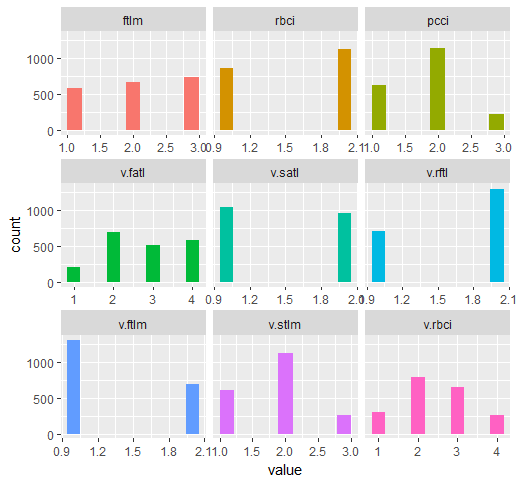
Fig.32. Variables del conjunto DT$ train, discretizadas con la función mdlp
El gráfico del conjunto DT1.d con todas las variables y con las mejores se muestra más abajo.
plot_num(env$DT1.d$train)
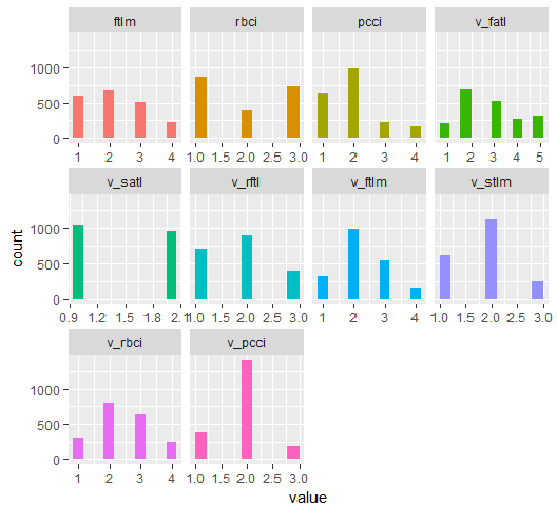
Fig.33. Variables del conjunto DT1 d$train, discretizadas con la función smbinning (todas)
plot_num(env$DT1.d$train[ ,env$best.dt1.d])
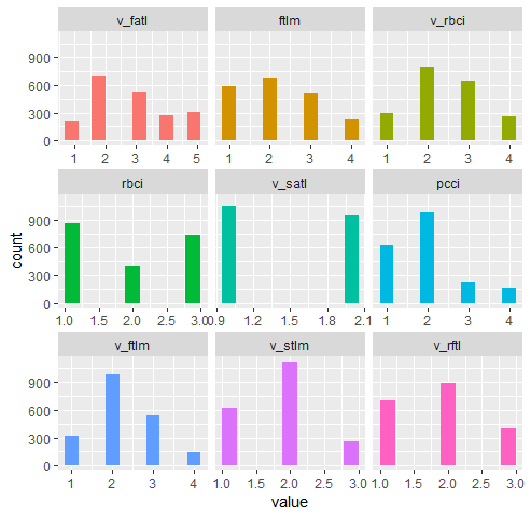
Fig.34. Variables del conjunto DT1.d$train, discretizadas con la función smbinning (loas mejores están dispuestas en orden creciente según la importancia de su información)
¿Qué podemos ver en los gráficos? La variables definidas como importantes son idénticas en ambos casos. Pero la división en rangos es diferente. Debemos comprobar qué variante da una mejor predicción con el modelo.
2.2. Evaluación analítica
Hay muchos métodos analíticos para identificar la importancia de los predictores según los criterios más diversos. Ya hemos analizado algunos de ellos antes. Ahora, me gustaría probar un acercamiento inusual a la elección de los predictores.
Usaremos el paquete varbvs. En la función homóloga se han implementado algoritmos rápidos para la instalación de modelos bayesianos de elección de variables, y el cálculo de los coeficientes bayesianos, donde el resultado (o variable objetivo) se modela con la regresión lineal o regresión logística. Estos algoritmos se basan en las aproximaciones variacionales descritas en "Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies" (P. Carbonetto and M. Stephens, Bayesian Analysis 7, 2012, pages 73-108). Este software se aplicó a grandes conjuntos de datos con más de un millón de variables y con miles de muestras.
La función varbvs() recibe una matriz, y la variable objetivo recibe un vector numérico (0, 1), como datos de entrada. Vamos a tomar nuestro conjunto con datos normalizados DTTanh.n$train y comprobar qué predictores se definirán como importantes según este método.
require(varbvs)
evalq({
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
fit <- varbvs(X = train[ ,-ncol(train)] ,
Z = NULL,
y = train[ ,ncol(train)] %>% as.vector(),
"binomial",
logodds = seq(-2,-0.5,0.1),
optimize.eta = T,
initialize.params = T,
verbose = T, nr = 100
)
print(summary(fit))
}, env)
Welcome to -- * *
VARBVS version 2.0.3 -- | | |
large-scale Bayesian -- || | | | || | | |
variable selection -- | || | | | | || || |||| || | ||
****************************************************************************
Copyright (C) 2012-2017 Peter Carbonetto.
See http://www.gnu.org/licenses/gpl.html for the full license.
Fitting variational approximation for Bayesian variable selection model.
family: binomial num. hyperparameter settings: 16
samples: 2000 convergence tolerance 1.0e-04
variables: 12 iid variable selection prior: yes
covariates: 0 fit prior var. of coefs (sa): yes
intercept: yes fit approx. factors (eta): yes
Finding best initialization for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00018 -1.204193e+03 6.1e-05 0003.3 NA 3.3e+00
Computing marginal likelihood for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00002 -1.204193e+03 3.2e-05 0003.3 NA 3.3e+00
Summary of fitted Bayesian variable selection model:
family: binomial num. hyperparameter settings: 16
samples: 2000 iid variable selection prior: yes
variables: 12 fit prior var. of coefs (sa): yes
covariates: 1 fit approx. factors (eta): yes
maximum log-likelihood lower bound: -1204.1931
Hyperparameters:
estimate Pr>0.95 candidate values
sa 3.49 [3.25,3.6] NA--NA
logodds -0.75 [-1.30,-0.50] (-2.00)--(-0.50)
Selected variables by probability cutoff:
>0.10 >0.25 >0.50 >0.75 >0.90 >0.95
3 3 3 3 3 3
Top 5 variables by inclusion probability:
index variable prob PVE coef* Pr(coef.>0.95)
1 1 ftlm 1.0000 NA 2.442 [+2.104,+2.900]
2 4 pcci 1.0000 NA 2.088 [+1.763,+2.391]
3 3 rbci 0.9558 NA 0.709 [+0.369,+1.051]
4 10 v.stlm 0.0356 NA 0.197 [-0.137,+0.529]
5 6 v.satl 0.0325 NA 0.185 [-0.136,+0.501]
*See help(varbvs) about interpreting coefficients in logistic regression.
Como podemos ver, se han definido los cinco mejores predictores (ftlm, pcci, rbci, v.stlm, v.satl). Estos entran en el grupo de los nueve mejores que definimos anteriormente, pero en otro orden y con otros pesos de importancia. Puesto que ya disponemos de un modelo, vamos a comprobar la calidad del resultado que obtendremos en los conjuntos de validación y prueba.
Conjunto de validación:
#-----------------
evalq({
val <- DTTanh.n$val %>% targ.int() %>%
as.matrix()
y = val[ ,ncol(val)] %>% as.vector()
pr <- predict(fit, X = val[ ,-ncol(val)] ,
Z = NULL)
}, env)
cm.val <- confusionMatrix(table(env$y, env$pr))
> cm.val
Confusion Matrix and Statistics
0 1
0 347 204
1 137 312
Accuracy : 0.659
95% CI : (0.6287, 0.6884)
No Information Rate : 0.516
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.3202
Mcnemar's Test P-Value : 0.0003514
Sensitivity : 0.7169
Specificity : 0.6047
Pos Pred Value : 0.6298
Neg Pred Value : 0.6949
Prevalence : 0.4840
Detection Rate : 0.3470
Detection Prevalence : 0.5510
Balanced Accuracy : 0.6608
'Positive' Class : 0
Siendo sinceros, el resultado no es impresionante en absoluto. Conjunto de prueba:
evalq({
test <- DTTanh.n$test %>% targ.int() %>%
as.matrix()
y = test[ ,ncol(test)] %>% as.vector()
pr <- predict(fit, X = test[ ,-ncol(test)] ,
Z = NULL)
}, env)
cm.test <- confusionMatrix(table(env$y, env$pr))
> cm.test
Confusion Matrix and Statistics
0 1
0 270 140
1 186 404
Accuracy : 0.674
95% CI : (0.644, 0.703)
No Information Rate : 0.544
P-Value [Acc > NIR] : < 2e-16
Kappa : 0.3375
Mcnemar's Test P-Value : 0.01269
Sensitivity : 0.5921
Specificity : 0.7426
Pos Pred Value : 0.6585
Neg Pred Value : 0.6847
Prevalence : 0.4560
Detection Rate : 0.2700
Detection Prevalence : 0.4100
Balanced Accuracy : 0.6674
'Positive' Class : 0
El resultado es casi el mismo. Esto significa que el modelo no ha sido re-entrenado y generaliza bien los datos.
Bien, los mejores según la versión de varbvs son ftlm, pcci, rbci, v.stlm, v.satl.
2.3. Neurored
Puesto que estamos estudiando las redes neuronales, vamos a comprobar qué predictores seleccionará la propia neurored como los más importantes.
Vamos a usar el paquete FCNN4R, que proporciona la interfaz para los principales programas de la biblioteca FCNN en C ++. FCNN se basa en una nueva representación de la red neuronal artificial que implica eficiencia, modularidad y capacidad de expansión. FCNN4R permite el aprendizaje estándar (backpropagation, Rprop, recocido simulado, gradiente estocástico) y también algoritmos de poda (minimum magnitude, Optimal Brain Surgeon), aunque veo este paquete como un motor de cálculo eficiente por encima de todo.
Los usuarios pueden implementar fácilmente su algoritmo usando métodos de gradiente rápidos junto con la funcionalidad de restauración de la red (eliminación de pesos y neuronas excesivas, reordenación de datos de entrada y unión de redes).
Las redes pueden ser exportadas a las funciones C, para integrarlas en cualquier solución programática.
Creamos una red completamente conectada con dos capas ocultas. Número de neuronas en cada capa: entrada = 12 (número de predictores), salida = 1. Iniciamos las neuronas con pesos aleatorios en el rango +/- 0.17. Establecemos la función de activación en cada capa de la neurored (excepto la entrada) = c("tanh", "tanh", "sigmoid"). Preparamos los conjuntos train/val/test.
Más abajo se muestra un script que ejecuta esta secuencia de acciones.
require(FCNN4R)
evalq({
mlp_net(layers = c(12, 8, 5, 1), name = "n.tanh") %>%
mlp_rnd_weights(a = 0.17) %>%
mlp_set_activation(layer = c(2, 3, 4),
activation = c("tanh", "tanh", "sigmoid"), #"threshold", "sym_threshold",
#"linear", "sigmoid", "sym_sigmoid",
#"tanh", "sigmoid_approx",
#"sym_sigmoid_approx"),
slope = 0) -> Ntanh #show()
#-------
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
test <- DTTanh.n$test %>% targ.int() %>% as.matrix()
val <- DTTanh.n$val %>% targ.int() %>% as.matrix()
}, env)
De entre los métodos de entrenamiento propuestos utilizaremos rprop. Establecemos las constantes: tol - nivel de error alcanzado el cual el entrenamiento debe ser detenido, max_ep - número de épocas después de cuyo cumplimiento el entrenamiento debe ser detenido, l2reg - coeficiente de regularización. Entrenamos la red con estos parámetros y evaluamos visualmente la red y el error de entrenamiento que tenemos.
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
net_rp <- mlp_teach_rprop(Ntanh,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_epochs = max_ep,
l2reg = l2reg,
u = 1.2, d = 0.5,
gmax = 50, gmin = 1e-06,
report_freq = 100)
}, env)
plot(env$net_rp$mse, t = "l",
main = paste0("max_epochs =", env$max_ep, " l2reg = ", env$l2reg))
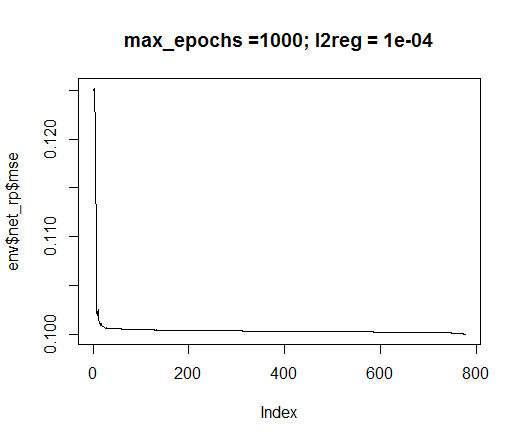
Fig.35. Error de entrenamiento de la neurored
evalq(mlp_plot(net_rp$net, FALSE), envir = env)
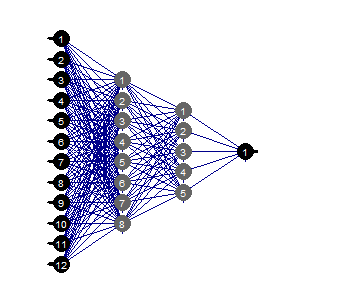
Fig.36. Estructura de la neurored
Poda (Prune)
La poda del valor mínimo es un algoritmo sencillo de utilizar. Aquí, los pesos con el menor valor absoluto se desconectan en cada paso. Este algoritmo requiere la redifusión de la red casi en cada paso, y da resultados subóptimos.
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
mlp_prune_mag(net_rp$net,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_reteach_epochs = max_ep,
report = FALSE,
plots = TRUE) -> net_rp_prune
}, env)
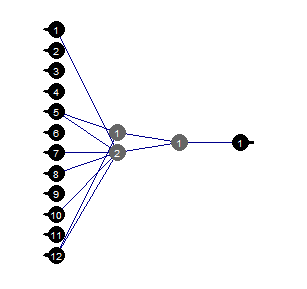
Fig.37. Neurored podada
Podemos ver que contando con la estructura concreta de la neurored, la configuración inicial, las funciones de activación y el error de aprendizaje, podremos arreglárnoslas perfectamente con la red de la estructura (12, 2, 1, 1). ¿Qué predictores fueron elegidos por la red neuronal?
evalq( best <- train %>% tbl_df %>% select(c(1,5,7,8,10,12)) %>% colnames(), env) env$best [1] "ftlm" "v.fatl" "v.rftl" "v.rstl" "v.stlm" [6] "v.pcci"
Las dos variables v.rstl y v.pcci no entran en el conjunto de las mejores 9, definido con anterioridad.
Me gustaría hacer hincapié en que aquí mostramos que una red neuronal puede seleccionar predictores importantes de forma independiente y automática. Esta elección depende tanto de los predictores, como de la estructura y los parámetros de la red.
¡Experimente!
Conclusión
En la siguiente parte vamos a hablar sobre cómo eliminar los ejemplos de ruido del conjunto, sobre cómo reducir el tamaño de las entradas y el efecto que esto tendrá, y sobre las formas de dividir los datos originales en train/val/test.
Anexos
1 Puede descargar FeatureTransformation.R, FeatureSelect.R, FeatureSelect_analitic.R FeatureSelect_NN.R y una captura con los resultados del funcionamiento de los scripts de la primera parte del artículo Part_1.RData desde Git /Part_II.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/3507
Examinamos en la práctica el método adaptativo del seguimiento del mercado
Neuroredes profundas (Parte I). Preparación de datos
Experto comercial universal: Indicador CUnIndicator y trabajo con órdenes pendientes (parte 9)
TradeObjects: Automatización del trading a base de objetos gráficos en MetaTrader
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso