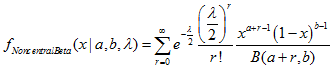#include <Graphics\Graphic.mqh>
#include <Math\Stat\NoncentralBeta.mqh>
#include <Math\Stat\Math.mqh>
#property script_show_inputs
//--- input parameters
input double a_par=2; // primer parámetro de la distribución beta (shape1)
input double b_par=5; // segundo parámetro de la distribución beta (shape2)
input double l_par=1; // parámetro de no-centralidad (lambda)
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
//--- desactivamos la exhibición del gráfico de precio
ChartSetInteger(0,CHART_SHOW,false);
//--- inicializamos el generador de números aleatorios
MathSrand(GetTickCount());
//--- generamos una muestra de la magnitud aleatoria
long chart=0;
string name="GraphicNormal";
int n=1000000; // número de valores en la muestra
int ncells=53; // número de intervalos en el histograma
double x[]; // centros de los intervalos del histograma
double y[]; // número de valores de la muestra que han entrado en el intervalo
double data[]; // muestra de valores aleatorios
double max,min; // valor máximo y mínimo en la muestra
//--- obtenemos la muestra de la distribución beta no central
MathRandomNoncentralBeta(a_par,b_par,l_par,n,data);
//--- calculamos los datos para construir el histograma
CalculateHistogramArray(data,x,y,max,min,ncells);
//--- obtenemos los límites de la secuencia y el salto para construir la curva teórica
double step;
GetMaxMinStepValues(max,min,step);
step=MathMin(step,(max-min)/ncells);
//--- obtenemos los datos calculados teóricamente en el intervalo [min,max]
double x2[];
double y2[];
MathSequence(min,max,step,x2);
MathProbabilityDensityNoncentralBeta(x2,a_par,b_par,l_par,false,y2);
//--- escalamos
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//--- mostramos el gráfico
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
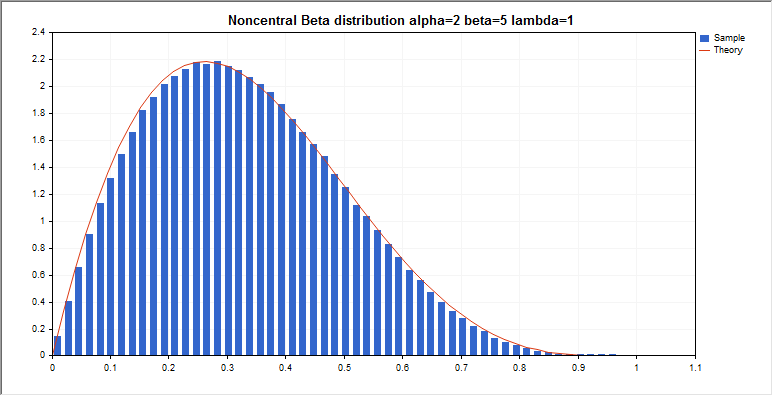
graphic.BackgroundMain(StringFormat("Noncentral Beta distribution alpha=%G beta=%G lambda=%G",
a_par,b_par,l_par));
graphic.BackgroundMainSize(16);
//--- plot all curves
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,"Sample").HistogramWidth(6);
//--- y ahora construimos la curva teórica de la densidad de la distribución
graphic.CurveAdd(x2,y2,CURVE_LINES,"Theory");
graphic.CurvePlotAll();
//--- plot all curves
graphic.Update();
}
//+------------------------------------------------------------------+
//| Calculate frequencies for data set |
//+------------------------------------------------------------------+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//--- establecemos los centros de los intervalos
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//--- rellenamos las frecuencias de entrada en el intervalo
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+------------------------------------------------------------------+
//| Calculates values for sequence generation |
//+------------------------------------------------------------------+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//--- calculamos la amplitud absoluta de la secuencia, para obtener la precisión de normalización
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//--- normalizamos los valores máximos y mínimos con la precisión establecida
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//--- el salto de generación de la secuencia también lo estableceremos a partir de la precisión indicada
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
}
|