Redes neuronales en el trading: Detección de anomalías en el dominio de la frecuencia (CATCH)

Introducción

Los mercados financieros modernos funcionan en tiempo real, donde se procesan cantidades gigantescas de datos cada segundo. Las cotizaciones bursátiles, los tipos de cambio, los volúmenes comerciales y los tipos de interés forman series temporales multivariantes complejas. El análisis de estos datos resulta fundamental para tráders e inversores. Ayuda a predecir los próximos movimientos del mercado y a identificar patrones ocultos.

Uno de los principales objetivos del análisis de las series temporales es la detección de anomalías. Las subidas inesperadas de los precios, los cambios repentinos de liquidez y la actividad comercial sospechosa pueden ser indicios de manipulación del mercado o de uso de información privilegiada. Si no se advierten a tiempo, las consecuencias pueden resultar catastróficas: desde grandes pérdidas hasta el colapso de instituciones financieras enteras.

Las anomalías son de dos tipos: puntuales y de subsecuencia. Las anomalías puntuales son valores atípicos bruscos, como un aumento repentino del volumen de transacciones en una sola acción. Son fáciles de detectar usando métodos estándar. Las anomalías subsiguientes son más complejas: son cambios que parecen normales pero que alteran las pautas conocidas del mercado. Por ejemplo, un cambio a largo plazo en la correlación entre valores, o una subida de precios anormalmente suave en mitad de un mercado volátil. Estas anomalías resultan especialmente importantes porque pueden indicar riesgos ocultos.

Uno de los métodos más eficaces para detectarlas es trasladar los datos al dominio de la frecuencia. En esta representación, los distintos tipos de anomalías se manifiestan en determinados rangos de frecuencia. Por ejemplo, los picos de volatilidad a corto plazo influyen en los componentes de alta frecuencia, mientras que los cambios de tendencia globales afectan a los componentes de baja frecuencia. No obstante, los métodos estándar suelen omitir detalles importantes, sobre todo en las frecuencias altas, donde se ocultan señales poco perceptibles pero críticas.

También es vital considerar los vínculos entre los distintos activos del mercado. Por ejemplo, si los futuros del petróleo caen bruscamente mientras las acciones de petróleo permanecen estables, esto podría ser señal de un desajuste en el mercado. Sin embargo, los modelos clásicos ignoran esas relaciones o las consideran de forma demasiado rígida, lo que reduce la precisión de las predicciones.

Una de las opciones para resolver estos problemas se propone en el artículo "CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching". Sus autores propusieron el nuevo framework CATCH que utiliza la transformada de Fourier para analizar los datos del mercado en el dominio de la frecuencia. Para detectar mejor las anomalías complejas, los autores del framework han desarrollado un mecanismo de parcheo de frecuencias que ayuda a simular el comportamiento normal de los activos con gran precisión. El módulo de correlación adaptativa permite identificar de forma automática correlaciones importantes entre instrumentos de mercado, ignorando el ruido.

El algoritmo CATCH

La arquitectura CATCH consta de tres módulos clave:

• Forward Module,
• Channel Fusion Module (CFM),
• Time-Frequency Reconstruction Module (TFRM).

Esta arquitectura se diseñó para permitir el análisis detallado de las características temporales y de frecuencia de los datos, así como la identificación de patrones ocultos entre canales. Este enfoque permite una detección eficaz de anomalías incluso en series temporales multivariantes complejas.

La primera etapa del procesamiento de datos es el Forward Module. Este incluye la normalización de datos, la transformación de la serie temporal en el dominio de la frecuencia mediante la transformada rápida de Fourier (FFT) y después la división en cortes de frecuencia (patches). La transformada de Fourier permite representar los datos temporales como funciones trigonométricas ortogonales, preservando las partes real e imaginaria del espectro de frecuencias de la serie temporal analizada.

A continuación, se realiza una partición en L parches de frecuencia de tamaño P con paso S. El parcheo se realiza sobre los datos de las partes reales e imaginarias del espectro de frecuencia con los mismos parámetros, después de lo cual se concatenan los datos, combinando las partes reales e imaginarias del espectro de cada segmento en un solo tensor.

En el siguiente paso, los parches se trasladan al espacio oculto usando una capa de proyección:

Este proceso es importante porque reduce la dimensionalidad de los datos al tiempo que conserva las características más importantes para su posterior análisis. De esta manera, puede mejorarse la capacidad de generalización del modelo y la precisión de la detección de anomalías.

El segundo utiliza el Channel Fusion Module (CFM), que identifica las interdependencias entre canales en cada banda de frecuencias. Para ello se utiliza el mecanismo Channel-Masked Transformer (CMT). Aquí, la máscara de canal M se crea con la ayuda de Mask Generator (MG). MG construye matrices de probabilidad D, que luego se binarizan usando el remuestreo de Bernoulli. Así, los valores altos en D conducen a unidades en M, lo que indica que existe un vínculo entre los canales.

El CMT procesa los parches considerando la atención enmascarada, que puede representarse como las siguientes expresiones matemáticas:

Para lograr una optimización eficaz en el contexto de la generación de máscaras y el ajuste de los mecanismos de atención, resulta importante desarrollar objetivos de optimización claros que mejoren la calidad de las máscaras resultantes. En este caso, el aspecto clave será aumentar explícitamente los coeficientes de atención entre los canales relevantes que se han identificado mediante la máscara. Esto alinea el mecanismo de atención con la correlación de canales más relevante y óptima, lo que a su vez mejora la calidad del modelo.

Una de las ventajas más importantes de este enfoque es la capacidad de evitar los efectos negativos que surgen cuando se incluyen canales irrelevantes en el proceso de atención. El mecanismo de enmascaramiento, sujeto al ajuste del enlace, centra eficazmente la atención en los canales más relevantes, minimizando los efectos de interferencias y la distorsiones. Este enfoque logra la robustez del mecanismo de atención, lo que mejora enormemente la precisión y la eficacia del modelo ante datos cambiantes.

El siguiente paso es una optimización iterativa del generador de máscaras, para así afinar más las correlaciones entre canales. Este proceso implica ajustar el mecanismo de atención en la capa enmascarada del Transformer canal por canal para captar y procesar completamente todas las relaciones posibles entre canales.

Para optimizar el mecanismo de enmascaramiento, los autores del framework sugieren utilizar la función de pérdida ClusteringLoss:

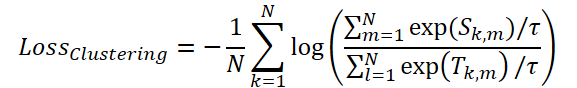
En el último paso, el Time-Frequency Reconstruction Module (TFRM) realiza la transformada inversa de Fourier (iFFT) para reconstruir las series temporales:

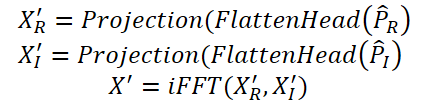
Las anomalías se identifican según el error de reconstrucción.

Mediante el uso de un exhaustivo análisis de datos basado en características temporales y de frecuencia, el modelo CATCH posibilita una detección fiable de anomalías.

A continuación se muestra la visualización del framework CATCH realizada por el autor.

Implementación con MQL5

Tras repasar los aspectos teóricos del framework CATCH, pasaremos a la parte práctica de nuestro artículo, donde implementaremos nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5.

En primer lugar, deberemos prestar especial atención al hecho de que en este framework casi todas las operaciones se realizan en el dominio de la frecuencia de los datos analizados. Se trata de una característica clave que determina el enfoque del procesamiento de los datos y la elección de los métodos matemáticos.

Como es sabido, la representación de una señal en el dominio de la frecuencia se realiza usando números complejos. En consecuencia, para el correcto funcionamiento del sistema será necesario garantizar un procesamiento eficaz de los datos complejos, incluidas las operaciones aritméticas.

Esta tarea ya ha sido parcialmente resuelta por nosotros mientras trabajábamos con el framework ATFNet. En aquel momento, establecimos los principios de procesamiento de los datos espectrales y desarrollamos enfoques metodológicos que ahora pueden utilizarse para crear la solución actual. Estos avances nos permitirán simplificar enormemente la aplicación de las funciones básicas.

Capa convolucional de datos complejos

Comenzaremos nuestro trabajo desarrollando una capa convolucional para trabajar con valores complejos. Como demuestra la práctica, las capas convolucionales son una de las herramientas más eficaces para procesar secuencias multivariantes. Por eso damos prioridad a la construcción de este componente.

Como de costumbre, primero construiremos algoritmos para el funcionamiento del nuevo objeto en el lado del contexto OpenCL. Llevar todas las operaciones clave al nivel de la GPU nos permite maximizar el paralelismo, algo fundamental cuando se procesan datos multidimensionales. A diferencia del cálculo secuencial en la CPU, aquí cada núcleo de la GPU realiza una parte de la tarea global, lo que da como resultado un modelo mucho más rápido. Tanto en el entrenamiento como durante la explotación.

Implementaremos las operaciones de pasada directa en el kernel FeedForwardComplexConv. En los parámetros de este kernel, transmitiremos los punteros a los 3 búferes de datos y una serie de constantes que definirán la estructura de datos.

Deberemos prestar especial atención al hecho de que todos los búferes de datos utilizan el tipo vectorial float2. Esta elección se debe a la necesidad de procesar eficazmente los números complejos, en los que cada magnitud está representada por un par de valores: la parte real y la parte imaginaria.

El uso de float2 nos ofrecerá algunas ventajas clave:

• Optimización de la carga y el almacenamiento de datos: gracias a la representación vectorial, podremos recuperar y escribir simultáneamente dos valores de los búferes, lo cual reducirá el número de operaciones de lectura y escritura.
• Aceleración por hardware: OpenCL proporciona soporte de hardware para trabajar con tipos vectoriales, lo cual permite acelerar las operaciones aritméticas.
• Representación uniforme de los datos: el uso de float2 hará que el código sea más legible y lógico, ya que cada variable se corresponde explícitamente con un número complejo.

__kernel void FeedForwardComplexConv(__global const float2 *matrix_w,
                                     __global const float2 *matrix_i,
                                     __global float2 *matrix_o,
                                     const int inputs,
                                     const int step,
                                     const int window_in,
                                     const int activation
                                    )
  {
   const size_t i = get_global_id(0);
   const size_t units = get_global_size(0);
   const size_t out = get_global_id(1);
   const size_t w_out = get_global_size(1);
   const size_t var = get_global_id(2);
   const size_t variables = get_global_size(2);

Se supone que el funcionamiento de este kernel se realizará en un espacio de tareas tridimensional. En la primera dimensión, especificaremos el número de elementos de la secuencia. La segunda será el número de filtros. Y la tercera dimensión del espacio del problema indicará el número de secuencias unitarias independientes en el tensor común de los datos de origen. En el cuerpo del kernel, identificaremos directamente el flujo actual de operaciones en el espacio de tareas en todas las dimensiones. Luego guardaremos los valores obtenidos en constantes locales.

A continuación, determinaremos los desplazamientos en los búferes de datos basándonos en los resultados de la identificación del flujo de operaciones. Esta operación es completamente idéntica al algoritmo utilizado en la capa neuronal convolucional de valores reales creada anteriormente, lo cual ha sido posible gracias al uso del tipo de datos vectorial para la representación de valores complejos.

int w_in = window_in;
int shift_out = w_out * (i + units * var);
int shift_in = step * i + inputs * var;
int shift = (w_in + 1) * (out + var * w_out);
int stop = (w_in <= (inputs - shift_in) ? w_in : (inputs - shift_in)) + inputs * var;

Con esto concluirá el trabajo preparatorio y pasaremos directamente a la operación convolucional. En este caso, los datos de origen y los parámetros del filtro entrenado serán cantidades complejas. El resultado de las operaciones también se representará mediante una cantidad compleja. Y realizaremos todas las operaciones matemáticas usando las funciones previamente creadas de operaciones básicas con magnitudes complejas.

En primer lugar, declararemos una variable local para almacenar temporalmente los resultados intermedios y transferiremos a ella el valor del elemento de desplazamiento entrenado.

   float2 sum = ComplexMul((float2)(1, 0), matrix_w[shift + w_in]);
#pragma unroll
   for(int k = 0; k <= stop; k ++)
      sum += IsNaNOrInf2(ComplexMul(matrix_i[shift_in + k], matrix_w[shift + k]), (float2)0);

Y a continuación, organizaremos un ciclo de multiplicación del vector de datos de origen por el vector de filtrado correspondiente, con los resultados sumados en una variable local.

Entonces, todo lo que deberemos hacer es aplicar la función de activación requerida y guardar el valor resultante en el búfer de resultados.

   switch(activation)
     {
      case 0:
         sum = ComplexTanh(sum);
         break;
      case 1:
         sum = ComplexDiv((float2)(1, 0), (float2)(1, 0) + ComplexExp(-sum));
         break;
      case 2:
         if(sum.x < 0)
           {
            sum.x *= 0.01f;
            sum.y *= 0.01f;
           }
         break;
      default:
         break;
     }
   matrix_o[out + shift_out] = sum;
  }

El siguiente paso consistirá en construir algoritmos de pasada inversa. Vamos a analizar el kernel de distribución del gradiente de error CalcHiddenGradientComplexConv. Aquí utilizaremos el mismo enfoque de representación de números complejos como una cantidad vectorial. Al mismo tiempo, añadiremos búferes de gradiente de error en los niveles de operación correspondientes en los parámetros del método.

__kernel void CalcHiddenGradientComplexConv(__global const float2 * matrix_w,
                                            __global const float2 * matrix_g,
                                            __global const float2 * matrix_o,
                                            __global float2 * matrix_ig,
                                            const int outputs,
                                            const int step,
                                            const int window_in,
                                            const int window_out,
                                            const int activation,
                                            const int shift_out
                                           )
  {
   const size_t i = get_global_id(0);
   const size_t inputs = get_global_size(0);
   const size_t var = get_global_id(1);
   const size_t variables = get_global_size(1);

Obsérvese que el objetivo de esta operación consistirá en transferir el gradiente de error al nivel de los datos de entrada según su influencia en la salida del modelo. Esto es lo que ha influido en los cambios en el espacio de tareas del trabajo del kernel. En nuestra aplicación, utilizaremos un espacio de tareas bidimensional. La primera dimensión apuntará a un elemento de la secuencia de datos de origen, mientras que la segunda apuntará a la secuencia unitaria de la serie multivariante.

En el cuerpo del kernel, al igual que antes, primero identificaremos el flujo actual de operaciones en todas las dimensiones del espacio de tareas. Los valores obtenidos se almacenarán como constantes locales.

A continuación, determinaremos los desplazamientos en los búferes de datos. Aquí cabe señalar que un elemento de los datos de origen podrá participar en varias operaciones convolucionales según el paso de ventana convolucional utilizado. Por consiguiente, deberemos recopilar el gradiente de error en todas esas operaciones. Por eso, definiremos los límites de los rangos en los que recopilaremos el gradiente de error.

float2 sum = (float2)0;
float2 out = matrix_o[i];
int start = i - window_in + step;
start = max((start - start % step) / step, 0) + var * inputs;
int stop = (i + step - 1) / step;
if(stop > (outputs / window_out))
   stop = outputs / window_out;
stop += var * outputs;

Una vez finalizados los trabajos preparatorios, organizaremos un ciclo de iteración de los rangos previamente definidos con un paso determinado y sumaremos los gradientes de error considerando los coeficientes de peso correspondientes.

#pragma unroll
   for(int h = 0; h < window_out; h ++)
     {
      for(int k = start; k < stop; k++)
        {
         int shift_g = k * window_out + h;
         int shift_w = (stop - k - 1) * step + i % step + h * (window_in + 1);
         if(shift_g >= outputs || shift_w >= (window_in + 1) * window_out)
            break;
         sum += ComplexMul(matrix_g[shift_out + shift_g], matrix_w[shift_w]);
        }
     }
   sum = IsNaNOrInf2(sum, (float2)0);

Ajustaremos el valor obtenido según la derivada de la función de activación de los datos de origen.

   switch(activation)
     {
      case 0:
         sum = ComplexMul(sum, (float2)1.0f - ComplexMul(out, out));
         break;
      case 1:
         sum = ComplexMul(sum, ComplexMul(out, (float2)1.0f - out));
         break;
      case 2:
         if(out.x < 0.0f)
           {
            sum.x *= 0.01f;
            sum.y *= 0.01f;
           }
         break;
      default:
         break;
     }
   matrix_ig[i] = sum;
  }

El resultado de las operaciones se almacenará en el elemento correspondiente del búfer de datos global.

Encontrará el código completo de los kernels presentados anteriormente en el artículo adjunto. Allí también se presentará el código completo de los kernels de optimización de los parámetros del filtro entrenado, que le sugiero dejar para el estudio autónomo. Y procederemos a organizar los procesos en el lado del programa principal.

Aquí crearemos un nuevo objeto CNeuronComplexConvOCL, cuya estructura se muestra a continuación.

class CNeuronComplexConvOCL    :  public CNeuronConvOCL
  {
protected:
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronComplexConvOCL(void)   {  activation = None;   }
                    ~CNeuronComplexConvOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint window_out, 
                          uint units_count, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronComplexConvOCL;   }
  };

Es bastante natural utilizar un objeto de capa convolucional de valores reales como clase padre. Esto nos permitirá utilizar plenamente la infraestructura de la clase padre, incluidos los objetos internos y las interfaces. No obstante, tendremos que hacer algunos ajustes en el funcionamiento de los métodos heredados.

En primer lugar, obviamente, estarán los métodos de pasada directa e inversa. Los redefiniremos para que funcionen con los nuevos kernels de programas OpenCL cuyos algoritmos se han descrito anteriormente. El algoritmo para colocar los kernels especificados en la cola de ejecución seguirá siendo el estándar. Por consiguiente, no nos detendremos en una revisión detallada de estos métodos. Podrá analizarlos por su cuenta, el código completo se ofrece en el archivo adjunto.

Sin embargo, nos tomaremos un momento para ver el algoritmo del método de inicialización de un nuevo objeto. Al fin y al cabo, trabajar con valores complejos conlleva cambios en los búferes de datos. Aquí debemos señalar que, aunque MQL5 permite trabajar con valores complejos, no hemos introducido nuevos objetos de búfer de datos: solo hemos aumentado el tamaño de los ya existentes. Esto hace que nuestra solución resulte más versátil y no requiera complejas modificaciones de los métodos.

La estructura de parámetros del método de inicialización se heredará completamente de la clase padre.

bool CNeuronComplexConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint step, uint window_out, 
                                 uint units_count, uint variables, 
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * units_count * window_out * variables,
                                                                         optimization_type, batch))
      return false;

En el cuerpo del método, primero llamaremos al método homónimo de capa completamente conectada, que será la clase padre de todos los objetos de capa neuronal de nuestra biblioteca, incluida la capa convolucional. No podremos utilizar el método homónimo de la clase padre directa debido a un desajuste en el tamaño del búfer de datos.

Observe que al definir el tamaño del objeto creado mediante el método de la clase padre, especificaremos que el tamaño de la capa sea 2 veces el tamaño calculado. Como no resulta difícil adivinar, esto se debe a la necesidad de almacenar las partes real e imaginaria de una magnitud compleja.

A continuación, almacenaremos las constantes de arquitectura del objeto en las variables internas.

iWindow = (int)window;
iStep = MathMax(step, 1);
activation = None;
iWindowOut = window_out;
iVariables = variables;

El siguiente paso consistirá en inicializar los búferes de datos heredados. Primero comprobaremos su actualidad y, de ser necesario, crearemos un nuevo objeto del búfer de parámetros entrenados.

if(CheckPointer(WeightsConv) == POINTER_INVALID)
  {
   WeightsConv = new CBufferFloat();
   if(CheckPointer(WeightsConv) == POINTER_INVALID)
      return false;
  }

A la hora de determinar el tamaño del búfer de los parámetros entrenados, deberemos considerar que aquí también estamos utilizando valores complejos. Por consiguiente, aumentaremos el tamaño del búfer 2 veces el valor calculado.

int count = (int)(2 * (iWindow + 1) * iWindowOut * iVariables);
if(!WeightsConv.Reserve(count))
   return false;

E inicializaremos el búfer con valores aleatorios.

float k = (float)(1 / sqrt(iWindow + 1));
for(int i = 0; i < count; i++)
  {
   if(!WeightsConv.Add((GenerateWeight() * 2 * k - k)*WeightsMultiplier))
    return false;
  }
if(!WeightsConv.BufferCreate(OpenCL))
   return false;

A continuación, según el método de optimización de los parámetros, inicializaremos el número necesario de búferes para guardar estos momentos de optimización de parámetros. Estos búferes se inicializarán inicialmente con valores cero.

   if(optimization == SGD)
     {
      if(CheckPointer(DeltaWeightsConv) == POINTER_INVALID)
        {
         DeltaWeightsConv = new CBufferFloat();
         if(CheckPointer(DeltaWeightsConv) == POINTER_INVALID)
            return false;
        }
      if(!DeltaWeightsConv.BufferInit(count, 0.0))
         return false;
      if(!DeltaWeightsConv.BufferCreate(OpenCL))
         return false;
     }
   else
     {
      if(CheckPointer(FirstMomentumConv) == POINTER_INVALID)
        {
         FirstMomentumConv = new CBufferFloat();
         if(CheckPointer(FirstMomentumConv) == POINTER_INVALID)
            return false;
        }
      if(!FirstMomentumConv.BufferInit(count, 0.0))
         return false;
      if(!FirstMomentumConv.BufferCreate(OpenCL))
         return false;
      //---
      if(CheckPointer(SecondMomentumConv) == POINTER_INVALID)
        {
         SecondMomentumConv = new CBufferFloat();
         if(CheckPointer(SecondMomentumConv) == POINTER_INVALID)
            return false;
        }
      if(!SecondMomentumConv.BufferInit(count, 0.0))
         return false;
      if(!SecondMomentumConv.BufferCreate(OpenCL))
         return false;
     }
//---
   return true;
  }

A continuación, finalizaremos el método retornando el resultado lógico de las operaciones al programa que realiza la llamada.

Con esto concluirá el análisis de los algoritmos para organizar el funcionamiento del objeto de capa convolucional de trabajo con magnitudes complejas. El código completo de este objeto y de todos sus métodos figura en el anexo del artículo.

Objeto de atención enmascarada a valores complejos

El siguiente bloque con el que trabajaremos, bastante amplio, será la creación de un objeto de atención enmascarada a valores complejos, que constituirá la base del Channel Fusion Module.

Ya hemos creado antes objetos de atención enmascarada que funcionan con valores reales. Ahora tendremos que construir un algoritmo para trabajar con valores complejos y, por supuesto, añadir algunas características del framework CATCH.

Como siempre, empezaremos a trabajar en un nuevo objeto construyendo los procesos en el lado del contexto OpenCL. El algoritmo de pasada directa se implementará en el kernel MaskAttentionComplex. En los parámetros del kernel pasaremos los punteros a los 5 búferes de datos y las 2 constantes que definen la estructura de los datos analizados. Como se supone que trabajaremos con valores complejos, los búferes destinados a transferir los datos iniciales y recibir los resultados, han recibido el tipo de vector float2. Sin embargo, el búfer de la matriz de enmascaramiento y los coeficientes de atención siguen conteniendo números reales porque representan una distribución de probabilidad.

__kernel void MaskAttentionComplex(__global const float2 *q,
                                   __global const float2 *kv,
                                   __global float2 *scores,
                                   __global const float *masks,
                                   __global float2 *out,
                                   const int dimension,
                                   const int heads_kv
                                  )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_local_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_local_size(1);
   const int heads = get_global_size(2);

Se supone que el funcionamiento del kernel se producirá en un espacio de tareas tridimensional. La primera dimensión será responsable de la dimensionalidad del tensor Query e indicará el número de elementos que se van a analizar. La segunda dimensión indicará la dimensionalidad del tensor Key, el número de elementos para buscar dependencias. A lo largo de esta dimensión, agruparemos los flujos en grupos de trabajo. Y la tercera dimensión indicará el número de cabezas de atención. En el cuerpo del kernel, identificaremos inmediatamente el flujo a lo largo de todas las dimensiones del espacio de tareas y almacenaremos los valores resultantes en constantes locales.

A partir de estas constantes, determinaremos el desplazamiento en todos los búferes de datos.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_k = dimension * (2 *  heads_kv * k + h_kv);
   const int shift_v = dimension * (2 *  heads_kv * k + heads_kv + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k;

Y guardaremos directamente el valor de la máscara en una variable local.

   const float mask = IsNaNOrInf(masks[shift_s], 0);

Aquí debemos señalar que para la entrada del kernel, esperamos un tensor de enmascaramiento dadas las cabezas de atención. En otras palabras, cada cabeza de atención tendrá su propia matriz de enmascaramiento de canales.

A continuación, declararemos un array en la memoria local del contexto OpenCL, que utilizaremos para el intercambio de datos dentro del grupo.

   const uint ls = min((uint)kunits, (uint)LOCAL_ARRAY_SIZE);
   float2 koef = (float2)(fmax((float)sqrt((float)dimension), (float)1), 0);
   __local float2 temp[LOCAL_ARRAY_SIZE];

Con esto concluirán los trabajos preparatorios y podremos pasar directamente al proceso de cálculo. Primero deberemos determinar los coeficientes de atención. Para ello, organizaremos un ciclo de multiplicación de los vectores de asesoramiento Query y Key. El valor exponencial del producto resultante se multiplicará por la máscara.

//--- Score
   float score = 0;
   float2 score2 = (float2)0;
   if(ComplexAbs(mask) >= 0.01)
     {
      for(int d = 0; d < dimension; d++)
         score2 = IsNaNOrInf2(ComplexMul(q[shift_q + d], kv[shift_k + d]), (float2)0);
      score = IsNaNOrInf(ComplexAbs(ComplexExp(ComplexDiv(score, koef))) * mask, 0);
     }

Tenga en cuenta que solo realizaremos esta operación si el coeficiente de enmascaramiento es mayor o igual que el valor de umbral. Así eliminaremos la influencia de canales irrelevantes.

A continuación, deberemos normalizar los valores obtenidos trasladando su dimensión de probabilidad mediante la función SoftMax. Para ello, organizaremos un proceso de síntesis de los valores resultantes dentro del grupo de trabajo. En primer lugar, organizaremos un ciclo de suma parcial de valores en los elementos del array local.

//--- sum of exp
#pragma unroll
   for(int i = 0; i < kunits; i += ls)
     {
      if(k >= i && k < (i + ls))
         temp[k % ls].x = (i == 0 ? 0 : temp[k % ls].x) + score;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Y luego, sumaremos el valor de los elementos de nuestro array.

   uint count = ls;
#pragma unroll
   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k].x += (k < count && (k + count) < kunits ? temp[k + count].x : 0);
      if(k + count < ls)
         temp[k + count].x = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Como resultado de todas las iteraciones del ciclo, el primer elemento del array local contendrá la suma de todos los valores dentro del grupo de trabajo. Y ahora tendremos que dividir el valor del coeficiente de atención obtenido en cada flujo de operaciones por el valor total calculado para obtener la representación normalizada deseada. El resultado de las operaciones se almacenará en el elemento correspondiente de la búfer global.

//--- score
   if(temp[0].x > 0)
      score = score / temp[0].x;
   scores[shift_s] = score;

Ahora nos quedará determinar la representación final del elemento analizado, considerando la influencia de otros canales. Para ello, deberemos multiplicar el vector de coeficientes de atención obtenidos por la matriz Value. Este proceso se complicará por la necesidad de realizar operaciones en flujos paralelos del grupo de trabajo, ya que cada flujo contendrá solo un factor de atención. Así que crearemos un sistema de ciclos completo. El ciclo exterior iterará los elementos de la fila correspondiente de la matriz Value.

//--- out
#pragma unroll
   for(int d = 0; d < dimension; d++)
     {
      float2 val = (score > 0 ? ComplexMul(kv[shift_v + d], (float2)(score,0)) : (float2)0);

Y en el cuerpo del ciclo guardaremos directamente el valor actual del búfer de datos global multiplicado por el factor de atención correspondiente en una variable local. No obstante, para reducir el número de costosos accesos a la memoria global, esta operación solo se realizará cuando el factor de atención sea mayor que "0". De lo contrario, podremos inicializar sin problemas la variable con un valor nulo sin acceder al búfer de datos global.

A continuación, tendremos que sumar los valores obtenidos en los flujos de operación paralelos del grupo de trabajo. Aquí organizaremos un proceso similar a la suma de coeficientes de atención. Primero sumaremos los valores individuales de los elementos del array local.

#pragma unroll
      for(int i = 0; i < kunits; i += ls)
        {
         if(k >= i && k < (i + ls))
            temp[k % ls] = (i == 0 ? (float2)0 : temp[k % ls]) + val;
         barrier(CLK_LOCAL_MEM_FENCE);
        }

Y luego sumaremos los valores de los elementos del array local.

      uint count = ls;
#pragma unroll
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : (float2)0);
         if((k + count) < ls)
            temp[k + count] = (float2)0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);

Solo necesitaremos un flujo de información para almacenar el valor recibido en el búfer de datos global.

      //---
      if(k == 0)
         out[shift_q + d] = temp[0];
      barrier(CLK_LOCAL_MEM_FENCE);
     }
  }

Aquí sincronizaremos necesariamente los flujos del grupo de trabajo y pasaremos a la siguiente iteración del ciclo.

Una vez que todas las iteraciones del sistema de ciclo se hayan completado con éxito, finalizaremos el kernel.

La siguiente etapa de nuestro trabajo consistirá en construir el proceso de distribución del gradiente de error usando operaciones de atención enmascarada sobre valores complejos. Lo implementaremos en el kernel MaskAttentionGradientsComplex.

__kernel void MaskAttentionGradientsComplex(__global const float2 *q, __global float2 *q_g,
                                            __global const float2 *kv, __global float2 *kv_g,
                                            __global const float *scores,
                                            __global const float *mask, __global float *mask_g,
                                            __global const float2 *gradient,
                                            const int kunits, const int heads_kv
                                           )
  {
//--- init
   const int q_id = get_global_id(0);
   const int d = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int dimension = get_global_size(1);
   const int heads = get_global_size(2);

La estructura de los parámetros del kernel se parecerá mucho a la de un kernel de pasada directa. Solo añadiremos los búferes de datos globales de los gradientes de error correspondientes. Sin embargo, hemos cambiado ligeramente la estructura del espacio de tareas. Se sigue usando el espacio de tareas tridimensional, solo que ahora la segunda dimensión indicará la dimensionalidad de los vectores internos, y no habrá fusión de flujos en grupos de trabajo.

En el cuerpo del kernel, identificaremos el flujo actual de operaciones en todas las dimensiones del espacio de tareas con los valores resultantes almacenados en constantes locales. Al igual que antes, los utilizaremos para determinar los desplazamientos en los búferes de datos globales.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h) + d;
   const int shift_s = (q_id * heads + h) * kunits;
   const int shift_g = h * dimension + d;
   float2 koef = (float2)(fmax(sqrt((float)dimension), (float)1), 0);

Una vez finalizados los trabajos preparatorios, pasaremos directamente a recopilar los gradientes de error. En primer lugar, definiremos el error a nivel del tensor Value.

Aquí deberemos recordar que el tensor Value se utiliza para generar todos los elementos de la secuencia resultante multiplicando por la matriz de coeficientes de atención. Como consecuencia, transferiremos los gradientes de error de los resultados de la atención al nivel del tensor Value, dados los coeficientes de atención correspondientes. Para ello, organizaremos un sistema de ciclos.

//--- Calculating Value's gradients
   int step_score = kunits * heads;
   if(h < heads_kv)
     {
#pragma unroll
      for(int v = q_id; v < kunits; v += qunits)
        {
         float2 grad = (float2)0;
         for(int hq = h; hq < heads; hq += heads_kv)
           {
            int shift_score = hq * kunits + v;
            for(int g = 0; g < qunits; g++)
              {
               float sc = IsNaNOrInf(scores[shift_score + g * step_score], 0);
               if(sc > 0)
                  grad += ComplexMul(gradient[shift_g + dimension * (hq - h + g  * heads)],
                                     (float2)(sc, 0));
              }
           }
         int shift_v = dimension * (2 *  heads_kv * v + heads_kv + h) + d;
         kv_g[shift_v] = grad;
        }
     }

El siguiente paso será distribuir el gradiente de error al nivel del tensor Query. Obviamente, cada elemento de este tensor afectará solo a un elemento del tensor de resultados. Así, podremos almacenar el valor del gradiente de error correspondiente en una variable local para reducir el número de accesos a la memoria global.

//--- Calculating Query's gradients
   float2 grad = 0;
   float2 out_g = IsNaNOrInf2(gradient[shift_g + q_id * dimension], (float2)0);
   int shift_val = (heads_kv + h_kv) * dimension + d;
   int shift_key = h_kv * dimension + d;
#pragma unroll
   for(int k = 0; (k < kunits && ComplexAbs(out_g) != 0); k++)
     {
      float2 sc_g = 0;
      float2 sc = (float2)(scores[shift_s + k], 0);
      for(int v = 0; v < kunits; v++)
         sc_g += IsNaNOrInf2(ComplexMul(
                                ComplexMul((float2)(scores[shift_s + v], 0),
                                           out_g * kv[shift_val + 2 * v * heads_kv * dimension]),
                                ((float2)(k == v, 0) - sc)), (float2)0);
      float m = mask[shift_s + k];
      mask_g[shift_s + k] = IsNaNOrInf(sc.x / m * sc_g.x + sc.y / m * sc_g.y, 0);
      grad += IsNaNOrInf2(ComplexMul(sc_g, kv[shift_key + 2*k*heads_kv*dimension]), (float2)0);
     }
   q_g[shift_q] = IsNaNOrInf2(ComplexDiv(grad, koef), (float2)0);

Sin embargo, al formar el valor resultante, se interactuará con una serie de valores del tensor Query y Value. Y para obtener el valor de error deseado, primero haremos descender el gradiente hasta la matriz de coeficientes de atención, y solo entonces transferiremos al tensor Query.

Nótese que aquí también transferiremos el gradiente de error a la matriz de enmascaramiento del canal.

En el último paso, transferiremos de forma similar el gradiente de error al nivel del tensor Key. El algoritmo repetirá casi completamente la distribución del gradiente de error al nivel de Query, solo que en este caso, nos moveremos a lo largo de la columna de la matriz de atención.

//--- Calculating Key's gradients
   if(h < heads_kv)
     {
#pragma unroll
      for(int k = q_id; k < kunits; k += qunits)
        {
         int shift_k = dimension * (2 *  heads_kv * k + h_kv) + d;
         grad = 0;
         for(int hq = h; hq < heads; hq++)
           {
            int shift_score = hq * kunits + k;
            float2 val = IsNaNOrInf2(kv[shift_k + heads_kv * dimension], (float2)0);
            for(int scr = 0; scr < qunits; scr++)
              {
               float2 sc_g = (float2)0;
               int shift_sc = scr * kunits * heads;
               float2 sc = (float2)(IsNaNOrInf(scores[shift_sc + k], 0), 0);
               if(ComplexAbs(sc) == 0)
                  continue;
               for(int v = 0; v < kunits; v++)
                  sc_g += IsNaNOrInf2(
                             ComplexMul(
                                ComplexMul((float2)(scores[shift_sc + v], 0),
                                           gradient[shift_g + scr * dimension]),
                                ComplexMul(val, ((float2)(k == v, 0) - sc))),
                             (float2)0);
               grad += IsNaNOrInf2(ComplexMul(sc_g, q[shift_q + scr * dimension]), (float2)0);
              }
           }
         kv_g[shift_k] = IsNaNOrInf2(ComplexDiv(grad, koef), (float2)0);
        }
     }
  }

Con esto concluirá nuestro análisis de los algoritmos para construir los procesos de atención enmascarada en el dominio de valores complejos en el lado del contexto OpenCL. Encontrará el código completo de los kernels presentados en el archivo adjunto.

La próxima etapa de nuestro trabajo consistirá en implementar los algoritmos para enmascarar la atención de los valores complejos en el lado del programa principal. Pero de eso hablaremos en el próximo artículo.

Conclusión

Hoy nos hemos familiarizado con los aspectos teóricos del framework CATCH, que combina la transformada de Fourier y el mecanismo de parcheo de frecuencias para detectar anomalías en series temporales multivariantes. Su principal ventaja reside en su capacidad para identificar pautas de mercado complejas que pasan desapercibidas cuando se analizan únicamente en el dominio temporal.

El uso de la representación de frecuencias permite una comprensión más profunda de la dinámica del mercado, mientras que el mecanismo de parcheo de frecuencias adapta el análisis a las condiciones cambiantes. El framework CATCH también tiene en cuenta las interconexiones entre activos, por lo que resulta más sensible a las anomalías sistémicas del mercado. A diferencia de los métodos tradicionales, no solo capta los saltos y picos obvios, sino que también reconoce dependencias complejas y ocultas que pueden pronosticar cambios en las tendencias del mercado.

En la parte práctica, hemos comenzado a trabajar en la implementación de nuestra propia visión de los enfoques propuestos por los autores del framework usando MQL5. En el próximo artículo continuaremos el trabajo iniciado; al final del mismo, evaluaremos la eficacia de las soluciones aplicadas sobre datos históricos reales.

Enlaces

• CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto para recopilar ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL