Redes neuronales en el trading: Optimización LSTM para la previsión de series temporales multivariantes (DA-CG-LSTM)

Introducción

El trading no son solo números en una pantalla: es un entorno dinámico en el que cada tick, cada vela, cada cambio en el volumen comercial supone un reflejo de las emociones, expectativas, temores y esperanzas humanas. Entender este ritmo, aprender a predecir hacia dónde se dirigirá el precio, es una tarea con la que luchan los tráders.

El enfoque se centra en series temporales multidimensionales. La forma clásica de presentar datos del mercado son: el precio del activo a lo largo del tiempo, el volumen de operaciones, indicadores, noticias, etc. Todos estos son datos que se pueden analizar, modelar y utilizar para realizar pronósticos.

Hasta hace no mucho, el mercado dependía de métodos clásicos probados en el tiempo, como ARIMA, SARIMA y otros. Estos modelos son cómodos, comprensibles y no requieren recursos informáticos colosales. Además, gestionaban bien la estacionalidad y las dependencias lineales, especialmente en condiciones de mercado tranquilas. Pero el mercado financiero no es estacionario, todo lo contario, es una mezcla: las noticias influyen en las expectativas, el sentimiento de los inversores cambia en segundos, las transacciones algorítmicas crean efectos de resonancia y todo esto da lugar a relaciones complejas, no lineales y a menudo caóticas. Los modelos tradicionales pueden indicar la dirección, pero no muestran los detalles.

Con la llegada de los métodos de aprendizaje profundo, la situación cambió drásticamente. Las redes neuronales recurrentes ( RNN ) permitieron considerar la historia de los cambios, pero tampoco fueron una panacea. Su limitación fundamental es la llamada "memoria corta". En otras palabras, dichos modelos solo pueden gestionar un contexto temporal limitado. A medida que aumenta la longitud de la secuencia original, olvidan rápidamente información importante del inicio de la serie temporal.

Para solucionar este problema se desarrollaron arquitecturas mejoradas como LSTM (Long Short-Term Memory) y GRU (Gated Recurrent Unit). Estos modelos dieron a las redes neuronales memoria: la capacidad de retener información importante durante periodos temporales más largos.

Sin embargo, también poseían sus limitaciones. A pesar de su capacidad para captar dependencias en un horizonte temporal más largo, aún son sensibles a la calidad de los datos básicos. Especialmente difíciles les resultan las situaciones en las que los aumentos repentinos del mercado resultan clave. Estas mutaciones a menudo no se registran en la memoria a largo plazo del modelo, especialmente si no están acompañadas de cambios notables en el contexto a largo plazo.

Para superar estas limitaciones, se propuso un mecanismo de (atención). Este permitía que los modelos se centraran eficazmente en secciones clave de una serie temporal, independientemente de su distancia respecto del momento actual. A diferencia de los LSTM, los mecanismos de atención no requieren procesar todos los pasos temporales secuencialmente y pueden centrarse de inmediato en la información verdaderamente importante. Esto mejoró drásticamente la capacidad de las redes neuronales para captar dependencias a largo plazo, especialmente en series temporales complejas y multidimensionales.

Pero aquí también hay un problema: estos modelos son buenos para captar dependencias a largo plazo, pero ignoran señales a corto plazo que pueden tener una importancia crítica. El mercado financiero no perdona los retrasos: un titular de noticias y el precio puede dispararse o desplomarse. Si el modelo no responde a tales mutaciones, pierde la oportunidad de cambiar su posición en el tiempo.

Los autores del artículo "A Dual-Staged Attention Based Conversion-Gated Long Short Term Memory for Multivariable Time Series Prediction" intentaron combinar lo mejor de los dos enfoques y propusieron el nuevo framework Dual-Staged Attention Conversion-Gated LSTM (DA-CG-LSTM). El modelo usa un mecanismo de atención dual. En la primera etapa, estima la importancia de las características y los intervalos temporales y luego, después del procesamiento en un bloque CG-LSTM especial, vuelve a analizar las dependencias temporales, fortaleciendo las señales importantes y debilitando las insignificantes.

Una ventaja adicional del modelo era su uso bien pensado de funciones de activación, lo que le ayudó a retener información a largo plazo y responder a picos de corto plazo.

El algoritmo DA-CG-LSTM

El framework DA-CG-LSTM es un modelo capaz de extraer características de series temporales multidimensionales. Su arquitectura combina dos capas de atención y una unidad recurrente modificada en forma de Conversion-Gated LSTM. Esto hace que el modelo resulte particularmente efectivo en problemas de pronóstico de procesos multidimensionales dinámicos.

Todo comienza con el suministro al modelo de una secuencia temporal multidimensional de datos de origen. Esta secuencia es una matriz X = [x1, x2, ..., xT] ∈ RT*n, donde cada línea xt es un vector de n características en el tiempo t. Pero el modelo no procesa esta información a ciegas. Primero, aprende a comprender qué señales y qué pasos temporales en esta historia resultan realmente importantes. Así comienza la primera etapa: la atención de entrada.

En primer lugar se analizan las características de cada momento temporal. El modelo calcula la importancia de cada característica x kt en el paso temporal t utilizando la fórmula:

Aquí We y be representan los pesos y desplazamientos entrenables de la capa lineal aplicada a cada vector de características de los datos de origen x t. Esta capa permite transformar los datos de origen en una representación latente más informativa, adecuada para la evaluación de significancia. Además, el vector v e, también entrenable, desempeña el papel de una máscara de atención interpretable: se usa para calcular la puntuación de importancia escalar. Este diseño permite que el modelo clasifique de manera flexible las características según su contribución, lo que resulta especialmente importante cuando se trabaja con series temporales ruidosas y multidimensionales.

Los coeficientes de importancia obtenidos se normalizan usando la función SoftMax, transformando el conjunto de estimaciones en una distribución de probabilidad sobre características:

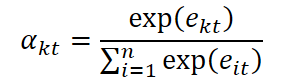
Con su ayuda se corrige el vector de datos inicial x ̃t, en el que cada característica se escala según su importancia.

Pero no vamos a quedarnos ahí. En el siguiente paso, el modelo analiza la importancia de cada paso temporal y determina qué puntos temporales deben enfatizarse durante el procesamiento. Para ello se usa una estructura similar:

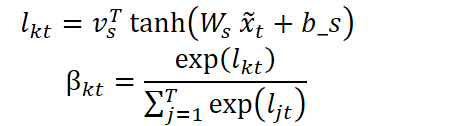
La secuencia resultante es una representación ponderada en el tiempo de:

Así, incluso antes de que comience el procesamiento recurrente, el modelo se centrará en la información que considera verdaderamente importante.

Luego, la secuencia se introduce en una unidad recurrente CG-LSTM modificada. Y aquí es donde ocurre el segundo nivel de magia. En el mecanismo LSTM estándar, los autores del framework trabajaron con las funciones de activación de las puertas de datos de origen y el olvido. Esto se hace para aumentar la sensibilidad del modelo ante los picos que acompañan a las mutaciones a corto plazo, mejorando al mismo tiempo la capacidad de recordar información a largo plazo.

En un bloque LSTM clásico, la puerta de datos de origen usa una función sigmoidea para tomar decisiones sobre qué información debe almacenarse. Sin embargo, la sigmoide es propensa a la saturación: para valores de entrada pequeños o grandes, su derivada se vuelve cercana a cero, lo cual reduce la efectividad del entrenamiento. Los autores del framework DA-CG-LSTM propusieron usar una combinación de la tangente sigmoidea e hiperbólica, que se expresa mediante la siguiente fórmula:

Este diseño evita la saturación en las primeras etapas del entrenamiento y mantiene la sensibilidad a fluctuaciones débiles pero sustanciales. En el contexto de series temporales financieras, esto resulta particularmente importante: por ejemplo, un cambio brusco en el volumen de transacciones o un aumento repentino en la volatilidad pueden indicar un cambio en el modo del mercado, y la detección temprana de estos patrones ofrece al modelo una ventaja de pronóstico.

La puerta del olvido CG-LSTM también se modifica. A diferencia del bloque LSTM estándar, aquí utilizamos una función que combina la sigmoide con la tangente hiperbólica inversa:

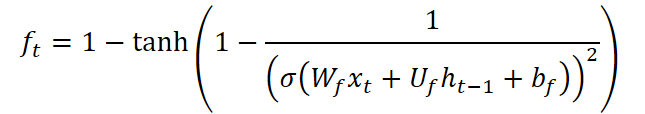
Esta fórmula tiene una propiedad única: la derivada de la función toma valores en el rango de 0 a aproximadamente 2,89, creando un efecto disperso en los datos. Es decir, el modelo se vuelve capaz de olvidar de forma más agresiva información irrelevante u obsoleta, concentrándose así en los cambios recientes. Esto resulta especialmente valioso en condiciones de mercado donde los eventos pasados rápidamente se vuelven irrelevantes y el éxito depende de reaccionar a las señales actuales.

A la salida del bloque CG-LSTM obtenemos una secuencia (h1, h2, ..., hT), donde cada ht lleva información de corto y largo plazo. Pero es importante no solo almacenar, sino también recordar correctamente. Esta es la tarea del segundo nivel de atención: el temporal.

Aquí el modelo parece mirar de nuevo su memoria, y calcula la importancia de cada estado oculto hj para el momento actual en el tiempo. Los valores obtenidos se normalizan usando SoftMax. Y sobre esta base se crea un vector de contexto: la quintaesencia de toda la historia temporal, que es procesada por el segundo bloque CG-LSTM.

Dado el estado oculto actual ht y el contexto enriquecido ct, el modelo produce la predicción final:

Donde f es típicamente una capa completamente conectada u otra estructura de salida del modelo.

La arquitectura DA-CG-LCTM no es solo inteligente, sino razonable. El modelo no lo recuerda todo, sino que hace una elección consciente: no reacciona a todos los ruidos, pero aprende a distinguir los picos de los patrones. En las tareas de previsión financiera esto resulta muy importante. El sistema es capaz de detectar señales similares a las del pasado, reconocer su fuerza y ajustar el pronóstico.

Por consiguiente, DA-CG-LSTM es un organismo vivo y dinámico que aprende, se adapta y extrae conclusiones basadas en el análisis estructurado de la información. Su fuerza no reside solo en sus ecuaciones formales, sino también en su claridad conceptual:

Atención + Memoria + Interpretación = Pronóstico Significativo

A continuación le presentamos la visualización del autor del framework DA-CG-LSTM.

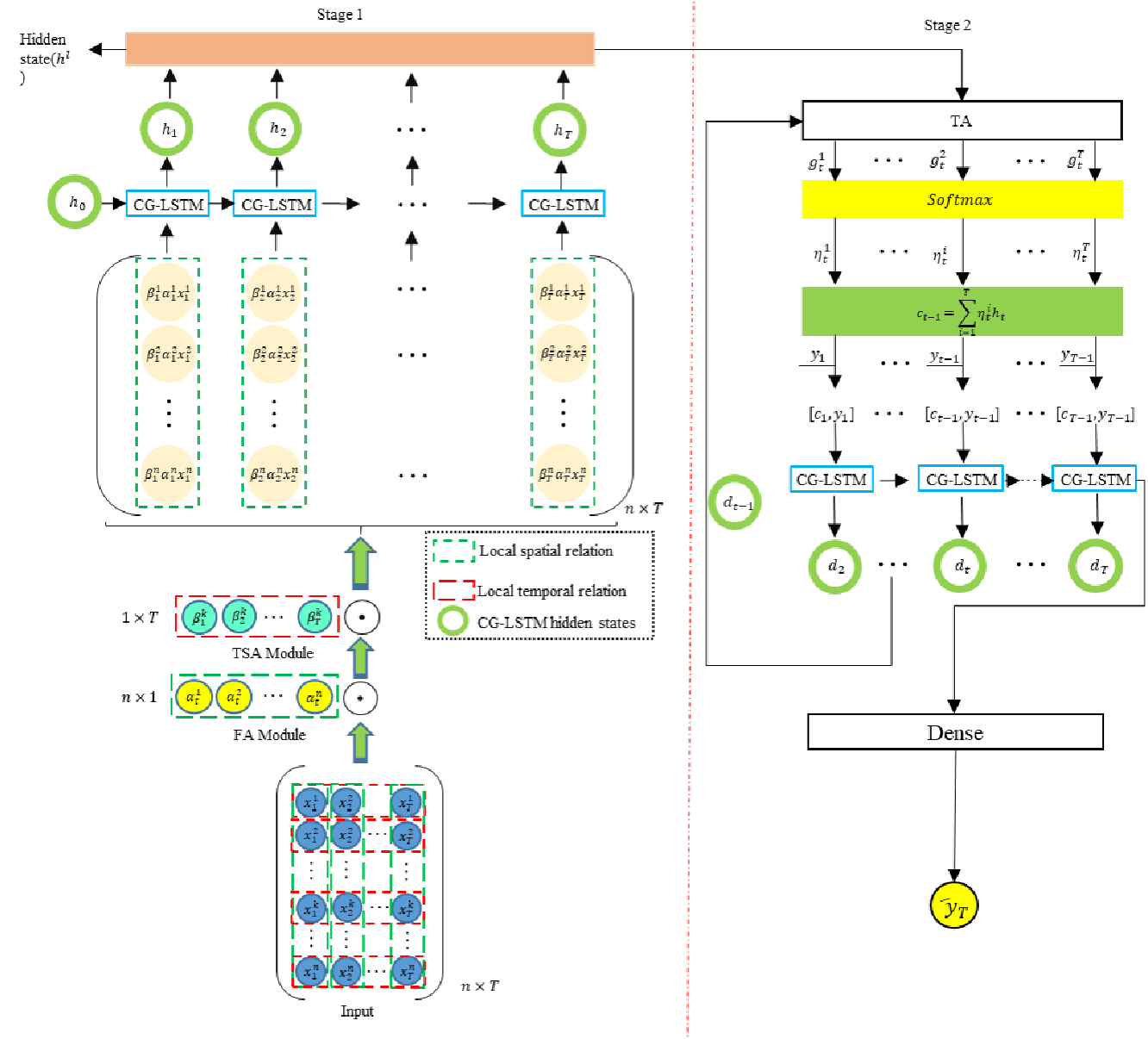
Implementación con MQL5

Tras revisar los aspectos teóricos del framework DA-CG-LSTM, podemos pasar a la parte práctica de nuestro trabajo, en la que analizaremos una opción para implementar nuestra propia visión de los enfoques propuestos utilizando MQL5.

Comenzaremos nuestro trabajo construyendo un bloque CG-LSTM modificado, cuya visualización del autor presentamos a continuación.

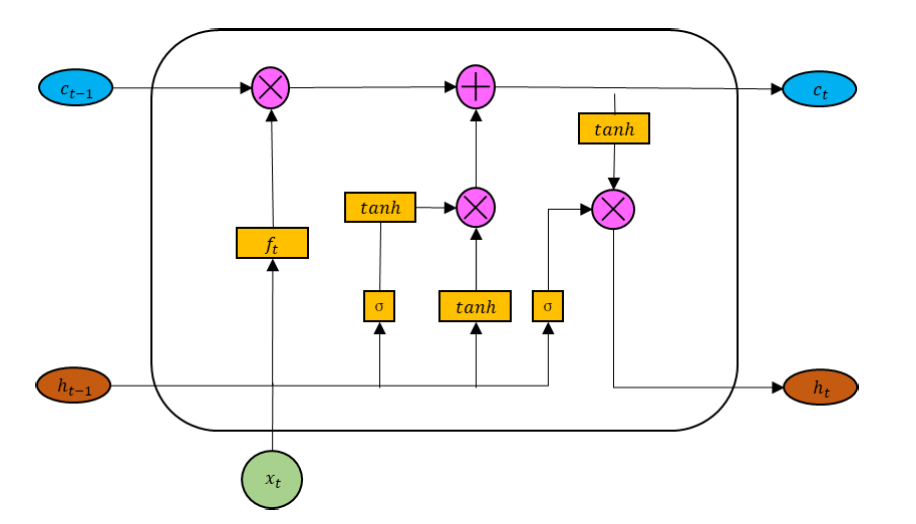
Vale la pena señalar aquí que, de manera similar al bloque LSTM clásico, el tensor de datos de origen se concatena con el estado oculto del bloque formado en el paso temporal anterior. El tensor resultante se usa para formar cuatro entidades: tres puertas y una representación del nuevo contexto. Para formar cada una de las entidades especificadas, se utiliza una capa lineal. Sin embargo, los resultados de las capas lineales se vuelven no lineales al usar diferentes funciones de activación.

El uso de 4 funciones de activación distintas para generar entidades individuales nos lleva a la necesidad de crear 4 capas completamente conectadas que se llamarán secuencialmente. Lo sé, esta no es la mejor opción. En nuestro trabajo, nos esforzamos por encontrar formas de maximizar la paralelización de las operaciones, lo cual acelerará el proceso de entrenamiento de modelos y la toma de decisiones en condiciones operativas.

Para lograr esto, al construir un bloque LSTM clásico, organizamos todo el proceso de pasada directa del bloque dentro de un solo kernel. En este caso, la formación de valores para cada entidad se realizaba en flujos paralelos del grupo de trabajo, con la posterior transferencia de valores entre ellos mediante el almacenamiento de datos en la memoria local. Esta implementación ha demostrado su eficacia. Sin embargo, al usar secuencias más complejas de funciones de activación propuestas por los autores del framework DA-CG-LSTM, nos topamos con la necesidad de crear búferes de datos adicionales para almacenar valores intermedios y la complicación general del algoritmo.

Por ello, en el marco de esta implementación, hemos decidido utilizar un enfoque alternativo. Para ello, dividiremos el proceso de pasada directa en 2 etapas. Primero, generaremos datos para las 4 entidades sin funciones de activación. Aquí podemos usar una capa simple completamente conectada o convolucional, cuyo tensor de salida sea un múltiplo del número de entidades generadas. Al trabajar con datos de origen multidimensionales, es preferible el uso de una capa convolucional, ya que permite organizar operaciones independientes para secuencias unitarias individuales.

En la segunda etapa, organizamos directamente el funcionamiento del bloque CG-LSTM, aplicando las funciones de activación necesarias a los datos obtenidos y construyendo procesos dentro del bloque.

Obviamente, comenzaremos nuestro trabajo implementando la segunda etapa en el lado del contexto OpenCL.

Modificamos el programa OpenCL

En primer lugar, organizaremos el proceso de pasada directa de nuestra visión de bloque CG-LSTM dentro del kernel CSLSTM_FeedForward. En los parámetros de este kernel solo obtendremos los punteros a 3 búferes de datos.

Uno de ellos contendrá los datos de origen (concatenated), que contendrán los valores de los cuatro componentes antes de aplicar las funciones de activación. Para minimizar la latencia al acceder a la memoria global y acelerar la lectura de los valores, los datos de este búfer se representan en formato float4, un tipo vector que permite leer cuatro elementos consecutivos a la vez en un solo acceso. Esta estructuración garantiza un uso más eficiente del ancho de banda de la memoria y permite cálculos más rápidos, especialmente al procesar grandes conjuntos de datos de origen.

Los otros dos búferes se usan para almacenar el contexto y los resultados.

__kernel void CSLSTM_FeedForward(__global const float4* __attribute__((aligned(16))) concatenated,
                                 __global float *memory,
                                 __global float *output)
  {
   uint id = (uint)get_global_id(0);
   uint total = (uint)get_global_size(0);       // hidden size
   uint idv = (uint)get_global_id(1);
   uint total_v = (uint)get_global_size(1);     // variables

Se supone que el funcionamiento de este kernel tiene lugar en un espacio de tareas bidimensional sin la creación de grupos de trabajo. La primera dimensión indica la dimensionalidad del estado oculto de la celda, mientras que la segunda indica el número de secuencias unitarias en los datos de origen. En el cuerpo del kernel, identificaremos inmediatamente el flujo en todas las dimensiones del espacio de tareas.

En función de los datos recibidos, determinaremos el desplazamiento en los búferes de datos e inmediatamente leeremos el bloque correspondiente de datos de origen en una variable local.

uint shift = id + total * idv;
float4 concat = concatenated[shift];

A continuación, añadiremos las funciones de activación necesarias a todas las entidades.

float fg = 1 - Activation(1 - 1 / pow(Activation(concat.s0, ActFunc_SIGMOID), 2), ActFunc_TANH);
float ig = Activation(Activation(concat.s1, ActFunc_SIGMOID), ActFunc_TANH);
float nc = Activation(concat.s2, ActFunc_TANH);
float og = Activation(concat.s3, ActFunc_SIGMOID);

Después de eso, actualizaremos los valores del contexto y el estado oculto.

float mem = IsNaNOrInf(memory[shift] * fg + ig * nc, 0);
float out = IsNaNOrInf(og * Activation(mem, ActFunc_TANH), 0);

Luego guardaremos los valores obtenidos en los elementos correspondientes de los búferes de datos globales y finalizaremos la operación del kernel.

 memory[shift] = mem;
 output[shift] = out;
} 

El código del kernel ha resultado compacto y fácil de leer, en gran parte debido al uso de un método auxiliar para seleccionar la función de activación. Esta solución no solo simplifica la lógica del cuerpo principal del kernel, sino que también hace que el código sea más modular y extensible. Además, la implementación de un mecanismo para comprobar la exactitud de los valores obtenidos aumenta la fiabilidad de toda la cadena computacional.

Tras finalizar el trabajo con el kernel de pasada directa, construiremos los procesos de pasada inversa. Podemos ver claramente que no se han utilizado parámetros entrenables durante la pasada directa. Todos ellos se colocan en la capa neuronal utilizada en la primera etapa. Por consiguiente, para implementar las operaciones de pasada inversa, solo necesitaremos distribuir correctamente el gradiente de error entre los participantes del proceso. Estas operaciones se realizarán en el kernel CSLSTM_CalcHiddenGradient.

Los parámetros del kernel de distribución de gradiente de error se complementarán con los búferes correspondientes, manteniendo al mismo tiempo el mismo espacio de tareas.

__kernel void CSLSTM_CalcHiddenGradient(__global const float4* __attribute__((aligned(16))) concatenated,
                                        __global float4* __attribute__((aligned(16))) grad_concat,
                                        __global const float* memory,
                                        __global const float* grad_output
                                       )
  {
   uint id = get_global_id(0);
   uint total = get_global_size(0);
   uint idv = get_global_id(1);
   uint shift = id + total * idv;

En el cuerpo del kernel, identificaremos el flujo actual en todas las dimensiones del espacio de tareas y determinaremos directamente el desplazamiento en los búferes de datos hacia los elementos correspondientes.

Vale la pena señalar que el cálculo de las derivadas de las funciones de activación complejas propuestas por los autores del framework DA-CG-LSTM requiere una serie de valores intermedios que no guardamos al realizar operaciones de pasada directa. Obviamente, almacenarlos requeriría importantes recursos de memoria. Y acceder a los búferes de datos globales supone una operación bastante costosa. Sin embargo, como el volumen principal de operaciones matriciales se ha trasladado a la capa neuronal interna de la primera etapa, podemos calcular de forma sencilla y con bastante rapidez los valores necesarios según los valores de las entidades antes de la función de activación.

Para este fin, leeremos los datos de origen antes de la activación en una variable local y calcularemos de nuevo las funciones, almacenando los resultados intermedios en variables locales. 

   float4 concat = concatenated[shift];                    // Pre-activation values for all 4 gates
// --- Forward reconstruction of gates ---
   float fg_s = Activation(concat.s0, ActFunc_SIGMOID);
   float fg = 1.0f - Activation(1.0f - 1.0f / pow(fg_s, 2), ActFunc_TANH);  // Forget gate (ft)
   float ig_s = Activation(concat.s1, ActFunc_SIGMOID);
   float ig = Activation(ig_s, ActFunc_TANH);              // Input gate (it)
   float nc = Activation(concat.s2, ActFunc_TANH);         // New content (ct~)
   float og = Activation(concat.s3, ActFunc_SIGMOID);      // Output gate (ot)
   float mem = memory[shift];                              // New memory state (ct)
   float mem_t = Activation(mem, ActFunc_TANH);            // tanh(ct)

Aquí calcularemos directamente el valor de la memoria en el paso temporal anterior utilizando el cálculo inverso.

// --- Reconstruct previous memory state (t-1) ---
   float prev_mem = IsNaNOrInf((mem - ig * nc) / fg, 0);

Tras completar el trabajo preparatorio, procederemos directamente a las operaciones de distribución del gradiente de error. Aquí primero leeremos el valor del gradiente en la salida del módulo desde el búfer global a una variable local.

// --- Gradients computation ---
   float out_g = grad_output[shift];

Y distribuiremos el valor obtenido entre las puertas de resultados y la memoria contextual utilizando las derivadas de las funciones de activación correspondientes.

float og_g = Deactivation(out_g * mem_t, og, ActFunc_SIGMOID);
float mem_g = Deactivation(out_g * og, mem_t, ActFunc_TANH);

A continuación, distribuiremos el gradiente del error de la memoria contextual entre la proyección del nuevo contexto y la puerta de los datos de origen.

float nc_g = Deactivation(mem_g * ig, nc, ActFunc_TANH);
float ig_g = Deactivation(Deactivation(mem_g * nc, ig, ActFunc_TANH), ig_s, ActFunc_SIGMOID);

Preste atención a las etapas de aplicación de las derivadas de las funciones de activación correspondientes al darse correcciones sucesivas del gradiente de error de las puertas de datos de entrada.

Finalmente, solo nos quedará el gradiente de error reducido al valor de la puerta de olvido antes de aplicar la función de activación. Como mencionamos antes, los autores del framework DA-CG-LSTM propusieron utilizar una función de activación bastante compleja. En consecuencia, distribuiremos el gradiente de error en varias etapas.

Primero, determinaremos el error en el valor de la puerta de olvido según el gradiente del error de memoria contextual y su valor anterior.

// ∂L/∂fg = ∂L/∂ct * mem_(t-1)
   float fg_g = mem_g * prev_mem;

Luego corregiremos el valor obtenido por la derivada de la función de activación de la tangente hiperbólica y la expresión interna compleja.

// Derivative of the complex forget gate:
// f(z) = 1 - tanh(1 - 1 / σ(z)^2)
   float fg_s_g = 2 / pow(fg_s, 3) * Deactivation(-fg_g, fg, ActFunc_TANH);
   fg_g = Deactivation(fg_s_g, fg_s, ActFunc_SIGMOID);

Y luego corregiremos la derivada de la sigmoide.

Y guardaremos los valores obtenidos en los elementos correspondientes del búfer de datos global.

// --- Write back gradients ---
   grad_concat[shift] = (float4)(fg_g, ig_g, nc_g, og_g);
  }

Con esto daremos por completo el trabajo en el lado del programa OpenCL. Podrá ver su código completo en el archivo adjunto.

Creación de un objeto CG-LSTM

A continuación trabajaremos en la parte principal del programa. Aquí crearemos un nuevo objeto CNeuronCGLSTMOCL, dentro del cual organizaremos el trabajo de nuestro bloque CG-LSTM. Más abajo resumimos la estructura del nuevo objeto:

class CNeuronCGLSTMOCL : public CNeuronBaseOCL
  {
protected:
   CNeuronBaseOCL    cConcatenateInputs;
   CNeuronConvOCL    cProjection;
   //---
   virtual bool      CSLSTM_feedForward(void);
   virtual bool      CSLSTM_CalcHiddenGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronCGLSTMOCL(void) {};
                    ~CNeuronCGLSTMOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons,
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint count, uint window, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override  const    {  return defNeuronCGLSTMOCL; }
   virtual bool      Clear(void) override;
   virtual CBufferFloat *getLSTMWeights(void) { return cProjection.GetWeightsConv(); }
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
  };

En la estructura presentada de la nueva clase, vemos el conjunto habitual de métodos redefinidos y 2 objetos internos, cuya funcionalidad conoceremos más a fondo durante la implementación de los métodos de la clase. Todos los objetos internos se declararán estáticamente, lo cual nos permitirá dejar vacíos el constructor y el destructor de la clase, La inicialización directa de los objetos declarados y heredados se realizará en el método Init.

En los parámetros del método de inicialización, obtendremos una serie de constantes que nos permitirán interpretar de forma inequívoca la arquitectura del objeto creado.

bool CNeuronCGLSTMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint count, uint window, uint variables,
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, count * variables, optimization_type, batch))
      return false;
   SetActivationFunction(None);

Algunos de los valores recibidos los transmitiremos directamente al método homónimo de la clase padre, donde ya están organizados los procesos de comprobación de los valores obtenidos y la inicialización de los objetos heredados.

Tenga en cuenta que aquí indicaremos explícitamente la ausencia de una función para el objeto creado.

Una vez completadas con éxito las operaciones del método de la clase padre, prepararemos los objetos declarados para su funcionalidad. En este caso solo hay 2. Uno de ellos es una capa completamente conectada para escribir el tensor concatenado de los datos de origen y el estado oculto de las últimas operaciones de pasada directa.

if(!cConcatenateInputs.Init(0, 0, OpenCL, (count + window) * variables, optimization, iBatch))
   return false;
cConcatenateInputs.SetActivationFunction(None);

Y aquí también indicaremos explícitamente la ausencia de una función de activación.

La segunda es una capa convolucional de proyección del tensor concatenado sobre 4 entidades.

if(!cProjection.Init(0, 1, OpenCL, count + window, count + window, count * 4, 1, variables, optimization, iBatch))
   return false;
cProjection.SetActivationFunction(None);

Como ya discutimos anteriormente, esta capa no utiliza una función de activación, lo cual indicamos explícitamente.

La inicialización de la capa convolucional merece especial atención. Al crearla, estableceremos explícitamente la longitud de la secuencia en uno. A primera vista, esto puede parecer una limitación, pero detrás de esta decisión hay una idea arquitectónica clara: al mismo tiempo, especificaremos el número de secuencias unitarias (independientes) que se procesarán en paralelo.

Este enfoque nos permitirá especificar para cada secuencia unitaria su propio conjunto de parámetros entrenables: una matriz de pesos aparte. Esto garantizará una completa independencia en su análisis y entrenamiento. Cada secuencia puede aprender en su propio contexto, respondiendo a patrones y regularidades específicas sin compartir parámetros con otras. Como resultado, obtendremos una representación más expresiva, adaptativa y estructuralmente flexible de los datos de origen, especialmente en problemas donde diferentes subsecuencias temporales tengan diferentes funciones semánticas o reflejen el comportamiento de factores de mercado individuales.

Este aislamiento de parámetros también juega un papel importante en el proceso de entrenamiento. En primer lugar, esta reduce la influencia mutua entre canales, lo que reduce el sobreentrenamiento con patrones dominantes. En segundo lugar, cada secuencia unitaria puede centrarse en sus propias propiedades de los datos. Este tipo de aprendizaje diferenciado hace que el modelo no solo resulte más preciso en tareas específicas, sino también mucho más resistente a las condiciones cambiantes del mercado.

Además, el entrenamiento independiente de filtros unitarios promueve una mejor generalización: el modelo memoriza datos con menor frecuencia y extrae patrones generales con mayor frecuencia. Esto resulta especialmente importante en series temporales financieras, donde los datos históricos pueden contener eventos únicos y no representativos. Al descomponer el proceso de aprendizaje en múltiples ramas aisladas, el modelo se vuelve capaz de reconocer señales típicas del mercado incluso en situaciones nuevas y nunca antes encontradas.

Y, obviamente, una característica especial de los modelos recurrentes es que utilizan sus propios datos de la pasada directa anterior. Por ello, borraremos todos los búferes de datos y solo entonces finalizaremos el método de inicialización.

   if(!Clear())
      return false;
//---
   return true;
  }

La siguiente etapa de nuestro trabajo será la construcción de los procesos de pasada directa, que organizaremos en el marco del método feedForward. Aquí debemos decir que todo es bastante simple. En los parámetros del método recibiremos el puntero al objeto de datos de origen, cuya relevancia comprobaremos de inmediato.

bool CNeuronCGLSTMOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Luego, de los parámetros de la capa de proyección, extraeremos las dimensionalidades del tensor de datos original y el estado oculto.

int hidden = (int)cProjection.GetFilters() / 4;
int inputs = (int)cProjection.GetWindow() - hidden;
int variables = (int)cProjection.GetVariables();

Después de lo cual, concatenaremos los datos de origen con los resultados de la pasada directa anterior en cuanto a las secuencias unitarias.

if(!Concat(NeuronOCL.getOutput(), getOutput(), cConcatenateInputs.getOutput(), inputs, hidden, variables))
   return false;

Proyectaremos los valores obtenidos sobre 4 entidades.

if(!cProjection.FeedForward(cConcatenateInputs.AsObject()))
   return false;

Y ahora todo lo que quedará es llamar al método de envoltorio para colocar el kernel de pasada directa creado anteriormente en la cola de ejecución CSLSTM_feedForward.

 return CSLSTM_feedForward();
}

Los métodos para colocar los kernels en la cola de ejecución se crean según el esquema con el que ya estamos familiarizados. Por consiguiente, en el marco de este artículo no nos detendremos en un examen detallado de su algoritmo.

Después de completar la construcción del método de pasada directa, pasaremos a la implementación de los procesos de pasada inversa. Como ya sabrá, el proceso aquí se divide en dos etapas: la distribución del gradiente de error y la optimización de los parámetros de entrenamiento.

En este caso, los parámetros entrenables estarán contenidos únicamente en la capa de proyección de los datos concatenados. Como consecuencia, el proceso de optimización de los parámetros entrenados del modelo se reducirá a una llamada al método de proyección homónimo.

bool CNeuronCGLSTMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   return cProjection.UpdateInputWeights(cConcatenateInputs.AsObject());
  }

El algoritmo para distribuir el gradiente de error entre los participantes del proceso calcInputGradients parece un poco más complicado. En los parámetros del método obtendremos el puntero al objeto de datos de origen. Este es el mismo objeto que analizamos en la pasada directa. Solo que esta vez necesitaremos transmitir el gradiente de error según la influencia de los datos de origen en el resultado final del modelo.

bool CNeuronCGLSTMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En el cuerpo del método, verificaremos directamente la relevancia del puntero obtenido. La necesidad de ejecutar este punto de control se ha discutido muchas veces en artículos anteriores.

A continuación, de manera similar al método de pasada directa, determinaremos las dimensionalidades de los datos de origen y el estado oculto.

int hidden = (int)cProjection.GetFilters() / 4;
int inputs = (int)cProjection.GetWindow() - hidden;
int variables = (int)cProjection.GetVariables();

En primer lugar, distribuiremos el gradiente de error entre las entidades llamando al método de envoltorio para agregarlo a la cola de ejecución del kernel correspondiente.

if(!CSLSTM_CalcHiddenGradient())
   return false;

Luego, haremos descender el gradiente de error al nivel del tensor concatenado de los datos de origen.

if(!cConcatenateInputs.calcHiddenGradients(cProjection.AsObject()))
   return false;

Y mediante concatenación inversa extraeremos el gradiente de error de los datos de origen.

if(!DeConcat(NeuronOCL.getGradient(), getPrevOutput(), cConcatenateInputs.getGradient(),
                                                             inputs, hidden, variables))
   return false;

Aquí vale la pena señalar que durante el proceso de inicialización de los objetos internos, deshabilitaremos intencionalmente las funciones de activación. Sin embargo, esto no excluye su uso para los datos de origen. Por consiguiente, verificaremos la presencia de la función de activación de los datos de origen y, de ser necesario, corregiremos los gradientes de error obtenidos usando las derivadas de las funciones de activación correspondientes.

   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(),
                                                                       NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

A continuación, finalizaremos el método retornando el resultado lógico de las operaciones al programa que realiza la llamada.

Con esto concluirá nuestra discusión de los algoritmos de construcción de los métodos para nuestra nueva clase CNeuronCGLSTMOCL. El código completo de esta clase y todos sus métodos se puede encontrar en el archivo adjunto.

Poco a poco, sin ni siquiera darnos cuenta, hemos agotado nuestro tiempo por hoy. Sin embargo, esta investigación requiere de una finalización lógica. Tomaremos un breve descanso y continuaremos desarrollando el presente tema. 

Conclusión

En este artículo, hemos presentado los aspectos teóricos del framework DA-CG-LSTM. A diferencia de los modelos tradicionales, su arquitectura incorpora varios mecanismos innovadores como el CG-LSTM y el mecanismo de atención dual, que permiten una extracción de dependencias más profunda y precisa en los datos. Estos componentes permiten el procesamiento eficiente de dependencias temporales complejas y la consideración de patrones tanto a largo como a corto plazo.

En la parte práctica del artículo, hemos presentado nuestra visión de la implementación del bloque CG-LSTM utilizando MQL5. Sin embargo, nuestro trabajo aún no ha concluido: lo continuaremos en el próximo artículo, llevándolo a su conclusión lógica.

Enlaces

• A Dual-Staged Attention Based Conversion-Gated Long Short Term Memory for Multivariable Time Series Prediction
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto para recopilar ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos offline
4	StudyOnline.mq5	Asesor	Asesor de entrenamiento de modelos online
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL