
Neuronale Netze im Handel: Hierarchischer Dual-Tower-Transformer (Hidformer)
Einführung
Neuronale Netzmodelle, die in der Lage sind, die zeitliche Struktur von Daten zu erfassen und verborgene Muster zu erkennen, sind besonders bei Finanzprognosen gefragt. Herkömmliche Ansätze für neuronale Netze stoßen jedoch an Grenzen, die mit der hohen Rechenkomplexität und der unzureichenden Interpretierbarkeit der Ergebnisse zusammenhängen. In den letzten Jahren haben daher Architekturen, die auf Aufmerksamkeitsmechanismen basieren, zunehmendes Interesse bei den Forschern geweckt, da sie eine genauere Analyse von Zeitreihen und Finanzdaten ermöglichen.
Modelle, die auf der Transformer-Architektur und ihren Modifikationen basieren, haben die größte Popularität erlangt. Eine solche Änderung, die in dem Artikel „Hidformer: Transformer-Style Neural Network in Stock Price Forecasting“ wird Hidformer genannt. Dieses Modell wurde speziell für die Zeitreihenanalyse entwickelt und konzentriert sich auf die Verbesserung der Vorhersagegenauigkeit durch optimierte Aufmerksamkeitsmechanismen, die effiziente Identifizierung langfristiger Abhängigkeiten und die Anpassung an die Merkmale von Finanzdaten. Der Hauptvorteil von Hidformer liegt in seiner Fähigkeit, komplexe zeitliche Zusammenhänge zu berücksichtigen, was besonders bei der Analyse von Aktienmärkten wichtig ist, wo die Preise von Vermögenswerten von zahlreichen Faktoren abhängen.
Die Autoren des Frameworks schlagen eine verbesserte Verarbeitung zeitlicher Abhängigkeiten, eine geringere Rechenkomplexität und eine höhere Vorhersagegenauigkeit vor. Dies macht Hidformer zu einem vielversprechenden Instrument für Finanzanalysen und -prognosen.
Der Algorithmus von Hidformer
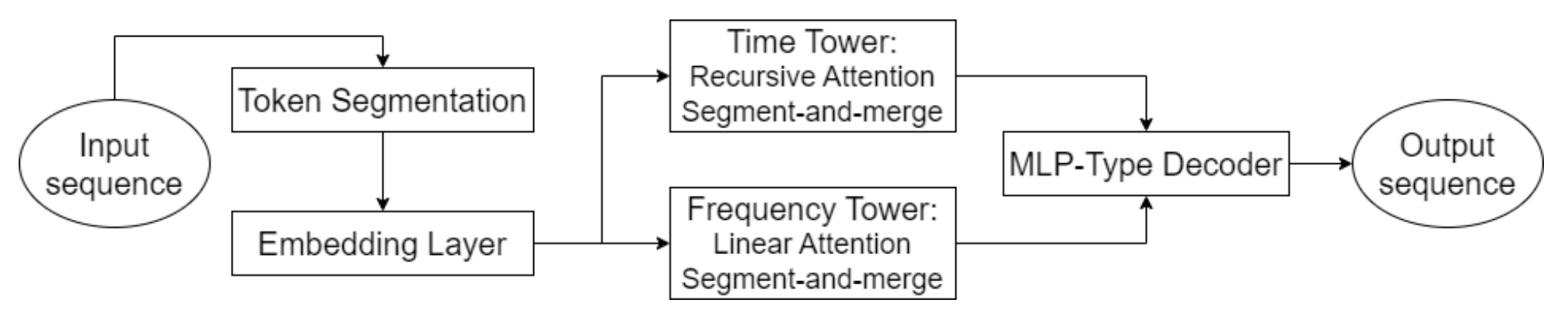
Eines der Hauptmerkmale von Hidformer ist die parallele Verarbeitung der Daten durch zwei Encoder. In der ersten werden die zeitlichen Merkmale analysiert, um Trends und Muster im Laufe der Zeit zu erkennen. Die zweite arbeitet im Frequenzbereich, wodurch das Modell tiefere Abhängigkeiten erkennen und das Marktrauschen eliminieren kann. Dieser Ansatz hilft, verborgene Muster in den Daten zu erkennen. Dies ist für die Vorhersage von Aktienkursen von entscheidender Bedeutung, da Signale durch Rauschen überlagert werden können. Die Eingabedaten werden in Teilsequenzen aufgeteilt, die dann in jeder Verarbeitungsstufe zusammengeführt werden, wodurch die Erkennung signifikanter Muster verbessert wird.
Diese Methode ist besonders nützlich für die Analyse von volatilen Vermögenswerten wie Technologieaktien oder Kryptowährungen, da sie hilft, fundamentale Trends von kurzfristigen Schwankungen zu trennen. Anstelle der standardmäßigen Multi-Head-Attention, die in der Transformer-Architektur verwendet wird, schlagen die Autoren von Hidformer vor, einen rekursiven Aufmerksamkeitsmechanismus im temporalen Encoder und einen linearen Aufmerksamkeitsmechanismus zu verwenden, um Abhängigkeiten im Frequenzspektrum zu erkennen. Dies verringert den Verbrauch von Rechenressourcen und verbessert die Stabilität der Vorhersagen, was das Modell bei der Arbeit mit großen Mengen von Marktdaten effizient macht.
Der Decoder des Modells basiert auf einem mehrschichtigen Perzeptron, das es ihm ermöglicht, die gesamte Preissequenz in einem einzigen Schritt zu prognostizieren. Dadurch werden Fehler vermieden, die sich sonst bei einer schrittweisen Vorausschätzung häufen würden. Diese Architektur ist besonders vorteilhaft für Finanzprognosen, da sie die Wahrscheinlichkeit einer Häufung von Ungenauigkeiten bei langfristigen Vorhersagen verringert.
Die Originalvisualisierung des Hidformer-Frameworks ist unten zu sehen.
Die Implementation in MQL5
Nach einem kurzen Überblick über die theoretischen Aspekte des Hidformer-Rahmens gehen wir nun dazu über, unsere eigene Interpretation der vorgeschlagenen Ansätze mit MQL5 zu implementieren. Wir beginnen mit der Implementierung der modifizierten Aufmerksamkeitsalgorithmen.
Schauen wir uns zunächst den rekursiven Aufmerksamkeitsalgorithmus an. Der ursprünglich für die Lösung von visuellen Dialogproblemen vorgeschlagene rekursive Aufmerksamkeitsmechanismus hilft dabei, den richtigen Kontext der aktuellen Anfrage auf der Grundlage des vorangegangenen Dialogverlaufs zu bestimmen. Es liegt auf der Hand, dass die rekursive Verarbeitung von Daten im Vergleich zur parallelen Berechnung der Aufmerksamkeit mehrerer Köpfe unsere Aufgabe nur verkompliziert. Andererseits können wir durch den rekursiven Ansatz vermeiden, die gesamte Historie zu verarbeiten, indem wir bei dem nächstgelegenen relevanten Element anhalten, das den erforderlichen Kontext enthält.
Diese Überlegungen führen uns zur Entwicklung eines Algorithmus für mehrstufige Aufmerksamkeit. Zuvor haben wir verschiedene Ansätze zur Erfassung lokaler und globaler Merkmale durch Anpassung des Aufmerksamkeitsfensters erörtert. Früher wurden jedoch verschiedene Aufmerksamkeitsstufen in separaten Komponenten verwendet. Ich schlage nun vor, den früheren mehrköpfigen Aufmerksamkeits-Algorithmus so zu ändern, dass jeder Kopf sein eigenes Kontextfenster erhält. Außerdem schlagen wir vor, das Kontextfenster nicht um das analysierte Element herum zu definieren, sondern vom Beginn der Sequenz an. Die neuesten Daten werden am Anfang der Sequenz gespeichert. Dieser Ansatz ermöglicht es uns, die analysierte Geschichte im Kontext der aktuellen Marktsituation zu bewerten.
Aufmerksamkeitsmodifikation in OpenCL
Zu Beginn werden wir die oben beschriebenen Änderungen auf der Seite von OpenCL implementieren. Zu diesem Zweck erstellen wir einen neuen Kernel MultiScaleRelativeAttentionOut, wobei wir den größten Teil seines Codes vom Spenderkernel kopieren MHRelativeAttentionOut. Die Parameterliste des Kernels wird unverändert übertragen.
__kernel void MultiScaleRelativeAttentionOut(__global const float * q, ///<[in] Matrix of Querys __global const float * k, ///<[in] Matrix of Keys __global const float * v, ///<[in] Matrix of Values __global const float * bk, ///<[in] Matrix of Positional Bias Keys __global const float * bv, ///<[in] Matrix of Positional Bias Values __global const float * gc, ///<[in] Global content bias vector __global const float * gp, ///<[in] Global positional bias vector __global float * score, ///<[out] Matrix of Scores __global float * out, ///<[out] Matrix of attention const int dimension ///< Dimension of Key ) { //--- init const uint q_id = get_global_id(0); const uint k_id = get_local_id(1); const uint h = get_global_id(2); const uint qunits = get_global_size(0); const uint kunits = get_local_size(1); const uint heads = get_global_size(2); const int shift_q = dimension * (q_id * heads + h); const int shift_kv = dimension * (heads * k_id + h); const int shift_gc = dimension * h; const int shift_s = kunits * (q_id * heads + h) + k_id; const int shift_pb = q_id * kunits + k_id; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); const uint window = fmax((kunits + h) / (h + 1), fmin(3, kunits)); float koef = sqrt((float)dimension);
Innerhalb der Methode führen wir zunächst vorbereitende Arbeiten durch. Hier definieren wir alle notwendigen Konstanten, einschließlich des Kontextfensters.
Beachten Sie, dass wir keinen separaten Puffer für die Weitergabe der einzelnen Kontextgrößen für jeden Aufmerksamkeitskopf erstellt haben. Stattdessen haben wir einfach die Länge der analysierten Sequenz durch die Aufmerksamkeitskopf-ID plus eins geteilt (da die IDs bei Null beginnen). So analysiert der erste Kopf die gesamte Sequenz, und die nachfolgenden Köpfe arbeiten mit immer kleineren Kontextfenstern.
Als Nächstes bestimmen wir die Aufmerksamkeitskoeffizienten. Jeder Ausführungsstrang berechnet einen Koeffizienten für ein bestimmtes Element. Operationen werden jedoch nur innerhalb des Kontextfensters durchgeführt. Elemente, die außerhalb des Fensters liegen, erhalten automatisch als Aufmerksamkeitsgewicht den Wert Null.
__local float temp[LOCAL_ARRAY_SIZE]; //--- score float sc = 0; if(k_id < window) { for(int d = 0; d < dimension; d++) { float val_q = q[shift_q + d]; float val_k = k[shift_kv + d]; float val_bk = bk[shift_kv + d]; sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + gp[shift_q + d] * val_bk; } sc = sc / koef; }
Um die Stabilität der Koeffizienten zu verbessern, verschieben wir die Werte in den Bereich der numerischen Stabilität. Dazu wird der maximale Koeffizient unter den berechneten Werten ermittelt, wobei Elemente außerhalb des Kontextfensters ausgeschlossen werden.
//--- max value for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id < window) if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? sc : fmax(temp[shift_local], sc)); } barrier(CLK_LOCAL_MEM_FENCE); } uint count = min(ls, kunits); //--- do { count = (count + 1) / 2; if(k_id < (window + 1) / 2) if(k_id < ls) temp[k_id] = (k_id < count && (k_id + count) < kunits ? fmax(temp[k_id + count], temp[k_id]) : temp[k_id]); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Erst dann berechnen wir den Exponentialwert jedes Koeffizienten abzüglich des Maximalwerts.
if(k_id < window) sc = IsNaNOrInf(exp(fmax(sc - temp[0], -120)), 0); barrier(CLK_LOCAL_MEM_FENCE);
Besondere Aufmerksamkeit muss jedoch den Operationen innerhalb des Kontextfensters gewidmet werden. Durch die Verschiebung des Maximums auf Null wird der maximale Exponent gleich eins. Alle anderen Koeffizienten liegen zwischen 0 und 1. Dadurch wird die Stabilität der SoftMax-Funktion verbessert. Da aber Koeffizienten außerhalb des Kontextfensters automatisch auf Null gesetzt wurden, würde die Berechnung ihres Exponenten das maximale Gewicht ergeben, was höchst unerwünscht ist. Daher müssen wir ihren Wert als Null beibehalten.
Anschließend addieren wir die Koeffizienten innerhalb der Arbeitsgruppe.
//--- sum of exp for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < count && k_id < (window + 1) / 2) temp[k_id] += ((k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Anschließend wird jeder Koeffizient normalisiert, indem er durch die berechnete Summe dividiert wird.
//--- score float sum = IsNaNOrInf(temp[0], 1); if(sum <= 1.2e-7f) sum = 1; sc /= sum; score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Die normalisierten Koeffizienten werden dann in den entsprechenden Datenpuffer geschrieben.
Nachdem wir die normalisierten Aufmerksamkeitsgewichte für die Sequenzelemente erhalten haben, können wir den angepassten Wert des aktuellen Elements berechnen. Dazu durchlaufen wir die Sequenz, multiplizieren den Wertetensor mit jedem Koeffizienten und summieren die Ergebnisse.
//--- out int shift_local = k_id % ls; for(int d = 0; d < dimension; d++) { float val_v = v[shift_kv + d]; float val_bv = bv[shift_kv + d]; float val = IsNaNOrInf(sc * (val_v + val_bv), 0); //--- sum of value for(int cur_v = 0; cur_v < kunits; cur_v += ls) { if(k_id >= cur_v && k_id < (cur_v + ls)) temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < count && (k_id + count) < kunits) temp[k_id] += temp[k_id + count]; if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- if(k_id == 0) out[shift_q + d] = IsNaNOrInf(temp[0], 0); barrier(CLK_LOCAL_MEM_FENCE); } }
Die Ausgaben werden in dem dafür vorgesehenen Datenpuffer gespeichert.
Durch die Beibehaltung der Nullgewichte können wir bestehende Tools zur Implementierung von Rückwärtsdurchlauf-Algorithmen verwenden. Damit ist unsere Arbeit auf der Seite von OpenCL abgeschlossen. Der vollständige Quellcode ist im Anhang enthalten.
Multiskalige Aufmerksamkeitsobjekte erstellen
Als Nächstes müssen wir im Hauptprogramm Aufmerksamkeitsobjekte mit mehreren Skalen erstellen. Um die Vorteile der Objektvererbung zu maximieren, haben wir einfach Objekte für Selbstaufmerksamkeits und Kreuzaufmerksamkeit auf der Grundlage bestehender Methoden erstellt und nur die Methode überschrieben, die den neu erstellten Kernel aufruft. Die Struktur der neuen Objekte ist unten dargestellt.
class CNeuronMultiScaleRelativeSelfAttention : public CNeuronRelativeSelfAttention { protected: //--- virtual bool AttentionOut(void); public: CNeuronMultiScaleRelativeSelfAttention(void) {}; ~CNeuronMultiScaleRelativeSelfAttention(void) {}; //--- virtual int Type(void) override const { return defNeuronMultiScaleRelativeSelfAttention; } };
class CNeuronMultiScaleRelativeCrossAttention : public CNeuronRelativeCrossAttention { protected: virtual bool AttentionOut(void); public: CNeuronMultiScaleRelativeCrossAttention(void) {}; ~CNeuronMultiScaleRelativeCrossAttention(void) {}; //--- virtual int Type(void) override const { return defNeuronMultiScaleRelativeCrossAttention; } };
Wir haben die klassische Methode verwendet, den Kernel in eine Warteschlange zu stellen. Wir haben ähnliche Methoden bereits mehrfach überprüft. Ich glaube, Sie werden keine Schwierigkeiten haben, sie zu verstehen. Der vollständige Code für diese Methoden ist im Anhang zu finden.
Rekursives Aufmerksamkeits-Objekt
Die oben implementierten Multiskalen-Aufmerksamkeitsobjekte ermöglichen es uns, Daten in verschiedenen Kontextfenstergrößen zu analysieren, aber dies ist nicht der von den Autoren von Hidformer vorgeschlagene rekursive Aufmerksamkeitsmechanismus. Wir haben lediglich die Vorbereitungsphase abgeschlossen.
Unser nächster Schritt besteht darin, ein rekursives Aufmerksamkeitsobjekt zu entwickeln, das in der Lage ist, aktuelle Daten im Kontext der zuvor beobachteten Geschichte zu analysieren. Dazu werden wir einige Techniken zur Entwicklung von Speichermodulen anwenden. Konkret werden wir den Kontext der beobachteten Zustände für eine bestimmte historische Tiefe speichern, die dann zur Bewertung des aktuellen Zustands verwendet wird. Wir werden diesen Algorithmus innerhalb der Methode CNeuronRecursiveAttention implementieren, deren Struktur unten dargestellt ist.
class CNeuronRecursiveAttention : public CNeuronMultiScaleRelativeCrossAttention { protected: CNeuronMultiScaleRelativeSelfAttention cSelfAttention; CNeuronTransposeOCL cTransposeSA; CNeuronConvOCL cConvolution; CNeuronEmbeddingOCL cHistory; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override { return false; } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override { return false; } public: CNeuronRecursiveAttention(void) {}; ~CNeuronRecursiveAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint history_size, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronRecursiveAttention; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool Clear(void) override; };
Die übergeordnete Klasse ist in diesem Fall das zuvor implementierte skalenübergreifende Objekt.
Innerhalb der Methode sehen wir eine vertraute Reihe von überschriebenen virtuellen Methoden und mehrere interne Objekte, deren Funktionen wir während der Implementierung der Vorwärts- und Rückwärtsdurchläufe untersuchen werden.
Alle internen Objekte werden als statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse leer lassen können. Die Initialisierung aller geerbten und neu deklarierten Objekte erfolgt in der Methode Init.
bool CNeuronRecursiveAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint history_size, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronMultiScaleRelativeCrossAttention::Init(numOutputs, myIndex, open_cl, window, window_key, units_count, heads, window_key, history_size, optimization_type, batch)) return false;
Die Methodenparameter enthalten eine Reihe von Konstanten, die die Architektur des erstellten Objekts klar definieren. Es ist wichtig zu beachten, dass unser Objekt, obwohl es von der Klasse der Kreuzaufmerksamkeit abgeleitet wurde, mit einem einzigen Strom von Eingangsdaten arbeitet. Der zweite Datenstrom, der für das korrekte Funktionieren der übergeordneten Klasse erforderlich ist, wird intern erzeugt. Die Sequenzlänge dieses zweiten Datenstroms wird durch den historischen Tiefenparameter history_size definiert.
Wie üblich rufen wir sofort die gleichnamige Methode der übergeordneten Klasse auf und übergeben ihr die erforderlichen Parameter. Erinnern Sie sich daran, dass die Elternmethode bereits alle erforderlichen Kontrollpunkte und Initialisierungsprozeduren für geerbte Objekte, einschließlich Basisschnittstellen, enthält.
Als Nächstes initialisieren wir die neu deklarierten internen Objekte. Das erste ist das mehrstufige Modul der Selbstaufmerksamkeit.
int index = 0; if(!cSelfAttention.Init(0, index, OpenCL, iWindow, iWindowKey, iUnits, iHeads, optimization, iBatch)) return false;
Mit Hilfe dieses Objekts lässt sich feststellen, welche Elemente der ursprünglichen Daten den größten Einfluss auf den aktuellen Zustand des analysierten Finanzinstruments haben.
Anschließend müssen wir den Kontext des aktuellen Umgebungszustands in den Speicher unseres rekursiven Aufmerksamkeitsblocks aufnehmen. Wir wollen den Kontext der einzelnen univariaten Sequenzen erhalten. Daher transponieren wir zunächst die Eingabedaten.
index++; if(!cTransposeSA.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch)) return false;
Dann extrahieren wir den Kontext der unitären Sequenzen mithilfe einer Faltungsschicht.
index++; if(!cConvolution.Init(0, index, OpenCL, iUnits, iUnits, iWindowKey, 1, iWindow, optimization, iBatch)) return false;
Man beachte, dass die Parameter der Faltungsschicht ein einzelnes Element der analysierten Sequenz angeben, während die Anzahl der unitären Sequenzen als Anzahl der unabhängigen Variablen übergeben wird. Dies ermöglicht eine völlig unabhängige Analyse von unitären Sequenzen, da jede ihren eigenen Satz von trainierbaren Parametern verwendet. Dies ermöglicht eine tiefere Analyse der ursprünglichen multimodalen Sequenz.
Als Nächstes verwenden wir eine Schicht zur Erzeugung von Einbettungen, um den Kontext des analysierten Umgebungszustands zu erfassen und ihn dem historischen Speicherstapel hinzuzufügen.
index++; uint windows[] = { iWindowKey * iWindow }; if(!cHistory.Init(0, index, OpenCL, iUnitsKV, iWindowKey, windows)) return false; //--- return true; }
Wenn alle Operationen erfolgreich abgeschlossen sind, geben wir einen logischen Erfolgswert an das aufrufende Programm zurück und beenden die Methode.
Unser nächster Schritt ist die Implementierung der Methode feedForward, deren Algorithmus ziemlich linear ist.
bool CNeuronRecursiveAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cSelfAttention.FeedForward(NeuronOCL)) return false;
Die Methode erhält einen Zeiger auf das Eingangsdatenobjekt, das die multimodale Zeitreihe enthält. Wir übergeben diesen Zeiger sofort an das Selbstaufmerksamkeits-Modul, um die Abhängigkeiten im aktuellen Umgebungszustand zu analysieren. Die Ergebnisse werden dann zur weiteren Verarbeitung umgesetzt.
if(!cTransposeSA.FeedForward(cSelfAttention.AsObject())) return false;
Wir extrahieren den Kontext von unitären Sequenzen mithilfe der Faltungsschicht.
if(!cConvolution.FeedForward(cTransposeSA.AsObject())) return false;
Wir übergeben die vorbereiteten Daten an den Einbettungsgenerator, der den Kontext des analysierten Zustands extrahiert und ihn dem Speicherstapel hinzufügt.
if(!cHistory.FeedForward(cConvolution.AsObject())) return false;
Nun müssen wir die zuvor erhaltenen Ergebnisse der Selbstaufmerksamkeit mit dem Kontext der historischen Sequenz anreichern. Zu diesem Zweck verwenden wir die entsprechende Methode der übergeordneten Klasse und übergeben ihr die erforderlichen Informationen.
return CNeuronMultiScaleRelativeCrossAttention::feedForward(cSelfAttention.AsObject(),
cHistory.getOutput());
}
Es ist erwähnenswert, dass wir für die Analyse des aktuellen Zustands im Kontext der zuvor beobachteten Zustände das zuvor erstellte Multiskalen-Aufmerksamkeitsobjekt verwenden. Bei diesem Ansatz wird den kürzlich beobachteten Daten mehr Gewicht beigemessen, während der Einfluss älterer Informationen verringert wird. Dennoch sind wir immer noch in der Lage, wichtige Punkte aus den „Tiefen des Gedächtnisses“ zu extrahieren.
Bevor wir die Methode beenden, geben wir dem Aufrufer einen booleschen Wert zurück, der den Erfolg oder Misserfolg der Initialisierung anzeigt.
Da die Selbstaufmerksamkeits-Ergebnisse im Vorwärtsdurchlauf zweimal verwendet werden, wirkt sich dies auf den in der Methode calcInputGradients implementierten Rückwärtsdurchlauf-Algorithmus aus.
bool CNeuronRecursiveAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Die Rückwärtsdurchlauf-Methode erhält einen Zeiger auf dasselbe Eingabedatenobjekt, aber jetzt müssen wir ihr den Gradienten des Fehlers übergeben, der seinem Einfluss auf die Ausgabe des Modells entspricht.
Innerhalb der Methode wird sofort die Gültigkeit des empfangenen Zeigers überprüft. Andernfalls können wir keine Daten an ein nicht existierendes Objekt übergeben, und weitere Operationen verlieren ihren Sinn. Deshalb fahren wir nur dann fort, wenn dieser Kontrollpunkt erfolgreich passiert wird.
Wie Sie wissen, entspricht der Informationsfluss der Vorwärts- und Rückwärtsdurchläufe konzeptionell vollständig und unterscheidet sich nur in der Richtung. Der Vorwärtsdurchlauf endet mit einem Aufruf der Methode der übergeordneten Klasse. Dementsprechend beginnt der Rückwärtsdurchlauf mit einem Aufruf der geerbten Methode. Letztere verteilt den zuvor erhaltenen Gradienten zwischen den beiden Datenströmen auf der Grundlage ihres Beitrags zum Endergebnis.
if(!CNeuronMultiScaleRelativeCrossAttention::calcInputGradients(cSelfAttention.AsObject(), cHistory.getOutput(), cHistory.getGradient(), (ENUM_ACTIVATION)cHistory.Activation())) return false;
Zunächst verteilen wir den Gradienten über den Hilfsdatenstrom, der dem Speicher des Objekts entspricht. Hier propagieren wir den Fehler bis hinunter zur Faltungsschicht, die den Kontext von univariaten Sequenzen extrahiert.
if(!cConvolution.calcHiddenGradients(cHistory.AsObject())) return false;
Dann wird sie an die Umsetzungsebene des Blocks der Selbstaufmerksamkeit weitergegeben.
if(!cTransposeSA.calcHiddenGradients(cConvolution.AsObject())) return false;
Als Nächstes müssen wir den Farbverlauf an die multiskalen Schichten der Selbstaufmerksamkeit weitergeben. Allerdings haben wir ihm zuvor bereits die Steigung des Hauptdatenstroms übermittelt, die erhalten bleiben muss. Dazu tauschen wir vorübergehend die Zeiger auf die Datenpuffer aus. Zunächst übergeben wir dem Objekt einen Zeiger auf einen freien Puffer, während wir den vorhandenen Puffer speichern.
CBufferFloat *temp = cSelfAttention.getGradient(); if(!cSelfAttention.SetGradient(cTransposeSA.getPrevOutput(), false) || !cSelfAttention.calcHiddenGradients(cTransposeSA.AsObject()) || !SumAndNormilize(temp, cSelfAttention.getGradient(), temp, iWindow, false, 0, 0, 0, 1) || !cSelfAttention.SetGradient(temp, false)) return false;
Dann propagieren wir den Fehlergradienten und summieren die Werte aus beiden Datenströmen. Danach versetzen wir die Pufferzeiger in ihren ursprünglichen Zustand zurück.
Schließlich propagieren wir den Gradienten auf die Ebene der Eingabedaten.
if(!NeuronOCL.calcHiddenGradients(cSelfAttention.AsObject())) return false; //--- return true; }
Am Ende der Methode geben wir einen logischen Erfolgswert zurück.
Der vollständige Code dieses Objekts und alle seine Methoden werden im Anhang zur weiteren Untersuchung bereitgestellt.
Lineare Aufmerksamkeit Objekt
Zusätzlich zu dem implementierten rekursiven Aufmerksamkeitsobjekt schlugen die Autoren des Frameworks auch vor, lineare Aufmerksamkeit im Turm zu verwenden, der für die Frequenzspektrumanalyse zuständig ist.
Lineare Aufmerksamkeit ist einer der Ansätze zur Optimierung des traditionellen Aufmerksamkeitsmechanismus in Transformer. Im Gegensatz zur klassischen Selbstaufmerksamkeit, die auf vollständig verknüpften Matrixoperationen mit quadratischer Komplexität beruht, reduziert die lineare Aufmerksamkeit die Rechenkomplexität, was sie für die Verarbeitung langer Sequenzen effizient macht.
Die lineare Aufmerksamkeit führt Faktorisierungen φ(Q) und φ(K) ein, die es ermöglichen, die Aufmerksamkeitsberechnung wie folgt darzustellen:
![]()
Vorteile der linearen Aufmerksamkeit
- Lineare Komplexität: Geringerer Rechenaufwand, der die Verarbeitung langer Sequenzen ermöglicht.
- Geringerer Speicherverbrauch: Es ist nicht erforderlich, die vollständige Score-Matrix der Abhängigkeitskoeffizienten zu speichern, was den Speicherbedarf verringert.
- Effizienz bei Online-Aufgaben: Lineare Aufmerksamkeit unterstützt die Streaming-Datenverarbeitung, da Aktualisierungen inkrementell erfolgen.
- Flexibilität bei der Kernelauswahl: Die verschiedene Funktionen von φ(x) ermöglichen die Anpassung des Aufmerksamkeitsmechanismus an bestimmte Aufgaben.
Die Implementierung des linearen Aufmerksamkeitsalgorithmus ist in dem Objekt CNeuronLinerAttention gekapselt, dessen Struktur im Folgenden dargestellt wird.
class CNeuronLinerAttention : public CNeuronBaseOCL { protected: uint iWindow; uint iWindowKey; uint iUnits; uint iVariables; //--- CNeuronConvOCL cQuery; CNeuronConvOCL cKey; CNeuronTransposeVRCOCL cKeyT; CNeuronBaseOCL cKeyValue; CNeuronBaseOCL cAttentionOut; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronLinerAttention(void) {}; ~CNeuronLinerAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronLinerAttention; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Hier sehen wir einen grundlegenden Satz überschriebener Methoden und mehrere interne Objekte, die eine Schlüsselrolle in dem von uns entwickelten Algorithmus spielen. Wir werden ihre Funktionalität bei der Implementierung der neuen Klassenmethoden genauer untersuchen.
Alle deklarierten Methoden sind statisch, sodass wir den Konstruktor und den Destruktor leer lassen können. Alle geerbten und deklarierten Objekte werden in der Methode Init initialisiert. Die Parameter dieser Methode umfassen mehrere Parameter, die die Architektur des erstellten Objekts definieren.
bool CNeuronLinerAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch)) return false;
Im Methodenrumpf wird sofort die gleichnamige Methode der Elternklasse aufgerufen. In diesem Fall handelt es sich um eine vollständig verbundene Schicht.
Als Nächstes speichern wir die wichtigsten Architekturparameter in internen Variablen und fahren mit der Initialisierung interner Objekte fort.
iWindow = window; iWindowKey = fmax(window_key, 1); iUnits = units_count; iVariables = variables;
Wir beginnen mit der Initialisierung der Faltungsschichten, die für die Erzeugung der Abfrage- (Query) und Schlüssel- (Key) Entitäten verantwortlich sind. Bei der Bildung von Abfragen verwenden wir eine sigmoidale Aktivierungsfunktion, die den Grad des Einflusses eines jeden Elements auf das Objekt angibt.
int index = 0; if(!cQuery.Init(0, index, OpenCL, iWindow, iWindow, iWindowKey, iUnits, iVariables, optimization, iBatch)) return false; cQuery.SetActivationFunction(SIGMOID); index++; if(!cKey.Init(0, index, OpenCL, iWindow, iWindow, iWindowKey, iUnits, iVariables, optimization, iBatch)) return false; cKey.SetActivationFunction(TANH);
Für die Schlüsselentitäten verwenden wir den hyperbolischen Tangens als Aktivierungsfunktion, mit der wir sowohl den positiven als auch den negativen Einfluss der einzelnen Elemente bestimmen können.
Anschließend initialisieren wir das Matrix-Transpositionsobjekt für Key:
index++; if(!cKeyT.Init(0, index, OpenCL, iVariables, iUnits, iWindowKey, optimization, iBatch)) return false; cKeyT.SetActivationFunction(TANH);
Und das Objekt, das für die Speicherung des Produkts der Matrizen Schlüssel (Key) und Wert (value) zuständig ist.
index++; if(!cKeyValue.Init(0, index, OpenCL, iWindow * iWindowKey, optimization, iBatch)) return false; cKeyValue.SetActivationFunction(None);
Beachten Sie, dass wir keine Ebene verwenden, um die Entität Wert zu erzeugen. Stattdessen planen wir, die rohen Eingangsdaten direkt zu verwenden.
Die Aufmerksamkeitsergebnisse werden in einem speziell erstellten internen Objekt gespeichert.
index++; if(!cAttentionOut.Init(0, index, OpenCL, Neurons(), optimization, iBatch)) return false; cAttentionOut.SetActivationFunction(None);
Wir werden die Schnittstellen der übergeordneten Klasse verwenden, um Restverbindungen zu erstellen. Um unnötiges Kopieren von Daten zu vermeiden, ersetzen wir den Zeiger auf den Gradientenpuffer.
if(!SetGradient(cAttentionOut.getGradient(), true)) return false; //--- return true; }
Bevor die Methode abgeschlossen wird, wird ein boolescher Wert an das aufrufende Programm zurückgegeben, der den Erfolg der Operationen anzeigt.
Sobald die Initialisierung abgeschlossen ist, wird der Algorithmus für den Vorwärtsdurchlauf in der Methode feedForward implementiert.
bool CNeuronLinerAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cQuery.FeedForward(NeuronOCL)) return false; if(!cKey.FeedForward(NeuronOCL) || !cKeyT.FeedForward(cKey.AsObject())) return false;
Die Methode erhält einen Zeiger auf die multidimensionale Sequenz von Eingabedaten, die unmittelbar zur Bildung der Entitäten Abfrage und Schlüssel verwendet wird.
Als Nächstes bestimmen wir den Einfluss jedes Objekts auf die analysierte Sequenz, indem wir die transponierte Schlüsselmatrix mit den Eingabedaten multiplizieren.
if(!MatMul(cKeyT.getOutput(), NeuronOCL.getOutput(), cKeyValue.getOutput(), iWindowKey, iUnits, iWindow, iVariables)) return false;
Um die Ergebnisse der linearen Aufmerksamkeit zu erhalten, multiplizieren wir den Abfragetensor mit dem Ergebnis der vorherigen Operation.
if(!MatMul(cQuery.getOutput(), cKeyValue.getOutput(), cAttentionOut.getOutput(), iUnits, iWindowKey, iWindow, iVariables)) return false;
Anschließend addieren wir die verbleibenden Verbindungen und normalisieren die Betriebsergebnisse.
if(!SumAndNormilize(NeuronOCL.getOutput(), cAttentionOut.getOutput(), Output, iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
Dann geben wir das logische Ergebnis der Operation an den Aufrufer zurück und beenden die Ausführung der Methode.
Als Nächstes müssen wir die Fehlergradienten auf alle internen Objekte und die Eingabedaten verteilen, und zwar entsprechend ihrem Beitrag zur Modellausgabe. Wie üblich werden diese Operationen in der Methode calcInputGradients durchgeführt, die einen Zeiger auf das Eingabedatenobjekt erhält. Diesmal wird es für das Schreiben von Ergebnissen verwendet.
bool CNeuronLinerAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Im Hauptteil der Methode wird sofort die Relevanz des empfangenen Zeigers geprüft. Wir haben bereits erwähnt, wie wichtig dieser Kontrollpunkt ist.
Aufgrund der Pufferzeigersubstitution geht der von der nächsten neuronalen Schicht empfangene Fehlergradient automatisch in das interne Ergebnisobjekt der linearen Aufmerksamkeit ein. Dann wird sie auf die Informationsströme verteilt.
if(!MatMulGrad(cQuery.getOutput(), cQuery.getGradient(), cKeyValue.getOutput(), cKeyValue.getGradient(), cAttentionOut.getGradient(), iUnits, iWindowKey, iWindow, iVariables)) return false; if(!MatMulGrad(cKeyT.getOutput(), cKeyT.getGradient(), NeuronOCL.getOutput(), cAttentionOut.getPrevOutput(), cKeyValue.getGradient(), iWindowKey, iUnits, iWindow, iVariables)) return false;
Es ist wichtig zu beachten, dass der Gradient, der auf die Eingabedaten übertragen werden soll, aus 4 Informationsflüssen besteht:
- Abfrage-Entität
- Schlüssel-Entität
- Schlüssel*Wert-Product
- Residuenverbindungen
In der vorherigen Operation haben wir den Gradienten aus dem Produkt von Schlüssel*Wert in einem freien Puffer gespeichert. Der Restgradient wird vollständig von der Ausgabe des aktuellen Objekts übertragen. Diese Gradienten werden noch nicht durch die Ableitung der Aktivierungsfunktion des Eingabeobjekts angepasst. Bei der Weitergabe des Gradienten durch die Faltungsschichten Abfrage/Schlüssel erfolgt jedoch eine Anpassung durch die entsprechenden Aktivierungsableitungen. Um die Konsistenz über alle Ströme hinweg zu gewährleisten, summieren wir die Gradienten und wenden die Ableitung der Aktivierungsfunktion des Eingabeobjekts an. Die Ergebnisse werden in einem freien Puffer gespeichert.
if(!SumAndNormilize(Gradient, cAttentionOut.getPrevOutput(), cAttentionOut.getPrevOutput(), iWindow, false, 0, 0, 0, 1)) return false; //--- if(NeuronOCL.Activation() != None) if(!DeActivation(NeuronOCL.getOutput(), cAttentionOut.getPrevOutput(), cAttentionOut.getPrevOutput(), NeuronOCL.Activation())) return false;
Wir passen auch die Gradienten anderer Ströme durch ihre jeweiligen Aktivierungsableitungen an.
if(cKeyT.Activation() != None) if(!DeActivation(cKeyT.getOutput(), cKeyT.getGradient(), cKeyT.getGradient(), cKeyT.Activation())) return false; if(cQuery.Activation() != None) if(!DeActivation(cQuery.getOutput(), cQuery.getGradient(), cQuery.getGradient(), cQuery.Activation())) return false;
Als Nächstes propagieren wir den Gradienten durch den Schlüsselinformationsfluss und akkumulieren die Ergebnisse.
if(!cKey.calcHiddenGradients(cKeyT.AsObject()) || !NeuronOCL.calcHiddenGradients(cKey.AsObject()) || !SumAndNormilize(NeuronOCL.getGradient(), cAttentionOut.getPrevOutput(), cAttentionOut.getPrevOutput(), iWindow, false, 0, 0, 0, 1)) return false;
Das Gleiche gilt für den Abfragefluss, woraufhin der kombinierte Gradient an das Eingabeobjekt übergeben wird.
if(!NeuronOCL.calcHiddenGradients(cQuery.AsObject()) || !SumAndNormilize(NeuronOCL.getGradient(), cAttentionOut.getPrevOutput(), NeuronOCL.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; //--- return true; }
Am Ende der Methode geben wir den booleschen Erfolgswert zurück.
Damit ist unsere Untersuchung der linearen Aufmerksamkeitsobjektmethoden abgeschlossen. Sie können den vollständigen Code der Klasse und alle ihre Methoden im Anhang einsehen.
Wir haben hart gearbeitet und das Ende dieses Artikels erreicht. Aber unsere Arbeit ist noch nicht beendet. Machen wir eine kurze Pause und machen wir im nächsten Artikel weiter, wo wir das Ganze zu einem logischen Abschluss bringen werden.
Schlussfolgerung
Wir haben den Hidformer untersucht, das bei Zeitreihenprognosen, einschließlich Finanzdaten, eine starke Leistung zeigt. Seine Besonderheit ist die Verwendung eines Dual-Tower-Codierers mit getrennter Analyse der Rohdaten als zeitliche Sequenz und ihrer Frequenzmerkmale. Dies verleiht Hidformer ein hohes Maß an Flexibilität und Anpassungsfähigkeit an wechselnde Marktbedingungen.
Im praktischen Teil des Artikels haben wir mehrere Komponenten implementiert, die von den Autoren von Hidformer vorgeschlagen wurden. Unsere Arbeit ist jedoch noch nicht abgeschlossen, und wir werden sie in naher Zukunft fortsetzen.
Referenzen
- Hidformer: Transformer-Style Neural Network in Stock Price Forecasting
- Hidformer: Hierarchical dual-tower transformer using multi-scale mergence for long-term time series forecasting
- Andere Artikel dieser Serie
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für die Probenahme mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Expert Advisor mit dem Modelltraining |
| 4 | Test.mq5 | Expert Advisor | Modellprüfung Expert Advisor |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Beschreibung des Systemzustands und der Modellarchitektur |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17069
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Von der Grundstufe bis zur Mittelstufe: Struct (I)
Von der Grundstufe bis zur Mittelstufe: Struct (I)
 Entwicklung eines Expert Advisors für mehrere Währungen (Teil 21): Vorbereitungen für ein wichtiges Experiment und Optimierung des Codes
Entwicklung eines Expert Advisors für mehrere Währungen (Teil 21): Vorbereitungen für ein wichtiges Experiment und Optimierung des Codes
 Neuronale Netze im Handel: Hierarchical Dual-Tower Transforme (letzter Teil)
Neuronale Netze im Handel: Hierarchical Dual-Tower Transforme (letzter Teil)
 Neuronale Netze im Handel: Speichererweitertes kontextbezogenes Lernen für Kryptowährungsmärkte (letzter Teil)
Neuronale Netze im Handel: Speichererweitertes kontextbezogenes Lernen für Kryptowährungsmärkte (letzter Teil)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Der Artikel Neural Networks in Trading: Hierarchical Two-Bar Transformer (Hidformer) wurde veröffentlicht:
Autor: Dmitriy Gizlyk
Hallo Dmitriy,
Laut OnTesterDeinit() sollte der Code im Tester-Modus (d.h. im StrategyTester) die NN-Dateien speichern.
Dies geschieht aber nicht. Auch dieses OnTesterDeinit() wird nicht aufgerufen, wie es scheint. Da ich keine der Druckanweisungen sehe.
Ist dies auf ein Update von MQL5 zurückzuführen? Oder warum speichert Ihr Code keine Dateien mehr?
Liegt das an einem Update von MQL5? Oder warum speichert Ihr Code keine Dateien mehr?
Lieber Andreas,
OnTesterDeinit läuft nur im Optimierungsmodus. Bitte beachten Sie die Dokumentation unter https://www.mql5.com/en/docs/event_handlers/ontesterdeinit.
Wir speichern keine Modelle im Tester, weil dieser EA sie nicht untersucht. Es ist notwendig, die Wirksamkeit des zuvor untersuchten Modells zu überprüfen.
Mit freundlichen Grüßen,
Dmitriy.