Redes neuronales en el trading: Detección de anomalías en el dominio de la frecuencia (Final)

MetaTrader 5 — Sistemas comerciales | 20 enero 2026, 12:18

Introducción

En el artículo anterior, presentamos el innovador framework CATCH para la detección de anomalías en series temporales multivariantes. El método de análisis de datos en el dominio de la frecuencia propuesto por los autores del framework permite no solo detectar anomalías puntuales en forma de valores atípicos y cambios bruscos, sino también detectar patrones más complejos y ocultos que escapan a los enfoques tradicionales. El framework CATCH usa la transformada de Fourier para pasar de la representación temporal de los datos a su forma espectral, lo que abre nuevas posibilidades al estudio detallado de las características de la secuencia analizada.

Una de las ventajas más importantes del CATCH es el uso de parches de frecuencia. En lugar de analizar todo el espectro, el modelo lo descompone en fragmentos individuales que se corresponden con una determinada gama de frecuencias. Este método permite analizar tanto las tendencias globales como los rasgos locales característicos de los componentes de alta frecuencia. Gracias a este enfoque, podemos distinguir y clasificar las distintas anomalías con gran precisión, ya sean pulsiones cortas o desviaciones más complejas a nivel de secuencias. Esta partición del espectro permite estudiar con más detalle la estructura de las series temporales.

Una parte importante del framework es el módulo adaptativo encargado de analizar las relaciones entre los distintos canales de datos. Este componente, que aplica el principio de atención enmascarada, ayuda al sistema a centrarse en las correlaciones más significativas, excluyendo la influencia de los factores de ruido y los datos irrelevantes. Dicho mecanismo mejora la calidad de la reconstrucción del comportamiento normal y aumenta considerablemente la solidez del modelo en un entorno de mercado volátil. A diferencia de los métodos tradicionales, que analizan los canales de forma aislada, CATCH permite considerar sus complejas interrelaciones. Esto resulta especialmente importante cuando tratamos con datos financieros, ya que los movimientos en un mercado pueden repercutir en otros segmentos.

La etapa final del funcionamiento de CATCH es la reconstrucción de la serie temporal original. Tras un análisis detallado en el dominio de la frecuencia y la identificación de posibles anomalías, el sistema realiza una transformación inversa, devolviendo los datos a una representación temporal familiar. La diferencia entre los valores iniciales y las series reconstruidas sirve como indicador fiable de las desviaciones, lo cual permite responder a tiempo a los cambios en la dinámica del mercado.

A continuación le mostramos la visualización del framework CATCH por parte del autor.

Visualización del framework CATCH por parte del autor

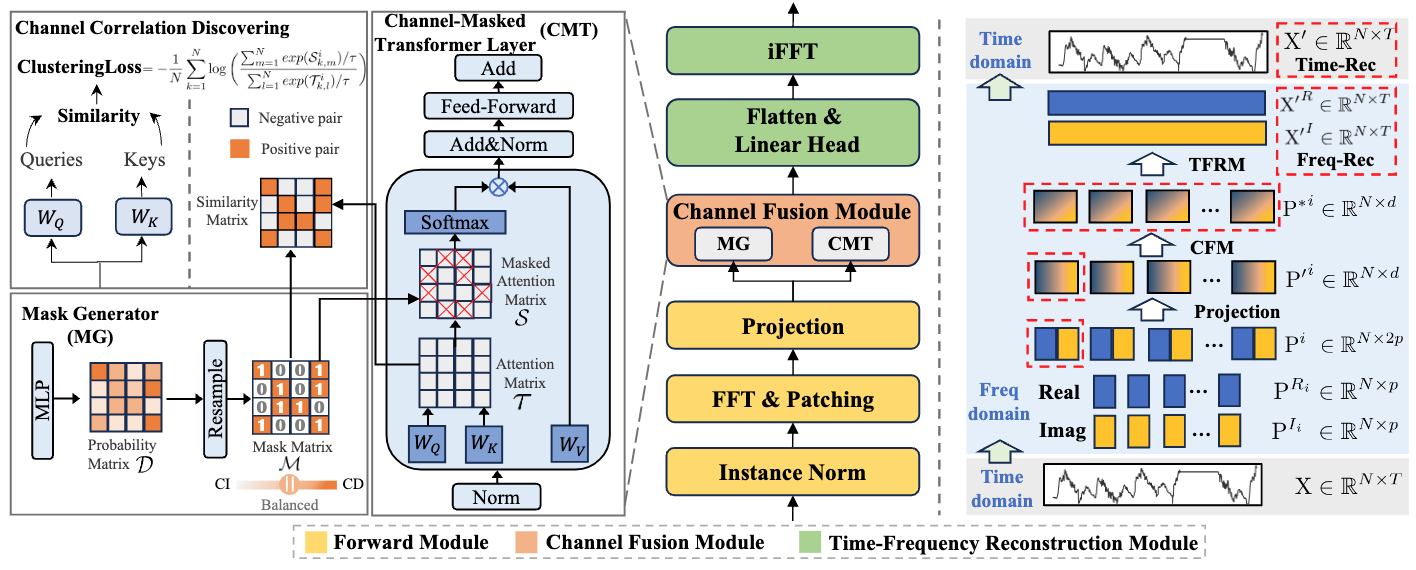
En la parte práctica del artículo anterior, comenzamos a implementar nuestra propia visión de los enfoques propuestos usando herramientas MQL5; concretamente, implementamos la capa convolucional de trabajo con valores complejos. Y también consideramos la implementación de las pasadas directa e inversa del módulo de atención enmascarada a magnitudes complejas en el lado del contexto OpenCL. Hoy continuaremos la labor iniciada.

Objeto de atención enmascarada a significados complejos

En el artículo anterior, analizamos los kernels MaskAttentionComplex y MaskAttentionGradientsComplex, que implementan los algoritmos de pasada directa e inversa del mecanismo de atención enmascarada en el dominio de magnitudes complejas. Vamos a continuar por donde lo dejamos. Y hoy organizaremos el módulo de atención enmascarada en el lado del programa principal. Para ello, crearemos un nuevo objeto CNeuronComplexMVMHMHMaskAttention, cuya estructura se muestra a continuación.

class CNeuronComplexMVMHMaskAttention :  public CNeuronBaseOCL
  {
protected:
   uint                       iWindow;
   uint                       iWindowKey;
   uint                       iHeads;
   uint                       iUnits;
   uint                       iVariables;
   //---
   CNeuronComplexConvOCL      cQKV;
   CNeuronBaseOCL             cQ;
   CNeuronBaseOCL             cKV;
   CNeuronConvOCL             cMask;
   CNeuronBaseOCL             cMHAttentionOut;
   CNeuronComplexConvOCL      cPooling;
   CNeuronBaseOCL             cResidual;
   CNeuronComplexConvOCL      cFeedForward[2];
   //---
   virtual bool               AttentionOut(void);
   virtual bool               AttentionInsideGradients(void);
   virtual bool               SumAndNormilize(CBufferFloat *tensor1, CBufferFloat *tensor2, CBufferFloat *out,
                                              int dimension, bool normilize = true, int shift_in1 = 0,
                                              int shift_in2 = 0, int shift_out = 0, float multiplyer = 0.5f) override;
   //---
   virtual bool               feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool               updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool               calcInputGradients(CNeuronBaseOCL *prevLayer) override;

public:
                     CNeuronComplexMVMHMaskAttention(void) {};
                    ~CNeuronComplexMVMHMaskAttention(void) {};
   //---
   virtual bool               Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint window, uint window_key, uint heads, 
                                   uint units_count, uint variables, 
                                   ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int                Type(void)   const   {  return defNeuronComplexMVMHMaskAttention;   }
   //---
   virtual bool               Save(int const file_handle) override;
   virtual bool               Load(int const file_handle) override;
   //---
   virtual bool               WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void               SetOpenCL(COpenCLMy *obj) override;
  };

Como podemos ver, la estructura presentada del nuevo objeto es bastante estándar para los módulos de atención, diversas variantes de los cuales ya hemos creado en nuestra biblioteca más de una vez. No obstante, hay una peculiaridad asociada al uso de magnitudes complejas. Se supone que la entrada de este objeto se suministra con los datos de origen ya en forma de valores complejos, por lo que omitiremos la etapa de transformación de datos. Y para la formación de las entidades Query, Key y Value utilizaremos la capa convolucional anteriormente creada para el trabajo con magnitudes complejas. Pero lo primero es lo primero.

Todos los objetos internos se declararán estáticamente, lo cual nos permitirá dejar vacíos el constructor y el destructor de la clase, mientras que la inicialización de los objetos declarados y heredados se realizará en el método Init. En los parámetros de este método obtendremos una serie de constantes que nos permitirán definir de forma única la arquitectura del objeto creado. Su estructura es bastante común para este tipo de objetos.

bool CNeuronComplexMVMHMaskAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                           uint window, uint window_key, uint heads,
                                           uint units_count, uint variables,
                                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
//---
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * window * units_count * variables,
                                                                      optimization_type, batch))
      return false;

En el cuerpo del método llamaremos directamente al método homónimo de la clase padre, que ya implementará el algoritmo de inicialización de objetos e interfaces heredados. A continuación, guardaremos en variables internas las constantes de la arquitectura del modelo obtenidas del programa externo.

   iWindow = window;
   iWindowKey = MathMax(window_key, 1);
   iUnits = units_count;
   iHeads = MathMax(heads, 1);
   iVariables = variables;

Luego trabajaremos con los objetos recién declarados. Y primero inicializaremos el objeto de generación de la matriz de enmascaramiento.

Aquí cabe señalar que los autores del framework proponen un módulo de generación de máscaras basado en una proyección entrenada de los datos de origen. En este caso, se utilizará la atención de varias cabezas con una máscara única para cada una.

Otro punto importante es que no se prestará atención a la secuencia completo del espectro de frecuencias. Los autores del framework CATCH proponen usar la atención solo dentro de parches separados que pertenezcan al mismo fragmento de frecuencia pero a secuencias unitarias diferentes.

Y, obviamente, a la salida del objeto de generación de máscaras deberíamos obtener una representación probabilística de la influencia de los canales individuales en forma de valores reales.

Para cumplir las restricciones anteriores, en nuestra implementación utilizaremos una capa convolucional regular con el doble del tamaño de la ventana (para abarcar la ventana de magnitudes complejas) y un número de filtros igual al vector de enmascaramiento para un elemento de la secuencia.

   uint index = 0;
   if(!cMask.Init(0, index, OpenCL, 2 * iWindow, 2 * iWindow, iVariables * iHeads,
                                         iUnits, iVariables, optimization, iBatch))
      return false;
   cMask.SetActivationFunction(SIGMOID);
   CBufferFloat *temp = cMask.GetWeightsConv();
   if(!temp ||
      !temp.Fill(0))
      return false;

Para mantener los resultados del objeto dentro del rango de valores requerido, utilizaremos una función de activación sigmoidal.

Tenga en cuenta que al inicializar el objeto, rellenaremos la matriz de parámetros entrenados con valores cero. Esto nos permitirá asignar inicialmente a todos los elementos una máscara de influencia igual al nivel "0,5". Durante el entrenamiento, los pesos se ajustarán cambiando la máscara de dependencia entre canales.

A continuación, inicializaremos el objeto de generación de entidades Query, Key y Value. Aquí ya utilizaremos una capa convolucional compleja, pues esperamos obtener valores complejos en la entrada y la salida del objeto.

   index++;
   if(!cQKV.Init(0, index, OpenCL, iWindow, iWindow, 3 * iWindowKey * iHeads,
                                    iUnits, iVariables, optimization, iBatch))
      return false;
   cQKV.SetActivationFunction(None);

Dividiremos el tensor total de las tres entidades en 2 componentes y separaremos la entidad Query en una matriz aparte. Para ello, inicializaremos 2 objetos adicionales.

   index++;
   if(!cQ.Init(0, index, OpenCL, 2 * iWindowKey * iHeads * iVariables * iUnits, optimization, iBatch))
      return false;
   cQ.SetActivationFunction(None);
   index++;
   if(!cKV.Init(0, index, OpenCL, 2 * cQ.Neurons(), optimization, iBatch))
      return false;
   cKV.SetActivationFunction(None);

Aquí es donde inicializaremos el objeto para almacenar los resultados de la atención multicabeza.

   index++;
   if(!cMHAttentionOut.Init(0, index, OpenCL, cQ.Neurons(), optimization, iBatch))
      return false;
   cMHAttentionOut.SetActivationFunction(None);

Y añadiremos una capa convolucional compleja para reducir la dimensionalidad de los resultados de la atención.

   index++;
   if(!cPooling.Init(0, index, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, 
                              iWindow, iUnits, iVariables, optimization, iBatch))
      return false;
   cPooling.SetActivationFunction(None);

De forma similar a la arquitectura del Transformer clásica, añadiremos una capa de preservación de enlaces residuales.

   index++;
   if(!cResidual.Init(0, index, OpenCL, cPooling.Neurons(), optimization, iBatch))
      return false;
   cResidual.SetActivationFunction(None);

Y detrás vendrán 2 capas convolucionales complejas del módulo FeedForward.

   index++;
   if(!cFeedForward[0].Init(0, index, OpenCL, iWindow, iWindow, 4 * iWindow,
                                  iUnits, iVariables, optimization, iBatch))
      return false;
   cFeedForward[0].SetActivationFunction(LReLU);
   index++;
   if(!cFeedForward[1].Init(0, index, OpenCL, 4 * iWindow, 4 * iWindow, iWindow,
                                       iUnits, iVariables, optimization, iBatch))
      return false;
   cFeedForward[1].SetActivationFunction(None);
   SetActivationFunction(None);
//---
   return true;
  }

Después, finalizaremos el método de inicialización del objeto, retornando previamente el resultado lógico de las operaciones al programa que realiza la llamada.

El siguiente etapa consistirá en construir el algoritmo de pasada directa dentro del método feedForward.

bool CNeuronComplexMVMHMaskAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En los parámetros de este método obtendremos el puntero al objeto de datos de origen, cuya relevancia comprobaremos inmediatamente.

Para mejorar la estabilidad del proceso de aprendizaje, normalizaremos los datos obtenidos.

   if(!NeuronOCL.SwapOutputs())
      return false;
   if(!SumAndNormilize(NeuronOCL.getPrevOutput(), NeuronOCL.getPrevOutput(), NeuronOCL.getOutput(),
                       iWindow, true, 0, 0, 0, 1))
      return false;

Aquí cabe señalar que los datos de origen resultantes se representarán mediante magnitudes complejas. Por consiguiente, hemos redefinido el método de suma y normalización de datos para poder manejarlo. Su código completo se encuentra en el archivo adjunto.

Tras la normalización, los datos de origen se utilizarán para generar los tensores de enmascaramiento y las entidades Query, Key, Value.

   if(!cMask.FeedForward(NeuronOCL))
      return false;
   if(!cQKV.FeedForward(NeuronOCL))
      return false;

Luego dividiremos el tensor total de entidades generadas en 2 separados.

   if(!NeuronOCL.SwapOutputs())
      return false;
   if(!DeConcat(cQ.getOutput(), cKV.getOutput(), cQKV.getOutput(), 2 * iWindowKey * iHeads,
                                              4 * iWindowKey * iHeads, iUnits * iVariables))
      return false;

Después transferiremos todos los datos preparados al kernel de pasada directa de la atención enmascarada. Esta operación se realizará en un método AttentionOut separado.

   if(!AttentionOut())
      return false;

A continuación, redimensionaremos los resultados de la atención multicabeza y sumaremos los valores resultantes con los datos de origen, creando enlaces residuales.

   if(!cPooling.FeedForward(cMHAttentionOut.AsObject()))
      return false;
   if(!SumAndNormilize(NeuronOCL.getOutput(), cPooling.getOutput(), cResidual.getOutput(), iWindow, true, 0, 0, 0, 1))
      return false;

Luego pasaremos los datos por 2 capas convolucionales del módulo FeedForward.

   if(!cFeedForward[0].FeedForward(cResidual.AsObject()))
      return false;
   if(!cFeedForward[1].FeedForward(cFeedForward[0].AsObject()))
      return false;

Y de nuevo añadiremos los enlaces residuales. Y almacenaremos el resultado de la operación en el búfer heredado de la interfaz de intercambio de datos con otras capas neuronales del modelo.

   if(!SumAndNormilize(cResidual.getOutput(), cFeedForward[1].getOutput(), getOutput(), iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Después, finalizaremos el método retornando el resultado lógico de las operaciones al programa que realiza la llamada.

Asimismo, debemos decir unas palabras sobre el método AttentionOut, en el que se pone en la cola de ejecución el kernel de atención enmascarada multicabeza MaskAttentionComplex. Últimamente, rara vez analizamos algoritmos de métodos de colocación de kernels de programas OpenCL en la cola de ejecución. Esto es comprensible. El algoritmo para poner un kernel en la cola de ejecución es bastante estándar. Así que no vemos necesidad de describir siempre las mismas operaciones. Pero en este caso hay un matiz relacionado con el funcionamiento del framework CATCH.

Como ya hemos mencionado, los autores del framework CATCH proponen realizar operaciones de atención enmascarada estrictamente entre elementos de la misma gama de frecuencias de diferentes secuencias unitarias. Simplemente, tomaremos parches idénticos de diferentes secuencias unitarias y analizaremos sus dependencias. Esto permitirá la detección independiente de dependencias de diferentes secuencias unitarias a diferentes frecuencias: las tendencias a largo plazo y a corto plazo estarán por separado. Sin embargo, no hemos considerado esta característica al crear el kernel unificado de atención enmascarada.

No obstante, tenemos la capacidad de organizar el proceso necesario gestionando el espacio de tareas de la puesta del kernel en la cola de ejecución. En primer lugar, examinaremos la dimensionalidad de los datos de origen recibidos como entrada al objeto. Luego obtendremos los datos segmentados de las secuencias multidimensionales, que pueden representarse como un tensor tridimensional {Variable, Segment, Dimension}. Además, al generar las entidades para la atención multicabeza, los resultados de la generación de cada una pueden representarse ya como un tensor de cuatro dimensiones {Variable, Segment, Head, Dimension}.

Aquí vale la pena señalar que el algoritmo de atención multicabeza que construimos realiza análisis independientes de cada una de las cabezas de atención. En consecuencia, si combinamos las dimensionalidades de los segmentos y las cabezas de atención representando cada segmento como una cabeza de atención independiente, obtendremos un análisis de las dependencias entre segmentos idénticos de secuencias unitarias diferentes, que es lo que se necesita para organizar el framework CATCH.

El método AttentionOut no contiene ningún parámetro. Y en el bloque de control de este método comprobaremos solo la relevancia del puntero al objeto de trabajo con el contexto OpenCL.

bool CNeuronComplexMVMHMaskAttention::AttentionOut(void)
  {
   if(!OpenCL)
      return false;

A continuación, declararemos los arrays para especificar el espacio de tareas y poner el kernel en la cola para su ejecución. Como ya hemos comentado, nos referiremos al número de secuencias unitarias en los datos analizados como la dimensionalidad de la secuencia. Y para el número de cabezas, especificaremos el producto del número dado de cabezas de atención por el número de segmentos de cada secuencia.

   uint global_work_offset[3] = {0};
   uint global_work_size[3] = {iVariables/*Q units*/, iVariables/*K units*/, iHeads * iUnits/*Heads*/};
   uint local_work_size[3] = {1, iVariables, 1};

Aquí fusionaremos los flujos de operaciones en grupos de trabajo a lo largo de la segunda dimensión del espacio de tareas.

A continuación, en los parámetros del kernel, pasaremos los punteros a los búferes de datos necesarios.

   ResetLastError();
   int kernel = def_k_MaskAttentionComplex;
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_q, cQ.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_kv, cKV.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_scores, cMask.getPrevOutIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_out, cMHAttentionOut.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_masks, cMask.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Aquí aprovecharemos la igualdad del tamaño de la matriz de coeficientes de atención y enmascaramiento del canal. Esta circunstancia garantizaba que no se creara un búfer adicional para almacenar temporalmente los coeficientes de atención. Su función la desempeñará el búfer libre del objeto de generación de la matriz de enmascaramiento.

Luego pasaremos los parámetros necesarios al kernel.

   if(!OpenCL.SetArgument(kernel, def_k_maskattcom_dimension, (int)iWindowKey))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(kernel, def_k_maskattcom_heads_kv, (int)(iHeads * iUnits)))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

En este caso, igualmente, especificaremos el producto del número de cabezas de atención indicado por el usuario por la longitud de la secuencia como el número de cabezas de atención para las entidades Key y Value.

Por último, pondremos el kernel en la cola de ejecución.

   if(!OpenCL.Execute(kernel, 3, global_work_offset, global_work_size, local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Y finalizaremos el método, retornando previamente el resultado lógico de las operaciones al programa que realiza la llamada.

Una vez completados los algoritmos de pasada directa, podemos construir los procesos de pasada inversa. Y primero, crearemos un método para distribuir los gradientes de error entre todos los objetos internos según su influencia en el resultado final del modelo calcInputGradients.

bool CNeuronComplexMVMHMaskAttention::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

En los parámetros del método, recibiremos en el mismo objeto de datos de origen que utilizamos en la pasada directa. Solo que esta vez tendremos que pasarle el gradiente de error según la influencia de los datos de origen. Y comprobaremos directamente la pertinencia del puntero recibido.

En esta fase, el búfer de interfaces externas de nuestro objeto contendrá el gradiente de error de la capa posterior. Sus valores se obtendrán sin corregir la derivada de la función de activación utilizada. Al fin y al cabo, hemos especificado deliberadamente su ausencia al inicializar el objeto. Esto se hace para crear libertades adicionales en la selección de las funciones de activación de los objetos internos. Y ahora corregiremos el gradiente de error obtenido mediante la derivada de la función de activación de la última capa convolucional del módulo FeedForward con los valores obtenidos que se le han transmitido.

   if(!DeActivation(cFeedForward[1].getOutput(), cFeedForward[1].getGradient(), Gradient, cFeedForward[1].Activation()))
      return false;

Y luego haremos descender el gradiente de error a través de las capas del módulo hasta el nivel del objeto de enlaces residuales después del módulo de atención.

   if(!cFeedForward[0].calcHiddenGradients(cFeedForward[1].AsObject()))
      return false;
   if(!cResidual.calcHiddenGradients(cFeedForward[0].AsObject()))
      return false;

Para el objeto de enlaces residuales, también especificaremos la ausencia de una función de activación. Y ahora repetiremos el procedimiento de ajuste de la derivada de la función de activación de la capa de escalado de los resultados de la atención multicabeza.

   if(!DeActivation(cPooling.getOutput(), cPooling.getGradient(), cResidual.getGradient(), cPooling.Activation()) ||
      !DeActivation(cPooling.getOutput(), cPooling.getPrevOutput(), Gradient, cPooling.Activation()) ||
      !SumAndNormilize(cPooling.getGradient(), cPooling.getPrevOutput(), cPooling.getGradient(), iWindow,
                                                                                       false, 0, 0, 0, 1))
      return false;

Sin embargo, aquí debemos decir que el objeto de enlaces residuales solo contiene el gradiente de error a lo largo de la línea troncal del módulo FeedForward. Nosotros, en cambio, necesitaremos añadir los datos y las líneas troncales de enlaces residuales. Por consiguiente, volveremos a corregir el gradiente de error del búfer de interfaces externas, pero mediante la derivada de la función de activación de la capa convolucional de los resultados de escalado de la atención multicabeza.

Me gustaría señalar que la reutilización de los datos del búfer de interfaces externas no significa que estén doblemente distorsionados. En el primer caso, guardaremos los resultados del ajuste en el búfer de la última capa del módulo FeedForward, mientras que los datos en el búfer de la interfaz permanecen en su forma original. Y ahora los resultados de las operaciones se escribirán en el búfer de la capa de proyección sin cambiar los datos de origen, que volveremos a utilizar cuando transfiramos los valores a través de la línea troncal de enlaces residuales a la capa de datos de origen.

Tras ajustar los valores, sumaremos la información de los dos flujos de información. Y luego distribuiremos el gradiente de error sobre las cabezas de atención.

   if(!cMHAttentionOut.calcHiddenGradients(cPooling.AsObject()))
      return false;
   if(!AttentionInsideGradients())
      return false;

Y llamaremos al método AttentionInsideGradients para distribuir el gradiente de error a través del proceso de atención. No nos detendremos en el algoritmo detallado del método anterior: lo dejaremos para su estudio individual. Su código completo figura en el archivo adjunto. Pero tenga en cuenta que el espacio de tareas y los parámetros para poner el kernel en la cola de ejecución deberán ser coherentes con la metodología propuesta para la pasada directa.

En el siguiente paso, combinaremos los gradientes de error de todas las entidades en un único tensor.

   if(!Concat(cQ.getGradient(), cKV.getGradient(), cQKV.getGradient(), 2 * iWindowKey * iHeads,
                                                  4 * iWindowKey * iHeads, iUnits * iVariables))
      return false;

Después, haremos descender el error al nivel de los datos de origen, corrigiendo previamente la derivada de la función de activación correspondiente.

   if(!DeActivation(cQKV.getOutput(), cQKV.getPrevOutput(), cQKV.getGradient(), cQKV.Activation()) ||
      !prevLayer.calcHiddenGradients(cQKV.AsObject()))
      return false;

Sin embargo, esto será solo un flujo de información. Así, añadiremos a los valores obtenidos los datos del flujo de información de enlaces residuales, corrigiéndolos previamente mediante la derivada de la función de activación del objeto de datos de origen.

En este caso, utilizaremos los datos tanto del módulo FeedForward como del búfer de interfaces externas.

   if(!DeActivation(prevLayer.getOutput(),cResidual.getPrevOutput(),cResidual.getGradient(),prevLayer.Activation()) ||
      !SumAndNormilize(prevLayer.getGradient(), cResidual.getPrevOutput(), cResidual.getPrevOutput(),
                       iWindow, false, 0, 0, 0, 1))
      return false;
   if(!DeActivation(prevLayer.getOutput(), cResidual.getGradient(), Gradient, prevLayer.Activation()) ||
      !SumAndNormilize(cResidual.getGradient(), cResidual.getPrevOutput(), cResidual.getPrevOutput(),
                       iWindow, false, 0, 0, 0, 1))
      return false;

Debemos recordar que los datos de origen también se utilizaban para generar la matriz de enmascaramiento. Por consiguiente, añadiremos a los datos recogidos anteriormente el gradiente de error en este flujo de información.

   if(!DeActivation(cMask.getOutput(), cMask.getGradient(), cMask.getGradient(), cMask.Activation()) ||
      !prevLayer.calcHiddenGradients(cMask.AsObject()) ||
      !SumAndNormilize(prevLayer.getGradient(), cResidual.getPrevOutput(), prevLayer.getGradient(),
                       iWindow, false, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Ahora que hemos recopilado el gradiente de error sobre todos los flujos de información al nivel de los datos de origen, podemos finalizar el método retornando el resultado lógico del método al programa que realiza la llamada.

Le propongo dejar el método de optimización de los parámetros del objeto para su estudio independiente. Su algoritmo es bastante simple, solo llamará a los métodos homónimos de los objetos internos. En el archivo adjunto figura el código completo del método. Allí también encontrará el código completo del objeto presentado y todos sus métodos. Ahora pasaremos a la siguiente fase de nuestro trabajo.

Creación del framework CATCH

Ya hemos hecho un trabajo preparatorio considerable construyendo los objetos individuales; ahora ha llegado el momento de ensamblarlos en un framework CATCH unificado. Sus algoritmos se construirán dentro del objeto CNeuronCATCH, cuya estructura le mostramos a continuación.

class CNeuronCATCH   :  public CNeuronTransposeOCL
  {
protected:
   CNeuronTransposeOCL        cTranspose;
   CNeuronBaseOCL             caFreqIn[2];
   CNeuronBaseOCL             cFreqConcat;
   CNeuronComplexConvOCL      caProjection[2];
   CNeuronComplexMVMHMaskAttention  caChannelFusion[2];
   CNeuronComplexConvOCL      caLinearHead[2];
   CNeuronBaseOCL             caFreqOut[2];
   //---
   virtual bool               FFT(CBufferFloat *inp_re, CBufferFloat *inp_im,
                                  CBufferFloat *out_re, CBufferFloat *out_im,
                                  uint variables, bool reverse = false);
   //---
   virtual bool               feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool               updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool               calcInputGradients(CNeuronBaseOCL *prevLayer) override;


public:
                     CNeuronCATCH(void) {};
                    ~CNeuronCATCH(void) {};
   //---
   virtual bool               Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint time_step, uint variables,
                                   uint window, uint step,
                                   uint window_key, uint heads,
                                   ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int                Type(void) override const   {  return defNeuronCATCH;   }
   //---
   virtual bool               Save(int const file_handle) override;
   virtual bool               Load(int const file_handle) override;
   //---
   virtual bool               WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void               SetOpenCL(COpenCLMy *obj) override;
  };

En la estructura presentada vemos un número bastante grande de objetos internos, cada uno de los cuales cumple una función diferente en el complejo algoritmo del framework. Pero hablaremos de su propósito durante la construcción de los métodos de la nueva clase. Ahora simplemente destacaremos que todos los objetos se declaran de forma estática, lo cual nos permite dejar vacíos el constructor y el destructor de la clase. La inicialización de todos los objetos se realizará en el método Init.

bool CNeuronCATCH::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                        uint time_step, uint variables,
                        uint window, uint step, uint window_key, uint heads,
                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, variables, time_step, optimization_type, batch))
      return false;

En los parámetros de este método obtendremos una serie de constantes que nos permitirán definir inequívocamente la arquitectura del objeto que se está inicializando. Algunos de ellos especifican la dimensionalidad de los datos de origen, mientras que otros definen la estructura de los flujos internos de información. Por ejemplo, time_step y variables especificarán el número de pasos temporales y secuencias unitarias en las series temporales multidimensionales de los datos de origen. Y window y step indicarán los parámetros de segmentación del espectro de frecuencias. Al mismo tiempo, window_key y heads, como no resulta difícil adivinar, son los principales parámetros del módulo de atención.

En el cuerpo del método, como es habitual, llamaremos inmediatamente al método homónimo de la clase padre. Esta vez, utilizaremos un objeto de transposición de datos como padre, y como habrá adivinado, esta elección no es aleatoria. Como entrada, esperamos que el objeto reciba una serie temporal multidimensional en forma de matriz, cada fila de la cual representará un vector que describirá el estado del entorno en un paso temporal. Sin embargo, el framework CATCH se basa en el análisis del espectro de frecuencias de secuencias unitarias individuales. Para mayor comodidad al trabajar con secuencias unitarias, tendremos que transponer el tensor resultante, y devolver los datos a la representación original en la salida. Planeamos realizar la última operación mediante el objeto padre, lo cual se refleja en los parámetros transmitidos.

Para transformar las series temporales en el dominio de la frecuencia, tenemos previsto usar el algoritmo de la transformada rápida de Fourier. Sin embargo, este algoritmo solo funcionará correctamente con secuencias cuya longitud sea un grado del número 2. No obstante, podemos aumentar la dimensionalidad de cualquier secuencia incrementándola con valores cero, lo que no afectará al resultado. Sin embargo, deberemos determinar el valor deseado más próximo.

//--- Calculate FFT size
   int power = int(MathLog(time_step) / M_LN2);
   if(power <= 0)
      return false;
   if(MathPow(2, power) != time_step)
      power++;
   uint FreqUinits = uint(MathPow(2, power));

Y, a continuación, determinar el número de segmentos según los parámetros de segmentación dados.

   if(window <= 0 || step <= 0)
      return false;
   int Segments = int((FreqUinits - int(window) + step - 1) / step);
   if(Segments <= 0)
      return false;

Con esto completaremos el trabajo preparatorio y pasaremos a inicializar los objetos internos. La primera capa será la de transposición de los datos de origen. Creo que sus parámetros de inicialización no plantean dudas.

   uint index = 0;
   if(!cTranspose.Init(0, index, OpenCL, time_step, variables, optimization, iBatch))
      return false;

A continuación, crearemos 2 búferes de datos para registrar las partes real e imaginaria del espectro de frecuencias tras la descomposición de Fourier.

   for(uint i = 0; i < caFreqIn.Size(); i++)
     {
      index++;
      if(!caFreqIn[i].Init(0, index, OpenCL, FreqUinits * variables, optimization, iBatch))
         return false;
      caFreqIn[i].SetActivationFunction(None);
     }

Y añadiremos un objeto de concatenación de datos de espectro de frecuencias.

   index++;
   if(!cFreqConcat.Init(0, index, OpenCL, 2 * FreqUinits * variables, optimization, iBatch))
      return false;
   cFreqConcat.SetActivationFunction(None);

Para segmentar el espectro de frecuencias, utilizaremos la capa convolucional de trabajo con magnitudes complejas, especificando los parámetros necesarios.

   index++;
   if(!caProjection[0].Init(0, index, OpenCL, window, step, 2 * window, Segments, variables, optimization, iBatch))
      return false;
   caProjection[0].SetActivationFunction(LReLU);

Y la segunda capa convolucional completará el trabajo de creación de las incorporaciones de nuestros parches.

   index++;
   if(!caProjection[1].Init(0, index, OpenCL,2*window,2*window,window_key, Segments, variables, optimization, iBatch))
      return false;
   caProjection[1].SetActivationFunction(TANH);

El análisis de las interdependencias entre los espectros de frecuencia de las secuencias unitarias individuales se realizará mediante dos módulos de atención sucesivos. En este caso, además, el primero trabajará directamente con las incorporaciones de parches creadas.

   index++;
   if(!caChannelFusion[0].Init(0, index, OpenCL,window_key,window_key,heads,Segments, variables, optimization, iBatch))
      return false;

Pero la arquitectura de la segunda capa de atención enmascarada entre canales variará con el número de segmentos. Si su número es múltiplo de 2, se realizará una combinación por pares de segmentos para encontrar las interdependencias de mayor rango.

   index++;
   if(Segments % 2 == 0)
     {
      if(!caChannelFusion[1].Init(0, index, OpenCL, 2 * window_key, window_key, heads, Segments / 2,
                                                                   variables, optimization, iBatch))
         return false;
     }
   else
      if(!caChannelFusion[1].Init(0, index, OpenCL, window_key, window_key, heads, Segments, variables,
                                                                                 optimization, iBatch))
         return false;

En caso contrario, repetiremos la arquitectura de la capa de atención anterior.

La dimensionalidad del tensor obtenido a partir de los resultados de los módulos de atención la reduciremos a la longitud del espectro de frecuencias de los datos de origen utilizando 2 capas convolucionales consecutivas de proyección.

   index++;
   if(!caLinearHead[0].Init(0, index, OpenCL, window_key, window_key, window, Segments, variables,
                                                                            optimization, iBatch))
      return false;
   caLinearHead[0].SetActivationFunction(LReLU);
   index++;
   if(!caLinearHead[1].Init(0, index, OpenCL, window * Segments, window * Segments, FreqUinits, 
                                                               variables, 1, optimization, iBatch))
      return false;
   caLinearHead[



1 ].SetActivationFunction(None);

La primera capa cambiará la dimensionalidad de los segmentos, mientras que la segunda ajustará la longitud de las secuencias unitarias.

Y añadiremos 2 objetos para separar las partes real e imaginaria del espectro de frecuencias antes de aplicar el algoritmo de la transformada inversa de Fourier.

   for(uint i = 0; i < caFreqOut.Size(); i++)
     {
      index++;
      if(!caFreqOut[i].Init(0, index, OpenCL, FreqUinits * variables, optimization, iBatch))
         return false;
      caFreqOut[i].SetActivationFunction(None);
     }
//---
   return true;
  }

En este punto ya hemos inicializado todos los objetos internos y podemos finalizar el método devolviendo el resultado lógico de las operaciones al programa que realiza la llamada.

A continuación, construiremos el proceso de pasada directa en el método feedForward. Como hemos mencionado anteriormente, en los parámetros del método obtendremos el puntero al objeto de datos de origen que contiene el tensor de series temporales multivariantes.

bool CNeuronCATCH::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

Primero transpondremos los datos obtenidos para procesarlos convenientemente en secuencias unitarias, tras lo cual los transferiremos al dominio de la frecuencia utilizando el algoritmo de la transformada rápida de Fourier.

   if(!FFT(cTranspose.getOutput(), NULL, caFreqIn[0].getOutput(), caFreqIn[1].getOutput(), iCount, false))
      return false;

Luego concatenaremos los resultados de la transformación de la frecuencia en un único tensor.

   if(!Concat(caFreqIn[0].getOutput(), caFreqIn[1].getOutput(), cFreqConcat.getOutput(), 1, 1, caFreqIn[0].Neurons()))
      return false;

Después, parchearemos el espectro de frecuencias e incorporaremos los datos utilizando dos capas de proyección convolucional.

   CNeuronBaseOCL *neuron = cFreqConcat.AsObject();
   for(uint i = 0; i < caProjection.Size(); i++)
     {
      if(!caProjection[i].FeedForward(neuron))
         return false;
      neuron = caProjection[i].AsObject();
     }

El siguiente paso consistirá en buscar interdependencias analizando los datos con módulos de atención enmascarada entre canales.

   for(uint i = 0; i < caChannelFusion.Size(); i++)
     {
      if(!caChannelFusion[i].FeedForward(neuron))
         return false;
      neuron = caChannelFusion[i].AsObject();
     }

Y retornaremos los datos a la dimensionalidad del espectro de frecuencias original.

   for(uint i = 0; i < caLinearHead.Size(); i++)
     {
      if(!caLinearHead[i].FeedForward(neuron))
         return false;
      neuron = caLinearHead[i].AsObject();
     }

A continuación, separaremos las partes real e imaginaria del espectro de frecuencias en objetos distintos.

   if(!DeConcat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), neuron.getOutput(), 1, 1, 
                                                                     caFreqOut[0].Neurons()))
      return false;
   if(!FFT(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caFreqOut[0].getPrevOutput(),
                                                caFreqOut[1].getPrevOutput(), iCount, true))
      return false;

Luego realizaremos una transformada de Fourier inversa, que devolverá los datos del espectro de frecuencias a la representación de la secuencia temporal. Sin embargo, aquí deberemos considerar que, como resultado de la transformada inversa de Fourier, obtendremos una serie temporal con una dimensionalidad igual a un grado del número 2, y esto podría diferir de la dimensionalidad de la serie temporal analizada, por lo que descartaremos los valores extra desconcatenando el tensor.

   if(!DeConcat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caFreqOut[0].getPrevOutput(), iWindow,
                                                       caFreqOut[0].Neurons() / iCount - iWindow, iCount))
      return false;

A los valores obtenidos les añadiremos los enlaces residuales de los datos de origen transpuestos, tras lo cual se normalizarán los resultados. Y realizaremos una transformación inversa de los datos en la representación original de la serie temporal.

   if(!SumAndNormilize(caFreqOut[0].getOutput(),cTranspose.getOutput(),caFreqOut[0].getOutput(),iWindow,true,0,0,0,1))
     return false;
//---
   return CNeuronTransposeOCL::feedForward(caFreqOut[0].AsObject());
  }

Con esto completaremos el método de pasada directa, y devolveremos el resultado lógico de las operaciones al programa que realiza la llamada.

La siguiente fase de nuestro trabajo consistirá en crear los procesos de pasada inversa para nuestros nuevos objetos. Y aquí deberemos prestar especial atención al método de distribución del error entre todos los participantes del proceso según su contribución al resultado total calcInputGradients.

bool CNeuronCATCH::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

En los parámetros del método obtendremos el puntero al objeto de datos de origen y comprobaremos inmediatamente la relevancia del puntero recibido. La necesidad de un punto de control de este tipo ya se ha debatido muchas veces.

A continuación, transpondremos el gradiente de error obtenido de la capa posterior a una representación de secuencias unitarias.

   if(!CNeuronTransposeOCL::calcInputGradients(caFreqOut[1].AsObject()))
      return false;
   if(!SumAndNormilize(caFreqOut[1].getGradient(),caFreqOut[1].getGradient(),cTranspose.getPrevOutput(),
                                                                              iWindow,false,0,0,0,0.5f))
     return false;

Y copiaremos los valores obtenidos en el búfer libre del objeto de transposición de datos de origen, que está implícito en el flujo de enlaces residuales.

Debemos recordar que la dimensionalidad de los resultados de la transformada inversa de Fourier puede superar la longitud de la serie temporal prevista. Como parte del pasada directa, descartaremos los valores redundantes. Aquí cabe señalar que, al realizar la pasada directa, hemos complementado con valores cero las series temporales analizadas hasta el tamaño requerido. Por consiguiente, en la parte descartada de los resultados de la transformada inversa de Fourier, esperamos obtener valores cero similares. Por consiguiente, para un correcto entrenamiento del modelo, lo correcto será especificar como gradiente de error de la parte descartada el resultado obtenido previamente con el signo opuesto.

   if((caFreqOut[0].Neurons() - iWindow) > 0)
      if(!SumAndNormilize(caFreqOut[1].getOutput(), caFreqOut[1].getOutput(), caFreqOut[1].getOutput(),
                                                                             1, false, 0, 0, 0, -0.5f))
         return false;

Luego concatenaremos los gradientes de error de los dos bloques en un único tensor.

   if(!Concat(caFreqOut[1].getGradient(), caFreqOut[1].getOutput(), caFreqOut[0].getGradient(), iWindow,
                                                              caFreqOut[0].Neurons() - iWindow, iCount))
      return false;

De esta forma, hemos obtenido el gradiente de error de la parte real de la señal reconstruida. Pero aún nos queda la parte imaginaria. Aquí debemos recordar que mediante la transformada inversa de Fourier recuperaremos la serie temporal a partir de su representación frecuencial. La propia serie temporal está representada por valores reales cuya parte imaginaria es igual a cero. Por consiguiente, el planteamiento para determinar el gradiente de error de la parte imaginaria será idéntico al del descarte de la parte real: solo cambiaremos el signo de los resultados obtenidos anteriormente.

   if(!SumAndNormilize(caFreqOut[1].getPrevOutput(), caFreqOut[1].getPrevOutput(), caFreqOut[1].getGradient(),
                                                                                    1, false, 0, 0, 0, -0.5f))
      return false;

Ahora podemos trasladar los gradientes de error al dominio de la frecuencia usando una transformada rápida de Fourier.

   if(!FFT(caFreqOut[0].getGradient(), caFreqOut[1].getGradient(), caFreqOut[0].getOutput(), caFreqOut[1].getOutput(),
                                                                                                       iCount, false))
      return false;

Y luego concatenaremos los resultados obtenidos en un único tensor combinando las partes real e imaginaria de las magnitudes complejas.

   if(!Concat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caLinearHead[1].getGradient(), 1, 1,
                                                                              caFreqOut[0].Neurons()))
      return false;

A continuación, pasaremos sucesivamente el gradiente de error a través de todos los objetos internos. Primero a través de los objetos de proyección final para los módulos de atención.

   if(!caLinearHead[0].calcHiddenGradients(caLinearHead[1].AsObject()))
      return false;

Mediante los módulos de atención, haremos descender el gradiente de error a las capas convolucionales de la incorporación.

   CObject *neuron = caLinearHead[0].AsObject();
   for(int i = int(caChannelFusion.Size()) - 1; i >= 0; i--)
     {
      if(!caChannelFusion[i].calcHiddenGradients(neuron))
         return false;
      neuron = caChannelFusion[i].AsObject();
     }

Y luego al nivel de los datos concatenados del espectro de frecuencias de los datos de origen.

   for(int i = int(caProjection.Size()) - 1; i >= 0; i--)
     {
      if(!caProjection[i].calcHiddenGradients(neuron))
         return false;
      neuron = caProjection[i].AsObject();
     }
//---
   if(!cFreqConcat.calcHiddenGradients(neuron))
      return false;

Aquí dividiremos el resultado obtenido en partes reales e imaginarias.

   if(!DeConcat(caFreqIn[0].getGradient(), caFreqIn[1].getGradient(), cFreqConcat.getGradient(), 1, 1,
                                                                               caFreqIn[0].Neurons()))
      return false;

Y luego, usando la transformada inversa de Fourier, devolveremos el gradiente de error a la representación de la serie temporal.

   if(!FFT(caFreqIn[0].getGradient(), caFreqIn[1].getGradient(), caFreqIn[0].getPrevOutput(),
                                                  caFreqIn[1].getPrevOutput(), iCount, false))
      return false;

Aquí solo resaltaremos la parte relevante de los datos relativos a los datos de origen.

   if(!DeConcat(cTranspose.getGradient(), caFreqIn[0].getGradient(), caFreqIn[0].getPrevOutput(), iWindow,
                                                        caFreqIn[0].Neurons() / iCount - iWindow, iCount))
      return false;
//---
   if(!SumAndNormilize(cTranspose.getGradient(),cTranspose.getPrevOutput(),cTranspose.getGradient(),iWindow,
                                                                                          false,0,0,0,1.0f))
     return false;

Y sumaremos con los datos de los enlaces residuales almacenados previamente.

Al final del método, transpondremos los gradientes de error a la representación de los datos de origen y, de ser necesario, corregiremos la derivada de la función de activación del objeto de datos de origen.

   if(!prevLayer.calcHiddenGradients(cTranspose.AsObject()))
      return false;
   if(prevLayer.Activation() != None)
     {
      if(!DeActivation(prevLayer.getOutput(), prevLayer.getGradient(), prevLayer.getGradient(), prevLayer.Activation()))
         return false;
     }
//---
   return true;
  }

Después retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

Con esto concluirá nuestra revisión de los algoritmos para construir nuestra propia visión de los enfoques propuestos por los autores del framework CATCH. El código completo de todos los objetos considerados y sus métodos se encuentra en el archivo adjunto al artículo.

Arquitectura de los modelos

Tras repasar los algoritmos para hacer realidad nuestra propia visión de los enfoques propuestos, diremos unas palabras sobre la arquitectura de los modelos entrenados. Al igual que en los artículos anteriores, entrenaremos 3 modelos: Un Codificador de estado del entorno, un Actor y un modelo predictivo de probabilidades de dirección de movimientos próximos. Implementaremos los planteamientos del framework CATCH en el Codificador de la descripción del estado del entorno analizado. Y gracias a que hemos reunido casi todo el framework en un único objeto, la arquitectura del modelo resultará visualmente sencilla.

bool CreateDescriptions(CArrayObj *&encoder, CArrayObj *&actor, CArrayObj *&probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }
//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

En primer lugar, como es habitual, utilizaremos una capa completamente conectada para registrar los datos de origen "brutos", seguida de un objeto de normalización de datos por lotes. En este se realizará el procesamiento primario de las series temporales multivariantes obtenidas y se convertirán las secuencias unitarias en una forma comparable.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, utilizaremos nuestro módulo CATCH. En él, utilizaremos la segmentación del espectro de frecuencias en 8 elementos, en pasos de 1. Esto nos permitirá analizar con más detalle las interdependencias en todo el espectro de frecuencias de los datos de origen.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronCATCH;
   prev_count=descr.count = HistoryBars;
     {
      int temp[]={BarDescr,8,32,4};       // Variables, Frequency window, Key Size, Heads
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
   descr.step=1;
   int prev_out=descr.windows[0];
   descr.batch = 1e4;
   descr.optimization=ADAM;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Luego ajustaremos los datos obtenidos en un estrecho margen de valores normalizados.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.step = BarDescr;
   descr.window_out = BarDescr;
   descr.layers = 1;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y retornaremos la distribución de sus datos de origen utilizando una capa de normalización inversa.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = HistoryBars * BarDescr;
   descr.layers = 1;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Las arquitecturas del Actor y el modelo de probabilidad predictiva de las probabilidades de las próximas direcciones se mantendrán prácticamente sin cambios respecto a los artículos anteriores. Le sugiero que se familiarice con ellas. Su código completo figura en los anexos. También encontrará los programas de interacción con el entorno y de entrenamiento de modelos, que se han portado sin ningún ajuste.

Simulación

Hoy hemos realizado un trabajo considerable para implementar los enfoques propuestos en el framework CATCH mediante MQL5 e integrar estos en los modelos entrenados, así que ha llegado el momento de la fase decisiva: probar la eficacia de las soluciones aplicadas con datos históricos reales. Esto permitirá evaluar los puntos fuertes y débiles de los planteamientos aplicados y determinar las posibilidades de optimización.

Para entrenar el modelo, hemos recopilado una muestra de entrenamiento de pasadas aleatorias en el simulador de estrategias de MetaTrader 5. Como base hemos usado los datos históricos del par de divisas EURUSD y el marco temporal M1 para todo el año 2024.

Los modelos entrenados se han probado con los datos históricos del periodo enero-marzo de 2025. Al mismo tiempo, hemos mantenido inalterados todos los parámetros del experimento, lo que garantiza la objetividad de los resultados obtenidos y permite una evaluación independiente de la eficacia de la estrategia. Este enfoque garantizará que el modelo no se limite a memorizar las características del conjunto de datos de entrenamiento, sino que demuestre realmente la capacidad de adaptarse a las nuevas condiciones del mercado.

A continuación podemos ver los resultados de las pruebas.

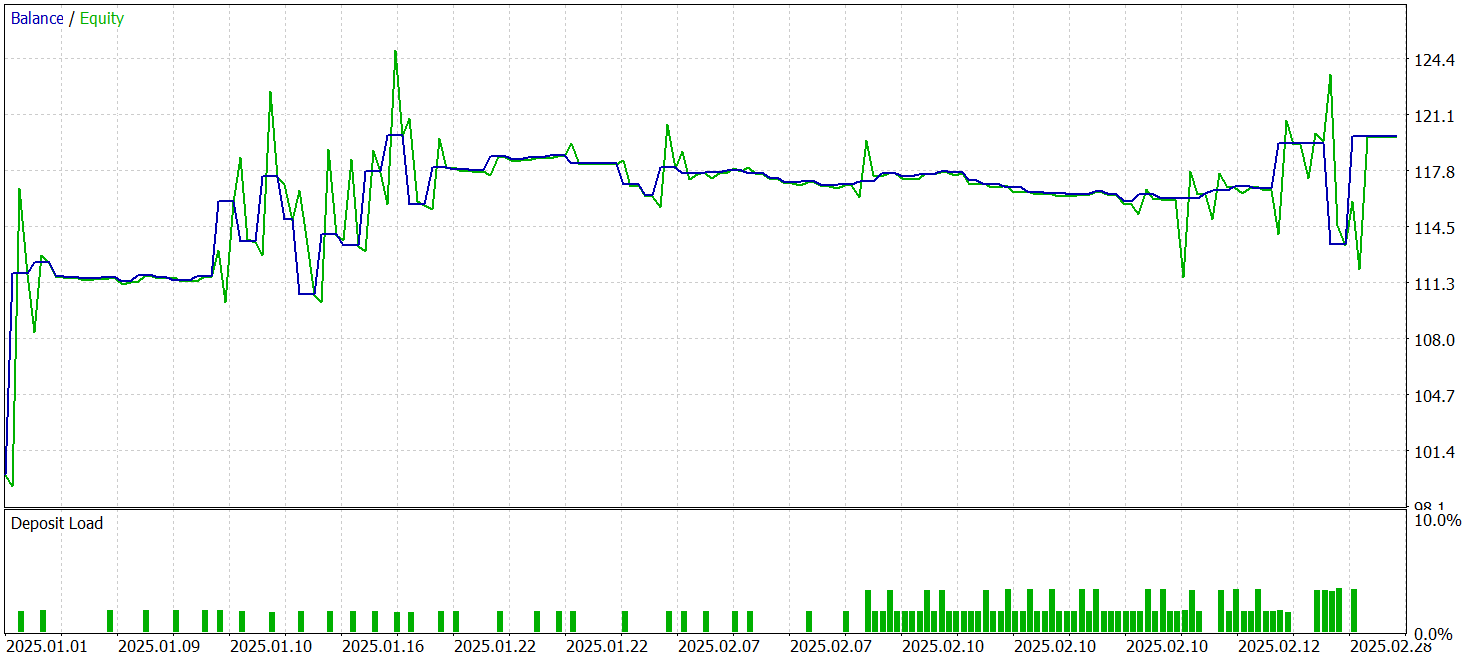
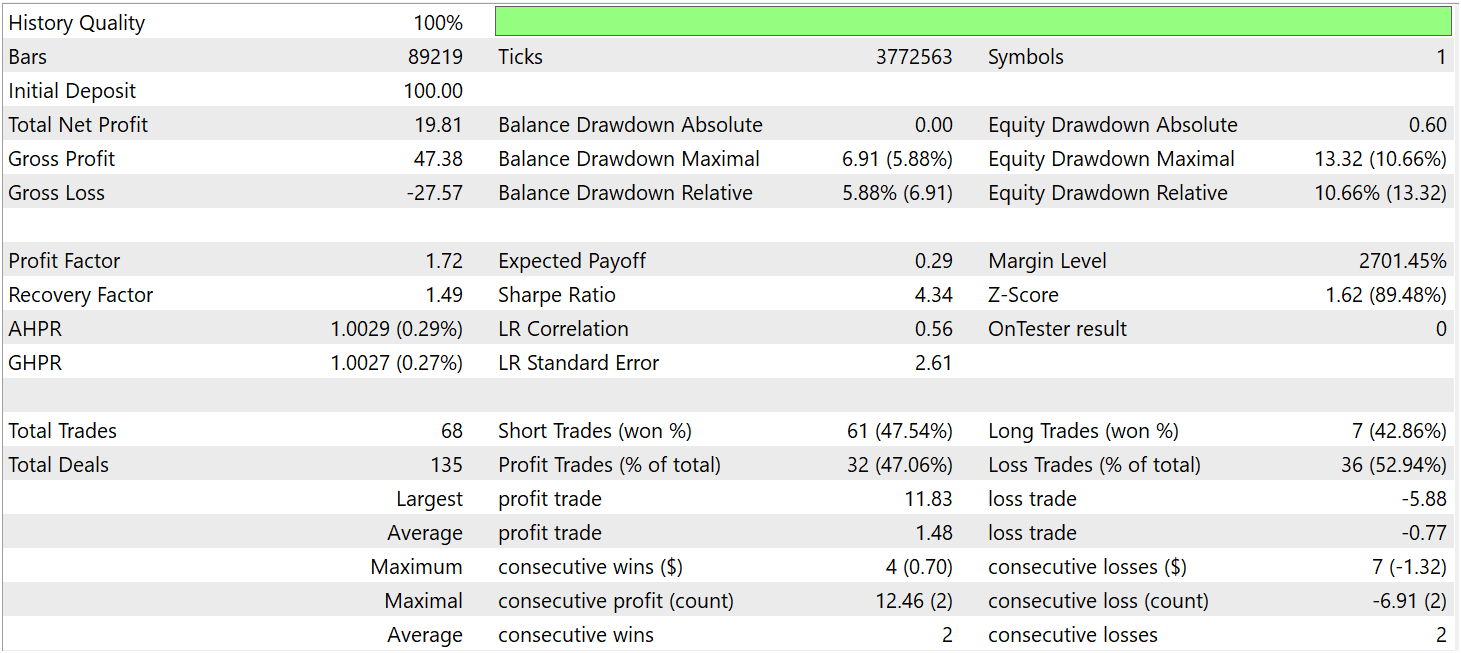
Durante el periodo de prueba, el modelo ha realizado 68 transacciones comerciales y 32 de ellas se han cerraron con beneficios, lo que supone algo más del 47%. Al mismo tiempo, la media de transacciones rentables es casi 2 veces superior al mismo indicador de transacciones no rentables. Como resultado, durante el periodo de prueba el modelo ha sido capaz de obtener beneficios, fijando el factor de beneficio en 1,72.

Conclusión

A lo largo de los dos artículos, hemos aprendido los aspectos teóricos del framework CATCH, un enfoque innovador que combina la transformada de Fourier y el mecanismo de parcheo de frecuencias para detectar anomalías en series temporales multivariantes. Su principal ventaja reside en su capacidad para revelar patrones complejos que permanecen invisibles cuando se analizan únicamente en el dominio temporal.

El uso de la representación de frecuencias permite profundizar en la estructura de la dinámica del mercado, mientras que el mecanismo de parcheo de frecuencias aporta flexibilidad al análisis, ayudando a adaptar el modelo a las condiciones cambiantes del entorno analizado. A diferencia de los métodos clásicos, CATCH no se limita a registrar saltos bruscos de precios y valores atípicos, sino que permite reconocer dependencias ocultas.

En la parte práctica, hemos implementado nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5, hemos entrenado el modelo y lo hemos probado con datos históricos reales. Los resultados indican que existe cierto potencial, pero este no se desarrollará si no llevamos a cabo una mayor optimización.

Enlaces

Programas utilizados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto para recopilar ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17675

Archivos adjuntos |

Descargar ZIP

MQL5.zip (2596.27 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Automatización de estrategias de trading en MQL5 (Parte 13): Algoritmo de trading para patrón Hombro-Cabeza-Hombro

En este artículo automatizamos el patrón Hombro-Cabeza-Hombro en MQL5. Analizamos su arquitectura, implementamos un EA para detectarlo y operar, y realizamos una prueba retrospectiva de los resultados. El proceso revela un algoritmo de negociación práctico con margen para mejoras.

Estrategias de reversión a la media con RSI2 de Larry Connors para operativa intradía

Larry Connors es un reconocido operador bursátil y autor, conocido principalmente por su trabajo en el ámbito del trading cuantitativo y estrategias como el RSI de dos períodos (RSI2), que ayuda a identificar condiciones de sobrecompra y sobreventa a corto plazo en los mercados. En este artículo, primero explicaremos la motivación detrás de nuestra investigación, luego recrearemos tres de las estrategias más famosas de Connors en MQL5 y las aplicaremos al trading intradía del CFD del índice S&P 500.

Asesor experto de scalping Ilan 3.0 Ai con aprendizaje automático

¿Recuerda el asesor experto Ilan 1.6 Dymanic? Hoy intentaremos mejorarlo usando el aprendizaje automático. Así, en el presente artículo reanimaremos el antiguo desarrollo y añadiremos aprendizaje automático con una tabla Q. Paso a paso.

Redes neuronales en el trading: Detección de anomalías en el dominio de la frecuencia (CATCH)

El framework CATCH combina la transformada de Fourier y el parcheo de frecuencias para detectar con precisión anomalías del mercado inaccesibles a los métodos tradicionales. En el presente artículo, analizaremos cómo este enfoque revela patrones ocultos en los datos financieros.