Características del Wizard MQL5 que debe conocer (Parte 41): Aprendizaje por refuerzo con redes neuronales (Deep-Q-Networks, DQN)

Introducción

Deep-Q-Networks (DQN) es otro algoritmo de aprendizaje por refuerzo, además del Q-Learning que analizamos en este artículo, pero que, a diferencia del Q-Learning, utilizan redes neuronales para pronosticar el valor q y la siguiente acción a realizar por el agente. Es similar/está relacionado con el Q-Learning en el sentido de que sigue interviniendo una tabla Q, en la que se almacena el conocimiento acumulado sobre acciones y estados de «episodios» anteriores. De hecho, comparte la misma página de Wikipedia que Q-Learning, como puede verse en los enlaces, donde se define esencialmente como una variante de Q-Learning.

La clase de señal junto con la clase de trailing stop y la clase de gestión monetaria son los tres módulos principales que necesitan ser definidos cuando se construye un Asesor Experto ensamblado con asistente. Ponerlos juntos a través del asistente MQL5 (MQL5 Wizard) se puede hacer siguiendo las guías que están aquí y aquí para los nuevos lectores. El código fuente adjunto al final de este artículo debe utilizarse siguiendo las guías de ensamblaje del asistente compartidas en estos enlaces. Estamos buscando, una vez más, definir una clase de señal personalizada para usar en un Asesor Experto ensamblado mediante un asistente.

Sin embargo, esta no es la única forma en que podemos examinar DQN, ya que también se pueden realizar y probar implementaciones para una clase de seguimiento personalizada o una clase de administración de dinero personalizada. Sin embargo, nos centraremos en la clase de señal porque determinar las condiciones largas y cortas en estos asesores expertos es fundamental y, en muchos casos, demuestra mejor el potencial de una configuración comercial. Este artículo se basa en artículos anteriores de esta serie, en los que nos centramos en técnicas o diferentes configuraciones que se pueden utilizar para desarrollar asesores expertos personalizados y, por lo tanto, una revisión de artículos anteriores para nuevos lectores sería una buena idea, especialmente si buscan diversificar su enfoque. Estos artículos cubren no solo una variedad de señales personalizadas, sino también implementaciones personalizadas de la clase de seguimiento y la clase de administración de dinero.

La configuración de DQN como vimos en el artículo de Q-Learning se implementa como un apoyo a la función de pérdida porque estamos viendo estrictamente el aprendizaje por refuerzo como una tercera forma de entrenamiento además del supervisado y el no supervisado. Esto, como se menciona en el artículo sobre Q-Learning, no significa que no pueda implementarse como un modelo independiente para su uso en el entrenamiento, sin un MLP subordinado. Esta forma alternativa de utilizar el aprendizaje por refuerzo se explorará en futuros artículos, en los que no habrá MLP subordinado y, en su lugar, las previsiones de acción del agente informarán sobre las condiciones largas y cortas.

Aprendizaje por refuerzo

Sin embargo, antes de comenzar, puede ser una buena idea hacer un rápido repaso de qué es el aprendizaje de refuerzo. Esta es una forma alternativa de entrenamiento de aprendizaje automático que en esencia se centra en las interacciones agente-entorno. El agente es la entidad que toma decisiones cuyo objetivo es aprender las mejores acciones para maximizar las recompensas acumuladas. El entorno es todo lo que está "fuera" del agente y que actúa como anfitrión de un crítico/observador, y proporciona retroalimentación al agente en forma de nuevos estados y recompensas (recompensas por proyecciones precisas del agente). Por tanto, el ciclo comienza con el agente observando el estado actual del entorno, haciendo previsiones de cambios en ese estado y luego seleccionando una acción adecuada para ese estado.

Los estados son representaciones del estado o la situación del entorno. Una vez que un agente selecciona o realiza una acción, se produce una transición en los estados del entorno de forma previa/simultánea, de modo que sus acciones se evalúan en función de su adecuación a este nuevo entorno. Esta valoración se cuantifica como «recompensas». Se utilizó una matriz Markov-Chain sin memoria para ponderar el proceso de decisión del agente en la previsión del siguiente estado, pero las transiciones reales vienen determinadas por el entorno, que en el caso de ese artículo venía marcado por una tabla cruzada entre la dirección del mercado y el horizonte temporal. Las acciones emprendidas por el agente, aunque pueden ser continuas (o un abanico infinito de posibilidades), a menudo son discretas, lo que significa que adoptan un conjunto predefinido de opciones que, en nuestro caso, eran vender, comprar o no hacer nada. Sin embargo, en nuestro caso, esta lista podría haberse ampliado para seguir, por ejemplo, el formato de las órdenes de mercado, de forma que no sólo se tuvieran en cuenta las órdenes de mercado, sino también las órdenes pendientes.

Del mismo modo, nuestra métrica de recompensas, que se reevaluaba en cada nueva barra, como la pérdida o el beneficio de la acción u orden anterior, podría «mejorarse» para cuantificar las excursiones favorables frente a las adversas como un ratio o cualquier otra métrica híbrida. Esta métrica de recompensa junto con el estado actual y la acción previa seleccionada se utilizan para actualizar la tabla Q, cuya fuente se compartió en la función «Critic Source» de la clase CQL. Como ya se ha mencionado anteriormente, estamos considerando estrictamente el aprendizaje por refuerzo como una alternativa al aprendizaje supervisado y al aprendizaje no supervisado, de forma que sirva para cuantificar estrictamente nuestra función de pérdida. Sin embargo, hay casos en los que el aprendizaje por refuerzo se aplica fuera de este escenario «definitivo» y se utiliza como un modelo independiente para hacer previsiones en las que las acciones del agente se aplican fuera del entrenamiento, y estos escenarios no se consideran aquí, pero podrían estudiarse en futuros artículos. 

Introducción al algoritmo Deep-Q-Networks

DQN se basa en Q-Learning, que fue el primer algoritmo de aprendizaje por refuerzo que estudiamos, y su objetivo principal, que sigue siendo el de DQN, es predecir los valores 'Q'. Estos, como se resumió anteriormente, son puntos de datos que clasifican varios estados del entorno y se registran en una tabla Q. La diferencia con el algoritmo Q-Learning radica en el uso de redes neuronales para pronosticar el próximo valor q, en lugar de depender de un Q-Map o una tabla que utiliza el algoritmo Q-Learning, como se demostró en nuestro primer artículo sobre aprendizaje de refuerzo. Además, hay una repetición de la experiencia y una red de objetivos como se describe en las secciones siguientes. Por lo tanto, la política 'épsilon-greedy' que se aplicaba anteriormente en el Q-Map ya no es aplicable a las DQN, ya que las redes neuronales están en juego.

Por lo tanto, el DQN mapea las recompensas futuras para cada acción posible en todos los estados aplicables con la ayuda de una red neuronal. Esta correspondencia de estados, que los operadores pueden considerar como distintas ponderaciones para cada acción posible (comprar/vender/conservar) en distintas condiciones de mercado (alcista/bajista/plano) proporciona ponderaciones, y estas ponderaciones determinan la posición comercial. Los DQN son expertos en el manejo de entornos de gran complejidad y dimensión, que forman parte de las principales características de los mercados financieros. Los mercados financieros son dinámicos y no lineales, con factores muy variables e independientes, como la evolución de los precios, los indicadores macroeconómicos y el sentimiento del mercado.

El Q-Learning tradicional tiende a tener problemas con esto ya que utiliza Q-Tables discretas con un número finito y manejable de estados, lo que contrasta con el DQN que es muy hábil dado su uso de redes neuronales. Las DQN también son buenas para captar las dependencias no lineales de los mercados en diversas clases de activos, que también sirven como señales de entrada en determinadas estrategias de negociación, por ejemplo, el carry trade del yen. Además, el uso de DQNs permite una mejor generalización, ya que la red puede adaptarse mejor a nuevos datos y condiciones del mercado, debido a que las redes neuronales suelen ser más flexibles que las Q-Tables. Esto es crucial en los mercados financieros, donde las condiciones pueden cambiar rápidamente y el agente debe adaptarse a situaciones desconocidas. Las DQN también resisten mejor el ruido del mercado que el Q-Learning tradicional. En los mercados financieros, las acciones de los agentes suelen tener recompensas diferidas (por ejemplo, mantener una posición que sólo puede dar beneficios al cabo de varios días o semanas). El uso por parte de DQN de la ecuación de Bellman con un factor de descuento (gamma) le permite evaluar las recompensas inmediatas y a largo plazo de forma que la red aprende a equilibrar entre beneficios rápidos y ganancias a largo plazo, algo esencial en la toma de decisiones estratégicas para carteras financieras.

Previsión de valores Q con DQN

Nosotros utilizamos DQN para normalizar la función de pérdida de un MLP, ya que para este artículo, como ya hemos mencionado, estamos considerando DQN estrictamente como un enfoque de entrenamiento alternativo y no como un modelo independiente que pueda utilizarse para realizar sus propias previsiones como un MLP típico. Este uso de DQN en el entorno rudimentario del <a>aprendizaje por refuerzo significa que nos estamos ciñendo prácticamente al enfoque que utilizamos en este artículo anterior. Por lo tanto, esto implica que tenemos una instancia de un MLP que actúa como el agente al que nos referimos como «DQN_ONLINE» en nuestra interfaz de clase de señal, que se abrevia a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalDQN   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis


   int                           m_train_set;                       //
   int                           m_epochs;                              // Epochs
   double                        m_learning_rate;                       // Alpha

   Elearning                     m_learning_type;

   double                        m_train_deposit;
   double                        m_train_criteria;

   double                        m_initial_weight;
   double                        m_initial_bias;
   
   int                           m_state_lag;
   int                           m_target_counts;
   int                           m_target_counter;

   Smlp                          m_mlp;
   Smlp                          m_dqn;
   Slearning                     m_learning;

public:
   void                          CSignalDQN(void);
   void                          ~CSignalDQN(void);

   //--- methods of setting adjustable parameters



...



...


protected:
   void                          GetOutput(int &Output);

   Cmlp                          *MLP,*DQN_ONLINE,*DQN_TARGET;
};

Esta red toma como entrada el estado actual y da como salida un vector o valores q para cada una de las acciones posibles. Su arquitectura de red, que puede ser ajustada o afinada por el lector, sigue una arquitectura 2-6-3 donde 2 es el tamaño de la capa de entrada. Su tamaño es 2 porque, como se indica en nuestro artículo anterior, aunque pueden ser "aplanados" como un único índice, en sentido estricto son un par de índices o coordenadas. Una coordenada mide el tipo de tendencia a corto plazo, mientras que la otra analiza la tendencia a largo plazo.

A la capa oculta simplemente se le asigna un tamaño de 6, sin embargo, como se indicó, este tamaño y la adición de capas ocultas adicionales se pueden personalizar a partir de lo que se utiliza aquí. Seleccionamos 6 a partir del tamaño de entrada multiplicado por el tamaño de salida. Entonces, nuestro tamaño de salida es 3, como fue el caso en el artículo de q-learning, donde esto representa la cantidad de acciones posibles que realiza un agente. Para resumir, estas acciones son comprar, vender o mantener. El resultado, que es un vector de las probabilidades de cada una de estas acciones, implica que la DQN es una red clasificadora. Esta salida de esta DQN de aprendizaje por refuerzo sirve como valor objetivo para la red MLP principal. Una vez que tengamos este resultado, podremos entrenar el MLP. Sin embargo, no hay que pasar por alto el entrenamiento de la DQN, y esto no sucede de la misma manera que en otras redes. En lugar de trabajar con otro conjunto de datos ubicuo de estados y valores 'Q', utilizamos otra red neuronal, que denominamos «DQN_TARGET», para proporcionar vectores objetivo con los que entrenar la red «DQN_ONLINE». Lo veremos a continuación.

El papel de una red objetivo

La red objetivo, al igual que la red en línea (la DQN anterior que proporciona el objetivo MLP), también toma un estado del entorno como entrada y genera un vector de valores 'Q' para cada acción posible. La principal diferencia con la red en línea es que las entradas del estado del entorno son para el estado que sigue al estado actual. Además, al ser otra red neuronal, uno esperaría que se entrenara por retropropagación, pero en cambio, en un intervalo preestablecido, simplemente copia la red en línea. La red objetivo proporciona valores objetivo más estables al calcular la diferencia temporal, lo que disminuye los riesgos de oscilaciones y divergencias durante el entrenamiento.

Sin una red objetivo independiente, el MLP madre y la red en línea, los valores objetivo cambiarían constantemente en un comportamiento oscilante inestable. Esto se debe a que ambas redes se actualizarían simultáneamente. Al utilizar la red objetivo, el proceso de aprendizaje se estabilizaría, ya que ambos algoritmos divergirían/oscilarían menos. Como ya se ha mencionado, la red objetivo no se retropropaga como un MLP normal, sino que copia la red en línea a intervalos determinados. Estos intervalos suelen ser de unos 10.000, y nuestro parámetro de entrada para modularlos se denomina «m_target_counts» y se asigna por defecto a sólo 65. Esto se debe a que estamos probando en el marco de tiempo diario durante sólo un año, por lo que tenemos 260 barras de precios para la prueba. Se trata de un parámetro ajustable, por lo que con un periodo de prueba más largo o un marco temporal menor, los 10.000 pasos son factibles. El cálculo del valor 'Q' objetivo se consigue mediante la siguiente fórmula:

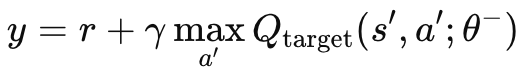
Donde:

• y: El valor Q objetivo, que representa la rentabilidad estimada (recompensa futura) partiendo del estado actual 's', tomando la acción 'a', y siguiendo la política óptima a partir de entonces.
• r: La recompensa inmediata recibida tras realizar la acción 'a' en el estado 's'.
• γ: El factor de descuento, que determina la importancia de las recompensas futuras. Es un valor comprendido entre 0 y 1.
• max a′ Qtarget(s′,a′;θ−): El valor Q máximo previsto para el siguiente estado 's′' sobre todas las posibles acciones 'a′', estimado por la red objetivo con parámetros θ-.

• Qtarget(s′,a′;θ−): El valor Q para el siguiente par estado-acción (s′,a′)(s', a')(s′,a′), predicho por la red objetivo.
• θ−: Los parámetros (pesos) de la red objetivo, que se actualizan periódicamente a partir de los parámetros de la red principal.
• 
  

Esta fórmula se implementa en MQL5 a través de la función objetivo crítico, que añadimos a la clase CQL que ya habíamos utilizado en nuestro artículo de introducción al aprendizaje por refuerzo. Esta función se enumera a continuación:

//+------------------------------------------------------------------+
// Critic Target for DQN
//+------------------------------------------------------------------+
vector Cql::CriticTarget(vector &Rewards, vector &TargetOutput)
{  vector _target = Rewards + (THIS.gamma * TargetOutput);
   return(_target);
}

Hay un problema de bootstrapping. En el Q-Learning tradicional, como vimos en el artículo anterior sobre aprendizaje por refuerzo, la red actualiza los valores 'Q' basándose en sus propias predicciones, lo que puede llevar a una cascada de errores (más comúnmente conocido como error de bootstrapping) si las predicciones son inexactas. Esto se debe a que los valores 'Q' de un estado dependen de los valores 'Q' de los estados siguientes, lo que puede dar lugar a una amplificación del error.

Por lo tanto, el papel de la red objetivo es mitigar esto proporcionando un objetivo de movimiento más lento. Como los parámetros de la red objetivo se actualizan con menos frecuencia (normalmente cada diez mil pasos), cambia más gradualmente que la red en línea. Esto reduce la velocidad a la que se propagan los errores, solucionando así el problema del arranque.

En situaciones donde tenemos dinámicas no lineales, como los entornos complejos de los mercados financieros o incluso otros como los videojuegos, las relaciones entre estados y recompensas tienden a ser altamente no lineales. Por lo tanto, la estabilidad introducida por la red objetivo es fundamental para que DQN aprenda de manera efectiva en estos entornos. Sin esta red objetivo, es más probable que la red en línea (DQN) diverja cuando se enfrenta a entornos complejos o que cambian rápidamente debido a las rápidas actualizaciones de los valores 'Q' y los objetivos.

Además, la red objetivo puede mejorarse añadiendo una extensión, que a menudo se conoce como Double DQN (doble DQN), la cual aborda el sesgo de sobreestimación. Esto se implementa utilizando las redes en línea y de destino por separado para seleccionar y evaluar acciones. Se trata de una disociación de los procesos de selección de acciones y de evaluación de acciones entre las redes en línea y las redes objetivo. La red en línea se utiliza para seleccionar la acción, mientras que la red objetivo la evalúa.

La repetición de la experiencia y su papel en el entrenamiento

La repetición de experiencias es una técnica de almacenamiento en búfer donde un agente DQN de aprendizaje de refuerzo almacena sus "experiencias" de estado, acción, recompensa y próximo estado en un búfer de repetición. Luego, estas experiencias se toman de manera aleatoria durante el entrenamiento para actualizar los pesos y sesgos del DQN del agente. Este enfoque es, como se esperaría, útil para romper la correlación secuencial al considerar solo puntos de datos consecutivos y, por lo tanto, podría ser más adecuado para escenarios del mundo real como los mercados financieros. En los mercados financieros, los puntos de datos consecutivos, ya sea en precio, volumen de contratos o volatilidad, tienden a estar altamente correlacionados ya que todos están influenciados por condiciones de mercado y comportamientos de los participantes similares. Entrenar a un agente DQN con datos tan correlacionados secuencialmente tiende a generar sobreajuste y falta de generalización, ya que el agente DQN se acostumbra a explotar patrones específicos que no se generalizan bien a diferentes condiciones de mercado.

Para romper estas correlaciones temporales, normalmente el DQN se entrena con minilotes de puntos de datos de experiencia muestreados aleatoriamente del búfer de reproducción. El muestreo aleatorio en particular ayuda a romper las correlaciones temporales, lo que da como resultado que el agente aprenda una mejor distribución de experiencias que se aproximan mejor a la dinámica subyacente del mercado. Además de una mejor generalización, el proceso de entrenamiento a largo plazo se estabiliza y converge mejor. Esto se debe a que la repetición de la experiencia reduce la varianza de las actualizaciones durante el proceso de formación.

Sin la repetición de la experiencia, las actualizaciones del peso de la red se producirían en ráfagas de muestras consecutivas altamente correlacionadas, sólo para ser interrumpidas por una actualización totalmente diferente de las condiciones del entorno, lo que tendería a hacer que todo el proceso de actualización fuera muy volátil, lo que podría conducir a la inestabilidad en el proceso de aprendizaje. Al tomar muestras aleatorias de un conjunto diverso de experiencias, el agente DQN realiza actualizaciones más suaves y estables, mejorando la convergencia hacia una política óptima.

La utilización eficaz de los datos históricos es algo que también permite la repetición de experiencias, ya que el agente vuelve a aprender de la experiencia varias veces (debido a la selección aleatoria), lo que resulta especialmente valioso en los mercados financieros, donde es difícil obtener grandes cantidades de datos diversos y representativos en un momento dado. En esencia, esto permite al DQN aprender de acontecimientos raros o significativos, como las caídas o subidas del mercado, aunque no estén ocurriendo actualmente. Esto hace que el agente esté más preparado y robusto para esos eventos, en caso de que ocurran.

La repetición de experiencias también aumenta el potencial de exploración del aprendizaje por refuerzo, en contraposición a la mera explotación. Reduce la probabilidad de que se produzca un «olvido catastrófico», en el que el agente toma muestras repetidamente de su memoria de repetición, lo que le permite reforzar el conocimiento de estrategias más antiguas y evitar que sean sobrescritas por experiencias más recientes; y, por último, permite instancias aún más especializadas de repetición de experiencias, como la repetición priorizada de experiencias, en la que las muestras de datos con mayores errores en la función de pérdida se priorizan por su mayor potencial de aprendizaje, lo que hace que el aprendizaje sea más eficiente y específico.

Mencionamos la repetición de experiencias en este artículo porque es un principio clave en DQN; sin embargo, mostraremos su capacidad en MQL5 en próximos artículos donde DQN será algo más que una función de pérdida híbrida, sino que será el modelo de previsión principal para nuestra clase de señal.

Toma de decisiones temporales

A menudo, las decisiones que se toman, incluso fuera del ámbito del comercio, en campos como la robótica o los juegos, tienen efectos retardados sobre los resultados futuros, que no son necesariamente inmediatos, sino que se manifiestan a lo largo de horizontes temporales más amplios. Los comunicados de prensa económica y los informes de las empresas son lo que podría venir a la mente de los comerciantes, pero esta relación establece una dependencia temporal. Esta relación temporal se considera en la ecuación de valor 'Q' anterior a través del factor gamma. Gamma permite un equilibrio entre las recompensas a corto y largo plazo, lo que da a los valores q de DQN la capacidad de mirar más allá y estimar el impacto acumulativo de las acciones a lo largo del tiempo. Se argumenta que el efecto de esto es que algunas recompensas se retrasan y gamma garantiza que el agente no ignore las recompensas a largo plazo mientras sigue controlando las inmediatas, lo que puede ser esencial al operar. Por ejemplo, a menudo las posiciones que se abren ante decisiones importantes sobre tasas de interés no producen inmediatamente variaciones favorables. Los periodos de excursión adversos suelen encabezar estas posiciones y, por lo tanto, la capacidad de tener y utilizar señales que tengan esto en cuenta, como las DQN, puede ser una ventaja.

Cambios en nuestro código anterior

Para utilizar nuestro DQN dentro de una función de pérdida híbrida, necesitamos en primer lugar añadir nuestra enumeración de pérdida personalizada para que tenga el siguiente aspecto:

//+------------------------------------------------------------------+
//| Custom Loss-Function Enumerator                                  |
//+------------------------------------------------------------------+
enum Eloss
{  LOSS_TYPICAL = -1,
   LOSS_SVR = 1,
   LOSS_QL = 2,
   LOSS_DQN = 3
};

Añadimos una nueva enumeración 'LOSS_DQN' que se seleccionará cuando la función de pérdida utilice DQN. Los cambios adicionales que tenemos que hacer como hicimos en el primer artículo sobre el aprendizaje por refuerzo están en la función de retropropagación, donde la selección del tipo de pérdida adecuado determina el valor utilizado en el cálculo de los deltas. Estos cambios son los siguientes:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }


....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }
   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss_typical);
   if(THIS.loss_custom == LOSS_SVR)
   {  _last_loss = SVR_Loss();
   }
   else if(THIS.loss_custom == LOSS_QL)
   {  

....

   }
   else if(THIS.loss_custom == LOSS_DQN)
   {  double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float);
      vector _rewards;
      _rewards.Init(Learning.dqn_target.Size());
      _rewards.Fill(0.0);
      if(_reward > 0.0)
      {  _rewards[0] = 1.0;
      }
      else if(_reward == 0.0)
      {  _rewards[1] = 1.0;
      }
      else if(_reward < 0.0)
      {  _rewards[2] = 1.0;
      }
      vector _target = QL.CriticTarget(_rewards, Learning.dqn_target);
      _last_loss = output.LossGradient(_target, THIS.loss_typical);
   }
   
....


}

Los otros cambios principales que hemos realizado en el código se encuentran en la clase CQL y ya se han destacado anteriormente, donde se introduce la fórmula del valor 'Q' para DQN. La función de salida get que utilizamos para generar los umbrales de condición no es muy diferente de la que consideramos en el artículo anterior sobre el Q-Learning básico. Se presenta a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalDQN::GetOutput(int &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  int _states = 2;
         vector _in, _in_old, _in_row, _in_row_old, _in_col, _in_col_old;
         if
         (
            _in_row.Init(_states) &&
            _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) &&
            _in_row.Size() == _states
            &&
            _in_row_old.Init(_states) &&
            _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, _states) &&
            _in_row_old.Size() == _states
            &&
            _in_col.Init(_states) &&
            _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) &&
            _in_col.Size() == _states
            &&
            _in_col_old.Init(_states) &&
            _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_state_lag + ii + 1, _states) &&
            _in_col_old.Size() == _states
         )
         {  _in_row -= _in_row_old;
            _in_col -= _in_col_old;
            //
            m_learning.ql_reward_max = _in_row.Max();
            m_learning.ql_reward_min = _in_row.Min();
            if(m_learning.ql_reward_max == m_learning.ql_reward_min)
            {  m_learning.ql_reward_max += m_symbol.Point();
            }
            MLP.Set(_in_row);
            MLP.Forward();
            //
            MLP.QL.THIS.environments = m_environments;
            //
            vector _in_e;
            _in_e.Init(1);
            MLP.QL.Environment(_in_row, _in_col, _in_e);
            //
            int _row = 0, _col = 0;
            MLP.QL.SetMarkov(int(_in_e[_states - 1]), _row, _col);
            _in.Init(2);
            _in[0] = _row;
            _in[1] = _col;
            DQN_ONLINE.Set(_in);
            DQN_ONLINE.Forward();
            //
            MLP.QL.SetMarkov(int(_in_e[_states - 2]), _row, _col);
            _in_old.Init(2);
            _in_old[0] = _row;
            _in_old[1] = _col;
            DQN_TARGET.Set(_in_old);
            DQN_TARGET.Forward();
            m_learning.dqn_target = DQN_TARGET.output;
            if(ii > 0)
            {  vector _target, _target_data, _target_data_old;
               if
               (
                  _target_data.Init(2) &&
                  _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) &&
                  _target_data.Size() == 2
                  &&
                  _target_data_old.Init(2) &&
                  _target_data_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, 2) &&
                  _target_data_old.Size() == 2
               )
               {  _target.Init(__MLP_OUTPUTS);
                  _target.Fill(0.0);
                  _target_data -= _target_data_old;
                  double _type = _target_data[1] - _in_row[1];
                  int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1));
                  _target[_index] = 1.0;
                  MLP.Get(_target);
                  if(i == m_epochs && ii == m_train_set)
                  {  DQN_ONLINE.Backward(m_learning, i);
                     if(m_target_counter >= m_target_counts)
                     {  DQN_TARGET = DQN_ONLINE;
                        m_target_counter = 0;
                     }
                     MLP.Backward(m_learning, i);
                  }
               }
            }
            Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2));
         }
      }
   }
}

Como ya se ha mencionado, tenemos 2 redes DQN, la red en línea y la red objetivo. Además, por supuesto, está el MLP padre que toma los cambios de precios cercanos como entradas, como en el artículo de Q-Learning. No deberíamos hacer referencia a la clase QL, además de llamar a la función objetivo crítica para obtener los valores 'Q' de DQN como se mencionó anteriormente. Sin embargo, debido a que la clase QL nos permite acceder a las coordenadas del estado del entorno (cuando se le proporciona un índice), así como componer un índice a partir de las coordenadas del estado, hacemos referencia a ella para obtener las entradas para las dos redes DQN. Como se mencionó, no utilizamos Q-Map para nuestros pronósticos, sino que confiamos en la red DQN en línea que está entrenada por la red objetivo. Tanto los DQN en línea como los de objetivos simplemente toman estados del entorno (antiguo y nuevo, respectivamente) y se entrenan para pronosticar un vector de valores 'Q' (para cada acción del agente).

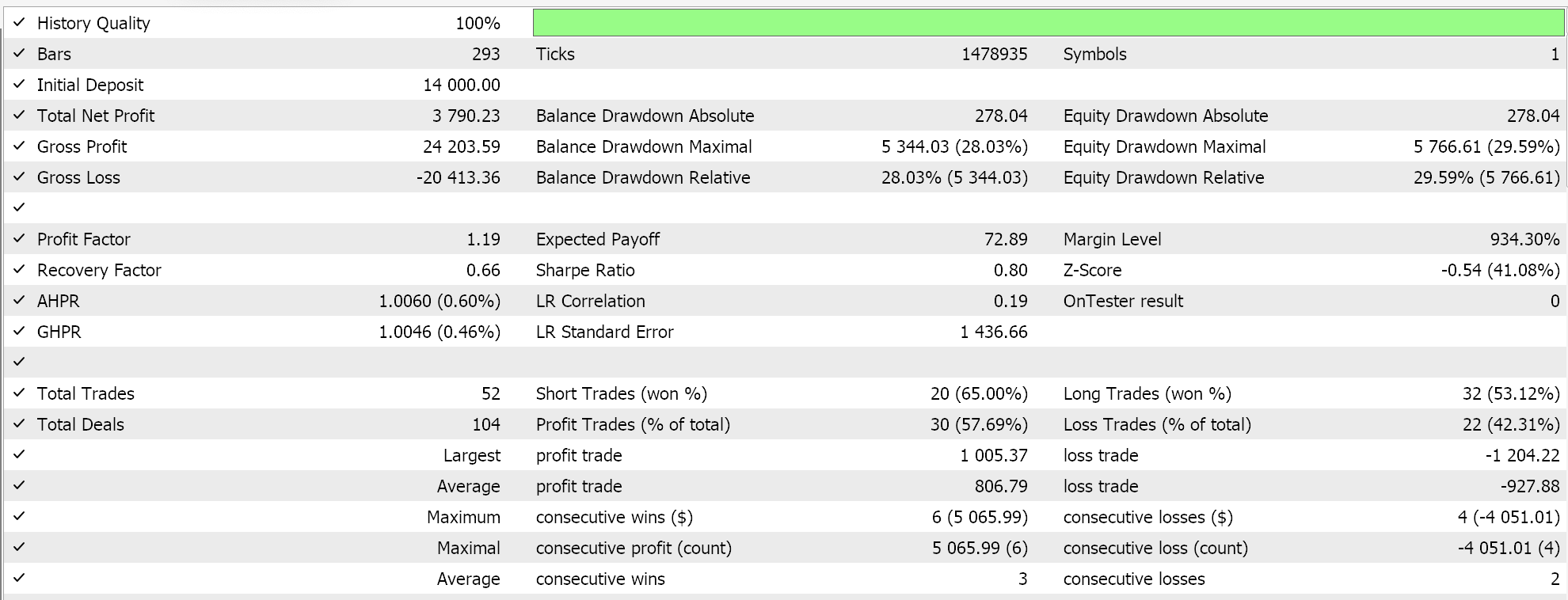
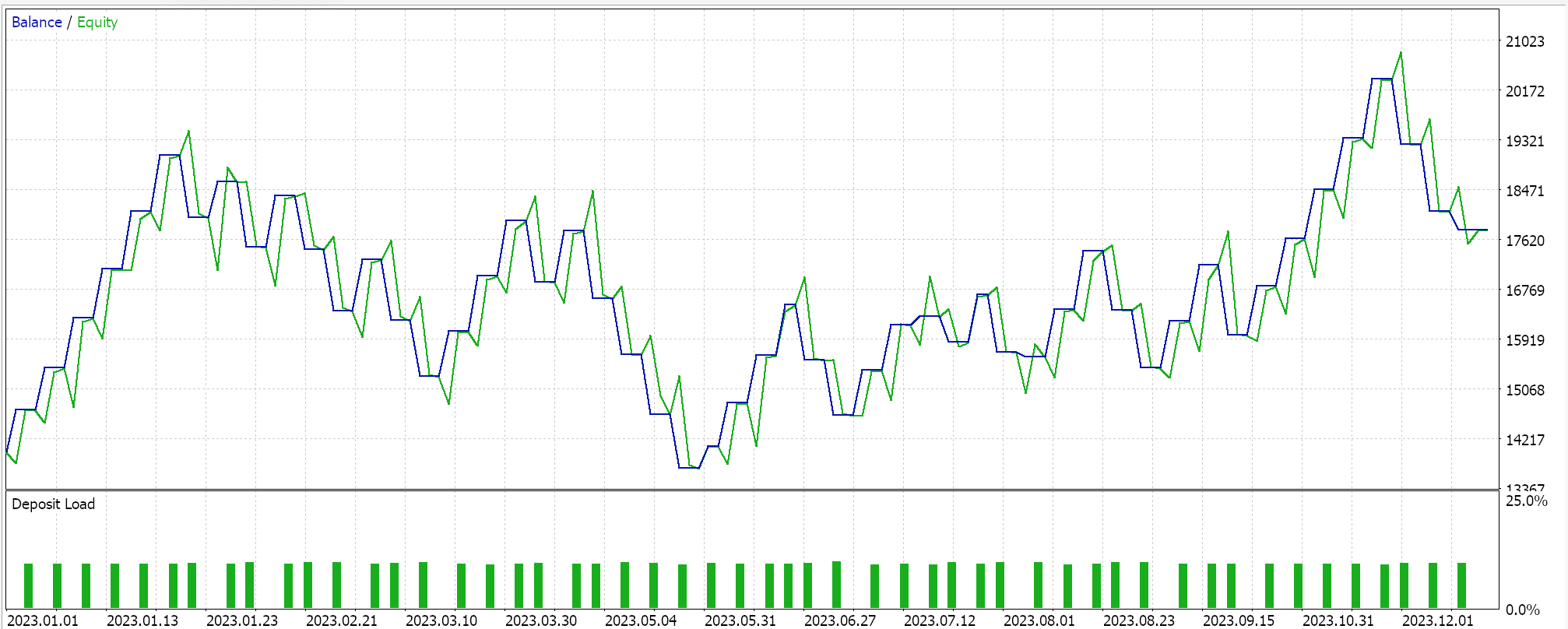
Informes del Probador de estrategias:

Probamos este MLP con entrenamiento de aprendizaje de refuerzo mediante redes Deep-Q en EURGBP para el año 2023 en el marco temporal diario. A continuación se presentan nuestros resultados, que pretenden demostrar estrictamente la comerciabilidad y no necesariamente la replicación en la acción futura del mercado.

Conclusión

Hemos examinado la implementación y las pruebas de un algoritmo alternativo al aprendizaje por refuerzo llamado Deep-Q-Networks en Asesores Expertos ensamblados con el asistente (MQL5 Wizard). El aprendizaje por refuerzo es el tercer método de entrenamiento en el aprendizaje automático, además del aprendizaje supervisado y el aprendizaje no supervisado, y aunque es estrictamente hablando un enfoque diferente de entrenamiento dentro del aprendizaje automático, en artículos posteriores consideraremos escenarios en los que puede servir como modelo principal y generador de señales.