Características del Wizard MQL5 que debe conocer (Parte 47): Aprendizaje por refuerzo con diferencia temporal

Introducción

La introducción al aprendizaje por diferencia temporal (Temporal Difference, TD) en el aprendizaje por refuerzo sirve como puerta de entrada para comprender cómo el TD se distingue de otros algoritmos, como Monte Carlo, Q-Learning y SARSA. Este artículo tiene como objetivo desentrañar las complejidades que rodean al aprendizaje TD, destacando su capacidad única para actualizar las estimaciones de valor de forma incremental basándose en información parcial de los episodios, en lugar de esperar a que estos se completen, como ocurre en los métodos Monte Carlo. Esta distinción convierte al aprendizaje TD en una herramienta poderosa, especialmente en entornos dinámicos que requieren actualizaciones rápidas de la política de aprendizaje.

En el último artículo sobre aprendizaje por refuerzo, analizamos el algoritmo Monte Carlo, que recopilaba información sobre recompensas a lo largo de múltiples ciclos antes de realizar una única actualización para cada episodio. Sin embargo, la diferencia temporal (TD) se basa en aprender de episodios parciales e incompletos, al igual que los algoritmos de Q-Learning y SARSA que abordamos anteriormente aquí y aquí.

A continuación se muestra un resumen tabulado de las principales diferencias entre TD, Q-Learning y SARSA.

Y, para recapitular, la fórmula para los pares acción-estado con actualización en la política, como SARSA por ejemplo, es la siguiente:

	Aprendizaje TD	Q-Learning	SARSA
Tipos de valores	Valores de estado V(s)	Valores de acción Q(s,a)	Valores de acción Q(s,a)
Enfoque de aprendizaje	Estimaciones de valores de estados futuros	Fuera de política	En política
Tipo de política	No depende de una política específica	Aprende la política óptima	Aprende la política de comportamiento actual
Actualizar objetivo	Valor del siguiente estado V(s′)	Máx. Q(s′,a′)	Q actual(s′,a′)
Exploración	A menudo requiere una política separada	Supone que el agente busca el óptimo	Más conservador
Comportamiento	Se mueve hacia el valor del siguiente estado	Codicioso; favorece la ruta óptima	Sigue la ruta de exploración real

Para recapitular algunos de los términos que hemos visto, en las actualizaciones de políticas, los pares acción-estado que se actualizaban eran los pares actuales y no necesariamente los óptimos o los que tenían los valores Q más altos. Si actualizamos los pares estado-acción con los valores Q más altos, entonces se trataría de un enfoque fuera de la política. Realizamos estas actualizaciones en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
// Update using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q_SA-action from Q_SA-Map
   double _sa = Q_SA[transition_act][e_row[1]][e_col[1]];
   double _v = Q_V[e_row[1]][e_col[1]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[1]][e_col[1]]);
   }
   Q_V[e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[1]][e_col[1]]);
}

//+------------------------------------------------------------------+
// Update using Off-policy
//+------------------------------------------------------------------+
void Cql::SetOffPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 0 represents highest valued Q_SA-action from Q_SA-Map
//as determined from Action() function above.
   double _sa = Q_SA[transition_act][e_row[0]][e_col[0]];
   double _v = Q_V[e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[0]][e_col[0]]);
   }
   Q_V[e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[0]][e_col[0]]);
}

Entre las funciones modificadas y revisadas se incluyen actualizaciones con la incorporación de un nuevo objeto «Q_V» que hemos representado como una matriz para facilitar la correspondencia con los respectivos estados del entorno, aunque podríamos haberlo representado fácilmente como un vector, ya que las coordenadas del estado del entorno se pueden asignar a un único índice entero. El antiguo mapa Q pasa a llamarse «Q_SA». Esta nueva denominación está en consonancia con los nuevos valores de seguimiento de objetos Q-Map independientes de las acciones, que es en lo que se centra TD, mientras que el cambio de nombre del antiguo Q-Map a Q_SA hace hincapié en sus valores de pares estado-acción, que se actualizan cada vez que se llama a la función. Nuestras implementaciones MQL5 anteriores se derivan de la siguiente fórmula para TD (que puede estar activada o desactivada):

Donde:

• V (s) : Valor del estado actual s
• V (s′) : Valor del siguiente estado s′
• α: Tasa de aprendizaje (controla cuánto ajustamos el valor actual)
• r: Recompensa recibida tras realizar la acción
• γ: Factor de descuento (determina la importancia de las recompensas futuras)
• Esta fórmula actualiza la estimación del valor de un estado V (s) basándose en la recompensa recibida y el valor estimado del siguiente estado V (s′)

Y, para recapitular, la fórmula para los pares acción-estado con actualización en la política, como SARSA por ejemplo, es la siguiente:

Donde:

• Q (s, a): Valor Q del par estado-acción actual (s, a)
• Q (s′, a′) : Valor Q del siguiente par estado-acción (s′, a′), donde a′ es la acción elegida por la política actual en el siguiente estado s′
• α: Tasa de aprendizaje
• r: Recompensa recibida tras realizar una acción a
• γ: Factor de descuento

Del mismo modo, la fórmula para las actualizaciones fuera de la política es la que se muestra a continuación:

Donde:

• Q (s, a): Valor Q del par estado-acción actual (s, a)
• max a′ ​Q (s′, a′): Valor Q máximo del siguiente estado s′ sobre todas las acciones posibles a′ (suponiendo que se tomará la mejor acción en s′).
• α: Tasa de aprendizaje
• r: Recompensa recibida tras realizar una acción a
• γ: Factor de descuento

A partir de las dos últimas fórmulas, queda claro que las actualizaciones específicas de cada acción proporcionan cierta información para la selección de la siguiente acción. Sin embargo, en el caso de la actualización TD, dado que agrega valores de todas las acciones y simplemente los asigna a su estado de entorno respectivo, la influencia de este proceso en la acción que se va a seleccionar no está bien definida.

Es por eso que al utilizar TD un modelo adicional, que en nuestro caso es una red neuronal de políticas, es necesario guiar la selección de la próxima acción del actor. Este modelo puede adoptar varias formas, pero para nuestros propósitos es simplemente un MLP de 3 capas de tamaño 3-9-3, donde la capa de salida proporciona una distribución de probabilidad para cada una de las 3 acciones posibles, que en nuestro caso siguen siendo comprar, vender y mantener. Este MLP será por tanto un clasificador y no un regresor. Indicamos el código de declaración de esta clase en la interfaz de clase de señal personalizada como se muestra a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalTD   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   
public:
   void                          CSignalTD(void);
   void                          ~CSignalTD(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   int               GetOutput(Cql *QL, CNeuralNetwork &PN);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   CNeuralNetwork    POLICY_NETWORK_BUY,POLICY_NETWORK_SELL;
};

El código fuente completo de nuestra clase de señal personalizada se adjunta al final de este artículo y está destinado a ser utilizado a través del asistente MQL5 para generar un Asesor Experto. Hay guías aquí y aquí para los lectores que sean nuevos en esto. Con nuestro código fuente adjunto, el lector puede realizar fácilmente cambios en el diseño de MLP cambiando no solo el número de capas, sino también su tamaño. Sin embargo, según nuestro diseño, la capa de entrada 3 está destinada a tomar como entradas la coordenada del entorno del eje x, el valor de transición o la lectura de la matriz Q_V actual y la lectura del entorno del eje y. El valor de transición se toma de la matriz Q_V que actualizamos en la configuración de la política de encendido y apagado, como ya se compartió en el código fuente anterior. Esta selección del valor de transición se maneja en la función Acción revisada como se indica a continuación:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   transition_value = Q_V[_next_row][_next_col];
   policy_history[1][0] = policy_history[0][0];
   policy_history[1][1] = policy_history[0][1];
   policy_history[1][2] = policy_history[0][2];
   policy_history[0][0] = _next_row;
   policy_history[0][1] = transition_value;
   policy_history[0][2] = _next_col;
   transition_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
   //if(transition_act!=1)printf(__FUNCSIG__+ " act is : %i ",transition_act);
}

Por lo tanto, la tesis predominante en nuestra red de políticas, la MLP antes mencionada, es que la acción adecuada que debe seleccionarse a continuación es una función del estado actual del entorno y su valor Q únicamente. Esto difiere de lo que hemos estado usando hasta aquí, donde se utilizó el Proceso de Decisión de Markov (MDP) para seleccionar la acción adecuada del Q-Map que renombramos en este artículo (código adjunto) a Q_SA. En todos los casos, hemos utilizado el MDP sin memoria calculando un búfer de secuencias recientes de estados del entorno. Estas secuencias de entorno, gracias a la función de Markov let, que se comparte nuevamente a continuación, nos brindan una proyección para el próximo estado del entorno.

//+------------------------------------------------------------------+
// Function to update markov matrix
//+------------------------------------------------------------------+
void Cql::LetMarkov(int OldRow, int OldCol, vector &E)  //
{  matrix _transitions;  // Count the transitions
   _transitions.Init(markov.Rows(), markov.Cols());
   _transitions.Fill(0.0);
   vector _states;  // Count the occurrences of each state
   _states.Init(markov.Rows());
   _states.Fill(0.0);
// Count transitions from state i to state ii
   for (int i = 0; i < int(E.Size()) - 1; i++)
   {  int _old_state = int(E[i]);
      int _new_state = int(E[i + 1]);
      _transitions[_old_state][_new_state]++;
      _states[_old_state]++;
   }
// Reset prior values to zero.
   markov.Fill(0.0);
// Compute probabilities by normalizing transition counts
   for (int i = 0; i < int(markov.Rows()); i++)
   {  for (int ii = 0; ii < int(markov.Cols()); ii++)
      {  if (_states[i] > 0)
         {  markov[i][ii] = double(_transitions[i][ii] / _states[i]);
         }
         else
         {  markov[i][ii] = 0.0;  // No transitions from this state
         }
      }
   }
}

Este proceso de determinación de los próximos estados gracias a MDP todavía se realiza con TD, aunque la diferencia aquí es que no podemos usar estas coordenadas del próximo estado proyectadas por sí solas para determinar la próxima acción. Anteriormente, cuando usábamos Q_SA, era cuestión de leer la acción con mayor ponderación de probabilidad a partir de las coordenadas del siguiente estado para saber qué se suponía que debía hacer el actor. Ahora bien, nuestra matriz equivalente, Q_V, solo nos da valores para cualquier coordenada de estado proporcionada, y aun así, determinar la próxima acción del actor es fundamental en el ciclo de aprendizaje de refuerzo.

Es por eso que presentamos una red de políticas, una MLP, que para nuestros propósitos hemos diseñado simplemente como un 3-9-3, que presenta una sola capa oculta de 9, que toma las 3 entradas mencionadas anteriormente de las dos coordenadas del entorno y su valor Q, y genera un vector de 3 que pretende capturar la distribución de probabilidad en las 3 posibles acciones de comprar, vender y mantener, siendo el valor con la puntuación más alta en el vector la acción recomendada.

Beneficios macro y propósito del TD

TD actualiza sus valores Q con más frecuencia que en Monte Carlo y las ventajas de esto en mercados financieros fluidos y que cambian rápidamente son obvias. Sin embargo, ¿qué lo diferencia de, por ejemplo, SARSA o Q-Learning desde el punto de vista de las ventajas? Intentaremos responder a esta pregunta analizando algunos ejemplos cotidianos.

Por definición, la principal diferencia entre TD y SARSA/Q-Learning es que TD se centra más en el aprendizaje basado en valores, donde solo se aprenden y actualizan los valores de estado, mientras que los otros dos algoritmos se centran en el emparejamiento estado-acción para realizar actualizaciones similares.

Escenario A

Supongamos que hay un sistema de gestión de inventario en un almacén que simplemente realiza un seguimiento de la cantidad de niveles de existencias en una multitud de productos. El objetivo de este sistema sería únicamente administrar los niveles de stock de inventario y garantizar que no haya exceso o defecto de ningún producto.

En esta situación, TD sería ventajoso sobre métodos como SARSA o Q-Learning simplemente por su enfoque en pares estado-valor, en lugar de pares estado-acción. Esto se debe a que, en este caso, el sistema solo necesitaría predecir el "valor" de cada estado (p. ej., el nivel general de existencias) sin evaluar cada acción específica (p. ej., realizar pedidos para cada SKU). Por lo tanto, en esta situación, sin la necesidad de una red de políticas MLP, el aprendizaje de TD puede actualizar la función de valor para el estado (niveles de inventario) sin calcular cada posible decisión de pedido para cada producto.

Además, la gestión del inventario puede tener cambios graduales en lugar de pares estado-acción abruptos que tienen retroalimentación de recompensa distinta. Dado que el aprendizaje TD trata con retroalimentación incremental, esto lo hace adecuado para entornos con transiciones suaves donde conocer el estado general es más importante que conocer el resultado de cada estado-acción. Finalmente, los entornos que tienen varias acciones y grandes espacios de estado-acción, como la gestión de inventario que es más compleja (donde necesitaríamos mapear un curso de acción para cada estado del nivel de inventario), Q-Learning y SARSA, aunque aplicables, seguramente tendrán un costo computacional, costos con los que TD nunca incurre debido a su aplicación holística más simple.

 

Escenario B

Considere un sistema de edificio inteligente que ajuste la configuración de calefacción, ventilación y aire acondicionado (HVAC) para minimizar el consumo de energía y mantener cómodos a sus ocupantes. Por lo tanto, sus objetivos de equilibrar las recompensas a corto plazo con los objetivos a largo plazo se alinean con la reducción de las facturas de energía y el mantenimiento del edificio a una temperatura y una calidad del aire óptimas, respectivamente.

En este caso, TD sería más adecuado que SARSA o Q-Learning porque los niveles de consumo de energía o la comodidad del usuario son métricas absolutas que no tienen ninguna acción asociada a ellas en función de sus valores. En este caso particular, para equilibrar las recompensas a corto y largo plazo, se pueden entrenar dos ciclos de aprendizaje de refuerzo para pronosticar ambas en paralelo. Las actualizaciones incrementales por ciclo de TD (en lugar de por episodio como vimos con Monte Carlo) también lo hacen ideal para este sistema de edificio inteligente, ya que las condiciones ambientales como la temperatura, la ocupación y la calidad del aire cambian gradualmente. Esto permite que TD proporcione un mecanismo de ajuste perfecto.

Finalmente, como se mencionó anteriormente, el equivalente de SARSA o Q-Learning vendrá con requisitos de memoria y cómputo adicionales ya que se requerirán acciones específicas para "remediar" cualquier déficit o exceso en los valores del estado del entorno.  

 

Escenario C

Un sistema de predicción y control del flujo de tráfico, cuyo objetivo es minimizar la congestión en múltiples intersecciones mediante la previsión del flujo de tráfico y el ajuste correspondiente de las señales semafóricas, constituye nuestro tercer posible caso de uso de TD. El aprendizaje automático (TD) también es ventajoso en esta situación, en comparación con SARSA o Q-Learning, ya que la principal preocupación es comprender y predecir el estado general del tráfico (como los niveles de congestión) en lugar de optimizar la acción de cada semáforo. El aprendizaje automático (TD) permite al sistema aprender el valor general de un estado del tráfico, en lugar del impacto de cada cambio específico en el semáforo.

El tráfico, que también es inherentemente dinámico y cambia continuamente a lo largo del día, influye en el modelo de actualización incremental de TD. Un algoritmo muy adaptable, a diferencia de Monte Carlo, que espera a que se complete el episodio antes de realizar actualizaciones. La reducción de la sobrecarga de procesamiento y memoria para TD también se aplica en este caso, especialmente si se tiene en cuenta lo entrelazados e interconectados que pueden estar los cruces de tráfico incluso en una ciudad relativamente pequeña. Los costos de computación y memoria seguramente serían un factor importante al implementar un sistema de predicción de flujo de tráfico, y TD contribuiría en gran medida a abordar este problema.

Escenario D

El mantenimiento predictivo en la fabricación presenta nuestro caso de uso final para el TD como algoritmo preferido en comparación con otros algoritmos de aprendizaje por refuerzo que hemos abordado hasta ahora. Consideremos un caso en el que una planta de fabricación busca predecir cuándo las máquinas necesitan mantenimiento para evitar tiempos de inactividad. Y al igual que con el sistema de edificios inteligentes, este sistema necesitaría equilibrar las recompensas a corto plazo (ahorro de costos de mantenimiento al retrasar los controles) con las ganancias a largo plazo (prevención de averías). El aprendizaje TD sería adecuado aquí porque puede actualizar el valor de salud general de la máquina a lo largo del tiempo basándose en una retroalimentación parcial, en lugar de rastrear acciones específicas (reparar o reemplazar) como lo harían SARSA o Q-learning.

TD también sería un mejor algoritmo porque la degradación de la máquina ocurre gradualmente y TD puede actualizar fácilmente el valor de salud de manera continua basándose en datos incrementales del sensor en lugar de esperar períodos más largos, lo que podría generar riesgos adicionales. Además, en una planta que tiene varias máquinas, el aprendizaje TD podría escalar bien, ya que el número de máquinas disminuye o aumenta porque se enfoca solo en rastrear el estado/salud de cada máquina y no tiene necesidad de almacenar y actualizar pares de acciones-estado específicos para cada máquina en la planta.

Estos son algunos casos, fuera del comercio financiero y los mercados, así que ahora consideremos cómo podemos aplicar esto específicamente como una clase de señal personalizada.

Estructuración de la clase de señal personalizada mediante el algoritmo TD

La clase de señal personalizada que construimos para implementar TD se basa en dos clases adicionales. Dado que es un algoritmo de aprendizaje por refuerzo, una de esas clases es la clase CQL. Ya hemos utilizado o hecho referencia a esta clase en todos los artículos anteriores; sin embargo, a continuación compartimos nuevamente su interfaz:

//+------------------------------------------------------------------+
//| Q_SA-Learning Class Interface.                                      |
//+------------------------------------------------------------------+
class Cql
{
protected:
   matrix            markov;
   void              LetMarkov(int OldRow, int OldCol, vector &E);

   vector            acts;
   matrix            environment;
   matrix            Q_SA[];
   matrix            Q_V;

public:
   void              Action(vector &E);
   void              Environment(vector &E_Row, vector &E_Col, vector &E);

   void              SetOffPolicy(double Reward, vector &E);
   void              SetOnPolicy(double Reward, vector &E);

   double            GetReward(double MaxProfit, double MaxLoss, double Float);
   vector            SetTarget(vector &Rewards, vector &TargetOutput);

   void              SetMarkov(int Index, int &Row, int &Col);
   int               GetMarkov(int Row, int Col);


   Sql               THIS;

   int               act[2];

   int               e_row[2];
   int               e_col[2];

   int               transition_act;
   double            transition_value;
   
   matrix            policy_history;

   vector            Q_Loss()
   {  vector _loss;
      _loss.Init(THIS.actions);
      _loss.Fill(0.0);
      for(int i = 0; i < THIS.actions; i++)
      {  _loss[i] = Q_SA[e_row[0]][e_col[0]][i];
      }
      return(_loss);
   }


   void              Cql(Sql &RL)
   {  //
      if(RL.actions > 0 && RL.environments > 0)
      {  policy_history.Init(2,2+1);
         policy_history.Fill(0.0);
         acts.Init(RL.actions);
         ArrayResize(Q_SA, RL.actions);
         for(int i = 0; i < RL.actions; i++)
         {  acts[i] = i + 1;
            Q_SA[i].Init(RL.environments, RL.environments);
         }
         Q_V.Init(RL.environments, RL.environments);
         environment.Init(RL.environments, RL.environments);
         for(int i = 0; i < RL.environments; i++)
         {  for(int ii = 0; ii < RL.environments; ii++)
            {  environment[i][ii] = ii + (i * RL.environments) + 1;
            }
         }
         markov.Init(RL.environments * RL.environments, RL.environments * RL.environments);
         markov.Fill(0.0);
         THIS = RL;
         ArrayFill(e_row, 0, 2, 0);
         ArrayFill(e_col, 0, 2, 0);
         ArrayFill(act, 0, 2, 1);
         transition_act = 1;
      }
   };
   void              ~Cql(void) {};
};

Esta es la clase principal de aprendizaje de refuerzo y algunas de sus clases que definen actualizaciones de políticas activadas y desactivadas ya se han compartido anteriormente. Además, esta clase suele ser suficiente para implementar el aprendizaje de refuerzo para una clase de señal personalizada; sin embargo, para TD, dado que no utilizamos ni confiamos únicamente en los valores del entorno para tomar decisiones comerciales, sino que optamos por continuar con la previsión de acciones adecuadas como lo hemos hecho en el pasado, necesitamos un modelo para hacer estas proyecciones.

Es por eso que se utiliza una clase adicional, la clase CNeuralNetwork, para definir este modelo como una red neuronal o MLP. De manera similar, su interfaz de clase se comparte a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CNeuralNetwork
{
protected:
   
   matrix               TransposeToCol(vector &V);
   matrix               TransposeToRow(vector &V);
   
public:
   CLayer               *layers[];
   double               m_learning_rate;
   ENUM_LOSS_FUNCTION   m_loss;
   void                 AddDenseLayer(ulong Neurons, ENUM_ACTIVATION_FUNCTION AF = AF_RELU, ulong LastNeurons = 0)
   {  ArrayResize(layers, layers.Size() + 1);
      layers[layers.Size() - 1] = new CLayer(Neurons, AF);
      if(LastNeurons  != 0)
      {  layers[layers.Size() - 1].AddWeights(LastNeurons);
      }
      else if(layers.Size() - 1 > 0)
      {  layers[layers.Size() - 1].AddWeights(layers[layers.Size() - 2].activations.Size());
      }
   };
   void                 Init(double LearningRate, ENUM_LOSS_FUNCTION LF)
   {  m_loss = LF;
      m_learning_rate = LearningRate;
   };
   
   vector               Forward(vector& Data);
   void                 Backward(vector& LabelAnswer);
   
   void                 CNeuralNetwork(){};
   void                 ~CNeuralNetwork()
   {  if(layers.Size() > 0)
      {  for(int i = 0; i < int(layers.Size()); i++)
         {  delete layers[i];
         }
      }
   };
};

Hemos realizado algunos cambios notables con respecto a la última clase CMLP que realizaba una función similar. El énfasis general estuvo puesto en la eficiencia; sin embargo, todavía es una versión beta, aunque para nuestros propósitos fue capaz de darnos algunos resultados. Además de los cambios de eficiencia que se realizaron principalmente en la función de retropropagación (Backward), y que son un trabajo en progreso, introdujimos una clase de capa y también cambiamos la forma en que se construye la red. La inicialización de la clase de señal personalizada ahora se ve de la siguiente manera: 

//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CSignalTD::CSignalTD(void) :    m_scale(5),
   m_use_markov(true),
   m_policy(true)

{
//--- initialization of protected data
   m_used_series = USE_SERIES_OPEN + USE_SERIES_HIGH + USE_SERIES_LOW + USE_SERIES_CLOSE + USE_SERIES_SPREAD + USE_SERIES_TIME;
   //
   RL.actions  = 3;//buy, sell, do nothing
   RL.environments = 3;//bullish, bearish, flat
   RL.use_markov = m_use_markov;
   RL.epsilon = m_epsilon;
   QL_BUY = new Cql(RL);
   QL_SELL = new Cql(RL);
   //
   POLICY_NETWORK_BUY.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_BUY.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_BUY.Init(0.0004,LOSS_BCE);
   //
   POLICY_NETWORK_SELL.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_SELL.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_SELL.Init(0.0004,LOSS_BCE);
}

Además de tener 2 clases CQL para manejar el aprendizaje de refuerzo en el lado de compra y venta respectivamente, ahora tenemos 2 redes de políticas para también hacer pronósticos de acción nuevamente en el lado de compra y venta respectivamente. La función de obtención de salida todavía se ejecuta de la misma manera que en artículos anteriores, con el cambio principal siendo que una instancia de la clase de red neuronal es una de sus entradas como red de políticas. Su nuevo listado es el siguiente:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CSignalTD::GetOutput(Cql *QL, CNeuralNetwork &PN)
{  int _td_act = 1;
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_row.Size() == m_scale+1
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale+1) &&
      _in_row_old.Size() == m_scale+1
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_col.Size() == m_scale+1
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale+1) &&
      _in_col_old.Size() == m_scale+1
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      _in_row.Resize(m_scale);
      _in_col.Resize(m_scale);
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
      PN.Forward(QL.policy_history.Row(1));
      vector _label;
      _label.Init(3);
      _label.Fill(0.0);
      if(_in_row[m_scale-1] > 0.0)
      {  _label[0] = 1.0;
      }
      else if(_in_row[m_scale-1] < 0.0)
      {  _label[2] = 1.0;
      }
      else if(_in_row[m_scale-1] == 0.0)
      {  _label[1] = 1.0;
      }
      PN.Backward(_label);
      vector _td_output = PN.Forward(QL.policy_history.Row(0));
      if(_td_output[0] >= _td_output[1] && _td_output[0] >= _td_output[2])
      {  _td_act = 0;
      }
      else if(_td_output[2] >= _td_output[0] && _td_output[2] >= _td_output[1])
      {  _td_act = 2;
      }
   }
   return(_td_act);
}

Con una red de políticas como una de sus entradas, ahora es posible realizar aprendizaje en línea o incremental ya que no entrenamos con un lote de datos antes de pronosticar, sino solo con los últimos datos de barra única. Solo debería haber una ejecución de retropropagación y una ejecución de avance, pero debido a que necesitamos cargar la información de la barra de precio actual en nuestra red neuronal antes de realizar la ejecución de retropropagación o de avance, realizamos una única ejecución de avance con la información de la barra anterior antes de ella, para cargar esta información. Nuestra función de avance también se modifica para devolver el vector de clasificación de salida del paso de avance. Tiene un tamaño de tres, donde cada valor en el índice respectivo proporciona una "probabilidad" o umbral de probabilidad de vender, mantener o comprar si queremos seguir el orden de indexación 0, 1, 2 respectivamente.

Entonces, para hacer un resumen de lo mencionado anteriormente, nos quedamos con el mismo entorno de aprendizaje de refuerzo simple y la configuración de acciones de 3 estados y 3 acciones. La elección de actualización de políticas es optimizable, como en el último artículo sobre aprendizaje de refuerzo que cubrió Monte Carlo. Sin embargo, cuando se realizan actualizaciones aquí, solo actualizan los valores Q de una nueva matriz introducida, la Q_V. Esto contrasta con lo que hemos hecho en el pasado, que era actualizar los valores Q en todo un mapa de entorno, para cada acción. La actualización de valores para cada acción fue constructiva para seleccionar la siguiente acción porque una vez que se utiliza el Proceso de Decisión de Markov para determinar las coordenadas del próximo estado del entorno, entonces simplemente se convierte en una cuestión de leer la acción con el Valor Q más alto y seleccionarla como nuestra próxima acción.

Con TD, nuestra matriz de entorno Q_V no tiene acciones con valores Q sino que solo tiene valores asignados a un entorno particular. Esto significa que para seleccionar o determinar el próximo curso de acción, se utiliza una red de políticas (una MLP en nuestro caso) para realizar estos pronósticos y sus entradas serían el valor del entorno actual (que es una suma de facto de todos los valores Q de las acciones aplicables en ese estado), así como las coordenadas del estado del entorno. El resultado, como también se mencionó, es una "distribución de probabilidad" entre las tres posibles acciones sobre qué acción sería la mejor dado el entorno actual y su valor.

Esta clase de señal personalizada se ensambla así con el asistente MQL5 en un Asesor Experto y, después de un breve período de optimización, para el año 2022 en el marco temporal de 1 hora que utiliza el símbolo GBP USD, una de las configuraciones favorables de ese período nos proporciona el siguiente informe:

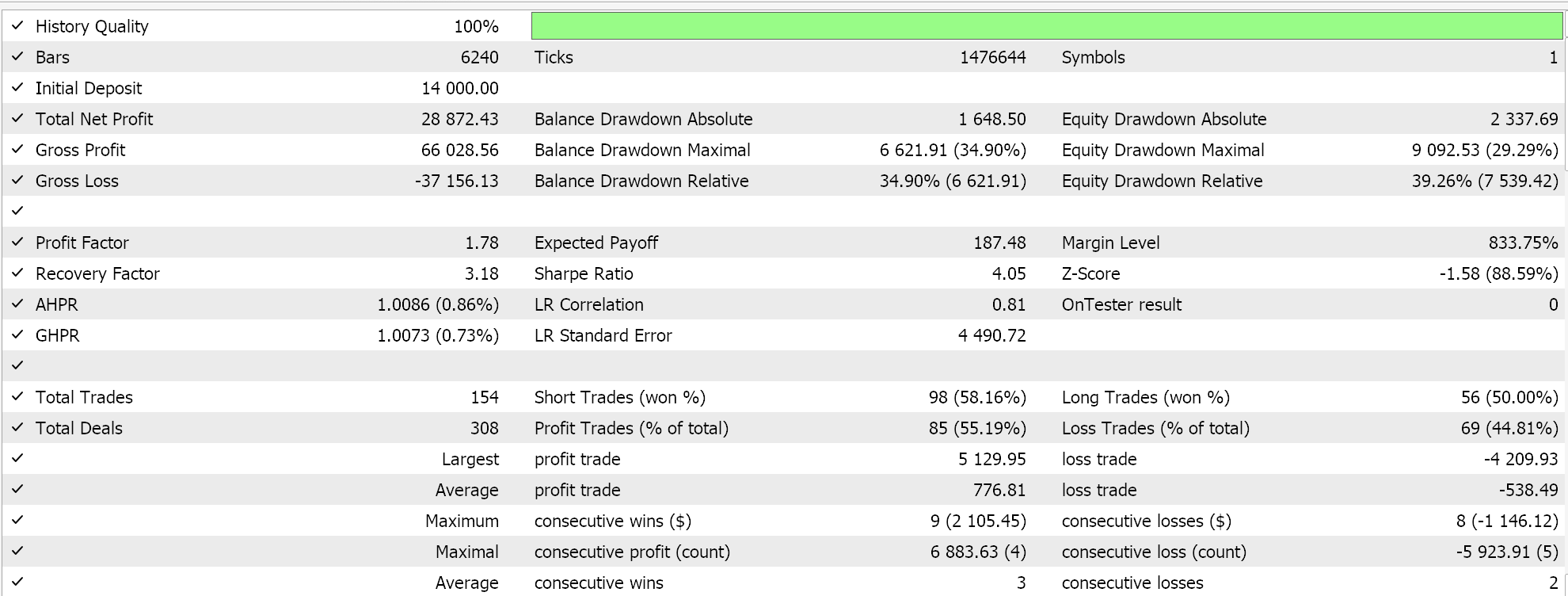
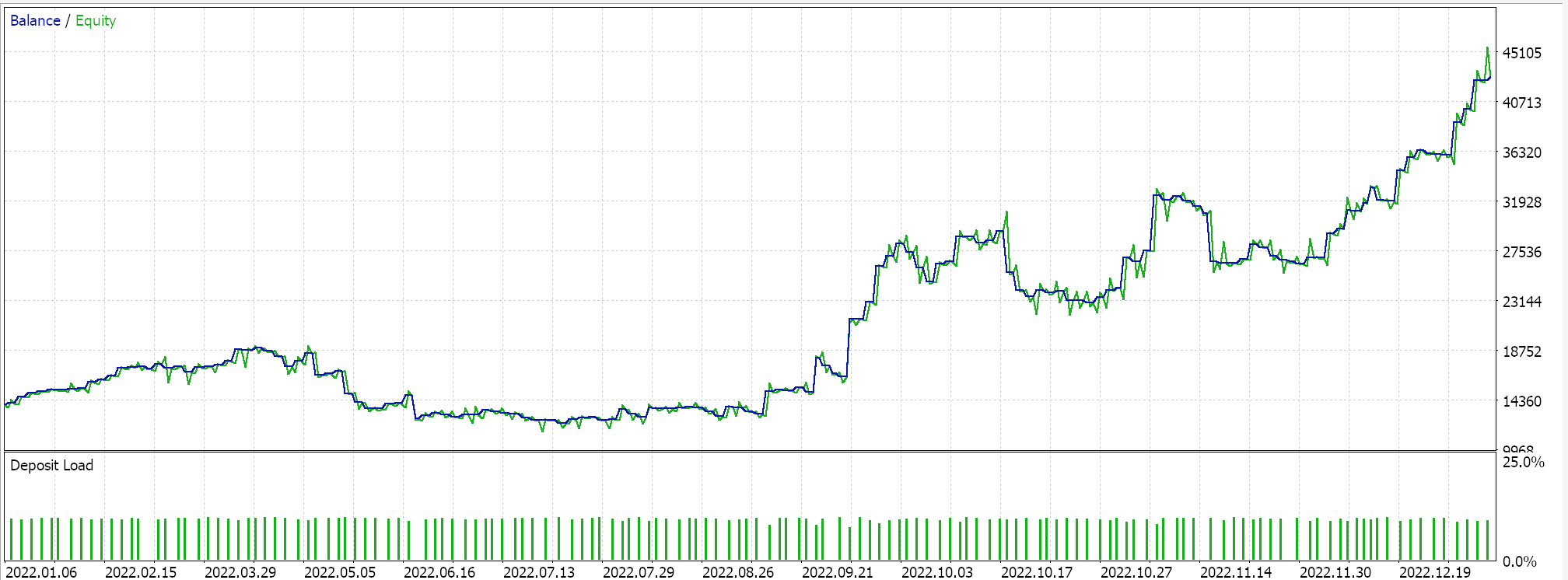
Estos resultados quizás hablan del potencial de nuestra clase de señal personalizada, pero sin denigrarlos, siempre se recomienda validar de forma cruzada las configuraciones de cualquier Asesor Experto antes de optar por implementarlo en un entorno en vivo. La validación cruzada y la diligencia de pruebas adicionales durante un período de tiempo más largo que el que hemos hecho aquí se dejan al lector para que las examine como crea conveniente.

Optimización y ajuste de la clase de señal con aprendizaje TD

En nuestras pruebas anteriores, solo optimizamos el epsilon, si utilizar la ponderación de Markov en el proceso de actualización y si realizar actualizaciones de políticas o actualizaciones fuera de políticas. Por supuesto, había parámetros adicionales típicos no relacionados con el TD, como los umbrales de apertura y cierre para las condiciones largas y cortas, el nivel de take profit, así como el umbral del precio de entrada en puntos.

Sin embargo, en el aprendizaje por refuerzo y en el aprendizaje por refuerzo, hay bastantes parámetros que hemos pasado por alto y hemos utilizado con valores preestablecidos. Estos son alfa y gamma, a los que se les asignan los valores 0.1 y 0.5 respectivamente. Estos dos parámetros son claves en las actualizaciones de políticas y podrían ser muy sensibles al rendimiento general de la clase de señal. Los otros parámetros clave que hemos pasado por alto al implementar nuestra clase de señal al asignarles efectivamente valores constantes son las configuraciones de las redes de políticas. Nos quedamos con una red 3-9-3 donde las funciones de activación en cada capa estaban todas preestablecidas, así como la tasa de aprendizaje. Cada uno de estos y probablemente todos ellos cuando se ajustan simultáneamente pueden tener grandes efectos en los resultados y el rendimiento de la clase de señal personalizada.

Conclusión

Hemos analizado el algoritmo de diferencia temporal del aprendizaje de refuerzo y hemos intentado destacar sus casos de uso que lo diferencian de otros algoritmos que ya hemos cubierto. Un aspecto que no hemos analizado y que es interesante para el aprendizaje de refuerzo en general es la disminución de la exploración con el paso del tiempo. La tesis o argumento detrás de esto es que a medida que un modelo de aprendizaje de refuerzo aprende con el tiempo, la necesidad de explorar nuevo territorio o seguir aprendiendo disminuye enormemente; por lo tanto, la explotación sería más importante. Esto es algo que los lectores pueden tener en cuenta cuando quieran personalizar el código adjunto para un uso posterior.

Otro aspecto podría ser hacer que épsilon sea variable, y no sólo disminuyéndola, que es lo que implica la descomposición anterior. La tesis de esto es que el aprendizaje de refuerzo debe ser muy dinámico y adaptable, a diferencia de los modelos de aprendizaje supervisado, que se basan en datos estáticos. Por lo tanto, el marco de aprendizaje de refuerzo de TD puede interactuar activamente con un entorno cambiante. Hemos considerado métodos de tasa de aprendizaje dinámico en un artículo anterior, y se podría argumentar que lo mismo podría considerarse para épsilon, de modo que la presunción de descomposición por sí sola no sirva como la única forma de mantener el aprendizaje de refuerzo en sus raíces.