Redes neuronales en el trading: Modelos de difusión direccional (DDM)

Introducción

El aprendizaje no supervisado de representaciones mediante modelos de difusión se ha convertido en un importante campo de investigación en visión por computadora. Los resultados experimentales de varios investigadores confirman la eficacia de los modelos de difusión en el entrenamiento de representaciones visuales significativas. La recuperación de datos distorsionados por determinados niveles de ruido proporciona una base adecuada para que el modelo aprenda conceptos visuales complejos, mientras que el aumento de la prioridad de unos niveles de ruido sobre otros durante el entrenamiento mejora el rendimiento de los modelos de difusión.

Los autores del artículo "Directional diffusion models for graph representation learning" propusieron utilizar modelos de difusión para el aprendizaje no supervisado de la representación de grafos. Sin embargo, en la práctica se encontraron con una limitación de los modelos de difusión vainilla. Sus experimentos demostraron que los datos de los grafos pueden tener estructuras anisótropas y direccionales distintas que resultan menos visibles en las imágenes. Los modelos de difusión estándar con un proceso de difusión directa isotrópico provocan una rápida disminución de la relación señal/ruido (Signal-to-Noise Ratio — SNR) interna, lo cual los hace menos eficaces en el estudio de estructuras anisótropas. Por lo tanto, se propusieron nuevos enfoques para capturar eficazmente dichas estructuras anisotrópicas. Se trata de modelos de difusión direccional, que pueden mitigar eficazmente el problema de la rápida disminución de la relación señal/ruido. El framework propuesto incorpora la generación de ruido direccional y dependiente de los datos durante la difusión directa. Las activaciones intermedias derivadas del modelo de absorción de ruido captan eficazmente la información semántica y topológica útil necesaria para las tareas posteriores.

En consecuencia, los modelos de difusión direccional ofrecen un enfoque generativo prometedor para el aprendizaje de representaciones de grafos. Los resultados de los experimentos realizados por los autores del método demuestran el rendimiento superior de los modelos en comparación con el aprendizaje contrastivo y los enfoques generativos. Cabe destacar que, en tareas de clasificación de grafos, los modelos de difusión direccional superan incluso a los modelos básicos de aprendizaje supervisado, lo que pone de relieve el enorme potencial de los modelos de difusión para el aprendizaje de representaciones de grafos.

La aplicación de modelos de difusión en el contexto del trading resulta prometedora a la hora de mejorar los métodos de representación y análisis de los datos del mercado. Los modelos de difusión direccional que tienen en cuenta las estructuras anisótropas de los datos pueden ser potencialmente útiles. Como los mercados financieros suelen caracterizarse por movimientos asimétricos y direccionales, los modelos de ruido direccional pueden reconocer con mayor eficacia las pautas estructurales de los movimientos de tendencia y corrección. Y esto pondrá de relieve las dependencias ocultas y los patrones estacionales.

1. El algoritmo DDM

Existen notables diferencias en las propiedades estructurales de los datos entre los grafos y las imágenes. Durante difusión directa vainilla, se añadirá sucesivamente ruido gaussiano isotrópico a los datos de origen hasta convertir la secuencia analizada en ruido blanco. Este proceso tiene sentido cuando los datos siguen distribuciones isotrópicas, ya que convierte gradualmente un punto de datos en ruido y genera datos ruidosos con una amplia gama de SNR. Sin embargo, en el caso de distribuciones de datos anisotrópicas, la adición de ruido isotrópico puede contaminar rápidamente la estructura de los datos, provocando una rápida reducción de la SNR a cero.

Como consecuencia, los modelos de eliminación de ruido no son capaces de entrenar representaciones de características significativas y discriminatorias que puedan utilizarse eficazmente para tareas posteriores. En cambio, con los modelos de difusión direccional que incluyen un proceso dependiente de los datos y la difusión direccional directa, la relación señal-ruido disminuye a un ritmo más lento. Esta reducción más lenta permite la extracción de representaciones de características de grano fino con diferentes SNR, preservando la información importante sobre las estructuras anisotrópicas. La información obtenida puede usarse para resolver problemas posteriores de clasificación de grafos y nodos.

El proceso de generación de ruido direccional consiste en convertir el ruido gaussiano isotrópico original en ruido anisótropo incorporando dos restricciones adicionales. Y estas dos limitaciones desempeñan un papel crucial en la mejora de los modelos de difusión.

Supongamos que Gt = (A, Xt) es la solución de trabajo en el t-ésimo paso de difusión directa, donde 𝐗t = {xt,1, xt,2, …, xt,N} representa las características estudiadas.

donde x0,i es el vector de características brutas del nodo i, μ ∈ ℛ y σ ∈ ℛ denotan los tensores de valores medios y desviaciones estándar de dimensionalidad d de las características sobre todos los N nodos, respectivamente, y ⊙ denota la multiplicación por elementos. Durante el entrenamiento de minipaquetes, μ y σ se calculan para los grafos dentro del paquete. El parámetro ɑt supone una gráfico de desviación fija y está parametrizado por la secuencia decreciente {β ∈ (0, 1)}.

A diferencia del proceso de difusión vainilla, los modelos de difusión direccional incluyen dos restricciones adicionales. Una de ellas predetermina la conversión del ruido gaussiano independiente de los datos en ruido anisótropo y dependiente de los paquetes. En esta restricción, cada coordenada del vector de ruido posee la misma media empírica y la misma desviación típica empírica que la coordenada correspondiente en los datos. Esto limita el proceso de difusión a la vecindad local del paquete, evitando una desviación excesiva y manteniendo la coherencia local. La otra restricción se introduce como una dirección angular que gira el ruido ε en el mismo hiperplano del objeto x0,i manteniendo la direccionalidad del objeto original. Esta restricción ayuda a mantener la estructura interna de los datos durante la difusión directa.

Estas dos restricciones funcionan como dúo para garantizar que el proceso de difusión directa tenga en cuenta la estructura básica de los datos y evite que las señales se difuminen rápidamente. Como resultado, la relación señal-ruido decae lentamente, lo cual permite a los modelos de difusión direccional extraer de manera eficaz representaciones de características significativas a diferentes escalas de SNR. Esto, a su vez, mejora el rendimiento de las tareas posteriores ofreciendo representaciones más fiables e informativas.

Los autores del método siguen la misma estrategia de aprendizaje que en los modelos de difusión vainilla y entrenan un modelo fθ que absorbe el ruido para aproximar el proceso de difusión inversa. Como la inversa del proceso directo con ruido direccional no puede expresarse en forma cerrada, se propuso que el modelo de reducción de ruido fθ predijese directamente la secuencia original.

A continuación le mostramos la visualización de autor del framework Directional diffusion models.

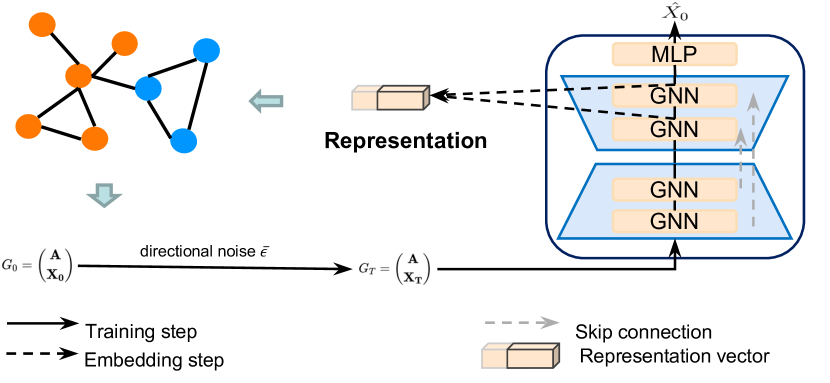
2. Implementación con MQL5

Tras repasar los aspectos teóricos del framework Directional diffusion models, pasaremos a la parte práctica de nuestro artículo, donde consideraremos una de las opciones para aplicar los enfoques propuestos utilizando MQL5.

Dividiremos nuestro trabajo en 2 bloques. En el primer paso, añadiremos ruido direccional a los datos analizados y, a continuación, implementaremos el framework dentro de una única clase.

2.1 Añadimos ruido direccional

Y antes de empezar, hablaremos del algoritmo de acción de la generación de ruido direccional. En primer lugar, necesitaremos el ruido de una distribución normal. Podemos obtenerlo fácilmente usando las bibliotecas MQL5 estándar.

A continuación, según el algoritmo propuesto por los autores del framework, deberemos convertirlo en ruido anisótropo dependiente de los datos de origen. Para ello, necesitaremos la media y la varianza de cada característica. Si lo pensamos detenidamente, ya hemos resuelto un problema similar al construir la capa de normalización por lotes CNeuronBatchNormOCL. Recordemos que el algoritmo de normalización por lotes toma los datos de origen con media cero y varianza unitaria. Sin embargo, la distribución de los datos cambia durante la fase de desplazamiento y escalado. Y probablemente podríamos tomar dicha información de la capa de normalización de los datos de origen. Además, ya hemos implementado el procedimiento para obtener los parámetros de la distribución original al construir la clase de normalización inversa CNeuronRevINDenormOCL. Pero este enfoque nos limitará a la hora de utilizar este framework.

Así que hemos ido un poco más lejos, y hemos decidido combinar la adición de ruido direccional con la normalización de los datos. Y aquí es donde nos surge la pregunta: ¿en qué momento añadimos el ruido?

De hecho, podemos añadir el ruido ANTES de normalizar los datos de origen. Pero en ese caso, distorsionaríamos el propio proceso de normalización. Al fin y al cabo, añadir ruido cambiará la distribución de los datos. Por lo tanto, al realizar la normalización con la media y la varianza previamente definidas en la salida, obtendremos una distribución desplazada. Y eso no resulta deseable.

La segunda opción sería añadir ruido a la salida de la capa de normalización. En este caso, tendremos que corregir el ruido gaussiano de los coeficientes de escalado y desplazamiento. Pero si nos fijamos en las fórmulas anteriores del algoritmo del autor, podremos ver que cuando se ajusta la dirección del ruido, este se desplaza hacia nuestro factor de desplazamiento. Como consecuencia, a medida que aumente el factor de desplazamiento, obtendremos ruido "asimétrico" desplazado. Lo cual tampoco resulta deseable.

Tras sopesar los pros y los contras, hemos optado por el camino inverso y añadido ruido entre la normalización de los datos y el paso del desplazamiento de escalado. En este caso, excluiremos el paso de transformación del ruido, ya que esperamos obtener datos con media cero y una varianza unitaria tras la normalización. Con esta distribución generaremos el ruido. Y para la etapa de escalado y desplazamiento, suministraremos los datos ya "ruidosos", lo que permitirá al modelo aprender los coeficientes correctos.

Ya hemos definido los principios de aplicación. Ahora podemos pasar al trabajo práctico. Implementaremos este algoritmo en el lado del contexto OpenCL. Para ello, crearemos un nuevo kernel BatchFeedForwardAddNoise. Diremos directamente que el algoritmo de este kernel está tomado en gran parte del kernel de pasada directa de la capa de normalización por lotes. No obstante, añadiremos un búfer de datos con ruido gaussiano y un coeficiente de valores atípicos ɑ.

__kernel void BatchFeedForwardAddNoise(__global const float *inputs, __global float *options,
                                       __global const float *noise, __global float *output,
                                       const int batch, const int optimization, 
                                       const int activation, const float alpha)
  {
   if(batch <= 1)
      return;
   int n = get_global_id(0);
   int shift = n * (optimization == 0 ? 7 : 9);

En el cuerpo del método, primero comprobaremos el tamaño del paquete de normalización, que deberá ser mayor que "1". Y luego determinaremos un desplazamiento en los búferes de datos basado en el ID del flujo actual.

A continuación, comprobaremos la presencia de números reales en el búfer de parámetros de normalización. Los elementos incorrectos se sustituirán por valores cero.

   for(int i = 0; i < (optimization == 0 ? 7 : 9); i++)
     {
      float opt = options[shift + i];
      if(isnan(opt) || isinf(opt))
         options[shift + i] = 0;
     }

Luego realizaremos la normalización de los datos de origen de acuerdo con el algoritmo de kernel básico.

   float inp = inputs[n];
   float mean = (batch > 1 ? (options[shift] * ((float)batch - 1.0f) + inp) / ((float)batch) : inp);
   float delt = inp - mean;
   float variance = options[shift + 1] * ((float)batch - 1.0f) + pow(delt, 2);
   if(batch > 0)
      variance /= (float)batch;
   float nx = (variance > 0 ? delt / sqrt(variance) : 0);

En esta fase, obtendremos los datos de origen normalizados con una media cero y una varianza unitaria. Y en este punto añadiremos el ruido, corregido previamente su dirección.

   float noisex = sqrt(alpha) * nx + sqrt(1-alpha) * fabs(noise[n]) * sign(nx);

Y luego ejecutaremos el algoritmo de escalado y desplazamiento con los resultados almacenados en los búferes de datos correspondientes, de forma similar a la implementación del kernel donante. Solo que esta vez aplicaremos escalado y desplazamiento a los valores ruidosos.

   float gamma = options[shift + 3];
   if(gamma == 0 || isinf(gamma) || isnan(gamma))
     {
      options[shift + 3] = 1;
      gamma = 1;
     }
   float betta = options[shift + 4];
   if(isinf(betta) || isnan(betta))
     {
      options[shift + 4] = 0;
      betta = 0;
     }
//---
   options[shift] = mean;
   options[shift + 1] = variance;
   options[shift + 2] = nx;
   output[n] = Activation(gamma * noisex + betta, activation);
  }

ya hemos implementado el algoritmo de pasada directa. ¿Y el de pasada inversa? Aquí debemos decir que, para realizar las operaciones de pasada directa, hemos decidido utilizar una implementación completa de los algoritmos de la capa de normalización por lotes. Lo que ocurre es que no entrenamos el ruido. En consecuencia, el gradiente de error se transferirá completamente a los datos de origen. Nuestro uso del coeficiente ɑ solo crea cierto desenfoque de la región centrada cerca de los datos de origen. Por lo tanto, podemos despreciar este coeficiente y transferir completamente el gradiente de error a la capa de datos de origen según el algoritmo de la capa de normalización por lotes.

Así completaremos el trabajo en el lado del programa OpenCL. Podrá ver su código completo en el archivo adjunto. Ahora comenzaremos a trabajar en la parte del programa principal, donde crearemos una nueva clase CNeuronBatchNormWithNoise. Como adivinará fácilmente, heredaremos la funcionalidad principal de la clase de normalización por lotes. Aquí, sin embargo, redefiniremos solo el método de pasada directa. A continuación, le mostraremos la estructura de la nueva clase.

class CNeuronBatchNormWithNoise  :  public CNeuronBatchNormOCL
  {
protected:
   CBufferFloat      cNoise;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   
public:
                     CNeuronBatchNormWithNoise(void) {};
                    ~CNeuronBatchNormWithNoise(void) {};
   //---
   virtual int       Type(void) const   {  return defNeuronBatchNormWithNoise;    }
  };

Como habrá notado, hemos intentado mantener nuestra nueva clase CNeuronBatchNormWithNoise lo más simple posible. No obstante, para organizar la funcionalidad requerida, necesitaremos un búfer para transmitir el ruido que generaremos en el lado del programa principal al contexto OpenCL. Sin embargo, no hemos redefinido ni el método de inicialización del objeto ni los métodos de gestión de archivos. Después de todo, no tiene sentido guardar ruido aleatorio. Por lo tanto, hemos sacado todo el trabajo al método feedForward, en cuyos parámetros obtendremos un puntero al objeto de datos de origen.

bool CNeuronBatchNormWithNoise::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!bTrain)
      return CNeuronBatchNormOCL::feedForward(NeuronOCL);

Aquí conviene señalar que solo añadiremos ruido al entrenar el modelo. Esto le permitirá aprender estructuras significativas de los datos de origen. Durante la explotación, sin embargo, queremos utilizar el modelo entrenado como un filtro, recuperando estructuras de datos significativas a partir de datos reales que contengan alguna fracción de valores de ruido. Por ello, durante la explotación simplemente realizaremos la normalización de los datos usando la clase padre.

El código adicional solo se ejecutará mientras se entrene el modelo. Primero comprobaremos la relevancia del puntero resultante al objeto de datos de origen.

if(!OpenCL || !NeuronOCL)
   return false;

Y luego lo almacenaremos en una variable interna.

PrevLayer = NeuronOCL;

Después comprobaremos el tamaño del paquete de normalización. Y si no es superior a 1, simplemente sincronizaremos las funciones de activación y finalizaremos el método con un resultado positivo. Porque en este caso el resultado del algoritmo de normalización será igual a los datos de origen. Y para evitar realizar trabajo innecesario, simplemente transmitiremos los datos de origen obtenidos a la capa posterior.

if(iBatchSize <= 1)
  {
   activation = (ENUM_ACTIVATION)NeuronOCL.Activation();
   return true;
  }

Si se superan con éxito todos los puntos de control anteriores, primero generaremos ruido a partir de una distribución normal.

double random[];
if(!Math::MathRandomNormal(0, 1, Neurons(), random))
   return false;

Después tendremos que transmitirlo al contexto OpenCL. Pero no hemos redefinido el método de inicialización del objeto. Así que primero comprobaremos nuestro búfer de datos para ver si hay suficientes elementos y el búfer creado previamente en el contexto.

if(cNoise.Total() != Neurons() ||
   cNoise.GetOpenCL() != OpenCL)
  {
   cNoise.BufferFree();
   if(!cNoise.AssignArray(random))
      return false;
   if(!cNoise.BufferCreate(OpenCL))
      return false;
  }

Si obtenemos un valor negativo en uno de los puntos de control, redimensionaremos el búfer y crearemos un nuevo puntero en el contexto OpenCL.

De lo contrario, simplemente copiaremos los datos en un búfer y los trasladaremos a la memoria contextual OpenCL.

else
  {
   if(!cNoise.AssignArray(random))
      return false;
   if(!cNoise.BufferWrite())
      return false;
  }

A continuación, ajustaremos el tamaño real de los paquetes y determinaremos aleatoriamente el nivel de ruido de los datos de origen.

iBatchCount = MathMin(iBatchCount, iBatchSize);
float noise_alpha = float(1.0 - MathRand() / 32767.0 * 0.01);

Y una vez hayamos preparado todos los datos necesarios, quedará pasarlos a los parámetros de nuestro kernel creado anteriormente.

uint global_work_offset[1] = {0};
uint global_work_size[1];
global_work_size[0] = Neurons();
int kernel = def_k_BatchFeedForwardAddNoise;
ResetLastError();
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_inputs, NeuronOCL.getOutputIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_noise, cNoise.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_options, BatchOptions.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_output, Output.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_activation, int(activation)))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_alpha, noise_alpha))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_batch, iBatchCount))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_optimization, int(optimization)))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
//---
if(!OpenCL.Execute(kernel, 1, global_work_offset, global_work_size))
  {
   printf("Error of execution kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                GetLastError(), __LINE__);
   return false;
  }
   iBatchCount++;
//---
   return true;
  }

Y poner el kernel en la cola de ejecución. De esta forma, controlaremos el proceso de las operaciones en cada paso. Y tras finalizar estas, devolveremos el resultado lógico de las mismas al programa externo.

Con esto concluiremos nuestra nueva clase CNeuronBatchNormWithNoise. Su código completo figura en el archivo adjunto.

2.2 Clase de framework DDM

Antes hemos implementado el objeto de adición de ruido direccional a los datos de origen. Ahora construiremos el framework Directional diffusion models en nuestra interpretación.

Debemos prestar atención de inmediato a que utilizaremos la estructura de los planteamientos propuestos por los autores del framework. Pero antes permítame algunas digresiones en el contexto de la resolución de nuestros problemas. En nuestra implementación, también utilizaremos la arquitectura en forma de U propuesta por los autores del método, pero sustituiremos las redes neuronales gráficas (GNN) por bloques del Codificador del Transformer. Además, los autores del método introducen datos ya ruidosos en la entrada del modelo, mientras que nosotros añadiremos ruido en el propio modelo. Pero lo primero es lo primero.

Para implementar nuestra solución, crearemos una nueva clase CNeuronDiffusion. Como objeto padre, utilizaremos un Transformer en forma de U. A continuación, le mostraremos la estructura de la nueva clase.

class CNeuronDiffusion  : public CNeuronUShapeAttention
  {
protected:
   CNeuronBatchNormWithNoise  cAddNoise;
   CNeuronBaseOCL             cResidual;
   CNeuronRevINDenormOCL      cRevIn;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronDiffusion(void) {};
                    ~CNeuronDiffusion(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint units_count, 
                          uint layers, uint inside_bloks, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronDiffusion;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

En la estructura de la clase presentada vemos la declaración de tres objetos, cuyo propósito conoceremos durante la implementación de los métodos de la clase. Usaremos los objetos heredados para construir la arquitectura básica del modelo de filtrado de ruido.

Todos los objetos nuevos se declararán estáticamente, lo que nos permitirá dejar vacíos el constructor y el destructor de la clase. La inicialización de todos los objetos se realizará en el método Init.

En los parámetros del método obtendremos las constantes básicas que definirán la arquitectura del objeto a crear. Debemos decir que en este caso hemos transferido completamente la estructura de los parámetros del método de la clase padre sin ningún cambio.

bool CNeuronDiffusion::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                            uint window, uint window_key, uint heads, 
                            uint units_count, uint layers, uint inside_bloks, 
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Sin embargo, durante la construcción de los nuevos algoritmos, cambiaremos ligeramente la secuencia de uso de los objetos heredados. Por lo tanto, en el cuerpo del método llamaremos al método homónimo de la clase básica, donde solo se inicializarán las interfaces principales.

A continuación, inicializaremos el objeto para normalizar los datos de origen con la adición de ruido. Este es el objeto que utilizaremos para el procesamiento inicial de los datos iniciales.

if(!cAddNoise.Init(0, 0, OpenCL, window * units_count, iBatch, optimization))
   return false;

Luego construiremos la estructura del transformador en forma de U. Aquí utilizaremos primero el bloque de atención multicabeza.

if(!cAttention[0].Init(0, 1, OpenCL, window, window_key, heads, units_count, layers, optimization, iBatch))
   return false; 

Y tras este, añadiremos una capa convolucional de reducción de la dimensionalidad.

if(!cMergeSplit[0].Init(0, 2, OpenCL, 2 * window, 2 * window, window, (units_count + 1) / 2, optimization, 
                                                                                                  iBatch))
   return false;

Y recursivamente formaremos los objetos de cuello.

 if(inside_bloks > 0)
   {
    CNeuronDiffusion *temp = new CNeuronDiffusion();
    if(!temp)
       return false;
    if(!temp.Init(0, 3, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, inside_bloks - 1, 
                                                                                     optimization, iBatch))
      {
       delete temp;
       return false;
      }
    cNeck = temp;
   }
 else
   {
   CNeuronConvOCL *temp = new CNeuronConvOCL();
   if(!temp)
      return false;
   if(!temp.Init(0, 3, OpenCL, window, window, window, (units_count + 1) / 2, optimization, iBatch))
     {
      delete temp;
         return false;
     }
   cNeck = temp;
     }

Aquí debemos señalar que hemos complicado un poco la arquitectura del modelo. Y con ello, el problema resuelto por el modelo. La cuestión es que hemos añadido recurrentemente objetos de difusión direccional similares como objeto de cuello, y esto significa que cada nueva capa añadirá ruido a los datos de origen. Como consecuencia, el modelo aprenderá a funcionar y a recuperar datos a partir de datos con mucho ruido.

Este enfoque no contradice la idea de los modelos de difusión, que son esencialmente modelos generativos, y se crearon para generar iterativamente datos a partir del ruido. Sin embargo, también podemos utilizar objetos de la clase padre en el cuello del modelo.

A continuación, añadiremos un segundo bloque de atención a nuestro modelo de supresión de ruido.

if(!cAttention[1].Init(0, 4, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, optimization,
                                                                                                     iBatch))
   return false;

Y una capa de convolución de recuperación de la dimensionalidad al nivel de los datos de origen.

if(!cMergeSplit[1].Init(0, 5, OpenCL, window, window, 2 * window, (units_count + 1) / 2, optimization, iBatch))
   return false;

Según la arquitectura del transformador en forma de U, complementaremos el resultado obtenido con los datos del enlace residual. Para registrarlos, crearemos una capa neuronal básica.

if(!cResidual.Init(0, 6, OpenCL, Neurons(), optimization, iBatch))
   return false;
if(!cResidual.SetGradient(cMergeSplit[1].getGradient(), true))
   return false;

A continuación, sincronizaremos los búferes de gradiente de la capa de enlace residual y la recuperación de la dimensionalidad.

Después añadiremos una capa de normalización inversa, que no mencionan los autores del framework, pero que se deduce de su lógica.

if(!cRevIn.Init(0, 7, OpenCL, Neurons(), 0, cAddNoise.AsObject()))
   return false;

La cuestión es que la versión del framework del autor no usa la normalización de datos. Se dice que se utilizan los datos de los grafos entrenados, que son procesados por redes de grafos. Y se espera que la salida del modelo produzca datos de origen sin ruido. Y durante el aprendizaje, el error de recuperación de datos se reducirá al mínimo. Nosotros, en cambio, usamos la normalización de datos en nuestra solución. Por lo tanto, para comparar los resultados con los valores reales, tendremos que devolver los datos a la distribución original. Precisamente este trabajo es el que realiza la capa de normalización inversa.

Ahora solo tenemos que sustituir los punteros a los búferes de datos para evitar operaciones de copiado innecesarias y devolver el resultado lógico de las transacciones al programa que realiza la llamada.

   if(!SetOutput(cRevIn.getOutput(), true))
      return false;
//---
   return true;
  }

Pero tenga en cuenta que en este caso solo estaremos sustituyendo el puntero al búfer de resultados. Esto dejará intacto el búfer de gradiente de error. Discutiremos las razones de esta decisión durante la revisión de los algoritmos de los métodos de pasada inversa.

Mientras tanto, pasaremos al método feedForward.

bool CNeuronDiffusion::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cAddNoise.FeedForward(NeuronOCL))
      return false;

En los parámetros del método, obtendremos el puntero al objeto de datos de origen, que pasaremos inmediatamente al método interno homónimo de la capa de adición de ruido.

Luego pasaremos los datos ruidosos a la primera unidad de atención.

if(!cAttention[0].FeedForward(cAddNoise.AsObject()))
   return false;

A continuación, cambiaremos la dimensionalidad de los datos y los pasaremos al objeto de cuello.

if(!cMergeSplit[0].FeedForward(cAttention[0].AsObject()))
   return false;
if(!cNeck.FeedForward(cMergeSplit[0].AsObject()))
   return false;

Los resultados obtenidos del cuello se introducirán en la entrada de la segunda unidad de atención.

if(!cAttention[1].FeedForward(cNeck))
   return false;

Después restauraremos la dimensionalidad de los datos a los datos de origen y realizaremos la suma con los datos ruidosos.

if(!cMergeSplit[1].FeedForward(cAttention[1].AsObject()))
   return false;
if(!SumAndNormilize(cAddNoise.getOutput(), cMergeSplit[1].getOutput(), cResidual.getOutput(),
                                                                        1, true, 0, 0, 0, 1))
   return false;

Y al final del método, retornaremos los datos al subespacio de la distribución de origen.

   if(!cRevIn.FeedForward(cResidual.AsObject()))
      return false;
//---
   return true;
  }

Después, todo lo que deberemos hacer es devolver el resultado lógico de las operaciones al programa que realiza la llamada.

Creo que el algoritmo para el método de pasada directa no planteará muchas dificultades. Pero con los métodos de distribución del gradiente de error calcInputGradients, no todo será tan sencillo. Y es aquí donde recordamos que estamos trabajando con un modelo de difusión.

bool CNeuronDiffusion::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

En los parámetros del método, al igual que sucede con la pasada directa, obtendremos el puntero al objeto de datos de origen. Solo que ahora tendremos que transmitirle el gradiente de error en función de la influencia de los datos de entrada en la salida del modelo. E inmediatamente comprobaremos la relevancia del puntero obtenido, porque de lo contrario todas las operaciones posteriores carecerán de sentido.

A continuación, quisiera recordarle que no hemos sustituido a propósito los punteros al búfer de gradiente de error durante la inicialización. Y en este punto, el gradiente de error recibido de la capa posterior solo se encontrará en el búfer de interfaz correspondiente. Esto nos permitirá resolver nuestro segundo problema, el entrenamiento del modelo de difusión. Como se menciona en la parte teórica de nuestro trabajo, el modelo de difusión se entrena para restablecer del ruido los datos de origen. Por lo tanto, determinaremos la desviación de los datos obtenidos a la salida de la capa durante la pasada directa con respecto a los datos obtenidos a la entrada sin ruido.

float error = 1;
if(!cRevIn.calcOutputGradients(prevLayer.getOutput(), error) ||
   !SumAndNormilize(cRevIn.getGradient(), Gradient, cRevIn.getGradient(), 1, false, 0, 0, 0, 1))
   return false;

Pero en nuestro artículo, queremos establecer un filtro capaz de destacar las estructuras significativas en el contexto de la resolución del problema básico. Por lo tanto, al gradiente de error de recuperación de datos obtenido le añadiremos el gradiente de error obtenido de la línea troncal principal, que indicará el error del modelo principal.

A continuación, descenderemos el gradiente de error total a la capa de enlace residual.

if(!cResidual.calcHiddenGradients(cRevIn.AsObject()))
   return false;

En esta fase, ya explotaremos la sustitución de los búferes de datos y transferiremos el gradiente de error hasta el segundo nivel del bloque de atención.

if(!cAttention[1].calcHiddenGradients(cMergeSplit[1].AsObject()))
   return false;

Y luego pasaremos el gradiente de error por la cadena: cuello, capa de reducción de dimensionalidad, primer bloque de atención, objeto de adición de ruido.

if(!cNeck.calcHiddenGradients(cAttention[1].AsObject()))
   return false;
if(!cMergeSplit[0].calcHiddenGradients(cNeck.AsObject()))
   return false;
if(!cAttention[0].calcHiddenGradients(cMergeSplit[0].AsObject()))
   return false;
if(!cAddNoise.calcHiddenGradients(cAttention[0].AsObject()))
   return false;

Aquí deberemos detenernos y añadir el gradiente de error de enlace residual.

if(!SumAndNormilize(cAddNoise.getGradient(), cResidual.getGradient(), cAddNoise.getGradient(), 1, 
                                                                             false, 0, 0, 0, 1))
   return false;

Y entonces pasaremos el gradiente de error al nivel de datos de origen y finalizaremos el método, devuelto previamente el resultado lógico de las operaciones al programa que realiza la llamada.

   if(!prevLayer.calcHiddenGradients(cAddNoise.AsObject()))
      return false;
//---
   return true;
  }

Con esto concluiremos nuestra revisión de los algoritmos para construir los métodos de nuestra clase de framework de difusión direccional. Podrá leer el código completo de todos los métodos de esta clase en los anexos. También hay programas para interactuar con el entorno y modelos de entrenamiento que se han trasladado de trabajos anteriores sin modificaciones.

Las arquitecturas de los modelos también se han tomado prestadas del artículo anterior. El único cambio reside en que hemos sustituido la capa de construcción adaptativa de grafos del Codificador del entorno por una capa de difusión direccional entrenada.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDiffusion;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = BarDescr;
   descr.layers=2;
   descr.step=3;
   {
      int temp[] = {4};                                  // Heads
      if(ArrayCopy(descr.heads, temp) < (int)temp.Size())
         return false;
   }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

La arquitectura completa de los modelos entrenados figura en los anexos.

Ahora pasaremos a la fase final de nuestro trabajo: probaremos la eficacia de los enfoques aplicados con datos reales.

3. Simulación

Hemos realizado un trabajo considerable para implementar los enfoques de difusión direccional usando MQL5. Y ha llegado el momento de probar su eficacia para resolver tareas comerciales. Entrenaremos los modelos utilizando los enfoques propuestos con datos reales del instrumento EURUSD para 2023. Durante el entrenamiento hemos usado datos históricos del marco temporal H1.

Como antes, aplicaremos el entrenamiento offline del modelo con actualizaciones periódicas del conjunto de datos de entrenamiento para mantenerlo coherente con la política actual del Actor.

Antes hemos señalado que el nuevo modelo del codificador del estado del entorno está tomado casi por completo del artículo anterior. Y para comparar los resultados, probaremos el nuevo modelo conservando íntegramente los parámetros de prueba del modelo básico. A continuación resumimos los resultados de las pruebas de los tres primeros meses de 2024.

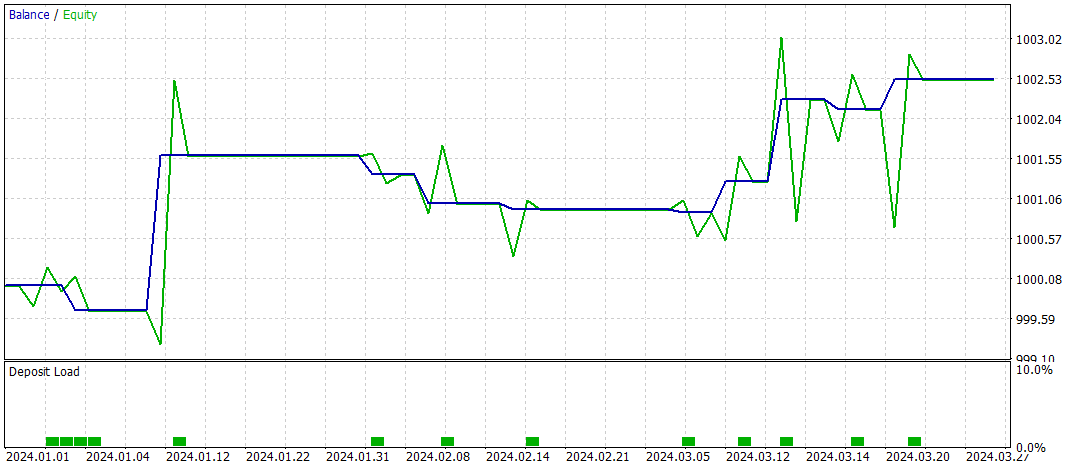
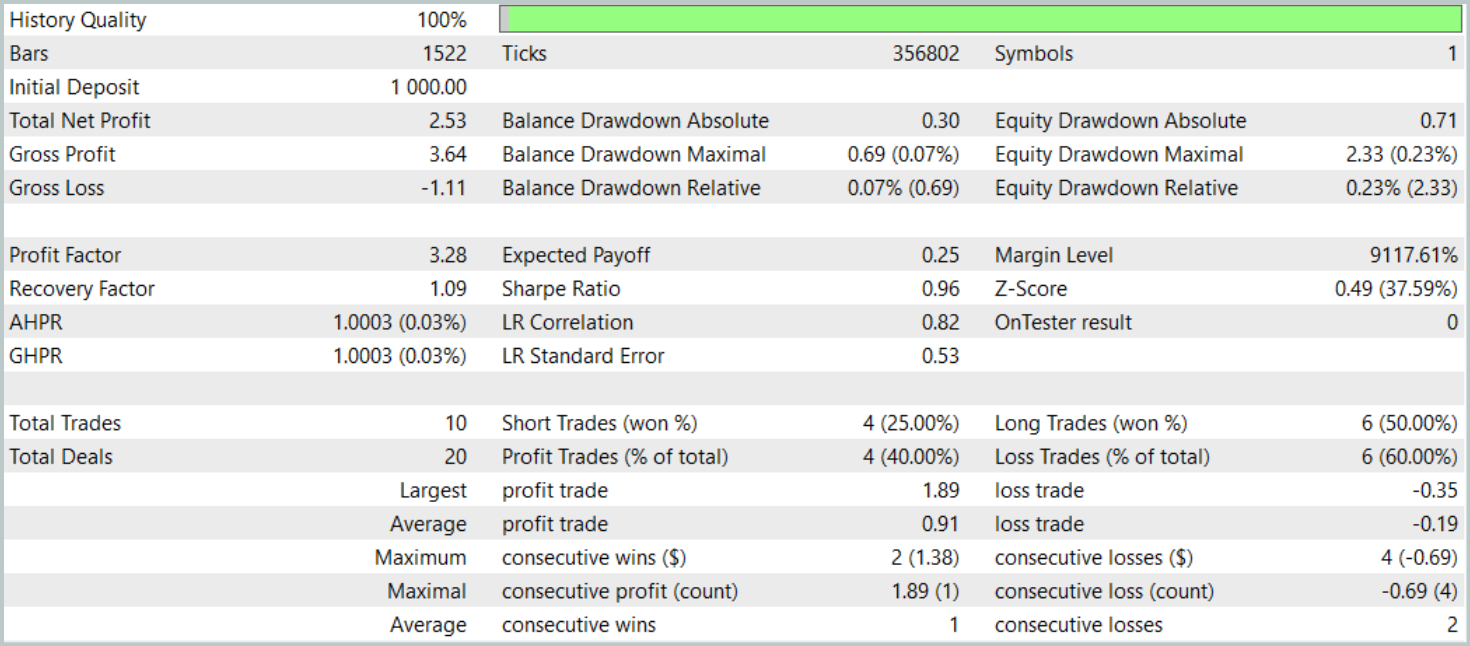
Durante el periodo de prueba, el modelo solo ha realizado 10 transacciones. Y eso es muy poco. Además, solo 4 de ellas se han cerrado con beneficios. No es un resultado que impresione. Sin embargo, la media y el máximo de las transacciones rentables son 5 veces superiores a los mismos indicadores de las transacciones deficitarias. Eso ha permitido al modelo fijar el factor de beneficio en 3,28.

En general, el modelo ha mostrado una buena relación beneficios/pérdidas, pero el número demasiado bajo de transacciones hace necesario buscar formas de aumentar la frecuencia de las mismas. Preferiblemente sin perder la calidad de las transacciones.

Conclusión

Los modelos de difusión direccional (Directional diffusion model — DDM) son una herramienta prometedora para analizar y presentar datos de mercado en el comercio. Como los mercados financieros presentan a menudo patrones anisótropos y direccionales debidos a complejas interacciones estructurales y factores externos, los modelos tradicionales de difusión con procesos isotrópicos no siempre son capaces de captar eficientemente estas características. Los DDM, con su capacidad para adaptarse a la direccionalidad de los datos mediante el uso de ruido direccional, permiten una mejor identificación de patrones y tendencias importantes, incluso ante altos niveles de ruido y volatilidad del mercado.

En la parte práctica, hemos implementado nuestra visión de los enfoques propuestos usando MQL5. Asimismo, hemos entrenado los modelos con datos históricos reales y los hemos probado más allá de la muestra de entrenamiento. Basándonos en los resultados de los experimentos realizados, podemos concluir que existe potencial para los DDM. Sin embargo, el modelo que hemos creado requiere una mayor optimización.

Enlaces

• Directional diffusion models for graph representation learning
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL