知っておくべきMQL5ウィザードのテクニック（第41回）：DQN (Deep-Q-Network)

はじめに

Deep-Q-Networks(DQN)（英語）は、この記事で取り上げたQ学習以外の、もう1つの強化学習アルゴリズムですが、Q学習とは異なり、ニューラルネットワークを使って、Q値とエージェントが次に取るべき行動を予測します。Q学習と似ている/関連しているのは、やはりQテーブルが関係していて、そこに以前の「エピソード」からの行動や状態に関する累積的な知識が保存される点です。実際、リンクからわかるように、DQNはQ学習と同じウィキペディアのページを共有しており、基本的にQ学習の変種として定義されています。

シグナルクラス、トレーリングストップクラス、マネーマネージメントクラスは、ウィザードで組み立てられたエキスパートアドバイザー(EA)を構築する際に定義する必要がある3つの主要モジュールです。新しい読者は、MQL5ウィザードを使ってそれらをまとめるためにこちらとこちらにあるガイドに従ってください。この記事の下に添付されているソースコードは、これらのリンクで共有されているウィザードの組み立てガイドに従って使用することを意図しています。ウィザードで組み立てられたEAで使用するカスタムシグナルクラスを定義することをもう一度考えてみましょう。

ただし、これはDQNを検査できる唯一の方法ではありません。カスタムトレーリングクラスまたはカスタム管理クラスの実装も作成してテストできます。なぜなら、これらのEAでロングとショートの条件を決定することは非常に重要であり、多くの場合、取引セットアップの可能性を最もよく示すからです。この記事は、本連載の以前の記事に基づいており、カスタマイズされたウィザードで組み立てられたEAの開発に使用できるテクニックやさまざまな設定について詳しく説明しています。そのため、特にアプローチの多様化を検討している新しい読者には、過去の記事を確認することをお勧めします。これらの記事は、様々なカスタムシグナルだけでなく、トレーリングクラスと資金管理クラスのカスタム実装もカバーしています。

Q学習の記事で見たようなDQNのセットアップは、損失関数のサポートとして実装されています。教師あり、教師なし以外の第3の学習方法として強化学習を厳密に捉えているからです。これは、Q学習の記事で述べられているように、下位のMLPなしで、訓練に使用する独立したモデルとして実装できないということではありません。この強化学習の代替的な使用方法については、今後の記事で検討する予定であり、そこでは下位MLPは存在せず、エージェントの行動予測が代わりに長短の条件を通知します。

強化学習の復習

始める前に、強化学習とは何かを簡単に復習しておくといいでしょう。これは、エージェントと環境の相互作用に焦点を当てた機械学習訓練の代替方法です。エージェントは意思決定主体であり、その目標は累積報酬を最大化するために最適な行動を学習することです。環境とは、Critic/観察者のホストとして働き、新しい状態や報酬（正確なエージェント予測に対する報酬）という形でエージェントにフィードバックを提供する、エージェントの「外」にあるすべてのものです。したがって、このサイクルは、エージェントが現在の環境状態を観察することから始まり、この状態の変化を予測し、この状態に適した適切な行動を選択します。

状態とは、環境の状態や状況を表すものです。エージェントが行動を選択したり実行したりすると、それに先立ち/同時に環境の状態が遷移し、その行動がこの新しい環境にどれだけ適していたかが評価されます。この評価は「報酬」として数値化されます。記憶のないマルコフ連鎖行列は、エージェントの次の状態を予測する意思決定プロセスを評価するのに使用されましたが、実際の遷移は環境によって決定され、その記事の場合、市場の方向と時間枠の範囲のクロステーブルによってマークされていました。エージェントがとる行動は、連続的（または無限の範囲の可能性）になることもありますが、多くの場合は離散的であり、つまり、事前定義された一連のオプションを実行します。このケースでは、販売、購入、または何もしないのいずれかです。しかし、私たちのケースでは、このリストは、例えば、成行注文だけでなく、未決注文も考慮するような成行注文の形式に従うように拡張することができました。

同様に、報酬インジケーターは、新しいバーごとに再評価され、前回の行動や注文による損失や利益として、有利なエクスカージョンと不利なエクスカージョンを比率やその他のハイブリッドインジケーターとして定量化するために「アップグレード」することができます。この報酬メトリックは、現在の状態および事前に選択された行動とともに、Qテーブルを更新するために使用されます。このためのソースは、CQLクラスのCriticSource関数で共有されています。すでに上で述べたように、ここでは強化学習を教師あり学習と教師なし学習の代替手段として厳密に検討しており、それによって損失関数を厳密に定量化します。ただし、強化学習がこの「決定的な」設定の外部に適用され、エージェントの行動が訓練の外部で適用される予測をおこなうための独立したモデルとして使用される例があり、これらのシナリオはここでは考慮されませんが、今後の記事で検討される可能性があります。 

DQNアルゴリズムの紹介

DQNは、私たちが最初に注目した強化学習アルゴリズムであるQ学習を基礎としており、その主要な目的は今でもDQNのものであるQ値の予測です。これらは、前述のように、さまざまな環境状態を分類するデータポイントであり、Qテーブルに記録されます。Q学習アルゴリズムとの違いは、最初の強化学習の記事で示したように、Q学習アルゴリズムで使用されるQマップやテーブルに頼るのではなく、次のQ値を予測する際にニューラルネットワークを使用する点にあります。さらに、以下のセクションで説明するように、経験再生とターゲットネットワークがあります。従って、以前はQマップ全体に適用されていたε-greedy方策 は、DQNではニューラルネットワークが活躍するため、もはや適用できません。

したがって、DQNは、ニューラルネットワークの助けを借りて、適用可能なすべての状態にわたって、それぞれの可能な行動に対する将来の報酬をマッピングします。トレーダーは、様々な市場状況（強気-弱気-保合）において、可能性のある各行動（買い-売り-ホールド）に対する様々な重み付けと考えることができるこの状態のマッピングは、重み付けを提供し、これらの重み付けが取引ポジションを決定します。DQNは、金融市場の主な特徴の一部である、複雑で高次元の環境を扱うことに長けています。金融市場は、価格変動、マクロ経済インジケーター、市場センチメントなど、非常に変動的で独立した要因を持つダイナミックで非線形な市場です。

従来のQ学習は、有限で管理可能な状態数を持つ離散Qテーブルを使用するため、これに苦戦する傾向があり、ニューラルネットワークを使用するDQNが非常に巧みであるのとは対照的です。DQNはまた、円キャリー取引など、特定の取引戦略におけるエントリシグナルとしても機能する、さまざまな資産クラスにわたる市場の非線形依存関係を捉えることに長けています。さらに、DQNを使用することで、ニューラルネットワークはQテーブルよりも柔軟である傾向があるため、ネットワークが新しいデータや市場の状況に適応しやすくなり、より優れた汎化が可能になります。これは、状況が急速に変化し、エージェントが不慣れな状況に適応しなければならない金融市場において極めて重要です。DQNはまた、従来のQ学習よりも市場ノイズに強いです。金融市場では、エージェントの行動にはしばしば遅延報酬がある（例えば、数日または数週間後にしか利益をもたらさないかもしれないポジションを保有するなど）。DQNは、割引係数（ガンマ）を持つベルマン方程式を使用することで、ネットワークが迅速な利益と長期的な利益のバランスを学習するように、即時的な報酬と長期的な報酬を評価することができます。これは、金融ポートフォリオの戦略的意思決定に不可欠なものです。

DQNによるQ値の予測

この記事では、DQNを代替訓練アプローチとして厳密に見ており、典型的なMLPのように独自の予測をおこなうために使用できる独立したモデルとして見ているわけではないので、MLPの損失関数を正規化するためにDQNを使用しています。初歩的な「強化学習」の設定でDQNを使うということは、この前の記事で使ったアプローチにほぼ忠実だということです。従って、以下に要約するシグナルクラスのインターフェイスでは、「DQN_ONLINE」と呼ぶエージェントとして機能するMLPのインスタンスを持っていることになります。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalDQN   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis


   int                           m_train_set;                       //
   int                           m_epochs;                              // Epochs
   double                        m_learning_rate;                       // Alpha

   Elearning                     m_learning_type;

   double                        m_train_deposit;
   double                        m_train_criteria;

   double                        m_initial_weight;
   double                        m_initial_bias;
   
   int                           m_state_lag;
   int                           m_target_counts;
   int                           m_target_counter;

   Smlp                          m_mlp;
   Smlp                          m_dqn;
   Slearning                     m_learning;

public:
   void                          CSignalDQN(void);
   void                          ~CSignalDQN(void);

   //--- methods of setting adjustable parameters



...



...


protected:
   void                          GetOutput(int &Output);

   Cmlp                          *MLP,*DQN_ONLINE,*DQN_TARGET;
};

このネットワークは、現在の状態を入力とし、可能な各行動に対するq値のベクトルを出力します。読者が調整または微調整できるネットワークアーキテクチャは、2-6-3アーキテクチャに従います（2は入力層のサイズ）。そのサイズが2であるのは、以前の記事で紹介したように、1つのインデックスとして「平坦化」することはできますが、厳密にはインデックスまたは座標のペアだからです。一方の座標は短期的なトレンドの種類を測定し、もう一方は長期的なトレンドを見ます。

隠れ層は単純に6のサイズが割り当てられているが、前述の通り、このサイズと隠れ層の追加は、ここで使われているものからカスタマイズすることができます。入力サイズ×出力サイズから6を選びました。つまり、出力サイズはQ学習の記事の場合と同じように3であり、これはエージェントが取りうる行動の数を表しています。復習すると、これらの行動は、買い、売り、またはホールドです。出力はそれぞれの行動をとる確率のベクトルであり、DQNは分類器ネットワークであることを意味します。  この強化学習DQNの出力は、親MLPネットワークの目標値として機能します。この出力が得られたら、MLPを訓練することができます。しかし、見逃せないのはDQNの訓練で、これは他のネットワークと同じようにはおこなわれません。「DQN_ONLINE」ネットワークを訓練するためのターゲットベクトルを提供するために、「DQN_TARGET」とラベル付けした別のニューラルネットワークを使用します。次にこれを見ます。

ターゲットネットワークの役割

ターゲットネットワークも、オンラインネットワーク（MLPのターゲットを提供する上記のDQN）と同様に、環境状態を入力とし、可能な各行動に対するq値のベクトルを出力します。オンラインネットワークとの主な違いは、環境状態の入力が現在の状態に続く状態であることです。さらに、これもニューラルネットワークであるため、バックプロパゲーションによる学習がおこなわれると予想されますが、その代わりに、あらかじめ設定された間隔で、オンラインネットワークをコピーするだけです。ターゲットネットワークは、時間差を計算する際に、より安定したターゲット値を提供し、訓練中の振動や発散のリスクを軽減します。

独立したターゲットネットワーク、マザーMLP、オンラインネットワークがなければ、ターゲット値は常に変化し、振動するような不安定な振る舞いをすることになります。両方のネットワークが同時に更新されるからです。ターゲットネットワークを使用することで、両アルゴリズムの発散や振動が少なくなり、学習プロセスが安定します。上述したように、ターゲットネットワークは通常のMLPのようにバックプロパゲートされるのではなく、一定の間隔でオンラインネットワークをコピーします。これらの間隔は通常約10,000の大きさで、これを調整するための入力パラメータは「m_target_counts」とラベル付けされ、デフォルトで65のみに割り当てられています。これは、1年間だけ日足でテストしているためで、テスト用の価格バーは260本あります。これは調整可能なパラメータなので、テスト期間を長くするか、時間枠を小さくすれば、10,000ステップは実現可能です。目標q値の算出は以下の式でおこなわれます。

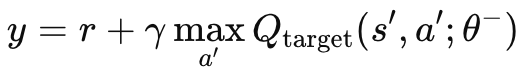
ここで

• y：目標Q値。現在の状態sから出発し、行動aをとり、その後最適な方針に従うと推定されるリターン（将来の報酬）を表します。
• r：状態sで行動aを起こした後に受け取る即時報酬
• γ：将来の報酬の重要性を決定する割引係数（0から1の間の値）
• max a′ Qtarget(s′,a′;θ−)： パラメータθ-を持つターゲットネットワークによって推定された、すべての可能な行動a′に対する次の状態s′の最大予測Q値

• Qtarget(s′,a′;θ−)： ターゲットネットワークが予測する次の状態-動作ペア(s′,a′)(s',a')(s′,a′)のQ値
• θ−：ターゲットネットワークのパラメータ（重み）で、メインネットワークのパラメータから定期的に更新されます。
• 
  

この式はMQL5ではCriticalTarget関数によって実装されており、強化学習の紹介記事ですでに使用したCQLクラスに追加しています。以下がその関数です。

//+------------------------------------------------------------------+
// Critic Target for DQN
//+------------------------------------------------------------------+
vector Cql::CriticTarget(vector &Rewards, vector &TargetOutput)
{  vector _target = Rewards + (THIS.gamma * TargetOutput);
   return(_target);
}

ブートストラップの問題があります。 強化学習に関する前回の記事で見たように、従来のQ学習では、ネットワークは自身の予測に基づいてQ値を更新するが、予測が不正確な場合、エラーの連鎖（より一般的にはブートストラップエラーと呼ばれる）を引き起こす可能性があります。これは、ある状態のq値が後続の状態のq値に依存するためで、潜在的に誤差が増幅される可能性があります。

したがって、ターゲットネットワークの役割は、動きの遅いターゲットを提供することでこれを軽減することです。ターゲットネットワークのパラメータの更新頻度は低いため（通常は数万ステップごと）、オンラインネットワークよりも緩やかに変化します。これにより、エラーが伝播する速度が遅くなり、ブートストラップ問題が解決されます。

金融市場のような複雑な環境や、ビデオゲームのような非線形のダイナミクスを持つ状況では、状態と報酬の関係は非常に非線形になりがちです。したがって、DQNがこのような環境で効果的に学習するためには、ターゲットネットワークによってもたらされる安定性が重要です。このターゲットネットワークがないと、複雑で急速に変化する環境に直面した場合、q値とターゲットの両方が急速に更新されるため、オンラインネットワーク(DQN)が発散する可能性が高くなります。

さらに、過大評価バイアスに対処するために、しばしば「ダブルDQN」と呼ばれる拡張機能を追加することで、ターゲットネットワークを改善することができます。これは、オンラインネットワークとターゲットネットワークの両方を別々に使用して、行動を選択し評価することで実施されます。これは、オンラインネットワークとターゲットネットワークの間で、行動選択と行動評価のプロセスを切り離すことです。オンラインネットワークは行動の選択に使われ、ターゲットネットワークはそれを評価します。

訓練における経験再生とその役割

経験再生は、強化学習DQNエージェントが、状態、行動、報酬、次の状態に関する「経験」を再生バッファに保存するバッファリング技術です。これらの経験は訓練中にランダムにサンプリングされ、エージェントのDQNの重みとバイアスを更新します。このアプローチは、予想されるように、連続するデータポイントのみを考慮することから逐次的な相関を断ち切るのに有効であり、したがって金融市場のような現実のシナリオにより適しています。金融市場では、価格や取引量、ボラティリティなど、連続したデータポイントは、いずれも同じような市場の状況や参加者の行動の影響を受けるため、相関性が高い傾向があります。このような連続的に相関するデータでDQNエージェントを訓練すると、DQN エージェントはさまざまな市場状況にうまく一般化されない特定のパターンを利用することに慣れてしまうため、過剰適合や一般化の欠如につながる傾向があります。

このような時間的相関を解消するために、通常、DQNは再生バッファからランダムにサンプリングされた経験データのミニバッチで学習されます。特にランダムサンプリングは、時間的相関関係を断ち切るのに役立ち、その結果、エージェントは市場の基本的なダイナミクスをよりよく近似した経験分布を学習することになります。より良い汎化だけでなく、長期的な訓練プロセスも安定し、収束も良くなります。これは、経験再生が訓練過程における更新のばらつきを減らすからです。

経験再生がなければ、ネットワークの重み更新は、相関性の高い連続したサンプルのバーストで起こり、異なる環境条件からのまったく異なる更新によって中断されるだけです。これにより、更新プロセス全体が非常に不安定になり、学習プロセスが不安定になる可能性があります。多様な経験のセットからランダムにサンプリングすることで、DQNエージェントはよりスムーズで安定した更新をおこない、最適なポリシーへの収束を改善します。

経験再生では、エージェントが（ランダム選択により）経験から複数回再学習するため、履歴データの効率的な利用も可能になります。これは、特定の時点で多様で代表的なデータを大量に取得することが困難な金融市場では特に貴重です。これは要するに、DQNが市場の暴落や暴騰のようなまれな、あるいは重要な出来事から学ぶことを可能にするということです。これによりエージェントは、万が一そのような事態が発生した場合に備え、より強固なものとなります。

経験再生はまた、単なる搾取とは対照的に、強化学習の探求の可能性を高めます。これにより、エージェントが再生バッファから繰り返しサンプルを採取する「壊滅的な忘却」の可能性が軽減され、古い戦略の知識を強化して、新しい経験によって上書きされるのを防ぐことができます。最後に、優先順位付けされた経験の再生など、経験の再生のさらに特殊なインスタンスが可能になります。優先順位付けされた経験の再生では、損失関数のエラーが大きいデータ サンプルが、学習の可能性が高くなることを考慮に入れて優先されるため、学習がより効率的で的を絞ったものになります。

この記事で経験再生について言及したのは、それがDQNの重要な原則だからです。ただし、今後の記事ではMQL5でのその機能を紹介します。そこでは、DQNは単なるハイブリッド損失関数ではなく、シグナルクラスの主要な予測モデルになります。

時間的意思決定

ロボット工学やゲームのような分野では、取引以外の意思決定でも、将来の結果に対して遅延効果をもたらすことがよくあります。トレーダーが思い浮かべるのは、経済ニュースのリリースと企業の業績でしょうが、この関係は時間的な依存関係を確立しています。この時間的関係は、γ係数を通して上記のq値式で考慮されています。γは、短期的な報酬と長期的な報酬のバランスをとることを可能にし、DQNのq値に、さらに先を見通し、長期にわたる行動の累積的な影響を推定する能力を与えます。この効果は、いくつかの報酬が遅延することであり、γはエージェントが長期的な報酬を無視しないようにする一方で、取引時に不可欠な即時的な報酬を監視し続けることを保証すると主張されています。例えば、主要な金利決定時にポジションを持ったとしても、すぐに有利な展開にはならないことが多いです。不利なエクスカーション期間は通常、これらのポジションの見出しとなるため、DQNのようにこれを考慮したシグナルを取得して使用する能力が有利になる可能性があります。

以前のコードの変更点

ハイブリッド損失関数の中でDQNを利用するには、まずカスタム損失列挙を以下のように追加する必要があります。

//+------------------------------------------------------------------+
//| Custom Loss-Function Enumerator                                  |
//+------------------------------------------------------------------+
enum Eloss
{  LOSS_TYPICAL = -1,
   LOSS_SVR = 1,
   LOSS_QL = 2,
   LOSS_DQN = 3
};

損失関数がDQNを使用する場合に選択される新しい列挙、LOSS_DQNを追加します。強化学習に関する最初の記事でおこなったように、バックプロパゲーション関数に追加の変更が必要です。この関数で適切な損失タイプを選択することで、デルタの計算に使われる値が決まります。これらの変更点は以下の通りです。

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }


....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }
   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss_typical);
   if(THIS.loss_custom == LOSS_SVR)
   {  _last_loss = SVR_Loss();
   }
   else if(THIS.loss_custom == LOSS_QL)
   {  

....

   }
   else if(THIS.loss_custom == LOSS_DQN)
   {  double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float);
      vector _rewards;
      _rewards.Init(Learning.dqn_target.Size());
      _rewards.Fill(0.0);
      if(_reward > 0.0)
      {  _rewards[0] = 1.0;
      }
      else if(_reward == 0.0)
      {  _rewards[1] = 1.0;
      }
      else if(_reward < 0.0)
      {  _rewards[2] = 1.0;
      }
      vector _target = QL.CriticTarget(_rewards, Learning.dqn_target);
      _last_loss = output.LossGradient(_target, THIS.loss_typical);
   }
   
....


}

コードに加えたその他の主な変更はCQLクラスで、DQNのq値式が導入されたことはすでに述べました。条件閾値の生成に使用するget output関数は、基本的なQ学習に関する以前の記事で検討したものと大きな違いはありません。以下に紹介します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalDQN::GetOutput(int &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  int _states = 2;
         vector _in, _in_old, _in_row, _in_row_old, _in_col, _in_col_old;
         if
         (
            _in_row.Init(_states) &&
            _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) &&
            _in_row.Size() == _states
            &&
            _in_row_old.Init(_states) &&
            _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, _states) &&
            _in_row_old.Size() == _states
            &&
            _in_col.Init(_states) &&
            _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) &&
            _in_col.Size() == _states
            &&
            _in_col_old.Init(_states) &&
            _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_state_lag + ii + 1, _states) &&
            _in_col_old.Size() == _states
         )
         {  _in_row -= _in_row_old;
            _in_col -= _in_col_old;
            //
            m_learning.ql_reward_max = _in_row.Max();
            m_learning.ql_reward_min = _in_row.Min();
            if(m_learning.ql_reward_max == m_learning.ql_reward_min)
            {  m_learning.ql_reward_max += m_symbol.Point();
            }
            MLP.Set(_in_row);
            MLP.Forward();
            //
            MLP.QL.THIS.environments = m_environments;
            //
            vector _in_e;
            _in_e.Init(1);
            MLP.QL.Environment(_in_row, _in_col, _in_e);
            //
            int _row = 0, _col = 0;
            MLP.QL.SetMarkov(int(_in_e[_states - 1]), _row, _col);
            _in.Init(2);
            _in[0] = _row;
            _in[1] = _col;
            DQN_ONLINE.Set(_in);
            DQN_ONLINE.Forward();
            //
            MLP.QL.SetMarkov(int(_in_e[_states - 2]), _row, _col);
            _in_old.Init(2);
            _in_old[0] = _row;
            _in_old[1] = _col;
            DQN_TARGET.Set(_in_old);
            DQN_TARGET.Forward();
            m_learning.dqn_target = DQN_TARGET.output;
            if(ii > 0)
            {  vector _target, _target_data, _target_data_old;
               if
               (
                  _target_data.Init(2) &&
                  _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) &&
                  _target_data.Size() == 2
                  &&
                  _target_data_old.Init(2) &&
                  _target_data_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, 2) &&
                  _target_data_old.Size() == 2
               )
               {  _target.Init(__MLP_OUTPUTS);
                  _target.Fill(0.0);
                  _target_data -= _target_data_old;
                  double _type = _target_data[1] - _in_row[1];
                  int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1));
                  _target[_index] = 1.0;
                  MLP.Get(_target);
                  if(i == m_epochs && ii == m_train_set)
                  {  DQN_ONLINE.Backward(m_learning, i);
                     if(m_target_counter >= m_target_counts)
                     {  DQN_TARGET = DQN_ONLINE;
                        m_target_counter = 0;
                     }
                     MLP.Backward(m_learning, i);
                  }
               }
            }
            Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2));
         }
      }
   }
}

すでに述べたように、オンラインネットワークとターゲットネットワークの2つのDQNネットワークがあります。加えて、もちろん、Q学習の記事のように、近い価格変動を入力とする親LPもあります。上記のようにDQNのq値を得るためにCriticalTarget関数を呼び出す以外に、QLクラスを参照すべきではありません。しかし、QLクラスは、状態座標からインデックスを合成するだけでなく、（インデックスが与えられたときに）環境の状態座標にアクセスできるため、2つのDQNネットワークの入力を得るためにQLクラスを参照しています。前述の通り、予測にq-mapを使用せず、ターゲットネットワークによって訓練されたオンラインDQNネットワークに依存しています。オンラインDQNもターゲットDQNも、単純に環境状態（それぞれ古い状態と新しい状態）を受け取り、q値のベクトル（各エージェントの行動）を予測するように学習されます。

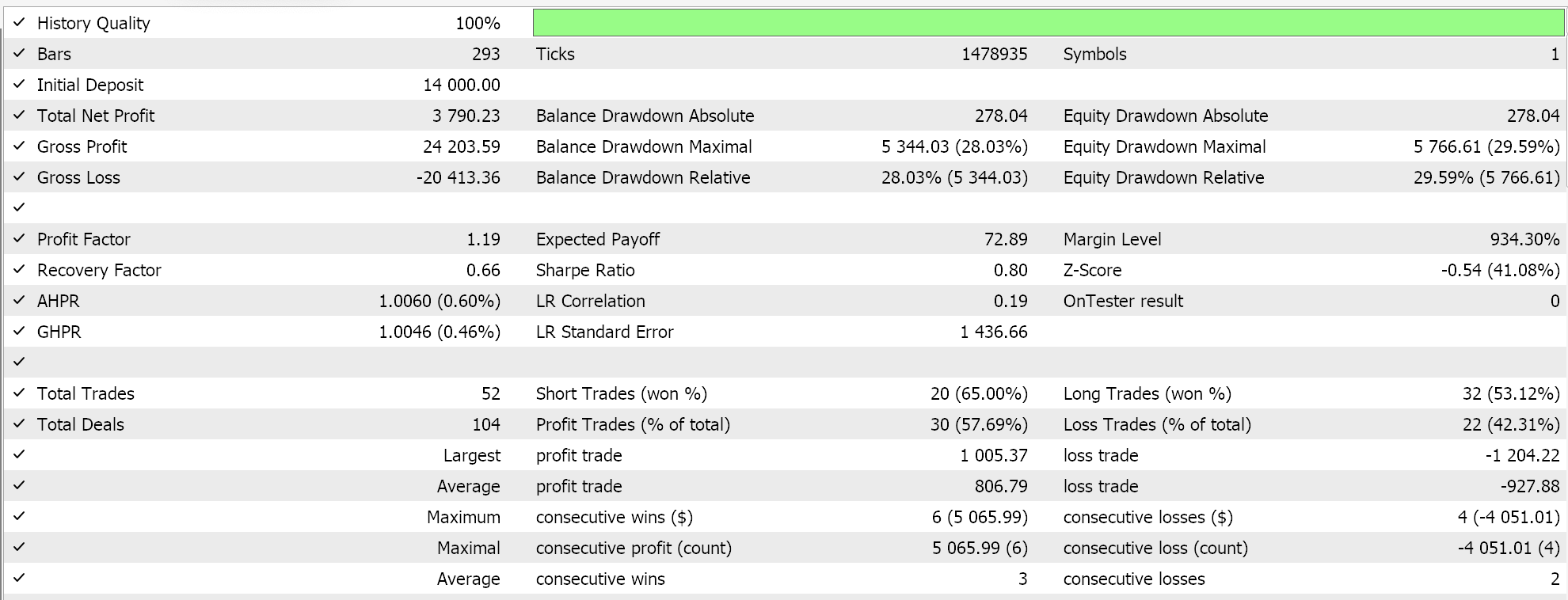
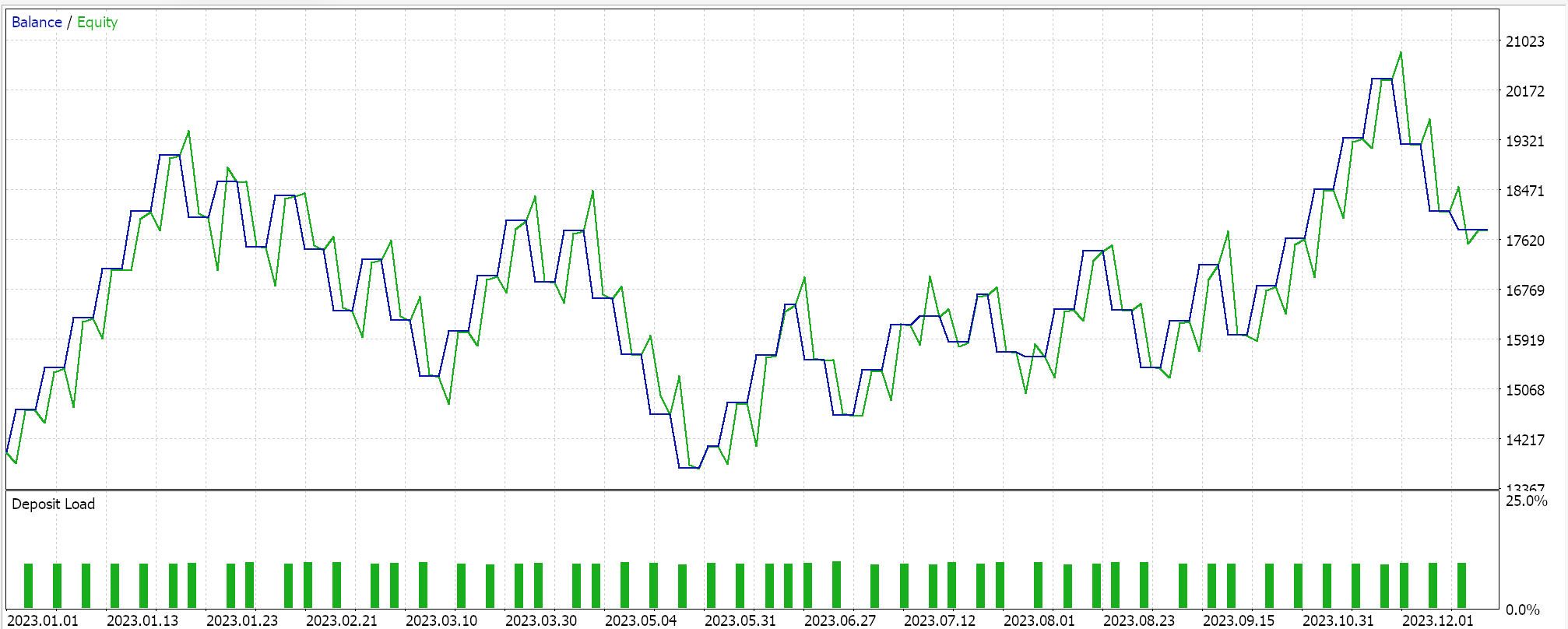
ストラテジーテスターのレポート

このMLPを、DQNを用いた強化学習訓練により、2023年のEURGBPで日次時間軸でテストします。以下はその結果ですが、これはあくまでも取引可能性を示すものであり、必ずしも将来の市場動向で再現できるものではありません。

結論

ウィザードで組み立てられたEAにおいて、DQA (Deep-Q-Network)と呼ばれる強化学習に代わるアルゴリズムの実装とテストを見てきました。強化学習は、教師あり学習、教師なし学習と並ぶ、機械学習における第3の学習方法であり、厳密に言えば、機械学習における学習方法としては異なるアプローチですが、この後の記事では、実際に強化学習が主要なモデルやシグナル発生器として機能するシナリオについて考えてみたいと思います。