MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 41): Deep-Q-Networks

Einführung

Tiefes Q-Lernen (DQN) ist neben Q-Lernen ein weiterer Algorithmus des verstärkenden Lernens, den wir uns in diesem Artikel angesehen haben, aber im Gegensatz zum Q-Learning verwenden sie neuronale Netze, um den q-Wert und die nächste Aktion des Agenten vorherzusagen. Es ist dem Q-Learning insofern ähnlich/verwandt, als dass eine Q-Tabelle involviert ist, in der das kumulative Wissen über Aktionen und Zustände aus früheren „Episoden“ gespeichert wird. Tatsächlich teilt es sich die gleiche Wikipedia-Seite mit Q-Learning, wie aus den Links ersichtlich ist, wo es im Wesentlichen als eine Variante von Q-Learning definiert wird.

Die Signalklasse zusammen mit den Klassen für Trailing-Stop und dem Money-Management sind die drei Hauptmodule, die beim Aufbau eines assistentengestützten Expert Advisors definiert werden müssen. Die Zusammenstellung mit Hilfe des MQL5-Assistenten kann anhand der Anleitungen hier und hier für neue Leser erfolgen. Der am Ende dieses Artikels beigefügte Quellcode ist für die Verwendung der Assistenten-Bauanleitungen gedacht, die unter diesen Links aufgeführt sind. Auch hier geht es um die Definition einer nutzerdefinierten Signalklasse für die Verwendung in einem vom Assistenten zusammengestellten Expert Advisor.

Dies ist jedoch nicht die einzige Möglichkeit, DQN zu untersuchen, da auch Implementierungen für eine nutzerdefinierte Trailing-Klasse oder eine nutzerdefinierte Money-Management-Klasse erstellt und getestet werden können. Wir konzentrieren uns jedoch auf die Signalklasse, da die Bestimmung der Kauf- und Verkaufs-Bedingungen in diesen Expert Advisors von entscheidender Bedeutung ist und in vielen Fällen das Potenzial eines Handels-Setups am besten demonstriert. Dieser Artikel baut auf früheren Artikeln dieser Serie auf, in denen wir auf Techniken oder verschiedene Setups eingehen, die bei der Entwicklung von maßgeschneiderten, mit einem Assistenten ausgestatteten Expert Advisors verwendet werden können, und so wäre ein Rückblick auf frühere Artikel für neue Leser eine gute Idee, insbesondere wenn sie ihren Ansatz diversifizieren möchten. Diese Artikel behandeln nicht nur eine Vielzahl von nutzerdefinierten Signalen, sondern auch nutzerdefinierte Implementierungen der Trailing-Klasse und der Money-Management-Klasse.

DQN-Setups, wie wir sie im Q-Learning-Artikel gesehen haben, werden als Unterstützung für die Verlustfunktion implementiert, da wir das Reinforcement Learning als eine dritte Art des Trainings neben dem überwachten und unbeaufsichtigten Training betrachten. Wie in dem Artikel über das q-learning erwähnt, bedeutet dies nicht, dass es nicht als unabhängiges Modell für das Training ohne ein untergeordnetes MLP implementiert werden kann. Diese alternative Art der Nutzung des Verstärkungslernens wird in zukünftigen Artikeln erforscht, wobei es keinen untergeordneten MLP geben wird und die Handlungsprognosen des Agenten stattdessen die langen und kurzen Bedingungen informieren werden.

Rekapitulieren wir Reinforcement Learning

Bevor wir uns damit befassen, ist es vielleicht eine gute Idee, kurz zu wiederholen, was Reinforcement Learning ist. Dies ist ein alternativer Weg zum maschinellen Lernen, der sich im Kern auf die Interaktion zwischen Agent und Umgebung konzentriert. Der Agent ist die Entscheidungsinstanz, deren Ziel es ist, die besten Handlungen zu erlernen, um den kumulativen Nutzen zu maximieren. Die Umwelt ist alles, was sich „außerhalb“ des Agenten befindet und als Wirt für einen Kritiker/Beobachter fungiert und dem Agenten Rückmeldungen in Form von neuen Zuständen und Belohnungen (Belohnungen für genaue Projektionen des Agenten) gibt. Der Zyklus beginnt also damit, dass der Agent den aktuellen Zustand der Umwelt beobachtet, Vorhersagen über Veränderungen dieses Zustands trifft und dann eine für diesen Zustand geeignete Aktion auswählt.

Zustände sind Darstellungen des Zustands oder der Situation der Umwelt. Sobald ein Agent eine Handlung auswählt oder ausführt, findet vorher/gleichzeitig ein Übergang in den Zuständen der Umwelt statt, sodass seine Handlungen danach beurteilt werden, wie geeignet sie für diese neue Umwelt waren. Diese Bewertung wird als „Belohnung“ quantifiziert. Die Matrix einer Markov-Kette ohne Erinnerung wurde verwendet, um den Entscheidungsprozess des Agenten bei der Vorhersage des nächsten Zustands zu gewichten, aber die tatsächlichen Übergänge werden von der Umgebung bestimmt, die im Fall dieses Artikels durch eine Kreuztabelle zwischen Marktrichtung und Zeithorizont gekennzeichnet war. Die Handlungen des Agenten können zwar kontinuierlich sein (oder unendlich viele Möglichkeiten bieten), aber oft sind sie diskret, d. h. sie nehmen eine vordefinierte Anzahl von Optionen an, die in unserem Fall entweder Verkaufen, Kaufen oder Nichtstun sind. Diese Liste hätte jedoch in unserem Fall erweitert werden können, um z. B. dem Format für Marktaufträge zu folgen, sodass nicht nur Marktaufträge, sondern auch schwebende Aufträge berücksichtigt werden.

In ähnlicher Weise könnte unsere Belohnungsmetrik, die bei jedem neuen Balken neu bewertet wurde, als Verlust oder Gewinn aus der vorangegangenen Aktion oder dem vorangegangenen Auftrag „aufgewertet“ werden, um günstige Ausschläge zu ungünstigen Ausschlägen als Verhältnis oder eine andere hybride Metrik zu quantifizieren. Diese Belohnungsmetrik wird zusammen mit dem aktuellen Zustand und der zuvor gewählten Aktion verwendet, um die Q-Tabelle zu aktualisieren. Die Quelle hierfür wurde in der Funktion „Critical Source“ der CQL-Klasse geteilt. Wie bereits erwähnt, betrachten wir das Reinforcement Learning strikt als Alternative zum überwachten und unüberwachten Lernen, sodass es dazu dient, unsere Verlustfunktion streng zu quantifizieren. Es gibt jedoch Fälle, in denen das Verstärkungslernen außerhalb dieses „endgültigen“ Rahmens angewandt und als unabhängiges Modell zur Erstellung von Prognosen verwendet wird, bei denen die Aktionen des Agenten außerhalb des Trainings angewandt werden, und diese Szenarien werden hier nicht betrachtet, könnten aber in zukünftigen Artikeln untersucht werden. 

Einführung in den Deep Q-Network Algorithmus

DQN basiert auf Q-Learning, dem ersten Reinforcement-Learning-Algorithmus, den wir uns angesehen haben, und sein Hauptziel, das immer noch das von DQN ist, ist die Vorhersage von Q-Werten. Dabei handelt es sich, wie oben beschrieben, um Datenpunkte, die verschiedene Umgebungszustände klassifizieren und in einer Q-Tabelle protokolliert werden. Der Unterschied zum Q-Learning-Algorithmus besteht in der Verwendung neuronaler Netze bei der Vorhersage des nächsten q-Wertes im Gegensatz zur Verwendung einer Q-Map oder Tabelle, die vom Q-Learning-Algorithmus verwendet wird, wie in unserem ersten Artikel zum Reinforcement Learning gezeigt wurde. Darüber hinaus gibt es eine Erfahrungswiederholung und ein Zielnetz, wie in den folgenden Abschnitten beschrieben. Die Epsilon-Greedy-Politik, die zuvor auf die Q-Map angewendet wurde, ist daher bei DQNs nicht mehr anwendbar, da neuronale Netze im Spiel sind.

Das DQN bildet daher mit Hilfe eines neuronalen Netzes zukünftige Belohnungen für jede mögliche Handlung über alle anwendbaren Zustände ab. Diese Zuordnung von Zuständen, die sich Händler als verschiedene Gewichtungen für jede mögliche Aktion (Kaufen-Verkaufen-Halten) unter verschiedenen Marktbedingungen (auf-, ab-, seitwärts) vorstellen können, liefert Gewichtungen, und diese Gewichtungen bestimmen die Handelsposition. DQNs sind in der Lage, hochkomplexe und hochdimensionale Umgebungen zu handhaben, die zu den Hauptmerkmalen der Finanzmärkte gehören. Die Finanzmärkte sind dynamisch und nichtlinear, mit sehr variablen und unabhängigen Faktoren wie Preisänderungen, makroökonomischen Indikatoren und Marktstimmung.

Das traditionelle Q-Learning hat damit Schwierigkeiten, da es diskrete Q-Tabellen mit einer endlichen und überschaubaren Anzahl von Zuständen verwendet, was im Gegensatz zum DQN steht, das durch die Verwendung von neuronalen Netzen sehr geschickt ist. DQNs sind auch gut geeignet, um nicht-lineare Abhängigkeiten an den Märkten über verschiedene Anlageklassen hinweg zu erfassen, die auch als Einstiegssignale für bestimmte Handelsstrategien dienen, z. B. für den Yen-Carry-Trade. Darüber hinaus ermöglicht die Verwendung von DQNs eine bessere Generalisierung, bei der sich das Netzwerk besser an neue Daten und Marktbedingungen anpassen kann, da neuronale Netze in der Regel flexibler sind als Q-Tabellen. Dies ist auf den Finanzmärkten von entscheidender Bedeutung, wo sich die Bedingungen schnell ändern können und der Agent sich an ungewohnte Situationen anpassen muss. DQNs sind auch widerstandsfähiger gegen Marktstörungen als traditionelles Q-Learning. Auf den Finanzmärkten werden Agentenaktionen oft erst mit Verzögerung belohnt (z. B. das Halten einer Position, die erst nach mehreren Tagen oder Wochen einen Gewinn abwirft). Die Verwendung der Bellman-Gleichung mit einem Abzinsungsfaktor (gamma) ermöglicht es dem DQN, die unmittelbaren und die langfristigen Belohnungen zu bewerten, sodass das Netzwerk lernt, zwischen schnellen Gewinnen und langfristigen Gewinnen abzuwägen, was bei der strategischen Entscheidungsfindung für Finanzportfolios wesentlich ist.

Vorhersage von Q-Werten mit DQN

Wir verwenden DQN, um die Verlustfunktion eines MLP zu normalisieren, da wir in diesem Artikel, wie bereits erwähnt, DQN ausschließlich als alternativen Trainingsansatz betrachten und nicht als unabhängiges Modell, das wie ein typisches MLP zur Erstellung eigener Prognosen verwendet werden kann. Diese Verwendung von DQN in der rudimentären „Reinforcement Learning“-Einstellung bedeutet, dass wir uns fast an den Ansatz halten, den wir in diesem früheren Artikel verwendet haben. Dies bedeutet also, dass wir eine Instanz eines MLP haben, die als Agent fungiert, den wir in unserer Signalklassenschnittstelle, die im Folgenden kurz dargestellt wird, als „DQN_ONLINE“ bezeichnen:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalDQN   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis


   int                           m_train_set;                       //
   int                           m_epochs;                              // Epochs
   double                        m_learning_rate;                       // Alpha

   Elearning                     m_learning_type;

   double                        m_train_deposit;
   double                        m_train_criteria;

   double                        m_initial_weight;
   double                        m_initial_bias;
   
   int                           m_state_lag;
   int                           m_target_counts;
   int                           m_target_counter;

   Smlp                          m_mlp;
   Smlp                          m_dqn;
   Slearning                     m_learning;

public:
   void                          CSignalDQN(void);
   void                          ~CSignalDQN(void);

   //--- methods of setting adjustable parameters



...



...


protected:
   void                          GetOutput(int &Output);

   Cmlp                          *MLP,*DQN_ONLINE,*DQN_TARGET;
};

Dieses Netz nimmt als Eingabe den aktuellen Zustand und gibt einen Vektor oder q-Werte für jede der möglichen Aktionen aus. Seine Netzwerkarchitektur, die vom Leser angepasst oder fein abgestimmt werden kann, folgt einer 2-6-3-Architektur, wobei 2 die Größe der Eingabeschicht ist. Ihre Größe ist 2, weil, wie in unserem früheren Artikel mitgeteilt, die Werte zwar als ein einziger Index „abgeflacht“ werden können, aber streng genommen ein Paar von Indizes oder Koordinaten sind. Die eine Koordinate misst die Art des Trends auf kurze Sicht, während die andere den langfristigen Trend betrachtet.

Der versteckten Schicht wird einfach eine Größe von 6 zugewiesen, aber wie bereits erwähnt, kann diese Größe und die Hinzufügung zusätzlicher versteckter Schichten von dem hier verwendeten Wert abweichen. Wir haben 6 aus Eingabegröße mal Ausgabegröße gewählt. Unsere Ausgabegröße ist also 3, wie im Artikel über das q-learning, wo dies die Anzahl der möglichen Aktionen eines Agenten darstellt. Zusammenfassend kann man sagen, dass diese Aktionen Kaufen, Verkaufen oder Halten sind. Da die Ausgabe ein Vektor der Wahrscheinlichkeiten für jede dieser Aktionen ist, ist das DQN ein Klassifizierungsnetz.  Die Ausgabe dieses DQN mit Verstärkungslernen dient als Zielwert für das übergeordnete MLP-Netz. Sobald wir diese Ausgabe haben, können wir den MLP trainieren. Nicht zu vernachlässigen ist jedoch die Ausbildung des DQN, die nicht in der gleichen Weise wie bei anderen Netzen erfolgt. Anstatt sich durch einen weiteren allgegenwärtigen Datensatz von Zuständen und q-Werten zu arbeiten, verwenden wir ein anderes neuronales Netz, das wir als „DQN_TARGET“ bezeichnen, um Zielvektoren für das Training des „DQN_ONLINE“-Netzes bereitzustellen. Wir sehen uns das als Nächstes an.

Die Rolle eines Zielnetzes

Das Zielnetz nimmt wie das Online-Netz (das obige DQN, das das MLP-Ziel liefert) ebenfalls einen Umgebungszustand als Eingabe und gibt einen Vektor von q-Werten für jede mögliche Aktion aus. Der Hauptunterschied zum Online-Netz besteht darin, dass die Eingaben für den Umgebungszustand den Zustand betreffen, der auf den aktuellen Zustand folgt. Da es sich um ein weiteres neuronales Netz handelt, würde man erwarten, dass es durch Backpropagation trainiert wird, aber stattdessen kopiert es in einem vorgegebenen Intervall einfach das Online-Netz. Das Zielnetz liefert stabilere Zielwerte bei der Berechnung der zeitlichen Differenz, was das Risiko von Oszillationen und Divergenzen beim Training verringert.

Ohne ein unabhängiges Zielnetz, das Mutter-MLP und das Online-Netz würden sich die Zielwerte ständig in einem oszillierenden, instabilen Verhalten ändern. Der Grund dafür ist, dass beide Netze gleichzeitig aktualisiert werden würden. Durch die Verwendung des Zielnetzes würde sich der Lernprozess stabilisieren, da beide Algorithmen weniger divergieren/oszillieren würden. Wie bereits erwähnt, wird das Zielnetz nicht wie ein normales MLP rückwärts propagiert, sondern es kopiert das Online-Netz in bestimmten Abständen. Diese Intervalle haben in der Regel eine Größe von etwa 10.000, und unser Eingabeparameter für die Modulation dieses Wertes trägt die Bezeichnung „m_target_counts“ und ist standardmäßig auf nur 65 festgelegt! Das liegt daran, dass wir nur ein Jahr lang auf dem täglichen Zeitrahmen testen, sodass wir 260 Preisbalken zum Testen haben. Dies ist ein einstellbarer Parameter, sodass bei einem längeren Testzeitraum oder einem kleineren Zeitrahmen die 10.000 Schritte machbar sind. Die Berechnung des Ziel-Q-Werts erfolgt nach der folgenden Formel:

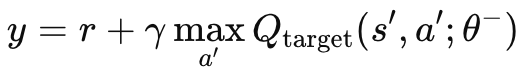
wobei:

• y: Der Q-Zielwert, der die geschätzte Rendite (zukünftige Belohnung) darstellt, ausgehend vom aktuellen Zustand s, der Durchführung der Aktion a und der anschließenden Befolgung der optimalen Strategie.
• r: Die unmittelbare Belohnung, die man erhält, wenn man im Zustand s eine Handlung a vornimmt.
• γ: Der Abzinsungsfaktor, der die Bedeutung zukünftiger Belohnungen bestimmt. Es ist ein Wert zwischen 0 und 1.
• max a′ Qtarget(s′,a′;θ−): Der maximale vorhergesagte Q-Wert für den nächsten Zustand s′ über alle möglichen Aktionen a′, geschätzt durch das Zielnetz mit den Parametern θ-.

• Qtarget(s′,a′;θ−): Der Q-Wert für das nächste Zustands-Aktionspaar (s′,a′)(s', a')(s′,a′), der vom Zielnetz vorhergesagt wird.
• θ−: Die Parameter (Gewichte) des Zielnetzes, die in regelmäßigen Abständen anhand der Parameter des Hauptnetzes aktualisiert werden.
• 
  

Diese Formel ist in MQL5 über die Funktion des kritischen Ziels implementiert, die wir an die CQL-Klasse anhängen, die wir bereits in unserem Einführungsartikel zum Reinforcement-Learning verwendet hatten. Diese Funktion ist unten aufgeführt:

//+------------------------------------------------------------------+
// Critic Target for DQN
//+------------------------------------------------------------------+
vector Cql::CriticTarget(vector &Rewards, vector &TargetOutput)
{  vector _target = Rewards + (THIS.gamma * TargetOutput);
   return(_target);
}

Es gibt ein Bootstrapping-Problem. Beim traditionellen Q-Learning, wie wir im vorherigen Artikel über das Verstärkungslernen gesehen haben, aktualisiert das Netzwerk die Q-Werte auf der Grundlage seiner eigenen Vorhersagen, was zu einer Kaskade von Fehlern führen kann (allgemeiner als Bootstrapping-Fehler bezeichnet), wenn die Vorhersagen ungenau sind. Dies liegt daran, dass die q-Werte für einen Zustand von den q-Werten der nachfolgenden Zustände abhängen, was zu einer Fehlerverstärkung führen kann.

Die Rolle des Zielnetzes besteht daher darin, dies zu mildern, indem es ein sich langsamer bewegendes Ziel darstellt. Da die Parameter des Zielnetzes weniger häufig aktualisiert werden (in der Regel alle paar zehntausend Schritte), ändert es sich allmählicher als das Online-Netz. Dadurch wird die Fehlerfortpflanzung verlangsamt und das Bootstrapping-Problem gelöst.

In Situationen, in denen eine nichtlineare Dynamik herrscht, wie z. B. in den komplexen Umgebungen der Finanzmärkte oder sogar in Videospielen, sind die Beziehungen zwischen Zuständen und Belohnungen in der Regel übermäßig nichtlinear. Die vom Zielnetz eingebrachte Stabilität ist daher entscheidend dafür, dass das DQN unter diesen Bedingungen effektiv lernen kann. Ohne dieses Zielnetz ist es wahrscheinlicher, dass das Online-Netz (DQN) in komplexen oder sich schnell verändernden Umgebungen aufgrund der schnellen Aktualisierung von Q-Werten und Zielen auseinander läuft.

Darüber hinaus kann das Zielnetz durch Hinzufügen einer Erweiterung verbessert werden, die oft als „doppelter DQN“ bezeichnet wird, um eine Verzerrung durch Überschätzung zu vermeiden. Dies wird dadurch erreicht, dass sowohl das Online- als auch das Zielnetz separat zur Auswahl und Bewertung von Aktionen genutzt werden. Es handelt sich um eine Entkopplung der Prozesse der Handlungsauswahl und Handlungsbewertung zwischen dem Online- und dem Zielnetz. Das Online-Netz wird für die Auswahl der Aktion verwendet, während das Zielnetz die Aktion bewertet.

Erfahrungswiederholung und ihre Rolle im Training

Erfahrungswiederholung ist eine Puffertechnik, bei der ein verstärkungslernender DQN-Agent seine „Erfahrungen“ mit Zustand, Aktion, Belohnung und nächstem Zustand in einem Wiederholungspuffer speichert. Diese Erfahrungen werden dann während des Trainings zufällig ausgewählt, um die DQN-Gewichte und Verzerrungen des Agenten zu aktualisieren. Dieser Ansatz ist erwartungsgemäß nützlich, um die sequentielle Korrelation aus der Betrachtung von nur aufeinanderfolgenden Datenpunkten zu brechen, und könnte daher für reale Szenarien wie die Finanzmärkte besser geeignet sein. Auf den Finanzmärkten sind aufeinanderfolgende Datenpunkte, ob Preise, Kontraktvolumen oder Volatilität, in der Regel stark korreliert, da sie alle von ähnlichen Marktbedingungen und dem Verhalten der Marktteilnehmer beeinflusst werden. Das Training eines DQN-Agenten auf solchen sequentiell korrelierten Daten führt tendenziell zu einer Überanpassung und zu einem Mangel an Generalisierung, da sich der DQN-Agent daran gewöhnt, spezifische Muster zu nutzen, die sich nicht gut auf unterschiedliche Marktbedingungen verallgemeinern lassen.

Um diese zeitlichen Korrelationen aufzubrechen, wird der DQN in der Regel auf Mini-Batches von zufällig ausgewählten Erfahrungsdatenpunkten aus dem Wiedergabepuffer trainiert. Insbesondere die Zufallsstichproben helfen, die zeitlichen Korrelationen aufzubrechen, was dazu führt, dass der Agent eine bessere Verteilung der Erfahrungen erlernt, die der zugrunde liegenden Dynamik des Marktes besser entspricht. Neben einer besseren Generalisierung stabilisiert sich der Trainingsprozess langfristig und konvergiert auch besser. Der Grund dafür ist, dass die Erfahrungswiederholung die Varianz der Aktualisierungen während des Trainingsprozesses reduziert.

Ohne Erfahrungswiederholung würden die Aktualisierungen der Netzgewichte in Schüben von stark korrelierten aufeinanderfolgenden Stichproben erfolgen, nur um dann durch eine völlig andere Aktualisierung aufgrund anderer Umgebungsbedingungen unterbrochen zu werden, was den gesamten Aktualisierungsprozess sehr unbeständig machen und möglicherweise zu Instabilität im Lernprozess führen würde. Durch die zufällige Auswahl aus einer Vielzahl von Erfahrungen führt der DQN-Agent sanftere und stabilere Aktualisierungen durch und verbessert so die Konvergenz zu einer optimalen Strategie.

Die effiziente Nutzung historischer Daten ist etwas, das die Erfahrungswiedergabe ebenfalls ermöglicht, da der Agent (aufgrund der Zufallsauswahl) mehrfach aus den Erfahrungen lernt, was besonders auf den Finanzmärkten wertvoll ist, wo es schwierig ist, zu jedem beliebigen Zeitpunkt große Mengen an unterschiedlichen und repräsentativen Daten zu erhalten. Dies ermöglicht es dem DQN, aus seltenen oder bedeutenden Ereignissen, wie z. B. Marktzusammenbrüchen oder -erholungen, zu lernen, auch wenn sie gerade nicht stattfinden. Dadurch ist der Agent besser auf solche Ereignisse vorbereitet und robuster, falls sie eintreten sollten.

Die Wiederholung von Erfahrungen erhöht auch das Explorationspotenzial des Verstärkungslernens, im Gegensatz zur reinen Ausbeutung. Es verringert die Wahrscheinlichkeit des „katastrophalen Vergessens“, bei dem der Agent wiederholt Proben aus seinem Wiederholungspuffer nimmt, was es ihm ermöglicht, das Wissen über ältere Strategien zu festigen und zu verhindern, dass diese durch neuere Erfahrungen überschrieben werden. Und schließlich ermöglicht es sogar noch speziellere Instanzen der Erfahrungswiedergabe wie die priorisierte Erfahrungswiedergabe, bei der Datenproben mit den größeren Verlustfunktionsfehlern aufgrund ihres höheren Lernpotenzials priorisiert werden, wodurch das Lernen effizienter und gezielter wird.

Wir erwähnen die Erfahrungswiederholung in diesem Artikel, weil sie ein Schlüsselprinzip des DQN ist; wir werden jedoch seine Fähigkeit in MQL5 in den kommenden Artikeln zeigen, wo DQN mehr als nur eine hybride Verlustfunktion sein wird, sondern das primäre Prognosemodell für unsere Signalklasse sein wird.

Zeitliche Entscheidungsfindung

Häufig haben Entscheidungen, auch außerhalb des Handels in Bereichen wie der Robotik oder dem Glücksspiel, verzögerte Auswirkungen auf künftige Ergebnisse, die nicht unbedingt sofort eintreten, sondern sich über einen längeren Zeithorizont erstrecken. Wirtschaftsnachrichten und Unternehmensbesetzungen sind das, was den Händlern in den Sinn kommen könnte, aber diese Beziehung stellt eine zeitliche Abhängigkeit her. Diese zeitliche Beziehung wird in der obigen q-Wert-Gleichung durch den Gamma-Faktor berücksichtigt. Gamma ermöglicht ein Gleichgewicht zwischen kurzfristigen und langfristigen Belohnungen, was den DQN-Q-Werten die Möglichkeit gibt, weiter in die Zukunft zu blicken und die kumulativen Auswirkungen von Maßnahmen im Laufe der Zeit abzuschätzen. Es wird argumentiert, dass dies zur Folge hat, dass einige Belohnungen verzögert werden, und Gamma stellt sicher, dass der Agent langfristige Belohnungen nicht ignoriert, während er die unmittelbaren Belohnungen im Auge behält, was beim Handel wichtig sein kann. So führen beispielsweise Positionen, die bei wichtigen Zinsentscheidungen eröffnet werden, oft nicht sofort zu günstigen Ausschlägen. Die ungünstigen Ausschlagsperioden bringen diese Positionen in der Regel in die Schlagzeilen, und daher kann die Möglichkeit, über Signale zu verfügen, die dies berücksichtigen, wie die DQNs, einen Vorteil darstellen.

Änderungen an unserem früheren Code

Um unseren DQN in einer hybriden Verlustfunktion zu verwenden, müssen wir zunächst unsere benutzerdefinierte Verlustaufzählung anhängen, die wie folgt aussieht:

//+------------------------------------------------------------------+
//| Custom Loss-Function Enumerator                                  |
//+------------------------------------------------------------------+
enum Eloss
{  LOSS_TYPICAL = -1,
   LOSS_SVR = 1,
   LOSS_QL = 2,
   LOSS_DQN = 3
};

Wir fügen eine neue Enumeration „LOSS_DQN“ hinzu, die ausgewählt wird, wenn die Verlustfunktion DQN verwendet. Weitere Änderungen, die wir wie im ersten Artikel über Reinforcement Learning vornehmen müssen, betreffen die Backpropagation-Funktion, bei der die Auswahl des geeigneten Verlusttyps den Wert bestimmt, der zur Berechnung der Deltas verwendet wird. Diese Änderungen sind wie folgt:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network arch! ");
      return;
   }


....

//COMPUTE DELTAS
   vector _last, _last_derivative;
   _last.Init(inputs.Size());
   if(hidden_layers == 0)
   {  _last = weights[hidden_layers].MatMul(inputs);
   }
   else if(hidden_layers > 0)
   {  _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]);
   }
   _last.Derivative(_last_derivative, THIS.activation);
   vector _last_loss = output.LossGradient(label, THIS.loss_typical);
   if(THIS.loss_custom == LOSS_SVR)
   {  _last_loss = SVR_Loss();
   }
   else if(THIS.loss_custom == LOSS_QL)
   {  

....

   }
   else if(THIS.loss_custom == LOSS_DQN)
   {  double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float);
      vector _rewards;
      _rewards.Init(Learning.dqn_target.Size());
      _rewards.Fill(0.0);
      if(_reward > 0.0)
      {  _rewards[0] = 1.0;
      }
      else if(_reward == 0.0)
      {  _rewards[1] = 1.0;
      }
      else if(_reward < 0.0)
      {  _rewards[2] = 1.0;
      }
      vector _target = QL.CriticTarget(_rewards, Learning.dqn_target);
      _last_loss = output.LossGradient(_target, THIS.loss_typical);
   }
   
....


}

Die anderen wichtigen Änderungen, die wir am Code vorgenommen haben, befinden sich in der CQL-Klasse und wurden bereits oben hervorgehoben, wo die q-Wert-Formel für DQN eingeführt wurde. Die Get-Output-Funktion, die wir für die Generierung der Bedingungsschwellenwerte verwenden, unterscheidet sich nicht wesentlich von der Funktion, die wir in dem früheren Artikel über das grundlegende q-learning betrachtet haben. Sie wird im Folgenden dargestellt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalDQN::GetOutput(int &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  int _states = 2;
         vector _in, _in_old, _in_row, _in_row_old, _in_col, _in_col_old;
         if
         (
            _in_row.Init(_states) &&
            _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) &&
            _in_row.Size() == _states
            &&
            _in_row_old.Init(_states) &&
            _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, _states) &&
            _in_row_old.Size() == _states
            &&
            _in_col.Init(_states) &&
            _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) &&
            _in_col.Size() == _states
            &&
            _in_col_old.Init(_states) &&
            _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_state_lag + ii + 1, _states) &&
            _in_col_old.Size() == _states
         )
         {  _in_row -= _in_row_old;
            _in_col -= _in_col_old;
            //
            m_learning.ql_reward_max = _in_row.Max();
            m_learning.ql_reward_min = _in_row.Min();
            if(m_learning.ql_reward_max == m_learning.ql_reward_min)
            {  m_learning.ql_reward_max += m_symbol.Point();
            }
            MLP.Set(_in_row);
            MLP.Forward();
            //
            MLP.QL.THIS.environments = m_environments;
            //
            vector _in_e;
            _in_e.Init(1);
            MLP.QL.Environment(_in_row, _in_col, _in_e);
            //
            int _row = 0, _col = 0;
            MLP.QL.SetMarkov(int(_in_e[_states - 1]), _row, _col);
            _in.Init(2);
            _in[0] = _row;
            _in[1] = _col;
            DQN_ONLINE.Set(_in);
            DQN_ONLINE.Forward();
            //
            MLP.QL.SetMarkov(int(_in_e[_states - 2]), _row, _col);
            _in_old.Init(2);
            _in_old[0] = _row;
            _in_old[1] = _col;
            DQN_TARGET.Set(_in_old);
            DQN_TARGET.Forward();
            m_learning.dqn_target = DQN_TARGET.output;
            if(ii > 0)
            {  vector _target, _target_data, _target_data_old;
               if
               (
                  _target_data.Init(2) &&
                  _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) &&
                  _target_data.Size() == 2
                  &&
                  _target_data_old.Init(2) &&
                  _target_data_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, 2) &&
                  _target_data_old.Size() == 2
               )
               {  _target.Init(__MLP_OUTPUTS);
                  _target.Fill(0.0);
                  _target_data -= _target_data_old;
                  double _type = _target_data[1] - _in_row[1];
                  int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1));
                  _target[_index] = 1.0;
                  MLP.Get(_target);
                  if(i == m_epochs && ii == m_train_set)
                  {  DQN_ONLINE.Backward(m_learning, i);
                     if(m_target_counter >= m_target_counts)
                     {  DQN_TARGET = DQN_ONLINE;
                        m_target_counter = 0;
                     }
                     MLP.Backward(m_learning, i);
                  }
               }
            }
            Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2));
         }
      }
   }
}

Wie bereits oben erwähnt, haben wir 2 DQN-Netze, das Online-Netz und das Zielnetz. Hinzu kommt natürlich die übergeordnete MLP, die, wie im Artikel über das Q-Learning, enge Preisänderungen als Inputs verwendet. Wir sollten uns nicht auf die Klasse QL beziehen, außer dass wir die kritische Zielfunktion aufrufen, um die q-Werte von DQN zu erhalten, wie oben erwähnt. Da die Klasse QL jedoch den Zugriff auf die Koordinaten des Umgebungszustands (bei Angabe eines Index) sowie die Zusammensetzung des Index aus den Zustandskoordinaten ermöglicht, beziehen wir uns auf sie, um die Eingaben für die beiden DQN-Netze zu erhalten. Wie bereits erwähnt, verwenden wir für unsere Prognosen nicht die q-map, sondern stützen uns auf das Online-DQN-Netz, das vom Zielnetz trainiert wird. Sowohl die Online- als auch die Ziel-DQNs nehmen einfach Umgebungszustände (alte bzw. neue) und werden darauf trainiert, einen Vektor von q Werten (für jede Agentenaktion) vorherzusagen.

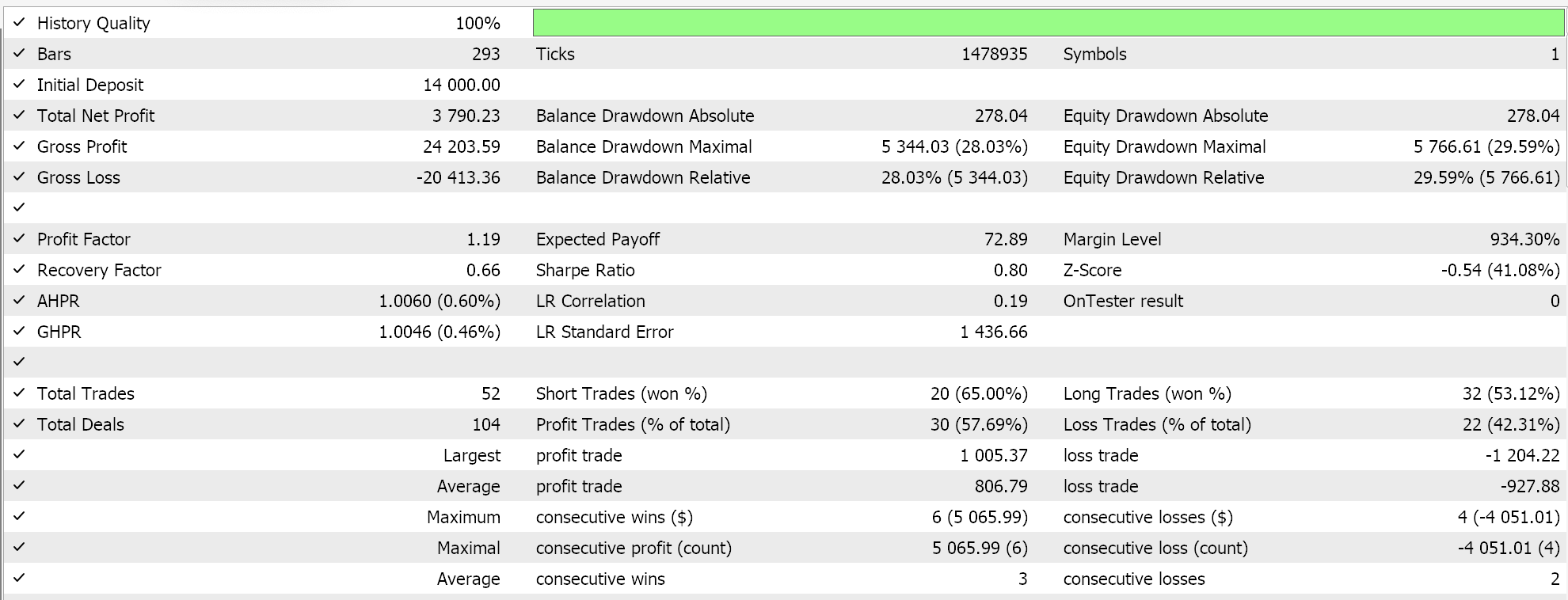
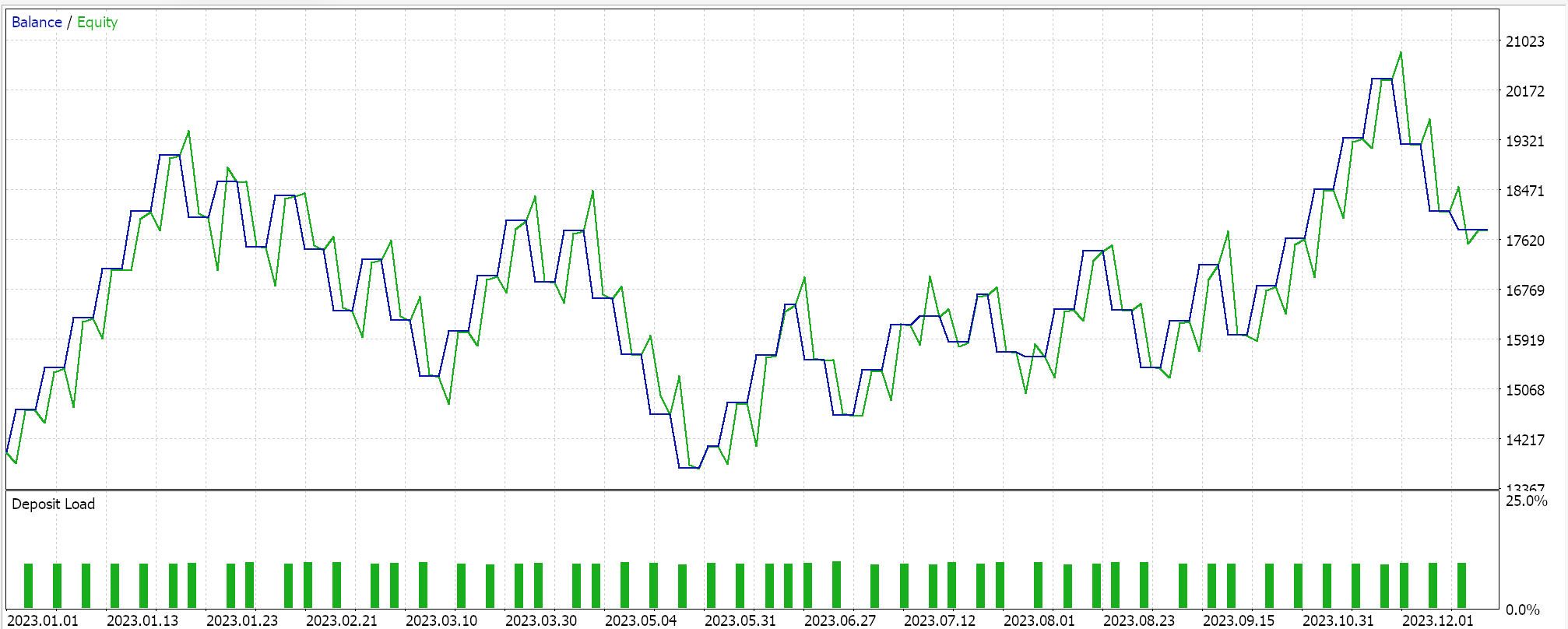
Strategie-Tester Berichte:

Wir testen diesen MLP mit Reinforcement-Learning-Training über Deep-Q-Netze auf EURGBP für das Jahr 2023 im täglichen Zeitrahmen. Nachfolgend sind unsere Ergebnisse aufgeführt, die lediglich die Handelbarkeit demonstrieren sollen und nicht unbedingt eine Replikation auf das zukünftige Marktgeschehen darstellen.

Schlussfolgerung

Wir haben uns mit der Implementierung und dem Testen eines alternativen Algorithmus zum Reinforcement-Learning namens Deep-Q-Networks in assistentengestützten Expert Advisors beschäftigt. Reinforcement-Learning ist neben dem überwachten und dem unüberwachten Lernen die dritte Trainingsmethode im maschinellen Lernen, und obwohl es sich streng genommen um einen anderen Trainingsansatz innerhalb des maschinellen Lernens handelt, werden wir in den folgenden Artikeln Szenarien betrachten, in denen es tatsächlich als primärer Modell- und Signalgenerator dienen kann.