您应当知道的 MQL5 向导技术（第 41 部分）：深度-Q-网络
175
0
概述
深度-Q-网络（DQN）是另一种强化学习算法，除了我们在本文中看到的 Q-学习 之外，但它们与 “Q-学习” 不同，使用神经网络来预测 q-值和代理人下一步欲采取的动作。它与 “Q-学习” 类似/相关，因为仍然涉及 “Q-表”，其中累积自先前“局次”得来的动作和状态的知识。事实上，它与 “Q-学习” 共享同样的维基百科页面，如从链接中可见，其中它基本上被定义为 “Q-学习” 的变体。
信号类、尾随止损类、和资金管理类一起，是向导汇编智能系统时需要定义的三个主要构建模块。通过 MQL5 向导将它们放到一起，可按 这里 和 这里 为新读者提供的指南来完成。本文底部附带的源代码，意在遵照这些链接中分享的向导汇编指南使用。我们再次寻求定义一个自定义信号类，以便能在向导汇编的智能系统中使用。
不过，这并非我们验证 DQN 的唯一途径，正如自定义尾随类、或自定义资金管理类的实现，也可以制作和测试。不过，我们专注于信号类，因为判定这些智能系统的做多和做空条件至关重要，在许多情况下，更好地展示交易设置的潜力。本文以本系列中的前几篇文章为基础，其中我们详细讲述了开发自定义向导汇编智能系统时可用的技术、或不同设置，故此对于新读者来说，回顾过去的文章将是一个好主意，尤其若他们正在寻求多样化的实现方式。这些文章不仅涵盖各种自定义信号，还涵盖了自定义尾随类、及资金管理类的实现。
就像我们在 “Q-学习” 文章中所见，DQN 设置的实现是作为对损失函数的支持，因为严格来讲我们将强化学习视为除有监督和无监督之外的第 3 种训练方式。正如 “Q-学习” 文章中提到的，这并非意味着它作为独立的模型实现，不能在没有从属 MLP 的情况下用于训练。这种使用强化学习的替代方式将在以后的文章中探讨，其中不会有从属的 MLP，代理人的动作预测将替换为通知做多和做空条件。
强化学习回顾
在我们起跳之前，或许快速回顾一下什么是强化学习是个好主意。这是机器学习训练的一种替代方式，其核心专注于代理人与环境的互动。代理人是决策实体，其目标是学习最佳动作，以便最大化累积奖励。环境是代理人“外部”的一切事物，充当评论者/观察者的宿主，并向代理人提供新状态和奖励形式的反馈（代理人准确预测的奖励）。因此，该循环从代理人观察当前环境状态开始，预测该状态的变化，然后选择适合该状态的相应动作。
状态是环境状态或状况的表示。一旦代理人选择或执行一个动作，环境状态的转换就会先期/同时发生，这样就会评估他的动作是否适合这个新环境。这种评估被量化为 “奖励”。无记忆马尔可夫（Markov）链矩阵权衡代理人的决策过程，来预测下一个状态时，但实际的转换是由环境判定的，在该文情况中，环境由市场方向和时间帧横向范围之间的交叉表标记。代理人所采取的动作，虽然可以是连续的（或无限范围的可能性），但它们往往是离散的，这意味着它们采取一组预定义的选项，而在我们的例子中，要么卖出、买入，要么什么都不做。尽管清单如此，在我们的例子中，其已被扩展如下，即是说市价单格式，如此不仅考虑到市价单，而且挂单也参与其中。
类似地，我们的奖励量值，在每根新柱线上都重新估算，在于来自先前操作或订单的亏损或盈利都可“升级”，从而将有利或不利的游离值量化为比率、或任何其它混合量值。该奖励量值与当前状态和先期选择的动作一起用于更新 Q-表，其来源在 CQL 类的 'CriticSource' 函数中分享。如上所述，我们严格地将强化学习视为监督学习和无监督学习的备案，如此这般它作用于严格量化我们的损失函数。然而，有些实例，其中强化学习被应用于 “决定性 ”设置之外，并被当作一个独立模型用来进行预测，其中代理人的动作被应用于训练之外，这些场景在此不予考虑，但可能会在未来的文章中加以考察。
深度 Q-网络算法概述
DQN 建立在 “Q-学习” 的基础上，其是我们研究的第一个强化学习算法，它的主要意图仍如 DQN，即预测 q-值。如上回顾，这些数据点对各种环境状态进行分类，并记录在 Q-表之中。与 “Q-学习” 算法的不同之处在于，使用神经网络来预测下一个 q-值，反比 Q-学习算法所依赖的 Q-映射（或表格），正如我们在第一篇强化学习文章中所演示的那样。此外，还有经验回放和目标网络，如以下各章节所述。因此，以前穿插在 Q-映射中应用的 ”ε-贪婪“ 政策不再适用于 DQN，因为神经网络正在发挥作用。
因此，DQN 在神经网络的辅助下，映射了跨越所有适用状态中每个可能动作的未来奖励。该状态映射交易者认为其是跨越各种市场条件（看涨-看跌-持平）中，每种可能动作（买入-卖出-持有）所提供的不同权重，这些权重决定了交易仓位。DQN 擅长处理高度复杂、和高维的环境，这些都是金融市场主要特征的一部分。金融市场是动态且非线性的，具有高度可变和独立的因素，像是价格变化、宏观经济指标、和市场情绪。
传统的 Q-学习 往往会受其阻碍阻，因为它使用状态数量有限且可管理的离散 Q-表，这与 DQN 形成鲜明对比，它十分搭配给定神经网络所用。DQN 还擅长捕捉各种资产类别的市场非线性依赖关系，而这也可当作某些交易策略的入场信号，例如日元套利交易。甚至，DQN 的运用，能够更好地普适，其网络能够更好地适应新的数据和市场条件，因神经网络往往比 q-表 更灵活。这在金融市场中至关重要，其中条件变化迅速，代理人必须适应不熟悉的情况。DQN 对市场噪音的适应能力也比传统的 “Q-学习” 更强。在金融市场中，代理人动作往往具有延迟奖励（譬如，持仓或许仅在若干天或周之后才有盈利）。DQN 使用带有贴现因子（gamma）的贝尔曼（Bellman）方程，令其能够评估短期和长期回报，如此网络学会了在快速盈利和长期收益之间取得平衡，这些在金融投资组合的策略决策中是本质。
依靠 DQN 预测 Q-值
我们正用 DQN 来归一化 MLP 的损失函数，因在本文中，如前所述，我们严格将 DQN 视为一种替代训练方式，而非像典型的 MLP 那样可自行预测的独立模型。在基本的 “强化学习” 设置中使用 DQN，意味着我们几乎坚持了我们在上一篇文章中所用的方式。由此意味着我们有一个 MLP 实例，它充当代理人，我们在信号类接口中将其称为 'DQN_ONLINE'，简要介绍如下：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CSignalDQN : public CExpertSignal { protected: int m_actions; // LetMarkov possible actions int m_environments; // Environments, per matrix axis int m_train_set; // int m_epochs; // Epochs double m_learning_rate; // Alpha Elearning m_learning_type; double m_train_deposit; double m_train_criteria; double m_initial_weight; double m_initial_bias; int m_state_lag; int m_target_counts; int m_target_counter; Smlp m_mlp; Smlp m_dqn; Slearning m_learning; public: void CSignalDQN(void); void ~CSignalDQN(void); //--- methods of setting adjustable parameters ... ... protected: void GetOutput(int &Output); Cmlp *MLP,*DQN_ONLINE,*DQN_TARGET; };
该网络取当前状态作为输入，并为每个可能的动作输出一个向量或 q-值。其网络架构可由读者调整或优调，遵循 2-6-3 架构，其中 2 是输入层的大小。其大小是 2，因为正如我们早前文章中所分享的，尽管有能力“扁平化”作为单个索引，但严格上，它是一对索引或坐标。一个坐标衡量覆盖短期的趋势类型，而另一个坐标衡量覆盖长期的趋势。
隐藏层大小被简单地分配为 6 ，不过如注，该大小和添加的其它隐藏层，能够据其所用的内容自定义。我们挑选了 6，来自输入大小与输出的倍数。故此，我们的输出大小为 3，就像 q-学习 文章中的情况一样，其表示代理人可能采取的动作数量。概言之，这些动作是买入、卖出、或持有。输出是执行这些动作的概率向量，这就意味着 DQN 是一个分类器网络。强化学习 DQN 的输出当作父级 MLP 网络的目标值。一旦我们得到该输出，我们就能训练 MLP。不过，DQN 的训练是不可忽视的，而其它网络不会以同样方式发生。与其费力地研究无处不在的状态和 q-值数据集，我们宁可使用另一个神经网络，为其贴上标签 “DQN_TARGET”，以便提供目标向量来训练 “DQN_ONLINE” 网络。接下来，我们考察这个。
目标网络的角色
目标网络，与在线网络（上面提供 MLP 目标的 DQN）一样，也采用环境状态作为输入，并为每个可能的动作输出 q-值向量。与在线网络的主要区别在于，环境状态输入是针对跟随当前状态的状态。此外，作为另一个神经网络，人们会期望它通过反向传播进行训练，但取而代之的是，在预设间隔内，它只是复制在线网络。在计算时态差别时，目标网络提供更稳定的目标值，从而降低了训练过程中振荡和发散的风险。
若无独立的目标网络、母级 MLP 和在线网络，目标值将在不稳定的振荡行为中持续变化。这是因为两个网络的更新是并发的。通过使用目标网络，学习过程将会是稳定的，因为两种算法的发散/振荡都会减少。如上所述，目标网络不像常规 MLP 那样反向传播，而是按设定间隔复制在线网络。这些间隔的大小通常约为 10,000 个，我们用于调制的输入参数标记为 'm_target_counts'，默认情况下仅赋值为 65 个！这是因为我们仅在日线时间帧上测试了一年，故我们有 260 根价格柱线进行测试。这是一个可调整参数，故配合更长测试周期、或较小的时间帧内，10,000 步是可行的。目标 q-值的计算按以下公式达成：
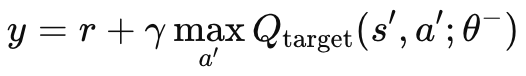
其中：
- y：目标 Q-值，表示从当前状态 s 开始，采取动作 a，然后遵循最优政策的预计回报（未来奖励）。
- r：在状态 s 中执行动作 a 后获得的即时奖励。
- γ：折扣系数，它决定了未来奖励的重要性。它是一个介于 0 和 1 之间的数值。
- max a′ Qtarget(s′,a′;θ−)：覆盖所有可能的动作 a′，下一个状态 s′的最大预测 Q-值，由目标网络依据参数 θ− 估算。
- Qtarget(s′,a′;θ−)：目标网络预测的下一个状态-动作对 (s′,a′)(s', a')(s′,a′), 的 Q-值。
- θ−：目标网络的参数（权重），其会据主网络的参数定期更新。
该公式的 MQL5 实现是通过关键目标函数，我们将其附加到我们在强化学习介绍性文章中曾用到的 CQL 类之中。该函数如下所示：
//+------------------------------------------------------------------+ // Critic Target for DQN //+------------------------------------------------------------------+ vector Cql::CriticTarget(vector &Rewards, vector &TargetOutput) { vector _target = Rewards + (THIS.gamma * TargetOutput); return(_target); }
这里有一个引导问题。正如我们在上一篇关于强化学习的文章中所见，在传统的 Q-学习中，网络基于自己的预测更新 q-值，如若预测不准确，则可能会导致一连串的错误（通常称为引导错误）。这是因为一个状态的 q-值取决于后续状态的 q-值，这可能会导致误差放大。
由此，目标网络的角色是通过提供慢速移动的目标来缓解这一点。由于目标网络的参数更新频率较低（通常每几万步一次），故它的变化比在线网络更缓慢。这会减慢误差的传播速度，从而管控引导问题。
在我们拥有非线性动态的状况下，诸如金融市场的复杂环境，甚至像是视频游戏，状态和奖励之间的关系往往是高度非线性的。因此，目标网络引入的稳定性，对于 DQN 在这些设置下有效学习至关重要。若没有这个目标网络，在面对复杂或快速变化的环境时，由于 q-值和目标的快速更新，在线网络（DQN）更可能发散。
此外，可以通过添加一个扩展来改进目标网络，该扩展通常被称为“双 DQN”，用于解决高估偏差。其实现是通过使用在线网络和目标网络两者，分开选择和评估动作。它在线网络和目标网络之间，解耦了动作选择、与动过评估过程。在线网络用来选择动作，而目标网络则对其进行评估。
经验回放及其在训练中的角色
经验回放是一种缓冲技术，其中强化学习 DQN 代理人将其状态、动作、奖励、和下一个状态的“经验”存储在回放缓冲区之中。然后，在训练期间从这些经验里随机采样，从而更新代理人的 DQN 权重和乖离。正如人们所期望的那样，该方式对于打破仅参考连续数据点的顺序相关性很实用，故而能够更适合金融市场等真实世界的场景。在金融市场中，连续的数据点，无论是价格、合约量、还是波动性，往往都是高度相关的，因为它们都受到相似的市场条件和参与者行为的影响。依据这种顺序相关的数据上训练 DQN 代理人往往会导致过度拟合、并缺乏普适性，因为 DQN 代理人习惯于利用特定形态，然其不能很好地普适不同市场条件。
为了打破这些时态相关性，典型情况下，DQN 依据从回放缓冲区随机采样的小批量经验数据点进行训练。随机抽样尤其有助于打破时态相关性，从而令代理人学习更好的经验分布，更好地逼近市场的底层动态。除了更好的普适化之外，覆盖长期的训练过程变得更加稳定，也能更好地收敛。这是因为经验回放在训练过程中降低了更新的变化。
若无经验回放，网络权重更新会因连续样本的高度相关而突然爆发，仅会被来自不同环境条件的完全不同的更新打断，而这趋于令整个更新过程非常不稳定，并导致学习过程不稳定。通过从一组不同的经验中随机采样，DQN 代理人执行更新更流畅、更稳定，从而提高朝最优策略的收敛性。
经验回放还能有效利用历史数据，因为代理人会多次从经验中重新学习（由于随机选择），这在金融市场尤其有价值，因为在任何特定时间获得大量多样化、和有代表性的数据都是具有挑战性的。这本质上令 DQN 能够从罕见、或重大事件中学习，譬如市场崩盘或反弹，即便它们目前并没发生。若它们发生，这样代理人在应对这些事件时就更有准备和健壮性。
相较仅仅是利用，经验回放还增强了强化学习的探索潜力。它降低了代理人从其回放缓冲区重复采样的“灾难性遗忘”的似然性，令其能够加强对旧策略的了解，并防止它们被新经验覆盖；最后，它允许更专业的经验回放实例，例如优先经验回放，其中损失函数误差较大的数据样本因其更高的学习潜力而被优先考虑，从而令学习更加高效和有针对性。
我们在本文中提及经验回放，因为它是 DQN 中的一个关键原则；不过，我们将在以后的文章中展示它在 MQL5 中的能力，其中 DQN 将不仅仅是一个混合损失函数，而是我们信号类的主要预测模型。
时态决策
往往所做决策，即使在交易之外，像是机器人或游戏等领域，也会对未来成果有延迟影响，其不一定是立竿见影的，但会在覆盖更长时间横截面内起作用。交易者可能会留意经济新闻发布和公司公示，但这种关系建立了时间依赖性。在上面的 q-值方程中，通过 Gamma 因子来研究这种时态关系。Gamma 允许在短期和长期奖励之间取得平衡，这令 DQN 的 q-值能够进一步向前看，并估测动作随时间推移的累积影响。有种论调，这样做的效果会令一些奖励被延迟，而 gamma 确保代理人不会忽视长期奖励，同时仍然密切关注眼前的奖励，这在交易时可能是本质性的。举例，在重大利率决策时开仓，往往不会立即产生有利的走位。这些持仓的开头通常是不利的走位区间，因此要考虑使用具有这种能力的信号，像是 DQN 可能是一个优势。
修改我们之前的代码
为了在混合损失函数中使用我们的 DQN，我们首先需要追加我们的自定义损失枚举，如下所示：
//+------------------------------------------------------------------+ //| Custom Loss-Function Enumerator | //+------------------------------------------------------------------+ enum Eloss { LOSS_TYPICAL = -1, LOSS_SVR = 1, LOSS_QL = 2, LOSS_DQN = 3 };
我们添加了一个新的枚举 'LOSS_DQN'，可选择使用 DQN 充当损失函数。正如我们在第一篇强化学习文章中所做的那样，我们要做的其它修改是在反向传播函数当中，其中选择合适损失类型去决定用于计算增量的数值。这些修改如下：
//+------------------------------------------------------------------+ //| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON. | //+------------------------------------------------------------------+ //| | //| -Extra Validation check of MLP architecture settings is performed| //| at run-time. | //| Chcecking of 'validation' parameter should ideally be performed | //| at class instance initialisation. | //| | //| -Run-time Validation of learning rate, decay rates and epoch | //| index is performed as these are optimisable inputs. | //+------------------------------------------------------------------+ void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1) { if(!validated) { printf(__FUNCSIG__ + " invalid network arch! "); return; } .... //COMPUTE DELTAS vector _last, _last_derivative; _last.Init(inputs.Size()); if(hidden_layers == 0) { _last = weights[hidden_layers].MatMul(inputs); } else if(hidden_layers > 0) { _last = weights[hidden_layers].MatMul(hidden_outputs[hidden_layers - 1]); } _last.Derivative(_last_derivative, THIS.activation); vector _last_loss = output.LossGradient(label, THIS.loss_typical); if(THIS.loss_custom == LOSS_SVR) { _last_loss = SVR_Loss(); } else if(THIS.loss_custom == LOSS_QL) { .... } else if(THIS.loss_custom == LOSS_DQN) { double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float); vector _rewards; _rewards.Init(Learning.dqn_target.Size()); _rewards.Fill(0.0); if(_reward > 0.0) { _rewards[0] = 1.0; } else if(_reward == 0.0) { _rewards[1] = 1.0; } else if(_reward < 0.0) { _rewards[2] = 1.0; } vector _target = QL.CriticTarget(_rewards, Learning.dqn_target); _last_loss = output.LossGradient(_target, THIS.loss_typical); } .... }
我们对代码所做的其它主要修改是在 CQL 类之中，上面已经高亮显示了 DQN 的 q-值公式。我们生成条件阈值的 GetOutput 函数与我们之前关于基本 q-学习 的文章中研究的没有太大区别。它如下所示：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalDQN::GetOutput(int &Output) { m_learning.rate = m_learning_rate; for(int i = m_epochs; i >= 1; i--) { MLP.LearningType(m_learning, i); for(int ii = m_train_set; ii >= 0; ii--) { int _states = 2; vector _in, _in_old, _in_row, _in_row_old, _in_col, _in_col_old; if ( _in_row.Init(_states) && _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) && _in_row.Size() == _states && _in_row_old.Init(_states) && _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, _states) && _in_row_old.Size() == _states && _in_col.Init(_states) && _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, _states) && _in_col.Size() == _states && _in_col_old.Init(_states) && _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_state_lag + ii + 1, _states) && _in_col_old.Size() == _states ) { _in_row -= _in_row_old; _in_col -= _in_col_old; // m_learning.ql_reward_max = _in_row.Max(); m_learning.ql_reward_min = _in_row.Min(); if(m_learning.ql_reward_max == m_learning.ql_reward_min) { m_learning.ql_reward_max += m_symbol.Point(); } MLP.Set(_in_row); MLP.Forward(); // MLP.QL.THIS.environments = m_environments; // vector _in_e; _in_e.Init(1); MLP.QL.Environment(_in_row, _in_col, _in_e); // int _row = 0, _col = 0; MLP.QL.SetMarkov(int(_in_e[_states - 1]), _row, _col); _in.Init(2); _in[0] = _row; _in[1] = _col; DQN_ONLINE.Set(_in); DQN_ONLINE.Forward(); // MLP.QL.SetMarkov(int(_in_e[_states - 2]), _row, _col); _in_old.Init(2); _in_old[0] = _row; _in_old[1] = _col; DQN_TARGET.Set(_in_old); DQN_TARGET.Forward(); m_learning.dqn_target = DQN_TARGET.output; if(ii > 0) { vector _target, _target_data, _target_data_old; if ( _target_data.Init(2) && _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) && _target_data.Size() == 2 && _target_data_old.Init(2) && _target_data_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, 2) && _target_data_old.Size() == 2 ) { _target.Init(__MLP_OUTPUTS); _target.Fill(0.0); _target_data -= _target_data_old; double _type = _target_data[1] - _in_row[1]; int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1)); _target[_index] = 1.0; MLP.Get(_target); if(i == m_epochs && ii == m_train_set) { DQN_ONLINE.Backward(m_learning, i); if(m_target_counter >= m_target_counts) { DQN_TARGET = DQN_ONLINE; m_target_counter = 0; } MLP.Backward(m_learning, i); } } } Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2)); } } } }
如上所述，我们有 2 个 DQN 网络，在线网络和目标网络。此外，当然，父级 MLP 取收盘价变化作为输入，就像 q-学习 文章中一样。除了如上所述调用关键目标函数来获取 DQN 的 q-值之外，我们不应该引用 QL 类。不过，由于 QL 类允许我们访问环境状态坐标（当给定索引时），以及从状态坐标组合为索引，因此我们引用它来获取两个 DQN 网络的输入。如前所述，我们没有使用 q-映射 进行预测，而是依赖于经目标网络训练的在线 DQN 网络。在线和目标 DQN 都简单地采用环境状态（分别为旧和新），并经训练来预测 q-值的向量（针对每名代理人动作）。
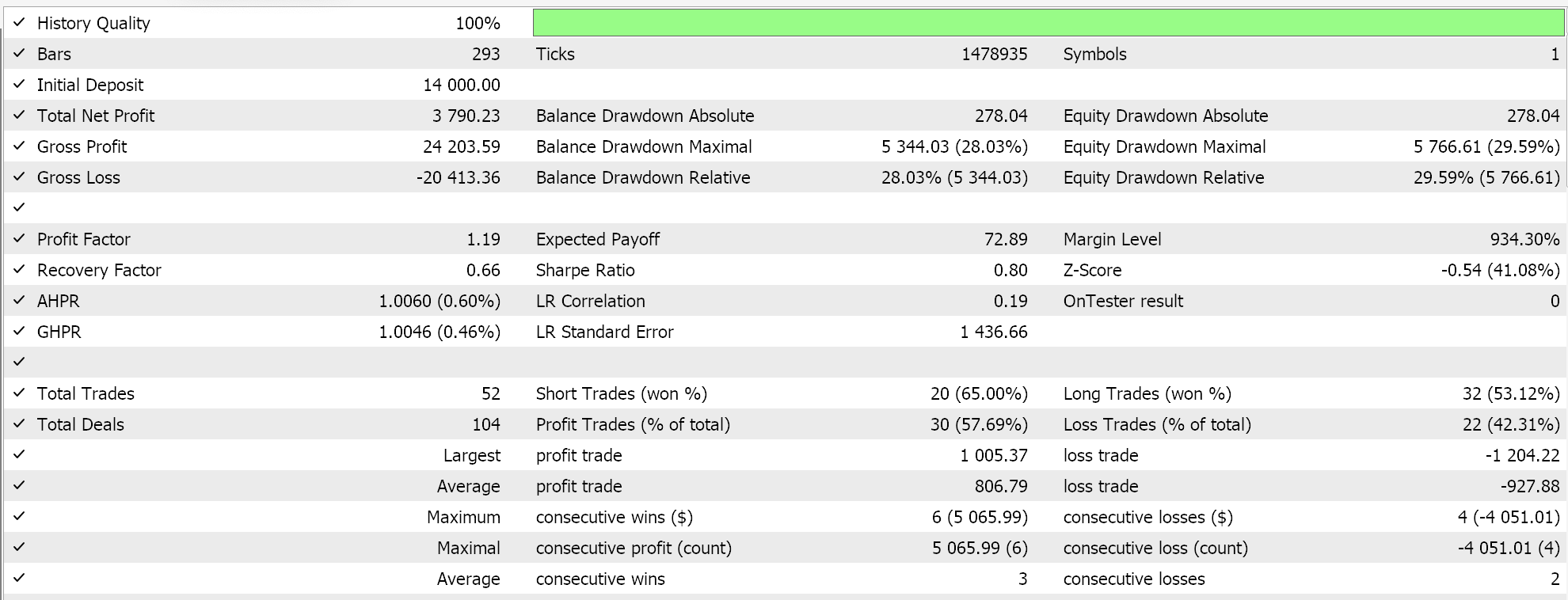
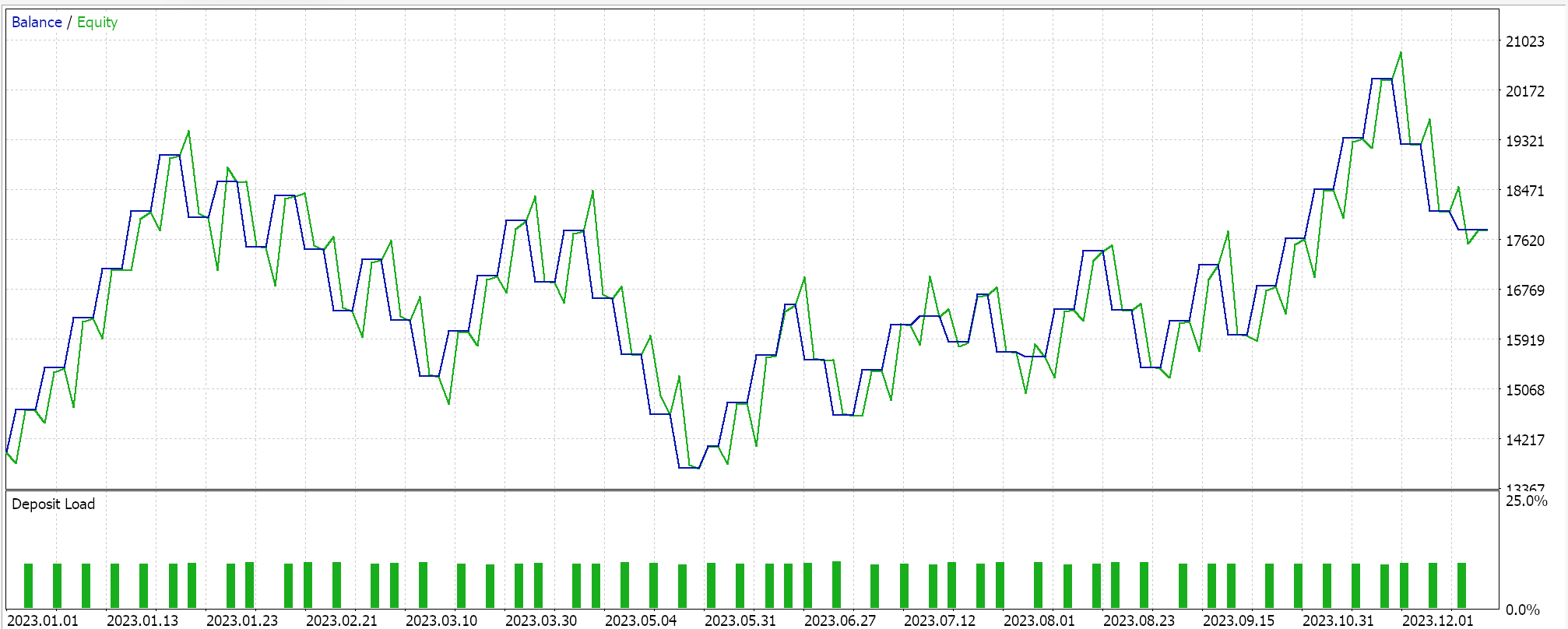
策略测试器报告：
我们通过 “深度-Q-网络” 依据 2023 年 EURGBP 的日线时间帧，配以强化学习训练来测试这个 MLP。以下是我们的结果，其中严格证明可交易性，但不一定在未来的市场动作上复现。
结束语
我们已考察了称为 “深度-Q-网络” 的强化学习替代算法的实现，并用向导汇编的智能系统进行了测试。强化学习是继监督学习和无监督学习之外机器学习训练的第三种方法，尽管严格来说它是一种机器学习训练的不同方式，但在后续文章中，我们将研究它能实际用作主要模型和信号发生器的场景。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/16008
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
开发多币种 EA 交易（第 18 部分）：考虑远期的自动化组选择
基于Python和MQL5的特征工程（第二部分）：价格角度
交易中的神经网络：广义 3D 引用表达分段
