Hibridación de algoritmos basados en poblaciones. Esquema secuencial y paralelo

Contenido:

1. Introducción
2. Experimento con GWO y COA
3. Experimento con ESG y SDSm
4. Conclusiones

1. Introducción

Vamos a analizar las tres variantes principales de hibridación de algoritmos de optimización:

1. Combinación de estrategias de búsqueda de algoritmos en un único conjunto genérico. Cada algoritmo será un individuo único con su propio conjunto de habilidades y capacidades. La mezcla de sus construcciones lógicas, en las que todos contribuyen, enriquecerá la diversidad de las propiedades en la búsqueda común del éxito. Es una danza de diferentes estilos en la que cada paso complementará y realzará el movimiento general. Un ejemplo de este enfoque sería el algoritmo híbrido de optimización de forrajeo bacteriano combinado con el algoritmo genético que hemos comentado anteriormente en este artículo.

2. Funcionamiento secuencial de cada uno de los algoritmos dividiendo las iteraciones en el funcionamiento parcial de uno y el funcionamiento final del otro, como pasándose el testigo. Los algoritmos serían equipos deportivos, cada uno especializado en una etapa diferente de la carrera. Pasar el testigo entre ellos implica transferir conocimientos y resultados, creando una transición fluida y eficaz de una etapa a la siguiente, como la armonía de un equipo bien coordinado, dejando inalterado el número total de iteraciones.

3. El funcionamiento paralelo de cada algoritmo y la posterior combinación de los mejores resultados únicos se asemejaría a la creatividad colectiva, donde cada algoritmo es un artista que pone su energía única en el lienzo común del mundo. En cada iteración se fusionan los mejores resultados, donde cada retoque complementa y amplía la comprensión del problema estudiado, creando una visión compartida de la solución óptima.

Estas variantes de hibridación de algoritmos abren un amplio abanico de posibilidades para la combinación creativa de distintos enfoques y estrategias que nos lleven a adquirir nuevos conocimientos y mejorar el campo de la optimización. Al igual que en el mundo del arte, donde una variedad de estilos y técnicas inspiran creaciones únicas, en el mundo de la optimización una combinación armoniosa de distintos algoritmos puede conducirnos a resultados óptimos y a una exploración eficaz de problemas complejos.

En un mundo de búsqueda constante de soluciones óptimas, donde cada paso en el espacio de opciones importa, es importante no solo saber buscar, sino saber encontrar con confianza para lograr el resultado deseado. El estudio experimental que realizamos en nuestro anterior artículo en el campo de los algoritmos de optimización basados en poblaciones, en el que situábamos forzosamente los algoritmos en el punto del mínimo global para alcanzar el punto del máximo global, nos reveló un aspecto importante: la dependencia del éxito respecto a las condiciones iniciales. Algunos algoritmos tenían dificultades para salir del punto de mínimo, perdiendo eficacia, mientras que otros eran brillantes ejemplos de estabilidad universal, con poca dependencia de la posición inicial. Algunos exploraban con éxito el espacio de búsqueda al principio del proceso, al tiempo que otros intentaban mejorar significativamente los resultados en fases posteriores. Estas características únicas de cada algoritmo pueden explotarse con éxito potenciando sus aspectos positivos y reduciendo sus puntos débiles. Esperamos que la combinación de distintas estrategias pueda ofrecer métodos más eficaces que permitan explorar con éxito el espacio y mejorar los resultados en las distintas fases del trabajo. Debemos añadir que, gracias a la normalización, la hibridación de algoritmos se ha hecho más accesible. Todos los algoritmos de poblaciones se reúnen ahora en una sola clase, lo cual abre la puerta a combinaciones creativas y posibilidades totalmente nuevas.

2. Experimento con GWO y COA

Para el experimento, tomaremos dos algoritmos con prestaciones y características distintas: GWO y COAm. Mientras que GWO se encuentra en la parte inferior de la tabla de clasificación, COAm se sitúa en el centro. Vamos a intentar averiguar qué resultados pueden obtenerse utilizando sus combinaciones en el trabajo secuencial y paralelo. En este artículo, no analizaremos la mezcla de elementos lógicos de las estrategias de búsqueda, ya que esto es algo muy específico de cada combinación de algoritmos y no puede considerarse en un único artículo.

El algoritmo del Lobo Gris (Grey Wolf Optimizer, GWO) es un algoritmo estocástico metaheurístico basado en la simulación de la caza en recintos cerrados de una manada de lobos grises.
Principales características del algoritmo GWO:

• Modelización del comportamiento de las manadas. El algoritmo utiliza la estructura jerárquica de una manada de lobos, donde cada lobo desempeña un papel distinto (alfa, beta, delta, omega).
  
• Búsqueda del máximo global. Los lobos alfa, beta y delta se consideran los más adaptables y se encuentran más cerca de sus presas, mientras que los demás lobos intentan acercarse a ellas. El GWO se precipita rápidamente hacia un posible extremo global.
  
• Adaptabilidad. Mientras el algoritmo está en funcionamiento, los lobos se reorganizan constantemente para adaptarse a las condiciones cambiantes.
  

El algoritmo de optimización del cuco (Cuckoo Optimization Algorithm — COAm) es uno de los últimos algoritmos heurísticos inspirados en la naturaleza. y se basa en el parasitismo de algunas especies de cucos.
Principales características del algoritmo COAm:

• Modelización del comportamiento de los cucos. El algoritmo usa la estrategia de cría del cuco, que pone sus huevos en los nidos de otros pájaros.
• Búsqueda del máximo global. Los huevos del nido se interpretan como posibles soluciones al problema de optimización, mientras que el huevo del cuco representa una nueva solución.
  
• Adaptabilidad. Si el huevo cuco es de mayor calidad que el huevo del progenitor, será sustituido. De lo contrario, el huevo del progenitor se quedará en el nido.

Así pues, la hibridación de estos algoritmos permitiría (presumiblemente) aprovechar sus ventajas combinadas para resolver problemas de optimización con mayor eficacia. La figura 1 muestra un esquema del funcionamiento de GWO y COAm. Al final de la primera etapa, cuando algunas de las iteraciones se asignan a GWO, los estados de los agentes de un algoritmo son transferidos al otro. Cada agente renace en una nueva especie, en este caso el lobo se convierte en cuco, manteniéndose la posición de los individuos en la población.

Figura 1. Algoritmo híbrido, GWO+COA

Veamos el teórico curso de los acontecimientos:

1. Inicio:
   - Empezaremos con 10 000 iteraciones, que es un recurso limitado, por lo que cada iteración será crítica para alcanzar la solución óptima.
2. Paso 1 (0—5000 iteraciones):
   - Dividiremos el número total de iteraciones por la mitad y empezaremos con el algoritmo GWO.
   - Debido a la rápida propagación de los lobos por el espacio de búsqueda, convergerán rápidamente hacia un posible extremo global a mediados del periodo.
3. Paso 2 (5 000 — 10 000 iteraciones):
   - Después de las primeras 5 000 iteraciones, transferiremos la posición de los lobos a la posición de los cucos en estos puntos.
   - La búsqueda del cuco con el vuelo de Levy recibirá el testigo para afinar aún más el extremo.
4. Resultado:
   - Es de esperar que, como resultado de esta combinación de los algoritmos GWO y COA con vuelo de Levy, podamos alcanzar un extremo global más preciso y estable en un número limitado de iteraciones. 

Así, el uso de la estrategia anterior optimizará el proceso de búsqueda del extremo global en un número limitado de iteraciones, ofreciendo el equilibrio necesario entre la velocidad de convergencia y la precisión del resultado.

Ahora declararemos la clase "C_AO_GWO_COAm", descendiente de la clase "C_AO". El constructor de la clase establecerá valores por defecto para los parámetros de optimización, como el tamaño de la población "popSize" y la relación "ratio" entre los algoritmos GWO y COAm. Esta clase permitirá usar los dos algoritmos de forma secuencial, sin influir en el manejo de los mismos y permitiendo utilizar nuestro banco de pruebas sin modificaciones.

La clase también definirá los métodos para el establecimiento de los parámetros, "SetParams", la inicialización de la optimización, "Init", el desplazamiento, "Moving" y la actualización de la solución global, "Revision", así como la inserción de los valores de las coordenadas en los agentes, "Injection".

Las variables importantes de la clase incluirán "ratio" (la relación entre GWO y COAm), y los objetos de las clases "C_AO_GWO" y "C_AO_COAm" para implementar el Grey Wolf Optimizer y el Cuckoo Optimization Algorithm, respectivamente.

También tendremos variables en la clase para monitorear el número de épocas y la época actual para cada uno de los algoritmos (GWO y COAm).

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GWO_COAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_GWO_COAm () { }
  C_AO_GWO_COAm ()
  {
    ao_name = "GWO_COAm";
    ao_desc = "Grey Wolf Optimizer and Cuckoo Optimization Algorithm M";

    popSize = 50;    //population size
    ratio   = 0.5;   //the ratio of GWO and COAm

    ArrayResize (params, 2);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "ratio";   params [1].val = ratio;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    ratio   = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double ratio;  //the ratio of GWO and COAm

  private: //-------------------------------------------------------------------
  C_AO_GWO  AO1;
  C_AO_COAm AO2;

  int epochCount;
  int epochNow;

  int epochGWO;
  int epochCOAm;
};
//——————————————————————————————————————————————————————————————————————————————

El método "Init" de la clase "C_AO_GWO_COAm" se utilizará para inicializar el proceso de optimización. Aquí se fijarán los valores iniciales, se crearán los agentes y se establecerán los parámetros de inicialización de los algoritmos GWO y COAm.

1. El éxito de la inicialización estándar se comprobará usando el método "StandardInit", que utiliza los parámetros transmitidos para establecer el rango de búsqueda mínimo y máximo.
2. El número de épocas para cada uno de los algoritmos GWO y COAm se calculará en función del "ratio" y del número total de épocas "epochCount".
3. Los parámetros de los algoritmos GWO y COAm se establecerán e inicializarán mediante los métodos "SetParams" e "Init".
4. El método retornará "true" si la inicialización se ha realizado correctamente.

Este método proporcionará la configuración inicial y la inicialización de los algoritmos GWO y COAm para optimizar el problema con los parámetros y las restricciones que se han establecido.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_GWO_COAm::Init (const double &rangeMinP  [], //minimum search range
                          const double &rangeMaxP  [], //maximum search range
                          const double &rangeStepP [], //step search
                          const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochCount   = epochsP;
  epochNow     = 0;

  epochGWO  = int(epochCount *ratio);
  epochCOAm = epochCount - epochGWO;

  AO1.params [0].val = popSize;
  AO2.params [0].val = popSize;

  AO1.SetParams ();
  AO2.SetParams ();

  AO1.Init (rangeMinP, rangeMaxP, rangeStepP, epochGWO);
  AO2.Init (rangeMinP, rangeMaxP, rangeStepP, epochCOAm);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

En el código del método "Moving" de la clase "C_AO_GWO_COAm", el valor de la variable "epochNow" se incrementará en uno. El contador "epochNow" se utilizará para determinar las etapas que ejecutan respectivamente primero GWO y después COAm.

Si "epochNow" es menor que "epochGWO", se llamará al método "Moving" del objeto "AO1" (GWO), tras lo cual los elementos del array de agentes "AO1.a" se copiarán en el array de agentes "a".

En caso de que "epochNow" sea igual a "epochGWO", se llamará al método "Moving" del objeto "AO2" (COAm) y, a continuación, los valores del array "AO1.a" se incorporarán en los elementos correspondientes del array "AO2.a", es decir, la propia transformación de lobos en cucos. Por último, todos los elementos del array "AO2.a" se copiarán en el array "a" para hacer referencia a los agentes "a" en el programa a ejecutar.

Este método garantizará que los agentes se muevan secuencialmente en cada época de optimización según los algoritmos GWO y COAm seleccionados.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  epochNow++;

  if (epochNow < epochGWO)
  {
    AO1.Moving ();
    for (int i = 0; i < popSize; i++)
    {
      a [i] = AO1.a [i];
    }
    return;
  }

  AO2.Moving ();

  if (epochNow == epochGWO)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        AO2.Injection (i, c, AO1.a [i].c [c]);
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    a [i] = AO2.a [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método de "Revision" realizará la transferencia del valor de adaptabilidad calculado de los agentes a los agentes correspondientes de los algoritmos.

Según el valor de las variables "epochNow" y "epochGWO", se realizarán las acciones para los algoritmos GWO o COAm:

1. Copiado del valor de adaptabilidad a los agentes.
2. Ejecución del método Revision.
3. Ejecución de la actualización global de la solución.
   

Así, este método implementará la lógica de actualización de la solución global con la solución de los algoritmos GWO y COAm según la fase de ejecución actual de los respectivos algoritmos.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  if (epochNow < epochGWO)
  {
    for (int i = 0; i < popSize; i++) AO1.a [i].f = a [i].f;

    AO1.Revision ();

    if (AO1.fB > fB)
    {
      fB = AO1.fB;
      ArrayCopy (cB, AO1.cB, 0, 0, WHOLE_ARRAY);
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++) AO2.a [i].f = a [i].f;

    AO2.Revision ();

    if (AO2.fB > fB)
    {
      fB = AO2.fB;
      ArrayCopy (cB, AO2.cB, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

En la visualización del rendimiento del algoritmo híbrido, destacará el siguiente fenómeno: El GWO se atasca a menudo en los extremos locales, poniendo fin prematuramente a su rápido movimiento. En cambio, el algoritmo COA deja tras de sí una estela de resultados variados, generando una dispersión a veces impresionante en los puntos finales.

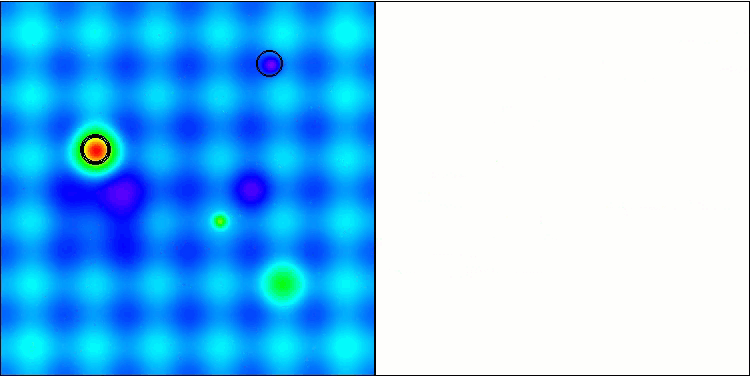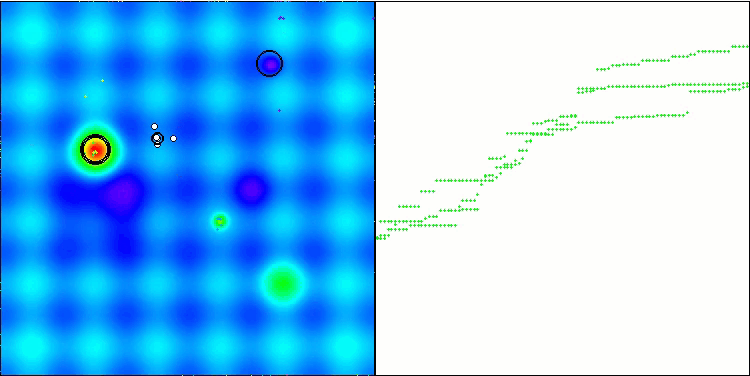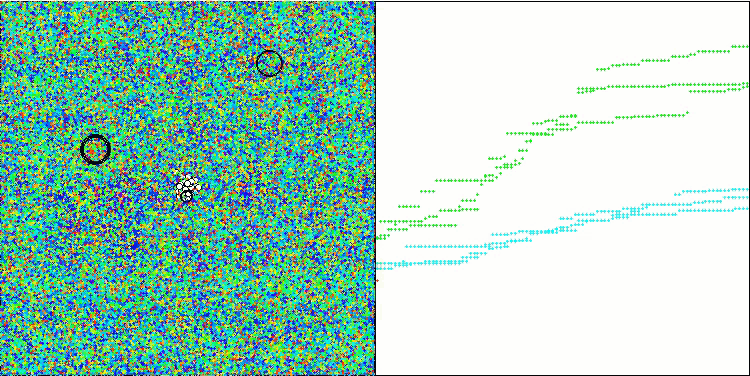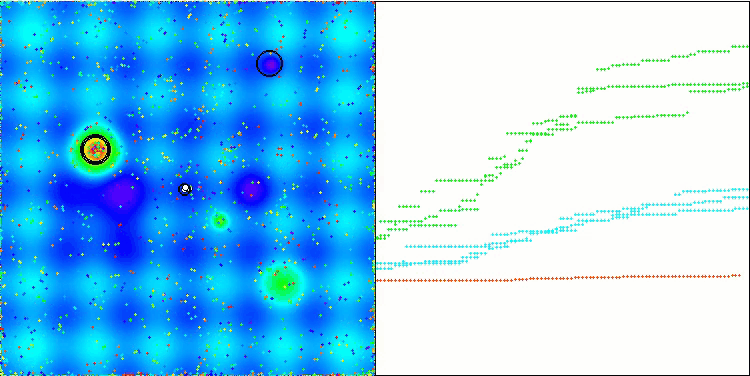
GWO-COAm en la función de prueba Hilly

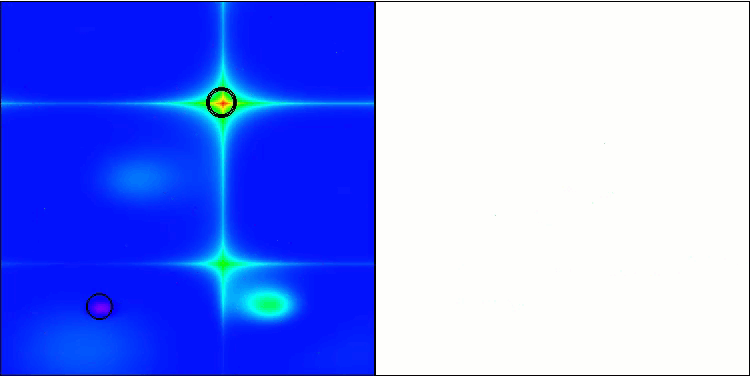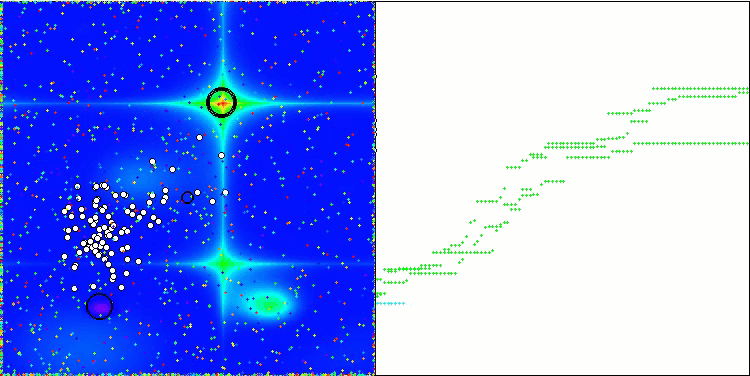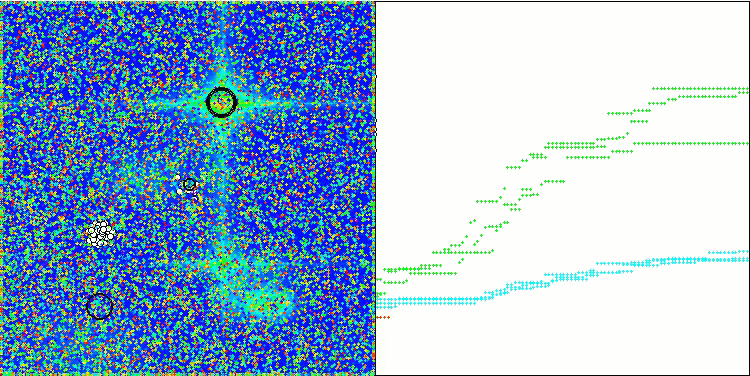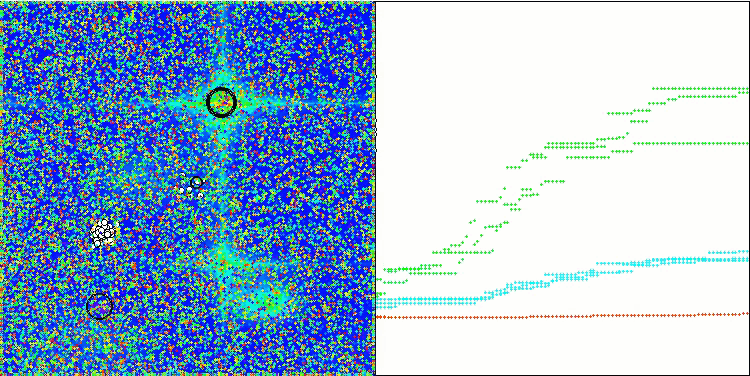
GWO-COAm en la función de prueba Forest

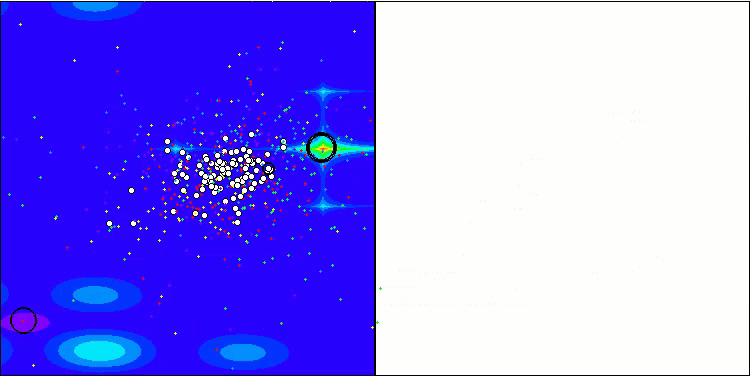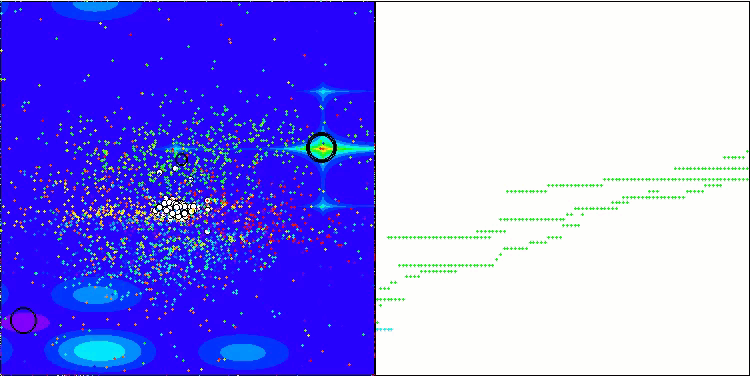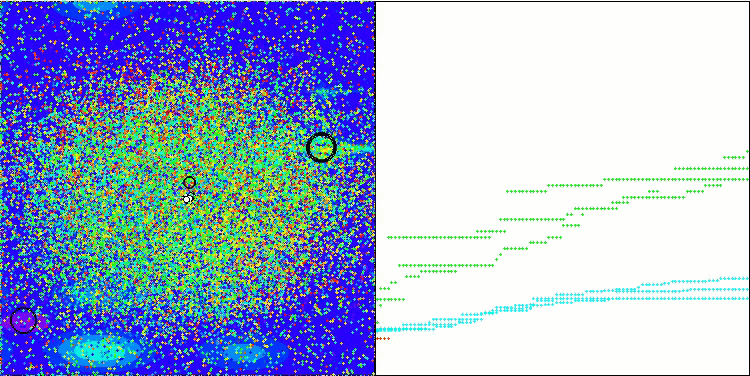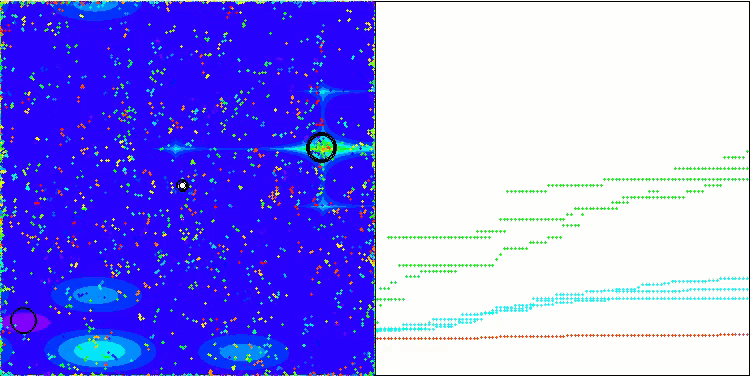
GWO-COAm en la función de prueba Megacity

Así pues, ya hemos realizado un experimento para intentar crear un algoritmo híbrido combinando los algoritmos GWO y COAm secuencialmente. Sin embargo, esto no nos ha traído los resultados deseados (mejoras en el rendimiento del mejor). El GWO se atasca a menudo en máximos locales y deja de moverse, mientras que el algoritmo COAm no logra recoger el testigo y se caracteriza por una gran variación de los resultados finales en función del número de ejecuciones experimentales.

Impresión de los resultados del algoritmo GWO-COAm según el esquema secuencial:

GWO_COAm|Grey Wolf Optimizer and Cuckoo Optimization Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.729041499138184
25 Hilly's; Func runs: 10000; result: 0.4465971838522985
500 Hilly's; Func runs: 10000; result: 0.2685674823439256
=============================
5 Forest's; Func runs: 10000; result: 0.6963174902735325
25 Forest's; Func runs: 10000; result: 0.347940898514357
500 Forest's; Func runs: 10000; result: 0.16776831572853218
=============================
5 Megacity's; Func runs: 10000; result: 0.5492307692307692
25 Megacity's; Func runs: 10000; result: 0.2464615384615385
500 Megacity's; Func runs: 10000; result: 0.10724615384615484
=============================
All score: 3.55917 (39.55%)

El resultado es comparable al del funcionamiento aparte de COAm. La mejora se nota, pero desgraciadamente es leve. Sin embargo, en inicios individuales autónomos, el COAm produce a veces resultados comparables.

Vamos a tratar de crear un híbrido que combine el funcionamiento en paralelo con el intercambio en cada iteración de las mejores posiciones de los agentes de los dos algoritmos, que no solo trabajarán de forma independiente, sino que también intercambiarán entre sí las mejores soluciones para un objetivo común.

Ahora vamos a intentar utilizar el funcionamiento en paralelo de los algoritmos GWO y COAm. Para ello, prácticamente no tendremos que cambiar la clase del algoritmo conjunto. Aquí mostraremos solo el código de los métodos que requieren cambios significativos.

A diferencia del esquema secuencial, en el esquema en paralelo ejecutaremos a la vez los métodos Moving de ambos algoritmos. Después, copiaremos los agentes de estos algoritmos en los agentes de la clase fusionada para enviarlos al cálculo de la función de aptitud. Así, este método combinará los datos de los dos objetos "AO1" y "AO2" en el array de objeto actual "a".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Moving ()
{
  AO1.Moving ();
  AO2.Moving ();

  int cnt = 0;
  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO1.a [i];
    cnt++;
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    a [cnt] = AO2.a [i];
    cnt++;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Las diferencias entre el método "Moving" para el esquema de funcionamiento paralelo y el esquema secuencial son las siguientes: tras transmitir los valores de adaptabilidad a los agentes de los objetos "AO1" y "AO2", ejecutar sus métodos "Revision" y actualizar la solución global, se copiarán de un algoritmo al otro dos agentes de cada uno. Esto significa que los dos mejores agentes se intercambiarán entre algoritmos, lo cual ayudará a enriquecer ambos algoritmos con las mejores características del otro, mejorando su rendimiento en la resolución de problemas. Este enfoque permitirá compartir las mejores soluciones alcanzadas por cada algoritmo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GWO_COAm::Revision ()
{
  int cnt = 0;

  for (int i = 0; i < popSize / 2; i++)
  {
    AO1.a [i].f = a [cnt].f;
    cnt++;

    if (AO1.a [i].f > fB)
    {
      fB = AO1.a [i].f;
      ArrayCopy (cB, AO1.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  for (int i = 0; i < popSize / 2; i++)
  {
    AO2.a [i].f = a [cnt].f;
    cnt++;

    if (AO2.a [i].f > fB)
    {
      fB = AO2.a [i].f;
      ArrayCopy (cB, AO2.a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  AO1.Revision ();
  AO2.Revision ();
  
  S_AO_Agent temp [];
  ArrayResize (temp, popSize / 2);
  
  for (int i = 0; i < 2; i++) temp [i] = AO1.a [i]; 

  for (int i = 0; i < 2; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      AO1.Injection (i, coords - 1, AO2.a [i].c [c]);
      AO2.Injection (i, coords - 1, temp  [i].c [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Impresión de los resultados del algoritmo GWO-COAm usando el esquema paralelo:

GWO_COAm|Grey Wolf Optimizer and Cuckoo Optimization Algorithm M|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6930620289919492
25 Hilly's; Func runs: 10000; result: 0.4389512737634269
500 Hilly's; Func runs: 10000; result: 0.26733735583025275
=============================
5 Forest's; Func runs: 10000; result: 0.6512995888741085
25 Forest's; Func runs: 10000; result: 0.33119611021722106
500 Forest's; Func runs: 10000; result: 0.16858175021299981
=============================
5 Megacity's; Func runs: 10000; result: 0.4615384615384615
25 Megacity's; Func runs: 10000; result: 0.23015384615384615
500 Megacity's; Func runs: 10000; result: 0.1059538461538471
=============================
All score: 3.34807 (37.20%)

Desgraciadamente, no se ha producido ninguna mejora en el rendimiento.

3. Experimento con ESG y SDSm

Las hibridaciones de GWO y COAm comentadas anteriormente han utilizado algoritmos de diferentes "categorías de peso". Quizá para estos fines sea necesario usar algoritmos cercanos en capacidades, para que realmente se complementen. Por lo tanto, realizaremos dos experimentos más sobre los esquemas en serie y en paralelo. Para ello, usaremos los algoritmos ESG y SDSm.

Combinando estos dos algoritmos en un híbrido, podremos crear una combinación única de aleatoriedad y dinámica social.

El algoritmo de búsqueda por difusión estocástica (Stochastic Diffusion Search, SDSm) es un algoritmo de optimización basado en poblaciones.

Las principales características del algoritmo son:

• Evaluación parcial de las decisiones. Los agentes realizan una evaluación parcial de las hipótesis (soluciones candidatas al problema de búsqueda), lo cual reduce la complejidad computacional del algoritmo.
• Difusión de soluciones prometedoras. Los agentes intercambian información sobre hipótesis a través de la comunicación directa cara a cara. Las soluciones de alta calidad pueden identificarse a partir de grupos de agentes que tengan la misma hipótesis.
• Razonamiento matemático. El SDSm muestra un profundo fundamento matemático, lo que lo hace más fiable y predecible.

El SDSm es un método de optimización evolutiva que combina la búsqueda aleatoria y la difusión para resolver problemas de optimización en espacios multidimensionales.

El algoritmo de evolución de grupos sociales (ESG) es un algoritmo de optimización multipoblacional.

Las principales características del algoritmo son:

• Grupos sociales. El algoritmo no trabaja con partículas individuales, sino con grupos sociales unidos por la cooperación y las experiencias compartidas. Cada grupo posee su propio centro de decisión y un conjunto de partículas como agentes de optimización.
• Movimiento colectivo. Las partículas de los grupos sociales interactúan y se mueven de forma conjunta en el espacio de parámetros. Esto permite a los grupos explorar distintas regiones del espacio de parámetros y compartir información sobre las mejores soluciones halladas.
• Experiencias locales y globales. Cada grupo social almacena información sobre la mejor solución dentro de él (experiencia local). También hay un mejor resultado general entre todos los grupos (experiencia global).

El ESG supone una arquitectura sencilla con una gran convergencia y pocos requisitos en cuanto a los recursos informáticos.

El código para los experimentos en serie y en paralelo será exactamente el mismo que el anterior, salvo que tendremos que sustituir la declaración de los objetos correspondientes de estas clases en lugar de GWO y COAm.

Impresión de los resultados del algoritmo ESG-SDSm usando el esquema secuencial:

ESG_SDSm|Evolution_of_Social_Groups and Stochastic Diffusion Search M|200.0|0.5|
=============================
5 Hilly's; Func runs: 10000; result: 0.9642488921252973
25 Hilly's; Func runs: 10000; result: 0.7526240638447592
500 Hilly's; Func runs: 10000; result: 0.2961693434072249
=============================
5 Forest's; Func runs: 10000; result: 0.9897783503200446
25 Forest's; Func runs: 10000; result: 0.7608845505131734
500 Forest's; Func runs: 10000; result: 0.2130287247171918
=============================
5 Megacity's; Func runs: 10000; result: 0.82
25 Megacity's; Func runs: 10000; result: 0.5421538461538462
500 Megacity's; Func runs: 10000; result: 0.11932307692307798
=============================
All score: 5.45821 (60.65%)

Impresión de los resultados del algoritmo ESG-SDSm usando el esquema paralelo:

ESG_SDSm|Evolution_of_Social_Groups and Stochastic Diffusion Search M|200.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9561232188424761
25 Hilly's; Func runs: 10000; result: 0.7493199026465321
500 Hilly's; Func runs: 10000; result: 0.3176797705433513
=============================
5 Forest's; Func runs: 10000; result: 0.9726744619317564
25 Forest's; Func runs: 10000; result: 0.7494321306074204
500 Forest's; Func runs: 10000; result: 0.22498291462144127
=============================
5 Megacity's; Func runs: 10000; result: 0.836923076923077
25 Megacity's; Func runs: 10000; result: 0.5261538461538462
500 Megacity's; Func runs: 10000; result: 0.13435384615384738
=============================
All score: 5.46764 (60.75%)

Los resultados del esquema de hibridación en serie y en paralelo han resultado muy próximos y se encuentran dentro del error normal de los algoritmos estocásticos y ligeramente por debajo de los resultados de estos algoritmos por separado.

4. Conclusiones

Los algoritmos analizados en este artículo como componentes para la hibridación se han seleccionado para abarcar distintas posiciones en la tabla de clasificación actual y averiguar el impacto de las distintas prestaciones de cada algoritmo en el resultado global. ¿Es importante que los algoritmos sean aproximadamente iguales en su capacidad de búsqueda para garantizar un análisis equilibrado y una comparación justa sobre su impacto en los resultados?

En este artículo, hemos considerado varios algoritmos de optimización como componentes para la hibridación. Nuestro objetivo consiste en abarcar una amplia gama de algoritmos que ocupen distintas posiciones en la tabla de clasificación actual para averiguar cómo afecta el diferente rendimiento de cada algoritmo al resultado global.

Queda por saber si resulta importante que los algoritmos sean aproximadamente iguales en la capacidad de búsqueda. Quizá no importe si el objetivo principal es encontrar la mejor solución.

Para los experimentos, hemos elegido algoritmos que difieren mucho en sus capacidades, como GWO y COA. Estos algoritmos suponen dos enfoques distintos de la optimización, y combinarlos puede aportarnos valiosas enseñanzas. Como contrapeso, también hemos seleccionado algoritmos muy próximos en rendimiento, como ESG y SDSm.

A continuación le mostramos la tabla de clasificación actual de algoritmos. Incluye todos los algoritmos que hemos analizado y se actualizará a medida que dispongamos de nuevos datos.

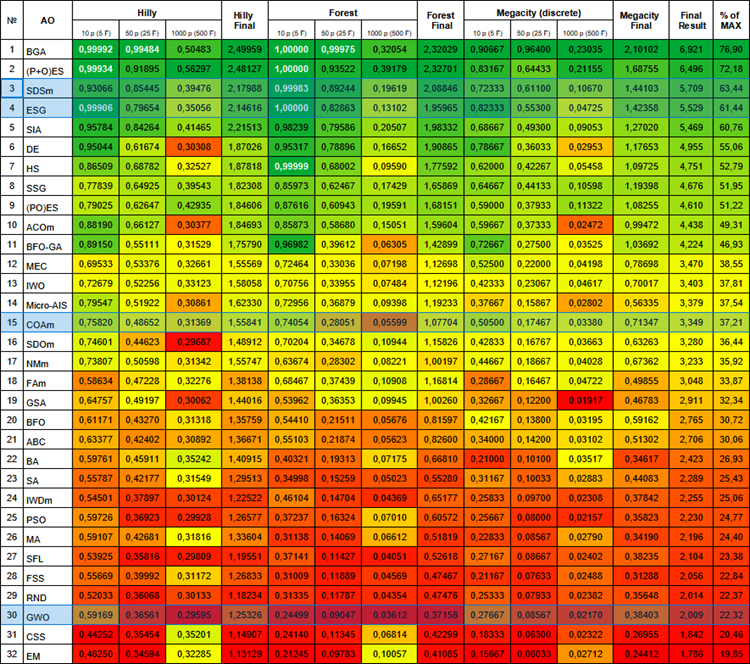
Tabla de clasificación de algoritmos basados en las poblaciones.

Al intentar crear un método híbrido que conecte el funcionamiento en paralelo y el intercambio de las mejores posiciones de los agentes de los algoritmos ESG y SDSm, también en un esquema secuencial, nos hemos encontrado con un fenómeno ambiguo. En nuestra investigación,hemos descubierto que la combinación de ambos enfoques da lugar a un resultado medio en lugar de a una sinergia y una mejora. Es probable que la interacción entre estas diferentes estrategias no haya sido lo suficientemente eficaz, impidiendo la plena integración de sus principios fundamentales.

De los experimentos se desprende que tanto los esquemas de hibridación secuenciales como los paralelos no han producido los resultados deseados en estas condiciones, lo cual pone de relieve la importancia de seleccionar cuidadosamente los algoritmos para que la fusión tenga éxito. Es necesario que los algoritmos posean intrínsecamente ciertas cualidades: o son buenos buscando y malos refinando, o viceversa. Solo entonces las técnicas de hibridación podrán mejorar el rendimiento de ambos algoritmos. La hibridación exitosa usando la fusión de las lógicas de los algoritmos (según el primer esquema) pone de relieve el potencial de este enfoque, pero requiere un esfuerzo considerable, una intervención cuidadosa y el desarrollo de una lógica de fusión conjunta para lograr resultados óptimos.

Esta observación pone de relieve la importancia no solo de las características individuales de los algoritmos, sino también de su interacción en el contexto de la hibridación. Al igual que en la vida salvaje, donde la combinación de distintas especies puede dar lugar a adaptaciones únicas, en el mundo de la optimización la combinación de algoritmos requiere de afinación y armonía. Quizá sea en las combinaciones inesperadas y en los intentos fallidos donde encontremos las claves de nuevos descubrimientos y mejoras en el campo de la optimización.

Así, esta experiencia revela la importancia de realizar con todo cuidado el análisis y la selección de los algoritmos a la hora de crear métodos de optimización híbridos. Para lograr resultados satisfactorios en la búsqueda de soluciones óptimas, debemos tener en cuenta no solo las características individuales de cada algoritmo, sino también su interacción dentro de un problema concreto.

Por favor, pruebe, experimente, cree y combine; como siempre, el conjunto completo de herramientas y los códigos fuente se encuentran adjuntos en el archivo del artículo.