Neural networks made easy (Part 22): Unsupervised learning of recurrent models
Contents
- Introduction
- 1. Features of training recurrent models
- 2. Implementation
- 3. Testing
- Conclusion
- List of references
- Programs used in the article
Introduction
The last two articles in our series were devoted to autoencoders. Their architecture makes it possible to train various neural networks models on unlabeled data using the backpropagation algorithm. The model learns to compress the initial data while selecting the main features. Our experiments have confirmed the effectiveness of autoencoder models. Pay attention that we used fully connected neural layers to train autoencoders. Such models work with a fixed input data window. The algorithm we have built can training any models operating with a fixed input data window. But the architecture of recurrent models is different. To make a decision on the activation of neurons, such models also use their previous state, in addition to the initial data. This feature should be taken into account when building an autoencoder.
1. Features of training recurrent models
Let us start by recalling the organization of recurrent models and their purpose. Take a look at the price chart. It displays historical data relating to the price movement. Each bar is a description of the boundaries of the range in which the symbol price fluctuated in a specific time interval. Note that this is "historical data". It means they will not change. New bars appear over time, But the old ones do not change. At each specific point in time, we have unchanged historical data and one last candle, which has not been completely formed and can change until its time interval closes.
By analyzing historical data, we try to predict the most likely future price movement. The depth of the analyzed history varies in each case. This is probably one of the main problems related to the use of neural networks with a fixed initial data amount. Small historical data windows limit the possibilities of analysis. Excessively large windows complicate the model and its learning. Therefore, when choosing the size of the input data window, the architect of such a model has to compromise and determine the "golden mean".
On the other hand, we are dealing with historical data. Whatever window size we choose, at each model iteration we will retransmit more than 99% of the information to it. The model will then reprocess this data. This does not look like an efficient use of resources. But neither fully connected nor convolutional models remember anything about previously processed information.
The above problems can be solved by utilizing recurrent networks. The idea is as follows. The state of each neuron depends on the source data processing result. Therefore, we can assume that the state of the neuron is a compressed form of the source data. Therefore, we can feed the source data along with the previous state into the neuron. Thus, the new state of the neuron will depend both on the current state of the system we are analyzing and on the previous state, information about which is compressed in the previous state of the neuron.
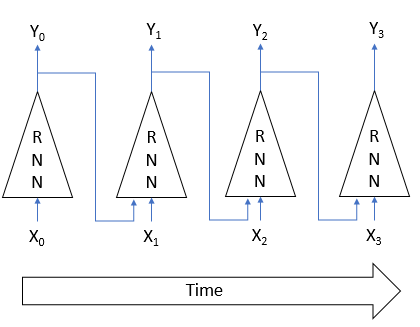
This approach enables the model to remember several states of the system. The use of activation functions and weight coefficients with the absolute value of less than 1 gradually reduces the influence of the earliest historical data. As a result, we have a model with a fairly predictable memory horizon.
By using such models with memory, we are not limited to the historical data window used for decision making. Also, we reduce the amount of retransmitted information since the model will already remember about it. Due to these advantages, recurrent models can be viewed as one of the high-priority areas in solving time series processing problems.
However, the use of these features requires special recurrent model training approaches. For example, getting back to the architecture of autoencoders, if we equate the input Xi and the output Yi of the model in the figure above, then in order to restore the original data from the latent state, there is no need to remember the previous state. Therefore, the model will nullify the influence of historical data during the training process. It will only evaluate the current state. If the recurrent model loses its ability to remember, it will lose its main advantage.
So, when developing our model architecture, we must take this fact into account. The learning process should be organized so that the model will be forced to access the data of previous iterations.
In autoencoder construction, the decoder architecture in most cases almost mirrors the encoder architecture. The same practice is preserved when working with recurrent models. Oddly enough, one of the first such architectures was used for supervised learning. The authors of the paper entitled " Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation" proposed the RNN Encoder-Decoder as a model for statistical machine translation. The encoder and decoder of this model were recurrent networks. The encoder compressed the phrase of the source language to a certain latent state. And then the decoder "unwrapped" it to a phrase in the target language. It is very similar to an autoencoder, isn't it?
The use of a recurrent model enabled the transfer of a phrase to the encoder one word at a time, which made it possible to train the model on phrases of various lengths. After receiving a complete phrase, the encoder transmitted the latent state to the decoder. The decoder also, one word at a time, gave the translation of the phrase in the target language.
After training on labeled phrases in English and French, the authors obtained a model capable of returning semantically and syntactically meaningful phrases.
Unsupervised learning of recurrent models is well presented in the article "Unsupervised Learning of Video Representations using LSTMs which was published in February 2015. The article authors conducted a series of experiments training recurrent autoencoders on various video materials. The performed both the restoration of the data input into the encoder and the prediction of the probable continuation of the video sequence.
The article presents various architectures of autoencoders. But they all use LSTM blocks for signal encoding and decoding. The best results were achieved when training the model with 1 encoder and 2 decoders. One decoder was responsible for restoring the original data, and the second decoder predicted the most likely continuation of the video sequence.
The use of recurrent blocks in the encoder allows the frame-by-frame transmission of the original video into the model. Depending on the task, recurrent decoder blocks return the reconstructed or predicted video sequence frame by frame.
In addition, the authors of the article show that recurrent models pretrained using unsupervised algorithms provide quite good results in tasks related to motion recognition on video after additional training using supervised algorithms, even on a relatively small amount of labeled data.
The materials presented in these two articles suggest that such an approach can be successful in solving our problems.
However, I will make a slight deviation from the proposed models in my implementation. All of them used recurrent blocks in the decoder and returned decoded data frame by frame. This fully corresponded to the translation and video analysis tasks. This may give good results in predicting the next bar. But I have not done any such experiments yet. In the general case, when analyzing the market situation, we evaluate it as a complete picture covering a rather long time interval. Therefore, we will gradually transfer changes in the market situation to the model in small portions. The model should then evaluate the situation taking into account current and previously received data. This means that the latent state should contain information about the widest possible time interval.
To achieve this effect, we will use recurrent blocks only in the encoder. In the decoder, we will also use fully connected neural layers while restoring the data transferred to the encoder in several iterations.
2. Implementation
Next, we move on to the practical part of our article. We will build our recurrent encoder based on the previously discussed LSTM blocks, the structure of which is shown in the figure below. The block consists of 4 fully connected neural layers. Three of them perform the function of gates that regulate the flow of information. The fourth one transforms the source data.
The LSTM block uses 2 recurrent information flows: memory and hidden state.
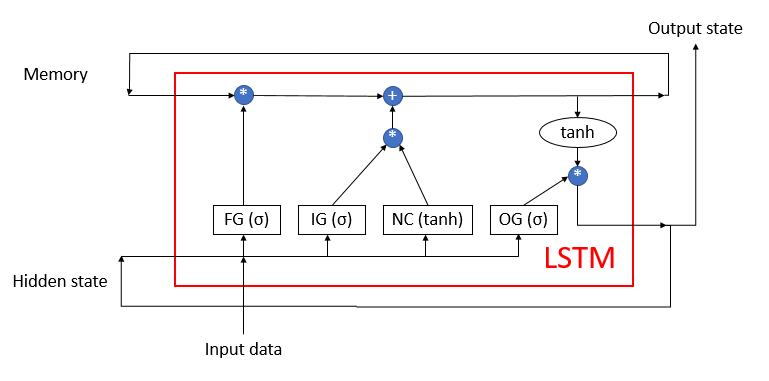
We have previously recreated the LSTM block algorithm using MQL5. Now we will repeat it using the OpenCL technology. To implement the algorithm, let us create a new class CNeuronLSTMOCL. Inherit the main set of buffers and methods from the base class CNeuronBaseOCL, which we will use as the parent class.
The structure of methods and class variables is presented below. The class methods are quite recognizable: these are the feed forward and backward methods which we override in each new class. The purpose of the variables needs to be explained.
class CNeuronLSTMOCL : public CNeuronBaseOCL { protected: CBufferFloat m_cWeightsLSTM; CBufferFloat m_cFirstMomentumLSTM; CBufferFloat m_cSecondMomentumLSTM; int m_iMemory; int m_iHiddenState; int m_iConcatenated; int m_iConcatenatedGradient; int m_iInputs; int m_iWeightsGradient; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronLSTMOCL(void); ~CNeuronLSTMOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronLSTMOCL; } };
First of all, we see 3 data buffers here:
- m_cWeightsLSTM — a matrix of weight coefficients of the LSTM block
- m_cFirstMomentumLSTM — a matrix of the first momentum of updating the weights
- m_cSecondMomentumLSTM — a matrix of the second momentum of updating the weights
Please pay attention to the following. As mentioned above, the LSTM block contains 4 fully connected neural layers. At the same time, we declare only one buffer for the weight matrix m_cWeightsLSTM. This buffer will contain the weights of all 4 neural layers. The use of a concatenated buffer will allow us to parallelize all 4 neural layers simultaneously. We will consider the parallelism organizing mechanism in more detail a little later when considering the implementation of each method.
The same applies to momentum buffers m_cFirstMomentumLSTM and m_cSecondMomentumLSTM.
In the latest terminal builds, MetaQuotes Ltd implemented a number of improvements. They also affected the OpenCL technology we use. In particular, they increased the maximum number of possible OpenCL objects and added the possibility of using the technology on video cards without double support. This will reduce the total time required to train the model, since now there is no need to load data from the CPU memory before calling each kernel and or to unload it back after it is executed. It is enough to load all the initial data once into the OpenCL context memory before starting the training process and to copy the result after the end of training.
Moreover, it allows us to declare some buffers only in the context of OpenCL without creating a mirror buffer in the main memory of the device. This refers to buffers for storing temporary information. Therefore, for a number of buffers, we will only create a variable to store a pointer to the buffer in the OpenCL context:
- m_iMemory — a pointer to the memory buffer
- m_iHiddenState — a pointer to the hidden state buffer
- m_iConcatenated — a pointer to the concatenated result buffer of four internal neural layers
- m_iConcatenatedGradient — a pointer to the concatenated buffer of error gradients at the level of results of four internal neural layers
- m_iWeightsGradient — a pointer to the buffer of error gradients at the level of the weight matrix of four internal neural layers.
We assign initial values to all variables in the class constructor.
CNeuronLSTMOCL::CNeuronLSTMOCL(void) : m_iMemory(-1), m_iConcatenated(-1), m_iConcatenatedGradient(-1), m_iHiddenState(-1), m_iInputs(-1) {}
In the class destructor, we free all used buffers.
CNeuronLSTMOCL::~CNeuronLSTMOCL(void) { if(!OpenCL) return; OpenCL.BufferFree(m_iConcatenated); OpenCL.BufferFree(m_iConcatenatedGradient); OpenCL.BufferFree(m_iHiddenState); OpenCL.BufferFree(m_iMemory); OpenCL.BufferFree(m_iWeightsGradient); m_cFirstMomentumLSTM.BufferFree(); m_cSecondMomentumLSTM.BufferFree(); m_cWeightsLSTM.BufferFree(); }
Continuing the implementation of our class methods, let us create a method for initializing the object of our LSTM block. Following the rules of inheritance, we will override the CNeuronLSTMOCL::Init method while preserving the parameters of a similar method of the parent class. The initialization method will receive in parameters the number of neurons of the next layer, the index of the neuron, the pointer to the OpenCL context object, the number of neurons of the current layer, the parameter optimization method, and the batch size.
In the method body, we first call a similar method of the parent class. Thus, we will initialize the inherited objects of the parent class and control the received initial data. Do not forget to check the operation execution result.
Next, we need to initialize the data buffers declared above. At this stage we cannot fully initialize all buffers because we do not have the required source data. In the parameters, we receive the number of neurons in the current layer and the number of neurons in the next layer. But we do not know the number of neurons in the previous layer. Therefore, we do not know the size of the buffer required to store the weights of the LSTM block. So, at this stage, we create only those data buffers, the size of which depends only on the number of elements in the current layer.
bool CNeuronLSTMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch)) return false; //--- m_iMemory = OpenCL.AddBuffer(sizeof(float) * numNeurons * 2, CL_MEM_READ_WRITE); if(m_iMemory < 0) return false; m_iHiddenState = OpenCL.AddBuffer(sizeof(float) * numNeurons, CL_MEM_READ_WRITE); if(m_iHiddenState < 0) return false; m_iConcatenated = OpenCL.AddBuffer(sizeof(float) * numNeurons * 4, CL_MEM_READ_WRITE); if(m_iConcatenated < 0) return false; m_iConcatenatedGradient = OpenCL.AddBuffer(sizeof(float) * numNeurons * 4, CL_MEM_READ_WRITE); if(m_iConcatenatedGradient < 0) return false; //--- return true; }
Do not forget to control the results at each step.
After creating the object initialization methods, move on to organizing a feed forward pass of the LSTM block. As you know, with the use of OpenCL technology, the calculations are performed directly in the OpenCL context on the GPU. In the code of the main program, we only call the necessary program. Therefore, before writing a method of the class, we need to supplement our OpenCL program with the appropriate kernel.
The LSTM_FeedForward kernel will be responsible for organizing a feed forward pass in the OpenCL program. To correctly organize the process, we need to feed pointers to 5 data buffers and one constant to the kernel:
- inputs — source data buffer:
- inputs_size — number of elements in the source data buffer
- weights — weight matrix buffer
- concatenated — concatenated buffer with the results of all internal layers
- memory — memory buffer
- output — results buffer (also serves as the hidden state buffer).
__kernel void LSTM_FeedForward(__global float* inputs, uint inputs_size, __global float* weights, __global float* concatenated, __global float* memory, __global float* output ) { uint id = (uint)get_global_id(0); uint total = (uint)get_global_size(0); uint id2 = (uint) get_local_id(1);
We will run the buffer in a two-dimensional task space. In the first dimension, we will indicate the number of elements in the current LSTM block. The second dimension is equal to the four threads by the number of internal neural layers. Note that the number of elements in the LSTM block determines the number of elements in each of the internal layers as well as the number of elements in the memory and the hidden state.
Therefore, in the kernel body, we first determine the ordinal number of the thread in each dimension. We also determine the number of tasks in the first dimension.
The entire LSTM block feed forward process can be conditionally divided into two subprocesses:
- calculation of values of internal neural layers
- implementation of the data flow from neural layers to LSTM block output
The execution of the second process is impossible until the first one is fully complete. This is because the execution of the second subprocess requires the values of all four neurons, at least within the current LSTM block element. Therefore, we need the synchronization of data threads along the second dimension. The current implementation of OpenCL allows thread synchronization within a local group. So, we will build our local groups according to the 2nd dimension of tasks.
Next, we will implement the calculation of the weighted sum of the source data and the hidden state. First, calculate the weighted sum of the hidden state.
float sum = 0; uint shift = (id + id2 * total) * (total + inputs_size + 1); for(uint i = 0; i < total; i += 4) { if(total - i > 4) sum += dot((float4)(output[i], output[i + 1], output[i + 2], output[i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += output[k] + weights[shift + k]; }
Then add the weighted sum of the initial data.
shift += total; for(uint i = 0; i < inputs_size; i += 4) { if(total - i > 4) sum += dot((float4)(inputs[i], inputs[i + 1], inputs[i + 2], inputs[i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += inputs[k] + weights[shift + k]; } sum += weights[shift + inputs_size];
Finally, add the value of the bias neuron.
After calculating the weighted sum, we need to calculate the value of the activation function. A sigmoid is used as an activation function for the gate. A hyperbolic tangent is used for the new content layer. The required activation function will be determined by the thread identifier in the second dimension.
if(id2 < 3) concatenated[id2 * total + id] = 1.0f / (1.0f + exp(sum)); else concatenated[id2 * total + id] = tanh(sum); //--- barrier(CLK_LOCAL_MEM_FENCE);
As mentioned above, for the correct execution of the algorithm, synchronization of threads along the 2nd dimension of the task space is needed. We will use the barrier function to synchronize the threads.
To implement the process of information transfer between internal layers, we only need one thread for each element of the LSTM block. Therefore, after the threads are synchronized, the process will be performed only for the thread with the 0 thread ID in the second dimension of the task space.
if(id2 == 0) { float mem = memory[id + total] = memory[id]; float fg = concatenated[id]; float ig = concatenated[id + total]; float og = concatenated[id + 2 * total]; float nc = concatenated[id + 3 * total]; //--- memory[id] = mem = mem * fg + ig * nc; output[id] = og * tanh(mem); } //--- }
This completes work with the forward pass kernel. Now, it can be called from the main program. First, create the required constants.
#define def_k_LSTM_FeedForward 32 #define def_k_lstmff_inputs 0 #define def_k_lstmff_inputs_size 1 #define def_k_lstmff_weights 2 #define def_k_lstmff_concatenated 3 #define def_k_lstmff_memory 4 #define def_k_lstmff_outputs 5
Then we can start creating the feed forward pass method of our class. Similar to the same method of any other previously considered class, this method received in the parameters a pointer to the object of the previous neural layer. IN the method body, we should immediately validate the pointer.
bool CNeuronLSTMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || NeuronOCL.Neurons() <= 0 || NeuronOCL.getOutputIndex() < 0 || !OpenCL) return false;
When initializing the class, we could not initialize all the data buffers, because we did not know the number of neurons in the previous layer. Now we have the pointer to the previous neural layer. So, we can request the number of neurons in this layer and create the required data buffers. Before doing so, make sure that the buffers have not been yet earlier. This feed forward method call can be not the first one. The variable containing the number of elements in the previous layer will serve as a kind of flag.
if(m_iInputs <= 0) { m_iInputs = NeuronOCL.Neurons(); int count = (int)((m_iInputs + Neurons() + 1) * Neurons()); if(!m_cWeightsLSTM.Reserve(count)) return false; float k = (float)(1 / sqrt(Neurons() + 1)); for(int i = 0; i < count; i++) { if(!m_cWeightsLSTM.Add((2 * GenerateWeight()*k - k)*WeightsMultiplier)) return false; } if(!m_cWeightsLSTM.BufferCreate(OpenCL)) return false; //--- if(!m_cFirstMomentumLSTM.BufferInit(count, 0)) return false; if(!m_cFirstMomentumLSTM.BufferCreate(OpenCL)) return false; //--- if(!m_cSecondMomentumLSTM.BufferInit(count, 0)) return false; if(!m_cSecondMomentumLSTM.BufferCreate(OpenCL)) return false; if(m_iWeightsGradient >= 0) OpenCL.BufferFree(m_iWeightsGradient); m_iWeightsGradient = OpenCL.AddBuffer(sizeof(float) * count, CL_MEM_READ_WRITE); if(m_iWeightsGradient < 0) return false; } else if(m_iInputs != NeuronOCL.Neurons()) return false;
After completing the preparatory work, pass pointers to the data buffers and the value of the required constant to the parameters of the feed forward kernel. Remember to control the execution of operations.
if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_inputs, NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_concatenated, m_iConcatenated)) return false; if(!OpenCL.SetArgument(def_k_LSTM_FeedForward, def_k_lstmff_inputs_size, m_iInputs)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_memory, m_iMemory)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_outputs, getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_weights, m_cWeightsLSTM.GetIndex())) return false;
Next, we define the problem space and the shift in it up to the 1st iteration. In this case we specify the problem space in two dimensions and the size of the local groups to be combined in two dimensions. In the first case, we specify the total number of current layer elements in the 1st dimension. For a local group, we specify only one element in the first dimension. In the second dimension, in both cases, we indicate four elements, according to the number of internal neural layers. This allows us to create local groups of four threads each. The number of such local groups will be equal to the number of elements in the current neural layer.
uint global_work_offset[] = {0, 0}; uint global_work_size[] = {Neurons(), 4}; uint local_work_size[] = {1, 4};
Thus, by synchronizing threads in each local group, we synchronize the calculation of the values of all four internal neural layers in the context of each individual element of the current layer. This is quite enough to implement the correct calculation of the feed forward pass of the entire LSTM block.
Next, we put our kernel in the execution queue.
if(!OpenCL.Execute(def_k_LSTM_FeedForward, 2, global_work_offset, global_work_size, local_work_size)) return false; //--- return true; }
This concludes the feed forward pass of the LSTM block, and we can move on to implementing the backpropagation pass. As in the previous case, we need to supplement the OpenCL program before creating the class methods. With the feed-forward pass, we managed to combine the entire forward pass into one kernel. This time we need three kernels.
In the first kernel LSTM_ConcatenatedGradient, we will implement the propagation of the gradient back to the internal layer results. In parameters, the kernel receives pointers to 4 data buffers. Three of them will contain the initial data: the buffer of gradients from the next layer, the memory state and the concatenated buffer of results of internal neural layers. The fourth buffer will be used to write the results of the kernel operation.
The kernel will be called in a one-dimensional problem space according to the number of elements in our LSTM block.
In the kernel body, we first define the thread identifier and the total number of threads. Then, moving along the backpropagation path of the signal, we determine the error gradient at the result level of the output gate, at the memory level, at the level of the new content neural layer, at the level of the new content gate. And then the error is determined at the forget gate level.
__kernel void LSTM_ConcatenatedGradient(__global float* gradient, __global float* concatenated_gradient, __global float* memory, __global float* concatenated ) { uint id = get_global_id(0); uint total = get_global_size(0); float t = tanh(memory[id]); concatenated_gradient[id + 2 * total] = gradient[id] * t; //output gate float memory_gradient = gradient[id] * concatenated[id + 2 * total]; memory_gradient *= 1 - pow(t, 2.0f); concatenated_gradient[id + 3 * total] = memory_gradient * concatenated[id + total]; //new content concatenated_gradient[id + total] = memory_gradient * concatenated[id + 3 * total]; //input gate concatenated_gradient[id] = memory_gradient * memory[id + total]; //forget gate }
After that, we need to propagate the error gradient through the inner layers of the LSTM block to the previous neural layer. To do this, create the LSTM_HiddenGradient level. When developing the OpenCL architecture of the program, I decided to combine the gradient distributions to the level of the previous layer and to the level of the weight matrix within this kernel. So, the kernel receives in parameters pointers to 6 data buffers and 2 constants. The kernel is to be called in a one-dimensional problem space.
__kernel void LSTM_HiddenGradient(__global float* concatenated_gradient, __global float* inputs_gradient, __global float* weights_gradient, __global float* hidden_state, __global float* inputs, __global float* weights, __global float* output, const uint hidden_size, const uint inputs_size ) { uint id = get_global_id(0); uint total = get_global_size(0);
In the kernel body, define the thread identifier and the total number of threads. Also, determine the size of one vector of the weight matrix.
uint weights_step = hidden_size + inputs_size + 1;
Next, loop through all the elements of the concatenated input data buffer, which includes the hidden state and the current state received from the previous neural layer. Loop iterations start from the current thread ID, while the loop iteration step is equal to the total number of running threads. This approach enables iteration over all elements of the concatenated source data layer, regardless of the number of running threads.
for(int i = id; i < (hidden_size + inputs_size); i += total) { float inp = 0;
At this step, in the loop body, we implement the division of the operations thread depending on the element being analyzed. If the element belongs to a hidden state, then save the hidden state in a private variable. The relevant value from the results buffer should be transferred to the buffer, as at the next iteration it will be in the hidden state.
if(i < hidden_size)
{
inp = hidden_state[i];
hidden_state[i] = output[i];
}
If the current element belongs to the input data buffer of the previous neuron layer, transfer the value of the initial data to a private variable and calculate the error gradient for the corresponding neuron of the previous layer.
else { inp = inputs[i - hidden_size]; float grad = 0; for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[g]; grad += temp * (1 - temp) * weights[i + g * weights_step]; } for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[g]; grad += temp * (1 - pow(temp, 2.0f)) * weights[i + g * weights_step]; } inputs_gradient[i - hidden_size] = grad; }
After propagating the error gradient to the previous neural layer, distribute the error gradient to the appropriate LSTM block weights.
for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[g]; weights[i + g * weights_step] = temp * (1 - temp) * inp; } for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[g]; weights[i + g * weights_step] = temp * (1 - pow(temp, 2.0f)) * inp; } }
At the end of the kernel, propagate the error gradient to the bias neurons of each weight vector.
for(int i = id; i < 4 * hidden_size; i += total) { float temp = concatenated_gradient[(i + 1) * hidden_size]; if(i < 3 * hidden_size) weights[(i + 1) * weights_step] = temp * (1 - temp); else weights[(i + 1) * weights_step] = 1 - pow(temp, 2.0f); } }
After propagating the error gradient back to the previous neural layer level and the weight matrix, we need to implement the weight updating process. I decided not to implement the full range of parameter optimization methods. Instead, I will implement the Adam method which I use most often. By analogy with my implementation, you can add any other method for optimizing model parameters.
So, the model parameters are updated in the LSTM_UpdateWeightsAdam kernel. The error gradient at the weight matrix level has already been calculated in the previous layer and has been written to the weights_gradient buffer. So, in this kernel, we only need to implement the process of updating the model parameters. To implement the parameter update process by the Adam method, we need two additional buffers to record the first and second momentum. In addition, we will need training hyperparameters. This data will be passed in the kernel parameters.
__kernel void LSTM_UpdateWeightsAdam(__global float* weights, __global float* weights_gradient, __global float *matrix_m, __global float *matrix_v, const float l, const float b1, const float b2 ) { const uint id = get_global_id(0); const uint total = get_global_size(0); const uint id1 = get_global_id(1); const uint wi = id1 * total + id;
As you know, the weight matrix is a two-dimensional matrix. Therefore, we will call the kernel in a two-dimensional task space.
In the body of the kernel, determine the ordinal number of the thread in both dimensions and the total number of threads running in the first dimension. By these constants, determine the shift in the buffers to the desired weight. Next, run the algorithm to update the corresponding element of the weight matrix.
float g = weights_gradient[wi]; float mt = b1 * matrix_m[wi] + (1 - b1) * g; float vt = b2 * matrix_v[wi] + (1 - b2) * pow(g, 2); float delta = l * (mt / (sqrt(vt) + 1.0e-37f) - (l1 * sign(weights[wi]) + l2 * weights[wi] / total)); weights[wi] = clamp(weights[wi] + delta, -MAX_WEIGHT, MAX_WEIGHT); matrix_m[wi] = mt; matrix_v[wi] = vt; };
We finish with the changes to the OpenCL program here and move on to implementing methods on the side of the main program.
We first create constants to work with the above created kernels.
#define def_k_LSTM_ConcatenatedGradient 33 #define def_k_lstmcg_gradient 0 #define def_k_lstmcg_concatenated_gradient 1 #define def_k_lstmcg_memory 2 #define def_k_lstmcg_concatenated 3 #define def_k_LSTM_HiddenGradient 34 #define def_k_lstmhg_concatenated_gradient 0 #define def_k_lstmhg_inputs_gradient 1 #define def_k_lstmhg_weights_gradient 2 #define def_k_lstmhg_hidden_state 3 #define def_k_lstmhg_inputs 4 #define def_k_lstmhg_weeights 5 #define def_k_lstmhg_output 6 #define def_k_lstmhg_hidden_size 7 #define def_k_lstmhg_inputs_size 8 #define def_k_LSTM_UpdateWeightsAdam 35 #define def_k_lstmuw_weights 0 #define def_k_lstmuw_weights_gradient 1 #define def_k_lstmuw_matrix_m 2 #define def_k_lstmuw_matrix_v 3 #define def_k_lstmuw_l 4 #define def_k_lstmuw_b1 5 #define def_k_lstmuw_b2 6
Next, we move on to the methods of our class. Let us start by creating the error gradient backpropagation method calcInputGradients. In the parameters, the method receives a pointer to the object of the previous neural layer. Immediately check the validity of the received pointer.
bool CNeuronLSTMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || NeuronOCL.Neurons() <= 0 || NeuronOCL.getGradientIndex() < 0 || NeuronOCL.getOutputIndex() < 0 || !OpenCL) return false;
Check the availability of the necessary data buffers in the OpenCL context.
if(m_cWeightsLSTM.GetIndex() < 0 || m_cFirstMomentumLSTM.GetIndex() < 0 || m_cSecondMomentumLSTM.GetIndex() < 0) return false; if(m_iInputs < 0 || m_iConcatenated < 0 || m_iMemory < 0 || m_iConcatenatedGradient < 0 || m_iHiddenState < 0 || m_iInputs != NeuronOCL.Neurons()) return false;
If all the checks are successful, proceed to the kernel call. In accordance with the error gradient algorithm, we will first call the LSTM_ConcatenatedGradient kernel.
First, transfer initial data to the kernel parameters.
if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_concatenated, m_iConcatenated)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_concatenated_gradient, m_iConcatenatedGradient)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_gradient, getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_memory, m_iMemory)) return false;
define the dimension of the problem space. Put the kernel in the execution queue.
uint global_work_offset[] = {0}; uint global_work_size[] = {Neurons()}; if(!OpenCL.Execute(def_k_LSTM_ConcatenatedGradient, 1, global_work_offset, global_work_size)) return false;
Here we also implement the call of the second kernel for error gradient propagation LSTM_HiddenGradient. Pass the parameters to the kernel.
if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_concatenated_gradient, m_iConcatenatedGradient)) return false; if(!OpenCL.SetArgument(def_k_LSTM_HiddenGradient, def_k_lstmhg_hidden_size, Neurons())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_hidden_state, m_iHiddenState)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs, NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs_gradient, NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs_size, m_iInputs)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_output, getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_weeights, m_cWeightsLSTM.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_weights_gradient, m_iWeightsGradient)) return false;
Use the already created arrays to specify the problem space and put the kernel in the execution queue.
if(!OpenCL.Execute(def_k_LSTM_HiddenGradient, 1, global_work_offset, global_work_size)) return false; //--- return true; }
Again, do not forget to implement all operations. This will allow you to timely track errors and prevent the critical termination of the program at the most inopportune moment.
After propagating the error gradient, to complete the algorithm, we need to implement the updateInputWeights method for updating the model parameters. The method receives in parameters a pointer to the object of the previous layer. But we have already defined the error gradient at the level of the weight matrix. Therefore, the presence of a pointer to the object of the previous layer is more related to the implementation of method overriding rather than the need to transfer data. In this case, the state of the received pointer does not affect the method result, so we do not check it. Instead, check the availability of the required internal buffers in the context of OpenCL.
bool CNeuronLSTMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!OpenCL || m_cWeightsLSTM.GetIndex() < 0 || m_iWeightsGradient < 0 || m_cFirstMomentumLSTM.GetIndex() < 0 || m_cSecondMomentumLSTM.GetIndex() < 0) return false;
Next, pass parameters to the kernel.
if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_weights, m_cWeightsLSTM.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_weights_gradient, m_iWeightsGradient)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_matrix_m, m_cFirstMomentumLSTM.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_matrix_v, m_cSecondMomentumLSTM.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_l, lr)) return false; if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_b1, b1)) return false; if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_b2, b2)) return false;
Define the problem space and put the kernel into the execution queue.
uint global_work_offset[] = {0, 0}; uint global_work_size[] = {m_iInputs + Neurons() + 1, Neurons()}; if(!OpenCL.Execute(def_k_LSTM_UpdateWeightsAdam, 2, global_work_offset, global_work_size)) return false; //--- return true; }
This concludes our work on organizing the backpropagation algorithm. Our class CNeuronLSTMOCL is ready for the first testing. But we know that we need to save the trained model and then restore it to a working state. Therefore, we will add methods for file operations.
As in all previously considered architectures of neural layers, the Save method is used to save data. In the parameters, this method receives the file handle for writing data.
In the method body, we first call a similar method of the parent class. That allows the implementation of all the necessary controls with almost one line of code and saving of objects inherited from the parent class. Check the parent class method execution result.
After that, save the number of neurons in the previous layer. Also, save the weight and momentum matrices.
bool CNeuronLSTMOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; if(FileWriteInteger(file_handle, m_iInputs, INT_VALUE) < sizeof(m_iInputs)) return false; if(!m_cWeightsLSTM.BufferRead() || !m_cWeightsLSTM.Save(file_handle)) return false; if(!m_cFirstMomentumLSTM.BufferRead() || !m_cFirstMomentumLSTM.Save(file_handle)) return false; if(!m_cSecondMomentumLSTM.BufferRead() || !m_cSecondMomentumLSTM.Save(file_handle)) return false; //--- return true; }
After saving the data, we need to create the load method to restore the object from the saved data. As already mentioned, data is read from a file in strict accordance with the write sequence. As in the data saving method, this method received in parameters a file handle for reading the file. We immediately call a similar method of the parent class.
bool CNeuronLSTMOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
Next, we read the number of neurons in the previous layer and the weight and momentum buffers saved earlier. After loading each buffer, initiate the creation of mirror data buffers in the OpenCL context. Remember to control the execution of operations.
m_iInputs = FileReadInteger(file_handle); //--- m_cWeightsLSTM.BufferFree(); if(!m_cWeightsLSTM.Load(file_handle) || !m_cWeightsLSTM.BufferCreate(OpenCL)) return false; //--- m_cFirstMomentumLSTM.BufferFree(); if(!m_cFirstMomentumLSTM.Load(file_handle) || !m_cFirstMomentumLSTM.BufferCreate(OpenCL)) return false; //--- m_cSecondMomentumLSTM.BufferFree(); if(!m_cSecondMomentumLSTM.Load(file_handle) || !m_cSecondMomentumLSTM.BufferCreate(OpenCL)) return false;
This method should not only read data from a file, but also restore the full functionality of the trained model. Therefore, after reading the data from the file, we also have to create temporary data buffers, information about which was not saved to the file.
if(m_iMemory >= 0) OpenCL.BufferFree(m_iMemory); m_iMemory = OpenCL.AddBuffer(sizeof(float) * 2 * Neurons(), CL_MEM_READ_WRITE); if(m_iMemory < 0) return false; //--- if(m_iConcatenated >= 0) OpenCL.BufferFree(m_iConcatenated); m_iConcatenated = OpenCL.AddBuffer(sizeof(float) * 4 * Neurons(), CL_MEM_READ_WRITE); if(m_iConcatenated < 0) return false; //--- if(m_iConcatenatedGradient >= 0) OpenCL.BufferFree(m_iConcatenatedGradient); m_iConcatenatedGradient = OpenCL.AddBuffer(sizeof(float) * 4 * Neurons(), CL_MEM_READ_WRITE); if(m_iConcatenatedGradient < 0) return false; //--- if(m_iHiddenState >= 0) OpenCL.BufferFree(m_iHiddenState); m_iHiddenState = OpenCL.AddBuffer(sizeof(float) * Neurons(), CL_MEM_READ_WRITE); if(m_iHiddenState < 0) return false; //--- if(m_iWeightsGradient >= 0) OpenCL.BufferFree(m_iWeightsGradient); m_iWeightsGradient = OpenCL.AddBuffer(sizeof(float) * m_cWeightsLSTM.Total(), CL_MEM_READ_WRITE); if(m_iWeightsGradient < 0) return false; //--- return true; }
Operations with the CNeuronLSTMOCL class methods are complete.
Next, we only need to add new kernels in the OpenCL context connection procedure and pointers to a new type of neural layers in the dispatcher methods of our base neural layer.
The complete code of all methods and classes is available in the attachment below.
3. Testing
The new neural layer class is ready, and we can move on to creating a model for test training. A new recurrent autoencoder model was built based on the variational autoencoder model from the previous article. That model was saved to a new file named "rnn_vae.mq5". The encoder architecture was changed: we added recurrent LSTM blocks there.
Please note that we only feed the last 10 candlesticks to the input of our recurrent encoder.
int OnInit() { //--- .................. .................. //--- Net = new CNet(NULL); ResetLastError(); float temp1, temp2; if(!Net || !Net.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false)) { printf("%s - %d -> Error of read %s prev Net %d", __FUNCTION__, __LINE__, FileName + ".nnw", GetLastError()); HistoryBars = iHistoryBars; CArrayObj *Topology = new CArrayObj(); if(CheckPointer(Topology) == POINTER_INVALID) return INIT_FAILED; //--- 0 CLayerDescription *desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; int prev = desc.count = 10 * 12; desc.type = defNeuronBaseOCL; desc.optimization = ADAM; desc.activation = None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = prev; desc.batch = 1000; desc.type = defNeuronBatchNormOCL; desc.activation = None; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; prev = desc.count = 500; desc.type = defNeuronLSTMOCL; desc.activation = None; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; prev = desc.count = prev/2; desc.type = defNeuronLSTMOCL; desc.activation = None; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; prev = desc.count = 50; desc.type = defNeuronLSTMOCL; desc.activation = None; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = prev/2; desc.type = defNeuronVAEOCL; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = (int) HistoryBars; desc.type = defNeuronBaseOCL; desc.activation = TANH; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = (int) HistoryBars * 2; desc.type = defNeuronBaseOCL; desc.activation = TANH; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = (int) HistoryBars * 4; desc.type = defNeuronBaseOCL; desc.activation = TANH; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 9 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = (int) HistoryBars * 12; desc.type = defNeuronBaseOCL; desc.activation = TANH; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net = new CNet(Topology); delete Topology; if(CheckPointer(Net) == POINTER_INVALID) return INIT_FAILED; dError = FLT_MAX; } else { CBufferFloat *temp; Net.getResults(temp); HistoryBars = temp.Total() / 12; delete temp; } //--- .................. .................. //--- return(INIT_SUCCEEDED); }
As previously discussed in this article, in order to organize the training of a recurrent block, we need to add conditions to force the model to look into "memory". For learning purposes, let us create a data stack. And after each iteration of the feed-forward pass, we will remove information about the oldest candle from the stack and add information about the new one to the end of the stack.
Thus, the stack will always contain information about several historical states of the analyzed model. The history depth will be determined by an external parameter. We will pass this stack to the autoencoder as target values. If the stack size exceeds the value of the initial data at the encoder input, the autoencoder will have to look into the memory of past states.
.................. .................. Net.feedForward(TempData, 12, true); TempData.Clear(); if(!Net.GetLayerOutput(1, TempData)) break; uint check_total = check_data.Total(); if(check_total >= check_count) { if(!check_data.DeleteRange(0, check_total - check_count + 12)) return; } for(int t = TempData.Total() - 12 - 1; t < TempData.Total(); t++) { if(!check_data.Add(TempData.At(t))) return; } if((total-it)>(int)HistoryBars) Net.backProp(check_data); .................. ..................
The model testing parameters were the same: EURUSD, H1, last 15 years. Default indicator settings. Input data about the last 10 candles into the encoder. The decoder is trained to decode the last 40 candles. Testing results are shown in the chart below. Data is input into the encoder after the formation of each new candle is completed.
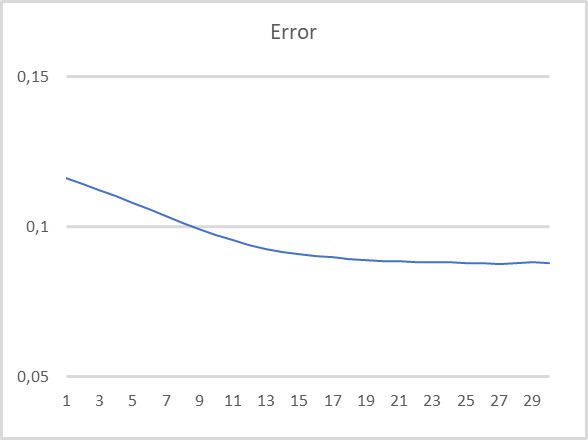
As you can see in the chart, the test results confirm the viability of this approach for unsupervised pre-training of recurrent models. During test training of the model, after 20 learning epochs, the model error almost stabilized with a loss rate of less than 9%. Also, information about at least 30 previous iterations is stored in the latent state of the model.
Conclusion
In this article, we got dealt with recurrent model training using autoencoders. In the practical part of the article, we created a recurrent autoencoder and performed its test training. The results of our experiment allow us to conclude that the proposed approach to unsupervised training of recurrent models using autoencoders is viable. The model showed pretty good results when restoring data for the last 30 iterations in testing.
List of references
- Neural networks made easy (Part 4): Recurrent networks
- Neural networks made easy (Part 14): Data clustering
- Neural networks made easy (Part 15): Data clustering using MQL5
- Neural networks made easy (Part 16): Practical use of clustering
- Neural networks made easy (Part 17): Dimensionality reduction
- Neural networks made easy (Part 18): Association rules
- Neural networks made easy (Part 19): Association rules using MQL5
- Neural networks made easy (Part 20): Autoencoders
- Neural networks made easy (Part 21): Variational autoencoders (VAE)
- Unsupervised Learning of Video Representations using LSTMs
- Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | rnn_vae.mq5 | EA | Recurrent autoencoder training Expert Advisor |
| 2 | VAE.mqh | Class library | Variational autoencoder latent layer class library |
| 3 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 4 | NeuroNet.cl | Code Base | OpenCL program code library |
…
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/11245
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 CCI indicator. Three transformation steps
CCI indicator. Three transformation steps
 Learn how to design a trading system by Alligator
Learn how to design a trading system by Alligator
 Neural networks made easy (Part 21): Variational autoencoders (VAE)
Neural networks made easy (Part 21): Variational autoencoders (VAE)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Hi, As I see this error on clang size, Not mql5.
i do not understand please elaborate
thank you
i do not understand please elaborate
thank you
At first, try to reinstall OpenCL driver to your device.
At first, try to reinstall OpenCL driver to your device.
hello i have tried that and it still didn't work ....the same error has been there from article 8 and i haven't found a way to solve it
the error points on the CNET ::save function on the point of declaration of bool result=layers.Save(handle); and points to the "layers" variable
hello i have tried that and it still didn't work ....the same error has been there from article 8 and i haven't found a way to solve it
the error points on the CNET ::save function on the point of declaration of bool result=layers.Save(handle); and points to the "layers" variable
What you see in MetaTrader 5 Options
What you see in MetaTrader 5 Options
this right here am i correct