Neural networks made easy (Part 17): Dimensionality reduction

MetaTrader 5 — Trading systems | 2 August 2022, 08:45

3 653

Dmitriy Gizlyk

Introduction

We continue to study models and unsupervised learning algorithms. We have already considered data clustering algorithms. In this article, I will explore a solution of problems related to dimensionality reduction. Essentially, these are certain data compression algorithms that are widely used in practice. Let us study the implementation of one of these algorithms and see how it can be used in building our trading model.

1. Understanding the dimensionality reduction problem

Every new day, new hour and new moment provides a huge amount of information in all spheres of human life. With the constantly spreading information technology in today world, people try to save and process as much information as possible. However, the soring of large amounts of information requires large data storages. Furthermore, extensive computing resources are required to process this information. One of the possible solutions to this problem is recording the available information in a more concise form. Moreover, if the compressed form preserves the full data context, less resources will be required for its processing.

For example, when we deal with pattern recognition on a 200*200 pixel image, each pixel is written in the color format which occupies 4 bytes in memory. The ability to represent each pixel in one of 16.5 million colors would be excessive for this problem. In most cases, the model performance will not be affected if we reduce the gradation to, say, 16 or 32 colors. In this case, we will only use 1 byte to write the color number of each pixel. Of course, we would need one-time cost to write the color matrix, 64 bytes for 16 colors and 128 bytes for 32 colors. This is not a big price to pay for reducing the size of all our images by 4 times. Actually, such a problem can be solved using the data clustering method already known to us. However, this might not be the most efficient way.

Another area of use for dimensionality reduction techniques is data visualization. For example, you have data describing certain system states, represented by 10 parameters. You need to find a way to visualize this data. 2D and 3D images are most preferred for human perception. Well, you could create several slides with different variations of 2-3 parameters. But this would not provide a complete picture of the system state. In most cases, different states in different slides will merge into one point. But these may be different states.

Therefore, we need to find such an algorithm that would help us translate all our system states from 10 parameters to a two- or three-dimensional space. Also, the algorithm should divide our system states while maintaining their relative position. Of course, it should lose as little information as possible.

You may think "This is all very interesting, but what is the practical use in trading?" Let us look at the terminal. How many indicators does it offer? Well, many of them may have certain data correlation. But each of them provides at least one value describing the market situation. And what if we multiply this by the number of trading instruments? Furthermore, different variations of indicators and analyzed timeframes can infinitely increase the number of parameters describing the current market state.

Of course, we will not study all instruments and all possible indicators in one model. But nevertheless, we can use a combination of many of them when searching for the most suitable combination. This will complicate the model and increase its training time. Therefore, by reducing the dimensionality of the initial data while maintaining the maximum information we both reduce the model training cost and reduce the decision-making time. And thus, the reaction to market behavior can be lightning fast. So, trades will be executed by a very good price.

Please note that dimensionality reduction algorithms are always used only for data preprocessing. This is because they only return a compressed form of the source data. The data is then saved or used for further processing. This can include data visualization or processing by some other model.

Thus, to construct a trading system, we can use minimum required information to describe the current market state and compress it using one of the dimensionality reduction algorithms. We should expect that the reduction process will eliminate some noise and correlating data. Then, we will input the reduced data into our trading decision making model.

I hope the idea is clear. To implement it the dimensionality reduction algorithm, I suggest using one of the most popular Principal Component Analysis methods. This algorithm has proven itself in solving various problems and it can be replicated on new data. This allows reducing incoming data and transferring it to the decision-making model to generate real-time trading decisions.

2. Principal Component Analysis (PCA) method

Principal component analysis was invented by the English mathematician Karl Pearson in 1901. Since then, it has been successfully used in many science fields.

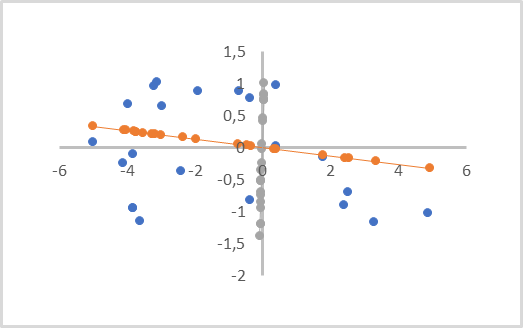
To understand the essence of the method, I propose to take the simplified task related to the reducing the dimension of a two-dimensional data array to a vector. From a geometric point of view, this can be represented as a projection of points of a plane onto a straight line.

In the figure below, the initial data is represented by blue dots. There are two projections, on the orange and gray lines, with dots of the corresponding color. As you can see, the average distance from the initial points to their orange projections is smaller than the similar distances to the gray projections. Gray projections have overlapping of projections of points. So, the orange projection is more preferable, as it separates all individual points and loses less data when reducing the dimension (distance from points to their projections).

Such a line is called the principal component. That is why the method is called Principal Component Analysis.

From a mathematical point of view, each principal component is a numerical vector which size is equal to the dimension of the original data. The product of the vector of original data describing one system state by the corresponding vector of the principal component generates the projection point of the analyzed state on the straight line.

Depending on the original data dimension and the requirements for dimensionality reduction, there can be several principal components, but no more than the original data dimension. When rendering a volumetric projection, there will be three of them. When compressing data, the allowable error is usually a loss of up to 1% of data.

Principal component method

Visually this looks similar to a linear regression. But these are completely different methods, and they produce different results.

A linear regression represents a linear dependence of one variable on another. Also, the distances are minimized perpendicular to the coordinate axes. Such a line can pass in any part of the plane.

In the principal component analysis, the values along all axes are absolutely independent and equivalent. Distances perpendicular to the line but not to the axes are minimized. The principal component line always passes through the origin. Therefore, all initial data must be normalized before applying this method. At least they should be centered around the origin. In other words, we need to center the data relative to 0 in each dimension.

Another important feature of the principal component analysis method is that its application results in a matrix of orthogonal vectors of principal components. It means that there is absolutely no correlation between all principal component vectors. This fact has a positive impact on the entire learning process of the future decision making model, which receives reduced data as input.

From a mathematical point of view, the principal component analysis method can be represented as a spectral decomposition of the covariance matrix of the initial data. And the covariance matrix can be found by the following formula.

Covariance matrix formula

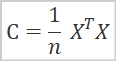
where

C is covariance matrix,
X is original data matrix,
n is the number of elements in the source data.

As a result of this operation, we get a square covariance matrix. Its size is equal to the number of features describing system states. Variances of features will be located along the main diagonal of the matrix. And other elements of the matrix represent the degree of covariance of the corresponding feature pairs.

At the next stage, we need to perform a singular value decomposition of the resulting covariance matrix. The singular value decomposition of a matrix is a rather complex mathematical process. But the introduction of matrices and matrix operations in MQL5 has greatly simplified this process, since this operation has already been implemented for matrices. Therefore, let us proceed immediately to the results of the singular value decomposition.

As a result of the singular value decomposition of the matrix, we obtain three matrices, the product of which is equal to the original matrix. The second matrix ∑ is a diagonal matrix which is equal to the original matrix in size. Along the main diagonal of this matrix lie singular numbers which represent the dispersion of values along the axes of singular vectors. Singular numbers are non-negative and are arranged in descending order. All other elements of the matrix are equal to 0. Therefore, it is often represented as a vector.

U and V are unitary square matrices containing left and right singular vectors, respectively. The size of the U matrix has the same number of rows as the original matrix, while matrix V has the same number of columns as the original matrix.

In our case, when we execute the singular value decomposition of the square covariance matrix, matrices U and V have the same size.

For dimensionality reduction purposes, we will use the matrix U. Since singular numbers are located in descending orders, we can simply take the require number of the first columns of the matrix U. Let us denote the new matrix as the matrix UR . To reduce the dimensionality, we can simply multiply the original data matrix by the newly created matrix UR.

The question arises here: Down to which value will the reduction be optimal? If the task were to visualize data, such a question would not arise. The selection of the final dimension between 1 and 3 would depend on the desired projection. Our task is to reduce data with the minimal information loss and to pass it to another decision model. Therefore, the main criterion is the amount of lost information.

The best option for determining the retained data amount is to calculate the ratio of singular values corresponding to the singular vectors used.

Ratio of transmitted information

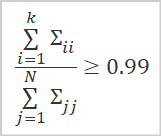
where

k is the number of vectors used
N is the total number of singular values.

In practice, this number of columns k is usually chosen so that the value of the above ratio is at least 0.99. This corresponds to retaining 99% of the information.

Now that we have considered the general theoretical aspects, we can proceed to the method implementation.

3. PCA implementation using MQL5

To implement the Principal Component Analysis algorithm, we will create a new class CPCA, inherited from the CObject base class. The code of the new class will be saved to the pca.mqh file.

We will use matrix operations to implement this class. Therefore, the model training result, i.e. the matrix UR, will be saved to the matrix m_Ureduce.

In addition, let us declare three more local variables. These are the model training status b_Studied and two vectors v_Means and v_STDs, to which we will save the values of arithmetic means and standard deviations for further data normalization.

class CPCA : public CObject
  {
private:
   bool              b_Studied;
   matrix            m_Ureduce;
   vector            v_Means;
   vector            v_STDs;

In the class constructor, indicate the false value in the model training state flag b_Studied and initialize the matrix m_Ureduce with the zero size. Leave the class destructor empty since we do not create any nested objects inside the class.

CPCA::CPCA()   :  b_Studied(false)
  {
   m_Ureduce.Init(0, 0);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPCA::~CPCA()
  {
  }

Next, we will recreate the model training method Study. The method receives the original data matrix in parameters and returns the logical result of the operation.

As mentioned above, to execute principal component analysis, it is necessary to use normalized data. Therefore, before we proceed to the implementation of the main method algorithm, we will normalize the initial data using the below formula.

Data normalization

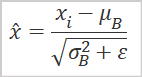
The use of matrix operations simplifies this task. Now we do not need to create loop systems. To find the arithmetic mean values for all features, we can use the Mean matrix operations method; in it we specify the dimension to count values. As a result of the operation, we immediately get a vector containing the arithmetic mean values for all features.

The denominator of the data normalization formula contains the square root of the variance, which corresponds to the standard deviation. Again, we can use matrix operations. The STD method returns a vector of standard deviations for the specified dimension. We only need to add a small constant to eliminate the divide-by-zero error.

Save the resulting vectors in the corresponding variables v_Means and v_STDs. Such a normalization of the initial data should be executed both at the stage of model training and at the stage of operation.

Next, normalize the data. For this purpose, prepare the matrix X with the size equal to the original data size. Implement a loop with the number of iterations equal to the number of rows in the source data matrix.

In the loop body, normalize initial data and save the operation result in the previously created matrix X. The use of vector operations eliminates the need to create a nested loop.

bool CPCA::Study(matrix &data)
  {
   matrix X;
   ulong total = data.Rows();
   if(!X.Init(total,data.Cols())
      return false;
   v_Means = data.Mean(0);
   v_STDs = data.STD(0) + 1e-8;
   for(ulong i = 0; i < total; i++)
     {
      vector temp = data.Row(i) - v_Means;
      temp /= v_STDs;
      X = X.Row(temp, i);
     }

After normalizing the original data, we proceed directly to the implementation of the principal component analysis algorithm. As mentioned above, we need to calculate the covariance matrix first. Thanks to matrix operations, this easily fits into one code line. In order not to create unnecessary objects, I overwrite the operations result in our matrix X.

   X = X.Transpose().MatMul(X / total);

According to the above algorithm, the next operation is the singular value decomposition of the covariance matrix. As a result of this operation, we expect to get three matrices: left singular vectors, singular values, and right singular vectors. As we have already discussed, only the elements of the of singular values matrix along the main diagonal can have non-zero values. Therefore, to save resources in the MQL5 implementation, a vector of singular values is returned instead of a matrix.

Before calling the function, we declare two matrices and vector to receive the results. After that we can call SVD matrix vector for the singular value decomposition. In the parameters we pass to the method matrices and a vector for recording the operation results of the operation.

   matrix U, V;
   vector S;
   if(!X.SVD(U, V, S))
      return false;

Now that we have obtained orthogonal matrices of singular vectors, we need to determine to level down to which we will reduce the dimension of the original data. As a general practice, we will retain at least 99% of the information contained in the original data.

Following the above logic, we first determine the total sum of all elements of the singular values vector. Also, be sure to check that the resulting value is greater than 0. It cannot be negative as singular values are not negative. In addition, we must exclude the divide-by-zero error.

After that, we calculate the cumulative sums of the values of the singular values vector and divide the resulting vector by the total sum of singular values.

As a result, we will get a vector of increasing values with a maximum value equal to 1.

Now, to determine the number of required columns, we need to find the position of the first element in the vector that is greater than or equal to the threshold information retaining value. In the above example it is 0.99. This corresponds to retaining 99% of the information.

   double sum_total = S.Sum();
   if(sum_total<=0)
      return false;
   S = S.CumSum() / sum_total;
   int k = 0;
   while(S[k] < 0.99)
      k++;

We just have to resize the matrix and transfer its contents to our class matrix. After that, switch the model training flag and exit the method.

   if(!U.Resize(U.Rows(), k + 1))
      return false;
//---
   m_Ureduce = U;
   b_Studied = true;
   return true;
  }

After we have created a model training method, i.e. we have determined the original data dimensionality reduction matrix, we can also create the ReduceM method to reduce the input data. It will receive in parameters the original data and will return a matrix of reduced dimension.

Of course, the input data must be comparable to the data used in the model training stage. Here we are talking about the quantity and quality of system state describing features, not about the number of observations.

At the beginning of the method, we create a block of controls, in which we check the model training flag. Here, we also check if the number of columns in the initial data matrix (number of features) is equal to the number of rows in the reduction matrix m_Ureduce. If any of the conditions is not met, exit the method, and return a zero-size matrix.

matrix CPCA::ReduceM(matrix &data)
  {
   matrix result;
   if(!b_Studied || data.Cols() != m_Ureduce.Rows())
      return result.Init(0, 0);

After successfully passing the block of controls, normalize the original data before performing dimensionality reduction. The normalization algorithm is similar to the one that we discussed above when training the model. The only difference is that this time we do not calculate the arithmetic mean and standard deviation. Instead, we use the corresponding vectors which were saved during training. Thus, we ensure the comparability of new results and those obtained during training.

   ulong total = data.Rows();
   if(!X.Init(total,data.Cols()))
      return false;
   for(ulong r = 0; r < total; r++)
     {
      vector temp = data.Row(r) - v_Means;
      temp /= v_STDs;
      result = result.Row(temp, r);
     }

Prior to completing the method algorithm, we need to multiply the matrix of normalized values to a reducing matrix and return the operation result to the caller.

   return result.MatMul(m_Ureduce);
  }

We have built methods for training the model which reduces the dimensionality of the original data. Thanks to the use of matrix operations, the resulting code is quite concise and we did not have to dive deep into mathematics. But this is the first code in our library that is written using matrix operations. Previously, we used dynamic arrays in CBufferDouble objects. Therefore, to provide the compatibility of our objects, it is necessary to create an interface for transferring data from a dynamic buffer to a matrix and vice versa.

To organize this process, we will create two methods: FromBuffer and FromMatrix. The first method will receive parameters with a dynamic data buffer and the size of the vector describing one system state. It will return the matrix into which the buffer contents will be transferred.

In the method body, we first organize a block of controls, in which we check the validity of the pointer to the initial data buffer object. Then we check whether the buffer size is multiple of the vector describing one state of the analyzed system.

matrix CPCA::FromBuffer(CBufferDouble *data, ulong vector_size)
  {
   matrix result;
   if(CheckPointer(data) == POINTER_INVALID)
     {
      result.Init(0, 0);
      return result;
     }
//---
   if((data.Total() % vector_size) != 0)
     {
      result.Init(0, 0);
      return result;
     }

If all checks are executed successfully, determine the number of rows in the matrix and initialize the result matrix.

   ulong rows = data.Total() / vector_size;
   if(!result.Init(rows, vector_size))
     {
      result.Init(0, 0);
      return result;
     }

Next, organize a system of nested loops in which we move all the contents of the dynamic buffer to the matrix.

   for(ulong r = 0; r < rows; r++)
     {
      ulong shift = r * vector_size;
      for(ulong c = 0; c < vector_size; c++)
         result[r, c] = data[(int)(shift + c)];
     }
//---
   return result;
  }

Once the loop system is complete, exit the method and return the created matrix to the caller.

The second method FromMatrix executes the reverse operation. In parameters, we input a matrix with data into the method and receive a dynamic data buffer at the output.

In the method body, we first create a new object of the dynamic array and then check the operation result.

CBufferDouble *CPCA::FromMatrix(matrix &data)
  {
   CBufferDouble *result = new CBufferDouble();
   if(CheckPointer(result) == POINTER_INVALID)
      return result;

Then reserve the size of the dynamic array large enough to store the entire contents of the matrix.

   ulong rows = data.Rows();
   ulong cols = data.Cols();
   if(!result.Reserve((int)(rows * cols)))
     {
      delete result;
      return result;
     }

Next, it is necessary to transfer the contents of the matrix to a dynamic array. This operation is performed within a system of two nested loops.

   for(ulong r = 0; r < rows; r++)
      for(ulong c = 0; c < cols; c++)
         if(!result.Add(data[r, c]))
           {
            delete result;
            return result;
           }
//---
   return result;
  }

After all loop operations have successfully completed, we exit the method and return the created data buffer object to the caller.

It should be noted here that we do not save a pointer to the created object. Therefore, any operations related to its state monitoring and to removing it from memory after operation completion must be organized on the side of the calling program.

Let us create similar methods to work with vectors. Data from the buffer to the vector will be moved using with an overloaded method FromBuffer. The reverse operation will be performed in the FromVector method. The algorithms for constructing methods are similar to those given above. The full code of the methods is provided in the attachment below.

After creating the data transfer methods, we can create an overload of the model training method, which will receive in the parameters a dynamic data buffer and the size of one system state describing vector. The method construction algorithm is quite simple. We first transfer data from a dynamic buffer to a matrix using the previously considered method FromBuffer. Then we call the previously considered model training method by passing the resulting matrix into it.

bool CPCA::Study(CBufferDouble *data, int vector_size)
  {
   matrix d = FromBuffer(data, vector_size);
   return Study(d);
  }

Let us create a similar overload for the dimensionality reduction method ReduceM. The only difference from the training method overloading is that in the method parameters we only pass the initial data buffer, without specifying the size of the vector describing one system state. This is related to the fact that by this time the model has already been trained and the size of the state description vector should be equal to the number of rows in the reduction matrix.

Another difference of this method is that to prevent excessive data transfer, we first check whether the model has been trained and whether he buffer size is multiple of the size of the state description vector. Only after all checks are passed successfully, we call the data transfer method.

matrix CPCA::ReduceM(CBufferDouble *data)
  {
   matrix result;
   result.Init(0, 0);
   if(!b_Studied || (data.Total() % m_Ureduce.Rows()) != 0)
      return result;
   result = FromBuffer(data, m_Ureduce.Rows());
//---
   return ReduceM(result);
  }

To obtain a reduced dimension matrix in the form of a dynamic data buffer, we will create two more overloaded methods Reduce. One of them will receive a dynamic data buffer with initial data in parameters. The second one will receive the matrix. Their code is shown below.

CBufferDouble *CPCA::Reduce(CBufferDouble *data)
  {
   matrix result = ReduceM(data);
//---
   return FromMatrix(result);
  }

CBufferDouble *CPCA::Reduce(matrix &data)
  {
   matrix result = ReduceM(data);
//---
   return FromMatrix(result);
  }

It may seem strange, but despite the difference in the method parameters, their contents are exactly the same. But this is easily explained by the use of the ReduceM method overloads.

We have considered the class functionality. Next, we will need to create methods for working with files. As we remember, any model that has once been trained should be able to quickly restore its operation for later use. As always, we start with the data saving method Save.

But before proceeding with the construction of the data saving method algorithm, let us look at our class structure and think about what we should save to a file.

Among the private class variables, we have one model training flag b_Studied, the dimensionality reduction matrix m_Ureduce and two vectors for the arithmetic mean v_Means and the standard deviation v_STDs. In order to be able to fully restore the model's performance, we need to save all these elements.

class CPCA : public CObject
  {
private:
   bool              b_Studied;
   matrix            m_Ureduce;
   vector            v_Means;
   vector            v_STDs;
   //---
   CBufferDouble     *FromMatrix(matrix &data);
   CBufferDouble     *FromVector(vector &data);
   matrix            FromBuffer(CBufferDouble *data, ulong vector_size);
   vector            FromBuffer(CBufferDouble *data);

public:
                     CPCA();
                    ~CPCA();
   //---
   bool              Study(CBufferDouble *data, int vector_size);
   bool              Study(matrix &data);
   CBufferDouble     *Reduce(CBufferDouble *data);
   CBufferDouble     *Reduce(matrix &data);
   matrix            ReduceM(CBufferDouble *data);
   matrix            ReduceM(matrix &data);
   //---
   bool              Studied(void)  {  return b_Studied; }
   ulong             VectorSize(void)  {  return m_Ureduce.Cols();}
   ulong             Inputs(void)   {  return m_Ureduce.Rows();   }
   //---
   virtual bool      Save(const int file_handle);
   virtual bool      Load(const int file_handle);
   //---
   virtual int       Type(void)  { return defUnsupervisedPCA; }
  };

When we build various models, all previously considered methods for saving data receive in parameters a file handle for writing data. The similar method of this class is no exception. In the method body, we immediately check the validity of the received handle.

bool CPCA::Save(const int file_handle)
  {
   if(file_handle == INVALID_HANDLE)
      return false;

Next, we save the value of the model training flag. Because its state determines the need to save other data. If the model has not yet been trained, there is no need to save empty vectors and matrix. In this case, we complete the method.

   if(FileWriteInteger(file_handle, (int)b_Studied) < INT_VALUE)
      return false;
   if(!b_Studied)
      return true;

If the model is trained, we proceed with the saving of the remaining elements. First we save the reduction matrix. In the MQL5 language, the data saving function for matrices has not yet been implemented. But we have a method to write to a data buffer file. We will take advantage of this method.

First, let us move data from the matrix to a dynamic data buffer. Then, save the number of columns in the matrix. Next, call the relevant method to save the data buffer. Note that in the method of data moving from the matrix to the buffer we did not save the object pointer. Also, I already mentioned that any operations related to such object memory clearing should be performed by the caller. Therefore, after we complete operations related to data saving, delete the created object.

   CBufferDouble *temp = FromMatrix(m_Ureduce);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(FileWriteLong(file_handle, (long)m_Ureduce.Cols()) <= 0)
     {
      delete temp;
      return false;
     }
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;

Let us use a similar algorithm to save vector data.

   temp = FromVector(v_Means);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;

   temp = FromVector(v_STDs);
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   if(!temp.Save(file_handle))
     {
      delete temp;
      return false;
     }
   delete temp;
//---
   return true;
  }

After successful completion of all operations, exit the method with the true result.

Data is restored from the file in the Load method, in the same order. We first check the validity of the file handle to load the data.

bool CPCA::Load(const int file_handle)
  {
   if(file_handle == INVALID_HANDLE)
      return false;

We then read the state of the model's training flag. If the model has not yet been trained, exit the method with a positive result. There is no need to perform any work related to the reduction of matrix and vectors, as they will be overwritten during model training. If you try to perform data dimensionality reduction before training, the method will check the state of the training flag and will be completed with a negative result.

   b_Studied = (bool)FileReadInteger(file_handle);
   if(!b_Studied)
      return true;

For the trained model, we will first create a dynamic buffer object. Then, count the number of columns in the reduction matrix. Load the contents of the reduction matrix to the data buffer.

After successful data loading, simply transfer the context of the dynamic buffer into our matrix.

   CBufferDouble *temp = new CBufferDouble();
   if(CheckPointer(temp) == POINTER_INVALID)
      return false;
   long cols = FileReadLong(file_handle);
   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   m_Ureduce = FromBuffer(temp, cols);

Using a similar algorithm, we will load the contents of the vectors.

   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   v_Means = FromBuffer(temp);

   if(!temp.Load(file_handle))
     {
      delete temp;
      return false;
     }
   v_STDs = FromBuffer(temp);

After successfully loading all the data, delete the dynamic data buffer object and exit the method with a positive result.

   delete temp;
//---
   return true;
  }

This completes the principal component method class. The complete code of all methods and functions is available in the attachment.

4. Testing

The operation of our class of the principal component analysis method was performed in 2 stages. In the first test I trained the model. For this purpose, I created the pca.mq5 expert Advisor based on the kmeans.mq5 EA which we considered in the previous article. The changes affected only the object of the used model and the Train model training function.

Again, at the beginning of the procedure, determine the start date of the training period.

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

Then we download the quotes and the values of the indicators used.

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
      return;
   if(!ArraySetAsSeries(Rates, true))
      return;
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

After that, we group the received data into one matrix.

   int total = bars - (int)HistoryBars;
   matrix data;
   if(!data.Init(total, 8 * HistoryBars))
     {
      ExpertRemove();
      return;
     }
//---
   for(int i = 0; i < total; i++)
     {
      Comment(StringFormat("Create data: %d of %d", i, total));
      for(int b = 0; b < (int)HistoryBars; b++)
        {
         int bar = i + b;
         int shift = b * 8;
         double open = Rates[bar]
                       .open;
         data[i, shift] = open - Rates[bar].low;
         data[i, shift + 1] = Rates[bar].high - open;
         data[i, shift + 2] = Rates[bar].close - open;
         data[i, shift + 3] = RSI.GetData(MAIN_LINE, bar);
         data[i, shift + 4] = CCI.GetData(MAIN_LINE, bar);
         data[i, shift + 5] = ATR.GetData(MAIN_LINE, bar);
         data[i, shift + 6] = MACD.GetData(MAIN_LINE, bar);
         data[i, shift + 7] = MACD.GetData(SIGNAL_LINE, bar);
        }
     }

Call the model training method.

   ResetLastError();
   if(!PCA.Study(data))
     {
      printf("Runtime error %d", GetLastError());
      return;
     }

After successful training, save the model to a file and call the Expert Advisor to complete its work.

   int handl = FileOpen("pca.net", FILE_WRITE | FILE_BIN);
   if(handl != INVALID_HANDLE)
     {
      PCA.Save(handl);
      FileClose(handl);
     }
//---
   Comment("");
   ExpertRemove();
  }

The full EA code can be found in the attachment.

As a result of EA performance on historical data over the past 15 years, the dimension of the initial data was reduced from 160 elements to 68. That is, we have a reduction in the source data size by almost 2.4 times, with the risk of losing only 1% of information.

At the next testing stage, we used a pre-trained principal component analysis model. After reducing source data size, we input the class operation results into a fully connected perceptron. For this test, we created the EA pca_net.mq5 based on a similar EA from the previous article kmeans_net.mq5. The perceptron was trained using historical data for the last two years.

Perceptron training results on reduced data

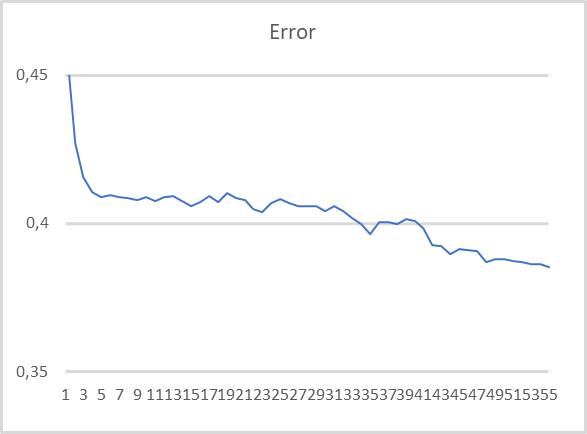
As can be seen in the graph, when training the model on compressed data, there is a fairly stable tendency to error reduction. After 55 training epochs, the error size has not stabilized yet. This means that further error reduction is possible if we continue training.

Conclusion

In this article, we considered the solution of another type of problem using unsupervised learning algorithms: Dimensionality Reduction. To solve such problems, we have created the CPCA class, in which we have implemented the algorithm of the principal component analysis method. This is quite an efficient data compression method, which provides a predictable information loss threshold.

When testing the created class, we compress the original data by almost 2.4 times, with the risk of losing only 1% of information. This is a pretty good result which enables an increase in the efficiency of a model trained on compressed data.

In addition, one of the great features of the principal component method is the use of an orthogonal matrix for dimensionality reduction. This reduces the correlation between features in compressed data almost to 0. This property also improves the efficiency of subsequent model training using compressed data. This is confirmed by the results of the second test.

At the same time, please be warned against using the principal components method in an attempt to combat model overfitting. This is pretty bad practice. In such cases, it is better to use regularization methods.

And here is one more observation from general practice. Although quite a small amount of information is lost in the process of data compression, it anyway happens. Therefore, the use of dimensionality reduction methods is recommended only if training models without using it did not produce the expected results.

Also, we have studies new matrix operations. Special thanks to MetaQuotes for the implementation of such operations in the MQL5 language. The use of matrix operations greatly simplifies code writing when creating or models related to solving artificial intelligence problems.

List of references

Programs used in the article

#	Name	Type	Description
1	pca.mq5	Expert Advisor	Expert Advisor to train the model
2	pca_net.mq5	EA	Expert Advisor to test passing the data to the second model
3	pсa.mqh	Class library	Library for implementing principal component analysis method
4	kmeans.mqh	Class library	Library for implementing the k-means method
5	unsupervised.cl	Code Base	OpenCL program code library to implement the k-means method
6	NeuroNet.mqh	Class library	A library of classes for creating a neural network
7	NeuroNet.cl	Code Base	OpenCL program code library

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/11032

Attached files |

Download ZIP

MQL5.zip (70.9 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.