
Neural networks made easy (Part 19): Association rules using MQL5
Contents
- Introduction
- 1. How the method can be used in trading
- 2. FP Growth algorithm implementation
- 3. Testing
- Conclusion
- List of references
- Programs used in the article
Introduction
In the previous article, we started learning association rules mining algorithms which belong to unsupervised learning methods. We have considered two algorithms for solving this type of problems: Apriori and FP Growth. The bottleneck of the Apriori algorithm is its large number of database calls aimed at determining the support of Frequent Pattern candidates. The FP Growth method solves this issue by building a tree which includes the entire database. All further operations are carried out with the FP tree, without accessing the database. This increases the problem solving speed, as the FP tree is located in RAM. Accessing it is much faster than a full iteration of the database.
1. How the method can be used in trading
Before proceeding to constructing the association rule mining algorithm using MQL5, let's think about how they can be used in trading.
Association rule mining algorithms were created to search for stable dependencies between binary features in the database. Therefore, such algorithms can be used to find some stable relationships between various features. This can be various patterns consisting of multiple indicators and/or instruments. The algorithm does not care if each separate feature represents different metrics or it is the values of the same metric in different time intervals. The algorithm evaluates each feature as being independent. Thus, we can try to combine this algorithm with the developments in supervised learning methods. Let us add a few target features to the training sample of historical data. The algorithm should find association rules which will lead to the formation of our target values.
We have an algorithm and an idea of how to use it to solve our practical problems. Let us look at how it can be implemented using MQL5. Then we will test the idea in practice.
2. FP Growth algorithm implementation
To implement the FP Growth algorithm considered in the previous article, let us remember that its construction is based on a decision tree. The MQL5 Standard Library has the CTree class for building a binary tree. Unfortunately, the binary tree option is not entirely convenient for us, since the number of branches from one node of an FP tree can be more than 2 (the maximum available in the binary implementation). Therefore, before building the algorithm itself, let us create the CMyTreeNode class to implement a tree node with multiple branches.
2.1. Tree node class implementation
This class will be derived from the standard MQL5 class of a dynamic array of objects CArrayObj. This class has been selected as a parent because it has the required functionality related to the creation and maintaining of a dynamic array of objects which, in our case, are the branch nodes.
Additionally, to implement the functionality required by the algorithm, three new variables have been added into the class:
- m_cParent — a pointer to the object of the previous parent node. It will be empty for the tree root
- m_iIndex — index of a feature in the source database; to be used to identify features
- m_dSupport — a variable to receive feature support value
class CMyTreeNode : public CArrayObj { protected: CMyTreeNode *m_cParent; ulong m_iIndex; double m_dSupport; public: CMyTreeNode(); ~CMyTreeNode(); }
In the class constructor, set initial values of the variables and clear the dynamic array. Leave the class destructor empty.
CMyTreeNode::CMyTreeNode() : m_iIndex(ULONG_MAX), m_dSupport(0) { Clear(); }
To work with hidden class variables, we will create a number of methods will be used in the FP Growth algorithm creation process. I will provide the explanation of the method purposes along with their use.
class CMyTreeNode : public CArrayObj { ........ public: ........ //--- methods of access to protected data CMyTreeNode* Parent(void) const { return(m_cParent); } void Parent(CMyTreeNode *node) { m_cParent = node; } void IncreaseSupport(double support) { m_dSupport += support; } double GetSupport(void) { return m_dSupport; } void SetSupport(double support) { m_dSupport = support; } ulong ID(void) { return m_iIndex; } void ID(ulong ID) { m_iIndex = ID; } };
To calculate the confidence level, let us create the GetConfidence method. In it, we first check the pointer to the predecessor node and if it is valid, divide the current node support by the parent node support.
Note that the FP tree building algorithm is organized so that the support of any node cannot be greater than the support of the parent node. Therefore, the result of the method operations will always be positive and will not be greater than 1.
We do not have zero divide checks as tree nodes are added based on existing transactions. Therefore, if a node is in the tree, then its feature has appeared in the database at least once and it has the minimum support.
double CMyTreeNode::GetConfidence(void) { CMyTreeNode *parent = Parent(); if(!parent) return 1; //--- double result = m_dSupport / parent.GetSupport(); return result; }
Also, we add a method that creates a new branch node AddNode. In the method parameter, we pass the feature ID in the source database of the training sample and the support of the node. The method returns a pointer to the created object.
In the method body, we create a new instance of the tree node and immediately check the operation result. If an error occurs, return an invalid object pointer.
Next, we specify the ID of the created node and pass to it a pointer to the current object as the parent object.
Add a new object to the dynamic array of the current node and check the operation result. If error occurs while adding an object to the array, delete the created object and exit the method, while returning an invalid pointer.
At the end of the method, save the support specified in the parameters in the new object and exit the method.
CMyTreeNode *CMyTreeNode::AddNode(const ulong ID, double support = 0) { CMyTreeNode *node = new CMyTreeNode(); if(!node) return node; node.ID(ID); if(!Add(node)) { delete node; return node; } node.Parent(GetPointer(this)); //--- if(support > 0) node.SetSupport(support); return node; }
Once we have created a new object, we should be able to delete it. The method for deleting an object by its index in a dynamic array already exists in the parent class. To expand the functionality, let us create the DeleteNode method for deleting a node by the feature ID.
The method receives the ID of the feature to be deleted and returns the boolean result of the operation.
In the method body, implement a loop to find a node with the specified ID in the dynamic array of the current node. The loop will iterate through elements in the range from 0 to the m_data_total variable value. The variable contains the number of active elements of the dynamic array, and it is controlled by the parent class.
In the method body, extract from the dynamic array the next element and validate the pointer. An element with an invalid pointer is immediately deleted by calling the Delete method of the parent class, with the specified index of the element to be deleted.
Note that the Delete method returns the boolean result of the operation. If an element is successfully deleted from the dynamic array, decrease the counter of loop iterations and move on to the next array. We only decrement the loop iterations counter and do not change the value of the m_data_total variable. This is because its value is already changed in the method of the Delete parent class.
If an error occurs while removing an invalid element form the dynamic array simply move on to the next element of the array. We do not terminate the method with the false result, since the method task is not to clear the dynamic array from invalid objects. This is only a helper feature. The main task of the method is to delete a specific element. Therefore, we continue the method execution until the required element is found.
When the required element of the dynamic array is found, call the previously mentioned Delete method of the parent class. This time we exit the method while returning the object deletion result.
If the element is not found after a complete iteration through all elements of the dynamic array, exit the method with the false result.
bool CMyTreeNode::DeleteNode(const ulong ID) { for(int i = 0; i < m_data_total; i++) { CMyTreeNode *temp = m_data[i]; if(!temp) { if(!Delete(i)) continue; return DeleteNode(ID); } if(temp.ID() != ID) continue; return Delete(i); } //--- return false; }
Talking further about the methods of the new class of the tree node CMyTreeNode, I would like to pay your attention to the Mining method. This method is responsible for finding paths in our FP tree up to the feature we are analyzing. Before we proceed to the description of the method algorithm, I must say that it is created taking into account the intended use in trading. Therefore, it slightly digresses from the basic algorithm.
First of all, we will not determine association rules for all features, but only for our target values. Therefore, while building rule trees, we are very likely to encounter a situation where the desired feature is not a leaf, but a node containing subsequent elements along the path. But we cannot ignore subsequent nodes, since they can increase the likelihood of a target result. Therefore, they should be taken into account when selecting paths to the analyzed feature.
Another point that I paid attention to when constructing this method is as follows. According to the algorithm, we first need to find all paths to the analyzed feature in the FP tree. After that we can calculate support values for each feature in the selected paths. I decided to perform these two subtasks within one method.
Please note that to build an FP tree it is only planned to use the CMyTreeNode class instances. Therefore, to perform a depth-first search, we will use a recursive method call.
Now let us look at the implementation of these tasks in the Mining method our class. In the method parameters, we pass pointers to a vector for writing element support values, a matrix for writing the paths, an identifier of the feature being analyzed, and a minimum confidence level. The method will return the boolean result of the operation.
In the method body, first check whether the analyzed node is the desired feature. To do this, compare the ID of our node and the ID of the desired node received in the parameters. If they are equal, check the confidence level of the node in the current branch. The level is determined using the previously considered GetConfidence method. The confidence level must not be less than the minimum allowed value. Otherwise, exit the method with the true result.
bool CMyTreeNode::Mining(vector &supports, matrix &paths, const ulong ID, double min_conf) { if(ID == m_iIndex) if(GetConfidence() < min_conf) return true;
The next block implements further search towards tree depth. Here, first save the support value of the current node into a local variable. Then, run a loop to iterate through all the branches from the current node to the depth of the tree. The method will be recursively called for all branches.
Note that with the recursive method we pass the desired identifier only until we find the corresponding node. After that we pass the ULONG_MAX constant into the tree depth, instead of the desired identifier. This is because due to the FP tree construction specifics, before we find the path to the desired item, the pattern confidence is likely to be less than 100%. As we further progress along the path, the probability of the desired feature will be 100%. Otherwise, we would have built a different path, bypassing the desired node.
Of course, such a situation is excluded when we use a custom algorithm. When determining rules for all features, by the time we start working on any of them in our FP tree, it will be a leaf without subsequent nodes. This is because all features with lower support will have been processed and deleted from the tree.
Thus, when we deviate from the algorithm, we must evaluate the impact of the changes on the entire process and make appropriate adjustments to the algorithm. In this case, we will have to add into the list all the paths which include the desired feature. This is the path from the desired feature to the tree root and all paths from any of the subsequent node to the tree root which pass through the desired feature. For this purpose, we need to inform further nodes that the desired feature has been found between the node and the root. Such a flag occurs when the ID of the desired feature changes to the ULONG_MAX constant.
After the positive result of the recursive method, for the next node, we subtract the support value from the local variable created before the loop with the support of the current node. If the next node ID is equal to the desired one, delete the processed node.
double support = m_dSupport; for(int i = 0; i < m_data_total; i++) { CMyTreeNode *temp = m_data[i]; if(!temp) { if(Delete(i)) i--; continue; } if(!temp.Mining(supports, paths, (ID == m_iIndex ? ULONG_MAX : ID), min_conf)) return false; support -= temp.GetSupport(); if(temp.ID() == ID) if(Delete(i)) i--; }
You can see that in the previous block, we only called the same method recursively for subsequent nodes, but we did not save the found paths. The saving will be performed in the next method block. This block will be executed for nodes with the desired attribute and for subsequent ones. For this, we need to check the ID of the current node and that received in parameters. In addition, the support of the current node after the execution of recursive methods must be greater than "0". Also, the current node cannot be the root. It means that it must have at least one predecessor node. This is because we need to use something as an antecedent for the rule.
If the control is passed successfully, increase the size of the path matrix by 1 row and fill in the added row with zero values.
Next, implement a propagation loop from the current node to the tree root. The current and all predecessor nodes are assigned the remaining support of the current node in our path line. Also, add the same value in the accumulative support vector for the corresponding items.
After the parent iteration is complete, exit the method with a positive result.
if(ID == m_iIndex || ID == ULONG_MAX) if(support > 0 && !!m_cParent) { CMyTreeNode *parent = m_cParent; ulong row = paths.Rows(); if(!paths.Resize(row + 1, paths.Cols())) return false; if(!paths.Row(vector::Zeros(paths.Cols()), row)) return false; supports[m_iIndex] += support; while(!!parent) { if(parent.ID() != ULONG_MAX) { supports[parent.ID()] += support; paths[row, parent.ID()] = support; } parent = parent.Parent(); } } //--- return true; }
Let me explain how the method works using a small example, because its construction is slightly beyond the scope of the PF Growth algorithm described above. Suppose the source database has the following transactions: "AB" repeated twice, one "ABC", "ABCD" repeated three times, and one "ABCDE". As a result, the following path has formed in the FP tree: "A7-B7-C5-D4-E1". When analyzing item "C" we need to restore from the tree all paths containing this item.
We start by calling a method on the root element "A" and instructing it to find the "C". Here we recursively call the method for the node "B". Continue up to the leaf "E". Since the "E" leaf has no successor nodes, start processing at block 2 of our method and write the paths. Here, we first save the "ABCDE" path and write support 1 for all nodes. It means that there was 1 such path in the source database. Then exit the method, passing control to a higher level.
At the "D" node level save the path "ABCD". From the support of node "D", subtract the "E" leaf support (4-1=3). Register the resulting value as the support of all items of this path. As you can see, this corresponds to the initial data, where we had 3 identical transactions in the training sample. Instead of repeating the transaction three times, we use item support values.
Similarly, save path "ABC" with the support equal to 1. Path "AB" is not saved as it does not contain the analyzed feature.
Find the entire code of all class methods in the file MyTreeNode.mqh attached below.
2.2. Implementation of the association rule mining class
Let us continue to build the FP Growth association rule mining algorithm. The main functionality will be described in another class CAssocRules. The structure of this class is shown below. As you can see, most of the methods are hidden "under the hood". But first things first.
class CAssocRules : public CObject { protected: CMyTreeNode m_cRoot; CMyTreeNode m_cBuyRules; CMyTreeNode m_cSellRules; vector m_vMin; vector m_vStep; int m_iSections; matrix m_mPositions; matrix m_BuyPositions; matrix m_SellPositions; //--- bool NewPath(CMyTreeNode *root, matrix &path); CMyTreeNode *CheckPath(CMyTreeNode *root, vector &path); //--- bool PrepareData(matrix &data, matrix &bin_data, vector &buy, vector &sell, const int sections = 10, const double min_sup = 0.03); matrix CreatePath(vector &bin_data, matrix &positions); matrix CreatePositions(vector &support, const double min_sup = 0.03); bool GrowsTree(CMyTreeNode *root, matrix &bin_data, matrix &positions); double Probability(CMyTreeNode *root, vector &data, matrix &positions); public: CAssocRules(); ~CAssocRules(); //--- bool CreateRules(matrix &data, vector &buy, vector &sell, int sections = 10, double min_freq = 0.03, double min_prob = 0.3); bool Probability(vector &data, double &buy, double &sell); //--- methods for working with files virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); virtual bool Save(const string file_name); virtual bool Load(const string file_name); };
Among the class variables, there are three instances of the tree nodes described above:
- m_cRoot — we will use it to write down our FP tree
- m_cBuyRules — this one will be used to write down buy rules
- m_cSellRules — for sell rules
Matrices m_mPositions, m_BuyPositions and m_SellPositions will contain features and their support values sorted in descending order.
When testing all previous models, we checked the possibility of determining a fractal before the formation of the 3rd candle of the pattern. Therefore, I will determine two rule mining trees to define buy and sell fractals. If according to your problem you need to define rules for a larger number of target features, then you will need to create more private rule trees.
For example, you may have multiple target buy and sell levels. Unfortunately, association rule mining algorithms only operate with binary tables. Therefore, you will have to create a separate item for each target level and find association rules for it. You can use dynamic arrays to exclude a large number of private variables.
The method constructor and destructor are left empty, since in this class I did not use dynamic pointers to tree-building objects.
As mentioned above, association rule mining algorithms for work only with binary matrices. But data on the market situation is difficult to be classified as such. Therefore, they need to be pre-processed before use.
To simplify further use of the class, the algorithm does not require pre-processing of data from the user. Instead, it is implemented in the PrepareData method. In parameters, the method receives pointers to 2 matrices, 2 vectors and 2 constants. One matrix contains the original data, and the second is used to write the processed binary data. The vectors contain the target values. In our case, they are represented by binary data, so they do not require pre-processing. Pre-processing is needed for source data.
To convert the scalar units of the source data into binary ones, we will use the range of values for each feature and divide it into several intervals. The number of intervals is set by the 'sections' parameter. The minimum values and step size for each feature will be saved in the corresponding vectors m_vMin and m_vStep. The vectors will then be used to convert source data to binary during practical use.
Here we prepare the binary matrix by setting the required size and filling with zeros. We can also specify the identifiers for target features, which will later be added as the last columns in a matrix.
bool CAssocRules::PrepareData(matrix &data, matrix &bin_data, vector &buy, vector &sell, const int sections = 10, const double min_sup = 0.03) { //--- m_iSections = sections; m_vMin = data.Min(0); vector max = data.Max(0); vector delt = max - m_vMin; m_vStep = delt / sections + 1e-8; m_cBuyRules.ID(data.Cols() * m_iSections); m_cSellRules.ID(m_cBuyRules.ID() + 1); bin_data = matrix::Zeros(data.Rows(), m_cSellRules.ID() + 1);
Next, implement a loop through all the rows of the input data matrix. In the loop body, subtract the vector of minimum values from each row and divide the result by the step size. To exclude data beyond the range, let us limit the lower and higher values of the vector elements. As a result of these operations, the integer part of the number in each item of the vector indicates to which range of values we need to include the corresponding item of the source data. Each range for our binary matrix will be a separate feature.
Let us run a nested loop and fill the relevant row of the binary matrix. If the feature is active, change its value to "1". Inactive features will remain with zero values.
for(ulong r = 0; r < data.Rows(); r++) { vector pos = (data.Row(r) - m_vMin) / m_vStep; if(!pos.Clip(0, m_iSections - 1)) return false; for(ulong c = 0; c < pos.Size(); c++) bin_data[r, c * sections + (int)pos[c]] = 1; } if(!bin_data.Col(buy, m_cBuyRules.ID()) || !bin_data.Col(sell, m_cSellRules.ID())) return false;
After filling the binary matrix, we can immediately calculate the supports for each feature and sort them in descending order in the CreatePositions method. After sorting, exit the method with a positive result.
vector supp = bin_data.Sum(0) / bin_data.Rows(); m_mPositions = CreatePositions(supp, min_sup); //--- return true; }
Since we mentioned the CreatePositions feature sorting method, let us consider its algorithm. The method receives a support vector and a minimum support level in parameters.
The method body will contain a little preparatory work. This is because the received support values are represented by a vector, in which item values contain support values. The indexes of the items indicate the features. With a simple sorting of the vector items, we would lose connection with the source data features. Therefore, we need to create "feature id - support" pairs. The pair data will be saved to a matrix.
To do this, first create an identity matrix with 2 columns and the number of rows equal to the number of features in the original sample. Then calculate the cumulative sums of items by columns and reduce the values of the resulting matrix by "1". Thus, we get a matrix in which the columns contain values in ascending order from "0", which correspond to the row index. We only need to replace one column with the resulting support vector. Thus, we obtain a matrix: each row will contain a feature identifier and a support value corresponding to it.
matrix CAssocRules::CreatePositions(vector &support, const double min_sup = 0.03) { matrix result = matrix::Ones(support.Size(), 2); result = result.CumSum(0) - 1; if(!result.Col(support, 1)) return matrix::Zeros(0, 0);
We only need to sort the matrix rows in the support descending order. To do this, implement a loop with a bubble sort algorithm.
bool change = false; do { change = false; ulong total = result.Rows() - 1; for(ulong i = 0; i < total; i++) { if(result[i, 1] >= result[i + 1, 1]) continue; if(result.SwapRows(i, i + 1)) change = true; } } while(change);
After exiting the loop, we will have a matrix with sorted features. We only need to remove the features that do not meet the minimum support requirement from this matrix. To do this, find the first feature below the minimum support level and "cut off" all the features below this level.
int i = 0; while(result[i, 1] >= min_sup) i++; if(!result.Resize(i, 2)) return matrix::Zeros(0, 0); //--- return result; }
After successfully resizing the matrix, exit the method and return the resulting matrix.
Before moving on to public methods, let us look at a few more methods in which some of the repetitive functions will be performed. We need to create a path from binary data to transfer to the FP tree. This functionality will be executed in the CreatePath method. The method will receive pointers to the vector of binary data and the matrix of sorted features. It will then return a path matrix that will contain "feature id - support" pairs to be added to the FP tree.
Pay attention to the difference between the sorted feature matrix, which we obtained when preparing the data, and the matrix for adding the path to the FP tree. Both matrices will contain "feature identifier - support" pairs. But the first matrix contains all the features available in the source data and their support in the training sample. While the path matrix will contain only the features present in the analyzed transaction and the supports from this transaction which are indicated in the binary matrix.
Well, since we are dealing with a binary matrix, feature support values in each transaction must be the same. Later we will use the same method to build private rule trees. Earlier, we considered an example when describing the CMyTreeNode::Mining method. Instead of repeating one path, we used support levels several times in that example. So, to unify the operations we will use 1 method in 2 sub-processes. In this case, the introduction of the support level will be very useful.
At the beginning of the method, we save in local variables the sizes of the source data vector and the number of analyzed features, which is less than the size of the source data vector by the number of random features with support below the minimum.
Also, we prepare a matrix to write the results. It cannot be larger than the analyzes feature matrix. Also, we introduce a variable indicating the size of our path. At this stage, it is equal to "0".
Next, we run a loop in through all the analyzed features in descending order of their supports. In the loop body, we extract the identifier of the next checked feature. Check its value in the binary source data vector. If the feature is not active, move on to the next feature.
If the feature is active, add the feature id and its support from the binary source data vector to the path matrix. After that we increase the path size variable.
After exiting the loop, reduce the size of the path matrix to the number of filled elements and exit the method.
matrix CAssocRules::CreatePath(vector &bin_data, matrix &positions) { ulong size = bin_data.Size(); //--- ulong total = positions.Rows(); int vect_pos = 0; matrix path = matrix::Zeros(2, total); for(ulong c = 0; c < total; c++) { ulong pos = (ulong)positions[c, 0]; if(pos >= size) continue; if(bin_data[pos] == 0) continue; path[0, vect_pos] = (double)pos; path[1, vect_pos] = bin_data[pos]; vect_pos++; } if(!path.Resize(2, vect_pos)) return matrix::Zeros(0, 0); //--- return path; }
Another method we will need is the one for adding a path to our FP tree: NewPath. The method will receive a pointer to the root node of the tree and the previously created path matrix. Then, it will return the boolean result of the operation. In the method body, we first check the size of the resulting path. It should be greater than 0. Then, we increase the support of the root node and run a loop through all items of the path.
In the loop body, check the presence of the next node with the required ID and, if necessary, create a new node. Then increase the node support size. And move on to searching for the next node in the path.
After iterating through all items of the path, exit the method.
bool CAssocRules::NewPath(CMyTreeNode *root, matrix &path) { ulong total = path.Cols(); if(total <= 0) return false; CMyTreeNode *parent = root; root.IncreaseSupport(path[1, 0]); for(ulong i = 0; i < total; i++) { CMyTreeNode *temp = parent.GetNext((ulong)path[0, i]); if(!temp) { temp = parent.AddNode((int)path[0, i], 0); if(!temp) return false; } temp.IncreaseSupport(path[1, i]); parent = temp; } //--- return true; }
And finally, we move on to the method growing the FP tree: GrowsTree. It receives in parameters a pointer to the root node of the tree, a binary matrix of source data and a matrix of sorted analyzed features. Inside the method, run a loop through all the rows of the source data.
In the loop body, capture the next transaction from the training sample and create a path to add to the tree, using the CreatePath method. Check to make sure the received part is greater than 0. Then call the NewPath method to add the created path to our FP tree. Do not forget to check the operation result.
After a successful iteration through all transactions from the source data, exit the method with a positive result.
bool CAssocRules::GrowsTree(CMyTreeNode * root, matrix & bin_data, matrix &positions) { ulong rows = bin_data.Rows(); for(ulong r = 0; r < rows; r++) { matrix path = CreatePath(bin_data.Row(r), positions); ulong size = path.Cols(); if(size <= 0) continue; if(!NewPath(root, path)) return false; } //--- return true; }
Now let us combine all the methods described above into the public method CreateRules. In the method parameters, we pass a matrix of scalar source data (not binary), binary vectors of target values, the number of intervals for converting scalar values to binary, minimum support and minimum confidence.
In the method body, we first check the received source data. We primarily check the correspondence of the dimensions of the obtained matrix vectors, and the number of intervals, which must be greater than 0.
After the block of checks, convert the scalar source data into a binary form. This is done using the PrepareData method described above.
bool CAssocRules::CreateRules(matrix &data, vector &buy, vector &sell, int sections = 10, double min_sup = 0.03, double min_conf = 0.3) { if(data.Rows() <= 0 || data.Cols() <= 0 || sections <= 0 || data.Rows() != buy.Size() || data.Rows() != sell.Size()) return false; //--- matrix binary_data; if(!PrepareData(data, binary_data, buy, sell, sections)) return false;
Further, in order to move to the plane of relative units, divide the binary matrix values by the number of transactions in the training sample and build the FP tree using the GrowsTree method.
double k = 1.0 / (double)(binary_data.Rows()); if(!GrowsTree(GetPointer(m_cRoot), binary_data * k, m_mPositions)) return false;
After building the FP tree, we can move on to creating the rules. First, prepare a vector to write supports and a matrix to write paths. Then call the Mining method of our FP tree to find all paths with the Buy feature.
vector supports = vector::Zeros(binary_data.Cols()); binary_data = matrix::Zeros(0, binary_data.Cols()); if(!m_cRoot.Mining(supports, binary_data, m_cBuyRules.ID(),min_conf)) return false;
After successfully extracting all paths, reset the support for the Buy feature, thereby removing it from the processing of all paths. Also sort private supports in descending order. Call the CreatePositions method and write the result to the m_BuyPositions matrix. If, after sorting the features, we still have the ability to build rules (the sorted matrix still has features to use as an antecedent for the rule), then call the tree growing method and input the previously selected paths to it.
As a result of these operations, we will get a private rule tree with a root at the m_cBuyRules node.
supports[m_cBuyRules.ID()] = 0; m_BuyPositions = CreatePositions(supports, min_sup); if(m_BuyPositions.Rows() > 0) if(!GrowsTree(GetPointer(m_cBuyRules), binary_data, m_BuyPositions)) return false;
Similarly, create a rule tree for Sell features.
supports = vector::Zeros(binary_data.Cols()); binary_data = matrix::Zeros(0, binary_data.Cols()); if(!m_cRoot.Mining(supports, binary_data, m_cSellRules.ID(),min_conf)) return false; supports[m_cSellRules.ID()] = 0; m_SellPositions = CreatePositions(supports, min_sup); if(m_SellPositions.Rows() > 0) if(!GrowsTree(GetPointer(m_cSellRules), binary_data, m_SellPositions)) return false; //--- m_cRoot.Clear(); //--- return true; }
After selecting all the rules, clear the source FP tree object to free up computer resources. Then exit the method with a positive result.
The 'Probability' method has been created for practical use. As parameters, the method receives a scalar vector of source data and pointers to two variables of type double, which will be used to store the particular pattern confidence. The method algorithm uses all the methods discussed above. You can see them in the attachment.
The full code of all classes and methods is available in the attachment.
3. Testing
I have created an Expert Advisor (assocrules.mq5) to test the class using real data. The EA was tested in full compliance with all the parameters used in previous tests. I cannot say that the method determined all fractals without errors. But the created EA demonstrated interesting results, which are shown in the screenshot below.
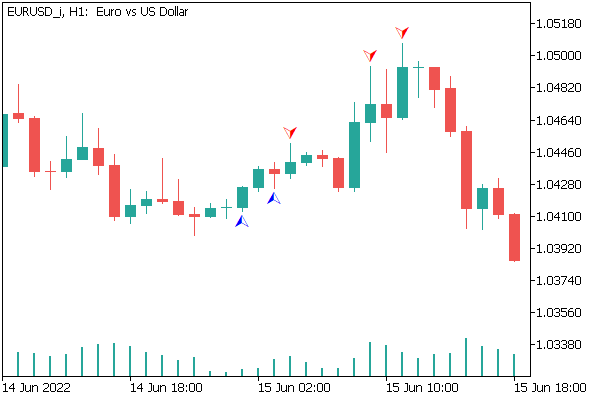
Conclusion
In this article, we considered another type of problem solved by unsupervised learning methods: Association rule mining. We have created a class for building association rules using the FP Growth algorithm. It was tested using an Expert Advisor which showed interesting results. Therefore, it can be concluded that such algorithms can be used to solve practical problems in trading.
List of references
- Neural networks made easy (Part 14): Data clustering
- Neural networks made easy (Part 15): Data clustering using MQL5
- Neural networks made easy (Part 16): Practical use of clustering
- Neural networks made easy (Part 17): Dimensionality reduction
- Neural networks made easy (Part 18): Association rules
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | assocrules.mq5 | Expert Advisor | Expert Advisor for training and testing the model |
| 2 | AssocRules.mqh | Class library | Class library for organizing the FP Growth algorithm |
| 3 | MyTreeNode.mqh | Class library | Tree node organization class library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/11141
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Learn how to design a trading system by DeMarker
Learn how to design a trading system by DeMarker
 Developing a trading Expert Advisor from scratch (Part 21): New order system (IV)
Developing a trading Expert Advisor from scratch (Part 21): New order system (IV)
 CCI indicator. Upgrade and new features
CCI indicator. Upgrade and new features
 Learn how to design a trading system by VIDYA
Learn how to design a trading system by VIDYA
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
hello teacher
I've tried to run the program, but with no success.
Ask for the parameters used to run.
Best regards
Anan Seti
hello teacher
I've tried to run the program, but with no success.
Ask for the parameters used to run.
Best regards
Anan Seti
You have run EA at tester. For study you must run EA at real-time. Don't worry. EA doesn't create any order.
Hello Dmitriy
This code compiles fine but when i put the EA on a graph the MT5 excludes this EA without any error
2022.12.01 10:24:01.046 Experts expert assocrules (EURUSD,H1) loaded successfully
2022.12.01 10:24:03.843 Experts expert assocrules (EURUSD,H1) removed
I updated all files in all directories but i couldn´t run this EA
Thank you
Rogerio
Hello Dmitriy
This code compiles fine but when i put the EA on a graph the MT5 excludes this EA without any error
2022.12.01 10:24:01.046 Experts expert assocrules (EURUSD,H1) loaded successfully
2022.12.01 10:24:03.843 Experts expert assocrules (EURUSD,H1) removed
I updated all files in all directories but i couldn´t run this EA
Thank you
Rogerio
Hello Rogerto.
It's just demo EA. And It doesn't create any orders.