
Neuronale Netze im Handel: Zweidimensionale Verbindungsraummodelle (letzter Teil)
Einführung
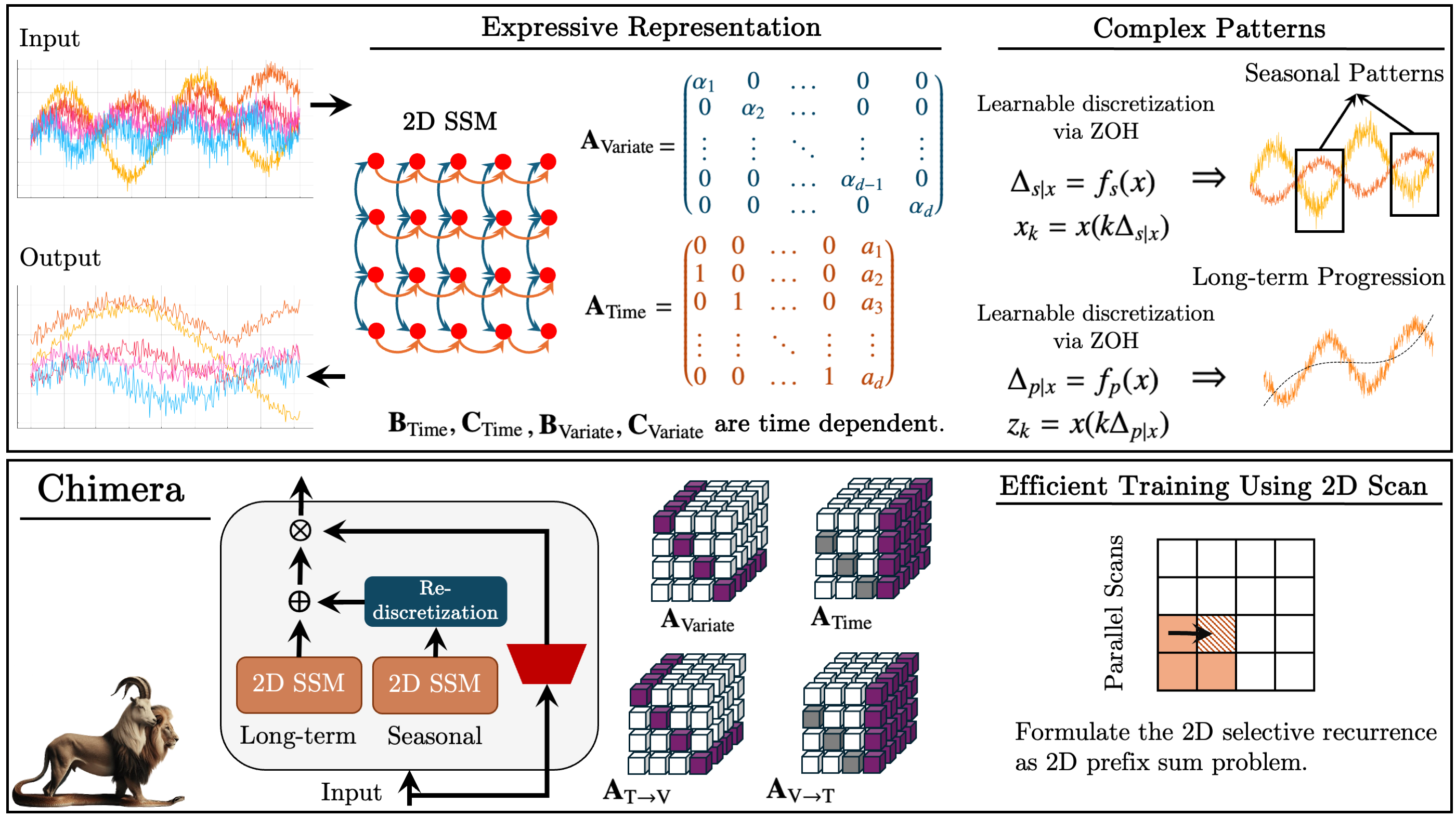
Im vorangegangenen Artikel haben wir den Chimera-Rahmen kennengelernt – ein zweidimensionales Zustandsraummodell (2D-SSM), das auf linearen Transformationen entlang der Zeitachse und der Achse der analysierten Variablen basiert. Es kombiniert Zustandsraummodelle entlang zweier Achsen und Mechanismen für deren Interaktion.
Zustandsraummodelle (State Space Models, SSM) sind in der Zeitreihenanalyse weit verbreitet, da sie die Modellierung komplexer Abhängigkeiten ermöglichen. Die traditionellen SSM berücksichtigen jedoch nur die zeitliche Achse, was ihre Anwendbarkeit auf mehrdimensionale Probleme einschränkt. Chimera erweitert dieses Konzept, indem es die Feature-Achse in den Modellierungsprozess einbezieht.
Der Rahmen arbeitet mit einer diskretisierten Form des 2D-SSM und führt die Diskretisierungsschritte Δ1 und Δ2 ein. Der erste Parameter betrifft die zeitlichen Abhängigkeiten, während der zweite die Beziehungen zwischen den Variablen regelt. Kleinere Werte von Δ1 helfen, langfristige Trends zu erfassen, während größere Werte saisonale Schwankungen hervorheben. In ähnlicher Weise regelt die Diskretisierung entlang der variablen Achse den Detaillierungsgrad der Analyse.
Um eine korrekte Prozessrekonstruktion zu gewährleisten, führen die Autoren des Frameworks strukturelle Beschränkungen für die Matrizen A1, A2 (zeitliche Abhängigkeiten) und A3, A4 (Beziehungen zwischen den Variablen) ein. Die kausale Natur des 2D-SSM schränkt den Informationstransfer entlang der Merkmalsachse ein; daher verwendet Chimera zwei Module, um die Abhängigkeiten mit vorhergehenden und nachfolgenden Merkmalen der analysierten Umgebung zu analysieren.
Die Flexibilität des Chimera-Rahmens ermöglicht die Verwendung der Parameter Bi, Ci, und Δi entweder als datenunabhängige Konstanten oder als Funktionen der Eingabedaten. Die Verwendung von kontextabhängigen Parametern macht das Modell anpassungsfähiger an die Bedingungen komplexer mehrdimensionaler Systeme.
Der Rahmen verwendet einen Stapel von 2D-SSMs mit nichtlinearen Transformationen zwischen den Schichten und nähert sich damit der Architektur von Deep Models an. Sie ermöglicht die Zerlegung von Zeitreihen in Trend- und saisonale Komponenten und bietet eine genaue Musteranalyse.
Nachfolgend sehen Sie die Visualisierung des Chimera-Rahmens durch die Autoren.
Im praktischen Teil des Artikels haben wir eine Architektur entwickelt, um die eigenen Vorstellungen der Autoren von den vorgeschlagenen Ansätzen mit Hilfe von MQL5 umzusetzen, und mit der Arbeit an deren Implementierung begonnen. Wir haben Änderungen am OpenCL-Programm untersucht. Wir haben die Struktur des 2D-SSM-Objekts entwickelt und seine Initialisierungsmethode vorgestellt. Heute arbeiten wir weiter an Algorithmen, um die vorgeschlagenen Ansätze in unsere eigenen Modelle zu integrieren.
2D-SSM Objekt
Zum Abschluss des vorangegangenen Artikels haben wir die Initialisierungsmethode des Objekts CNeuron2DSSMOCL untersucht, in dem wir die Funktionalität für die Konstruktion und das Training eines 2D-SSM implementieren wollen. Die Struktur dieses Objekts wird im Folgenden dargestellt.
class CNeuron2DSSMOCL : public CNeuronBaseOCL { protected: uint iWindowOut; uint iUnitsOut; CNeuronBaseOCL cHiddenStates; CLayer cProjectionX_Time; CLayer cProjectionX_Variable; CNeuronConvOCL cA; CNeuronConvOCL cB_Time; CNeuronConvOCL cB_Variable; CNeuronConvOCL cC_Time; CNeuronConvOCL cC_Variable; CNeuronConvOCL cDelta_Time; CNeuronConvOCL cDelta_Variable; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool feedForwardSSM2D(void); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradientsSSM2D(void); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuron2DSSMOCL(void) {}; ~CNeuron2DSSMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuron2DSSMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool Clear(void) override; };
Heute setzen wir diese Arbeit fort. Zunächst betrachten wir den Algorithmus für die Konstruktion der Methode für den Vorwärtsdurchlauf dieses Objekts: feedForward.
bool CNeuron2DSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *x_time = NULL; CNeuronBaseOCL *x_var = NULL;
In den Methodenparametern übergeben wir einen Zeiger auf das Eingabedatenobjekt, das wir sofort in einer lokalen Variablen speichern. Hier deklarieren wir auch zwei zusätzliche lokale Variablen, um Zeiger auf die Projektionsobjekte der Eingabedaten im Kontext von Zeit und Merkmalen zu speichern. In diesem Stadium müssen wir diese Projektionen noch erstellen.
Zur Bildung dieser Projektionen haben wir in der Initialisierungsmethode zwei interne Sequenzen erstellt und Zeiger auf ihre Objekte in den dynamischen Arrays cProjectionX_Time und cProjectionX_Variable gespeichert. Wir können sie nun verwenden, um die erforderlichen Hochrechnungen zu erhalten.
Zunächst wird die Projektion im zeitlichen Kontext erstellt. Wir haben den Zeiger auf das Eingabedatenobjekt bereits in einer lokalen Variablen gespeichert. Als Nächstes erstellen wir eine Schleife, die nacheinander die Objekte des Projektionsmodells im zeitlichen Kontext durchläuft.
//--- Projection Time int total = cProjectionX_Time.Total(); for(int i = 0; i < total; i++) { x_time = cProjectionX_Time.At(i); if(!x_time || !x_time.FeedForward(inp)) return false; inp = x_time; }
Innerhalb des Hauptteils der Schleife erhalten wir zunächst einen Zeiger auf das nächste Objekt in der Sequenz. Wir überprüfen die Gültigkeit des erhaltenen Zeigers. Nach erfolgreicher Übergabe dieses Kontrollpunkts rufen wir die Methode für den Vorwärtsdurchlauf des Objekts auf und übergeben ihm den Zeiger auf das Eingabedatenobjekt.
Anschließend speichern wir den Zeiger auf das aktuelle Objekt in der lokalen Variablen, die die Eingabedaten darstellt, und fahren mit der nächsten Iteration der Schleife fort.
Nach Abschluss aller Schleifeniterationen enthält die lokale Variable, die die Projektion der Eingabedaten in den zeitlichen Kontext enthält, einen Zeiger auf das letzte Objekt in der entsprechenden Sequenz. Der Puffer dieses Objekts enthält die Projektion, die wir benötigen.
Auf ähnliche Weise erhalten wir die Projektion der Eingabedaten in den Merkmalskontext.
//--- Projection Variable inp = NeuronOCL; total = cProjectionX_Variable.Total(); for(int i = 0; i < total; i++) { x_var = cProjectionX_Variable.At(i); if(!x_var || !x_var.FeedForward(inp)) return false; inp = x_var; }
Um die vier Projektionen der beiden verborgenen Zustände zu erhalten, genügt es, eine einzige Vorwärtspassagemethode der entsprechenden Projektionsobjekte aufzurufen. In seinen Parametern übergeben wir einen Zeiger auf das Objekt, das den verketteten Tensor der verborgenen Zustände enthält.
if(!cA.FeedForward(cHiddenStates.AsObject())) return false;
Die übrigen Parameter unseres 2D-SSM sind kontextabhängig. Daher werden als nächstes die Modellparameter auf der Grundlage der entsprechenden Projektionen der Eingabedaten erstellt. Zu diesem Zweck werden die Objekte zur Erzeugung von Modellparametern nacheinander durchlaufen und ihre Methoden für den Vorwärtsdurchlauf aufgerufen, wobei Zeiger auf die entsprechenden Objekte zur Projektion der Eingabedaten übergeben werden.
if(!cB_Time.FeedForward(x_time) || !cB_Variable.FeedForward(x_var)) return false; if(!cC_Time.FeedForward(x_time) || !cC_Variable.FeedForward(x_var)) return false; if(!cDelta_Time.FeedForward(x_time) || !cDelta_Variable.FeedForward(x_var)) return false;
In diesem Stadium haben wir die Vorbereitung der Parameter des zweidimensionalen Zustandsraummodells abgeschlossen. Wir müssen lediglich neue Werte für den verborgenen Zustand und die Modellausgaben erzeugen. Wie Sie wissen, wurden diese Prozesse im vorherigen Artikel in einen separaten Kernel verschoben, der auf der Seite vonOpenCL erstellt wurde. Jetzt genügt es, die Wrapper-Methode für diesen Kernel aufzurufen. Zuvor ist jedoch zu beachten, dass die Erzeugung eines neuen verborgenen Zustands die aktuellen Werte überschreibt, die wir für die Rückwärtsdurchlauf benötigen. Daher tauschen wir zunächst die Zeiger auf die Datenpufferobjekte aus und rufen dann die Wrapper-Methode feedForwardSSM2D auf.
if(!cHiddenStates.SwapOutputs()) return false; //--- return feedForwardSSM2D(); }
Der nächste Schritt unserer Arbeit ist die Entwicklung der Algorithmen für den Rückwärtsdurchlauf unseres Objekts. Schauen wir uns die Methode für die Fehlergradientenverteilung calcInputGradients an. In den Parametern dieser Methode erhalten wir einen Zeiger auf dasselbe Eingabedatenobjekt, aber dieses Mal müssen wir ihm den Fehlergradienten übergeben, der dem Einfluss der Eingabedaten auf das Gesamtergebnis des Modells entspricht.
bool CNeuron2DSSMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Die Datenübertragung ist nur möglich, wenn ein gültiger Zeiger auf das Objekt vorhanden ist. Daher besteht der erste Schritt des Algorithmus darin, den empfangenen Zeiger zu überprüfen, was dazu beiträgt, den Zugriff auf freigegebene oder nicht initialisierte Ressourcen zu verhindern. Dieser Ansatz ist von entscheidender Bedeutung, um die Stabilität des Rechenprozesses zu gewährleisten und Ausfälle bei der Datenverarbeitung zu verhindern.
Nach erfolgreichem Durchlaufen des Kontrollblocks beginnen die Operationen zur Verteilung des Fehlergradienten. Dieser Prozess wird von der Ebene der Ausgangsergebnisse des Modells zu den Eingangsdaten durchgeführt, wobei der Mechanismus des Rückwärtsdurchlaufs in Übereinstimmung mit dem Datenfluss des Vorwärtsdurchlaufs, jedoch in umgekehrter Reihenfolge, angewendet wird.
Wir haben die Methode des Vorwärtsdurchlaufs abgeschlossen, indem wir die Wrapper-Methode des Kernels aufgerufen haben, die versteckte Zustände erzeugt und die Ausgaben des 2D-SSM berechnet. Dementsprechend beginnt der Prozess der Fehlergradientenfortpflanzung mit dem Aufruf einer ähnlichen Wrapper-Methode, allerdings für den Kernel, der die Fehlerverteilung durchführt. Innerhalb dieses Kerns wird der Gradient korrekt auf die Elemente des 2D-SSM verteilt, und zwar entsprechend ihrem Beitrag zur Bildung des Modellergebnisses.
if(!calcInputGradientsSSM2D()) return false;
Es ist wichtig zu beachten, dass in diesem Stadium nur die Verteilung der Gradientenwerte auf die Strukturkomponenten des Modells vorgenommen wird. Eine direkte Anpassung der Werte durch die Ableitungen der Aktivierungsfunktionen der Objekte wird in diesem Kernel jedoch nicht vorgenommen. Bevor der Fehlergradient durch die internen Objekte des Modells propagiert wird, ist daher zu prüfen, ob diese Objekte Aktivierungsfunktionen enthalten. Falls erforderlich, sollte eine entsprechende Korrektur vorgenommen werden, um den Einfluss nichtlinearer Transformationen auf die propagierten Gradienten zu berücksichtigen. Dadurch wird sichergestellt, dass jeder Modellparameter unter Berücksichtigung seines tatsächlichen Beitrags zur Bildung des Ausgangssignals aktualisiert wird.
//--- Deactivation CNeuronBaseOCL *x_time = cProjectionX_Time[-1]; CNeuronBaseOCL *x_var = cProjectionX_Variable[-1]; if(!x_time || !x_var) return false; if(x_time.Activation() != None) if(!DeActivation(x_time.getOutput(), x_time.getGradient(), x_time.getGradient(), x_time.Activation())) return false; if(x_var.Activation() != None) if(!DeActivation(x_var.getOutput(), x_var.getGradient(), x_var.getGradient(), x_var.Activation())) return false; if(cB_Time.Activation() != None) if(!DeActivation(cB_Time.getOutput(), cB_Time.getGradient(), cB_Time.getGradient(), cB_Time.Activation())) return false; if(cB_Variable.Activation() != None) if(!DeActivation(cB_Variable.getOutput(), cB_Variable.getGradient(), cB_Variable.getGradient(), cB_Variable.Activation())) return false; if(cC_Time.Activation() != None) if(!DeActivation(cC_Time.getOutput(), cC_Time.getGradient(), cC_Time.getGradient(), cC_Time.Activation())) return false; if(cC_Variable.Activation() != None) if(!DeActivation(cC_Variable.getOutput(), cC_Variable.getGradient(), cC_Variable.getGradient(), cC_Variable.Activation())) return false; if(cDelta_Time.Activation() != None) if(!DeActivation(cDelta_Time.getOutput(), cDelta_Time.getGradient(), cDelta_Time.getGradient(), cDelta_Time.Activation())) return false; if(cDelta_Variable.Activation() != None) if(!DeActivation(cDelta_Variable.getOutput(), cDelta_Variable.getGradient(), cDelta_Variable.getGradient(), cDelta_Variable.Activation())) return false; if(cA.Activation() != None) if(!DeActivation(cA.getOutput(), cA.getGradient(), cA.getGradient(), cA.Activation())) return false;
Als Nächstes fahren wir mit dem Prozess der Verteilung von Fehlergradienten durch die internen Objekte unseres 2D-SSM fort. Zunächst müssen wir die Gradientenwerte durch die Objekte weitergeben, die für die Generierung der kontextabhängigen Modellparameter verantwortlich sind. Ich möchte Sie daran erinnern, dass diese Parameter auf der Grundlage der entsprechenden Projektionen der Eingangsdaten gebildet werden.
Hier ist es wichtig zu beachten, dass die Projektionsobjekte der Eingabedaten bereits am Hauptprozess der Bildung der Ausgabe des Modells beteiligt sind und während der vorangegangenen Operationen Fehlergradientenwerte erhalten haben. Um die zuvor ermittelten Werte zu erhalten, tauschen wir die Zeiger auf die entsprechenden Datenpuffer aus.
//--- Gradient to projections X CBufferFloat *grad_x_time = x_time.getGradient(); CBufferFloat *grad_x_var = x_var.getGradient(); if(!x_time.SetGradient(x_time.getPrevOutput(), false) || !x_var.SetGradient(x_var.getPrevOutput(), false)) return false;
Anschließend wird der Fehlergradient sequentiell durch die Objekte propagiert, die die kontextabhängigen Parameter bilden, und in jeder Phase werden die resultierenden Werte mit den zuvor gespeicherten Werten akkumuliert.
//--- B -> X if(!x_time.calcHiddenGradients(cB_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cB_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
//--- C -> X if(!x_time.calcHiddenGradients(cC_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cC_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
//--- Delta -> X if(!x_time.calcHiddenGradients(cDelta_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cDelta_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
Nachdem die Fehlergradienten von allen Informationsflüssen erfolgreich propagiert wurden, stellen wir die Objektzeiger auf ihren ursprünglichen Zustand zurück.
if(!x_time.SetGradient(grad_x_time, false) || !x_var.SetGradient(grad_x_var, false)) return false;
In diesem Stadium haben wir die Werte des Fehlergradienten auf der Ebene der Projektionen der Eingabedaten in beiden Kontexten erhalten. Als Nächstes müssen wir die Gradienten durch die entsprechenden internen Projektionsmodelle propagieren. Dazu legen wir Schleifen an, die rückwärts über die Objekte der entsprechenden Sequenzen iterieren.
//--- Projection Variable int total = cProjectionX_Variable.Total() - 2; for(int i = total; i >= 0; i--) { x_var = cProjectionX_Variable[i]; if(!x_var || !x_var.calcHiddenGradients(cProjectionX_Variable[i + 1])) return false; }
//--- Projection Time total = cProjectionX_Time.Total() - 2; for(int i = total; i >= 0; i--) { x_time = cProjectionX_Time[i]; if(!x_time || !x_time.calcHiddenGradients(cProjectionX_Time[i + 1])) return false; }
Beachten Sie, dass wir bei der Ausbreitung des Fehlergradienten durch die internen Modelle der kontextuellen Projektionen bei der ersten Schicht jeder Sequenz anhalten. Es sollte betont werden, dass unsere beiden Projektionssequenzen ihre Werte auf der Grundlage der Eingabedaten generieren, die wir als Methodenparameter von dem externen Programm erhalten. Nun müssen wir den Fehlergradienten von beiden internen Projektionsmodellen an das Eingabedatenobjekt übergeben.
Wie in solchen Fällen üblich, propagieren wir den Fehlergradienten zunächst durch einen Informationsfluss.
//--- Projections -> inputs if(!NeuronOCL.calcHiddenGradients(x_var.AsObject())) return false;
Dann tauschen wir die Zeiger auf die Objekte des Gradientenpuffers aus und verbreiten die Fehler über den zweiten Informationsfluss.
grad_x_time = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(x_time.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(x_time.AsObject()) || !SumAndNormilize(grad_x_time, NeuronOCL.getGradient(), grad_x_time, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(grad_x_time, false)) return false; //--- return true; }
Schließlich werden die Werte beider Informationsflüsse summiert und die Datenpufferzeiger in ihren ursprünglichen Zustand zurückversetzt.
Es ist zu beachten, dass wir den Fehlergradienten nicht auf das verborgene Zustandsobjekt übertragen, da dieses Objekt nur zur Datenspeicherung verwendet wird und keine trainierbaren Parameter enthält.
Nachdem wir nun die Fehlergradientenwerte auf alle internen Objekte verteilt haben, müssen wir nur noch das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurückgeben und die Ausführung der Methode abschließen.
Damit schließen wir unsere Untersuchung der Algorithmen ab, die zur Konstruktion der Methoden des Objekts CNeuron2DSSMOCL verwendet werden. Der vollständige Code dieses Objekts und alle seine Methoden werden im Anhang zur weiteren Untersuchung bereitgestellt.
Das Chimera-Modul
Der nächste Schritt unserer Arbeit ist der Bau des Chimera-Moduls. Die Autoren des Frameworks schlagen vor, zwei parallele 2D-SSMs mit unterschiedlichen Diskretisierungsstufen und Restverbindungen zu verwenden. Die Kombination von zwei unabhängigen Zustandsraummodellen, die auf unterschiedlichen Diskretisierungsebenen arbeiten, ermöglicht eine tiefere Analyse von Abhängigkeiten und erlaubt die Konstruktion von hocheffizienten Vorhersagemodellen, die an multiskalige Daten angepasst sind.
Die Verwendung von 2D-SSMs mit unterschiedlichen Diskretisierungsparametern ermöglicht eine differenzierte Analyse von Zeitreihen. Das Hochfrequenzmodell erfasst langfristige Muster, während sich das Niederfrequenzmodell auf die Identifizierung saisonaler Zyklen konzentriert. Diese Trennung verbessert die Vorhersagegenauigkeit, da sich jedes Modell an seinen eigenen Teil der Daten anpasst und Informationsverluste und Fehler, die durch übermäßige Aggregation zeitlicher Merkmale entstehen, minimiert werden. Die Hinzunahme eines Diskretisierungsmoduls ermöglicht es, die Ergebnisse der beiden Modelle in eine vergleichbare Form zu bringen.
Ein weiterer Vorteil des Chimera-Moduls ist die Verwendung von Restverbindungen, die eine effiziente Informationsübertragung zwischen den Modellebenen gewährleisten. Sie ermöglichen es, dass Gradienten während des Rückwärtsdurchlauf erhalten bleiben und weitergegeben werden, wodurch ein Verschwinden des Gradienten verhindert wird. Dies ist besonders wichtig beim Training tiefer Modelle, bei denen der Gradientenabstieg oft Probleme mit der numerischen Stabilität verursacht. Das Modell wird robuster gegenüber Informationsverlusten während der Datenübertragung zwischen den Schichten, und der Trainingsprozess wird stabiler, selbst wenn mit langen Zeitreihen gearbeitet wird.
Wir implementieren den vorgeschlagenen Mechanismus in das Objekt CNeuronChimera; seine Struktur wird im Folgenden vorgestellt.
class CNeuronChimera : public CNeuronBaseOCL { protected: CNeuron2DSSMOCL caSSM[2]; CNeuronConvOCL cDiscretization; CLayer cResidual; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronChimera(void) {}; ~CNeuronChimera(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronChimera; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool Clear(void) override; };
In der vorgestellten Struktur sehen wir eine vertraute Reihe von überschriebenen Methoden und mehrere interne Objekte, deren Funktionalität sich leicht aus ihren Namen erschließen lässt.
Alle internen Objekte werden statisch deklariert, sodass der Konstruktor und der Destruktor der Klasse leer bleiben können. Die Initialisierung aller Objekte wird in der Methode Init durchgeführt.
bool CNeuronChimera::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_out * window_out, optimization_type, batch)) return false; SetActivationFunction(None);
In den Methodenparametern erhalten wir eine Reihe von Konstanten, die die Architektur des zu erstellenden Objekts eindeutig definieren. Es sei darauf hingewiesen, dass die Liste der Parameter vollständig von der analogen Methode des zuvor beschriebenen ObjektsCNeuron2DSSMOCL übernommen wird und die Architektur eines der internen 2D-SSMs spezifiziert.
Wie üblich beginnt der Initialisierungsalgorithmus mit einem Aufruf der Methode der übergeordneten Klasse. In diesem Fall handelt es sich um die Basisschicht, die vollständig verbunden ist.
Als Nächstes fahren wir mit der Initialisierung der internen Objekte fort. Wie bereits erwähnt, verwenden wir zwei zweidimensionale Zustandsraummodelle mit unterschiedlichen Detaillierungsgraden. In der Objektstruktur werden die internen Modelle als Array caSSM dargestellt. Um die Objekte dieses Arrays zu initialisieren, organisieren wir eine Schleife.
int index = 0; for(int i = 0; i < 2; i++) { if(!caSSM[i].Init(0, index, OpenCL, window_in, (i + 1)*window_out, units_in, units_out, optimization, iBatch)) return false; index++; }
Das erste Zustandsraummodell wird mit den vom externen Programm erhaltenen Parametern initialisiert. Das zweite Modell erhält eine doppelte Dimensionalität des Merkmalsraums für die Ausgabeergebnisse, wodurch es komplexere Abhängigkeiten erfassen kann. Da beide Modelle mit einem gemeinsamen Satz von Eingabedaten arbeiten, bleiben die wichtigsten Konfigurationsparameter unverändert, wodurch die Integrität und Konsistenz der Struktur gewährleistet wird.
Als Nächstes initialisieren wir die zusätzliche Diskretisierungsschicht, die eine Projektion der Ergebnisse des zweiten Modells in den Unterraum des ersten Modells erzeugt. Dies ist eine Standard-Faltungsschicht, die den Merkmalsraum auf die angegebene Größe reduziert.
if(!cDiscretization.Init(0, index, OpenCL, 2 * window_out, 2 * window_out, window_out, units_out, 1, optimization, iBatch)) return false; cDiscretization.SetActivationFunction(None);
Um Datenverluste zu vermeiden, deaktivieren wir die Aktivierungsfunktion für dieses Objekt.
Nach der Initialisierung der Informationsflussobjekte für die beiden Zustandsraummodelle fahren wir mit der Organisation der restlichen Verbindungen fort. In diesem Stadium ergibt sich ein Problem bei der Summierung von Tensoren, die sich in ihrer Größe entlang einer oder mehrerer Achsen unterscheiden können. Um dieses Problem zu lösen, müssen die Eingabedaten zunächst in den angegebenen Ergebnisunterraum projiziert werden. Zu diesem Zweck wird ein internes Datenprojektionsmodell erstellt, ähnlich wie bei den zuvor besprochenen kontextuellen Projektionsmodellen. Dieser Ansatz ermöglicht eine korrekte Ausrichtung der Datendimensionen, wodurch die Stabilität der Architektur und die genaue Verarbeitung der zeitlichen Abhängigkeiten gewährleistet werden.
Zunächst bereiten wir ein dynamisches Array vor, um Zeiger auf die Modellobjekte zu speichern, und deklarieren lokale Variablen für die vorübergehende Speicherung dieser Zeiger.
//--- Residual cResidual.Clear(); cResidual.SetOpenCL(OpenCL); CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL;
Wir erstellen ein Objekt zur Datentransposition, gefolgt von einer Faltungsschicht, die Einheitssequenzen in die angegebene Zeitreihendimensionalität projiziert.
transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) || !cResidual.Add(transp)) { delete transp; return false; } index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, units_in, units_in, units_out, window_in, 1, optimization, iBatch) || !cResidual.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Dieser Ansatz ermöglicht es uns, strukturelle Abhängigkeiten innerhalb einzelner Einheitsfolgen der analysierten multivariaten Zeitreihen zu erhalten.
Daran schließt sich ein weiterer Block an, der aus einem Transpositionsobjekt und einer Faltungsschicht besteht, die eine Projektion der Eingabedaten entlang der Merkmalsachse vornehmen.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, window_in, units_out, optimization, iBatch) || !cResidual.Add(transp)) { delete transp; return false; } index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, window_in, window_in, window_out, units_out, 1, optimization, iBatch) || !cResidual.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Man beachte, dass beide Faltungsschichten keine Aktivierungsfunktionen verwenden, was eine Projektion der Eingabedaten mit minimalem Informationsverlust ermöglicht.
Am Ausgang des Objekts wollen wir drei Informationsflüsse zusammenfassen. Wie in solchen Fällen üblich, propagieren wir den Fehlergradienten in vollem Umfang entlang aller Zweige. Um unnötige Datenkopiervorgänge zu vermeiden, synchronisieren wir Zeiger auf die Puffer für die Fehlergradienten. Es ist jedoch erwähnenswert, dass die für die Datenprojektion verwendeten Faltungsschichten Aktivierungsfunktionen enthalten können. In diesem speziellen Fall haben wir sie natürlich nicht verwendet und hätten diesen Aspekt ignorieren können. Aber um eine universellere Lösung zu schaffen, dürfen wir sie nicht übersehen. Daher wird der Fehlergradient erst an die Faltungsschichten weitergegeben, nachdem er durch die Ableitung der aktiven Aktivierungsfunktion korrigiert wurde.
if(!SetGradient(caSSM[0].getGradient(), true)) return false; //--- return true; }
Schließlich geben wir ein boolesches Ergebnis an das aufrufende Programm zurück und schließen die Initialisierungsmethode ab.
Sobald die Initialisierung abgeschlossen ist, wird der Algorithmus für den Vorwärtsdurchlauf in der Methode feedForward implementiert.
bool CNeuronChimera::feedForward(CNeuronBaseOCL *NeuronOCL) { for(uint i = 0; i < caSSM.Size(); i++) { if(!caSSM[i].FeedForward(NeuronOCL)) return false; }
Der Algorithmus des Vorwärtsdurchlaufs ist recht einfach. In den Methodenparametern übergeben wir einen Zeiger auf das Eingabedatenobjekt, das wir an die internen Zustandsraummodelle übergeben. Zu diesem Zweck organisieren wir eine Schleife, die über die internen 2D-SSMs iteriert und nacheinander deren Methoden für die Vorwärtsdurchläufe aufruft.
Nach Abschluss aller Schleifeniterationen projizieren wir die erhaltenen Ergebnisse in eine vergleichbare Form.
if(!cDiscretization.FeedForward(caSSM[1].AsObject())) return false;
Als Nächstes müssen wir eine Projektion der Eingabedaten in den Ergebnisunterraum erhalten. Zu diesem Zweck organisieren wir eine Schleife, die sequentiell über die Objekte des internen Projektionsmodells iteriert und dabei die Methoden für die Vorwärtsdurchläufe der entsprechenden Objekte aufruft.
CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *current = NULL; for(int i = 0; i < cResidual.Total(); i++) { current = cResidual[i]; if(!current || !current.FeedForward(inp)) return false; inp = current; }
Schließlich werden die Ergebnisse der drei Informationsflüsse summiert und die Daten anschließend normalisiert.
if(!SumAndNormilize(caSSM[0].getOutput(), cDiscretization.getOutput(), Output, 1, false, 0, 0, 0, 1) || !SumAndNormilize(Output, current.getOutput(), Output, cDiscretization.GetFilters(), true, 0, 0, 0, 1)) return false; //--- return true; }
Danach geben wir das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurück und schließen die Ausführung der Methode ab.
Hinter der scheinbaren Einfachheit des Algorithmus für den Vorwärtsdurchlauf verbirgt sich jedoch die Verwendung von drei Informationsflüssen, was zu einer gewissen Komplexität bei der Organisation des Prozesses der Fehlergradientenverteilung führt. Dieser Prozess ist in der Methode calcInputGradients implementiert.
bool CNeuronChimera::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
In den Methodenparametern übergeben wir einen Zeiger auf das Eingabedatenobjekt, in das wir nun den Fehlergradienten entsprechend seinem Einfluss auf das Endergebnis des Modells übergeben müssen. Und im Hauptteil der Methode prüfen wir sofort die Relevanz des empfangenen Zeigers. Die Notwendigkeit einer solchen Validierung wurde bereits erörtert.
Als Nächstes korrigieren wir den Fehlergradienten, den wir von den nachfolgenden Objekten erhalten, durch die Aktivierungsfunktion der Projektionsschicht des zweiten 2D-SSM und übertragen ihn auf die Ebene dieses Modells.
if(!DeActivation(cDiscretization.getOutput(), cDiscretization.getGradient(), Gradient, cDiscretization.Activation())) return false; if(!caSSM[1].calcHiddenGradients(cDiscretization.AsObject())) return false;
In ähnlicher Weise passen wir den Fehlergradienten durch die Ableitung der Aktivierungsfunktion der letzten Schicht des internen Eingangsdaten-Projektionsmodells an und propagieren ihn sequentiell durch die Objekte dieser Sequenz.
CNeuronBaseOCL *residual = cResidual[-1]; if(!residual) return false; if(!DeActivation(residual.getOutput(), residual.getGradient(), Gradient, residual.Activation())) return false; for(int i = cResidual.Total() - 2; i >= 0; i--) { residual = cResidual[i]; if(!residual || !residual.calcHiddenGradients(cResidual[i + 1])) return false; }
In diesem Stadium erreichen wir den Schritt, den Fehlergradienten entlang aller drei Zweige an die Eingangsdatenebene weiterzugeben. Bei der Gradientenfortpflanzung werden die zuvor gespeicherten Werte überschrieben. Glücklicherweise haben wir bereits gelernt, wie wir mit diesem Problem umgehen können. Zunächst propagieren wir den Fehlergradienten von einem Zustandsraummodell.
if(!NeuronOCL.calcHiddenGradients(caSSM[0].AsObject())) return false;
Dann tauschen wir den Datenpufferzeiger aus und propagieren den Fehlergradienten entlang des zweiten Zweigs, gefolgt von der Summierung der Daten aus den beiden Informationsflüssen.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(residual.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(caSSM[1].AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1)) return false;
Auf die gleiche Weise fügen wir die Werte des dritten Informationsflusses hinzu.
if(!NeuronOCL.calcHiddenGradients((CObject*)residual) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false) ) return false; //--- return true; }
Erst nach der Summierung der Daten aus allen Informationsflüssen werden die Objektzeiger wieder in ihren ursprünglichen Zustand versetzt.
Wir geben das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurück und schließen die Ausführung der Methode ab.
Damit schließen wir die Analyse der Algorithmen zur Implementierung des Chimera-Rahmens mit MQL5 ab. Der vollständige Code für die vorgestellten Objekte und alle ihre Methoden ist im Anhang verfügbar.
Modell der Architektur
In den vorangegangenen Abschnitten haben wir umfangreiche Arbeit geleistet, um die von den Autoren des Chimera-Rahmenwerks vorgeschlagenen Methoden mit MQL5 zu implementieren. Die Autoren des Frameworks empfehlen jedoch die Verwendung einer Architektur, die aus einem Stapel solcher Objekte besteht, zwischen denen Nichtlinearitäten organisiert sind. Die Verwendung einer solchen Architektur trägt dazu bei, ein flexibles und anpassungsfähiges System zu schaffen, das in der Lage ist, dynamisch auf Änderungen der Betriebsbedingungen zu reagieren. Daher werden wir kurz auf die Architektur der trainierbaren Modelle eingehen.
Vorab sei gesagt, dass wir im Rahmen dieses Experiments die Chimera-Ansätze in einem Multitasking-Lernsystem implementiert haben.
Die Architektur der trainierten Modelle wird in der Methode CreateDescriptions definiert.
bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
In den Methodenparametern erhalten wir Zeiger auf zwei dynamische Arrays, in denen wir Beschreibungen der Modellarchitekturen speichern müssen. Im Hauptteil der Methode prüfen wir die Relevanz der erhaltenen Zeiger und erstellen gegebenenfalls neue Instanzen von Objekten.
Zunächst beschreiben wir die Architektur des Akteurs, die auch den Zustands-Encoder-Block der Umgebung umfasst. Für die Modelleingabe planen wir, unbearbeitete Rohdaten zu verwenden, die den Zustand der Umwelt beschreiben. Diese Daten werden an eine vollständig verknüpfte Schicht von ausreichender Größe weitergeleitet.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Daran schließt sich eine Batch-Normalisierungsschicht an, in der die Eingangsdaten primär verarbeitet und in eine vergleichbare Form gebracht werden.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Die verarbeiteten Daten werden dann in das erste Chimera-Modul eingespeist, an dessen Ausgang wir eine mehrdimensionale zeitliche Sequenz erwarten, die aus 64 Elementen mit jeweils 16 Merkmalen besteht.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {BarDescr, 16}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {HistoryBars, 64}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Darauf folgt eine Faltungsschicht mit einer SoftPlus-Aktivierungsfunktion zur Einführung von Nichtlinearität.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = 64; descr.window = 16; descr.step = 16; descr.window_out = 16; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
In ähnlicher Weise fügen wir zwei weitere Chimera-Module hinzu, indem wir Nichtlinearitäten zwischen ihnen einfügen.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {16, 32}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {64, 32}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = 32; descr.window = 32; descr.step = 32; descr.window_out = 16; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {16, 32}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {32, 16}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Gleichzeitig reduzieren wir in Analogie zum ResNeXt-Rahmenwerk die Sequenzlänge und erhöhen proportional die Dimensionalität des Merkmalsraums.
Danach folgt der Entscheidungskopf, der aus drei aufeinander folgenden, vollständig verknüpften Schichten besteht.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 512; descr.batch = 1e4; descr.activation = TANH; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.activation = TANH; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = SoftPlus; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Die Ergebnisse ihrer Arbeit werden mit Hilfe einer Batch-Normalisierungsschicht normalisiert.
//--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Wie bei den zuvor besprochenen Modellen wird am Ausgang des Akteurs ein Risikomanagementmodul hinzugefügt.
//--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMacroHFTvsRiskManager; //--- Windows { int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = 10; descr.window_out = 16; descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 12 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Das Modell zur Schätzung der Wahrscheinlichkeit der Richtung der bevorstehenden Kursbewegung wurde nahezu unverändert aus dem vorherigen Artikel übernommen. Die Aktivierungsfunktionen in den verborgenen Schichten wurden nur geringfügig angepasst. Daher werden wir sie hier nicht im Detail untersuchen. Eine vollständige Beschreibung der Modellarchitekturen finden Sie im Anhang. Der komplette Code zum Trainieren und Testen der Modelle wird dort ebenfalls zur Verfügung gestellt und wurde ohne Änderungen aus der vorherigen Arbeit übernommen.
Tests
Nach Abschluss der Implementierung unserer eigenen Interpretation der von den Autoren des Chimera-Rahmens vorgeschlagenen Ansätze gehen wir zur letzten Phase unserer Arbeit über – dem Training und Testen der Modelle auf realen historischen Daten.
Zum Trainieren der Modelle haben wir einen Trainingsdatensatz verwendet, der beim Training der zuvor besprochenen Modelle gesammelt wurde. Dieser Trainingsdatensatz wurde mit historischen Daten des Währungspaares EURUSD für das gesamte Jahr 2024 auf dem Zeitrahmen M1 erstellt. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt. Eine ausführliche Beschreibung der Vorbereitung des Trainingsdatensatzes finden Sie unter diesem Link.
Das Testen der trainierten Modelle wurde im MetaTrader 5 Strategy Tester mit historischen Daten vom Januar 2025 durchgeführt, wobei die anderen Trainingsparameter unverändert blieben. Die Testergebnisse werden im Folgenden vorgestellt.
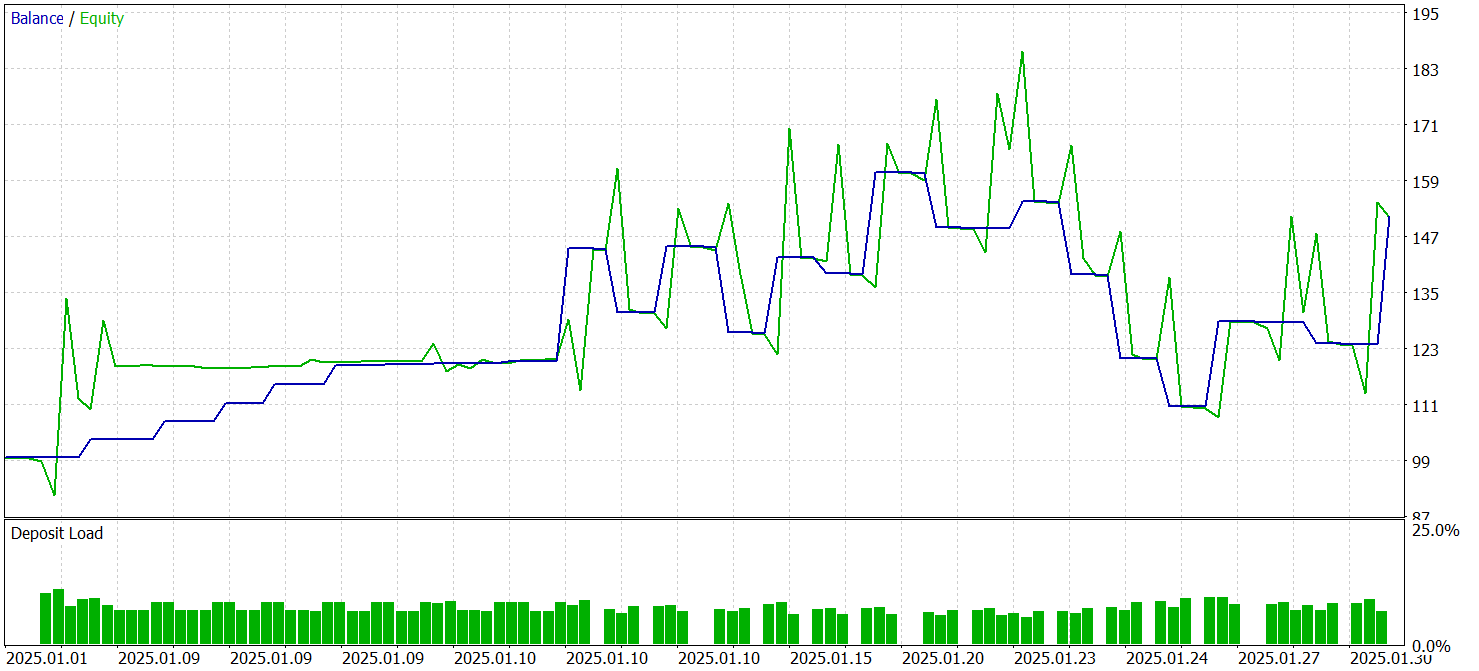
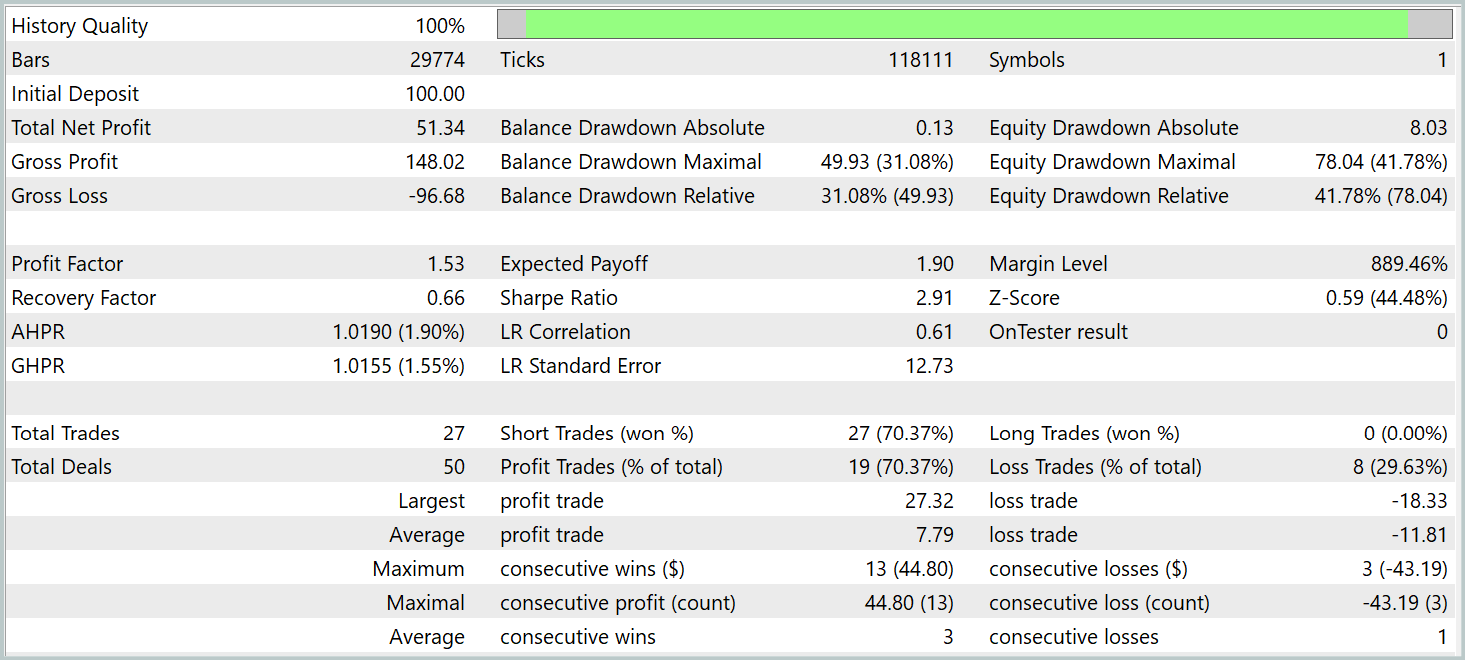
Den Testergebnissen zufolge war das Modell in der Lage, einen Gewinn zu erzielen. Mehr als 70 % der Handelsgeschäfte wurden mit einem Gewinn abgeschlossen. Der Gewinnfaktor wurde mit 1,53 angegeben.
Es sind jedoch einige Punkte zu beachten. Die Modelle wurden mit dem Zeitrahmen M1 getestet. Gleichzeitig führte das Modell nur 27 Handelsgeschäfte aus, was für den Hochfrequenzhandel auf dem minimalen Zeitrahmen recht wenig ist. Außerdem eröffnete das Modell nur Verkaufspositionen, was ebenfalls Fragen aufwirft.
Auch die Haltedauer der Position gibt Anlass zur Sorge. Die schnellste Position wurde sozusagen fast eine Stunde nach der Eröffnung geschlossen. Die durchschnittliche Haltezeit beträgt mehr als 14 Stunden. Und das, obwohl das Modell im Zeitrahmen M1 getestet wurde.
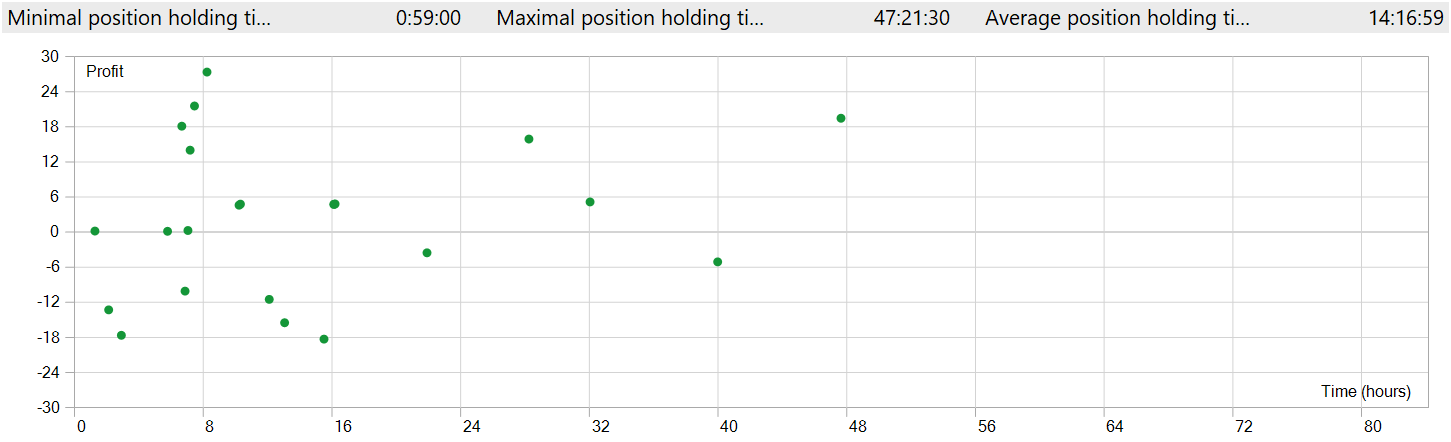
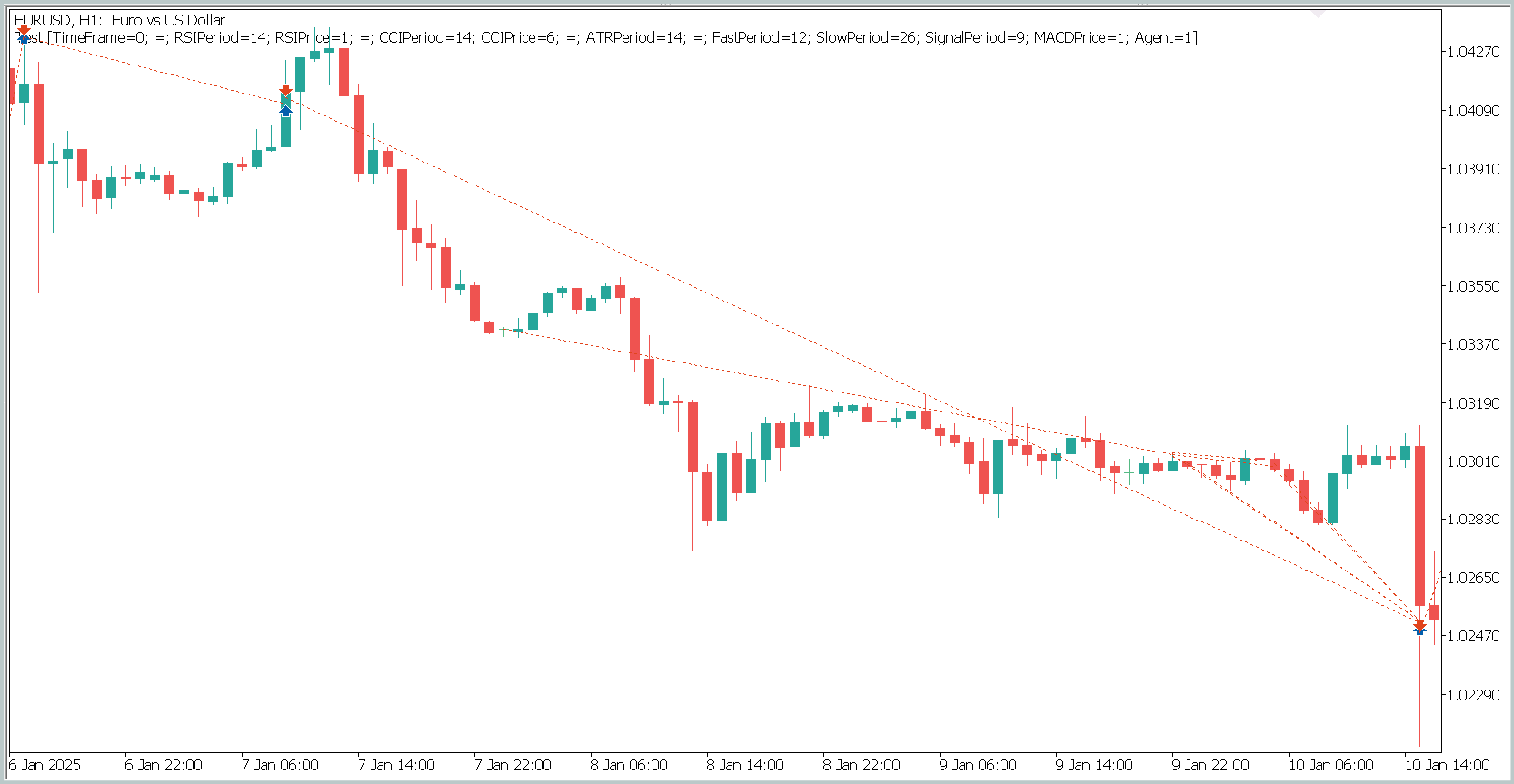
Um Positionseröffnungen und -schließungen in einem einzigen Chart-Fenster anzeigen zu können, war es notwendig, den Zeitrahmen zu vergrößern. In dieser Form kann man deutlich beobachten, dass der Handel in Richtung des globalen Trends verläuft. Dies steht natürlich nicht im Einklang mit dem Begriff des Hochfrequenzhandels auf dem Zeitrahmen M1. Es ist jedoch offensichtlich, dass das implementierte Modell in der Lage ist, langfristige Trends zu erfassen, während kurzfristige Schwankungen ignoriert werden.
Schlussfolgerung
In den letzten beiden Artikeln haben wir den Chimera-Rahmen betrachtet, der auf einem zweidimensionalen Zustandsraummodell basiert. Mit diesem Ansatz werden innovative Techniken zur Modellierung multivariater Zeitreihen eingeführt, die es ermöglichen, komplexe Beziehungen sowohl im zeitlichen Kontext als auch im Merkmalsraum zu berücksichtigen.
Im praktischen Teil unserer Arbeit haben wir unsere Interpretation der Rahmenansätze in MQL5 umgesetzt. Das konstruierte Modell wurde an realen historischen Daten trainiert und getestet. Die Testergebnisse fielen etwas unerwartet aus. Während des Testzeitraums war das Modell in der Lage, einen Gewinn zu erwirtschaften. Entgegen den Erwartungen beobachteten wir jedoch einen Handel in Richtung des globalen Trends mit langen Positionshaltezeiten, obwohl das Modell auf dem M1-Zeitrahmen getestet wurde.
Referenzen
- Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models
- Andere Artikel aus dieser Reihe
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor für die Probenahme |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für die Probenahme mit der Methode Real-ORL |
| 3 | Study.mq5 | Expert Advisor | Expert Advisor für das Training des Modells |
| 4 | Test.mq5 | Expert Advisor | Expert Advisor für den Modeltest |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Beschreibung des Systemzustands und der Modellarchitektur |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Code Base | OpenCL-Programmcode |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17241
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Indikator für die Stärke eines Währungspaares in reinem MQL5
Indikator für die Stärke eines Währungspaares in reinem MQL5
 Algorithmus der erfolgreichen Gastronomen (SRA)
Algorithmus der erfolgreichen Gastronomen (SRA)
 Eine alternative Log-datei mit der Verwendung der HTML und CSS
Eine alternative Log-datei mit der Verwendung der HTML und CSS
 Wie können jahrhundertealte Funktionen Ihre Handelsstrategien aktualisieren?
Wie können jahrhundertealte Funktionen Ihre Handelsstrategien aktualisieren?
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.