Neuronale Netze im Handel: Hybride Graphsequenzmodelle (letzter Teil)
Einführung
Im vorangegangenen Artikel haben wir die theoretischen Aspekte des einheitlichen Graphensequenzsystems GSM+ untersucht, einer innovativen Datenverarbeitungsmethode, die die Vorteile mehrerer architektonischer Lösungen kombiniert. GSM++ umfasst drei Schlüsselschritte: die Tokenisierung des Graphen, die Kodierung lokaler Knoten und die Kodierung globaler Abhängigkeiten. Diese Struktur erhöht die Effizienz bei der Arbeit mit graphenstrukturierten Daten und verbessert die analytischen Fähigkeiten für komplexe Aufgaben im Finanzwesen und in anderen Bereichen, die Zeitreihen und strukturierte Datenanalysen beinhalten.
Ein entscheidendes Element des Systems ist die hierarchische Graphen-Tokenisierung, die die Umwandlung komplexer Daten in eine kompakte sequentielle Darstellung ermöglicht. Die in GSM++ verwendete Tokenisierungsmethode bewahrt die topologischen und zeitlichen Merkmale der Originaldaten und verbessert die Genauigkeit der Merkmalsextraktion erheblich. Darüber hinaus trägt dieser Ansatz zur Senkung der Rechenkosten bei der Analyse großer Datensätze bei und bietet ein ausgewogenes Verhältnis zwischen Verarbeitungsgeschwindigkeit und Analysetiefe. Je nach Aufgabenstellung kann der Detaillierungsgrad der Analyse angepasst werden, was die Methodik vielseitig und flexibel macht.
Herkömmliche Analysemethoden stoßen häufig auf Informationsredundanz, was den Rechenaufwand erhöht und die Erkennung von Mustern erschwert. Die Verwendung adaptiver Kodierungsmechanismen ermöglicht jedoch die Extraktion der wichtigsten Knotenmerkmale und deren effiziente Weiterleitung an nachfolgende Analyseschichten. Dadurch wird die Menge an irrelevanten Informationen reduziert und die Fähigkeit des Modells, lokale Beziehungen zwischen Knoten zu erkennen, verbessert. Ein weiterer Vorteil der lokalen Kodierung ist ihre Fähigkeit, sich dynamisch an Änderungen der Quelldaten anzupassen, was besonders auf volatilen Finanzmärkten von Bedeutung ist, wo plötzliche Veränderungen die Prognosegenauigkeit erheblich beeinträchtigen können.
Die analytischen Fähigkeiten werden durch den Einsatz eines hybriden Encoders, der rekurrente Modelle und Transformer kombiniert, weiter verbessert. Dieser Ansatz nutzt die Stärken beider Methoden: Rekurrente Mechanismen verarbeiten Zeitreihen effizient, indem sie Ereignisfolgen erfassen, während Transformer mit Selbstaufmerksamkeits-Mechanismen komplexe, ordnungsunabhängige Abhängigkeiten effektiv identifizieren. Diese Kombination verbessert nicht nur die Modellgenauigkeit, sondern erhöht auch die Robustheit gegenüber der Marktdynamik. Darüber hinaus kann sich der hybride Encoder an verschiedene Szenarien anpassen und ermöglicht ein konfigurierbares Gleichgewicht zwischen Vorhersagegenauigkeit und Recheneffizienz je nach den spezifischen Anforderungen der Aufgabe.
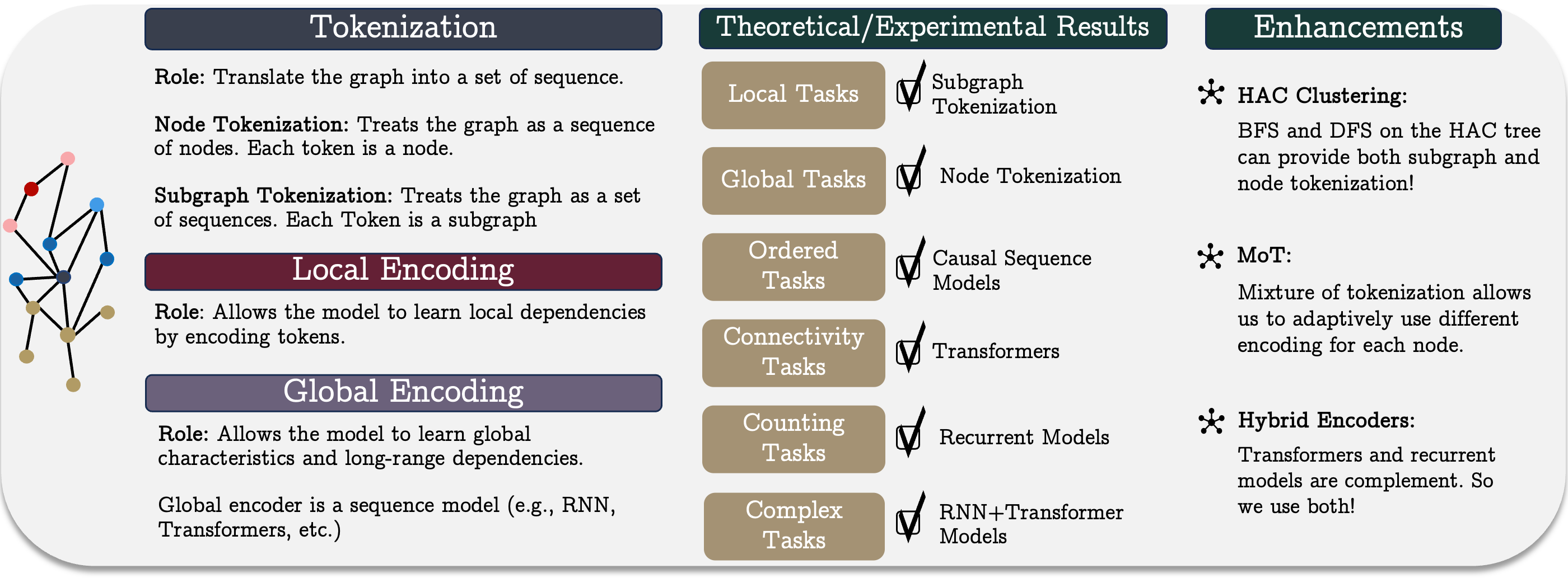
Im praktischen Teil des letzten Artikels haben wir begonnen, unsere eigene Interpretation des GSM++ mit MQL5 zu implementieren. In Anbetracht der hohen Volatilität von Finanzdaten haben wir uns entschieden, das von den Autoren vorgeschlagene hierarchische ähnlichkeitsbasierte Clustering (HAC) nicht zu verwenden. Stattdessen haben wir uns für ein trainierbares, gemischtes Tokenisierungsmodul entschieden, das die Flexibilität und Anpassungsfähigkeit des Modells bei der Arbeit mit realen Marktdaten deutlich erhöht.
Der implementierteMoT-Algorithmus (Mixture of Tokenization) verwendet vier verschiedene Token-Typen pro Balken, was eine detailliertere Marktdatenanalyse ermöglicht. Für dieses Experiment verwenden wir die folgenden Ansätze zur Kodierung der Quelldaten:
- Tokenisierung des Knoten – jeder Balken wird als separates Analyseelement behandelt, was die Bewertung seiner individuellen Merkmale und die Identifizierung von Schlüsselparametern ermöglicht, die die nachfolgenden Entwicklungen beeinflussen.
- Tokenisierung der Kanten – analysiert Abhängigkeiten zwischen benachbarten Balken und erkennt kurzfristige Korrelationen und Trends, die für die Vorhersage kurzfristiger Veränderungen nützlich sind.
- Tokenisierung des Subgraphs – untersucht Gruppen von Balken, um komplexere Strukturen und stabile Muster zu erkennen, die für strategische Prognosen wichtig sind.
- Tokenisierung einzelner einheitlicher Sequenzen im Subgraph – ermöglicht eine eingehende Analyse univariater Sequenzen und ihrer gegenseitigen Abhängigkeiten, was für die Aufdeckung versteckter Muster in den Daten von entscheidender Bedeutung ist.
Diese Token werden mit Hilfe des Systems von Attention-Pooling-Mechanismus kombiniert, der aus dem R-MAT. Diese Methode ermöglicht es dem Modell, sich auf die wichtigsten Merkmale zu konzentrieren und weniger relevante Daten zu vernachlässigen, was die Entscheidungsfindung erheblich verbessert. Der Hauptvorteil von Attention Pooling ist die Fähigkeit, komplexe Datenstrukturen effizient zu handhaben und dabei die wichtigsten Merkmale hervorzuheben, während die Auswirkungen des Rauschens minimiert werden.
Um diesen Ansatz umzusetzen, haben wir das Objekt CNeuronMoT, das die Basisfunktionalität von CNeuronMHAttentionPooling erbt, um eine effiziente Anwendung des Attention-Pooling-Algorithmus zu gewährleisten. Dieser modulare Aufbau erhöht die Anpassungsfähigkeit des Modells, verbessert die Verarbeitung von Marktdaten und steigert die Qualität der Preisbewegungsanalyse und -prognose, was es zu einem wertvollen Werkzeug für den algorithmischen Handel macht.
Die nächste Stufe der Datenverarbeitung ist die lokale Knotencodierung. In unserer Implementierung verwenden wir ein zuvor entwickeltes Modul zur adaptiven Merkmalsglättung. Node-Adaptive Feature Smoothing (NAFS) erzeugt informativere Knoteneinbettungen, indem es sowohl die Graphenstruktur als auch die individuellen Knotenmerkmale berücksichtigt. Bei diesem Ansatz wird davon ausgegangen, dass verschiedene Knotenpunkte unterschiedliche Glättungsstufen erfordern können. Dies ermöglicht eine adaptive Verarbeitung jedes Knotens im Kontext seiner Nachbarschaft. NAFS wendet einen kombinierten Glättungsansatz niedriger und hoher Ordnung an, der sowohl lokale als auch globale Abhängigkeiten innerhalb des Graphen effektiv erfasst.
NAFS verwendet eine Ensemble-Feature-Aggregationsmethode. Dieser Ansatz verbessert die Robustheit des Modells gegenüber Rauschen und die Zuverlässigkeit der Kodierung. Zu den wichtigsten Vorteilen des NAFS-Moduls gehören:
- Flexible Datenfilterung, die die wichtigsten Merkmale hervorhebt und Rauschen eliminiert.
- Optimierung des Rechenaufwands, der bei der Analyse großer Graphen und hochfrequenter Marktdaten entscheidend sind.
- Anpassungsfähigkeit an veränderte Bedingungen durch dynamische Anpassung der Glättungsparameter.
- Verbesserte Modellgenauigkeit durch eine ausgewogene Kombination aus detaillierter Analyse und hoher Generalisierungsfähigkeit.
Die letzte Kernkomponente von GSM++ ist der Hybrid-Encoder. Die Autoren des Frameworks schlagen eine Kombination aus dem Modul Mamba mit einem Transformer vor. In unserer Implementierung folgen wir diesem Konzept. Aber wir verfeinern es weiter, indem wir Mamba durch Chimäre und den Transformer durch Hidformer ersetzen.
Chimera verwendet zweidimensionale Zustandsraummodelle (2D-SSM), die Abhängigkeiten sowohl entlang der zeitlichen Achse als auch einer zusätzlichen Dimension, die mit der Graphentopologie zusammenhängt, effektiv modellieren. Dieser Ansatz erweitert die Möglichkeiten zur Analyse komplexer Marktbeziehungen erheblich. Zu den Vorteilen von Chimera gehören:
- Zweidimensionale Kodierung von Abhängigkeiten, die die Erkennung verborgener Marktmuster und die Vorhersagegenauigkeit verbessert.
- Erhöhte Modellaussagekraft, die eine tiefere Analyse komplexer nichtlinearer Vermögensbeziehungen ermöglicht.
- Anpassungsfähigkeit an dynamische Marktveränderungen, damit das Modell schnell auf sich verändernde Bedingungen reagieren kann.
Hidformer verfügt über eine Dual-Stream-Architektur, die im Gegensatz zum klassischen Transformer die Verarbeitung der Eingabedaten in zwei Pfade trennt: Ein Encoder analysiert zeitliche Abhängigkeiten, während der andere Frequenzkomponenten der Marktdaten verarbeitet. Diese Konstruktion ermöglicht eine genauere Modellierung der Marktdynamik. Die wichtigsten Vorteile von Hidformer sind:
- Trennung von Zeit- und Frequenzanalyse zur Verbesserung der Genauigkeit der Markttrendprognosen.
- Verwendung rekursiver Aufmerksamkeit im zeitlichen Kodierer und linearer Aufmerksamkeit im Frequenzkodierer, wodurch die Rechenkomplexität verringert und die Effizienz verbessert wird.
Die Integration von Chimera und Hidformer in GSM++ hat somit das Potenzial, eine hohe Genauigkeit bei der Kodierung von Abhängigkeiten zu erreichen, den Einfluss des Marktrauschens zu minimieren und die Zuverlässigkeit der analytischen Prognosen zu erhöhen.
Einstellung des SSM-Modul
Es ist erwähnenswert, dass bei der Prüfung des Modells, das mit Chimera erstellten, eine längere Verweildauer in der Position beobachtet wurde. Damals wurde die Hypothese aufgestellt, dass das Modell nur langfristige Trends erfasst und kurzfristige Schwankungen ignoriert. Um dieser Einschränkung zu begegnen, haben wir beschlossen, das zuvor implementierte Objekt leicht zu verändern und ein zusätzliches internes zweidimensionales Zustandsraummodell hinzuzufügen. Die aktualisierten Algorithmen sind im Objekt CNeuronChimeraPlus implementiert, dessen Struktur im Folgenden beschrieben wird.
class CNeuronChimeraPlus : public CNeuronChimera { protected: CNeuron2DSSMOCL cSSMPlus; CLayer cDiscretizationPlus; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronChimeraPlus(void) {}; ~CNeuronChimeraPlus(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronChimeraPlus; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool Clear(void) override; };
Wie aus der Struktur des neuen Objekts ersichtlich ist, haben wir das zuvor erstellteObjekt CNeuronChimera nicht vollständig umgeschrieben. Im Gegenteil, sie wurde als übergeordnete Klasse verwendet, sodass wir alle zuvor implementierten Funktionen erben konnten. Das Hinzufügen eines dritten 2D-SSM-Moduls zusammen mit dem entsprechenden Datenprojektionsblock macht es jedoch erforderlich, die üblichen virtuellen Methoden außer Kraft zu setzen. Die Initialisierung sowohl von neu deklarierten als auch von geerbten Objekten erfolgt in der Methode Init, deren Parameterstruktur vollständig von der entsprechenden Methode der Elternklasse geerbt wird.
bool CNeuronChimeraPlus::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronChimera::Init(numOutputs, myIndex, open_cl, window_in, window_out, units_in, units_out, optimization_type, batch)) return false;
Innerhalb des Methodenkörpers rufen wir zunächst die entsprechende Methode der übergeordneten Klasse auf, die bereits die Mechanismen zur Parametervalidierung und Initialisierung der geerbten Komponenten implementiert.
Nach der erfolgreichen Ausführung der Methodenoperationen der übergeordneten Klasse fahren wir mit der Initialisierung der neu deklarierten Objekte fort, die die erweiterten Funktionen des Modells bereitstellen. Eine der wichtigsten Komponenten, die in dieser Phase hinzugefügt wurden, ist das zusätzliche zweidimensionale Zustandsraummodul (2D-SSM).
Es ist wichtig zu beachten, dass die Methode der übergeordneten Klasse bereits zwei 2D-SSM-Module initialisiert hat, die jeweils eine bestimmte Aufgabe erfüllen. Ein Modul arbeitet innerhalb der angegebenen Ergebnisdimensionen und bietet eine Standardkodierung räumlicher Abhängigkeiten, während das zweite Modul einen erweiterten Merkmalsraum verwendet, der die Erfassung komplexerer und mehrstufiger Beziehungen zwischen Analyseelementen ermöglicht.
Um die Verallgemeinerungsfähigkeit des Modells zu erhöhen und die Genauigkeit der Marktdatenverarbeitung zu verbessern, unterscheidet sich das zusätzliche 2D-SSM-Modul von den bestehenden Modulen, indem es innerhalb des spezifizierten Merkmalsraums arbeitet, aber mit einer erweiterten Projektion entlang der zeitlichen Dimension. Diese Architektur ermöglicht eine genauere Analyse von Zeitreihen und räumlich verteilten Marktdaten.
int index = 0; if(!cSSMPlus.Init(0, index, OpenCL, window_in, window_out, units_in, 2 * units_out, optimization, iBatch)) return false;
Anschließend müssen die Ergebnisse in den vorgesehenen Unterraum projiziert werden. Hier ist anzumerken, dass wir nicht sofort Projektionen entlang der zeitlichen Dimension durchführen können. Daher müssen wir eine kleine interne Sequenz von Objekten zusammenstellen.
Wir beginnen mit der Vorbereitung eines dynamischen Arrays und lokaler Variablen zur Speicherung von Zeigern auf die zu erstellenden Objekte.
CNeuronTransposeOCL *transp = NULL; CNeuronConvOCL *conv = NULL; cDiscretizationPlus.Clear(); cDiscretizationPlus.SetOpenCL(OpenCL);
Zunächst erstellen wir ein Datentranspositionsobjekt, mit dem wir die Daten in das gewünschte Format umwandeln können.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, 2 * units_out, window_out, optimization, iBatch) || !cDiscretizationPlus.Add(transp)) { delete transp; return false; }
Als Nächstes fügen wir eine Faltungsdatenprojektionsschicht entlang der angegebenen zeitlichen Dimension hinzu.
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, 2 * units_out, 2 * units_out, units_out, window_out, 1, optimization, iBatch) || !cDiscretizationPlus.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Anschließend werden die Daten mit Hilfe eines weiteren Transpositionsobjekts in ihre ursprüngliche Darstellung zurückgeführt.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, window_out, units_out, optimization, iBatch) || !cDiscretizationPlus.Add(transp)) { delete transp; return false; } transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation()); //--- return true; }
Damit ist die Initialisierung der internen Objekte abgeschlossen, und die Methode schließt mit der Rückgabe eines logischen Ergebnisses an das aufrufende Programm ab.
Als Nächstes müssen wir den Algorithmus des Vorwärtsdurchlaufs in der Methode feedForward implementieren. Es ist zu beachten, dass die Ausgabe der entsprechenden übergeordneten Klassenmethode eine Datennormalisierung beinhaltet. Wie Sie wissen, wird durch diesen Vorgang die Datenverteilung verändert. Die Summierung dieser normalisierten Werte mit den nicht normalisierten Ergebnissen des hinzugefügten Informationsstroms könnte zu einer unvorhersehbaren Verzerrung zugunsten eines der Wege führen. Um dies zu verhindern, schreiben wir die Methode feedForward komplett um.
bool CNeuronChimeraPlus::feedForward(CNeuronBaseOCL *NeuronOCL) { for(uint i = 0; i < caSSM.Size(); i++) { if(!caSSM[i].FeedForward(NeuronOCL)) return false; } if(!cSSMPlus.FeedForward(NeuronOCL)) return false;
Die Methode erhält einen Zeiger auf das Eingabedatenobjekt, der sofort an die gleichnamigen Methoden der internen Zustandsraummodelle weitergegeben wird. Diese Modelle liefern Ergebnisse in drei verschiedenen Projektionen.
Anschließend bringen wir die Ergebnisse des Zustandsraummodells mithilfe interner Diskretisierungsobjekte in eine vergleichbare Form.
if(!cDiscretization.FeedForward(caSSM[1].AsObject())) return false; CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *current = NULL; for(int i = 0; i < cDiscretizationPlus.Total(); i++) { current = cDiscretizationPlus[i]; if(!current || !current.FeedForward(inp)) return false; inp = current; }
Zusätzlich erhalten wir eine Projektion der Eingabedaten entlang des Restverbindungsweges.
inp = NeuronOCL; for(int i = 0; i < cResidual.Total(); i++) { current = cResidual[i]; if(!current || !current.FeedForward(inp)) return false; inp = current; }
Schließlich werden die vier Informationsströme summiert. In diesem Fall wird die Normalisierung der Werte erst in der letzten Phase vorgenommen.
inp = cDiscretizationPlus[-1]; if(!SumAndNormilize(caSSM[0].getOutput(), cDiscretization.getOutput(), Output, 1, false, 0, 0, 0, 1) || !SumAndNormilize(Output, inp.getOutput(), Output, 1, false, 0, 0, 0, 1) || !SumAndNormilize(Output, current.getOutput(), Output, cDiscretization.GetFilters(), true, 0, 0, 0, 1)) return false; //--- return true; }
Wir geben das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurück und schließen die Ausführung der Methode ab.
Der nächste Schritt unserer Arbeit ist die Entwicklung der Algorithmen für die Rückwärtsdurchgänge. Sie sind in zwei Methoden implementiert: calcInputGradients und updateInputWeights. Die erste betrifft die Verteilung der Fehlergradienten auf die beteiligten Objekte. Im zweiten Schritt werden die trainierbaren Parameter der Modelle angepasst. In diesem Stadium können wir, anders als bei der Methode feedForward, die Funktionalität der übergeordneten Klasse nutzen.
Die Gradientenverteilungsmethode erhält einen Zeiger auf dasselbe Eingabedatenobjekt, das nun mit Fehlergradientenwerten aufgefüllt werden muss, die den Einfluss der Eingabedaten auf die Modellausgabe widerspiegeln.
bool CNeuronChimeraPlus::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!CNeuronChimera::calcInputGradients(NeuronOCL)) return false;
Anders als beim Standardansatz wird die Gültigkeit des Zeigers nicht geprüft, sondern er wird sofort an die gleichnamige Methode der Elternklasse übergeben. Es implementiert bereits Kontrollpunkte und den Algorithmus zur Verteilung der Fehlergradienten auf die drei vererbten Informationsströme (zwei 2D-SSMs und den Restverbindungspfad).
Anschließend wird der Gradient nur über den hinzugefügten Pfad weitergegeben. Zunächst wird der von den nachfolgenden Objekten erhaltene Fehlergradient durch die Ableitung der Aktivierungsfunktion der letzten Schicht im hinzugefügten Diskretisierungsmodell angepasst.
CNeuronBaseOCL *current = cDiscretizationPlus[-1]; if(!current || !DeActivation(current.getOutput(), current.getGradient(), Gradient, current.Activation())) return false;
Die angepassten Werte werden dann in umgekehrter Reihenfolge durch den Diskretisierungsblock geleitet. Dazu iterieren wir rückwärts durch die Elemente und rufen nacheinander die entsprechenden Methoden der jeweiligen Objekte auf.
for(int i = cDiscretizationPlus.Total() - 2; i >= 0; i--) { current = cDiscretizationPlus[i]; if(!current || !current.calcHiddenGradients(cDiscretizationPlus[i + 1])) return false; }
Der Fehlergradient wird dann durch das zweidimensionale Zustandsraummodell propagiert.
if(!cSSMPlus.calcHiddenGradients(current.AsObject())) return false;
Schließlich wird der Gradient auf das Niveau der Eingabedaten zurückgeführt. Der Puffer des Eingabedatenobjekts enthält bereits den Gradienten, der sich durch die drei vererbten Informationsströme fortpflanzt. Um die Daten zu erhalten, wird daher der Zeiger auf den Fehlergradientenpuffer vorübergehend ersetzt, damit die neu berechneten Werte erhalten bleiben.
current = cResidual[0]; CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(current.getGradient(), false) || !NeuronOCL.calcHiddenGradients(cSSMPlus.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false)) return false; //--- return true; }
Als Nächstes propagieren wir den Fehlergradienten vom zweidimensionalen Zustandsraummodell auf die Ebene der Eingabedaten. Dann addieren wir die erhaltenen Werte mit den zuvor gesammelten.
Wir setzen die Zeiger auf die Datenpuffer in ihren ursprünglichen Zustand zurück.
Damit ist die Überprüfung der Algorithmen für das erweiterte Chimera-Modul abgeschlossen. Der vollständige Code der Klasse CNeuronChimeraPlus und alle ihre Methoden sind in den beigefügten Dateien zu finden.
Aufbau des Hybriddecoders
Nach der Konstruktion des aufgerüsteten Chimera-Moduls geht es an die Entwicklung des Hybrid-Encoders. Wie bereits erwähnt, enthält er in unserer Implementierung das Chimera-Modul und den Hidformer-Block. Das Hidformer-Objekt erhält Daten über den analysierten Systemzustand als Eingabe und erzeugt einen Tensor von Agentenaktionen als Ausgabe. Und in diesem Zusammenhang wäre es wahrscheinlich korrekter, unser neues Objekt als Hybriddecoder zu bezeichnen. Die Objektstruktur wird im Folgenden dargestellt.
class CNeuronHypridDecoder : public CNeuronHidformer { protected: CNeuronChimeraPlus cChimera; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronHypridDecoder(void){}; ~CNeuronHypridDecoder(void){}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint stack_size, uint nactions, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronHypridDecoder; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool Clear(void) override; };
Die Struktur deklariert nur ein internes Objekt – das modifizierte Chimera-Modul, dessen Algorithmen oben beschrieben wurden. Das Objekt CNeuronHidformer wird als übergeordnete Klasse verwendet, wodurch eine redundante Duplizierung von Funktionen vermieden wird und eine effiziente Wiederverwendung bereits implementierter Methoden und Strukturen ermöglicht wird, ohne dass explizit eine zusätzliche Instanz innerhalb des Objekts erzeugt werden muss. Dennoch müssen wir die üblichen virtuellen Methoden außer Kraft setzen.
Das interne Objekt wird statisch deklariert, sodass der Konstruktor und Destruktor der neuen Klasse leer bleiben. Die Initialisierung dieser deklarierten und geerbten Objekte wird in der Methode Init durchgeführt.
bool CNeuronHypridDecoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, uint stack_size, uint nactions, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronHidformer::Init(numOutputs, myIndex, open_cl, window_key, window_key, nactions, heads, layers, stack_size, nactions, optimization_type, batch)) return false;
Die Methodenparameter enthalten eine Reihe von Konstanten, die die Architektur des zu erstellenden Objekts eindeutig definieren. Es ist zu beachten, dass die Parameterstruktur vollständig von der gleichnamigen Methode der Elternklasse geerbt wird. Beim Aufruf der Methode der übergeordneten Klasse werden die empfangenen Werte jedoch nicht in der gleichen Form übergeben. Der Grund dafür ist, dass die Methode feedForward der übergeordneten Klasse nicht die Rohdaten des externen Programms, sondern die Ausgaben des internen Chimera-Moduls empfangen soll. Dementsprechend werden bei der Initialisierung von geerbten Objekten der Elternklasse die Ergebnisdimensionen des internen Moduls als Eingangsdaten angegeben. Hier wird die Merkmalsdimensionalität auf den Wert des internen Zustandsvektors gesetzt. Die Länge der Sequenz entspricht dem Aktionsraum des Agenten. Mit anderen Worten: Das Chimera-Modul gibt einen latenten Zustandstensor aus, bei dem jede Zeile ein Token darstellt, das einem separaten Element der Aktionen des Agenten entspricht.
Nach erfolgreicher Ausführung der Methode der Elternklasse wird die gleichnamige Methode des Chimera-Moduls aufgerufen, wobei die Dimensionen der Eingabedaten und die gewünschten Dimensionen des Ergebnistensors angegeben werden.
if(!cChimera.Init(0, 0, OpenCL, window, window_key, units_count, nactions, optimization, iBatch)) return false; //--- return true; }
Die Methode gibt dann ein logisches Ausführungsergebnis zurück, womit der Vorgang abgeschlossen ist.
Sie haben vielleicht bemerkt, dass der Algorithmus der Objektinitialisierungsmethode recht einfach ist. Die gleiche Einfachheit gilt auch für die anderen Methoden. So erhält die Methode feedForward einen Zeiger auf das Eingabedatenobjekt, der sofort an die gleichnamige Methode des Chimera-Moduls übergeben wird.
bool CNeuronHypridDecoder::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cChimera.FeedForward(NeuronOCL)) return false; return CNeuronHidformer::feedForward(cChimera.AsObject()); }
Die Ergebnisse werden dann an die gleichnamige Methode der übergeordneten Klasse übergeben. Das logische Ergebnis wird an das aufrufende Programm zurückgegeben. Dann schließen wir die Methode ab.
Die übrigen Methoden dieser Klasse können unabhängig voneinander überprüft werden. Der vollständige Code des EAs befindet sich im Anhang.
Modell der Architektur
Nachdem wir die einzelnen Bausteine von GSM++ fertiggestellt haben, fahren wir mit dem Zusammenbau der gesamten Modellarchitektur fort. In diesem Fall trainieren wir ein einziges Modell – den Actor. Die Architekturbeschreibung wird mit der Methode CreateDescriptions bereitgestellt.
bool CreateDescriptions(CArrayObj *&actor) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; }
Die Methode erhält einen Zeiger auf ein dynamisches Array zur Speicherung der Folge von Objekten, die die Modellarchitektur beschreiben. Wir überprüfen sofort die Gültigkeit des Zeigers. Falls erforderlich, wird eine neue Objektinstanz erstellt.
Als Nächstes erstellen wir Beschreibungen für die Eingabedatenebene. Wie üblich wird eine vollständig verbundene Schicht von ausreichender Größe verwendet.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Das Modell erhält Rohdaten vom Terminal. Die erste Vorverarbeitung erfolgt durch das Modell. Zu diesem Zweck wird eine Batch-Normalisierungsschicht angewendet, um die unterschiedlichen Werte der Eingabedaten zu standardisieren.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Danach folgt das Modul für die gemischte Tokenisierung.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMoT; descr.window = BarDescr; descr.count = HistoryBars; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Anschließend wird das S3-Modul verwendet, um die optimale Token-Permutationsmethode zu lernen. Es ermittelt die beste Reihenfolge der Elemente unter Berücksichtigung ihrer gegenseitigen Abhängigkeiten und ihrer Bedeutung innerhalb der gesamten Datenstruktur.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronS3; descr.count = HistoryBars; descr.window = BarDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Die verarbeiteten Daten werden dann an den lokalen Kodierer des Knoten weitergeleitet, der durch das NAFS-Modul implementiert wird.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronNAFS; descr.count = HistoryBars; descr.window = BarDescr; descr.window_out = BarDescr; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Der Tensor Agent-Action wird vom Hybrid-Decoder-Modul erzeugt, dessen Algorithmen oben beschrieben wurden.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronHypridDecoder; //--- Windows { int temp[] = {BarDescr, 120, NActions}; //Window, Stack Size, N Actions if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = HistoryBars; descr.window_out = 32; descr.step = 4; // Heads descr.layers = 3; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Es ist wichtig zu erwähnen, dass die Architektur, die wir für den Agenten entwickelt haben, ausschließlich auf die Analyse von Umweltzuständen ausgerichtet ist. Für eine umfassende Risikobewertung ist dies jedoch unzureichend, da das Modell die verfügbaren Vermögenswerte und ihre Auswirkungen auf die Entscheidungsfindung nicht berücksichtigt.
Um dieses Problem zu lösen, wird die Architektur um einen Block für das Risikomanagement erweitert, der aus den zuvor betrachteten Modellen übernommen wurde.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMacroHFTvsRiskManager; //--- Windows { int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = 10; descr.window_out = 16; descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- return true; }
Nach der Erstellung der Architekturbeschreibung gibt die Methode ein logisches Ausführungsergebnis an das aufrufende Programm zurück.
Der vollständige Code der Architekturbeschreibungsmethode ist im Anhang enthalten. Der Anhang enthält auch Trainings- und Testskripte, die aus früheren Arbeiten kopiert wurden. Sie sind für eine unabhängige Überprüfung verfügbar.
Tests
Wir haben umfangreiche Arbeiten zur Umsetzung unserer Interpretation der von den Autoren von GSM vorgeschlagenen Ansätze durchgeführt. Wir haben nun eine kritische Phase erreicht – die Bewertung der Wirksamkeit der umgesetzten Lösungen anhand echter historischer Daten.
Es ist anzumerken, dass die letzten neuronalen Schichten des Agenten genau der Architektur entsprechen, die in unserer Implementierung von Hidformer verwendet wird. Es wird die gleiche Struktur des Risikomanagementmoduls verwendet, und am Ausgang des Hybriddecoders wird das Objekt CNeuronHidformer eingesetzt. Aufgrund dieser architektonischen Ähnlichkeit ist es sinnvoll, die Leistung des neuen Modells mit der von Hidformer zu vergleichen.
Um einen fairen Vergleich zu ermöglichen, wurden beide Modelle auf demselben Datensatz trainiert, der zuvor für das Training von Hidformer verwendet wurde. Erinnern Sie sich daran:
- Der Trainingssatz besteht aus historischen EURUSD M1-Daten für das gesamte Kalenderjahr 2024.
- Alle analysierten Indikatorparameter bleiben ohne zusätzliche Optimierung auf den Standardwerten und eliminieren so den Einfluss externer Faktoren.
- Die Tests des trainierten Modells wurden mit historischen Daten vom Januar 2025 durchgeführt, wobei alle anderen Parameter unverändert blieben, um einen objektiven Vergleich zu gewährleisten.
Die Testergebnisse werden im Folgenden vorgestellt.
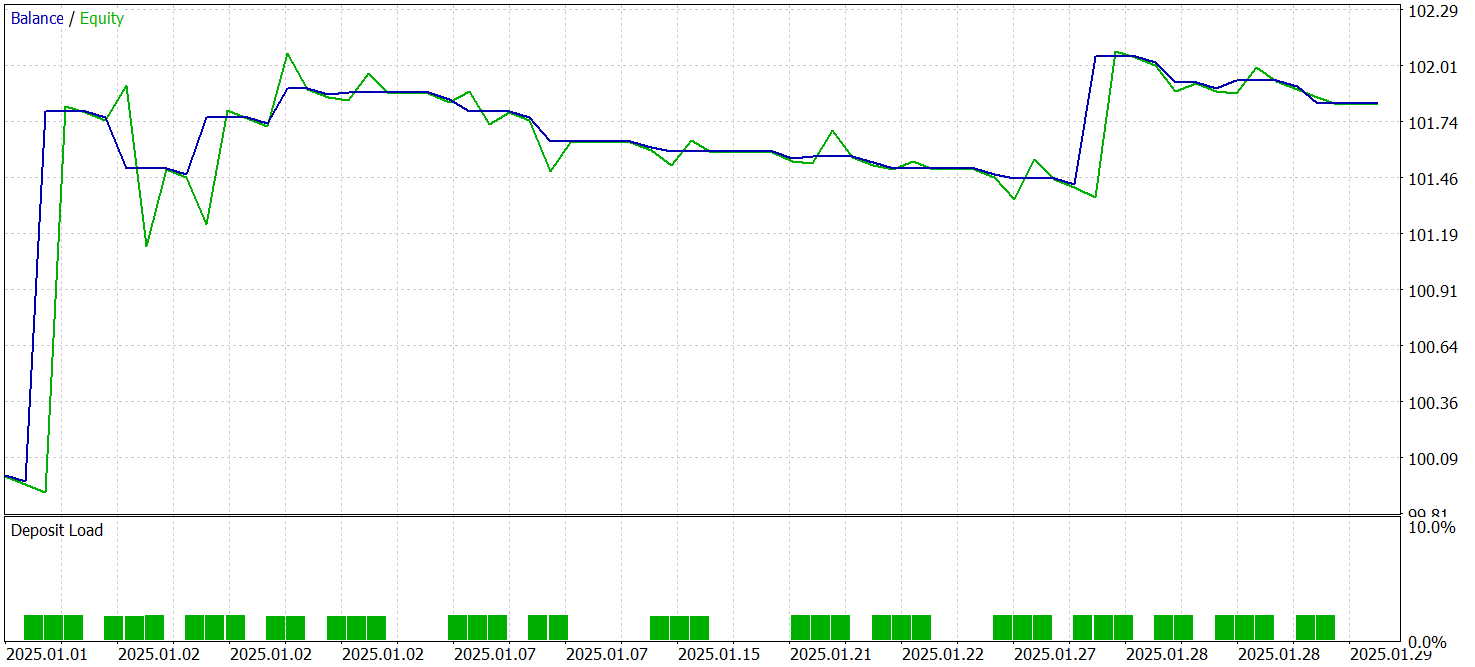
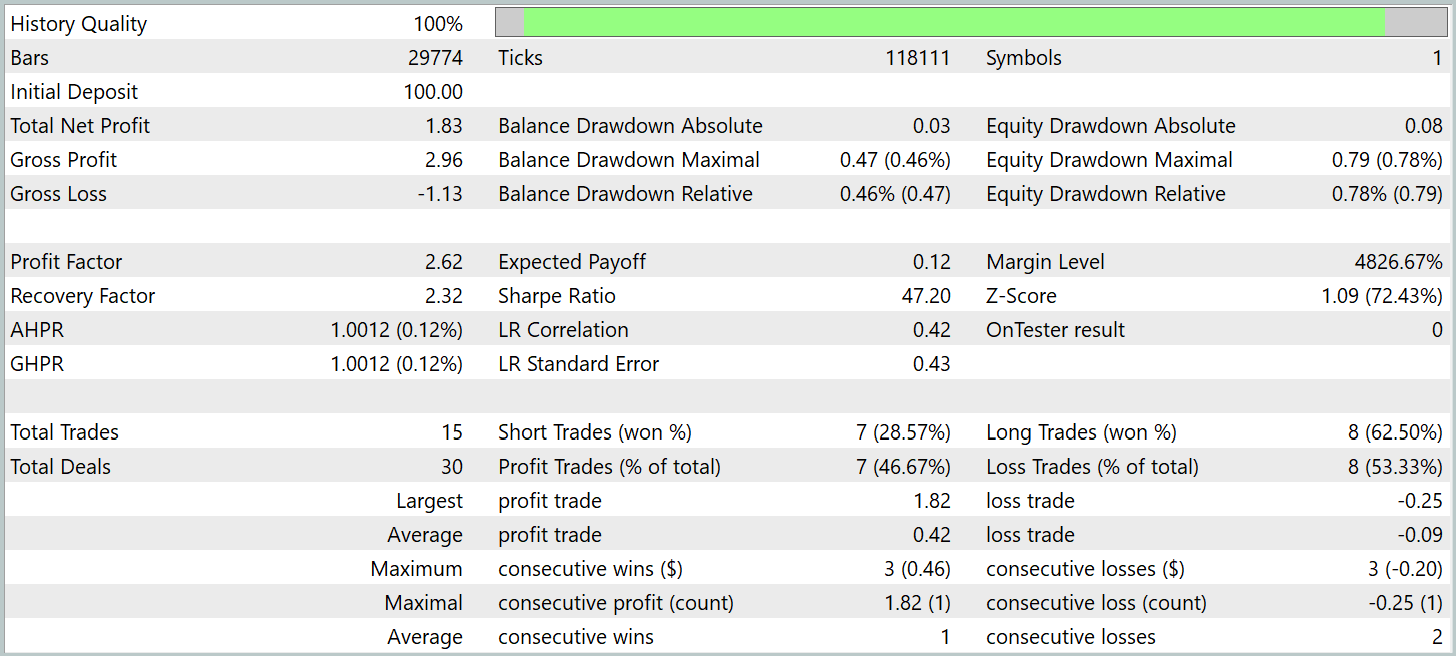
Während des Testzeitraums führte das Modell 15 Handelsgeschäfte aus, was für den Hochfrequenzhandel auf dem M1-Zeitrahmen relativ wenig ist. Dieser Wert liegt sogar noch unter dem des Basismodells von Hidformer. Nur 7 Handelsgeschäfte waren gewinnbringend, was 46,67 % entspricht. Dies ist ebenfalls niedriger als der Basiswert von 62,07 %. Hier sehen wir eine geringere Genauigkeit der Verkaufsposition. Allerdings war ein leichter Rückgang der Verlustgröße bei gleichzeitiger relativer Zunahme der gewinnbringenden Handelsgrößen zu verzeichnen.
Lag das Verhältnis von durchschnittlich gewinnbringenden zu verlustbringenden Geschäften beim Basismodell bei 1,6, so liegt dieses Verhältnis beim neuen Modell bei über 4. Dadurch verdoppelte sich der Gesamtgewinn im Testzeitraum nahezu, und der Gewinnfaktor stieg entsprechend an. Dies deutet darauf hin, dass die neue Architektur der Verlustminimierung und der Gewinnmaximierung bei erfolgreichen Geschäften Vorrang einräumt. Dies kann langfristig zu stabileren Finanzergebnissen führen. Aufgrund des kurzen Testzeitraums und der geringen Anzahl von Handelsgeschäften lassen sich jedoch keine Rückschlüsse auf die langfristige Leistung des Modells ziehen.
Schlussfolgerung
Wir haben das Unified Graph Sequence Processing, GSM++, erforscht, das fortschrittliche Methoden zur Analyse von Marktdaten kombiniert. Sein Hauptvorteil liegt in der hybriden Datendarstellung, die eine hierarchische Tokenisierung, eine lokale Knotencodierung und eine globale Abhängigkeitscodierung umfasst. Dieser mehrstufige Ansatz extrahiert effizient signifikante Muster und bildet hochinformative Einbettungen, die für die Prognose von Finanzzeitreihen entscheidend sind.
Im praktischen Teil dieser Arbeit haben wir unsere eigene Interpretation der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Es ist wichtig, darauf hinzuweisen, dass es erhebliche Unterschiede zwischen unserer Implementierung und den ursprünglichen Methoden der Autoren gibt. Daher gelten alle Testergebnisse ausschließlich für die implementierte Lösung.
Das trainierte Modell hat gezeigt, dass es in der Lage ist, mit Daten, die außerhalb der Stichprobe liegen, Gewinne zu erzielen. Allerdings nicht in dem Umfang, den wir uns wünschen würden. Dies deutet auf das Potenzial der implementierten Ansätze hin, aber es sind weitere Arbeiten erforderlich, einschließlich des Trainings auf einem repräsentativeren Datensatz, umfassender Tests und der Optimierung der analysierten Indikatoren und ihrer Parameter. Das Modell identifiziert Muster in den Trainingsdaten, anstatt sie zu erstellen.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor für die Probenahme |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für die Probenahme mit der Methode Real-ORL |
| 3 | Study.mq5 | Expert Advisor | Expert Advisor für das Training des Modells |
| 4 | Test.mq5 | Expert Advisor | Expert Advisor für den Modeltest |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Beschreibung des Systemzustands und der Modellarchitektur |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Code Base | OpenCL-Programmcode |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17310
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
 Die Komponenten View und Controller für Tabellen im MQL5 MVC-Paradigma: Container
Die Komponenten View und Controller für Tabellen im MQL5 MVC-Paradigma: Container
 Eine alternative Log-datei mit der Verwendung der HTML und CSS
Eine alternative Log-datei mit der Verwendung der HTML und CSS
 Erforschung des maschinellen Lernens im unidirektionalen Trendhandel am Beispiel von Gold
Erforschung des maschinellen Lernens im unidirektionalen Trendhandel am Beispiel von Gold
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.