
Neuronale Netze im Handel: Hybride Graphsequenzmodelle (GSM++)
In den letzten Jahren haben Graphen-Transformer, die aus den Bereichen der Verarbeitung natürlicher Sprache und der Computer Vision übernommen wurden, besondere Aufmerksamkeit auf sich gezogen. Ihre Fähigkeit, langfristige Abhängigkeiten zu modellieren und effizient mit unregelmäßigen Finanzstrukturen umzugehen, macht sie zu einem vielversprechenden Instrument für Aufgaben wie Volatilitätsprognosen, die Erkennung von Marktanomalien und die Entwicklung optimaler Anlagestrategien. Die klassischen Transformer stehen jedoch vor einer Reihe grundlegender Probleme, darunter hohe Rechenkosten und Schwierigkeiten bei der Anpassung an ungeordnete Graphenstrukturen.
Die Autoren von „Best of Both Worlds: Advantages of Hybrid Graph Sequence Models“ schlagen ein einheitliches Graphensequenzmodell, GSM++, vor, das die Stärken verschiedener Architekturen kombiniert, um eine effektive Methode zur Darstellung und Verarbeitung von Graphen zu schaffen. Das Modell besteht aus drei Schlüsselschritten: Tokenisierung des Graphen, lokale Kodierung der Knoten und globale Kodierung der Abhängigkeiten. Dieser Ansatz ermöglicht es dem Modell, sowohl lokale als auch globale Beziehungen in Finanzsystemen zu erfassen, was es vielseitig und für eine breite Palette von Aufgaben einsetzbar macht.
Eine Kernkomponente des vorgeschlagenen Modells ist die hierarchische Graphen-Tokenisierungsmethode, die Marktdaten in eine kompakte sequentielle Darstellung umwandelt, wobei ihre topologischen und zeitlichen Merkmale erhalten bleiben. Im Gegensatz zu herkömmlichen Zeitreihenkodierungsmethoden verbessert dieser Ansatz die Qualität der Merkmalsextraktion und vereinfacht die Verarbeitung großer Mengen von Marktdaten. Die Kombination von hierarchischer Tokenisierung mit einer hybriden Architektur, die Transformer und rekurrente Mechanismen umfasst, führt zu einer überlegenen Leistung bei mehreren Aufgaben. Dies macht die Methode zu einem leistungsstarken Werkzeug für die Bearbeitung komplexer Finanzdaten.
Empirische Studien und theoretische Analysen, die von den Autoren des Systems von GSM++ durchgeführt wurden, zeigen, dass das vorgeschlagene Modell nicht nur mit traditionellen Graphen-Transformer konkurriert, sondern diese auch in mehreren Schlüsselmetriken übertrifft.
Der Algorithmus von GSM++
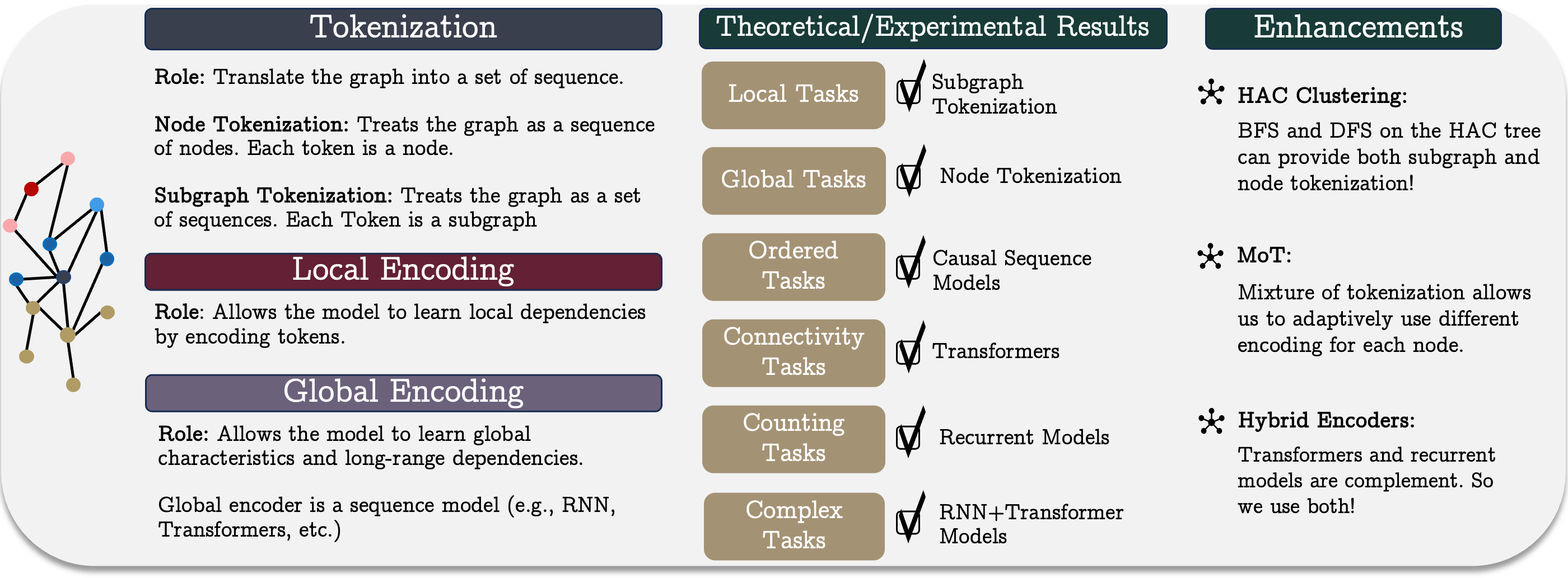
Das einheitliche Graphensequenzmodell stellt einen konzeptionellen Rahmen dar, der drei Schlüsselphasen umfasst: Tokenisierung, lokale Kodierung und globale Kodierung. Diese Methode ermöglicht eine effiziente Darstellung und Analyse komplexer Graphenstrukturen, was besonders auf den Finanzmärkten wichtig ist. Komplexe Marktsysteme, die zahlreiche Teilnehmer und Interaktionen umfassen, erfordern leistungsstarke Modellierungswerkzeuge, die in der Lage sind, nichtlineare Abhängigkeiten und versteckte Korrelationen zu erfassen.
Die Tokenisierung spielt eine grundlegende Rolle bei der Umwandlung einer Graphenstruktur in eine sequenzielle Darstellung, die für sequenzbasierte Modelle geeignet ist. Zu den primären Tokenisierungsstrategien gehören die Tokenisierung von Knoten oder Kanten und die Tokenisierung von Teilgraphen. Die Wahl der Tokenisierungsmethode wirkt sich erheblich auf die Effektivität des Modells aus, da sie bestimmt, wie vollständig die Strukturinformationen des Graphen erhalten bleiben und welche organisatorischen Merkmale bei der Analyse berücksichtigt werden.
Die Knoten- oder Kanten-Tokenisierung behandelt den Graphen als eine Abfolge von Einzelelementen und lässt deren Verbindungen untereinander unberücksichtigt. Die Erhaltung von Strukturinformationen erfordert eine zusätzliche Positions- oder Strukturkodierung. Der größte Nachteil dieser Methode ist die hohe Rechenkomplexität, da die Sequenzlänge der Anzahl der Knoten oder Kanten entspricht, was das Modelltraining erschwert. Sie ist jedoch nützlich, wenn detaillierte Informationen über jedes Systemelement benötigt werden – beispielsweise bei der Entwicklung individueller Anlagestrategien auf der Grundlage mikroskopischer Merkmale. Im Hochfrequenzhandel ermöglicht dieser Ansatz eine genauere Analyse kurzfristiger Marktschwankungen und die Erkennung abnormaler Handelsmuster.
Die Tokenisierung von Untergraphen reduziert die Rechenkosten, indem sie den Graphen als eine Folge von Untergraphen darstellt und so die Fähigkeit des Modells verbessert, lokale Strukturen zu erfassen. Dieser Ansatz ist besonders nützlich für Finanzanwendungen, z. B. für die Analyse von Handelsmustern, bei denen die Teilgraphen Clustern korrelierter Vermögenswerte oder Gruppen von Anlegern entsprechen. Die Interaktionen zwischen Vermögenswerten haben oft einen verborgenen Netzwerkcharakter, und die auf Subgraphen basierende Analyse hilft dabei, beständige Marktmuster aufzudecken, die für das Portfoliomanagement, die Liquiditätsbewertung und Arbitragestrategien von entscheidender Bedeutung sind.
Jede Tokenisierungsmethode hat Vorteile und Einschränkungen, sodass die Wahl von der jeweiligen Aufgabe abhängt. In einigen Fällen erreichen hybride Ansätze, die beide Strategien kombinieren, ein besseres Gleichgewicht zwischen der Genauigkeit der Datendarstellung und der Recheneffizienz.
Auf der Grundlage dieser Ideen haben die Autoren von GSM++ einen hierarchischen Tokenisierungsalgorithmus vorgeschlagen, der auf dem Clustering von Knoten nach Ähnlichkeit basiert (Hierarchical Affinity Clustering, HAC).
Der Algorithmus beginnt damit, dass er jeden Knoten des Graphen als separaten Cluster behandelt. Bei jedem Schritt werden zwei Cluster, die durch die am wenigsten „teure“ Kante (bestimmt durch die Ähnlichkeit ihrer Kodierungen) verbunden sind, zusammengeführt. Dieser Prozess wird so lange fortgesetzt, bis der gesamte Graph zu einem einzigen Cluster verschmolzen ist. Das Ergebnis ist ein hierarchischer Baum, wobei die Wurzel den gesamten Graphen darstellt und die Blätter den ursprünglichen Knoten entsprechen.
Dieser Ansatz bietet zwei wesentliche Vorteile. Erstens werden die Knoten so angeordnet, dass ähnliche Elemente näher beieinander liegen, was die Graphendarstellung in Modellen verbessert. Zweitens ermöglicht es die Kodierung von Graphen auf mehreren Ebenen und damit eine flexible Strukturanalyse. Es werden zwei Strategien zur Durchquerung von Bäumen entwickelt: die Deep-First-Suche (DFS) und die Breadth-First-Suche (BFS). Das DFS erzeugt Knotenfolgen, die ihre hierarchische Position widerspiegeln. BFS erzeugt Sequenzen, in denen ähnliche Knoten nebeneinander liegen.
Diese Tokenisierungsmethode bewahrt die lokale Struktur des Graphen und arbeitet effizient mit rekurrenten Modellen, insbesondere bei Aufgaben, die eine globale Konnektivitätsanalyse erfordern.
Zusätzlich wird eine hierarchische Positionskodierungsmethode verwendet, die die kürzesten Pfade zwischen den Knoten und ihre Positionen in der Clusterhierarchie berücksichtigt. Experimente zeigen, dass diese Kodierung die Qualität der Graphendarstellung deutlich verbessert.
Da verschiedene Knoten je nach Graphenstruktur und Aufgabe unterschiedliche Tokenisierungsmethoden erfordern können, wurde der Ansatz „Mix of Tokenization“ (MoT) vorgeschlagen. Es ermöglicht jedem Knoten, die am besten geeignete Kodierungsmethode zu verwenden, indem es optimale Tokenizer auswählt und deren Darstellungen kombiniert.
Nach der Tokenisierung werden die Daten in Vektordarstellungen umgewandelt, um lokale Graphmerkmale zu untersuchen. In diesem Stadium werden üblicherweise Graph Neural Networks (GNNs) verwendet, da sie lokale Abhängigkeiten zwischen den Knoten effizient erfassen. Auf den Finanzmärkten hilft dies bei der Analyse von Korrelationen zwischen Vermögenswerten, der Erkennung lokaler Anomalien und der Erstellung von Prognosen auf der Grundlage von Mikrostrukturdaten. Aufgrund ihrer Anpassungsfähigkeit und ihrer Fähigkeit, komplexe Muster zu extrahieren, werden GNNs im algorithmischen Handel und bei der Vorhersage der Marktvolatilität eingesetzt.
Die globale Kodierung ist entscheidend für die Modellierung langfristiger Abhängigkeiten innerhalb des Graphen. Die sequenzielle Kodierung wird angewandt, um komplexe Beziehungen zwischen Strukturelementen zu erkennen. In Finanzanwendungen ermöglicht dies die Modellierung makroökonomischer Trends, die Analyse des Einflusses globaler Faktoren auf die Märkte und die Entwicklung von Strategien auf der Grundlage tiefgreifender Datenverknüpfungen. Langfristige Finanztrends, wie die Auswirkungen der Geldpolitik oder globaler Wirtschaftskrisen, erfordern Algorithmen, die in der Lage sind, komplexe Abhängigkeiten über mehrere Zeithorizonte hinweg zu erfassen.
Bei der Auswahl eines Sequenzmodells für das Graphentraining stellt sich eine wichtige Frage: Welches Modell ist am effektivsten? Der Standardansatz erlaubt es, verschiedene Sequenzkodierer mit unterschiedlichen Tokenisierungsmethoden zu kombinieren, wodurch mehrere mögliche Architekturen entstehen. Es besteht jedoch kein eindeutiger Konsens darüber, welche für bestimmte Graph-Aufgaben am besten geeignet sind.
Zählaufgaben erfordern die Bestimmung der Anzahl von Knoten eines bestimmten Typs. Aufmerksamkeitsbasierte Modelle ohne kausale Abhängigkeiten können solche Aufgaben nicht korrekt lösen. Das wirft die Frage auf: Können rekurrente Modelle, die die Reihenfolge berücksichtigen, dieses Problem lösen?
Wenn die Breite des rekurrenten Modells mit der Anzahl der verschiedenen Knotenklassen übereinstimmt, kann es diese genau zählen. Dies zeigt die Effektivität von rekurrenten Modellen bei Aufgaben, bei denen die sequenzielle Struktur wichtiger ist als die Graphentopologie.
Bestimmte Graphenaufgaben, wie z. B. algorithmische Schlussfolgerungen, erfordern die strikte Einhaltung der Knotenreihenfolge. Moderne Sequenzmodelle beruhen meist auf kausalen Abhängigkeiten, die bei der Integration mit Graphenmodellen berücksichtigt werden müssen. Die Forschung zeigt, dass eine übermäßige Informationskomprimierung die Repräsentationstreue beeinträchtigen kann. Bei rekurrenten Modellen nimmt die Empfindlichkeit gegenüber den Ausgangsdaten mit dem Abstand zwischen den Elementen ab, während bei Transformern die Empfindlichkeit konstant bleibt. Allerdings neigen beide Modelle mit zunehmender Tiefe zum Zusammenbruch der Darstellung.
Informationen, die am Anfang einer Sequenz stehen, haben eine höhere Chance, behalten zu werden. Dies führt zu einem U-förmigen Effekt, bei dem die Zeichen am Anfang und am Ende der Sequenz ihre Bedeutung besser behalten als die in der Mitte. Dieses Verhalten ist sowohl bei Transformern als auch bei rekurrenten Modellen zu beobachten. Daher sollten bei der Anordnung von Knoten in einer Sequenz wichtige Elemente näher beieinander liegen, um die gegenseitige Beeinflussung zu verstärken.
Konnektivitätsbezogene Aufgaben erfordern eine globale Graphenstrukturanalyse. Konnektivität kann als binäres Klassifikationsproblem betrachtet werden. Studien zeigen, dass Transformer mit ausreichender Tiefe und Einbettungsgröße solche Aufgaben effektiv lösen können. Rekurrente Modelle und Transformer mit begrenzter Aufmerksamkeit erfordern jedoch wesentlich mehr Parameter oder Tiefe, um ähnliche Ergebnisse zu erzielen.
Wiederkehrende Modelle sind am effektivsten, wenn die Daten eine natürliche Ordnung aufweisen und die Tokenisierung die Graphenstruktur berücksichtigt. Die Knotenlokalität, die den maximalen Abstand zwischen benachbarten Knoten definiert, ist ein wichtiger Parameter. Bei Graphen mit begrenzter Lokalität kann ein kompaktes rekurrentes Modell die Konnektivität effizient bestimmen. Festparameter-Transformer hingegen haben mit solchen Aufgaben zu kämpfen.
Die Wahl eines Modells erfordert das Verständnis von Kompromissen bei der Graphenanalyse. Bei der Untersuchung der verschiedenen Architekturen wurden mehrere wichtige Feststellungen getroffen:
- Transformer eignen sich hervorragend für Verbindungsaufgaben mit minimalen Parametern. Sie sind besonders nützlich für komplexe Graphen, die parallele Berechnungen erfordern. Ihre Fähigkeit, kontextabhängige Darstellungen zu bilden, macht sie für die Analyse komplexer Netzwerke und Graphen sehr leistungsfähig.
- Rekurrente neuronale Netze (RNNs) funktionieren gut auf Graphen, deren Knotenpunktverbindungen eine klar lokalisierte Struktur aufweisen. Sie benötigen weniger Parameter und Berechnungen und sind daher energieeffizient und für Datenströme geeignet.
- Hybridmodelle, die RNNs und Transformer kombinieren, nutzen die Vorteile beider Architekturen. Sie schaffen ein Gleichgewicht zwischen Rechenkomplexität und Vorhersagegenauigkeit, insbesondere dann, wenn sowohl der globale Kontext als auch lokale Details entscheidend sind.
- Zustandsraummodelle sind sehr effektiv, wenn eine strenge Elementordnung wichtig ist. Sie verfügen über ein Langzeitgedächtnis, was sie für die Zeitreihenanalyse und die Modellierung sequenzieller Aktionen in agentenbasierten Systemen nützlich macht.
- Die spärliche Aufmerksamkeit (Sparse attention)reduziert die Rechenkosten für den Transformer, insbesondere bei großen Graphen. Ihre effektive Nutzung erfordert zusätzliche Mechanismen zur Identifizierung der wichtigsten Knotenverbindungen, was die Implementierung erschweren kann.
Die Modellauswahl hängt also von der Struktur der Eingabedaten und den verfügbaren Rechenressourcen ab. Transformer eignen sich für komplexe Graphen mit ausgeprägten globalen Abhängigkeiten, RNNs sind optimal für lokalisierte Sequenzen, und Zustandsraummodelle zeichnen sich bei Aufgaben aus, die eine strikte Operationsreihenfolge erfordern. Hybride Ansätze ermöglichen ein Gleichgewicht zwischen Recheneffizienz und Vorhersagegenauigkeit, was sie zu einer vielseitigen Wahl für viele Anwendungsszenarien macht.
Auf der Grundlage dieser Analyse stellen die Autoren das Systems von GSM++ vor, das eine hierarchische, auf Ähnlichkeit basierende Knoten-Tokenisierung, Faltungs-GNNs als lokalen Encoder und einen hybriden globalen Encoder mit Mamba- und Transformer-Modulen umfasst.
Die Implementation in MQL5
Nachdem wir die theoretischen Aspekte der von den Autoren von GSM++ vorgeschlagenen Ansätze besprochen haben, kommen wir nun zum praktischen Teil unserer Arbeit. In diesem Abschnitt konzentrieren wir uns auf die Umsetzung unserer eigenen Interpretation der diskutierten Ansätze mit Hilfe von MQL5-Tools.
Es sei darauf hingewiesen, dass das allgemeine Konzept der ursprünglichen Ansätze zwar beibehalten wurde, sich unsere Umsetzung jedoch im Detail deutlich unterscheidet.
In erster Linie haben wir bei unserer Implementierung auf hierarchisches ähnlichkeitsbasiertes Clustering (HAC) verzichtet. Man kann davon ausgehen, dass es sich bei den Kerzen auf dem Chart eines Finanzinstruments um dynamische und sich entwickelnde Objekte handelt, die sich nicht einfach standardisieren lassen. Ihre Analyse und Clusterbildung ist ein komplexer, vielschichtiger Prozess, der einen viel tieferen und umfassenderen Ansatz erfordert.
Daher verwenden wir wie bisher trainierbare Module für die Tokenisierung der Repräsentationen der untersuchten Balken. Dieser Ansatz ermöglicht es uns, die Flexibilität und Anpassungsfähigkeit des Modells unter realen Datenbedingungen beizubehalten, was bei der Arbeit mit Finanzmärkten besonders wichtig ist.
Nichtsdestotrotz verwenden wir in unserer Implementierung den vorgeschlagenen Mix of Tokenization (MoT) Algorithmus, wenn auch in einer etwas modifizierten und angepassten Form, um den Besonderheiten unserer Aufgabe gerecht zu werden. Die Autoren von GSM++ schlagen vor, ein trainierbares Clustermodell zu verwenden, um die beiden relevantesten Tokenisierungsalgorithmen auszuwählen, woraufhin die Ergebnisse dieser Algorithmen summiert werden, um die endgültige Darstellung zu erzeugen. Im Gegensatz dazu bereiten wir vier verschiedene Arten von Token für jeden Balken vor und kombinieren ihre Ergebnisse mit einem Attention Pooling-Algorithmus, der von R-MAT ausgeliehen wurde.
Dieser Ansatz verbessert die Qualität der Analyse erheblich, da er die Berücksichtigung von mehr Aspekten der Daten und eine präzisere Extraktion der relevanten Informationen ermöglicht. In unserer Arbeit werden die folgenden Tokenisierungsvarianten verwendet:
- Knoten-Tokenisierung – jeder Balken steht für ein separates analytisches Element, das das Modell verarbeitet, um Daten zu extrahieren.
- Kanten-Tokenisierung – konzentriert sich auf Interaktionen zwischen zwei aufeinanderfolgenden Balken und hebt wichtige Verbindungen zwischen verschiedenen Teilen der Daten hervor.
- Tokenisierung von Teilgraphen – ermöglicht die Bildung komplexerer Strukturen durch die Berücksichtigung von Verbindungen zwischen mehreren Balken innerhalb einer einzigen Gruppe.
- Subgraphen-Tokenisierung einzelner unitärer Sequenzen – bietet eine detaillierte Analyse struktureller Sequenzen, die eine Datenverarbeitung auf tieferer Ebene ermöglicht.
Die Verwendung dieser Tokenisierungsmethoden ermöglicht die Berücksichtigung sowohl einzelner Elemente als auch ihrer Wechselbeziehungen, wodurch die Qualität der Informationsdarstellung für jeden Balken erheblich verbessert und die Gesamtleistung des Modells gesteigert wird. Die Kombination aller Token durch Attention Pooling ermöglicht es dem Modell, sich flexibel anzupassen und sich auf die wichtigsten Merkmale zu konzentrieren, was die Entscheidungsfindung verbessert.
Um diese Lösung zu implementieren, erstellen wir ein neues Objekt, CNeuronMoT. Seine Struktur ist unten dargestellt.
class CNeuronMoT : public CNeuronMHAttentionPooling { protected: CNeuronConvOCL cNodesTokenizer; CNeuronConvOCL cEdgesTokenizer; CNeuronConvOCL cSubGraphsTokenizer; CLayer cUnitarSubGraphsTokenizer; CNeuronBaseOCL cConcatenate; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronMoT(void){}; ~CNeuronMoT(void){}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronMoT; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Das übergeordnete Objekt ist in diesem Fall CNeuronMHAttentionPooling, das bereits den Attention-Pooling-Algorithmus implementiert, der in der Ausgabestufe des Moduls zur Kombination verschiedener Tokenisierungsvarianten verwendet werden soll. Dieser Ansatz bietet mehrere wesentliche Vorteile.
Erstens wird durch die Verwendung der übergeordneten Klasse Code-Redundanz vermieden, sodass das Attention-Pooling-Modul nicht in anderen Objekten oder Komponenten neu implementiert werden muss. Stattdessen integrieren wir eine fertige und optimierte Implementierung des Algorithmus, die ein hohes Maß an Abstraktion beibehält und die Wartung des Codes vereinfacht.
Zweitens werden alle Vorgänge im Zusammenhang mit der Token-Kombination und -Verarbeitung über die Funktionalität der übergeordneten Klasse ausgeführt. Dies vereinfacht die Systemarchitektur erheblich und verbessert die Ressourceneffizienz, da die übergeordnete Klasse bereits alle notwendigen Methoden und Algorithmen für die Aufmerksamkeitsverarbeitung enthält. Dadurch wird die Duplizierung von Funktionen minimiert und die Modularität und Erweiterbarkeit verbessert.
Die Struktur des neuen Objekts enthält eine vertraute Reihe von virtuellen überschreibbaren Methoden, die für die Implementierung unseres Modells unerlässlich sind. Diese Methoden bieten Flexibilität und ermöglichen die Anpassung des Objektverhaltens je nach den Anforderungen der Aufgabe.
Darüber hinaus enthält die Klasse mehrere interne Objekte, die in unserem Algorithmus eine wichtige Rolle spielen. Darüber hinaus enthält die Klasse mehrere interne Objekte, die eine wichtige Rolle bei der Erstellung unseres Algorithmus spielen. Ihr spezifischer Zweck wird bei der Implementierung der Klassenmethoden im Detail erläutert, wobei ihre Funktionsweise und ihr Zusammenspiel ausführlich beschrieben werden.
Alle internen Objekte werden als statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse leer lassen können. Die Initialisierung aller deklarierten und geerbten Objekte wird wie üblich in der Methode Init durchgeführt.
bool CNeuronMoT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronMHAttentionPooling::Init(numOutputs, myIndex, open_cl, window, units_count, 4, optimization_type, batch)) return false;
Die Methodenparameter erhalten Konstanten, die die Dimensionalität der Eingabedaten beschreiben. Bitte beachten Sie, dass diese Implementierung eine Ausgabe in der gleichen Dimensionalität erwartet. Folglich werden die Parameter sofort an die gleichnamige Methode der Elternklasse übergeben, die bereits die Initialisierung für alle geerbten Objekte und Schnittstellen implementiert.
Nach erfolgreicher Ausführung der Methode der übergeordneten Klasse fahren wir mit der Initialisierung der neu deklarierten Objekte fort. Zunächst initialisieren wir das Knoten-Tokenization-Objekt. Sie ist als Faltungsschicht implementiert, wobei die Größe des Faltungsfensters, der Schritt und die Anzahl der Filter dem Vektor entsprechen, der ein einzelnes Sequenzelement beschreibt.
Dieser Ansatz ermöglicht eine effiziente Verarbeitung sequenzieller Daten, wobei jedes Element (Knoten) als Vektor dargestellt wird, der bestimmten Merkmalen entspricht. Durch die Faltung können wichtige lokale Merkmale extrahiert werden, die die Grundlage für die anschließende Datenverarbeitung und Tokenisierung bilden. Die Anpassung der Faltungsparameter an den Elementbeschreibungsvektor gewährleistet eine nahtlose Integration der Faltungsschicht in die Gesamtmodellstruktur, wodurch Effizienz und Konsistenz über alle Verarbeitungsstufen hinweg erhalten bleiben.
int index = 0; if(!cNodesTokenizer.Init(0, index, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cNodesTokenizer.SetActivationFunction(SoftPlus);
Als Nächstes initialisieren wir die Faltungsschicht für die Kanten-Tokenisierung. Im Gegensatz zum vorherigen Objekt verwenden wir hier das Faltungsfenster von zwei aufeinanderfolgenden Elementen. Dies ermöglicht die Modellierung von Wechselwirkungen und Verbindungen zwischen benachbarten Elementen, was für eine tiefergehende Strukturanalyse wichtig ist.
index++; if(!cEdgesTokenizer.Init(0, index, OpenCL, 2 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cEdgesTokenizer.SetActivationFunction(SoftPlus);
Es ist zu beachten, dass die Verwendung eines Doppelfensters mit einem einzigen Schritt die Sequenzlänge im Allgemeinen um ein Element reduziert. Die anschließende Token-Kombination erfordert jedoch eine Kompatibilität der Tensordimensionen über alle Stufen hinweg. Daher wird die ursprüngliche Sequenzlänge beibehalten, indem fehlende Elemente am Ende mit Nullen aufgefüllt werden.
In ähnlicher Weise initialisieren wir die Subgraph-Tokenization-Faltungsschicht, indem wir das Fenster auf drei Sequenzelemente erweitern und alle anderen Parameter beibehalten.
index++; if(!cSubGraphsTokenizer.Init(0, index, OpenCL, 3 * iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; cSubGraphsTokenizer.SetActivationFunction(SoftPlus);
Auf allen Tokenisierungsebenen wenden wir die SoftPlus-Aktivierungsfunktion an. Diese Wahl bietet mehrere Vorteile. SoftPlus ist sanft und monoton, vermeidet scharfe Sprünge und verbessert die Stabilität des Trainings. Im Gegensatz zu ReLU gibt es bei SoftPlus keinen abrupten Übergang von Null zu positiven Werten, was Probleme mit „toten Neuronen“ verhindert.
Außerdem ist die SoftPlus-Ableitung immer positiv, was eine gute Differenzierbarkeit und eine reibungslose Aktualisierung der Gewichte während der Backpropagation ermöglicht. Dies ist besonders wichtig für komplexe neuronale Netze, die präzise und stabile Parametereinstellungen erfordern.
Durch die Anwendung von SoftPlus auf allen Tokenisierungsebenen wird ein flexibleres und stabileres Modell geschaffen, das die für die Verarbeitung und Analyse komplexer sequentieller Daten erforderliche Glattheit und Robustheit gewährleistet.
Die Erzeugung von Token für unitäre Sequenzen einer mehrdimensionalen Zeitreihe erfordert mehrere aufeinander folgende Operationen. Um diese Funktion auszuführen, müssen wir mehrere aufeinanderfolgende Operationen durchführen, die wir in einem internen Modell zusammenfassen und Zeiger auf Objekte speichern, die in dem dynamischen Array cUnitarSubGraphsTokenizer gespeichert sind.
Wir initialisieren zunächst ein dynamisches Array und deklarieren lokale Variablen für die temporäre Speicherung von Objektzeigern.
cUnitarSubGraphsTokenizer.Clear(); cUnitarSubGraphsTokenizer.SetOpenCL(OpenCL); CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL;
Um die Arbeit mit unitären Sequenzen zu erleichtern, transponieren wir die Eingabedaten.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, iUnits, iWindow, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(transp)) { delete transp; return false; }
Dann verwenden wir eine Faltungsschicht, um Teilgraphen-Token zu erzeugen. Auch hier analysieren wir 3-Element-Untergraphen. Jedes Element wird durch einen einzigen Wert dargestellt, und die Anzahl der analysierten Variablen entspricht der Anzahl der unitären Sequenzen.
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, 3, 1, 1, iUnits, iWindow, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(SoftPlus);
Dieser Ansatz ermöglicht eine detaillierte Analyse von Übergängen und Mustern innerhalb einzelner unitärer Sequenzen.
Die erzeugten Werte werden dann in ihren ursprünglichen Zustand zurückversetzt.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, iWindow, iUnits, optimization, iBatch) || !cUnitarSubGraphsTokenizer.Add(transp)) { delete transp; return false; } transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Schließlich initialisieren wir das Objekt, das für die Verkettung der Ergebnisse aus den verschiedenen Tokenisierungsansätzen verantwortlich ist.
index++; if(!cConcatenate.Init(0, index, OpenCL, 4 * iWindow * iUnits, optimization, iBatch)) return false; cConcatenate.SetActivationFunction(None); //--- return true; }
Beachten Sie, dass die Aktivierung für das Verkettungsobjekt absichtlich deaktiviert ist. Natürlich verwenden wir dieselben Aktivierungsfunktionen für alle Token-erzeugenden Objekte. Wir könnten sie in das Verkettungsobjekt verschieben, was den Gradientenverteilungsalgorithmus im Backpropagation-Durchgang etwas vereinfachen könnte. Im Allgemeinen erlauben wir jedoch die Verwendung unterschiedlicher Aktivierungsfunktionen für einzelne Token-Generierungsobjekte. In diesem Fall würde die Angabe einer Aktivierungsfunktion für das Verkettungsobjekt die Daten nur verzerren.
Am Ende der Methode geben wir das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurück.
Als Nächstes müssen wir den Algorithmus für den Vorwärtsdurchlauf in der Methode feedForward implementieren. Der Algorithmus ist recht einfach.
bool CNeuronMoT::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cNodesTokenizer.FeedForward(NeuronOCL)) return false; if(!cEdgesTokenizer.FeedForward(NeuronOCL)) return false; if(!cSubGraphsTokenizer.FeedForward(NeuronOCL)) return false;
Die Methode erhält einen Zeiger auf das Objekt, das die Eingabedaten enthält, die an die entsprechenden Methoden der internen Objekte auf verschiedenen Tokenisierungsebenen weitergegeben werden.
Für die Tokengenerierung in unitäre Sequenzen durchläuft eine Schleife die Objekte des internen Modells.
CNeuronBaseOCL *prev = NeuronOCL, *current = NULL; for(int i = 0; i < cUnitarSubGraphsTokenizer.Total(); i++) { current = cUnitarSubGraphsTokenizer[i]; if(!current || !current.FeedForward(prev)) return false; prev = current; }
Alle generierten Token werden in einem einzigen Tensor zusammengefasst, der die Sequenzelemente darstellt.
if(!Concat(cNodesTokenizer.getOutputIndex(), cEdgesTokenizer.getOutputIndex(), cSubGraphsTokenizer.getOutputIndex(), current.getOutputIndex(), cConcatenate.getOutputIndex(), iWindow, iWindow, iWindow, iWindow, iUnits)) return false;
Der resultierende Tensor wird an die gleichnamige Methode der Elternklasse weitergegeben, um die endgültige Graphendarstellung zu erhalten.
return CNeuronMHAttentionPooling::feedForward(cConcatenate.AsObject());
}
Wir geben das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurück und schließen die Ausführung der Methode ab.
Obwohl die Methode feedForward konzeptionell einfach ist, führt sie vier parallele Informationsströme aus, was die Gradientenverteilung erschwert. Sein Algorithmus ist in der Methode calcInputGradients implementiert.
bool CNeuronMoT::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Die Methode erhält einen Zeiger auf das gleiche Quelldatenobjekt. Diesmal müssen wir auch den Fehlergradienten im Einfluss der Eingabedaten auf die Modellausgabe einbeziehen. Daten können nur an ein gültiges Objekt übergeben werden. Daher wird zunächst die Gültigkeit des Zeigers überprüft.
Der Fehlergradient von nachfolgenden Objekten wird unter Verwendung der übergeordneten Klasse bis zum Token-Verkettungsobjekt verteilt.
if(!CNeuronMHAttentionPooling::calcInputGradients(cConcatenate.AsObject())) return false;
Der Gradient wird dann auf alle Informationsströme aufgeteilt.
CNeuronBaseOCL *current = cUnitarSubGraphsTokenizer[-1]; if(!current || !DeConcat(cNodesTokenizer.getGradient(), cEdgesTokenizer.getGradient(), cSubGraphsTokenizer.getGradient(), current.getGradient(), cConcatenate.getGradient(), iWindow, iWindow, iWindow, iWindow, iUnits)) return false;
Als Nächstes müssen wir den Fehlergradienten auf alle Informationsströme verteilen.
Aus dem Verkettungsobjekt erhalten wir den Fehlergradienten, der noch nicht um die Ableitung der Aktivierungsfunktion bereinigt wurde. Daher müssen wir, bevor wir mit den Operationen der einzelnen Informationsströme beginnen, die Werte an die Ableitungen der entsprechenden Aktivierungsfunktionen anpassen.
Zunächst verteilen wir den Fehlergradienten entlang univariater Sequenzen. Zunächst überprüfen wir das Vorhandensein der Aktivierungsfunktion und passen gegebenenfalls die erhaltenen Werte an.
if(current.Activation() != None && !DeActivation(current.getOutput(), current.getGradient(), current.getGradient(), current.Activation())) return false;
Als Nächstes führen wir eine Backpropagation-Schleife über die Objekte des internen Modells durch und rufen nacheinander die entsprechenden Methoden auf.
for(int i = cUnitarSubGraphsTokenizer.Total() - 2; i >= 0; i--) { current = cUnitarSubGraphsTokenizer[i]; if(!current || !current.calcHiddenGradients(cUnitarSubGraphsTokenizer[i + 1])) return false; }
Danach propagieren wir den Fehlergradienten auf die Ebene der Quelldaten.
if(!NeuronOCL.calcHiddenGradients(current.AsObject())) return false;
In diesem Stadium haben wir den Fehlergradienten über nur einen Zweig an die Quelldatenebene weitergegeben. Wir müssen dies für drei weitere Zweige tun.
Um die zuvor ermittelten Werte zu erhalten, tauschen wir die Zeiger auf die entsprechenden Datenpuffer aus.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(current.getPrevOutput(), false)) return false;
Sobald wir sicher sind, dass die zuvor gewonnenen Daten gespeichert wurden, propagieren wir die Gradienten entlang der übrigen Zweige. Hier überprüfen wir nacheinander das Vorhandensein der Aktivierungsfunktion und passen die Werte ggf. an die entsprechende Ableitung der Aktivierungsfunktion an.
if(cNodesTokenizer.Activation() != None && !DeActivation(cNodesTokenizer.getOutput(), cNodesTokenizer.getGradient(), cNodesTokenizer.getGradient(), cNodesTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cNodesTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
Dann propagieren wir den Fehlergradienten auf die Ebene der Quelldaten und summieren ihn mit den zuvor akkumulierten Werten. Wiederholen Sie die Vorgänge für den nächsten Zweig.
if(cEdgesTokenizer.Activation() != None && !DeActivation(cEdgesTokenizer.getOutput(), cEdgesTokenizer.getGradient(), cEdgesTokenizer.getGradient(), cEdgesTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cEdgesTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
if(cSubGraphsTokenizer.Activation() != None && !DeActivation(cSubGraphsTokenizer.getOutput(), cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.getGradient(), cSubGraphsTokenizer.Activation())) return false; if(!NeuronOCL.calcHiddenGradients(cSubGraphsTokenizer.AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, iWindow, false, 0, 0, 0, 1)) return false;
Nach erfolgreicher Weitergabe von Fehlergradienten über alle Informationsströme hinweg setzen wir die Zeiger in ihren ursprünglichen Zustand zurück, geben das boolesche Ergebnis der Operation an den Aufrufer zurück und beenden die Methode.
if(!NeuronOCL.SetGradient(temp, false)) return false; //--- return true; }
Damit schließen wir den Überblick über den algorithmischen Aufbau der Methoden des adaptiven gemischten Tokenisierungsobjekts CNeuronMoT ab. Die vollständige Implementierung dieses Objekts und alle seine Methoden finden Sie im Anhang.
Wir haben das Ende dieses Artikels erreicht, aber unsere Arbeit ist noch nicht abgeschlossen. Lassen Sie uns eine kurze Pause einlegen und die Arbeit im nächsten Teil fortsetzen.
Schlussfolgerung
In diesem Artikel haben wir einen innovativen Ansatz für die Verwendung hybrider Graphsequenzmodelle (GSM++) untersucht, der die Leistungsfähigkeit von Graphstrukturen mit der sequentiellen Datenanalyse kombiniert. Diese Modelle bieten eine hohe Prognose- und Analysegenauigkeit und verarbeiten effizient komplexe Finanzdaten. Darüber hinaus optimieren sie die Nutzung von Rechenressourcen, was sie für die Arbeit mit großen Datenmengen besonders wertvoll macht. Ein entscheidender Vorteil von GSM++ ist seine Fähigkeit, sich an die sich schnell ändernden Marktbedingungen anzupassen.
Im praktischen Teil haben wir unsere eigene Vision der vorgeschlagenen Ansätze umgesetzt und ein gemischtes Tokenisierungsmodul konstruiert. Im nächsten Artikel werden wir diese Arbeit fortsetzen und die Wirksamkeit unserer Implementierung an realen historischen Daten testen.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Expert Advisor für die Probenahme |
| 2 | ResearchRealORL.mq5 | Expert Advisor | Expert Advisor für die Probenahme mit der Methode Real-ORL |
| 3 | Study.mq5 | Expert Advisor | Expert Advisor für das Training des Modells |
| 4 | Test.mq5 | Expert Advisor | Expert Advisor für den Modeltest |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Beschreibung des Systemzustands und der Modellarchitektur |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Code Base | OpenCL-Programmcode |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17279
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Verwendung von Deep Reinforcement Learning zur Verbesserung des Ilan Expert Advisor
Verwendung von Deep Reinforcement Learning zur Verbesserung des Ilan Expert Advisor
 Swap-Arbitrage am Devisenmarkt: Aufbau eines synthetischen Portfolios und Generierung eines konsistenten Swapflusses
Swap-Arbitrage am Devisenmarkt: Aufbau eines synthetischen Portfolios und Generierung eines konsistenten Swapflusses
 Marktsimulation (Teil 10): Sockets (IV)
Marktsimulation (Teil 10): Sockets (IV)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.