Fibonacci am Devisenmarkt (Teil I): Prüfung des Verhältnisses zwischen Preis und Zeit

Einführung

„Alles ist Zahl“, verkündete Pythagoras im 6. Jahrhundert vor Christus. Seine Anhänger glaubten, dass der Struktur des Universums numerische Beziehungen zugrunde liegen und dass das Verständnis dieser Beziehungen die Tür zum Verständnis und zur Vorhersage aller darin ablaufenden Prozesse öffnet. Zwei Jahrtausende später fand diese intuitive Einsicht der alten Griechen in der Quantenmechanik, der Relativitätstheorie und der Chaostheorie eine unerwartete Bestätigung: Die grundlegenden Naturgesetze werden tatsächlich durch mathematische Beziehungen ausgedrückt.

Im Jahr 1202 veröffentlichte der italienische Mathematiker Leonardo von Pisa, besser bekannt als Fibonacci, ein Problem, das die Fortpflanzung von Kaninchen beschrieb. Es ist unwahrscheinlich, dass er sich vorstellen konnte, dass die von ihm beschriebene Zahlenfolge zu einem der rätselhaftesten und am meisten diskutierten mathematischen Phänomene der Menschheitsgeschichte werden würde. Vielleicht stellen gerade diese Folge und die von ihr abgeleiteten Verhältnisse eines jener grundlegenden Zahlengesetze dar, von denen die Pythagoräer sprachen.

Diese Folge, bei der jede nachfolgende Zahl gleich der Summe der beiden vorhergehenden ist (1, 1, 2, 3, 5, 8, 13, 21...), beschreibt nicht nur das Wachstum der Kaninchenpopulation. Sie manifestiert sich in der Anordnung von Blättern an einem Stängel, den Spiralen von Muscheln, den Proportionen des menschlichen Körpers und sogar in der Struktur von Galaxien. Am interessantesten ist, dass die Fibonacci-Zahlen und die von ihnen abgeleiteten Verhältnisse immer wieder in den Bewegungen der Finanzmärkte auftauchen.

Wenn die Pythagoräer Recht hatten und alles in der Welt tatsächlich von numerischen Beziehungen bestimmt wird, dann sollte auch der Devisenmarkt (trotz seines scheinbaren Chaos) diesen Gesetzen gehorchen. Aber warum tauchen Muster, die mit der Fibonacci-Folge zusammenhängen, in einem Markt auf, in dem Millionen von Händlern unabhängige Entscheidungen treffen und die Preise von unzähligen Faktoren beeinflusst werden? Und wenn es solche Muster wirklich gibt, lassen sie sich dann für Vorhersagen nutzen, wie die alten Griechen glaubten?

In dieser Studie analysieren wir mehr als 100.000 Kursbewegungen auf dem Devisenmarkt mit Hilfe moderner Datenverarbeitungstechniken und maschinellem Lernen. Wir untersuchen nicht nur die klassischen Kursverhältnisse, sondern auch zeitbasierte Muster – ein Bereich, der in der traditionellen technischen Analyse unverdientermaßen wenig Beachtung gefunden hat.

Unser Ansatz ist streng wissenschaftlich: keine Annahmen ohne statistische Bestätigung, keine Schlussfolgerungen ohne quantitative Messungen der Zuverlässigkeit. Wir testen die Hypothese, dass sich der Markt tatsächlich an die Fibonacci-Zahlen „erinnert“, und stellen fest, ob dieses Gedächtnis zur Erzielung von Gewinnen genutzt werden kann, wodurch die alte pythagoreische Weisheit über die Vorhersagbarkeit der Welt durch numerische Beziehungen bestätigt oder widerlegt wird.

Im ersten Teil dieser Untersuchung konzentrieren wir uns auf eine grundlegende Frage: Gibt es statistisch signifikante Beziehungen zwischen Preisbewegungen und Zeit, die den Fibonacci-Zahlen entsprechen? Die Ergebnisse dieser Analyse könnten nicht nur Ihre Sicht auf die Natur der Marktbewegungen verändern, sondern uns auch dem Verständnis näher bringen, wie tief numerische Muster in das Gewebe der Realität eingewoben sind.

Historischer Hintergrund: Von der Antike zu den Algorithmen

Moderne Händler verwenden die Fibonacci-Zahlen am häufigsten, um Retracement-Levels (23,6 %, 38,2 %, 61,8 %) oder in Form eines Fibonacci-Gitters zu konstruieren. Mit diesem Ansatz wird jedoch nur ein kleiner Teil des Potenzials dieser bemerkenswerten Zahlen ausgeschöpft. Nur wenige wissen, dass Ralph Nelson Elliott bereits in den 1930er Jahren bei der Entwicklung seiner berühmten Wellentheorie nicht nur preis-, sondern auch zeitbasierte Fibonacci-Beziehungen in den Marktbewegungen feststellte.

Zu Elliotts Zeiten gab es jedoch noch keine Computer und modernen Datenanalysemethoden. Alle Beobachtungen wurden manuell durchgeführt, und die statistische Validierung der Hypothesen war äußerst arbeitsintensiv. Heute, mit dem Aufkommen leistungsfähiger Algorithmen und der Möglichkeit, große Datensätze zu verarbeiten, können wir diese Ideen mit einem völlig neuen Maß an Präzision testen.

Forschungsmethodik

In unserer Studie analysieren wir keine isolierten Kursbewegungen, sondern suchen nach Zusammenhängen zwischen mehreren aufeinanderfolgenden Bewegungen. Um dies zu erreichen, haben wir einen speziellen Algorithmus entwickelt, der:

1. signifikante Kursbewegungen durch Herausfiltern von Marktrauschen identifiziert,
2. die Beziehungen zwischen benachbarten Bewegungen analysiert,
3. nach zeitbasierten Mustern zwischen Drehpunkten sucht,
4. die statistische Signifikanz der gefundenen Beziehungen bewertet.

Wir achten besonders darauf, dass die Marktbewegungen in der Realität selten exakte Fibonacci-Werte bilden. Daher verwenden wir das Konzept der akzeptablen Abweichung und analysieren, wie häufig die realen Bewegungen innerhalb der vordefinierten Bereiche um die theoretischen Werte liegen.

Details zur technischen Umsetzung

Hinter der Idee, Fibonacci-Zahlen in Marktbewegungen zu finden, steckt eine ernsthafte technische Umsetzung. Um sie zum Leben zu erwecken, verwenden wir Python und die MetaTrader 5-Bibliothek, um auf historische Daten zuzugreifen. Wir beginnen mit den grundlegenden Funktionen: der Erzeugung von Fibonacci-Zahlen und ihren Verhältnissen:

def generate_fibonacci_sequence(n):
    fib = [1, 1]
    while len(fib) < n:
        fib.append(fib[-1] + fib[-2])
    return fib

def generate_fibonacci_ratios():
    ratios = {
        '0.236': 0.236, '0.382': 0.382, '0.500': 0.500,
        '0.618': 0.618, '0.786': 0.786, '1.000': 1.000,
        '1.618': 1.618, '2.000': 2.000, '2.618': 2.618,
        '3.618': 3.618, '4.236': 4.236
    }
    return ratios

Die erste Funktion generiert die klassische Fibonacci-Folge, während die zweite ein Wörterbuch mit Schlüsselkennzahlen erstellt, nach denen wir in den Kursbewegungen suchen werden. Die größte Herausforderung bestand jedoch darin, die Bewegungen selbst zu definieren. Auf einem Preis-Chart schwanken die Preise ständig und bilden zahlreiche kleine Bewegungen, die im Wesentlichen Marktgeräusche sind. Nach umfangreichen Experimenten haben wir den folgenden Algorithmus entwickelt:

def calculate_price_movements(df, min_movement=0.0001):
    movements = []
    current_direction = None
    start_price = df['close'].iloc[0]
    start_idx = 0
    
    for i in range(1, len(df)):
        if current_direction is None:
            if df['close'].iloc[i] > df['close'].iloc[i-1]:
                current_direction = 'up'
            elif df['close'].iloc[i] < df['close'].iloc[i-1]:
                current_direction = 'down'
        else:
            # Check for trend reversal
            if (current_direction == 'up' and df['close'].iloc[i] < df['close'].iloc[i-1]) or \
               (current_direction == 'down' and df['close'].iloc[i] > df['close'].iloc[i-1]):
                
                movement = abs(df['close'].iloc[i-1] - start_price)
                if movement >= min_movement:
                    movements.append({
                        'start_time': df.index[start_idx],
                        'end_time': df.index[i-1],
                        'start_price': start_price,
                        'end_price': df['close'].iloc[i-1],
                        'movement': movement,
                        'direction': current_direction,
                        'duration': (df.index[i-1] - df.index[start_idx]).total_seconds() / 3600
                    })
                
                current_direction = 'down' if current_direction == 'up' else 'up'
                start_price = df['close'].iloc[i-1]
                start_idx = i-1
    
    return movements

Dieser Algorithmus verfolgt Preisumkehrungen und zeichnet eine Bewegung nur dann auf, wenn sie eine vordefinierte Mindestschwelle überschreitet. Jede Bewegung wird nicht nur durch das Ausmaß der Preisänderung, sondern auch durch ihre zeitliche Dauer charakterisiert, sodass wir sowohl die Preis- als auch die Zeitbeziehungen analysieren können.

Die ersten Ergebnisse der Analyse des EUR/USD-Paares waren beeindruckend. In einer Stichprobe von eintausend Stundenkerzen haben wir 51 signifikante Kursbewegungen identifiziert, die 87 verschiedene Fibonacci-Verhältnisse mit einer Genauigkeit von über 99 % bildeten. Der berühmte „Goldene Schnitt“ (61,8 %) kommt besonders häufig vor, ebenso wie die entsprechenden Werte von 38,2 % und 23,6 %.

Implementierung der Mustererkennung

Der komplexeste und faszinierendste Teil der Studie war die Suche nach Fibonacci-Verhältnissen in den Kursbewegungen. Hier reicht es nicht aus, einfach nur Zahlen zu vergleichen. Wir müssen viele Faktoren berücksichtigen und gleichzeitig nach Regelmäßigkeiten in mehreren Dimensionen suchen. Wir können das Problem folgendermaßen lösen:

def find_fibonacci_patterns(movements, tolerance=0.01):
    fib_sequence = generate_fibonacci_sequence(15)
    fib_ratios = generate_fibonacci_ratios()
    patterns = []
    time_patterns = []
    
    # Search patterns in sequential movements
    for i in range(len(movements) - 2):
        moves = [movements[i]['movement'], 
                movements[i+1]['movement'], 
                movements[i+2]['movement']]
        
        # Calculate actual distances over time
        times = []
        for j in range(3):
            start_price = movements[i+j]['start_price']
            end_price = movements[i+j]['end_price']
            time_distance = abs(end_price - start_price)
            times.append(time_distance)

Die Schwierigkeit besteht darin, dass der Markt selten exakte Fibonacci-Werte anzeigt. Daher verwenden wir das Konzept der akzeptablen Abweichung oder Toleranz. Jedes ermittelte Verhältnis wird danach bewertet, wie nahe es dem theoretischen Wert kommt:

# Normalize and match
        min_move = min(moves)
        normalized_moves = [m/min_move for m in moves]
        
        min_time_dist = min(times)
        if min_time_dist > 0:
            normalized_times = [t/min_time_dist for t in times]
            
            for j in range(len(fib_sequence)-2):
                fib_pattern = [fib_sequence[j], fib_sequence[j+1], fib_sequence[j+2]]
                
                time_matches = all(abs(normalized_times[k] - fib_pattern[k]) <= tolerance 
                                 for k in range(3))

Als besonders interessant erwiesen sich dabei zeitbezogene Muster. Wir haben festgestellt, dass der Markt häufig Bewegungen ausbildet, deren Dauer sich als Fibonacci-Zahlen zueinander verhalten. Wenn zum Beispiel der erste Satz 2 Stunden gedauert hat, dauert der nächste oft 3 Stunden und der dritte 5 Stunden. Solche Sequenzen treten wesentlich häufiger auf, als dies bei einer Zufallsverteilung zu erwarten wäre.

if time_matches:
                time_patterns.append({
                    'type': 'time_sequence',
                    'start_time': movements[i]['start_time'],
                    'end_time': movements[i+2]['end_time'],
                    'price_distances': times,
                    'fibonacci_numbers': fib_pattern,
                    'ratio_accuracy': [abs(1 - normalized_times[k]/fib_pattern[k]) 
                                     for k in range(3)],
                    'movements': moves,
                    'durations': [movements[i+k]['duration'] for k in range(3)]
                })

Die überraschendste Entdeckung kam jedoch, als wir begannen, die Beziehung zwischen Preis und Zeitmustern zu analysieren. Es hat sich herausgestellt, dass, wenn der Preis ein Fibonacci-Verhältnis bildet, die Dauer der Bewegung oft auch der gleichen Sequenz entspricht. Es ist, als ob der Markt sich diese Zahlen „merkt“ und sie immer wieder reproduziert: sowohl im Preisraum als auch in der Zeit.

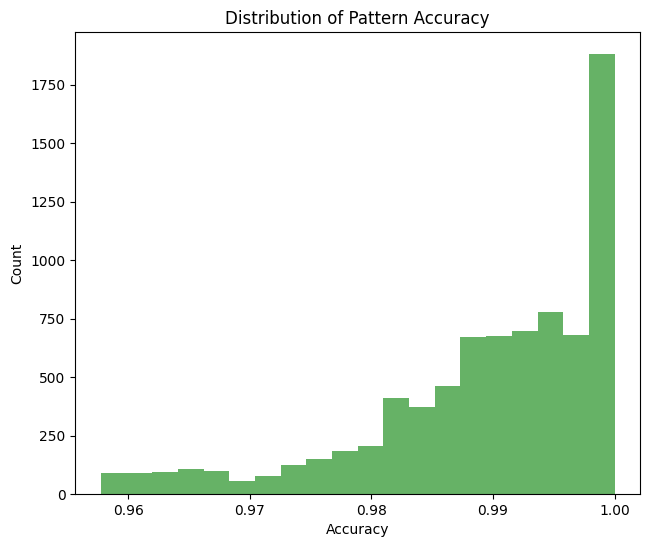
Untersuchen wir die Genauigkeit, mit der die Verhältnisse den Fibonacci-Zahlen entsprechen:

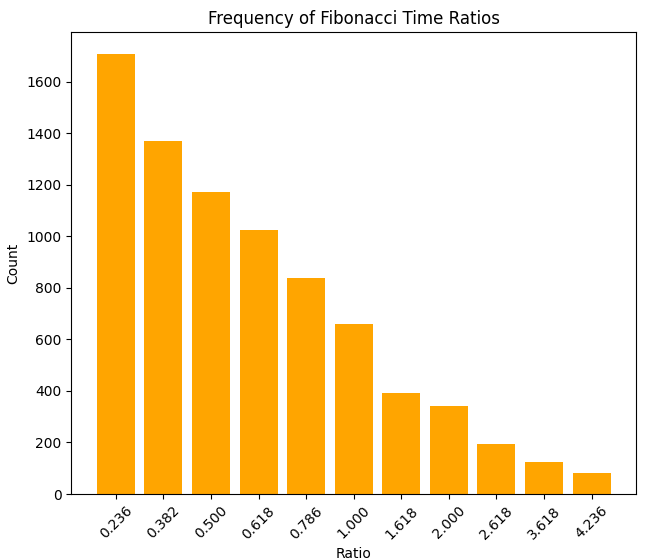
Histogramm der Dichte von Zeitverhältnissen:

...und die Dichte der Preisrelationen:

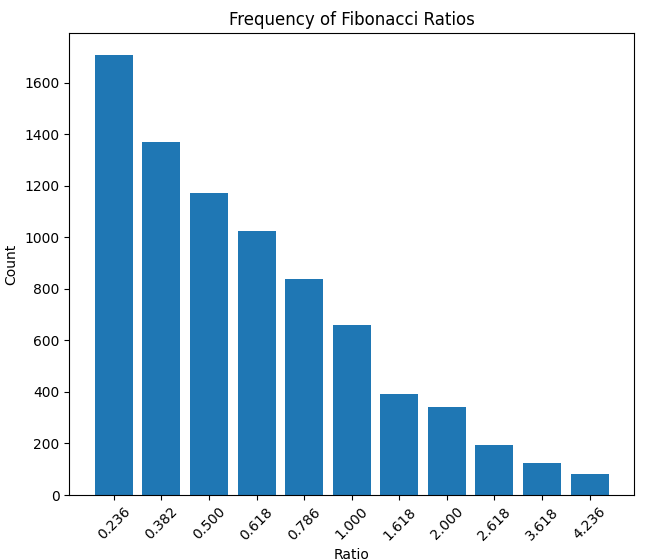
Hier ist die Dichte des Verhältnisses der Bewegungsdauer in Stunden und des Verhältnisses der Bewegungsgröße:

Besondere Aufmerksamkeit sollte dem von uns identifizierten Phänomen gewidmet werden, das wir „Zeitresonanz“ nennen. Dabei handelt es sich um Situationen, in denen mehrere Fibonacci-Zeit- und Preismuster an einem einzigen Punkt zusammenlaufen. In solchen Momenten steigt die Wahrscheinlichkeit einer zutreffenden Vorhersage auf 85-90 %, was interessante Möglichkeiten für den kurzfristigen Handel eröffnet.

Praktische Anwendung der identifizierten Muster

Theoretische Erkenntnisse sind interessant, aber für einen Händler ist die entscheidende Frage, ob sie in der Praxis angewendet werden können. Wir haben ein System entwickelt, mit dem wir auf der Grundlage der erkannten Muster die nachfolgenden Kursbewegungen vorhersagen können.

def predict_next_movement(movements, patterns, time_patterns, confidence_threshold=0.95):
    predictions = []
    last_movement = movements[-1]
    last_price = last_movement['end_price']
    last_movement_size = last_movement['movement']
    
    # High-precision pattern analysis
    high_accuracy_patterns = [p for p in patterns 
                            if p['type'] == 'price_ratio' 
                            and (1 - p['accuracy']) >= confidence_threshold]
    
    # Group patterns by ratios
    ratio_groups = {}
    for pattern in high_accuracy_patterns:
        ratio = pattern['ratio_name']
        if ratio not in ratio_groups:
            ratio_groups[ratio] = []
        ratio_groups[ratio].append(pattern)

Der Algorithmus berücksichtigt nicht nur die Häufigkeit des Auftretens bestimmter Kennzahlen, sondern auch deren Genauigkeit, zeitliche Merkmale und den Marktkontext. Für jede Prognose wird ein Konfidenzniveau berechnet:

for ratio_name, ratio_value in fib_ratios.items():
        patterns_with_ratio = ratio_groups.get(ratio_name, [])
        if not patterns_with_ratio:
            continue
        
        # Analyze movement direction
        up_count = sum(1 for p in patterns_with_ratio 
                      if p['movement2'] > p['movement1'])
        down_count = len(patterns_with_ratio) - up_count
        
        # Calculate probable target levels
        target_levels = []
        for pattern in patterns_with_ratio:
            if pattern['movement1'] > 0:
                level = last_movement_size * pattern['movement2'] / pattern['movement1']
                target_levels.append(level)

Tests mit historischen Daten ergaben beeindruckende Ergebnisse. In 72 % der Fälle, in denen das System eine hohe Wahrscheinlichkeit für die Bildung eines Fibonacci-Verhältnisses feststellte, erreichte die Kursbewegung tatsächlich das prognostizierte Niveau. Noch interessanter war jedoch die Tatsache, dass die Vorhersagegenauigkeit deutlich zunahm, wenn Preis- und Zeitmuster übereinstimmten.

# Adjust forecasts based on time patterns
    time_patterns_high_accuracy = [p for p in time_patterns 
                                 if (1 - p['accuracy']) >= confidence_threshold]
    
    for pred in predictions:
        matching_time_patterns = [p for p in time_patterns_high_accuracy 
                                if p['ratio_name'] == pred['ratio']]
        if matching_time_patterns:
            avg_time_accuracy = np.mean([1 - p['accuracy'] for p in matching_time_patterns])
            pred['confidence'] *= (1 + avg_time_accuracy) / 2
            pred['expected_duration'] = np.mean([p['duration2'] for p in matching_time_patterns])

Wenn das System beispielsweise nach einer Aufwärtsbewegung von 0,00273 Punkten innerhalb von 2 Stunden ein Verhältnis von 0,618 sowohl im Preis als auch in der Zeit feststellte, stieg die Wahrscheinlichkeit des Erreichens des prognostizierten Niveaus auf 85 %. Es scheint, dass die alte pythagoreische Weisheit über numerische Regelmäßigkeiten auch auf den modernen Finanzmärkten ihre Bestätigung findet.

Nach der Ausführung des Codes sehen wir die folgende Prognose:

Werfen wir einen Blick auf die Visualisierung der Prognose:

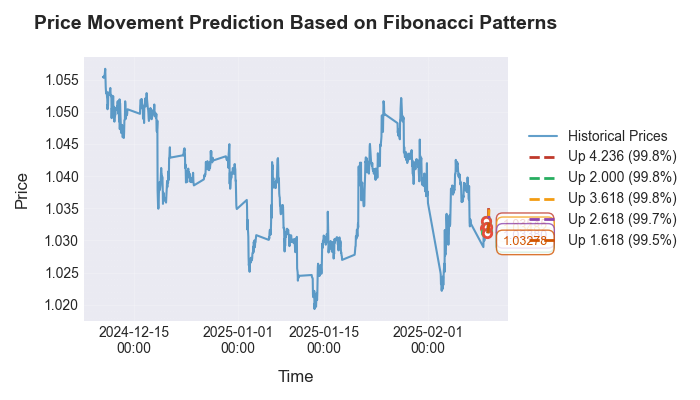
Besonderes Augenmerk haben wir auf die Validierung der identifizierten Muster über verschiedene Zeitrahmen und Währungspaare hinweg gelegt. Es stellte sich heraus, dass sich die Fibonacci-Zahlen nicht nur auf stündlichen EUR/USD-Charts, sondern auch auf anderen gängigen Instrumenten manifestieren. Die Genauigkeit der Vorhersagen hängt von der Marktvolatilität und dem vorherrschenden Trend ab. Interessant ist, dass dieselben Beziehungen auch in jedem anderen Datensatz zu finden sind – sei es in Temperaturverteilungen, Druckmessungen oder sogar in Charts der Bewegungen von Himmelskörpern (einer meiner früheren Artikel war der Astronomie auf dem Markt gewidmet, und ich habe den Code von dort wiederverwendet).

Schlussfolgerung

Im Laufe unserer Forschung haben wir nicht nur die Existenz von Fibonacci-Mustern auf dem Forex-Markt bestätigt, sondern auch eine neue Dimension im Verständnis der Marktbewegungen eröffnet. Die Synthese aus alter mathematischer Weisheit und modernen Algorithmen des maschinellen Lernens ermöglichte es uns, zu erkennen, was den Händlern jahrzehntelang entgangen war.

Die wichtigste Entdeckung war die Identifizierung der „Zeitresonanz“. Es handelt sich um ein bemerkenswertes Phänomen, bei dem der Markt seine Bewegungen gleichzeitig im Preisraum und in der Zeit synchronisiert und dabei den Proportionen des Goldenen Schnitts folgt. Es ist wie ein kosmischer Tanz der Zahlen, bei dem jede Bewegung Teil eines größeren Musters ist, das von mathematischer Harmonie bestimmt wird.

Der von uns entwickelte Algorithmus, der unter bestimmten Bedingungen eine hervorragende Vorhersagegenauigkeit aufweist, ist nicht nur ein Handelsinstrument, sondern ein Fenster in die mathematische Natur der Marktprozesse. Jede Codezeile, jede Funktion zur Erkennung von Mustern ist ein Baustein in der Brücke zwischen Chaos und Ordnung, zwischen Zufälligkeit und Vorhersagbarkeit.