Neuronale Netze im Handel: Ein hybrider Handelsrahmen mit prädiktiver Kodierung (StockFormer)

Einführung

Das Verstärkungslernen (Reinforcement Learning, RL) wird zunehmend auf komplexe Probleme im Finanzbereich angewandt, einschließlich der Entwicklung von Handelsstrategien und Portfoliomanagement. Die Modelle werden trainiert, um historische Daten über die Preisentwicklung von Vermögenswerten, Handelsvolumina und technische Indikatoren zu analysieren. Die meisten bestehenden Methoden gehen jedoch davon aus, dass die analysierten Daten alle Abhängigkeiten zwischen den Anlagen vollständig erfassen. In der Praxis ist dies nur selten der Fall, insbesondere in einem sehr volatilen Marktumfeld mit starkem Rauschen.

Herkömmliche Ansätze berücksichtigen häufig weder die kurz- und langfristigen Renditeprognosen noch die Korrelationen zwischen den einzelnen Vermögenswerten. Erfolgreiche Anlagestrategien beruhen jedoch in der Regel auf einem umfassenden Verständnis dieser Faktoren. Um dieses Problem anzugehen, wurde in dem Artikel „StockFormer: Learning Hybrid Trading Machines with Predictive Coding“ der StockFormer vorgesterllt, ein hybrides Handelssystem, das Predictive Coding mit der Flexibilität von RL-Agenten kombiniert. Die prädiktive Kodierung, die in der Verarbeitung natürlicher Sprache und im Computersehen weit verbreitet ist, ermöglicht die Extraktion informativer verborgener Zustände aus verrauschten Eingabedaten, eine Fähigkeit, die besonders in Finanzanwendungen wertvoll ist.

Der StockFormer integriert drei modifizierte Transformer-Zweige, die jeweils für die Erfassung verschiedener Aspekte der Marktdynamik zuständig sind:

• Langfristige Trends
• Kurzfristige Trends
• Instrumentübergreifende Abhängigkeiten

Jeder Zweig enthält einen Mechanismus, den Diversified Multi-Head Attention (DMH-Attn), der den ursprünglichen Transformer erweitert, indem er einen einzelnen Block von FeedForward durch mehrere parallele Blöcke ersetzt. Auf diese Weise kann das Modell verschiedene zeitliche Muster über Teilräume hinweg erfassen und gleichzeitig wichtige Informationen bewahren.

Um die Handelsstrategien zu optimieren, werden die latenten Zustände, die von diesen drei Zweigen erzeugt werden, mit Hilfe von Multi-Head-Attention adaptiv zu einem einheitlichen Zustandsraum verschmolzen, der dann vom RL-Agenten verwendet wird.

Das Erlernen der Politik erfolgt mit Hilfe der Methode Akteur–Kritiker. Entscheidend ist, dass das Gradienten-Feedback des Kritiker-Moduls zur Verbesserung des Moduls für die prädiktive Codierung zurückgeführt wird, wodurch eine enge Integration zwischen prädiktiver Modellierung und Optimierung der Politik gewährleistet wird.

Experimente, die mit drei öffentlichen Datensätzen durchgeführt wurden, haben gezeigt, dass StockFormer sowohl bei der Vorhersagegenauigkeit als auch bei den Anlagerenditen die bestehenden Methoden deutlich übertrifft.

Der StockFormer-Algorithmus

StockFormer befasst sich mit Prognosen und Handelsentscheidungen auf den Finanzmärkten durch RL. Eine wesentliche Einschränkung herkömmlicher Methoden besteht darin, dass sie nicht in der Lage sind, dynamische Abhängigkeiten zwischen Vermögenswerten und deren künftige Entwicklung effektiv zu modellieren. Dies ist besonders wichtig auf Märkten, auf denen sich die Bedingungen schnell und unvorhersehbar ändern. StockFormer löst diese Herausforderung durch zwei zentrale Schritte: prognoseorientiertes Codieren und Training der Handelsstrategie.

In der ersten Phase nutzt StockFormer das selbstüberwachte Lernen, um versteckte Muster aus verrauschten Marktdaten zu extrahieren. Dadurch kann das Modell sowohl kurz- und langfristige Dynamiken als auch instrumentübergreifende Abhängigkeiten erfassen. Mit diesem Ansatz extrahiert das Modell wichtige verborgene Zustände, die dann im nächsten Schritt für Handelsentscheidungen verwendet werden.

Die Finanzmärkte weisen sehr unterschiedliche zeitliche Muster über mehrere Vermögenswerte hinweg auf, was die Gewinnung effektiver Darstellungen aus Rohdaten erschwert. Um dieses Problem zu lösen, modifiziert StockFormer den mehrköpfigen Aufmerksamkeit-Mechanismus des ursprünglichen Transformers, indem das einzelne FeedForward-Netzwerk (FFN) durch eine Gruppe paralleler FFNs ersetzt wird. Ohne die Anzahl der Parameter zu erhöhen, stärkt dieses Design die Fähigkeit der mehrköpfigen Aufmerksamkeit, Merkmale zu zerlegen, und verbessert so die Modellierung heterogener zeitlicher Muster über Teilräume hinweg.

Dieses erweiterte Modul wird diversifizierte mehrköpfige Aufmerksamkeit (Diversified Multi-Head Attention, DMH-Attn) genannt. Bei den Entitäten von Query, Key und Value der Dimension dmodel beginnt der Prozess mit der Aufteilung der Ausgangsmerkmale Z der mehrköpfige Aufmerksamkeit in h Gruppen entlang der Kanaldimension, wobei h die Anzahl der Aufmerksamkeitsköpfe ist. Ein spezielles FFN wird dann auf jede Gruppe in Z angewendet:

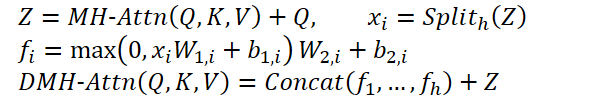
MH-Attn bezeichnet hier die Aufmerksamkeit mehrerer Köpfe. 𝑓𝑖 sind Ausgangsmerkmale jedes FFN-Kopfes, die zwei lineare Projektionen mit ReLU-Aktivierung zwischen ihnen enthalten.

Jeder Zweig im modernisierten Transformer in StockFormer ist in zwei Module unterteilt: einen Encoder und einen Decoder. Beide werden beim Training der prädiktiven Kodierung verwendet, aber nur der Kodierer wird bei der Strategieoptimierung eingesetzt. Das Modell umfasst L Encoderschichten und M Decoderschichten. Der endgültige Encoderausgang XLenc wird in jede Decoderschicht eingespeist. Der Prozess der Berechnungen auf der l-ten Kodierschicht und der m-ten Dekodierschicht kann wie folgt beschrieben werden:

• Encoderschicht:

• Decoderschicht:

Dabei sind Xl,enc und Xm,dec die Ausgänge des Encoders bzw. des Decoders. Die Eingaben für die erste Encoder- und Decoderschicht bestehen aus Rohdaten mit Positionseinbettungen. Die endgültige Decoderausgabe wird durch eine Projektionsschicht geleitet, um prädiktive Kodierungsergebnisse zu erzeugen.

Das Modul für vermögensübergreifende Abhängigkeiten identifiziert dynamische Korrelationen zwischen Zeitreihen. In jedem Zeitschritt t verarbeitet es identische Eingaben in Encoder und Decoder. Für die Börsendaten verwendeten die Autoren des Rahmens technische Indikatoren wie MACD, RSI und SMA.

Beim Training werden die Daten in zwei Teile aufgeteilt:

1. Kovarianzmatrix. Die Kovarianzmatrix wird für die täglichen Schlusskurse aller Vermögenswerte über ein festes Zeitfenster vor dem Zeitpunkt t berechnet.
2. Maskierte Statistik. Dieser Teil enthält die Hälfte der Zeitreihen, die nach dem Zufallsprinzip mit Nullen maskiert werden, während der Rest als sichtbare Merkmale dient. Zum Testzeitpunkt verwenden wir vollständige (unmaskierte) Daten.

Ziel ist es, maskierte Statistiken auf der Grundlage der Kovarianzmatrix und der übrigen Merkmale zu rekonstruieren. Diese prädiktive Codierungsaufgabe zwingt den Transformer-Encoder, Abhängigkeiten zwischen den Assets zu lernen.

Kurz- und langfristige Prognosemodule in StockFormer zielen darauf ab, die Renditen für jeden Vermögenswert über verschiedene Zeithorizonte vorherzusagen.

Das Modul für kurzfristige Prognosen sagt die Renditen des nächsten Tages für den Vermögenswert voraus (H = 1). Zu diesem Zweck geben wir die analysierten Statistiken für T Tage in den Encoder ein. Der Decoder erhält dieselbe Statistik, allerdings für den analysierten Zeitpunkt.

Das langfristige Modul funktioniert ähnlich, liefert aber Prognosen über einen längeren Zeitraum. Dadurch wird das Modell ermutigt, eine erweiterte Marktdynamik zu erfassen.

Für das Training der kurzfristigen und langfristigen Prognosemodule wird eine kombinierte Verlustfunktion verwendet, die sowohl den Regressionsfehler als auch den Fehler in der Aktienrangliste berücksichtigt. Der Regressionsfehler minimiert die Diskrepanz zwischen prognostizierter und tatsächlicher Rendite, während der Rangfolgefehler sicherstellt, dass Vermögenswerte mit höherer Rendite bevorzugt werden.

Die beiden Zweige des Modells ermöglichen es StockFormer, die Marktdynamik über verschiedene Zeithorizonte hinweg zu erfassen, sodass der RL-Agent genauere und besser informierte Handelsentscheidungen treffen kann.

In der zweiten Trainingsstufe integriert StockFormer drei Arten von latenten Repräsentationen: srelat,t, slong,t und sshort,t in den einheitlichen Zustandsraum St unter Verwendung einer Kaskade von Mehrkopf-Aufmerksamkeitsblöcken. Der Prozess beginnt mit der Verschmelzung von kurzfristigen und langfristigen Prognosen. Hier dient die langfristige Vorhersagedarstellung als Query, da sie weniger durch kurzfristiges Rauschen beeinträchtigt wird. Das Ergebnis dieses Schritts wird dann mit der latenten Darstellung der Abhängigkeiten von Vermögenswerten abgeglichen, die als Key und Value im nachfolgenden Aufmerksamkeitsmodul verwendet wird.

Das Modell wird dann trainiert, um mit Hilfe des Ansatzes von Akteur–Kritiker die optimale Handelsstrategie zu ermitteln. Einer der Hauptvorteile des StockFormers ist die Integration der Phasen der prognoseorientierten Codierung und der Politik-Optimierung. Die Bewertungen des Kritikers helfen, die Qualität der Extraktion latenter Repräsentationen zu verfeinern, sodass das Modell die Beziehungen zwischen den Vermögenswerten besser analysieren und das Rauschen in den Eingabedaten besser verarbeiten kann.

Die originale Visualisierung des Systems des StockFormer finden Sie unten.

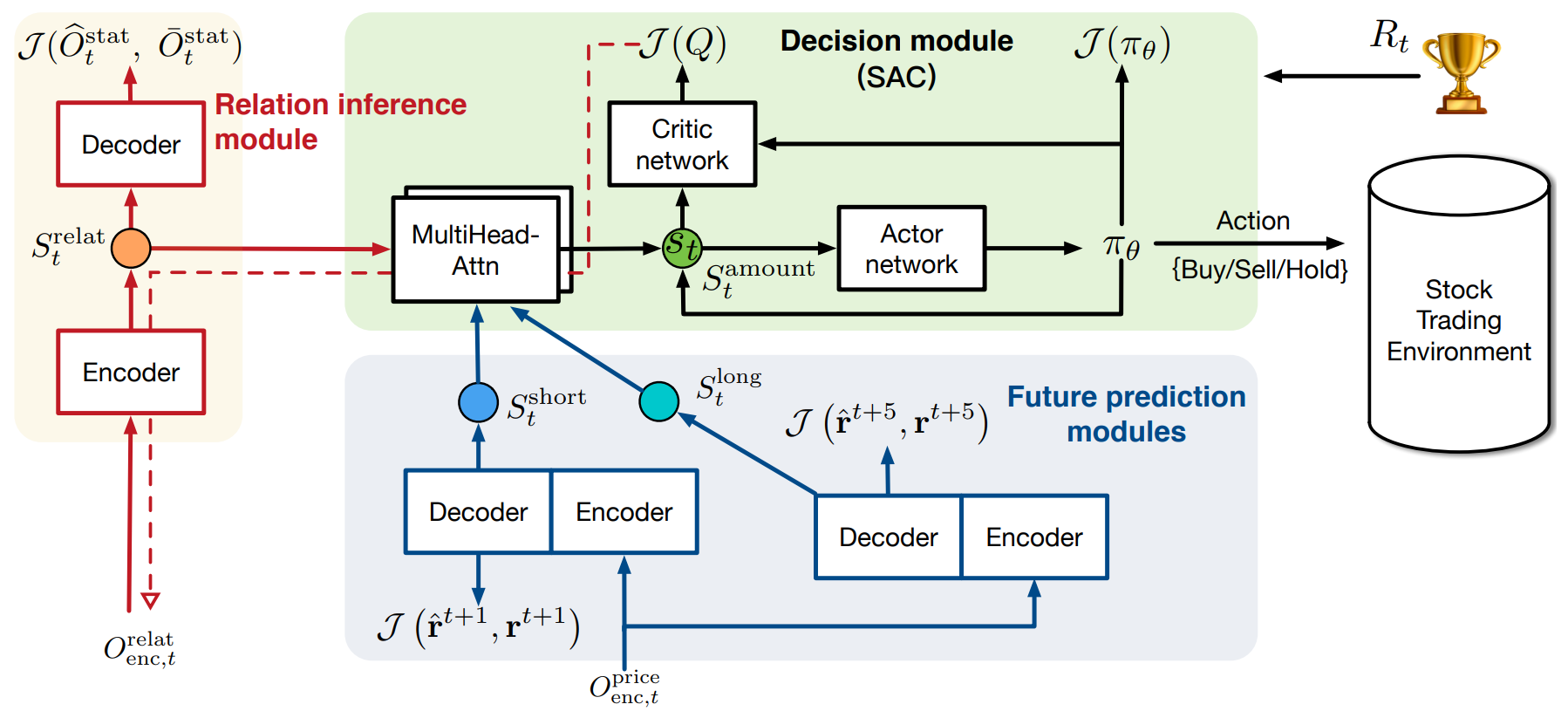
Die Implementation in MQL5

Nachdem wir die theoretischen Grundlagen von StockFormer erläutert haben, wenden wir uns der Implementierung der vorgeschlagenen Methoden in MQL5 zu. Wie in der theoretischen Beschreibung hervorgehoben wurde, besteht die wichtigste architektonische Änderung in der Einführung eines mehrköpfigen Blocks von FeedForward. Die Umsetzung dieses Blocks ist der erste Schritt unserer Arbeit.

Bei der Implementierung des von den Autoren des StockFormer-Rahmens vorgeschlagenen mehrköpfigen FeedForward-Blocks werden die Ausgaben des mehrköpfigen Selbstaufmerksamkeit-Blocks für jedes Sequenzelement in h gleiche Gruppen unterteilt, wobei jede Gruppe von einem eigenen MLP mit eindeutigen trainierbaren Parametern verarbeitet wird.

Es ist wichtig, darauf hinzuweisen, dass sich der Ansatz zur Bildung von Köpfen hier von dem unterscheidet, der im herkömmlichen mehrköpfigen Aufmerksamkeitsblock verwendet wird. In der mehrköpfigen Selbstaufmerksamkeit wurden mehrere Versionen der Entitäten von Query, Key und Value aus einer einzigen Sequenz-Element-Einbettung erzeugt. In diesem Fall schlagen die Autoren von StockFormer jedoch vor, den Repräsentationsvektor eines Sequenzelements direkt in mehrere gleiche Gruppen aufzuteilen. Jede Gruppe wird dann von ihrem eigenen MLP verarbeitet. Dieser Ansatz ermöglicht natürlich die Erstellung mehrerer Köpfe, ohne die Anzahl der trainierbaren Parameter zu erhöhen. Außerdem behält der Ausgangstensor dieselbe Dimensionalität, sodass eine Projektionsschicht wie bei MH Selbstaufmerksamkeit nicht erforderlich ist. Aus diesem Grund können wir jedoch keine bestehenden Faltungsschichten verwenden, wie es früher möglich war. Das heißt, wir müssen eine alternative Lösung finden.

Einerseits könnte man erwägen, den dreidimensionalen Tensor zu transponieren, um die Lösung für Faltungsschichten mit unabhängiger Analyse von eindimensionalen Sequenzen anzupassen. StockFormer enthält jedoch eine beträchtliche Anzahl solcher Ebenen. Daher würde das Umsetzen von Daten vor und nach dem FeedForward-Block in jeder Schicht sowohl die Trainings- als auch die Inferenzzeit erheblich verlängern. Daher wurde beschlossen, eine Mehrkopfvariante der Faltungsschicht zu entwickeln. Bevor diese neue Komponente in das Hauptprogramm implementiert werden kann, sind jedoch einige Anpassungen auf Seiten von OpenCL erforderlich.

Ausweitung des OpenCL-Programms

Wir beginnen mit der Konstruktion des Kerns des Vorwärtsdurchlauf FeedForward für die neue Mehrkopf-Faltungsschicht FeedForwardMHConv. Es ist anzumerken, dass die Parameterstruktur und ein Teil des Algorithmus vom Kernel der bestehenden Faltungsschicht entlehnt wurden. Die Fusionskopf-Kennung und die Gesamtzahl der Köpfe wurden als zusätzliche Dimension in den Aufgabenraum eingeführt.

__kernel void FeedForwardMHConv(__global float *matrix_w,
                                __global float *matrix_i,
                                __global float *matrix_o,
                                const int inputs,
                                const int step,
                                const int window_in,
                                const int window_out,
                                const int activation
                               )
  {
   const size_t i = get_global_id(0);
   const size_t h = get_global_id(1);
   const size_t v = get_global_id(2);
   const size_t total = get_global_size(0);
   const size_t heads = get_global_size(1);

Im Kernelkörper identifizieren wir den Thread über alle Dimensionen des Aufgabenraums hinweg. Anschließend werden die Eingangs- und Ausgangsdimensionen für jeden Faltungskopf sowie die Offsets in den globalen Datenpuffern bestimmt, die den zu analysierenden Elementen entsprechen.

   const int window_in_h = (window_in + heads - 1) / heads;
   const int window_out_h = (window_out + heads - 1) / heads;
   const int shift_out = window_out * i + window_out_h * h;
   const int shift_in = step * i + window_in_h * h;
   const int shift_var_in = v * inputs;
   const int shift_var_out = v * window_out * total;
   const int shift_var_w = v * window_out * (window_in_h + 1);
   const int shift_w_h = h * window_out_h * (window_in_h + 1);

Sobald diese vorbereitenden Arbeiten abgeschlossen sind, gehen wir dazu über, die Faltungsoperationen zwischen den Eingabedaten und dem trainierbaren Filter zu konstruieren. In einem einzigen Thread führen wir eine Faltung für einen Kopf der Eingabedaten mit dem entsprechenden Filter durch. Um dies zu erreichen, organisieren wir ein System von verschachtelten Schleifen. Die äußere Schleife iteriert über die Elemente der Ausgabeschicht, die dem gegebenen Faltungskopf entsprechen.

   float sum = 0;
   float4 inp, weight;
   int stop = (window_in_h <= (inputs - shift_in) ? window_in_h : (inputs - shift_in));
//---
   for(int out = 0; (out < window_out_h && (window_out_h * h + out) < window_out); out++)
     {
      int shift = (window_in_h + 1) * out + shift_w_h;

In der äußeren Schleife berechnen wir zunächst den Offset im Puffer der trainierbaren Parameter. Anschließend wird eine innere Schleife eingeleitet, um die Elemente des auf die Eingabedaten angewandten Faltungsfensters zu durchlaufen.

      for(int k = 0; k <= stop; k += 4)
        {
         switch(stop - k)
           {
            case 0:
               inp = (float4)(1, 0, 0, 0);
               weight = (float4)(matrix_w[shift_var_w + shift + window_in_h], 0, 0, 0);
               break;
            case 1:
               inp = (float4)(matrix_i[shift_var_in + shift_in + k], 1, 0, 0);
               weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + window_in_h], 0, 0);
               break;
            case 2:
               inp = (float4)(matrix_i[shift_var_in + shift_in + k],
                              matrix_i[shift_var_in + shift_in + k + 1], 1, 0);
               weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1],
                                 matrix_w[shift_var_w + shift + window_in_h], 0);
               break;
            case 3:
               inp = (float4)(matrix_i[shift_var_in + shift_in + k], matrix_i[shift_var_in + shift_in + k + 1],
                              matrix_i[shift_var_in + shift_in + k + 2], 1);
               weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1],
                                 matrix_w[shift_var_w + shift + k + 2], matrix_w[shift_var_w + shift + shift_w_h]);
               break;
            default:
               inp = (float4)(matrix_i[shift_var_in + shift_in + k], matrix_i[shift_var_in + shift_in + k + 1],
                              matrix_i[shift_var_in + shift_in + k + 2], matrix_i[shift_var_in + shift_in + k + 3]);
               weight = (float4)(matrix_w[shift_var_w + shift + k], matrix_w[shift_var_w + shift + k + 1],
                                 matrix_w[shift_var_w + shift + k + 2], matrix_w[shift_var_w + shift + k + 3]);
               break;
           }

Um die Berechnungen zu optimieren, verwenden wir integrierte Vektormultiplikationsfunktionen, die eine effizientere Nutzung der Prozessorressourcen ermöglichen. Dementsprechend laden wir zunächst die erforderlichen Werte aus externen Puffern in lokale Vektorvariablen und führen dann Vektormultiplikationen durch, bevor wir zur nächsten Iteration der inneren Schleife übergehen.

         sum += IsNaNOrInf(dot(inp, weight), 0);
        }

Nach Abschluss aller Iterationen der inneren Schleife wenden wir die Aktivierungsfunktion an und speichern das Ergebnis in dem entsprechenden Ausgabepufferelement. Der Prozess wird dann mit der nächsten Iteration der äußeren Schleife fortgesetzt.

      sum = IsNaNOrInf(sum, 0);
      //---
      matrix_o[shift_var_out + out + shift_out] = Activation(sum, activation);;
     }
  }

Am Ende aller Schleifeniterationen enthält der Ausgabepuffer alle erforderlichen Werte, und die Kernelausführung ist abgeschlossen.

Wir gehen nun zur Konstruktion der Algorithmen für die Rückwärtsdurchläufe über. Hier ist anzumerken, dass wir anders als beim Vorwärtsdurchlauf die Faltungskopfkennung nicht als Dimension in den Aufgabenraum einführen können.

Erinnern Sie sich daran, dass wir während des Prozesses der Gradientenverteilung die Einflusswerte jedes Eingabeelements auf die Ausgabe akkumulieren. In Fällen, in denen die Schrittweite des Faltungsfensters kleiner als seine Größe ist, kann ein einzelnes Eingabeelement die Elemente des Ergebnissensors über mehrere Faltungsspitzen hinweg beeinflussen.

Aus diesem Grund führen wir in diesem Fall die Anzahl der Aufmerksamkeitsköpfe als zusätzlichen externen Parameter des Kerns CalcHiddenGradientMHConv ein. Die Kennung des spezifischen Faltungskopfes wird dann während der Akkumulation der Fehlergradienten ermittelt.

__kernel void CalcHiddenGradientMHConv(__global float *matrix_w,
                                       __global float *matrix_g,
                                       __global float *matrix_o,
                                       __global float *matrix_ig,
                                       const int outputs,
                                       const int step,
                                       const int window_in,
                                       const int window_out,
                                       const int activation,
                                       const int shift_out,
                                       const int heads
                                      )
  {
   const size_t i = get_global_id(0);
   const size_t inputs = get_global_size(0);
   const size_t v = get_global_id(1);

Im Kernelkörper identifizieren wir den aktuellen Thread im zweidimensionalen Aufgabenraum, der auf das Eingabedatenelement und den univariaten Sequenzbezeichner verweist. Danach bestimmen wir die Werte der Konstanten, einschließlich der Verschiebung in den Datenpuffern, sowie die Fensterabmessungen und die Anzahl der Filter für einen Fusionskopf. 

   const int shift_var_in = v * inputs;
   const int shift_var_out = v * outputs;
   const int shift_var_w = v * window_out * (window_in + 1);
   const int window_in_h = (window_in + heads - 1) / heads;
   const int window_out_h = (window_out + heads - 1) / heads;

Hier legen wir auch den Bereich des Ausgabefensters fest, der durch das analysierte Element der Quelldaten beeinflusst wird.

   float sum = 0;
   float out = matrix_o[shift_var_in + i];
   const int w_start = i % step;
   const int start = max((int)((i - window_in + step) / step), 0);
   int stop = (w_start + step - 1) / step;
   stop = min((int)((i + step - 1) / step + 1), stop) + start;
   if(stop > (outputs / window_out))
      stop = outputs / window_out;

Nach der Vorarbeit gehen wir dazu über, Fehlergradienten aus allen abhängigen Elementen des Ergebnistensors zu sammeln. Um dies zu erreichen, organisieren wir ein System von Schleifen. Die äußere Schleife durchläuft die abhängigen Elemente innerhalb des zuvor definierten Fensters.

   for(int k = start; k < stop; k++)
     {
      int head = (k % window_out) / window_out_h;

Im Hauptteil der äußeren Schleife definieren wir zunächst den Faltungskopf für ein einzelnes Element des Ergebnissensors und organisieren dann eine verschachtelte Schleife zur Iteration über die Filter.

      for(int h = 0; h < window_out_h; h ++)
        {
         int shift_g = k * window_out + head * window_out_h + h;
         int shift_w = (stop - k - 1) * step + (i % step) / window_in_h +
                       head * (window_in_h + 1) + h * (window_in_h + 1);
         if(shift_g >= outputs || shift_w >= (window_in_h + 1) * window_out)
            break;
         float grad = matrix_g[shift_out + shift_g + shift_var_out];
         sum += grad * matrix_w[shift_w + shift_var_w];
        }
     }

Innerhalb des Körpers der verschachtelten Schleife wird der Fehlergradient über alle Filter eines einzelnen Fusionskopfes akkumuliert, bevor zur nächsten Iteration des Schleifensystems übergegangen wird.

Nachdem die Gradienten aller abhängigen Elemente gesammelt wurden, wird der kumulierte Wert um die Ableitung der Aktivierungsfunktion angepasst und das Ergebnis im entsprechenden Element des Datenpuffers gespeichert:

   matrix_ig[shift_var_in + i] = Deactivation(sum, out, activation);
  }

An diesem Punkt sind die Operationen des Gradientenverteilungskerns abgeschlossen. Was den Kernel für die Parameteraktualisierung betrifft, so schlage ich vor, dass Sie ihn unabhängig überprüfen. Der vollständige Programmcode von OpenCL ist im Anhang zu diesem Artikel zu finden. Wir gehen nun zum nächsten Schritt unserer Arbeit über: der Implementierung der mehrköpfigen neuronalen Faltungsschicht im Hauptprogramm.

Mehrköpfige Faltungsschicht

Um die Faltungsfunktionalität auf der Seite des Hauptprogramms zu implementieren, führen wir ein neues Objekt ein, CNeuronMHConvOCL. Wie zu erwarten, wurde die bestehende Faltungsschicht als übergeordnete Klasse verwendet. Die Struktur des neuen Objekts wird im Folgenden dargestellt.

class CNeuronMHConvOCL  :  public CNeuronConvOCL
  {
protected:
   uint              iHeads;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMHConvOCL(void)  :  iHeads(1)   {};
                    ~CNeuronMHConvOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint window_out, 
                          uint units_count, uint variables, uint heads, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronMHConvOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
  };

In dieser Struktur wird nur eine interne Variable eingeführt, um die angegebene Anzahl von Faltungsspitzen zu speichern. Alle anderen für die Verarbeitung erforderlichen Objekte und Variablen werden von der übergeordneten Klasse geerbt. Darüber hinaus werden die Methoden der Vorwärts- und Rückwärtsdurchläufe überschrieben, die als Wrapper für den Aufruf der zuvor beschriebenen Kernel dienen. Der Kernel-Planungsalgorithmus bleibt unverändert und bedarf daher keiner weiteren Erläuterung. In diesem Artikel konzentrieren wir uns ausschließlich auf die Initialisierungsmethode Init, die fast vollständig von Grund auf neu implementiert wurde.

In der Parameterstruktur der Methode wurde nur ein einziges neues Element hinzugefügt, das es ermöglicht, die Anzahl der Faltungsköpfe vom aufrufenden Programm zu übergeben.

bool CNeuronMHConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                            uint window, uint step, uint window_out, 
                            uint units_count, uint variables, uint heads, 
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronProofOCL::Init(numOutputs, myIndex, open_cl, window, step, 
                             units_count * window_out * variables, ADAM, batch))
      return false;

Innerhalb der Methode rufen wir zunächst die entsprechende Initialisierungsmethode der übergeordneten Unterstichprobenebene auf, die in diesem Fall als Vorgängerobjekt fungiert. Anschließend weisen wir die Werte der externen Parameter lokalen Variablen zu.

   iWindowOut = window_out;
   iVariables = variables;
   iHeads = MathMax(MathMin(heads, window), 1);

Als Nächstes müssen wir den Tensor der trainierbaren Parameter mit Zufallswerten initialisieren. Zuvor definieren wir jedoch die Dimensionalität dieses Tensors. Seine Größe hängt von der Anzahl der univariaten Reihen in der zu analysierenden multimodalen Sequenz, der Gesamtzahl der Filter und der Größe des Faltungsfensters für einen einzelnen Kopf ab.

   const int window_h = int((iWindow + heads - 1) / heads);
   const int count = int((window_h + 1) * iWindowOut * iVariables);

Beachten Sie, dass wir uns auf die Gesamtzahl der Filter in allen Fusionsköpfen beziehen, während wir nur das Faltungsfenster eines einzelnen Kopfes verwenden. Es lässt sich leicht ableiten, dass die Anzahl der trainierbaren Parameter für einen einzelnen Faltungskopf gleich dem Produkt aus der Anzahl der Filter pro Kopf und der Größe seines Eingabefensters plus einem Bias-Term (Fi * (Wi + 1)) ist. Um die Gesamtzahl der Parameter für eine einzige univariate Sequenz zu erhalten, wird dieser Wert einfach mit der Anzahl der Köpfe (Fi * (Wi + 1) * H) multipliziert. Es ist auch klar, dass die Anzahl der Filter pro Kopf, multipliziert mit der Anzahl der Köpfe, die Gesamtzahl der vom Nutzer angegebenen Filter ergibt.

Der nächste Schritt besteht darin, die Gültigkeit des Zeigers auf das Pufferobjekt, das die trainierbaren Parameter enthält, zu überprüfen und gegebenenfalls ein neues Objekt zu erstellen.

   if(!WeightsConv)
     {
      WeightsConv = new CBufferFloat();
      if(!WeightsConv)
         return false;
     }

Wir reservieren die erforderliche Anzahl von Elementen im Puffer und organisieren eine Schleife, um den Puffer mit Zufallswerten zu füllen.

   if(!WeightsConv.Reserve(count))
      return false;
   float k = (float)(1 / sqrt(window_h + 1));
   for(int i = 0; i < count; i++)
     {
      if(!WeightsConv.Add((GenerateWeight() * 2 * k - k) * WeightsMultiplier))
         return false;
     }
   if(!WeightsConv.BufferCreate(OpenCL))
      return false;

Nachdem wir den Puffer erfolgreich mit Zufallswerten gefüllt haben, übertragen wir ihn in den OpenCL-Kontextspeicher. Als Nächstes erstellen wir Impulspuffer und füllen sie mit Nullwerten.

   if(!FirstMomentumConv)
     {
      FirstMomentumConv = new CBufferFloat();
      if(!FirstMomentumConv)
         return false;
     }
   if(!FirstMomentumConv.BufferInit(count, 0.0))
      return false;
   if(!FirstMomentumConv.BufferCreate(OpenCL))
      return false;
//---
   if(!SecondMomentumConv)
     {
      SecondMomentumConv = new CBufferFloat();
      if(!SecondMomentumConv)
         return false;
     }
   if(!SecondMomentumConv.BufferInit(count, 0.0))
      return false;
   if(!SecondMomentumConv.BufferCreate(OpenCL))
      return false;
   if(!!DeltaWeightsConv)
      delete DeltaWeightsConv;
//---
   return true;
  }

An dieser Stelle schließen wir unsere Diskussion über die Methoden des Mehrkopf-Faltungsschichtobjekts CNeuronMHConvOCL ab. Die vollständige Implementierung dieser Klasse und aller ihrer Methoden finden Sie im Anhang.

Der mehrköpfige Block von FeedForward

Wir haben nun den ersten Baustein für den Aufbau des Systems von StockFormer geschaffen. Als Nächstes werden wir ihn verwenden, um den mehrköpfige Block von FeedForward innerhalb des neuen Objekts cneuronmhfeedforward zu implementieren, dessen Struktur unten dargestellt ist.

class CNeuronMHFeedForward   :  public CNeuronBaseOCL
  {
protected:
   CNeuronMHConvOCL  acConvolutions[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMHFeedForward(void) {};
                    ~CNeuronMHFeedForward(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out,
                          uint units_count, uint variables, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const override   {  return defNeuronMHFeedForward;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

In der Struktur des neuen Objekts deklarieren wir ein Array, das aus zwei internen mehrköpfigen Faltungsschichten besteht, und überschreiben die bekannte Reihe von virtuellen Methoden. Diese internen Objekte werden statisch deklariert, was es uns ermöglicht, den Konstruktor und den Destruktor leer zu lassen. Die Initialisierung aller deklarierten und geerbten Objekte wird in der Methode Init durchgeführt.

bool CNeuronMHFeedForward::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                uint window, uint window_out,
                                uint units_count, uint variables, uint heads,
                                ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch))
      return false;

Die Initialisierungsmethode empfängt Konstanten, die die Architektur des zu erstellenden Objekts definieren. Einige dieser Parameter werden sofort an die entsprechende Initialisierungsmethode der übergeordneten Klasse übergeben, um die geerbten Basisschnittstellen einzurichten.

Anschließend initialisieren wir die erste Faltungsschicht und geben GELU als Aktivierungsfunktion an.

   if(!acConvolutions[0].Init(0, 0, OpenCL, window, window, window_out, units_count, variables, heads, 
                                                                                  optimization, iBatch))
      return false;
   acConvolutions[0].SetActivationFunction(GELU);

Danach initialisieren wir die zweite Faltungsschicht, diesmal ohne Aktivierungsfunktion.

   if(!acConvolutions[1].Init(0, 1, OpenCL, window_out, window_out, window, units_count, variables, heads, 
                                                                                     optimization, iBatch))
      return false;
   acConvolutions[1].SetActivationFunction(None);

Es ist zu beachten, dass wir beim Aufruf der Initialisierungsmethode der zweiten Faltungsschicht die Parameter für die Anzahl der Filter und die Größe des Eingabefensters vertauschen.

Am Ausgang des FeedForward-Blocks werden Residuen-Verbindungen mit Normalisierung angewendet. Aus diesem Grund wird der Ergebnispuffer der Schnittstelle des Blocks nicht überschrieben. Wir überschreiben jedoch den Puffer für die Fehlergradienten, sodass die Gradienten von den Schnittstellen direkt in den entsprechenden Puffer der zweiten Faltungsschicht übertragen werden können.

   if(!SetGradient(acConvolutions[1].getGradient(), true))
      return false;
   SetActivationFunction(None);
//---
   return true;
  }

Wir deaktivieren auch die Aktivierungsfunktion für den Block selbst und schließen die Initialisierungsmethode ab, indem wir das logische Ergebnis der Ausführung an das aufrufende Programm zurückgeben.

Sobald die Initialisierung abgeschlossen ist, wird der Algorithmus des Vorwärtsdurchlaufs in der Methode feedForward implementiert. In diesem Fall ist die Umsetzung einfach. Wir rufen einfach die Vorwärtspassmethoden der internen Faltungsschichten nacheinander auf.

bool CNeuronMHFeedForward::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CObject *prev = NeuronOCL;
   for(uint i = 0; i < acConvolutions.Size(); i++)
     {
      if(!acConvolutions[i].FeedForward(prev))
         return false;
      prev = GetPointer(acConvolutions[i]);
     }

Die Ergebnisse werden dann mit den ursprünglichen Eingaben summiert, gefolgt von einer Normalisierung innerhalb der Elemente der zu analysierenden multimodalen Sequenz.

   if(!SumAndNormilize(NeuronOCL.getOutput(), acConvolutions[acConvolutions.Size() - 1].getOutput(),
                       Output, acConvolutions[0].GetWindow(), true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Die Methode schließt mit der Rückgabe des logischen Ergebnisses der Operation an das aufrufende Programm ab.

Der Algorithmus von calcInputGradients der Fehlergradientenverteilungsmethode sieht etwas komplizierter aus, da wir Gradienten entlang zweier Datenströme verteilen müssen.

bool CNeuronMHFeedForward::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Die Parameter dieser Methode enthalten einen Zeiger auf das Quelldatenobjekt; in dessen Puffer werden wir den Fehlergradienten übergeben, der entsprechend dem Einfluss der Eingabedaten auf die endgültige Modellausgabe verteilt wird. Und im Hauptteil der Methode prüfen wir sofort die Relevanz des empfangenen Zeigers.

Nach erfolgreicher Übergabe des Kontrollblocks organisieren wir eine Schleife der umgekehrten Iteration durch die internen Faltungsschichten, wobei wir die relevanten Methoden nacheinander aufrufen.

   for(int i = (int)acConvolutions.Size() - 2; i >= 0; i--)
     {
      if(!acConvolutions[i].calcHiddenGradients(acConvolutions[i + 1].AsObject()))
         return false;
     }

Nachdem der Fehlergradient über die interne Objektpipeline verteilt wurde, wird er anschließend auf die Ebene der Quelldaten übertragen. Mit diesem Vorgang ist der Hauptarbeitsablauf abgeschlossen.

   if(!NeuronOCL.calcHiddenGradients(acConvolutions[0].AsObject()))
      return false;

Als Nächstes müssen wir den Fehlergradienten entlang des zweiten Informationsstroms ausbreiten. Der Algorithmus ist hier in zwei Betriebszweige unterteilt, je nach Vorhandensein der Aktivierungsfunktion der Quelldaten. Da wir keine Aktivierungsfunktion haben, addieren wir einfach den kumulierten Fehlergradienten auf der Ebene der Quelldaten mit ähnlichen Werten am Ausgang unseres Blocks.

   if(NeuronOCL.Activation() == None)
     {
      if(!SumAndNormilize(NeuronOCL.getGradient(), Gradient, NeuronOCL.getGradient(),
                          acConvolutions[0].GetWindow(), false, 0, 0, 0, 1))
         return false;
     }
   else
     {
      if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getPrevOutput(), Gradient, NeuronOCL.Activation()) ||
         !SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getPrevOutput(), NeuronOCL.getGradient(),
                          acConvolutions[0].GetWindow(), false, 0, 0, 0, 1))
         return false;
     }
//---
   return true;
  }

Andernfalls müssten wir zunächst den Fehlergradienten der Ausgangsebene unseres Blocks um die Ableitung der Aktivierungsfunktion der Quelldaten anpassen. Erst dann würden wir die Daten aus den beiden Informationsströmen summieren.

Es bleibt nur noch, das Ergebnis der Operationen an das aufrufende Programm zurückzugeben und die Methode zu beenden.

Die Methode zur Anpassung der trainierbaren Parameter des Blocks zur Verringerung des Gesamtmodellfehlers, updateInputWeights, bleibt einer unabhängigen Untersuchung vorbehalten. Der Algorithmus ist recht einfach: Wir rufen einfach die entsprechenden Methoden der internen Objekte nacheinander auf. Die vollständige Implementierung des Objekts von dem mehrköpfige Block von FeedForward CNeuronMHFeedForward mit all seinen Methoden finden Sie im Anhang zu diesem Artikel.

Der Decoder von diversifizierter, mehrköpfiger Aufmerksamkeit

Nach dem Aufbau des Mehrkopf-FeedForward-Blocks gehen wir nun zur Konstruktion von Encoder- und Decoder-Objekten für diversifizierte Mehrkopf-Aufmerksamkeit über. Um die Algorithmen dieser Module zu implementieren, führen wir neue Objekte ein: CNeuronDMHAttention bzw. CNeuronCrossDMHAttention. Die Konstruktion dieser Objekte folgt einer weitgehend ähnlichen Struktur. Letzteres unterscheidet sich jedoch dadurch, dass es einen internen Kreuzaufmerksamkeits-Block enthält und mit zwei Quellen von Eingangsdaten arbeitet. Im Rahmen dieses Artikels schlage ich vor, sich auf den Decoder als das komplexere Objekt zu konzentrieren. Sobald die Algorithmen klar sind, wird das Verständnis des Encoders keine größeren Schwierigkeiten bereiten.

Als übergeordnete Klasse für beide Objekte verwenden wir CNeuronRMAT, die den zugrunde liegenden Algorithmus des sequentiellen Modells bereitstellt.

class CNeuronCrossDMHAttention   :  public CNeuronRMAT
  {
protected:
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput,
                                                                   CBufferFloat *SecondGradient, 
                                                        ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;

public:
                     CNeuronCrossDMHAttention(void)  {};
                    ~CNeuronCrossDMHAttention(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint window_cross, uint units_cross,
                          uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronCrossDMHAttention; }
  };

In der Struktur des Decoder-Objekts können wir nur die Überschreibung virtueller Methoden beobachten. Die interne Objektstruktur wird in der Initialisierungsmethode Init definiert, deren Parameter die Schlüsselkonstanten enthalten, die die Architektur des Objekts bestimmen.

bool CNeuronCrossDMHAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint window_key, uint units_count,
                                    uint window_cross, uint units_cross, uint heads,
                                    uint layers, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Im Hauptteil der Methode rufen wir zunächst die Initialisierungsmethode der übergeordneten Klasse der vollständig verbundenen Schicht auf, um die geerbten Schnittstellen einzurichten.

Als Nächstes löschen wir das dynamische Array, das für die Speicherung von Zeigern auf die internen Objekte des Moduls verwendet wird, und erstellen mehrere lokale Variablen für die temporäre Datenspeicherung.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   CNeuronRelativeSelfAttention *attention = NULL;
   CNeuronRelativeCrossAttention *cross = NULL;
   CNeuronMHFeedForward *conv = NULL;
   bool use_self = units_count > 0;
   int layer = 0;

Sobald diese Vorbereitungsphase abgeschlossen ist, wird eine Schleife mit der Anzahl der Iterationen organisiert, die der angegebenen Anzahl der internen Schichten des diversifizierten Multi-Head-Attention-Decoders entspricht.

   for(uint i = 0; i < layers; i++)
     {
      if(use_self)
        {
         attention = new CNeuronRelativeSelfAttention();
         if(!attention ||
            !attention.Init(0, layer, OpenCL, window, window_key, units_count, heads, optimization, iBatch) ||
            !cLayers.Add(attention)
           )
           {
            delete attention;
            return false;
           }
         layer++;
        }

Innerhalb der Schleife erstellen wir zunächst einen Block relativer Selbstaufmerksamkeit, um die Abhängigkeiten im primären Eingabedatenstrom zu analysieren. Es ist wichtig zu beachten, dass der Selbstaufmerksamkeits-Block nur dann instanziiert wird, wenn die Sequenzlänge des primären Eingangsstroms größer als „1“ ist. Andernfalls sind keine Daten für eine Abhängigkeitsanalyse verfügbar.

Dann fügen wir ein Modul für relative Kreuzaufmerksamkeit hinzu.

      cross = new CNeuronRelativeCrossAttention();
      if(!cross ||
         !cross.Init(0, layer, OpenCL, window, window_key, units_count, heads, 
                              window_cross, units_cross, optimization, iBatch) ||
         !cLayers.Add(cross)
        )
        {
         delete cross;
         return false;
        }
      layer++;

Jede interne Schicht des Decoders wird mit einem mehrköpfigen FeedForward-Block abgeschlossen, nach dem wir zur nächsten Iteration der Schleife übergehen.

      conv = new CNeuronMHFeedForward();
      if(!conv ||
         !conv.Init(0, layer, OpenCL, window, 2 * window, units_count, 1, heads, optimization, iBatch) ||
         !cLayers.Add(conv)
        )
        {
         delete conv;
         return false;
        }
      layer++;
     }

Nach der Initialisierung des vollständigen Satzes interner Objekte werden die Schnittstellenzeiger durch Verweise auf diese Objekte ersetzt und die Methode abgeschlossen, wobei ein logisches Ergebnis an das aufrufende Programm zurückgegeben wird.

   SetOutput(conv.getOutput(), true);
   SetGradient(conv.getGradient(), true);
//---
   return true;
  }

Der Algorithmus der FeedForward-Methode besteht aus sequentiellen Aufrufen der jeweiligen Methoden der internen Objekte. Ich schlage vor, die Untersuchung dieser Frage als eigenständige Aufgabe zu betrachten. Widmen wir uns stattdessen dem Algorithmus calcInputGradients zur Verteilung der Fehlergradienten.

bool CNeuronCrossDMHAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                   CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondInput || !SecondGradient)
      return false;

Die Parameter dieser Methode umfassen Zeiger auf die Eingabedatenobjekte und ihre entsprechenden Fehlergradienten, in die die Ergebnisse der Operationen geschrieben werden. Daher validieren wir innerhalb des Methodenkörpers zunächst die erhaltenen Zeiger.

Es ist wichtig hervorzuheben, dass während des Vorwärtsdurchlaufs die zweite Eingangsdatenquelle gleichermaßen von den Kreuzaufmerksamkeits-Modulen aller Decoderschichten genutzt wird. Folglich müssen wir die Fehlergradienten aus allen Informationsflüssen aggregieren. Wie in solchen Fällen üblich, benötigen wir einen internen Puffer zur Datenspeicherung. Da kein solcher Puffer in dem neuen Objekt definiert wurde, verwenden wir einen der ungenutzten Puffer, die von der übergeordneten Klasse geerbt wurden.

Zunächst wird die Größe des geerbten Puffers überprüft und gegebenenfalls angepasst.

   if(PrevOutput.Total() != SecondGradient.Total())
     {
      PrevOutput.BufferFree();
      if(!PrevOutput.BufferInit(SecondGradient.Total(), 0) ||
         !PrevOutput.BufferCreate(OpenCL))
         return false;
     }

Als Nächstes initialisieren wir den Fehlergradientenpuffer für die zweite Datenquelle mit Nullwerten. Dieser Schritt stellt sicher, dass die Gradienten des aktuellen Durchgangs nicht mit den Werten der vorherigen Durchgänge kumuliert werden.

   if(!SecondGradient.Fill(0))
      return false;

Anschließend erstellen wir lokale Variablen für die temporäre Datenspeicherung.

   CObject *next = cLayers[-1];
   CNeuronBaseOCL *current = NULL;

An diesem Punkt ist die Vorbereitungsphase abgeschlossen, und wir beginnen eine umgekehrte Iterationsschleife über die internen Objekte.

   for(int i = cLayers.Total() - 2; i >= 0; i--)
     {
      current = cLayers[i];
      if(!current ||
         !current.calcHiddenGradients(next, SecondInput, PrevOutput, SecondActivation))
         return false;
      if(next.Type() == defNeuronCrossDMHAttention)
         if(!SumAndNormilize(SecondGradient, PrevOutput, SecondGradient, 1, false, 0, 0, 0, 1))
            return false;
      next = current;
     }

Innerhalb dieser Schleife rufen wir nacheinander die entsprechenden Methoden der internen Objekte auf, wobei wir ständig den Typ des Objekts überprüfen, das für die Verteilung der Fehlergradienten verantwortlich ist. Tritt ein Kreuzaufmerksamkeits-Block auf, addieren wir den Fehlergradienten der zweiten Datenquelle zu den zuvor akkumulierten Werten.

Nach erfolgreicher Beendigung aller Iterationen der Schleife wird der Fehlergradient auf die Eingabedaten des Hauptstroms zurückübertragen.

   if(!NeuronOCL.calcHiddenGradients(next, SecondInput, PrevOutput, SecondActivation))
      return false;
   if(next.Type() == defNeuronCrossDMHAttention)
      if(!SumAndNormilize(SecondGradient, PrevOutput, SecondGradient, 1, false, 0, 0, 0, 1))
         return false;
//---
   return true;
  }

In diesem Stadium überprüfen wir erneut die Art des Objekts, das die Gradientenverteilung durchführt, und fügen gegebenenfalls den Fehlergradienten aus dem zweiten Informationsstrom zu den kumulierten Werten hinzu. Schließlich schließen wir die Methode ab, indem wir ein logisches Ergebnis an das aufrufende Programm zurückgeben.

Damit ist unser Überblick über die Konstruktionsalgorithmen für den Decoder der diversifizierten Mehrkopfaufmerksamkeit abgeschlossen. Die vollständige Implementierung dieses Objekts und alle seine Methoden finden Sie im Anhang. Dort finden Sie auch den vollständigen Code für alle anderen in diesem Artikel vorgestellten Objekte.

Wir haben nun die zentrale architektonische Einheit des Systems von StockFormer implementiert – das diversifizierte Mehrkopf-Aufmerksamkeitsmodul in Form des Encoders und Decoders der Transformer-Architektur. Die Autoren von StockFormer schlagen jedoch auch einen zweistufigen Trainingsprozess mit einem ausgeklügelten Mechanismus der Interaktion zwischen trainierbaren Modellen vor. Dies wird im nächsten Artikel besprochen.

Schlussfolgerung

Wir haben uns mit dem System StockFormer vertraut gemacht, dessen Autoren einen innovativen Ansatz für das Training von Handelsstrategien auf den Finanzmärkten vorschlagen. StockFormer kombiniert Methoden des „Predictive Coding“ mit „Deep Reinforcement Learning“. Sein Hauptvorteil liegt in der Fähigkeit, flexible Strategien zu trainieren, die die dynamischen Abhängigkeiten zwischen mehreren Vermögenswerten berücksichtigen und gleichzeitig ihr Verhalten sowohl auf kurze als auch auf lange Sicht vorhersagen. 

Der dreifach verzweigte prädiktive Kodierungsmechanismus extrahiert latente Darstellungen, die mit kurzfristigen Trends, langfristiger Dynamik und Abhängigkeiten zwischen den Vermögenswerten verbunden sind. Der kaskadierende, mehrköpfige Aufmerksamkeits-Mechanismus ermöglicht eine effiziente Integration dieser verschiedenen Repräsentationen in einen einheitlichen Zustandsraum.

Im praktischen Teil dieses Artikels haben wir die von den Autoren vorgeschlagene Modifikation des ursprünglichen Transformer-Algorithmus in MQL5 implementiert und in die Encoder- und Decoder-Module der diversifizierten Mehrkopfaufmerksamkeit integriert. Im nächsten Artikel werden wir diese Arbeit fortsetzen, indem wir die Architektur der trainierbaren Modelle und den Prozess ihres Trainings diskutieren.

Referenzen

• StockFormer: Learning Hybrid Trading Machines with Predictive Coding
• Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Expert Advisor für die Probennahme
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor für die Probenahme mit der Real-ORL-Methode
3	Study1.mq5	Expert Advisor	Predictive Learning Expert Advisor
4	Study2.mq5	Expert Advisor	Expert Advisor für politische Bildung
5	Test.mq5	Expert Advisor	Modellprüfung Expert Advisor
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	OpenCL-Programmcode-Bibliothek