Neuronale Netze im Handel: Ein selbstanpassendes Multi-Agenten-Modell (MASA)

Einführung

Computertechnologien werden zu einem integralen Bestandteil der Finanzanalytik und bieten innovative Ansätze zur Lösung komplexer Probleme. In den letzten Jahren hat das Verstärkungslernen (Reinforcement Learning, RL) seine Wirksamkeit beim dynamischen Portfoliomanagement unter den Bedingungen turbulenter Finanzmärkte bewiesen. Bestehende Methoden konzentrieren sich jedoch häufig auf die Maximierung der Rendite und schenken dem Risikomanagement nur unzureichend Beachtung - insbesondere bei Unsicherheiten durch Pandemien, Naturkatastrophen und regionale Konflikte.

Um dieser Einschränkung zu begegnen, führte die Studie „Developing A Multi-Agent and Self-Adaptive Framework with Deep Reinforcement Learning for Dynamic Portfolio Risk Management" MASA (Multi-Agent and Self-Adaptive) ein. MASA integriert zwei interagierende Agenten: Der erste optimiert die Rendite mit Hilfe des Algorithmus TD3, während der zweite die Risiken durch evolutionäre Algorithmen oder andere Optimierungsmethoden minimiert. Darüber hinaus beinhaltet MASA einen Marktbeobachter, der mit Hilfe von tiefen neuronalen Netzen Markttrends analysiert und Feedback gibt.

Die Autoren testeten MASA anhand der Daten der Indizes CSI 300, Dow Jones Industrial Average (DJIA) und S&P 500 über die letzten 10 Jahre. Ihre Ergebnisse zeigen, dass MASA die traditionellen RL-basierten Ansätze im Portfoliomanagement übertrifft.

1. Der MASA-Algorithmus

Um die Grenzen herkömmlicher Ansätze von RL zu überwinden, die dazu neigen, sich zu sehr auf die Optimierung der Rendite zu konzentrieren, schlagen die Autoren eine selbstadaptive Multi-Agenten-Architektur (MASA) vor. Diese Struktur verwendet zwei interaktive und reaktive Agenten (einer basiert auf RL, der andere auf einem alternativen Optimierungsalgorithmus), um ein grundlegend neues Multi-Agenten-RL-Schema zu schaffen. Ziel ist es, ein dynamisches Gleichgewicht zwischen den Portfoliorenditen und den potenziellen Risiken herzustellen, insbesondere unter volatilen Marktbedingungen.

Innerhalb dieser Architektur optimiert sich der Agent mit RL, das auf dem Algorithmus TD3 basiert, die Gesamtrendite des Portfolios. Gleichzeitig passt der alternative Optimierungsagent das vom Agenten RL generierte Portfolio an und minimiert die Risiken unter Berücksichtigung der vom Marktbeobachter gelieferten Einschätzungen der Marktentwicklung.

Diese klare funktionale Trennung ermöglicht es dem Modell, kontinuierlich zu lernen und sich an die zugrunde liegende Dynamik der Finanzmärkte anzupassen. Im Ergebnis führt MASA zu ausgewogeneren Portfolios, sowohl in Bezug auf die Rentabilität als auch auf das Risiko, im Vergleich zu Ansätzen, die ausschließlich auf RL basieren.

Wichtig ist, dass der Rahmen von MASA ein lose gekoppeltes, pipeline-ähnliches Berechnungsmodell für seine drei intelligenten, interagierenden Agenten verwendet. Der allgemeine Ansatz, der auf RL von Multi-Agenten basiert, gewährleistet also Widerstandsfähigkeit und Robustheit: Das System funktioniert auch dann noch effektiv, wenn einer der Agenten ausfällt.

Bevor der iterative Trainingsprozess beginnt, werden alle relevanten Informationen initialisiert, einschließlich der Politik des RL und der Marktzustandsdaten, die vom Marktbeobachtungsagenten verwaltet werden.

Während des Trainings werden Informationen über den aktuellen Marktzustand Ot (z. B. die jüngsten Aufwärts- oder Abwärtstrends des zugrunde liegenden Marktes während der letzten Handelstage) zur Analyse durch den Marktbeobachter gesammelt. Parallel dazu wird die Belohnung aus der zuvor ausgeführten Aktion At−1, Final als Feedback für den Algorithmus von RL verwendet, um die Verhaltensregeln des RL-Agenten zu verfeinern.

Der Marktbeobachter wird dann aktiviert, um die vorgeschlagene Risikogrenze σs,t und den Marktvektor Vm,t zu berechnen, die als zusätzliche Merkmale für die Aktualisierung sowohl des RL-Agenten als auch des Controllers in Reaktion auf die aktuellen Marktbedingungen dienen.

Um Flexibilität und Anpassungsfähigkeit zu gewährleisten, kann der Rahmen von MASA eine Vielzahl von Ansätzen einbeziehen, einschließlich algorithmischer Modelle oder tiefer neuronaler Netze. Noch wichtiger ist, dass sowohl RL-basierte als auch auf alternativer Optimierung basierende Agenten von Natur aus durch den kontinuierlichen Zugang zu aktuellen Marktinformationen geschützt sind, die das wertvollste Feedback aus dem Handelsumfeld liefern. Die vom Marktbeobachter gewonnenen Erkenntnisse werden ausschließlich als Zusatzinformationen verwendet, die eine schnellere Anpassung und eine bessere Leistung sowohl des RL-Agenten als auch des Controllers ermöglichen, insbesondere bei sehr volatilen Märkten.

In Worst-Case-Szenarien, in denen der Marktbeobachter aufgrund von „Rauschen“ irreführende Signale erzeugt, die die Entscheidungsfindung der anderen Agenten beeinflussen könnten, ermöglicht die adaptive Natur des Belohnungsmechanismus von RL dem System, sich während der nachfolgenden Trainingsiterationen wieder an die zugrunde liegende Handelsumgebung anzupassen. Darüber hinaus trägt die Fähigkeit des Marketbeobachters zur Selbstkorrektur im Laufe der Zeit dazu bei, die Auswirkungen irreführender Signale abzuschwächen und Stabilität über längere Handelshorizonte zu gewährleisten.

Experimentelle Ergebnisse zeigen, dass sowohl RL-basierte Agenten als auch alternative Optimierer erhebliche Leistungsverbesserungen aufweisen - selbst wenn der Market Observer mit relativ einfachen algorithmischen Methoden implementiert wird. Dieses Ergebnis unterstreicht die Robustheit von MASA, wenn es an komplexen Datensätzen wie dem CSI 300, dem DJIA und dem S&P 500 über einen Zeitraum von 10 Jahren getestet wird.

Um jedoch die langfristigen Auswirkungen der Eingaben des Marktbeobachters auf die beiden anderen Agenten, auf die der vorgeschlagene MASA-Rahmen angewandt werden sollte, vollständig zu verstehen, sind weitere Analysen über komplexere Datensätze und verschiedene Anwendungsbereiche erforderlich.

Nach der Aktivierung des Marktbeobachters generiert der RL-Agent die aktuelle Aktion At, RL in Form von Portfoliogewichten. Diese Gewichte können dann vom Controller überarbeitet werden, der einen alternativen Optimierungsalgorithmus anwendet, der seine eigene Risikomanagementstrategie sowie die vom Beobachter ermittelten Marktbedingungen berücksichtigt. Dank dieses lose gekoppelten, pipeline-basierten Modells funktioniert MASA als robustes Multi-Agenten-System (MAS), das die betriebliche Integrität aufrechterhält, selbst wenn ein Agent ausfällt.

Durch seinen belohnungsbasierten Mechanismus passt sich MASA nahtlos an sich ständig verändernde Umgebungen an. Die Entscheidungsagenten verbessern iterativ die Portfolioperformance im Hinblick auf Rendite- und Risikoziele, wobei sie sich auf das wertvolle Feedback des Marktbeobachters stützen. Gleichzeitig beinhaltet der Belohnungsmechanismus ein auf Entropie basierendes Divergenzmaß, um die Vielfalt der generierten Aktionen als intelligente und anpassungsfähige Strategie zu fördern, die für die Bewältigung der Volatilität der verschiedenen Finanzmärkte unerlässlich ist.

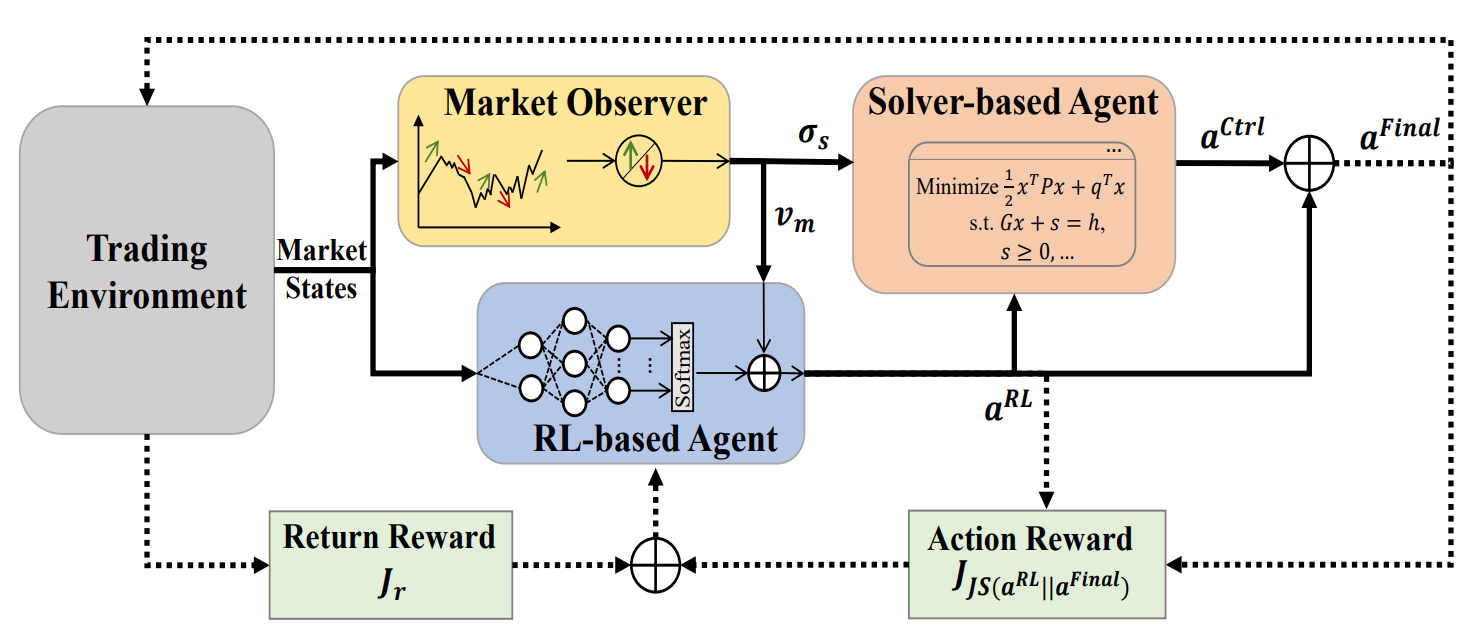
Die ursprüngliche Visualisierung des MASA-Rahmens ist unten zu sehen.

2. Implementation in MQL5

Nachdem wir uns mit den theoretischen Aspekten der Methode MASA beschäftigt haben, gehen wir nun zum praktischen Teil des Artikels über, in dem wir unsere Interpretation der vorgeschlagenen Ansätze mit MQL5 umsetzen.

Wie bereits erwähnt, besteht der MASA-Rahmen aus drei Agenten. Zur besseren Lesbarkeit und Übersichtlichkeit des Codes werden wir für jeden Agenten ein eigenes Objekt erstellen und diese später in einer einheitlichen Struktur zusammenfassen.

2.1 Der Marktbeobachter-Agent

Wir beginnen mit der Entwicklung des Agenten Market Observer (Marktbeobachter). Die Autoren von MASA betonen, dass eine Vielzahl von Algorithmen für die Marktanalyse eingesetzt werden kann – von einfachen analytischen Methoden bis hin zu fortgeschrittenen Deep-Learning-Modellen. Die Hauptaufgabe des Marktbeobachters besteht darin, die wichtigsten Trends zu erkennen, um die wahrscheinlichsten kommenden Bewegungen zu prognostizieren.

In unserer Implementierung verwenden wir einen hybriden Ansatz. Zunächst wenden wir einen stückweise linearen Darstellungsalgorithmus an, um aktuelle Markttendenzen zu erfassen. Als Nächstes analysieren wir die Abhängigkeiten zwischen den identifizierten Trends einzelner univariater Sequenzen mit Hilfe eines Aufmerksamkeitsmoduls mit relativer Positionskodierung. In der Ausgabestufe schließlich versuchen wir, das wahrscheinlichste Marktverhalten über einen definierten Planungshorizont mit Hilfe eines MLP zu prognostizieren.

Dieser zusammengesetzte Algorithmus für den Marktbeobachter wird in einem neuen Objekt CNeuronMarketObserver gekapselt. Seine Struktur wird im Folgenden dargestellt.

class CNeuronMarketObserver   :  public CNeuronRMAT
  {
public:
                     CNeuronMarketObserver(void)   {};
                    ~CNeuronMarketObserver(void)   {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint forecast,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMarketObserver; }
  };

Der Algorithmus folgt einer linearen Struktur. Für eine solche Struktur ist die Klasse CNeuronRMAT, die für die Unterstützung kleinerer linearer Modelle entwickelt wurde, eine geeignete Elternklasse für unser neues Objekt. Dies ermöglicht es uns, die Struktur des Marktbeobachters hauptsächlich innerhalb der Initialisierungsmethode Init zu definieren. Die Hauptfunktionalität wird bereits von der übergeordneten Klasse übernommen.

Die Parameter der Methode Init geben die Konstanten an, die die Architektur des Market Observer-Agenten definieren. Dazu gehören:

• window – die Größe des Vektors, der ein einzelnes Sequenzelement beschreibt (Anzahl der univariaten Zeitreihen);
• window_key – die Dimensionalität der internen Aufmerksamkeitskomponenten (Query, Key, Value ), Abfrage, Schlüssel, Wert;
• units_count – die historische Tiefe der für die Analyse verwendeten Daten;
• heads – die Anzahl der Aufmerksamkeitsköpfe;
• layers – die Anzahl der Aufmerksamkeitsebenen;
• forecast – der Prognosehorizont für die kommende Bewegung.

bool CNeuronMarketObserver::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint window_key, uint units_count,
                                 uint heads, uint layers, uint forecast,
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
//--- Init parent object
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * forecast,
                                                   optimization_type, batch))
      return false;

In dieser Methode rufen wir zunächst die Initialisierungsmethode der Basisschicht mit vollständiger Vernetzung auf, die als übergeordnete Klasse für alle neuronalen Schichten in unserer Bibliothek dient. Die Methode der Elternklasse sorgt für die Initialisierung der grundlegenden Schnittstellen unseres Objekts.

Hier sind zwei wichtige Punkte zu beachten: Zunächst rufen wir die Initialisierungsmethode der Basisklasse auf, nicht die der direkten Elternklasse. Der Grund dafür ist, dass sich die Architektur des Market Observer deutlich von der seiner Mutterklasse unterscheidet.

Zweitens geben wir beim Aufruf der übergeordneten Initialisierungsmethode die Objektgröße als das Produkt aus dem Planungshorizont und der Größe des Sequenzelementvektors an. Dies entspricht dem Tensor, den wir als Ausgabe des Marktbeobachters erwarten.

Anschließend wird das dynamische Array von Zeigern auf interne Objekte gelöscht:

//--- Clear layers' array
   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);

Damit sind die vorbereitenden Arbeiten abgeschlossen, und wir können mit der eigentlichen Konstruktion des Agenten zur Marktbeobachtung beginnen.

Das Modell erwartet als Eingabe eine multimodale Zeitreihe, die als eine Folge von Vektoren dargestellt wird, die einzelne Systemzustände (in unserem Fall Balken) beschreiben. Um jede univariate Sequenz richtig zu verarbeiten, müssen die eingehenden Daten zunächst transponiert werden.

//--- Tranpose input data
   int lay_count = 0;
   CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, lay_count, OpenCL, units_count, window, optimization, iBatch) ||
      !cLayers.Add(transp))
     {
      delete transp;
      return false;
     }

Dann transformieren wir sie in eine stückweise lineare Darstellung.

//--- Piecewise linear representation
   lay_count++;
   CNeuronPLROCL *plr = new CNeuronPLROCL();
   if(!plr ||
      !plr.Init(0, lay_count, OpenCL, units_count, window, false, optimization, iBatch) ||
      !cLayers.Add(plr))
     {
      delete plr;
      return false;
     }

Um Abhängigkeiten zwischen diesen univariaten Sequenzen zu analysieren, verwenden wir ein Aufmerksamkeitsmodul mit relativer Positionskodierung, das mit der erforderlichen Anzahl interner Schichten parametrisiert ist.

//--- Self-Attention for Variables
   lay_count++;
   CNeuronRMAT *att = new CNeuronRMAT();
   if(!att ||
      !att.Init(0, lay_count, OpenCL, units_count, window_key, window, heads, layers,
                                                                optimization, iBatch) ||
      !cLayers.Add(att))
     {
      delete att;
      return false;
     }

Auf der Grundlage der Ergebnisse des Aufmerksamkeitsblocks versuchen wir, die kommenden Werte für jede univariate Sequenz vorherzusagen. Hier verwenden wir einen Faltungsblock für die Residuem (CResidualConv) als MLP-Ersatz für die unabhängige Vorhersage der Werte jeder univariaten Zeitreihe.

//--- Forecast mapping
   lay_count++;
   CResidualConv *conv = new CResidualConv();
   if(!conv ||
      !conv.Init(0, lay_count, OpenCL, units_count, forecast, window, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }

Schließlich werden die vorhergesagten Ergebnisse in die Dimensionalität der ursprünglichen Eingabedaten zurückverwandelt.

//--- Back transpose forecast
   lay_count++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, lay_count, OpenCL, window, forecast, optimization, iBatch) ||
      !cLayers.Add(transp))
     {
      delete transp;
      return false;
     }

Um Datenkopiervorgänge zu minimieren, wenden wir eine Substitutionstechnik der Zeiger mit externen Schnittstellenpuffern für eine effiziente Speicherverwaltung an.

   if(!SetOutput(transp.getOutput(), true) ||
      !SetGradient(transp.getGradient(), true))
      return false;
//---
   return true;
  }

Die Methode schließt mit der Rückgabe des booleschen Ergebnisses der Operation an den Aufrufer ab.

Die Kernfunktionalität dieser Klasse wird von ihrem übergeordneten Objekt geerbt. Damit ist der Agent zur Marktbeobachtung nun vollständig. Der vollständige Quellcode dieser Klasse ist im Anhang enthalten.

2.2 Der RL-Agent

Der nächste Schritt ist der Aufbau des RL-Agenten. Im Rahmen von MASA arbeitet dieser Agent parallel zum Marktbeobachter, führt unabhängige Marktanalysen durch und trifft Entscheidungen auf der Grundlage der von ihm erlernten Strategie.

Die Autoren von MASA schlagen vor, den RL-Agenten mit einem TD3-basierten Modell zu implementieren. Wir gehen jedoch von einer anderen Architektur des RL-Agenten aus. Für die unabhängige Umweltanalyse verwenden wir das Rahmenwerk von PSformer. Die Entscheidungsfindung auf der Grundlage der durchgeführten Analyse wird durch ein leichtgewichtiges Perzeptron mit SAM-Optimierung übernommen.

Unser RL-Agent ist in einem neuen Objekt CNeuronRLAgent implementiert. Seine Struktur ist unten dargestellt.

class CNeuronRLAgent :  public   CNeuronRMAT
  {
public:
                     CNeuronRLAgent(void) {};
                    ~CNeuronRLAgent(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint segments, float rho,
                          uint layers, uint n_actions,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   override {  return defNeuronRLAgent;   }
  };

Ähnlich wie beim Market Observer verwenden wir hier die Vererbung von CNeuronRMAT, einer Basisklasse für lineare Modelle. Wir müssen also nur die Architektur des neuen Moduls in der Methode Init angeben.

bool CNeuronRLAgent::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint segments,
                          float rho, uint layers, uint n_actions,
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
//--- Init parent object
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, n_actions, optimization_type, batch))
      return false;

Die Methodenparameter sind denen des Marktbeobachters sehr ähnlich. Es gibt jedoch einige Unterschiede. So wird beispielsweise der Parameter für den Prognosehorizont durch den Aktionsraum des Agenten (n_actions) ersetzt. Zu den weiteren Parametern gehören segments (die Anzahl der Segmente) und rho (ein Unschärfekoeffizient).

In Init rufen wir den Basis-Initialisierer für vollständig verbundene Schichten auf und geben den Aktionsraum unseres RL-Agenten als Größe des Ausgabentensors an.

Anschließend wird das dynamische Array mit den internen Objektzeigern gelöscht.

//--- Clear layers' array
   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);

Die Eingabedaten des Modells werden zunächst an den PSformer übergeben, dessen erforderliche Anzahl von Schichten in einer Schleife erzeugt wird.

//--- State observation
   int lay_count = 0;
   for(uint i = 0; i < layers; i++)
    {
     CNeuronPSformer *psf = new CNeuronPSformer();
     if(!psf ||
        !psf.Init(0, lay_count, OpenCL, window, units_count, segments, rho, optimization,iBatch)||
        !cLayers.Add(psf))
       {
        delete psf;
        return false;
       }
     lay_count++;
    }

Der RL-Agent trifft dann Entscheidungen über die optimale Aktion, indem er die Ergebnisse der durchgeführten Analyse in einen Entscheidungsblock einspeist, der aus Faltungsschichten und voll verknüpften Schichten besteht. Die Faltungsschicht reduziert die Dimensionalität.

   CNeuronConvSAMOCL *conv = new CNeuronConvSAMOCL();
   if(!conv ||
      !conv.Init(n_actions, lay_count, OpenCL, window, window, 1, units_count,
                                                      1, optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(GELU);
   lay_count++;

Die vollständig verknüpfte Schicht erzeugt den Aktionstensor.

   CNeuronBaseSAMOCL *flat = new CNeuronBaseSAMOCL();
   if(!flat ||
      !flat.Init(0, lay_count, OpenCL, n_actions, optimization, iBatch) ||
      !cLayers.Add(flat))
     {
      delete flat;
      return false;
     }
   SetActivationFunction(SIGMOID);

Beachten Sie, dass wir in diesem Fall nicht die stochastische Politik des Akteurs verwenden. Es kann jedoch sein, dass wir sie in Zukunft noch verwenden müssen, worauf wir später noch eingehen werden.

Standardmäßig wird für den Aktionsvektor eine sigmoide Aktivierungsfunktion verwendet, die die Werte auf den Bereich zwischen 0 und 1 beschränkt. Dies kann bei Bedarf durch ein externes Programm übersteuert werden.

Wie zuvor ersetzen wir Zeiger auf Datenpuffer von externen Schnittstellen und geben dann das boolesche Ergebnis der Initialisierung zurück.

   if(!SetOutput(flat.getOutput(), true) ||
      !SetGradient(flat.getGradient(), true))
      return false;
//---
   return true;
  }

Damit ist das Objekt RL-Agent vollständig. Der vollständige Code dieser Klasse und alle ihre Methoden sind im Anhang zu finden.

2.3 Controller

Wir haben Objekte von zwei aus drei Bearbeitern konstruiert. Wir wenden uns nun der dritten Komponente zu: dem Controller-Agenten. Seine Aufgabe ist es, das Risiko zu bewerten und die Aktionen des RL-Agenten auf der Grundlage der vom Marktbeobachter durchgeführten Analyse des Umweltzustands anzupassen.

Der wesentliche Unterschied besteht darin, dass der Controller zwei Eingangsdatenquellen verarbeitet. Er muss nicht nur jeden Input einzeln bewerten, sondern auch ihre gegenseitigen Abhängigkeiten. Meiner Meinung nach eignet sich die Struktur des Transformer-Decoders hervorragend für diese Aufgabe. Anstelle der Standardmodule Selbstaufmerksamkeit (Self-Attention) und Kreuzaufmerksamkeit (Cross-Attention) verwenden wir jedoch Varianten der relativen Positionskodierung.

Der Controller ist als ein neues Objekt CNeuronControlAgent implementiert, das wiederum von CNeuronRMAT erbt. Da es mit zwei Eingangsströmen arbeitet, müssen mehrere Methoden neu definiert werden. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronControlAgent  :  public CNeuronRMAT
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, 
                                 CBufferFloat *SecondInput) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, 
                                        CBufferFloat *SecondInput, 
                                        CBufferFloat *SecondGradient, 
                                        ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, 
                                        CBufferFloat *SecondInput) override;

public:
                     CNeuronControlAgent(void) {};
                    ~CNeuronControlAgent(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint window_kv, uint units_kv, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronControlAgent; }
  };

Auch hier erfolgt die Initialisierung der internen Objekte in der Methode Init, die die Architektur des Transformer-Decoders festlegt.

bool CNeuronControlAgent::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                               uint window, uint window_key, uint units_count,
                               uint heads, uint window_kv, uint units_kv, uint layers,
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
//--- Init parent object
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, 
                                                     optimization_type, batch))
      return false;
//--- Clear layers' array
   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);

Wie in den vorangegangenen Fällen rufen wir die entsprechende Methode der Basisschicht mit vollständiger Verknüpfung auf und geben die Dimensionalität der Ausgänge auf der Ebene des Haupteingabetensors an. Danach löschen wir das dynamische Array der Zeiger.

Als Nächstes bauen wir die Architektur unseres Controller-Agenten auf. Erinnern Sie sich daran, dass der Marktbeobachter eine multimodale Zeitreihe ausgibt, eine Folge von Vektoren, die vorhergesagte Zustände der Umwelt (Balken) darstellen.

Zwei Ansätze sind möglich: Abgleich von RL-Agentenaktionen mit einzelnen Balken oder mit univariaten Sequenzen. Wir verstehen, dass der Marktbeobachter uns nur Prognosedaten zur Verfügung gestellt hat, deren Eintrittswahrscheinlichkeit bei weitem nicht 100% beträgt. Außerdem besteht die Möglichkeit, dass es bei absolut allen Werten zu Abweichungen kommt.

Lassen Sie uns logisch denken. Wie viele Informationen kann uns der Vektor, der eine Prognosekerze beschreibt, liefern, vorausgesetzt, dass jedes Element unterschiedliche Abweichungen aufweisen kann? Die Frage ist umstritten und schwer zu beantworten, ohne die Genauigkeit der einzelnen Prognosen zu kennen.

Betrachtet man hingegen eine separate univariate Reihe, so kann man neben den Einzelwerten auch den Trend der kommenden Bewegung erkennen. Da der Trend durch eine Reihe von Werten gebildet wird, könnte man logischerweise die Bestätigung eines Trends erwarten, auch wenn einige Elemente abweichen.

Außerdem weisen alle univariaten Sequenzen in unseren multimodalen Zeitreihen bestimmte Abhängigkeiten auf. Wenn also der vorhergesagte Trend einer univariaten Zeitreihe durch die Werte einer anderen bestätigt wird, steigt die Wahrscheinlichkeit einer solchen Prognose.

Aus diesem Grund haben wir beschlossen, die Abhängigkeit der Handlungen des Agenten von den vorhergesagten Werten der univariaten Sequenzen zu analysieren. Dementsprechend speisen wir zunächst die sekundäre Datenquelle in eine vorbereitete neuronale Schicht ein.

   int lay_count = 0;
   CNeuronBaseOCL *flat = new CNeuronBaseOCL();
   if(!flat ||
      !flat.Init(0, lay_count, OpenCL, window_kv * units_kv, optimization, iBatch) ||
      !cLayers.Add(flat))
     {
      delete flat;
      return false;
     }

Und dann formatieren wir sie in univariate Sequenzdarstellungen um.

   lay_count++;
   CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, lay_count, OpenCL, units_kv, window_kv, optimization, iBatch) ||
      !cLayers.Add(transp))
     {
      delete transp;
      return false;
     }
   lay_count++;

Als Nächstes müssen wir die Architektur unseres Decoders konstruieren. Die erforderliche Anzahl von Ebenen wird in einer Schleife erstellt. Die Anzahl der Iterationen wird durch die externen Parameter der Initialisierungsmethode bestimmt.

//--- Attention Action To Observation
   for(uint i = 0; i < layers; i++)
     {
      if(units_count > 1)
        {
         CNeuronRelativeSelfAttention *self = new CNeuronRelativeSelfAttention();
         if(!self ||
            !self.Init(0, lay_count, OpenCL, window, window_key, units_count, heads,
                                                               optimization, iBatch) ||
            !cLayers.Add(self))
           {
            delete self;
            return false;
           }
         lay_count++;
        }

Es ist wichtig zu wissen, dass im ursprünglichen Transformer-Decoder die Eingangsdaten zunächst von einem Selbstaufmerksamkeitsmodul verarbeitet werden, das die Abhängigkeiten zwischen den einzelnen Elementen der Quellsequenz analysiert. In unserer Implementierung ersetzen wir dieses Modul durch sein Gegenstück, das eine relative Positionskodierung verwendet. Wir erstellen dieses Modul jedoch nur, wenn die Ausgangssequenz mehr als ein Element enthält. Denn bei einem einzigen Element gibt es natürlich keine Abhängigkeiten, die zu analysieren wären. In diesem Fall wäre das Modul der Selbstaufmerksamkeit überflüssig.

Als Nächstes erstellen wir ein Kreuzaufmerksamkeitsmodul, das die Abhängigkeiten zwischen den Elementen der beiden Datenquellen analysiert.

      CNeuronRelativeCrossAttention *cross = new CNeuronRelativeCrossAttention();
      if(!cross ||
         !cross.Init(0, lay_count, OpenCL, window, window_key, units_count, heads, 
                                        units_kv, window_kv, optimization, iBatch) ||
         !cLayers.Add(cross))
        {
         delete cross;
         return false;
        }
      lay_count++;

Jede Decoderschicht wird dann mit einem Block FeedForward vervollständigt, für den wir einen Residual Convolutional Block verwenden.

      CResidualConv *ffn = new CResidualConv();
      if(!ffn ||
         !ffn.Init(0, lay_count, OpenCL, window, window, units_count, optimization, iBatch) ||
         !cLayers.Add(ffn))
        {
         delete ffn;
         return false;
        }
      lay_count++;
     }

Danach fahren wir mit der nächsten Schleifeniteration fort und konstruieren die folgende Decoderschicht.

Wie bei der Standardarchitektur des Transformer-Decoder wird der Ausgang des Faltungsblocks der Residuen normalisiert. Es kann jedoch auch erforderlich sein, den Aktionsraum des Akteurs auf einen bestimmten Bereich zu beschränken, was in der Regel durch eine Aktivierungsfunktion geschieht. Daher fügen wir nach der Konstruktion der erforderlichen Anzahl von Decoderschichten eine zusätzliche Faltungsschicht mit der angegebenen Aktivierungsfunktion hinzu.

   CNeuronConvSAMOCL *conv = new CNeuronConvSAMOCL();
   if(!conv ||
      !conv.Init(0, lay_count, OpenCL, window, window, window, units_count, 1,
                                                       optimization, iBatch) ||
      !cLayers.Add(conv))
     {
      delete conv;
      return false;
     }
   SetActivationFunction(SIGMOID);

Standardmäßig wird, wie beim RL-Agenten, die Sigmoidfunktion verwendet. Wir behalten jedoch die Möglichkeit, sie von einem externen Programm aus außer Kraft zu setzen.

Am Ende der Initialisierungsmethode ersetzen wir Zeiger auf die Schnittstellenpuffer und geben einen booleschen Wert an das aufrufende Programm zurück, der den Erfolg der Operation anzeigt.

//---
   if(!SetOutput(conv.getOutput(), true) ||
      !SetGradient(conv.getGradient(), true))
      return false;
//---
   return true;
  }

Nachdem die Initialisierung des neuen Objekts abgeschlossen ist, wird der Algorithmus des Vorwärtsdurchlaufs in der Methode feedForward konstruiert.

bool CNeuronControlAgent::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!SecondInput)
      return false;

In den Methodenparametern erhalten wir Zeiger auf zwei Eingabedatenobjekte. Der primäre Datenstrom wird als neuronale Schicht übergeben, und der sekundäre Datenstrom wird als Datenpuffer bereitgestellt. Der Einfachheit halber ersetzen wir den Ergebnispuffer einer eigens geschaffenen internen Schicht durch das in den Methodenparametern enthaltene Objekt.

   CNeuronBaseOCL *second = cLayers[0];
   if(!second)
      return false;
   if(!second.SetOutput(SecondInput, true))
      return false;

Anschließend transponieren wir den Tensor der sekundären Datenquelle, um die multimodale Zeitreihe als eine Folge von univariaten Reihen darzustellen.

   second = cLayers[1];
   if(!second || !second.FeedForward(cLayers[0]))
      return false;

Als Nächstes werden die verbleibenden internen neuronalen Schichten der Reihe nach durchlaufen, indem ihre Feedforward-Methoden aufgerufen und beide Datenquellen übergeben werden.

   CNeuronBaseOCL *first = NeuronOCL;
   CNeuronBaseOCL *main = NULL;
   for(int i = 2; i < cLayers.Total(); i++)
     {
      main = cLayers[i];
      if(!main ||
         !main.FeedForward(first, second.getOutput()))
         return false;
      first = main;
     }
//---
   return true;
  }

Nach erfolgreicher Beendigung aller Schleifeniterationen geben wir einfach ein boolesches Ergebnis an den Aufrufer zurück, das die erfolgreiche Ausführung signalisiert.

Wie man sieht, ist der Algorithmus des Vorwärtsdurchlaufs relativ einfach zu handhaben. Dies ist der Verwendung von vorgefertigten Blöcken zu verdanken, mit denen eine komplexere Architektur aufgebaut werden kann.

Bei der Implementierung des Algorithmus zur Verteilung des Fehlergradienten wird die Situation aufgrund der Verwendung einer sekundären Datenquelle noch schwieriger. Auf dem primären Datenpfad werden die Informationen sequentiell von einer internen Schicht zur nächsten weitergegeben. Die sekundäre Datenquelle wird jedoch von allen Decoderebenen gemeinsam genutzt. Speziell für alle Kreuzaufmerksamkeits-Module. Folglich muss der Fehlergradient für die Sekundärdaten von allen Kreuzaufmerksamkeits-Modulen erfasst werden. Ich schlage vor, dass Sie sich die Lösung für dieses Problem im Code ansehen.

Diese Logik ist in der Methode calcInputGradients implementiert. Die Methodenparameter enthalten Zeiger auf die beiden Eingabedatenströme und ihre entsprechenden Fehlergradienten. Unsere Aufgabe ist es, den Fehlergradienten zwischen den beiden Datenquellen entsprechend ihrem Beitrag zum endgültigen Ergebnis zu verteilen.

bool CNeuronControlAgent::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput,
                              CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondGradient)
      return false;

Innerhalb der Methode validieren wir zunächst die empfangenen Zeiger, da wir keine Daten an nicht existierende Objekte übergeben können.

Wie beim Vorwärtsdurchlauf wird die sekundäre Datenquelle in Form von Puffern dargestellt. Und wir ersetzen die Zeiger in der entsprechenden internen Ebene.

   CNeuronBaseOCL *main = cLayers[0];
   if(!main)
      return false;
   if(!main.SetGradient(SecondGradient, true))
      return false;
   main.SetActivationFunction(SecondActivation);
//---
   CNeuronBaseOCL *second = cLayers[1];
   if(!second)
      return false;
   second.SetActivationFunction(SecondActivation);

In diesem Stadium synchronisieren wir auch die Aktivierungsfunktionen der internen Schicht und der nachfolgenden Transpositionsschicht mit der Aktivierungsfunktion der Eingabedaten. Dadurch wird eine korrekte Gradientenausbreitung gewährleistet.

Die Transpositionsebene dient nun als sekundäre Datenquelle. Der Einfachheit halber speichern wir Zeiger auf seine Schnittstellenobjekte in lokalen Variablen.

   CBufferFloat *second_out = second.getOutput();
   CBufferFloat *second_gr = second.getGradient();
   CBufferFloat *temp = second.getPrevOutput();
   if(!second_gr.Fill(0))
      return false;

Und wir löschen den Gradientenpuffer von allen zuvor angesammelten Werten.

Dann iterieren wir rückwärts durch die internen neuronalen Schichten. Beachten Sie, dass wir in dieser Schleife nur mit Decoderobjekten arbeiten.

Da die ersten beiden internen Objekte für die Bearbeitung der sekundären Datenquelle reserviert sind.

   for(int i = cLayers.Total() - 2; i >= 2; i--)
     {
      main = cLayers[i];
      if(!main)
         return false;

Für jede Decoderschicht wird der Zeiger aus dem Array abgerufen und validiert.

Da nicht alle Decodermodule mit zwei Datenquellen arbeiten, verzweigt der Algorithmus je nach Objekttyp. Bei Kreuzaufmerksamkeits-Modulen wird zunächst der Fehlergradient der sekundären Datenquelle aus der aktuellen Ebene in einen Zwischenspeicher übertragen und dann mit den zuvor gespeicherten Ergebnissen akkumuliert.

      if(cLayers[i + 1].Type() == defNeuronRelativeCrossAttention)
        {
         if(!main.calcHiddenGradients(cLayers[i + 1], second_out, temp, SecondActivation) ||
            !SumAndNormilize(temp, second_gr, second_gr, 1, false, 0, 0, 0, 1))
            return false;
        }

Bei anderen Modulen wird der Fehlergradient einfach entlang des primären Pfades weitergegeben. Und dann geht es weiter mit der nächsten Iteration der Schleife.

      else
        {
         if(!main.calcHiddenGradients(cLayers[i + 1]))
            return false;
        }
     }

Nach Abschluss aller Iterationen werden die akkumulierten Gradienten an die Eingabedatenquellen zurückgegeben. Zunächst übergeben wir den Gradienten entlang des primären Pfads an die erste Datenquelle.

   if(!NeuronOCL.calcHiddenGradients(main.AsObject(), second_out, temp, SecondActivation))
      return false;

Es sei jedoch daran erinnert, dass die erste Decoderschicht entweder ein Selbstaufmerksamkeits- oder ein Kreuzaufmerksamkeits-Modul sein kann. Im letzteren Fall werden beide Datenquellen verwendet. Wir müssen also den Objekttyp überprüfen und gegebenenfalls den kumulierten Gradienten der zweiten Datenquelle hinzufügen.

   if(main.Type() == defNeuronRelativeCrossAttention)
     {
      if(!SumAndNormilize(temp, second_gr, second_gr, 1, false, 0, 0, 0, 1))
         return false;
     }

Schließlich geben wir den gesamten akkumulierten Gradienten entlang des sekundären Pfades an die entsprechende Eingangsquelle weiter.

   main = cLayers[0];
   if(!main.calcHiddenGradients(second.AsObject()))
      return false;
//---
   return true;
  }

Die Methode endet mit der Rückgabe eines logischen Ergebnisses an das aufrufende Programm.

Der Algorithmus zur Aktualisierung der Parameter, der in der Methode updateInputWeights implementiert ist, ist relativ einfach. Wir durchlaufen eine Schleife durch die internen Objekte, die trainierbare Parameter enthalten, und rufen die entsprechenden Aktualisierungsmethoden auf. Wir werden hier nicht ins Detail gehen. Es ist jedoch wichtig zu beachten, dass die konstruierte Objektarchitektur Module mit den für SAM optimierten Parametern verwendet. Daher muss die Iteration durch die internen Objekte in umgekehrter Reihenfolge durchgeführt werden.

Damit schließen wir unsere Diskussion über die Algorithmen ab, die zur Umsetzung der Methoden des Controller-Agenten verwendet werden. Der vollständige Code für die neue Klasse und alle ihre Methoden sind in den Anhängen enthalten.

Wir sind heute ein gutes Stück vorangekommen, auch wenn unsere Arbeit noch nicht abgeschlossen ist. Wir machen eine kurze Pause, und im nächsten Artikel werden wir das Projekt zu einem logischen Abschluss bringen.

Schlussfolgerung

Wir haben einen innovativen Ansatz für das Portfoliomanagement unter volatilen Finanzmarktbedingungen untersucht – den Rahmen von Multi-Agent Self-Adaptive (MASA). Der vorgeschlagene Rahmen kombiniert erfolgreich die Vorteile von RL-Algorithmen zur Renditeoptimierung, adaptive Optimierungsmethoden zur Risikominimierung und ein Marktbeobachtungsmodul zur Trendanalyse.

Im praktischen Teil haben wir jeden der vorgeschlagenen Agenten in MQL5 als eigenständiges Modul implementiert. Im nächsten Artikel werden wir sie in ein vollständiges System integrieren und die Leistung der implementierten Lösungen anhand echter historischer Daten bewerten.

Referenzen

• Developing A Multi-Agent and Self-Adaptive Framework with Deep Reinforcement Learning for Dynamic Portfolio Risk Management
• Andere Artikel aus dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Expert Advisor zum Sammeln von Beispielen
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor für das Sammeln von Beispielen nach der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modellausbildung Expert Advisor
4	Test.mq5	Expert Advisor	Modellprüfung Expert Advisor
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Bibliothek	OpenCL-Programmcode-Bibliothek