Redes neuronales en el trading: Modelo hiperbólico de difusión latente (HypDiff)
Introducción
Los grafos contienen la variedad y el significado de las topologías de los datos de origen. Estas características topológicas suelen reflejar principios físicos y modelos de desarrollo. Los modelos tradicionales de grafos aleatorios basados en la teoría de grafos requieren el uso de heurísticas artificiales para crear algoritmos con una topología determinada y son incapaces de modelar con flexibilidad una gran variedad de grafos complejos. Como consecuencia, se han desarrollado muchos modelos de aprendizaje profundo para la generación de grafos. Los modelos probabilísticos de difusión desarrollados con la función de reducción de ruido han demostrado una gran eficacia y potencial en la resolución de problemas de imagen.
Sin embargo, debido a la estructura irregular y no euclidiana de los grafos, la aplicación del modelo de difusión en este contexto posee dos limitaciones principales:
- Una alta complejidad computacional. La esencia de la generación de grafos consiste en procesar la discreción, la dispersión y otras propiedades topológicas de una estructura no euclidiana. Como la perturbación de ruido gaussiano utilizada en el modelo de difusión de vainilla no resulta adecuada para los datos discretos, el modelo de difusión de grafos discretos suele tener una alta complejidad temporal y espacial debido al problema de la dispersión estructural. Además, el modelo de difusión de grafos discretos se basa en un proceso de ruido gaussiano continuo para crear grafos totalmente conectados y ruidosos que pierden la información estructural y las propiedades topológicas básicas.
- La anisotropía de la estructura no euclidiana. A diferencia de los datos de estructuras regulares, las estructuras de incorporación de grafos no euclidianos "irregulares" son anisotrópicas en el espacio latente continuo. Las incorporaciones de nodos de grafos en el espacio euclidiano muestran una anisotropía significativa en varias direcciones concretas. La difusión isotrópica de la incorporación de nodos del grafo en el espacio latente procesará la información estructural anisotrópica como ruido, y esta información estructural útil se perderá en el proceso de reducción del ruido.
El espacio geométrico hiperbólico está ampliamente reconocido como un colector continuo ideal para representar estructuras discretas arborescentes o jerárquicas y se usa en diversos problemas de aprendizaje de grafos. Y según los autores del artículo "Hyperbolic Geometric Latent Diffusion Model for Graph Generation", la geometría hiperbólica tiene un gran potencial para resolver la anisotropía estructural no euclidiana en los procesos de difusión latente de los grafos. En el espacio hiperbólico, se observa que la distribución de incorporaciones de nodos tiende a ser globalmente isotrópica. En este caso, la anisotropía se conserva de manera local. Además, la geometría hiperbólica unifica las dimensiones angulares y radiales de las coordenadas polares y puede dotar a las dimensiones geométricas de semántica física e interpretabilidad. Curiosamente, la geometría hiperbólica puede proporcionar un espacio latente con características geométricas a priori del grafo.
Basándose en los hallazgos anteriormente mencionados, los autores del citado artículo pretenden seleccionar un espacio latente adecuado basado en la geometría hiperbólica para desarrollar un proceso de difusión eficiente en una estructura no euclidiana en problemas de generación de grafos que preserven la topología. Se resuelven dos grandes problemas de forma paralela:
- La aditividad de las distribuciones gaussianas continuas no está definida en el espacio latente hiperbólico;
- El desarrollo de un proceso de difusión anisotrópica eficiente para estructuras no euclidianas.
Para resolver estos problemas, se propuso un modelo de difusión latente en el espacio hiperbólico (HypDiff). Para el problema aditivo de la distribución gaussiana continua en el espacio hiperbólico, se propone un proceso de difusión basado en medidas radiales. Al mismo tiempo, se utilizó una restricción angular para limitar el ruido anisotrópico con el fin de preservar la aprioridad estructural, guiando el modelo de difusión hacia detalles más finos de la estructura del grafo.
1. El algoritmo HypDiff
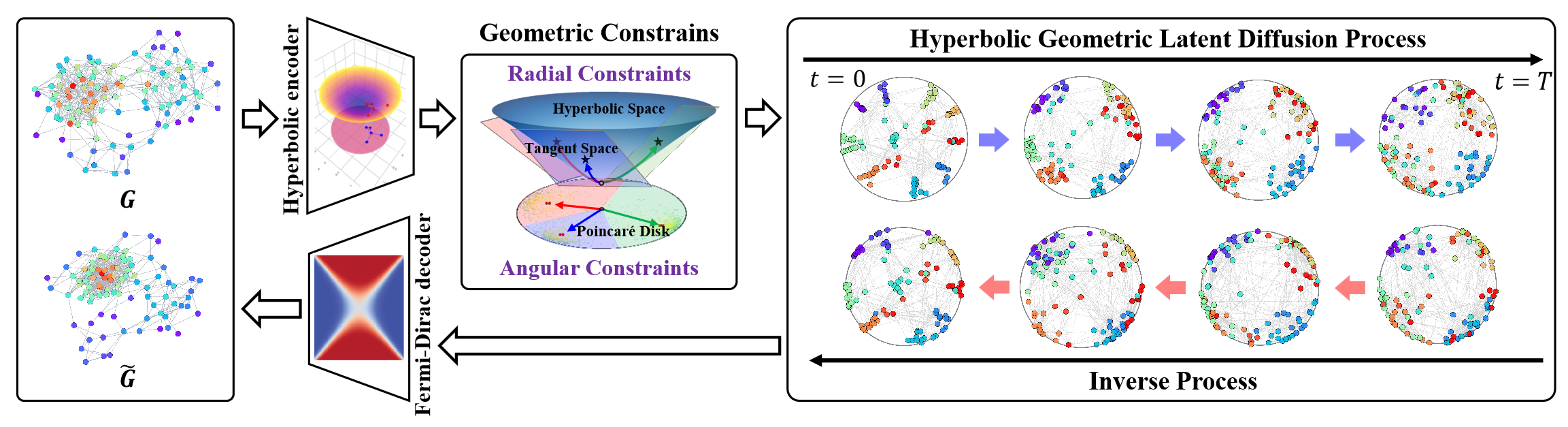
El modelo de difusión hiperbólica latente (HypDiff) resuelve dos problemas principales. Usa la geometría hiperbólica para abstraer una jerarquía implícita de los nodos del grafo e introduce dos restricciones geométricas para preservar importantes propiedades topológicas. Los autores del método utilizan una estrategia de aprendizaje en dos etapas. En primer lugar, entrenan un autocodificador hiperbólico para obtener incorporaciones de nodos preentrenados y, a continuación, entrenan un proceso geométrico hiperbólico de difusión latente.
Primero se integran los datos del grafo 𝒢 = (𝐗, A) en un espacio hiperbólico de baja dimensionalidad, lo que mejorará el proceso de difusión del grafo oculto.
El autocodificador hiperbólico propuesto por los autores del método consta de un codificador geométrico hiperbólico y un decodificador Fermi-Dirac. El codificador geométrico hiperbólico codifica el grafo 𝒢 = (𝐗, A) en el espacio geométrico hiperbólico para obtener una representación hiperbólica adecuada, mientras que el decodificador Fermi-Dirac decodifica nuevamente la representación hiperbólica en el dominio de datos del grafo. La variedad hiperbólica Hd y el espacio tangente 𝒯x pueden mapearse la una sobre el otro mediante representaciones exponenciales y logarítmicas. Los perceptrones multicapa (MLP) o las redes neuronales gráficas (GNN) pueden utilizarse para las representaciones exponenciales y logarítmicas como codificadores geométricos hiperbólicos. En su trabajo, los autores del método usaron redes neuronales convolucionales de grafos hiperbólicos (HGCN) como codificador geométrico hiperbólico.
Debido al fallo aditivo de la distribución gaussiana en el espacio hiperbólico, no se puede usar directamente la distribución normal riemanniana o la distribución normal envuelta. En lugar de la difusión de incorporación hiperbólica, se utiliza el espacio de producto de múltiplos de variedades. Los autores del método HypDiff propusieron un nuevo proceso de difusión en el espacio hiperbólico. Para una mayor eficiencia computacional, la distribución gaussiana del espacio hiperbólico se aproxima por la distribución gaussiana del plano tangente 𝒯μ.
A diferencia de la suma lineal en el espacio euclidiano, el espacio hiperbólico usa la suma de Möbius. Esto crea problemas para la difusión en la variedad hiperbólica. Además, el ruido isotrópico provoca una rápida disminución de la relación señal/ruido, lo cual dificulta la conservación de la información topológica.
La anisotropía del grafo en el espacio latente contiene un desplazamiento inductivo de la estructura del grafo, donde el problema más crítico reside en la determinación de las direcciones dominantes de las características anisotrópicas. Para resolver los problemas anteriores, los autores de HypDiff propusieron una estructura de difusión anisotrópica hiperbólica. La idea básica consiste en seleccionar la dirección de difusión principal (es decir, el ángulo) basándose en la clusterización de los nodos según su similitud, lo cual equivale a dividir el espacio latente hiperbólico en varios sectores. A continuación, los nodos de cada clúster se proyectan sobre el plano tangente a su centro para su difusión.
Los clústeres pueden obtenerse utilizando cualquier algoritmo de clusterización basado en similitudes en el paso de procesamiento previo.
El parámetro de clusterización hiperbólica k ∈ [1, n] representa el número de sectores que separan el espacio hiperbólico. La difusión anisotrópica hiperbólica es equivalente a la difusión direccional en el modelo de Klein 𝕂c,n con curvatura múltiple Ci ∈|k|, que supone una proyección aproximada sobre el conjunto de planos tangentes 𝒯𝐨i∈{|k|} de los centroides Oi∈{|k|}.
Esta propiedad establece elegantemente una conexión entre el algoritmo de aproximación propuesto por los autores de HypDiff y el modelo de curvatura múltiple de Klein.
El algoritmo propuesto muestra cierto comportamiento basado en el valor de k. Esto permite una representación más flexible y detallada de la anisotropía basada en la geometría hiperbólica, lo cual permite una mayor precisión y eficacia en la posterior adición de ruido y el entrenamiento del modelo.
La geometría hiperbólica puede describir de forma natural y geométrica el patrón de conexión de los nodos durante el crecimiento del grafo. La popularidad de un nodo puede abstraerse según sus coordenadas radiales, mientras que la similitud puede expresarse usando las distancias de las coordenadas angulares en el espacio hiperbólico.
El objetivo principal consiste en modelizar una difusión con crecimiento geométrico radial en la que este crecimiento radial sea consistente con las propiedades hiperbólicas.
La principal razón por la que el modelo de difusión general no funciona bien con grafos es la reducción de la relación señal-ruido rápida. En HypDiff, la dirección geodésica entre el punto central de cada clúster y el polo norte O se utiliza como dirección objetivo de la difusión cuando se imponen restricciones para procesos de difusión directa.
Siguiendo el proceso estándar de reducción de ruido y entrenamiento del modelo de ruido para modelar el proceso de difusión inversa, los autores de HypDiff usan la arquitectura DDM basada en UNET para entrenar la previsión X0.
Además, los autores de HypDiff demuestran que es posible realizar el muestreo simultáneamente en el mismo espacio tangente en lugar de efectuarlo en diferentes espacios tangentes de los centros de los clústeres para mejorar la eficacia.
A continuación le mostramos la visualización del framework HypDiff realizada por el autor.
2. Implementación con MQL5
Tras repasar los aspectos teóricos del marco HypDiff, vamos a pasar a la parte práctica de este artículo, donde implementaremos nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5. Y debemos decir de entrada que nos espera un "largo y fascinante viaje". Por lo tanto, deberá estar mentalmente preparado para trabajar mucho.
2.1 Complementamos el programa OpenCL
Y empezaremos nuestro trabajo añadiendo cambios a nuestro programa OpenCL. Primero tendremos que organizar la proyección de los datos de origen en el espacio hiperbólico. Durante la transformación de datos, deberemos considerar la posición de cada elemento en la secuencia, ya que el espacio hiperbólico combina los parámetros del espacio y el tiempo euclidianos. De forma similar a la aplicación del autor, utilizaremos el modelo de Lorentz. Realizaremos esta tarea en el kernel HyperProjection.
__kernel void HyperProjection(__global const float *inputs, __global float *outputs ) { const size_t pos = get_global_id(0); const size_t d = get_local_id(1); const size_t total = get_global_size(0); const size_t dimension = get_local_size(1);
En los parámetros de este kernel pasaremos los punteros a los búferes de datos: la secuencia a analizar y los resultados de la transformación. Luego definiremos los parámetros de los búferes que se pasarán directamente a través del espacio de tareas. La primera dimensión nos indicará la dimensionalidad de la secuencia analizada, mientras que la segunda dimensión nos indicará el tamaño del vector de descripción de un elemento de la secuencia analizada. En este caso, los flujos se agruparán en grupos de trabajo según la última dimensión.
Aquí deberemos considerar que el vector de descripción de un elemento de la secuencia contendrá 1 elemento más.
A continuación, declararemos un array local que nos permitirá organizar el intercambio de datos entre los flujos del grupo de trabajo.
__local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
Y luego definiremos las constantes de desplazamiento en los búferes de datos.
const int shift_in = pos * dimension + d; const int shift_out = pos * (dimension + 1) + d + 1;
Después cargaremos los datos iniciales del búfer global en los elementos locales del flujo de operaciones correspondiente y calcularemos los valores cuadráticos. Al mismo tiempo, comprobaremos la validez de los resultados de las operaciones anteriores.
float v = inputs[shift_in]; if(isinf(v) || isnan(v)) v = 0; //--- float v2 = v * v; if(isinf(v2) || isnan(v2)) v2 = 0;
A continuación, tendremos que calcular la norma del vector de datos de origen. Para ello, sumaremos el cuadrado de sus valores utilizando nuestro array local. Al fin y al cabo, cada flujo del grupo de trabajo contiene 1 elemento.
//--- if(d < ls) temp[d] = v2; barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += v2; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Aquí cabe señalar que necesitaremos la norma del vector solo para calcular el valor del primer elemento de nuestro vector que describe las coordenadas hiperbólicas del elemento de la secuencia analizada. Todos los demás elementos los trasladaremos sin cambios, pero con un desplazamiento de posición.
outputs[shift_out] = v;
Y para no realizar operaciones redundantes, determinaremos el valor del primer elemento del vector hiperbólico solo en el primer flujo de cada grupo de trabajo.
Aquí, primero calcularemos la proporción de desplazamiento en el elemento analizado en la secuencia original. Y a continuación restaremos el cuadrado del valor obtenido de la norma anterior calculada del vector de representación original del elemento analizado. Y sacaremos la raíz cuadrada del valor resultante.
if(d == 0) { v = ((float)pos) / ((float)total); if(isinf(v) || isnan(v)) v = 0; outputs[shift_out - 1] = sqrt(fmax(temp[0] - v * v, 1.2e-07f)); } }
Tenga en cuenta que para extraer la raíz cuadrada tomaremos de forma garantizada un valor superior a 0. Esto nos permitirá excluir errores en las operaciones y resultados no válidos.
Para implementar los algoritmos de pasada inversa, crearemos directamente el kernel HyperProjectionGrad, en el que implementaremos el proceso de distribución del gradiente de error a través de las operaciones de pasada directa descritas anteriormente. Y hay dos cosas a las que prestar atención. En primer lugar, la posición de un elemento en la secuencia será estática y no estará parametrizada. Por lo tanto, no le aplicaremos un gradiente de error.
En segundo lugar, el gradiente de error de los elementos restantes vendrá en dos flujos de información. La transferencia directa de datos posibilitará la transferencia directa del gradiente de error. Al mismo tiempo, se han utilizado todos los elementos del vector de descripción del elemento de la secuencia original para calcular la norma del vector implicado en la determinación del primer elemento de la representación hiperbólica. Por lo tanto, cada elemento deberá recibir su parte del gradiente de error del primer elemento del vector de representación hiperbólica.
Veamos la implementación de los enfoques descritos en código. En los parámetros del kernel HyperProjectionGrad se transmitirán ya 3 punteros a los búferes de datos. Asimismo, se añadirá un búfer de gradiente de error al nivel de los datos de origen (inputs_gr), mientras que el búfer de representación hiperbólica de la secuencia original se sustituirá por el correspondiente búfer de gradiente de error (outputs_gr).
__kernel void HyperProjectionGrad(__global const float *inputs, __global float *inputs_gr, __global const float *outputs_gr ) { const size_t pos = get_global_id(0); const size_t d = get_global_id(1); const size_t total = get_global_size(0); const size_t dimension = get_global_size(1);
El espacio de tareas del kernel lo dejaremos de forma similar al de la pasada directa, pero sin combinar los flujos en grupos de trabajo. En el cuerpo del kernel, primero identificaremos el flujo actual en el espacio de tareas. Y según los valores obtenidos determinaremos el desplazamiento en los búferes de datos.
const int shift_in = pos * dimension + d; const int shift_start_out = pos * (dimension + 1); const int shift_out = shift_start_out + d + 1;
En el bloque de carga de datos de los búferes globales, leeremos el valor del elemento analizado de la representación original y su gradiente de error al nivel de la representación hiperbólica.
float v = inputs[shift_in]; if(isinf(v) || isnan(v)) v = 0; float grad = outputs_gr[shift_out]; if(isinf(grad) || isnan(grad)) grad = 0;
A continuación, determinaremos la fracción del gradiente de error del primer elemento de la representación hiperbólica, que se definirá como el producto de su gradiente de error por el valor inicial del elemento analizado.
v = v * outputs_gr[shift_start_out]; if(isinf(v) || isnan(v)) v = 0;
Y no nos olvidaremos de comprobar la validez de los resultados en cada paso.
Luego almacenaremos el gradiente de error acumulado en el búfer de datos global correspondiente.
//---
inputs_gr[shift_in] = v + grad;
}
En esta fase, hemos organizado la proyección de los datos de origen en el espacio hiperbólico. Sin embargo, los autores del método proponen realizar el proceso de difusión en proyecciones del espacio hiperbólico sobre planos tangentes.
A primera vista, la proyección de los datos de una representación plana a una hiperbólica y viceversa para añadir ruido puede parecer un poco extraña. Pero la cuestión es que resulta muy probable que la representación plana original sea diferente de la proyección final. Al fin y al cabo, el plano de los valores iniciales y las proyecciones de la representación hiperbólica son planos diferentes.
Supongo que puede compararse con hacer un dibujo a partir de una fotografía de un objeto. En primer lugar, componemos en nuestra cabeza una representación tridimensional del objeto representado en la fotografía considerando nuestra experiencia y nuestros conocimientos a priori. A continuación, trasladamos al papel un dibujo del objeto presentado en vistas lateral, frontal y superior. Del mismo modo, HypDiff realiza proyecciones de los datos sobre múltiples planos tangentes con centros diferentes.
Para implementar dicha funcionalidad, crearemos el kernel LogMap. En los parámetros de este kernel obtendremos los punteros a 7 búferes de datos, lo cual nos bastará. Entre ellos, habrá 3 búferes de datos de origen:
- El búfer de características contendrá el tensor de incorporación de la representación hiperbólica de los datos de origen.
- El búfer de centroides contendrá las coordenadas de los centroides. Hacia ellos se han trazado planos tangentes sobre los que realizaremos las proyecciones de los datos iniciales.
- Los búferes curvatures representarán los parámetros de curvatura de los centroides correspondientes.
No resulta difícil adivinar que el búfer outputs está destinado a registrar los resultados de las operaciones. Asimismo, hemos añadido 3 búferes de datos adicionales para registrar los resultados intermedios que necesitaremos al realizar las operaciones de pasada inversa.
Y aquí debemos señalar que en nuestra implementación nos hemos alejado un poco del marco de los autores. La cuestión es que los autores de HypDiff agruparon los elementos de la secuencia analizada en la fase de preparación de los datos, y luego proyectaron a las tangentes solo elementos de grupos separados. Sin embargo, no realizaremos una división preliminar de los elementos de la secuencia en grupos. Por consiguiente, generaremos la proyección de todos los elementos a todas las tangentes. Obviamente, esto aumentará el número de operaciones a realizar. Pero, por otra parte, así enriqueceremos la representación del modelo de la secuencia analizada.
__kernel void LogMap(__global const float *features, __global const float *centroids, __global const float *curvatures, __global float *outputs, __global float *product, __global float *distance, __global float *norma ) { //--- identify const size_t f = get_global_id(0); const size_t cent = get_global_id(1); const size_t d = get_local_id(2); const size_t total_f = get_global_size(0); const size_t total_cent = get_global_size(1); const size_t dimension = get_local_size(2);
En el cuerpo del método, identificaremos el flujo actual de operaciones en el espacio de tareas tridimensional. La primera dimensión indicará un elemento de la secuencia original. La segunda estará en el centroide. Y la tercera, en la posición en el vector de descripción del elemento de secuencia analizado. En este caso, añadiremos los flujos en grupos de trabajo en la última dimensión.
A continuación, declararemos un array local de intercambio de datos dentro del grupo de trabajo.
//--- create local array __local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
Y luego definiremos las constantes de desplazamiento en los búferes de datos.
//--- calc shifts const int shift_f = f * dimension + d; const int shift_out = (f * total_cent + cent) * dimension + d; const int shift_cent = cent * dimension + d; const int shift_temporal = f * total_cent + cent;
Después cargaremos los datos iniciales de los búferes globales comprobando obligatoriamente la validez de los valores obtenidos.
//--- load inputs float feature = features[shift_f]; if(isinf(feature) || isnan(feature)) feature = 0; float centroid = centroids[shift_cent]; if(isinf(centroid) || isnan(centroid)) centroid = 0; float curv = curvatures[cent]; if(isinf(curv) || isnan(curv)) curv = 1.2e-7;
A continuación tendremos que calcular los productos de los tensores de los datos de origen y los centroides. Pero como estamos trabajando con una representación hiperbólica, utilizaremos el producto de Minkowski. Para ello, primero realizaremos la multiplicación de los valores escalares correspondientes.
//--- dot(features, centroids) float fc = feature * centroid; if(isnan(fc) || isinf(fc)) fc = 0;
Y sumaremos los valores obtenidos en el grupo de trabajo.
//--- if(d < ls) temp[d] = (d > 0 ? fc : -fc); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += fc; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float prod = temp[0]; if(isinf(prod) || isnan(prod)) prod = 0;
Obsérvese que, a diferencia de la multiplicación habitual de vectores en el espacio euclídeo, tomaremos el producto de los primeros elementos de los vectores con el valor inverso.
Luego comprobaremos la validez del resultado de las operaciones realizadas y guardaremos el valor obtenido en el elemento correspondiente del búfer global de almacenamiento temporal de datos. Necesitaremos este valor durante el pasada inversa.
product[shift_temporal] = prod;
Esto nos permitirá determinar la dirección y la magnitud del desplazamiento del elemento analizado desde el centroide.
//--- project float u = feature + prod * centroid * curv; if(isinf(u) || isnan(u)) u = 0;
Después determinaremos la norma de Minkowski del vector desplazamiento obtenido. Al igual que antes, tomaremos el cuadrado de cada elemento.
//--- norm(u) float u2 = u * u; if(isinf(u2) || isnan(u2)) u2 = 0;
Y sumaremos los valores obtenidos dentro del grupo de trabajo, tomando el cuadrado del primer elemento con signo contrario.
if(d < ls) temp[d] = (d > 0 ? u2 : -u2); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += u2; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float normu = temp[0]; if(isinf(normu) || isnan(normu) || normu <= 0) normu = 1.0e-7f; normu = sqrt(normu);
También necesitaremos este valor como parte de la pasada inversa. Así que lo guardaremos en el búfer de almacenamiento temporal de datos.
norma[shift_temporal] = normu;
En el siguiente paso, determinaremos la distancia del punto analizado hasta el centroide en el espacio hiperbólico con los parámetros de curvatura del centroide. En este caso, no volveremos a calcular el producto de los vectores, sino que utilizaremos el valor obtenido anteriormente.
//--- distance features to centroid float theta = -prod * curv; if(isinf(theta) || isnan(theta)) theta = 0; theta = fmax(theta, 1.0f + 1.2e-07f); float dist = sqrt(clamp(pow(acosh(theta), 2.0f) / curv, 0.0f, 50.0f)); if(isinf(dist) || isnan(dist)) dist = 0;
Luego verificaremos la validez del valor obtenido y guardaremos el resultado en el búfer global de almacenamiento temporal de datos.
distance[shift_temporal] = dist;
A continuación ajustaremos los valores del vector de desplazamiento.
float proj_u = dist * u / normu;
Y luego solo nos quedará realizar una proyección de los valores obtenidos sobre el plano tangente. Y aquí, de forma similar a la proyección de Lorentz realizada antes, tendremos que corregir el primer elemento del vector de proyección. Para ello, calcularemos el producto de los vectores de proyección y el centroide sin considerar los primeros elementos.
if(d < ls) temp[d] = (d > 0 ? proj_u * centroid : 0); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += proj_u * centroid; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Luego ajustaremos el valor del primer elemento de la proyección.
//--- if(d == 0) { proj_u = temp[0] / centroid; if(isinf(proj_u) || isnan(proj_u)) proj_u = 0; proj_u = fmax(u, 1.2e-7f); }
Y guardaremos los resultados obtenidos.
//---
outputs[shift_out] = proj_u;
}
Como podemos ver, el algoritmo del kernel ha resultado bastante engorroso, con un montón de conexiones complejas. Y esto dificulta bastante la comprensión de la trayectoria del gradiente de error dentro de la pasada inversa. Sin embargo, desenredar esta "maraña" dependerá de nosotros . Para ello, nos armaremos de una gran atención al detalle y nos pondremos manos a la obra. El algoritmo de pasada inversa se implementará en el kernel LogMapGrad.
__kernel void LogMapGrad(__global const float *features, __global float *features_gr, __global const float *centroids, __global float *centroids_gr, __global const float *curvatures, __global float *curvatures_gr, __global const float *outputs, __global const float *outputs_gr, __global const float *product, __global const float *distance, __global const float *norma ) { //--- identify const size_t f = get_local_id(0); const size_t cent = get_global_id(1); const size_t d = get_local_id(2); const size_t total_f = get_local_size(0); const size_t total_cent = get_global_size(1); const size_t dimension = get_local_size(2);
En los parámetros del kernel, añadiremos los búferes de gradiente de error en los niveles de los datos de origen y resultados, lo cual nos proporcionará 4 búferes de datos adicionales.
Dejaremos el espacio de tareas del kernel de la misma forma que en la pasada directa, solo que cambiaremos el principio de agrupación en grupos de trabajo. De hecho, ahora no solo tendremos que recopilar valores dentro de los vectores de los elementos individuales de la secuencia, sino también gradientes para los centroides. De hecho, cada centroide trabajará con todos los elementos de la secuencia analizada. Como consecuencia, también deberá obtener el gradiente de error de cada uno.
En el cuerpo del kernel, identificaremos el flujo de operaciones en todas las dimensiones del espacio de tareas. Después de eso, crearemos un array local de intercambio de datos entre los elementos del grupo de trabajo.
//--- create local array __local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
Y definiremos las constantes de desplazamiento en los búferes de datos globales.
//--- calc shifts const int shift_f = f * dimension + d; const int shift_out = (f * total_cent + cent) * dimension + d; const int shift_cent = cent * dimension + d; const int shift_temporal = f * total_cent + cent;
Después cargaremos los datos de los búferes globales. En primer lugar, extraeremos los datos de origen y los valores intermedios.
//--- load inputs float feature = features[shift_f]; if(isinf(feature) || isnan(feature)) feature = 0; float centroid = centroids[shift_cent]; if(isinf(centroid) || isnan(centroid)) centroid = 0; float centroid0 = (d > 0 ? centroids[shift_cent - d] : centroid); if(isinf(centroid0) || isnan(centroid0) || centroid0 == 0) centroid0 = 1.2e-7f; float curv = curvatures[cent]; if(isinf(curv) || isnan(curv)) curv = 1.2e-7; float prod = product[shift_temporal]; float dist = distance[shift_temporal]; float normu = norma[shift_temporal];
Y aquí calcularemos los valores del vector de desplazamiento del elemento secuencial analizado desde el centroide. A diferencia de las operaciones de pasada directa, ya tenemos todos los datos que necesitamos.
float u = feature + prod * centroid * curv; if(isinf(u) || isnan(u)) u = 0;
Ahora cargaremos el gradiente de error existente al nivel de los resultados.
float grad = outputs_gr[shift_out]; if(isinf(grad) || isnan(grad)) grad = 0; float grad0 = (d>0 ? outputs_gr[shift_out - d] : grad); if(isinf(grad0) || isnan(grad0)) grad0 = 0;
Obsérvese que cargamos el gradiente de error no solo del elemento analizado, sino también del primer elemento del vector de descripción del elemento de secuencia analizado. La razón aquí resulta similar a la descrita anteriormente para el kernel HyperProjectionGrad.
A continuación, inicializaremos las variables locales de acumulación del gradiente de error.
float feature_gr = 0; float centroid_gr = 0; float curv_gr = 0; float prod_gr = 0; float normu_gr = 0; float dist_gr = 0;
Primero trazaremos el gradiente de error a partir de la proyección de los datos sobre el plano tangente al vector de desplazamiento.
float proj_u_gr = (d > 0 ? grad + grad0 / centroid0 * centroid : 0);
Cabe señalar que el primer elemento del vector de desplazamiento no influirá en el resultado. Por lo tanto, su gradiente será "0". Los demás elementos han recibido tanto un gradiente de error directo como una fracción del primer elemento de los resultados.
Aquí determinaremos los primeros valores de los gradientes de error para los centroides. Los calcularemos en un ciclo, recogiendo los valores de todos los elementos de la secuencia.
for(int id = 0; id < dimension; id += ls) { if(d >= id && d < (id + ls)) { int t = d % ls; for(int ifeat = 0; ifeat < total_f; ifeat++) { if(f == ifeat) { if(d == 0) temp[t] = (f > 0 ? temp[t] : 0) + outputs[shift_out] / centroid * grad; else temp[t] = (f > 0 ? temp[t] : 0) + grad0 / centroid0 * outputs[shift_out]; } barrier(CLK_LOCAL_MEM_FENCE); }
Y después de recoger los gradientes de error de todos los elementos de la secuencia dentro del array local, usaremos un único flujo y transferiremos los valores recogidos a una variable local.
if(f == 0) { if(isnan(temp[t]) || isinf(temp[t])) temp[t] = 0; centroid_gr += temp[0]; } } barrier(CLK_LOCAL_MEM_FENCE); }
En este proceso, será esencial garantizar que todos los flujos de operaciones alcancen los puntos de barrera sin excepción.
A continuación, calcularemos el gradiente de error para los vectores de distancia, norma y desplazamiento.
dist_gr = u / normu * proj_u_gr;
float u_gr = dist / normu * proj_u_gr;
normu_gr = dist * u / (normu * normu) * proj_u_gr;
Aquí cabe señalar que los elementos del vector de desplazamiento son individuales en cada flujo. Pero la norma del vector y la distancia son valores discretos. Por lo tanto, tendremos que sumar los gradientes de error correspondientes dentro de un único elemento de la secuencia analizada. Primero recogeremos los gradientes de error para la distancia. Después sumaremos los valores a través de un array local.
for(int ifeat = 0; ifeat < total_f; ifeat++) { if(d < ls && f == ifeat) temp[d] = dist_gr; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += dist_gr; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); if(f == ifeat) { if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; dist_gr = temp[0];
Y determinaremos inmediatamente el gradiente de error para el parámetro de curvatura del centroide correspondiente y el producto de los vectores.
if(d == 0) { float theta = -prod * curv; float theta_gr = 1.0f / sqrt(curv * (theta * theta - 1)) * dist_gr; if(isinf(theta_gr) || isnan(theta_gr)) theta_gr = 0; curv_gr += -pow(acosh(theta), 2.0f) / (2 * sqrt(pow(curv, 3.0f))) * dist_gr; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; temp[0] = -curv * theta_gr; if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; curv_gr += -prod * theta_gr; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; } } barrier(CLK_LOCAL_MEM_FENCE);
Sin embargo, cabe señalar que el gradiente de error del parámetro de curvatura solo se acumulará para su posterior almacenamiento en el búfer de datos globales. Por el contrario, el gradiente de error del producto de vectores será un valor intermedio para la distribución posterior entre elementos influyentes. Por eso será importante que lo sincronicemos dentro del grupo de trabajo. Así que en esta etapa lo almacenaremos en un elemento del array local. Y luego lo moveremos a una variable local.
if(f == ifeat) prod_gr += temp[0]; barrier(CLK_LOCAL_MEM_FENCE);
Creo que se habrá dado cuenta del gran número de controles repetitivos. Esto complica un poco el código, pero se trata de una medida necesaria para pasar correctamente las barreras de sincronización de los flujos del grupo de trabajo.
A continuación, sumaremos de forma similar el gradiente de error de la norma del vector de desplazamiento.
if(d < ls && f == ifeat) temp[d] = normu_gr; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += normu_gr; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); if(f == ifeat) { normu_gr = temp[0]; if(isinf(normu_gr) || isnan(normu_gr)) normu_gr = 1.2e-7;
Luego corregiremos el gradiente de error del vector de desplazamiento.
u_gr += u / normu * normu_gr; if(isnan(u_gr) || isinf(u_gr)) u_gr = 0;
Y lo distribuiremos entre los datos de origen y el centroide.
feature_gr += u_gr; centroid_gr += prod * curv * u_gr; } barrier(CLK_LOCAL_MEM_FENCE);
También cabe señalar aquí que el gradiente de error del vector de desplazamiento deberá distribuirse al nivel del producto de los vectores y el parámetro de curvatura. Sin embargo, las entidades especificadas son valores escalares. Por consiguiente, tendremos que sumar los valores dentro de un único elemento de la secuencia analizada. Y en esta etapa, organizaremos la suma de los productos de los gradientes de error correspondientes del vector de desplazamiento por los elementos del centroide. Que será básicamente el producto de estos vectores.
//--- dot (u_gr * centroid) if(d < ls && f == ifeat) temp[d] = u_gr * centroid; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += u_gr * centroid; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Utilizaremos los valores obtenidos para distribuir el gradiente de error entre las entidades correspondientes.
if(f == ifeat && d == 0) { if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; prod_gr += temp[0] * curv; if(isinf(prod_gr) || isnan(prod_gr)) prod_gr = 0; curv_gr += temp[0] * prod; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; temp[0] = prod_gr; } barrier(CLK_LOCAL_MEM_FENCE);
A continuación, sincronizaremos el valor del gradiente de error al nivel del producto de los vectores dentro del grupo de trabajo.
if(f == ifeat) { prod_gr = temp[0];
Y distribuiremos el valor obtenido entre los datos de origen.
feature_gr += prod_gr * centroid * (d > 0 ? 1 : -1); centroid_gr += prod_gr * feature * (d > 0 ? 1 : -1); } barrier(CLK_LOCAL_MEM_FENCE); }
Una vez hayamos realizado correctamente todas las operaciones y se hayan recogido completamente los gradientes de error en las variables locales, transferiremos los valores resultantes a los búferes de datos globales.
//--- result features_gr[shift_f] = feature_gr; centroids_gr[shift_cent] = centroid_gr; if(f == 0 && d == 0) curvatures_gr[cent] = curv; }
Y finalizaremos el funcionamiento del kernel.
Como podemos ver, el algoritmo es bastante complejo, pero al mismo tiempo atractivo. Y para entenderlo deberemos prestar atención a los detalles.
Como ya hemos mencionado, la aplicación del marco HypDiff requiere un trabajo considerable. Solo hemos hablado de la implementación de los algoritmos en la parte del programa OpenCL, cuyo código completo estará disponible en el apéndice. Dicho esto, ya casi hemos agotado la extensión del artículo. Le propongo explorar más a fondo la implementación de los algoritmos del framework en la parte del programa central en el próximo artículo. Así, dividiremos el trabajo realizado en 2 bloques lógicos.
Conclusión
El uso de la geometría hiperbólica resuelve los problemas derivados del conflicto entre los datos de grafos discretos y el modelo de difusión continua. El marco HypDiff propone un método mejorado de generación de ruido gaussiano hiperbólico para resolver el problema del fallo aditivo de las distribuciones gaussianas en el espacio hiperbólico. Las restricciones geométricas de similitud angular se aplican al proceso de difusión anisotrópica para preservar la estructura local.
En la parte práctica del artículo, hemos empezado a aplicar los enfoques propuestos utilizando los recursos de MQL5. Sin embargo, el alcance del trabajo va más allá del ámbito de un solo artículo. Así que seguiremos construyendo el framework propuesto en el próximo artículo.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16306
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte V): Modelos profundos de Markov
Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte V): Modelos profundos de Markov
 De novato a experto: depuración colaborativa en MQL5
De novato a experto: depuración colaborativa en MQL5
 Redes neuronales en el trading: Modelo hiperbólico de difusión latente (Final)
Redes neuronales en el trading: Modelo hiperbólico de difusión latente (Final)
 Entrenamos un perceptrón multicapa usando el algoritmo de Levenberg-Marquardt
Entrenamos un perceptrón multicapa usando el algoritmo de Levenberg-Marquardt
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso