Нейросети в трейдинге: Гиперболическая модель латентной диффузии (HypDiff)
Введение
Графы содержат разнообразие и значимость топологий исходных данных. Эти топологические характеристики часто отражают физические принципы и модели развития. Традиционные модели случайных графов, базирующиеся на теории графов, требуют применения искусственных эвристик для создания алгоритмов определённой топологии и не способны гибко моделировать разнообразные сложные графы. В связи с этим было создано множество моделей глубокого обучения для генерации графов. Разработанные вероятностные модели диффузии с функцией шумоподавления показали высокую эффективность и потенциал в решении задач визуализации.
Однако из-за нерегулярной и не евклидовой структуры графов реализация диффузионной модели в данном контексте имеет два основных ограничения:
- Высокая вычислительная сложность. Суть генерации графов заключается в обработке дискретности, разреженности и других топологических свойств не евклидовой структуры. Поскольку возмущение гауссова шума, используемое в ванильной модели диффузии, не подходит для дискретных данных, модель диффузии дискретного графа обычно имеет высокую временную и пространственную сложность из-за проблемы структурной разреженности. Более того, модель диффузии дискретных графов опирается на непрерывный процесс гауссова шума для создания полностью связанных, зашумленных графов, которая теряет структурную информацию и лежащие в ее основе топологические свойства.
- Анизотропия не евклидовой структуры. В отличие от данных регулярной структуры, "нерегулярные" не евклидовые структуры эмбедингов графов анизотропные в непрерывном латентном пространстве. Эмбединги узлов графа в евклидовом пространстве демонстрируют значительную анизотропию в нескольких конкретных направлениях. Изотропная диффузия эмбединга узла графа в латентное пространство будет рассматривать анизотропную структурную информацию как шум, и эта полезная структурная информация будет потеряна в процессе шумоподавления.
Гиперболическое геометрическое пространство широко признано в качестве идеального непрерывного многообразия для представления дискретных древовидных или иерархических структур и используется в различных задачах обучения графов. И как утверждают авторы работы "Hyperbolic Geometric Latent Diffusion Model for Graph Generation", гиперболическая геометрия обладает большим потенциалом для решения не евклидовой структурной анизотропии в процессах латентной диффузии графов. В гиперболическом пространстве можно наблюдать, что распределение эмбедингов узлов имеет тенденцию быть изотропным глобально. При этом анизотропия сохраняется локально. Кроме того, гиперболическая геометрия унифицирует угловые и радиальные измерения полярных координат и может обеспечить геометрические измерения с физической семантикой и интерпретируемостью. Интересно, что гиперболическая геометрия может обеспечить латентное пространство с геометрическими априорными характеристиками графа.
Основываясь на вышеизложенных выводах, авторы указанной работы стремятся подобрать подходящее латентное пространство на основе гиперболической геометрии для разработки эффективного процесса диффузии в не евклидовую структуру в задачах генерации графов с сохранением топологии. Параллельно решаются 2 основные проблемы:
- Аддитивность непрерывных гауссовых распределений не определена в гиперболическом латентном пространстве;
- Разработка эффективного процесса анизотропной диффузии для неевклидовых структур.
С целью решения этих проблем была предложена модель латентной диффузии в гиперболическом пространстве (HypDiff). Для аддитивной задачи о непрерывном гауссовом распределении в гиперболическом пространстве предложен процесс диффузии, основанный на радиальных мерах. А угловое ограничение было использовано для ограничения анизотропного шума с целью сохранения структурной априорности, направляя диффузионную модель к более мелким деталям структуры графа.
1. Алгоритм HypDiff
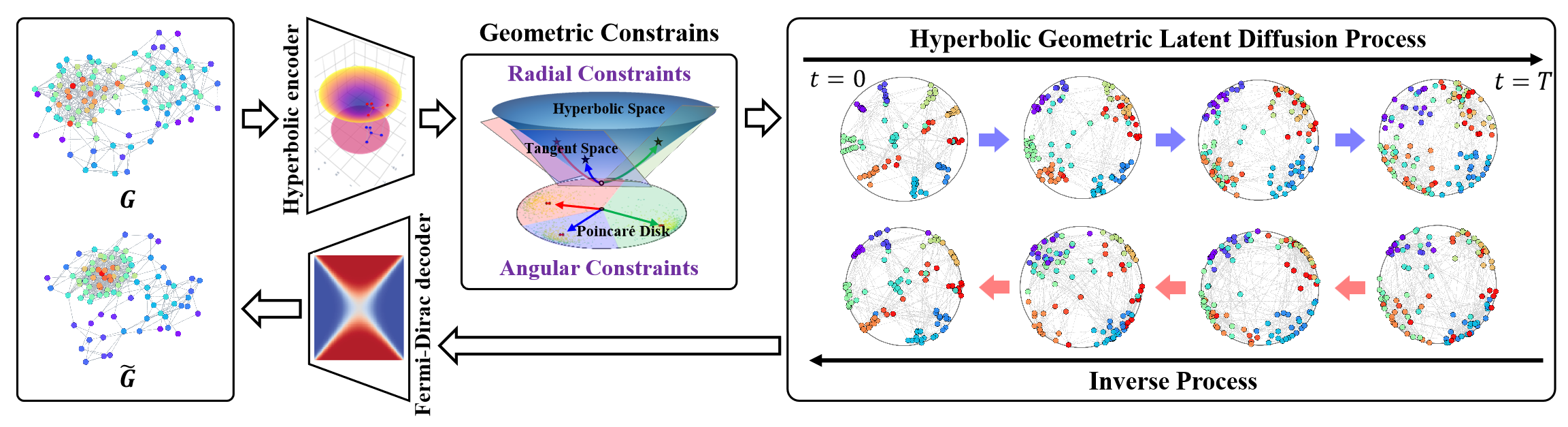
Модель латентной гиперболической диффузии (HypDiff) позволяет решить две основные проблемы. В ней используется гиперболическая геометрия для абстрагирования неявной иерархии узлов графа и вводится два геометрических ограничения для сохранения важных топологических свойств. Авторы метода применяют двухэтапную стратегию обучения. Сначала обучается гиперболический автоэнкодер для получения предварительно обученных эмбедингов узлов, а затем обучается процесс гиперболической геометрической латентной диффузии.
Сначала требуется интегрировать данные графа 𝒢 = (𝐗, A) в гиперболическое пространство с низкой размерностью, что позволит улучшить процесс скрытой диффузии графа.
Предложенный авторами метода гиперболический автоэнкодера состоит из гиперболического геометрического энкодера и декодера Ферми-Дирака. Гиперболический геометрический энкодер кодирует граф 𝒢 = (𝐗, A) в гиперболическое геометрическое пространство для получения подходящего гиперболического представления, а декодер Ферми-Дирака декодирует гиперболическое представление обратно в область данных графа. Гиперболическое многообразие Hd и касательное пространство 𝒯x могут быть отображены друг на друга с помощью экспоненциального и логарифмического отображений. Затем можно использовать многослойные перцептроны (MLP) или графовые нейронные сети (GNN) для экспоненциального и логарифмического представлений в качестве гиперболических геометрических энкодеров. В своей работе авторы метода использовали сверточные нейронные сети с гиперболическим графом (HGCN) в качестве гиперболического геометрического энкодера.
Из-за аддитивного сбоя гауссова распределения в гиперболическом пространстве нельзя напрямую использовать риманово нормальное распределение или обернутое нормальное распределение. Вместо гиперболической диффузии эмбедингов используется пространство произведения кратных многообразий. Авторы метода HypDiff предложили новый процесс диффузии в гиперболическом пространстве. Для вычислительной эффективности гауссово распределение гиперболического пространства аппроксимируется гауссовским распределением касательной плоскости 𝒯μ.
В отличие от линейного сложения в евклидовом пространстве, гиперболическое пространство использует сложение Мёбиуса. Это создает проблемы для диффузии по гиперболическому многообразию. Кроме того, изотропный шум приводит к быстрому снижению отношения сигнал/шум, что затрудняет сохранение топологической информации.
Анизотропия графа в латентном пространстве содержит индуктивное смещение структуры графа, где наиболее критической проблемой является определение доминирующих направлений анизотропных признаков. Для решения указанных проблем авторы HypDiff предложили гиперболическую анизотропную диффузионную структуру. Основная идея заключается в том, чтобы выбрать основное направление диффузии (т.е. угол) на основе кластеризации узлов по сходству. Что эквивалентно разделению гиперболического латентного пространства на несколько секторов. После чего проецируются узлы каждого кластера на касательную плоскость его центра для диффузии.
Кластеры могут быть получены с помощью любого алгоритма кластеризации на основе сходства на этапе предварительной обработки.
Параметр гиперболической кластеризации k ∈ [1, n] представляет собой количество секторов, разделяющих гиперболическое пространство. Гиперболическая анизотропная диффузия эквивалентна направленной диффузии в модели Клейна 𝕂c,n с множественной кривизной Ci ∈|k|, которая представляет собой приближенную проекцию на набор касательных плоскостей 𝒯𝐨i∈{|k|} центроидов Oi∈{|k|}.
Это свойство элегантно устанавливает связь между предложенным авторами HypDiff алгоритмом аппроксимации и моделью Клейна с множественной кривизной.
Предложенный алгоритм демонстрирует определенное поведение, основанное на значении k. Это позволяет более гибко и детально представить анизотропию на основе гиперболической геометрии, что позволяет повысить точность и эффективность при последующем добавлении шума и обучении модели.
Гиперболическая геометрия может естественно и геометрически описывать схему соединения узлов во время роста графа. Популярность узла может быть абстрагирована по его радиальным координатам, а сходство может быть выражено угловыми координатными расстояниями в гиперболическом пространстве.
Основная цель состоит в том, чтобы смоделировать диффузию с геометрическим радиальным ростом. В которой этот радиальный рост согласуется с гиперболическими свойствами.
Основная причина, по которой общая диффузионная модель не очень хорошо работает с графами, заключается в снижении быстрого отношения сигнал/шум. В HypDiff направление геодезии между центральной точкой каждого кластера и северным полюсом O используется в качестве целевого направления диффузии при наложении ограничений для процессов прямой диффузии.
Следуя стандартному процессу шумоподавления и обучения шумопоглощающей модели для моделирования процесса обратной диффузии, авторы HypDiff используют архитектуру DDM на основе UNET для обучения прогнозированию X0.
Кроме того, авторы HypDiff демонстрируют, что для повышения эффективности можно выполнять выборку одновременно в одном и том же тангенциальном пространстве вместо выборки в разных тангенциальных пространствах центров кластера.
Авторская визуализация фреймворка HypDiff представлена ниже.
2. Реализация средствами MQL5
После рассмотрения теоретических аспектов фреймворка HypDiff мы переходим к практической части данной статьи, в которой реализуем собственное видение предложенных подходов средствами MQL5. И сразу надо сказать, что нам предстоит "длительное и увлекательное путешествие". Поэтому следует морально подготовиться к выполнению большого объема работы.
2.1 Дополнение OpenCL-программы
И начнем мы свою работу с добавления изменений в нашу OpenCL-программу. Сначала нужно организовать проекцию исходных данных в гиперболическое пространство. В процессе трансформации данных необходимо учитывать положение каждого элемента в последовательности, так как гиперболическое пространство объединяет параметры евклидова пространства и времени. По аналогии с авторской реализацией, мы используем модель Лоренца. Эту задачу мы выполним в кернеле HyperProjection.
__kernel void HyperProjection(__global const float *inputs, __global float *outputs ) { const size_t pos = get_global_id(0); const size_t d = get_local_id(1); const size_t total = get_global_size(0); const size_t dimension = get_local_size(1);
В параметрах данного кернела мы будем передавать указатели на буфера данных: анализируемая последовательность и результаты преобразования. Непосредственно параметры передаваемых буферов мы определим через пространство задач. Первое измерение нам укажет на размерность анализируемой последовательности, а второе — на размер вектора описания одного элемента анализируемой последовательности. При этом потоки объединены в рабочие группы по последнему измерению.
Здесь надо обратить внимание, что вектор описания одного элемента последовательности будет содержать на 1 элемент больше.
Далее мы объявим локальный массив, который позволит нам организовать обмен данными между потоками рабочей группы.
__local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
И определим константы смещения в буферах данных.
const int shift_in = pos * dimension + d; const int shift_out = pos * (dimension + 1) + d + 1;
Загрузим из глобального буфера исходные данные в локальные элементы соответствующего потока операций и вычислим квадратичные значения. При этом проверим действительность результатов указанных операций.
float v = inputs[shift_in]; if(isinf(v) || isnan(v)) v = 0; //--- float v2 = v * v; if(isinf(v2) || isnan(v2)) v2 = 0;
Далее нам предстоит посчитать норму вектора исходных данных. Для этого мы суммируем квадрат его значений с помощью нашего локального массива. Ведь каждый поток рабочей группы содержит по 1 элементу.
//--- if(d < ls) temp[d] = v2; barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += v2; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Здесь стоит отметить, что норма вектора нам необходима только для вычисления значения первого элемента в нашем векторе описания гиперболических координат элемента анализируемой последовательности. Все остальные элементы мы переносим без изменений, но со смещением позиции.
outputs[shift_out] = v;
И чтобы не выполнять избыточные операции, определение значения первого элемента гиперболического вектора мы выполним только в первом потоке каждой рабочей группы.
Здесь мы сначала вычислим долю смещения в анализируемого элемента в исходной последовательности. А затем вычтем квадрат полученного значения рассчитанной выше нормы вектора исходного представления анализируемого элемента. И возьмем квадратный корень из полученного значения.
if(d == 0) { v = ((float)pos) / ((float)total); if(isinf(v) || isnan(v)) v = 0; outputs[shift_out - 1] = sqrt(fmax(temp[0] - v * v, 1.2e-07f)); } }
Обратите внимание, что для извлечения квадратного корня мы гарантированно берем значения больше 0. Это позволит нам исключить получения ошибок выполнения операций и получение недействительных результатов.
С целью реализации алгоритмов обратного прохода мы тут же создадим кернел HyperProjectionGrad, в котором реализуем процесс распределения градиентов ошибки через описанные выше операции прямого прохода. И тут следует обратить внимание на 2 момента. Во-первых, позиция элемента в последовательности статична и не параметризуется. Следовательно, к ней мы не проводим градиент ошибки.
Во-вторых, градиент ошибки остальных элементов приходит по 2 информационным потокам. Прямой перенос данных дает прямую передачу градиента ошибки. В то же время все элементы исходного вектора описания элемента последовательности использовались для вычисления нормы вектора, участвующей в определении первого элемента гиперболического представления. Следовательно, каждый элемент должен получить свою долю градиента ошибки от первого элемента вектора гиперболического представления.
Посмотрим на реализацию описанных подходов в коде. В параметрах кернела HyperProjectionGrad передается уже 3 указателя на буферы данных. Добавляется буфер градиентов ошибки на уровне исходных данных (inputs_gr). А буфер гиперболического представления исходной последовательности заменяется соответствующим буферов градиентов ошибки (outputs_gr).
__kernel void HyperProjectionGrad(__global const float *inputs, __global float *inputs_gr, __global const float *outputs_gr ) { const size_t pos = get_global_id(0); const size_t d = get_global_id(1); const size_t total = get_global_size(0); const size_t dimension = get_global_size(1);
Пространство задач кернела мы оставляем аналогичным прямому проходу, но уже не объединяем потоки в рабочие группы. В теле кернела мы сначала идентифицируем текущий поток в пространстве задач. И по полученным значениям определяем смещение в буферах данных.
const int shift_in = pos * dimension + d; const int shift_start_out = pos * (dimension + 1); const int shift_out = shift_start_out + d + 1;
В блоке загрузки данных из глобальных буферов мы считаем значение анализируемого элемента из исходного представления и его градиента ошибки на уровне гиперболического представления.
float v = inputs[shift_in]; if(isinf(v) || isnan(v)) v = 0; float grad = outputs_gr[shift_out]; if(isinf(grad) || isnan(grad)) grad = 0;
Затем мы определим долю градиента ошибки от первого элемента гиперболического представления, которая определяется как произведение его градиента ошибки на исходное значение анализируемого элемента.
v = v * outputs_gr[shift_start_out]; if(isinf(v) || isnan(v)) v = 0;
И не забываем на каждом этапе проверять действительность полученных результатов.
Суммарный градиент ошибки мы сохраним в соответствующем глобальном буфере данных.
//---
inputs_gr[shift_in] = v + grad;
}
На данном этапе мы организовали проекцию исходных данных в гиперболическое пространство. Однако авторы метода предлагают осуществлять процесс диффузии в проекциях гиперболического пространства на касательные плоскости.
На первый взгляд может показаться немного странным спроецировать данные из плоского представления гиперболическое и обратно для добавления шума. Но суть в том, что исходное плоское представление, с большой долей вероятности, будет отличаться от финальной проекции. Ведь плоскость исходных значений и проекции гиперболического представления это разные плоскости.
Наверное, это можно сравнить с составлением чертежа по фотографии предмета. Сначала мы в своей голове составляем объемное представление об изображенном на фотографии предмете с учетом своего опыта и априорных знаний. А затем переносим на бумагу чертеж представленного предмета в видах сбоку, спереди и сверху. Аналогично HypDiff делает проекции данных на несколько касательных плоскостей с различными центрами.
Для реализации такого функционала мы создадим кернел LogMap. В параметрах данного кернела мы получаем указатели на 7 буферов данных, что, согласитесь, довольно много. Среди них 3 буфера исходных данных:
- В буфере features представлен тензор эмбедингов гиперболического представления исходных данных.
- Буфер centroids содержит координаты центроидов. К ним проведены касательные плоскости, на которые нам предстоит сделать проекции исходных данных.
- В буферы curvatures представлены параметры кривизны соответствующих центроидов.
Не трудно догадаться, что буфер outputs предназначен для записи результатов операций. И мы добавили ещё 3 буфера данных для записи промежуточных результатов, которые нам понадобятся в процессе выполнения операций обратного прохода.
И здесь следует обратить внимание, что в своей реализации мы немного отошли от авторского фреймворка. Дело в том, что авторы HypDiff группировали элементы анализируемой последовательности на стадии подготовки данных. И осуществляли проекции на касательные только элементы отдельных групп. Мы же не будем осуществлять предварительное деление элементов последовательности на группы. Поэтому будем генерировать проекцию всех элементов на все касательные. Это конечно повысит количество выполняемых операций. Но с другой стороны обогатит представление модели об анализируемой последовательности.
__kernel void LogMap(__global const float *features, __global const float *centroids, __global const float *curvatures, __global float *outputs, __global float *product, __global float *distance, __global float *norma ) { //--- identify const size_t f = get_global_id(0); const size_t cent = get_global_id(1); const size_t d = get_local_id(2); const size_t total_f = get_global_size(0); const size_t total_cent = get_global_size(1); const size_t dimension = get_local_size(2);
В теле метода мы идентифицируем текущий поток операций в трехмерном пространстве задач. Первое измерение указывает на элемент исходной последовательности. Второе — на центроид. А третье — на позицию в векторе описания анализируемого элемента последовательности. В данном случае мы объединяем потоки в рабочие группы по последнему измерению.
Далее мы объявляем локальный массив обмена данными в пределах рабочей группы.
//--- create local array __local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
И определим константы смещения в буферах данных.
//--- calc shifts const int shift_f = f * dimension + d; const int shift_out = (f * total_cent + cent) * dimension + d; const int shift_cent = cent * dimension + d; const int shift_temporal = f * total_cent + cent;
После чего загрузим исходные данные из глобальных буферов с обязательной проверкой действительности полученных значений.
//--- load inputs float feature = features[shift_f]; if(isinf(feature) || isnan(feature)) feature = 0; float centroid = centroids[shift_cent]; if(isinf(centroid) || isnan(centroid)) centroid = 0; float curv = curvatures[cent]; if(isinf(curv) || isnan(curv)) curv = 1.2e-7;
Далее нам предстоит вычислить произведения тензоров исходных данных и центроидов. Но так как мы работаем с гиперболическим представлением, то воспользуемся произведением Минковского. Для этого мы сначала выполним умножение соответствующих скалярных значений.
//--- dot(features, centroids) float fc = feature * centroid; if(isnan(fc) || isinf(fc)) fc = 0;
И суммируем полученные значения в рамках рабочей группы.
//--- if(d < ls) temp[d] = (d > 0 ? fc : -fc); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += fc; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float prod = temp[0]; if(isinf(prod) || isnan(prod)) prod = 0;
Обратите внимание, что в отличие от привычного умножения векторов в евклидовом пространстве мы берем произведение первых элементов векторов с обратным значением.
Проверяем действительность результата выполненных операций и сохраняем полученное значение в соответствующем элементе глобального буфера временного хранения данных. Это значение нам понадобится в процессе обратного прохода.
product[shift_temporal] = prod;
Это позволяет нам определить направление и величину смещения анализируемого элемента от центроида.
//--- project float u = feature + prod * centroid * curv; if(isinf(u) || isnan(u)) u = 0;
Определим норму Минковского полученного вектора смещения. Как и ранее возьмем квадрат каждого элемента.
//--- norm(u) float u2 = u * u; if(isinf(u2) || isnan(u2)) u2 = 0;
И сложим полученные значения в рамках рабочей группы, взяв квадрат первого элемента с обратным знаком.
if(d < ls) temp[d] = (d > 0 ? u2 : -u2); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += u2; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); float normu = temp[0]; if(isinf(normu) || isnan(normu) || normu <= 0) normu = 1.0e-7f; normu = sqrt(normu);
Полученное значение нам так же понадобится в рамках обратного прохода. Поэтому мы сохраним его в буфере временного хранения данных.
norma[shift_temporal] = normu;
На следующем шаге мы определим расстояние от анализируемой точки до центроида в гиперболическом пространстве с параметрами кривизны центроида. При этом мы не будем повторно вычислять произведение векторов, а воспользуемся ранее полученным значением.
//--- distance features to centroid float theta = -prod * curv; if(isinf(theta) || isnan(theta)) theta = 0; theta = fmax(theta, 1.0f + 1.2e-07f); float dist = sqrt(clamp(pow(acosh(theta), 2.0f) / curv, 0.0f, 50.0f)); if(isinf(dist) || isnan(dist)) dist = 0;
Убедимся в действительности полученного значения и сохраним результат в глобальном буфере временного хранения данных.
distance[shift_temporal] = dist;
Скорректируем значения вектора смещения.
float proj_u = dist * u / normu;
И далее нам остается сделать проекцию полученных значений на касательную плоскость. И здесь, аналогично выполненной выше проекции Лоренца нам предстоит скорректировать первый элемент вектора проекции. Для этого мы вычислим произведение векторов проекции и центроида без учета первых элементов.
if(d < ls) temp[d] = (d > 0 ? proj_u * centroid : 0); barrier(CLK_LOCAL_MEM_FENCE); for(int i = ls; i < (int)dimension; i += ls) { if(d >= i && d < (i + ls)) temp[d % ls] += proj_u * centroid; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Скорректируем значение первого элемента проекции.
//--- if(d == 0) { proj_u = temp[0] / centroid; if(isinf(proj_u) || isnan(proj_u)) proj_u = 0; proj_u = fmax(u, 1.2e-7f); }
И сохраним полученные результаты.
//---
outputs[shift_out] = proj_u;
}
Как можно заметить, алгоритм кернела вышел довольно громоздким с большим количеством сложных связей. И это довольно усложняет понимание пути прохождения градиента ошибки в рамках обратного прохода. Но нам предстоит распутать этот "клубок". Давайте вооружимся пристальным вниманием к деталям и приступим к работе. Алгоритм обратного прохода реализован в кернеле LogMapGrad.
__kernel void LogMapGrad(__global const float *features, __global float *features_gr, __global const float *centroids, __global float *centroids_gr, __global const float *curvatures, __global float *curvatures_gr, __global const float *outputs, __global const float *outputs_gr, __global const float *product, __global const float *distance, __global const float *norma ) { //--- identify const size_t f = get_local_id(0); const size_t cent = get_global_id(1); const size_t d = get_local_id(2); const size_t total_f = get_local_size(0); const size_t total_cent = get_global_size(1); const size_t dimension = get_local_size(2);
В параметрах кернела мы добавили буферы градиентов ошибки на уровне исходных данных и результатов, что дало нам 4 дополнительных буфера данных.
Пространство задач кернела мы оставили аналогичным прямому проходу, только изменили принцип группировки в рабочие группы. Ведь теперь нам предстоит собирать значения не только в рамках векторов отдельных элементов последовательности, но и градиенты для центроидов. А ведь каждый центроид работает со всеми элементами анализируемой последовательности. Соответственно, и градиент ошибки должен получить от каждого.
В теле кернела мы идентифицируем поток операций во всех измерениях пространства задач. После чего создадим локальный массив обмена данными между элементами рабочей группы.
//--- create local array __local float temp[LOCAL_ARRAY_SIZE]; const int ls = min((int)dimension, (int)LOCAL_ARRAY_SIZE);
И определим константы смещения в глобальных буферах данных.
//--- calc shifts const int shift_f = f * dimension + d; const int shift_out = (f * total_cent + cent) * dimension + d; const int shift_cent = cent * dimension + d; const int shift_temporal = f * total_cent + cent;
После чего загрузим данные из глобальных буферов. Сначала извлекаем исходные данные и промежуточные значения.
//--- load inputs float feature = features[shift_f]; if(isinf(feature) || isnan(feature)) feature = 0; float centroid = centroids[shift_cent]; if(isinf(centroid) || isnan(centroid)) centroid = 0; float centroid0 = (d > 0 ? centroids[shift_cent - d] : centroid); if(isinf(centroid0) || isnan(centroid0) || centroid0 == 0) centroid0 = 1.2e-7f; float curv = curvatures[cent]; if(isinf(curv) || isnan(curv)) curv = 1.2e-7; float prod = product[shift_temporal]; float dist = distance[shift_temporal]; float normu = norma[shift_temporal];
И здесь же вычислим значения вектора смещения анализируемого элемента последовательности от центроида. В отличие от операций прямого прохода, у нас уже есть все необходимые данные.
float u = feature + prod * centroid * curv; if(isinf(u) || isnan(u)) u = 0;
А затем загрузим имеющийся градиент ошибки на уровне результатов.
float grad = outputs_gr[shift_out]; if(isinf(grad) || isnan(grad)) grad = 0; float grad0 = (d>0 ? outputs_gr[shift_out - d] : grad); if(isinf(grad0) || isnan(grad0)) grad0 = 0;
Обратите внимание, мы загружаем градиент ошибки не только анализируемого элемента, но и первого в векторе описания анализируемого элемента последовательности. Причина здесь аналогично описанной выше для кернела HyperProjectionGrad.
Далее мы инициализируем локальные переменные накопления градиентов ошибки.
float feature_gr = 0; float centroid_gr = 0; float curv_gr = 0; float prod_gr = 0; float normu_gr = 0; float dist_gr = 0;
Вначале мы проведем градиент ошибки от проекции данных на касательную плоскость до вектора смещения.
float proj_u_gr = (d > 0 ? grad + grad0 / centroid0 * centroid : 0);
Здесь стоит обратить внимание, что первый элемент вектора смещения не оказал влияния на результат. Следовательно, его градиент равен "0". При этом другие элементы получили как прямой градиент ошибки, так и долю от первого элемента результатов.
Тут же мы определим первые значения градиентов ошибки для центроидов. Их мы будем вычислять в цикле, собирая значения от всех элементов последовательности.
for(int id = 0; id < dimension; id += ls) { if(d >= id && d < (id + ls)) { int t = d % ls; for(int ifeat = 0; ifeat < total_f; ifeat++) { if(f == ifeat) { if(d == 0) temp[t] = (f > 0 ? temp[t] : 0) + outputs[shift_out] / centroid * grad; else temp[t] = (f > 0 ? temp[t] : 0) + grad0 / centroid0 * outputs[shift_out]; } barrier(CLK_LOCAL_MEM_FENCE); }
А после сбора градиентов ошибки от всех элементов последовательности в рамках локального массива, мы воспользуемся одним потоком и перенесем собранные значения в локальную переменную.
if(f == 0) { if(isnan(temp[t]) || isinf(temp[t])) temp[t] = 0; centroid_gr += temp[0]; } } barrier(CLK_LOCAL_MEM_FENCE); }
При этом не забываем следить, чтобы барьеры посетили все потоки операций без исключений.
Далее мы посчитаем градиент ошибки для векторов расстояний, нормы и смещений.
dist_gr = u / normu * proj_u_gr;
float u_gr = dist / normu * proj_u_gr;
normu_gr = dist * u / (normu * normu) * proj_u_gr;
Здесь стоит обратить внимание, что элементы вектора смещения индивидуальны в каждом потоке. А вот норма вектора и расстояние являются дискретными значениями. Поэтому нам предстоит суммировать соответствующие градиенты ошибки в рамках одного элемента анализируемой последовательности. Вначале мы соберем градиенты ошибки для расстояния. Суммировать значения мы будем через локальный массив.
for(int ifeat = 0; ifeat < total_f; ifeat++) { if(d < ls && f == ifeat) temp[d] = dist_gr; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += dist_gr; barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); if(f == ifeat) { if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; dist_gr = temp[0];
И сразу определим градиент ошибки для параметра кривизны соответствующего центроида и произведения векторов.
if(d == 0) { float theta = -prod * curv; float theta_gr = 1.0f / sqrt(curv * (theta * theta - 1)) * dist_gr; if(isinf(theta_gr) || isnan(theta_gr)) theta_gr = 0; curv_gr += -pow(acosh(theta), 2.0f) / (2 * sqrt(pow(curv, 3.0f))) * dist_gr; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; temp[0] = -curv * theta_gr; if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; curv_gr += -prod * theta_gr; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; } } barrier(CLK_LOCAL_MEM_FENCE);
Однако стоит обратить внимание, что градиент ошибки параметра кривизны только накапливается для последующего сохранения в глобальном буфере данных. В отличие от него, градиент ошибки произведения векторов является промежуточным значениям для последующего распределения между влияющими элементами. Поэтому нам важно синхронизировать его в рамках рабочей группы. Поэтому на данном этапе мы сохраним его в элементе локального массива. А затем перенесем его в локальную переменную.
if(f == ifeat) prod_gr += temp[0]; barrier(CLK_LOCAL_MEM_FENCE);
Думаю Вы заметили большое количество повторяющихся контролей. Это немного усложняет код, но является вынужденной мерой для организации корректного прохождения барьеров синхронизации потоков рабочей группы.
Далее мы аналогичным образом суммируем градиент ошибки нормы вектора смещения.
if(d < ls && f == ifeat) temp[d] = normu_gr; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += normu_gr; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); if(f == ifeat) { normu_gr = temp[0]; if(isinf(normu_gr) || isnan(normu_gr)) normu_gr = 1.2e-7;
И скорректируем градиент ошибки вектора смещения.
u_gr += u / normu * normu_gr; if(isnan(u_gr) || isinf(u_gr)) u_gr = 0;
И распределим его между исходными данными и центроидом.
feature_gr += u_gr; centroid_gr += prod * curv * u_gr; } barrier(CLK_LOCAL_MEM_FENCE);
Здесь же стоит обратить внимание, что градиент ошибки вектора смещения необходимо распределить на уровень произведения векторов и параметр кривизны. Однако указанные сущности являются скалярными значениями. Следовательно, нам предстоит суммировать значения в рамках одного элемента анализируемой последовательности. И на данном этапе мы организуем суммирование произведений соответствующих градиентов ошибки вектора смещения на элементы центроидов. Что, в принципе, является произведением этих векторов.
//--- dot (u_gr * centroid) if(d < ls && f == ifeat) temp[d] = u_gr * centroid; barrier(CLK_LOCAL_MEM_FENCE); for(int id = ls; id < (int)dimension; id += ls) { if(d >= id && d < (id + ls) && f == ifeat) temp[d % ls] += u_gr * centroid; barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (int)dimension); //--- do { count = (count + 1) / 2; if(f == ifeat) { if(d < count) temp[d] += ((d + count) < dimension ? temp[d + count] : 0); if(d + count < dimension) temp[d + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Полученные значения мы используем для распределения градиента ошибки на соответствующие сущности.
if(f == ifeat && d == 0) { if(isinf(temp[0]) || isnan(temp[0])) temp[0] = 0; prod_gr += temp[0] * curv; if(isinf(prod_gr) || isnan(prod_gr)) prod_gr = 0; curv_gr += temp[0] * prod; if(isinf(curv_gr) || isnan(curv_gr)) curv_gr = 0; temp[0] = prod_gr; } barrier(CLK_LOCAL_MEM_FENCE);
Далее мы синхронизируем значение градиента ошибки на уровне произведения векторов в рамках рабочей группы.
if(f == ifeat) { prod_gr = temp[0];
И распределяем полученное значение между исходными данными.
feature_gr += prod_gr * centroid * (d > 0 ? 1 : -1); centroid_gr += prod_gr * feature * (d > 0 ? 1 : -1); } barrier(CLK_LOCAL_MEM_FENCE); }
После успешного выполнения всех операций и полного сбора градиентов ошибки в локальных переменных, мы переносим полученные значений в глобальные буфера данных.
//--- result features_gr[shift_f] = feature_gr; centroids_gr[shift_cent] = centroid_gr; if(f == 0 && d == 0) curvatures_gr[cent] = curv; }
И завершаем работу кернела.
Как можно заметить, алгоритм достаточно сложен, но в то же время привлекателен. И его понимание требует внимания к деталям.
Как уже упоминалось, реализация фреймворка HypDiff предполагает значительный объем работы. Мы обсудили лишь реализацию алгоритмов на стороне OpenCL-программы, полный код которой доступен в приложении. При этом объем статьи уже практически исчерпан. И я предлагаю продолжить изучение реализации алгоритмов фреймворка на стороне основной программе в следующей статье. Таким образом мы разделим проделанную работу на 2 логических блока.
Заключение
Использование гиперболической геометрии позволяет решить проблемы конфликта между данными дискретного графа и моделью непрерывной диффузии. Фреймворк HypDiff предлагает усовершенствованный метод генерации гиперболического гауссова шума для решения проблемы аддитивного сбоя гауссовых распределений в гиперболическом пространстве. Геометрические ограничения углового подобия применяются к процессу анизотропной диффузии для сохранения локальной структуры.
В практической части статьи мы начали реализацию предложенных подходов средствами MQL5. Однако объем работ выходит за рамки одной статьи. И мы продолжим построение предложенного фреймворка в следующей статье.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения Моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Обучение многослойного персептрона с помощью алгоритма Левенберга-Марквардта
Обучение многослойного персептрона с помощью алгоритма Левенберга-Марквардта
 Машинное обучение и Data Science (Часть 23): Почему LightGBM и XGBoost лучше многих ИИ-моделей?
Машинное обучение и Data Science (Часть 23): Почему LightGBM и XGBoost лучше многих ИИ-моделей?
 Интеграция скрытых марковских моделей в MetaTrader 5
Интеграция скрытых марковских моделей в MetaTrader 5
 Анализ влияния погоды на валюты аграрных стран с использованием Python
Анализ влияния погоды на валюты аграрных стран с использованием Python
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования