Datenwissenschaft und ML (Teil 42): Forex-Zeitreihenvorhersage mit ARIMA in Python, alles was Sie wissen müssen
144
0
Inhalt
- Was ist eine Zeitreihenprognose?
- Einführung in ARIMA-Modelle
- Hauptkomponenten eines ARIMA-Modells
- ARIMA-Modell in Python
- Aufbau eines ARIMA-Modells für EURUSD
- Vorhersagen außerhalb der Stichprobe mit ARIMA
- Diagramme der Residuen des ARIMA-Modells
- SARIMA-Modell
- Schlussfolgerung
Was ist Zeitreihenprognose?
Bei der Zeitreihenprognose werden vergangene Daten verwendet, um zukünftige Werte in einer Folge von Datenpunkten vorherzusagen. Diese Abfolge ist in der Regel nach der Zeit geordnet, daher der Name Zeitreihe.
Kernvariablen in Zeitreihendaten
Wir können in unseren Daten so viele Merkmalsvariablen haben, wie wir wollen, aber alle Daten für Zeitreihenanalysen oder Prognosen müssen diese beiden Variablen enthalten.
- Zeit
Hierbei handelt es sich um eine unabhängige Variable, die die spezifischen Zeitpunkte angibt, zu denen die Datenpunkte beobachtet wurden. - Zielvariable
Dies ist der Wert, den wir versuchen, auf der Grundlage früherer Beobachtungen und möglicherweise anderer Faktoren vorherzusagen. (z. B. täglicher Börsenschlusskurs, stündliche Temperatur, Website-Traffic pro Minute).
Ziel der Zeitreihenprognose ist es, historische Muster und Trends in den Daten zu nutzen, um fundierte Vorhersagen über zukünftige Werte zu treffen.
Wir haben bereits über die Zeitreihenprognose mit normalen KI-Modellen gesprochen. In diesem Artikel befassen wir uns mit der Zeitreihenprognose anhand eines Modells, das für Zeitreihenprobleme entwickelt wurde und als ARIMA bekannt ist.
Die Zeitreihenprognose kann in zwei Arten unterteilt werden.
- Univariate Zeitreihenprognose
Hierbei handelt es sich um ein Problem der Zeitreihenprognose, bei dem ein Prädiktor zur Vorhersage seiner zukünftigen Werte verwendet wird. Zum Beispiel die Verwendung der aktuellen Schlusskurse einer Aktie zur Vorhersage künftiger Schlusskurse.
Dies ist die Art der Vorhersage, die ARIMA-Modelle leisten können. - Multivariate Zeitreihenprognosen
Es handelt sich um ein Problem der Zeitreihenprognose, bei dem mehrere Prädiktoren verwendet werden, um eine Zielvariable in der Zukunft vorherzusagen.
Ähnlich wie wir es in diesem Artikel getan haben.
Einführung in ARIMA-Modelle
ARIMA steht für Autoregressive Integrated Moving Average
Es gehört zu einer Klasse von Modellen, die eine gegebene Zeitreihe auf der Grundlage ihrer vergangenen Werte, d. h. ihrer Verzögerungen und der verzögerten Prognosefehler, erklären.
Die Gleichung kann zur Prognose zukünftiger Werte verwendet werden. Jede „nicht saisonale“ Zeitreihe, die Muster aufweist und kein zufälliges weißes Rauschen ist, kann mit ARIMA-Modellen modelliert werden.
ARIMA, die Abkürzung für AutoRegressive Integrated Moving Average, ist also ein Prognosealgorithmus, der auf der Idee beruht, dass allein die Informationen in den vergangenen Werten der Zeitreihe zur Vorhersage der zukünftigen Werte genutzt werden können.
ARIMA-Modelle werden durch drei Ordnungsparameter spezifiziert: (p, d, q),
wobei:
- p ist die Ordnung des AR-Terms
- q ist die Ordnung des MA-Terms
- d die Anzahl der Differenzierungen, die erforderlich sind, um die Zeitreihe stationär zu machen
Die Bedeutung von p, d, und q im ARIMA-Modell
Die Bedeutung von p
p ist die Ordnung des autoregressiven (AR) Terms. Es bezieht sich auf die Anzahl der Verzögerungen von Y, die als Prädiktoren verwendet werden sollen.
Die Bedeutung von d
Der Begriff Auto Regressive in ARIMA bedeutet, dass es sich um ein lineares Regressionsmodell handelt, das seine Verzögerungen als Prädiktoren verwendet. Lineare Regressionsmodelle funktionieren bekanntlich am besten, wenn die Prädiktoren nicht miteinander korreliert und unabhängig voneinander sind, sodass wir die Zeitreihe stationär machen müssen.
Der gängigste Ansatz, um die Reihe stationär zu machen, ist das Differenzieren. Das heißt, dass der vorherige Wert vom aktuellen Wert abgezogen wird. Je nach Komplexität der Reihe kann mehr als eine Differenzierung erforderlich sein.
Der Wert von d ist also die Mindestanzahl von Differenzierungen, die erforderlich ist, um die Reihe stationär zu machen. Wenn die Zeitreihe bereits stationär ist, ist d = 0.
Die Bedeutung von q
q ist die Ordnung des Terms Gleitender Durchschnitt (MA). Es bezieht sich auf die Anzahl der verzögerten Prognosefehler, die in das ARIMA-Modell einfließen sollen.
Schlüsselkomponenten eines ARIMA-Modells
Um ARIMA zu verstehen, müssen wir seine Bausteine dekonstruieren. Sobald wir die Komponenten aufgeschlüsselt haben, wird es einfacher zu verstehen, wie diese Zeitreihenvorhersagemethode als Ganzes funktioniert.
Der Name ARIMA kann in drei Teile (AR, I, MA) aufgeteilt werden, wie unten beschrieben.
Autoregressiver Teil AR(p)
Die autoregressive (AR) Komponente bildet einen Trend aus vergangenen Werten im AR-Rahmen für Vorhersagemodelle. Zur Verdeutlichung: Der „Autoregressionsrahmen“ funktioniert wie ein Regressionsmodell, bei dem man die Verzögerungen der eigenen Vergangenheitswerte der Zeitreihe als Regressoren verwendet.
Dieser Teil wird nach der folgenden Formel berechnet:
wobei:
-
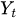ist der aktuelle Wert der Zeitreihe zum Zeitpunkt t. -
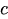ist der konstante Term. -
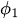bis 
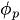sind die autoregressiven Parameter (Koeffizienten), die angeben, wie viel jeder verzögerte Wert zum aktuellen Wert beiträgt. -
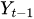bis 
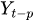sind die vergangenen Werte der Zeitreihenverzögerungen. -
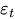ist der Fehlerterm zum Zeitpunkt t.
Der integrierte Teil I(d)
Der integrierte Teil (I) beinhaltet die Differenzierung der Zeitreihenkomponente, wobei zu beachten ist, dass unsere Zeitreihen stationär sein sollten, d. h., dass Mittelwert und Varianz über einen bestimmten Zeitraum konstant bleiben sollten.
Im Grunde genommen wird eine Beobachtung von einer anderen subtrahiert, sodass Trends und Saisonalität eliminiert werden. Durch Differenzierung erhalten wir Stationarität. Dieser Schritt ist notwendig, da er dazu beiträgt, dass sich das Modell an die Daten und nicht an das Rauschen anpasst.
Gleitender Durchschnitt MA(q) Teil
Die Komponente gleitender Durchschnitt (GMA) konzentriert sich auf die Beziehung zwischen einer Beobachtung und einem Restfehler. Wenn wir uns ansehen, wie die aktuelle Beobachtung mit den Fehlern der Vergangenheit zusammenhängt, können wir daraus einige hilfreiche Informationen über einen möglichen Trend in unseren Daten ableiten.
Wir können die Residuen als einen dieser Fehler betrachten, und das Konzept des gleitenden Durchschnittsmodells schätzt oder berücksichtigt ihre Auswirkungen auf unsere letzte Beobachtung. Dies ist besonders nützlich, um kurzfristige Änderungen in den Daten oder zufällige Schocks zu verfolgen und zu erfassen. Im (MA)-Teil einer Zeitreihe können wir wertvolle Informationen über ihr Verhalten gewinnen, die es uns wiederum ermöglichen, Prognosen und Vorhersagen mit größerer Genauigkeit zu treffen.
wobei:
-
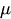ist eine Konstante. -
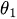ist der MA-Parameter. -
ist der vorherige Fehler. -
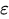ist der aktuelle Fehler.
ARIMA-Modell in Python
Ein ARIMA-Modell ist also einfach eine Kombination der drei oben beschriebenen Teile AR, I und MA, wie oben beschrieben. Die Gleichung lautet nun.
Die Herausforderung bei ARIMA-Modellen besteht nun darin, die richtigen Parameter (die p-, d- und q-Werte) zu finden. Da diese Werte für die Ausführung des Modells ausschlaggebend sind, müssen wir verstehen, wie man diese Werte findet.
Ermittlung der Ordnung des AR-Terms (p)
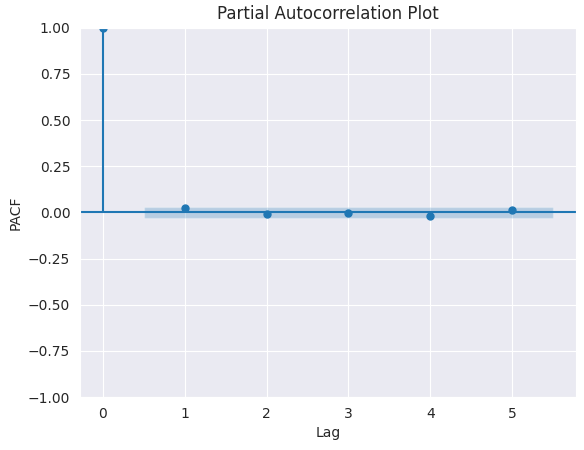
Die erforderliche Anzahl von AR-Termen lässt sich anhand der Darstellung der partiellen Autokorrelation (PACF) ermitteln.
Die partielle Autokorrelation kann als die Korrelation zwischen der Reihe und ihrer/seinen Verzögerung(en) nach Ausschluss der Beiträge der Zwischenverzögerungen beschrieben werden. PACF gibt also gewissermaßen die reine Korrelation zwischen einer Verzögerung und der Reihe wieder. Auf diese Weise werden wir wissen, ob diese Verzögerung im AR-Term benötigt wird oder nicht.
Wir installieren zunächst alle Abhängigkeiten in der Eingabeaufforderung (CMD). Die Datei requirements.txt ist am Ende dieses Beitrags angehängt.
pip install -r requirements.txt
Importieren
# Importing required libraries import pandas as pd import numpy as np import MetaTrader5 as mt5 # Use auto_arima to automatically select best ARIMA parameters import seaborn as sns import matplotlib.pyplot as plt import warnings import os # Suppress warning messages for cleaner output warnings.filterwarnings("ignore") # Set seaborn plot style for better visualization sns.set_style("darkgrid")
Abrufen der Daten von MetaTrader5.
# Getting (EUR/USD OHLC data) from MetaTrader5 mt5_exe_file = r"c:\Users\Omega Joctan\AppData\Roaming\Pepperstone MetaTrader 5\terminal64.exe" # Change this to your MetaTrader5 path if not mt5.initialize(mt5_exe_file): print("Failed to initialize Metatrader5, error = ",mt5.last_error) exit() # select a symbol into the market watch symbol = "EURUSD" timeframe = mt5.TIMEFRAME_D1 if not mt5.symbol_select(symbol, True): print(f"Failed to select {symbol}, error = {mt5.last_error}") mt5.shutdown() exit() rates = mt5.copy_rates_from_pos(symbol, timeframe, 1, 1000) # Get 1000 bars historically df = pd.DataFrame(rates) print(df.head(5)) print(df.shape)
PACF-Darstellung.
from statsmodels.graphics.tsaplots import plot_pacf import matplotlib.pyplot as plt plt.figure(figsize=(6,4)) plot_pacf(series.diff().dropna(), lags=5) plt.title("Partial Autocorrelation Plot") plt.xlabel('Lag') # X-axis label plt.ylabel('PACF') # Y-axis label plt.savefig("pacf plot.png") plt.show()
Ausgabe:
Um den richtigen Wert von p zu ermitteln, suchen wir nach der Verzögerung, nach der PACF in der Grafik abfällt (nahe Null und nicht mehr signifikant). Dieser Verzögerungswert ist der richtige Kandidat für p.
Aus dem obigen Chart geht hervor, dass der rechte p-Wert 0 ist (alle Verzögerungen über 0 sind unbedeutend).
Bestimmung der Reihenfolge der Differenzierung (d) in einem ARIMA-Modell
Wie bereits erläutert, besteht der Zweck der Differenzierung einer Zeitreihe darin, sie stationär zu machen, da das ARIMA-Modell von Stationarität ausgeht, aber wir sollten darauf achten, dass wir eine Zeitreihe nicht unter- oder überdifferenzieren.
Die richtige Differenzierungsreihenfolge ist die Mindestdifferenzierung, die erforderlich ist, um eine nahezu stationäre Reihe zu erhalten, die um einen definierten Mittelwert herum wandert, und die Auto Korrelationsfunktion (ACF) geht relativ schnell gegen Null.
Wenn die Autokorrelationen für eine große Anzahl von Verzögerungen (10 oder mehr) positiv sind, dann muss die Reihe weiter differenziert werden. Ist hingegen die Verzögerung 1 der Autokorrelation zu negativ, dann ist die Reihe wahrscheinlich überdifferenziert.
Wenn wir uns nicht zwischen zwei Ordnungen der Differenzierung entscheiden können, wählen wir die Ordnung, die die geringste Standardabweichung in der differenzierten Reihe ergibt.
Lassen Sie uns anhand der Schlusskurse des EURUSD die richtige Reihenfolge für die Differenzierung finden.
Zunächst müssen wir prüfen, ob die gegebene Reihe (in diesem Fall die Schlusskurse) stationär ist, indem wir den Augmented Dickey Fuller Test (ADF Test) aus dem Python-Paket statsmodels verwenden. Wir prüfen die Stationarität, weil wir nur die Reihenfolge der Differenzierung für eine nicht-stationäre Reihe finden wollen.
Die Nullhypothese (Ho) des ADF-Tests lautet, dass die Zeitreihe nicht stationär ist. Wenn also der p-Wert des Tests kleiner als das Signifikanzniveau (0,05) ist, lehnen wir die Nullhypothese ab und schließen daraus, dass die Zeitreihe tatsächlich stationär ist.
Wenn also in unserem Fall der P-Wert > 0,05 ist, gehen wir dazu über, die richtige Reihenfolge der Differenzierung zu finden.
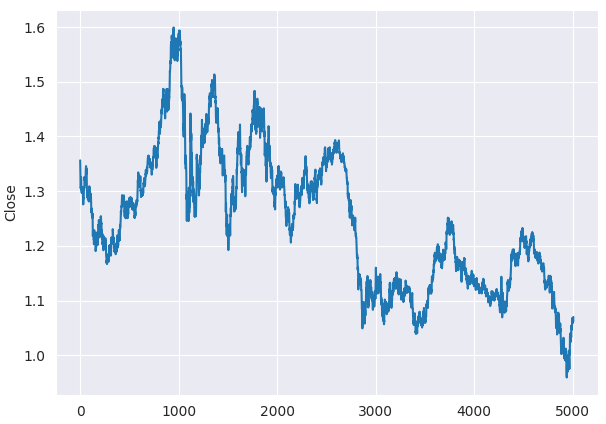
Schon vor dem ADF-Test können wir erkennen, dass die Schlusskurse des EURUSD nicht stationär sind, wenn wir uns das Liniendiagramm ansehen.
plt.figure(figsize=(7,5)) sns.lineplot(df, x=df.index, y="Close") plt.savefig("close prices.png")
Ausgabe:
Überprüfung der Stationarität.
from statsmodels.tsa.stattools import adfuller series = df["Close"] result = adfuller(series) print(f'p-value: {result[1]}')
Ausgabe:
p-value: 0.3707268514544181
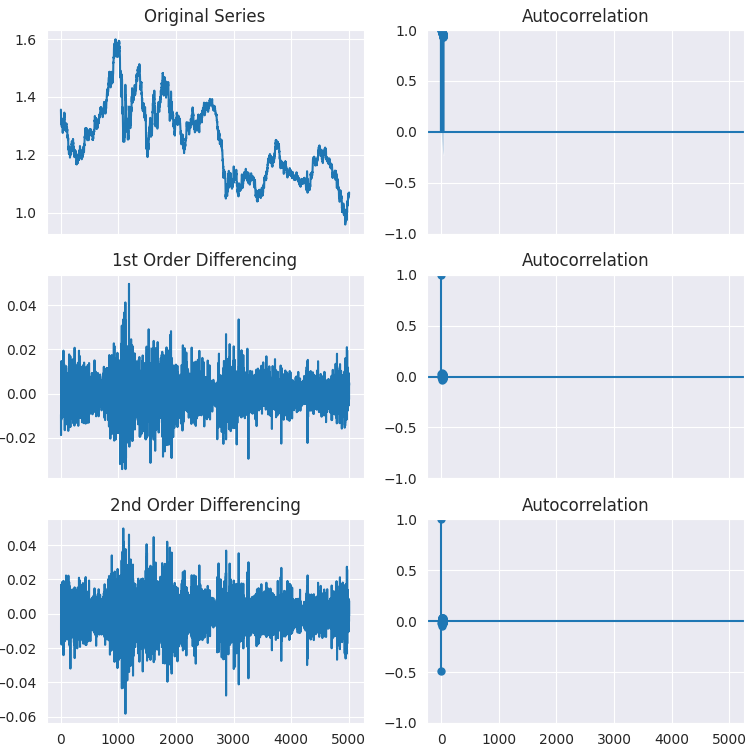
Wie Sie sehen können, ist der p-Wert weit größer als das Signifikanzniveau (0,05). Differenzieren wir die Reihe erst einmal, dann zum zweiten Mal, und sehen wir uns an, wie die Darstellung der Autocorrelation aussieht.
# Original Series fig, axes = plt.subplots(3, 2, sharex=True, figsize=(9, 9)) axes[0, 0].plot(series); axes[0, 0].set_title('Original Series') plot_acf(series, ax=axes[0, 1]) # 1st Differencing axes[1, 0].plot(series.diff().dropna()); axes[1, 0].set_title('1st Order Differencing') plot_acf(series.diff().dropna(), ax=axes[1, 1]) # 2nd Differencing axes[2, 0].plot(series.diff().diff()); axes[2, 0].set_title('2nd Order Differencing') plot_acf(series.diff().diff().dropna(), ax=axes[2, 1]) plt.savefig("acf plots.png") plt.show()
Ausgabe:
Wie aus den Diagrammen ersichtlich ist, erfüllt die erste Ordnung der Differenzierung ihre Aufgabe, da bei der zweiten Ordnung der Differenzierung kein signifikanter Unterschied im Ergebnis der Stationarität zu beobachten ist. Dies kann wiederum durch den ADF-Test überprüft werden.
result = adfuller(series.diff().dropna()) print(f'p-value d=1: {result[1]}') result = adfuller(series.diff().diff().dropna()) print(f'p-value d=2: {result[1]}')
Ausgabe:
p-value d=1: 0.0 p-value d=2: 0.0
Ermitteln der Ordnung des MA-Terms (q)
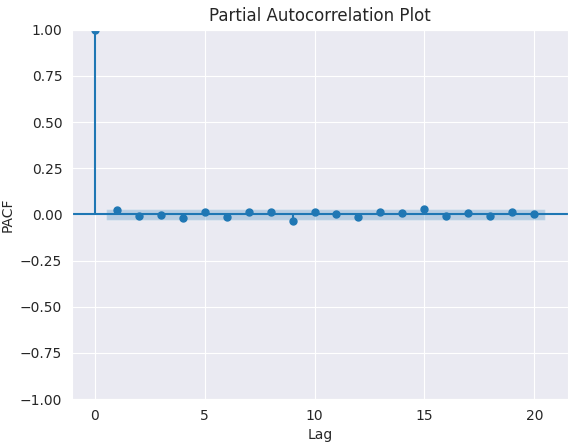
So wie wir die PACF-Darstellung für die Anzahl der AR-Terme (d) betrachtet haben, werden wir die ACF-Darstellung für die Anzahl der MA-Terme betrachten. Auch hier ist der MA-Term technisch gesehen der Fehler der verzögerten Prognose.
Die ACF-Darstellung zeigt uns, wie viele MA-Terme erforderlich sind, um jegliche Autokorrelation in der stationären Reihe zu entfernen.
plt.figure(figsize=(7,5)) plot_pacf(series.diff().dropna(), lags=20) plt.title("Partial Autocorrelation Plot") plt.xlabel('Lag') # X-axis label plt.ylabel('PACF') # Y-axis label plt.savefig("pacf plot finding q.png") plt.show()
Ausgabe:
Der beste Wert für q ist 0.
Die oben beschriebenen Methoden zur Ermittlung der p-, d- und q-Werte sind grob und manuell. Wir können diesen Prozess automatisieren und die Parameter ohne großen Aufwand mithilfe einer Hilfsfunktion von pmdarima mit dem Namen auto_arima ermitteln.
from pmdarima.arima import auto_arima model = auto_arima(series, seasonal=False, trace=True) print(model.summary())
Ausgabe:
Performing stepwise search to minimize aic ARIMA(2,1,2)(0,0,0)[0] intercept : AIC=-35532.282, Time=3.21 sec ARIMA(0,1,0)(0,0,0)[0] intercept : AIC=-35537.068, Time=0.49 sec ARIMA(1,1,0)(0,0,0)[0] intercept : AIC=-35537.492, Time=0.59 sec ARIMA(0,1,1)(0,0,0)[0] intercept : AIC=-35537.511, Time=0.74 sec ARIMA(0,1,0)(0,0,0)[0] : AIC=-35538.731, Time=0.25 sec ARIMA(1,1,1)(0,0,0)[0] intercept : AIC=-35535.683, Time=1.22 sec Best model: ARIMA(0,1,0)(0,0,0)[0] Total fit time: 6.521 seconds
Auf diese Weise erhalten wir dieselben Parameter wie bei der manuellen Analyse.
Erstellung eines ARIMA-Modells für EURUSD
Nachdem wir nun die Werte von p, d und q bestimmt haben, haben wir alles, was wir für die Anpassung (das Training) des ARIMA-Modells benötigen.
from statsmodels.tsa.arima.model import ARIMA arima_model = ARIMA(series, order=(0,1,0)) arima_model = arima_model.fit() print(arima_model.summary())
Ausgabe:
SARIMAX Results ============================================================================== Dep. Variable: Close No. Observations: 4007 Model: ARIMA(0, 1, 0) Log Likelihood 13987.647 Date: Mon, 26 May 2025 AIC -27973.293 Time: 16:59:38 BIC -27966.998 Sample: 0 HQIC -27971.062 - 4007 Covariance Type: opg ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ sigma2 5.427e-05 7.78e-07 69.768 0.000 5.27e-05 5.58e-05 =================================================================================== Ljung-Box (L1) (Q): 1.47 Jarque-Bera (JB): 1370.86 Prob(Q): 0.22 Prob(JB): 0.00 Heteroskedasticity (H): 0.49 Skew: 0.09 Prob(H) (two-sided): 0.00 Kurtosis: 5.86 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step).
Nun trainieren wir dieses Modell auf einigen Daten und verwenden es, um Prädiktion für Daten außerhalb der Stichprobe zu treffen, ähnlich wie wir es mit klassischen maschinellen Lernmodellen tun.
Wir beginnen mit der Aufteilung der Daten in Trainings- und Testproben.
series = df["Close"] train_size = int(len(series) * 0.8) train, test = series[:train_size], series[train_size:]
Anpassen des Modells an die Trainingsdaten.
from statsmodels.tsa.arima.model import ARIMA arima_model = ARIMA(train, order=(0,1,0)) arima_model = arima_model.fit() print(arima_model.summary())
Erstellung von Vorhersagen auf der Grundlage der Trainingsdaten.
predicted = arima_model.predict(start=1, end=len(train))
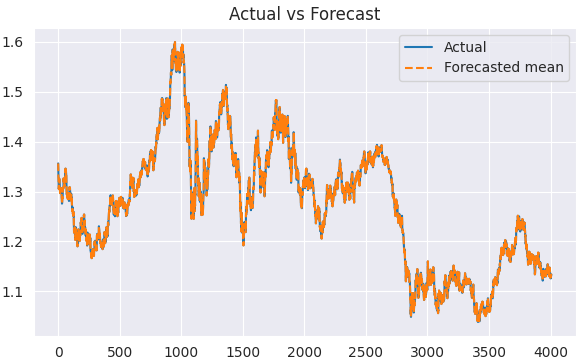
Visualisierung des Ergebnisses.
plt.figure(figsize=(7,4)) plt.plot(train.index, train, label='Actual') plt.plot(train.index, predicted, label='Forecasted mean', linestyle='--') plt.title('Actual vs Forecast') plt.legend() plt.show()
Ausgabe:
Da wir nun die tatsächlichen und die prognostizierten Werte haben, können wir das Modell mit einer beliebigen Bewertungstechnik oder Verlustfunktion unserer Wahl bewerten.
Zuvor wollen wir jedoch einen Weg finden, dieses ARIMA-Modell zu nutzen, um Prädiktion für die Daten außerhalb der Stichprobe zu treffen.
Prädiktion außerhalb der Stichprobe mit ARIMA
Im Gegensatz zu den klassischen Algorithmen des maschinellen Lernens verfolgen diese traditionellen Zeitreihenprognosemodelle einen anderen Ansatz, wenn es darum geht, Vorhersagen auf der Grundlage von Informationen zu treffen, die sie zuvor nicht gesehen haben.
In klassischen Frameworks für maschinelles Lernen und in Python-Bibliotheken gibt es eine Methode namens predict, die, wenn sie mit einem Array von Daten aufgerufen wird, eine Vorhersage/einen Schätzwert für den nächsten (zukünftigen) Wert bzw. die nächsten (zukünftigen) Werte trifft.
Bei ARIMA-Modellen sagt diese Methode nicht unbedingt die Zukunft voraus; sie ist nur dann nützlich, wenn es darum geht, Vorhersagen auf der Grundlage der In-Sample-Daten (der bereits im Modell vorhandenen Informationen), d. h. der Trainingsdaten, zu treffen.
Um dies zu verstehen, sollten wir den Unterschied zwischen Prädiktion und Prognose erörtern.
Unter Prädiktion versteht man die Schätzung unbekannter (zukünftiger oder anderer) Werte mit Hilfe eines beliebigen Modells, während sich die Prognose auf die Vorhersage zukünftiger Werte in Zeitreihendaten bezieht, indem zeitliche Muster und Abhängigkeiten genutzt werden.
Die Prädiktion kann auf Probleme wie die Klassifizierung der Marktrichtung oder die Schätzung der nächsten Schlusskurse angewandt werden, während die Prognose zur Vorhersage der nächsten Aktienkurse auf der Grundlage des/der aktuellen Wertes/Werte dient.
Im ARIMA-Modell wird die Methode zur Prädiktion typischerweise für die Vorhersage von Vergangenheitswerten verwendet, aus denen das Modell gelernt hat, weshalb es den Start- und Endindex benötigt. Sie kann auch die Anzahl der Schritte in der Vergangenheit annehmen, die Sie vorhersagen (auswerten) möchten.
predicted = arima_model.predict(start=1, end=len(train))
print(arima_model.predict(steps=10))
Um den/die zukünftigen Wert(e) vorherzusagen, müssen wir eine Methode namens forecast().
Wie bereits erwähnt, hängen traditionelle zeitreihenbasierte Modelle wie ARIMA von dem/den vorherigen Wert(en) ab, um den/die nächsten Wert(e) vorherzusagen, wie aus der Formel in Abbildung 03 ersichtlich ist.
Dies bedeutet, dass wir das Modell ständig mit neuen Informationen aktualisieren müssen, damit es relevant bleibt. Damit beispielsweise ein ARIMA-Modell eine Vorhersage für den morgigen Schlusskurs des EURUSD machen kann, muss dieses Modell mit dem heutigen Schlusskurs desselben Instruments (Symbols) gefüttert werden; dasselbe gilt für morgen und den folgenden Tag.
Das ist etwas ganz anderes als das, was wir beim klassischen maschinellen Lernen tun.
Lassen Sie uns nun Vorhersagen auf der Grundlage von Daten machen, die außerhalb der Stichprobe liegen.
# Fit initial model model = ARIMA(train, order=(0, 1, 0)) results = model.fit() # Initialize forecasts forecasts = [results.forecast(steps=1).iloc[0]] # First forecast # Update with test data iteratively for i in range(len(test)): # Append new observation without refitting results = results.append(test.iloc[i:i+1], refit=False) # Forecast next step forecasts.append(results.forecast(steps=1).iloc[0]) forecasts = forecasts[:-1] # remove the last element which is the predicted next value # Compare forecasts vs actual test data plt.plot(test.index, test, label="Actual") plt.plot(test.index, forecasts, label="Forecast", linestyle="--") plt.legend()
Die Methode append fügt neue (aktuelle) Informationen in das Modell ein. In diesem Fall wird der aktuelle Schlusskurs des EURUSD zur Prognose des nächsten Schlusskurses herangezogen.
refit=False, stellt sicher, dass das Modell nicht noch einmal trainiert wird. Auf diese Weise lässt sich das ARIMA-Modell effektiv aktualisieren.
Erstellen wir eine Funktion mit einer Reihe von Bewertungsmetriken, die wir zur Beurteilung der Leistung des ARIMA-Modells verwenden können.
import sklearn.metrics as metric from statsmodels.tsa.stattools import acf from scipy.stats import pearsonr def forecast_accuracy(forecast, actual): # Convert to numpy arrays if they aren't already forecast = np.asarray(forecast) actual = np.asarray(actual) metrics = { 'mape': metric.mean_absolute_percentage_error(actual, forecast), 'me': np.mean(forecast - actual), # Mean Error 'mae': metric.mean_absolute_error(actual, forecast), 'mpe': np.mean((forecast - actual) / actual), # Mean Percentage Error 'rmse': metric.mean_squared_error(actual, forecast, squared=False), 'corr': pearsonr(forecast, actual)[0], # Pearson correlation 'minmax': 1 - np.mean(np.minimum(forecast, actual) / np.maximum(forecast, actual)), 'acf1': acf(forecast - actual, nlags=1)[1], # ACF of residuals at lag 1 "r2_score": metric.r2_score(forecast, actual) } return metrics
forecast_accuracy(forecasts, test)
Ausgabe:
{'mape': 0.0034114761554881936,
'me': 6.360279441117738e-05,
'mae': 0.0037872155688622737,
'mpe': 6.825424905960248e-05,
'rmse': 0.005018824533752777,
'corr': 0.99656297100796,
'minmax': 0.0034008221524469695,
'acf1': 0.04637470541528736,
'r2_score': 0.9931220697334551} Der mape-Wert von 0,003 zeigt an, dass das Modell zu etwa 99,996 % genau ist, ein Wert, der sich auch im r2_score widerspiegelt.
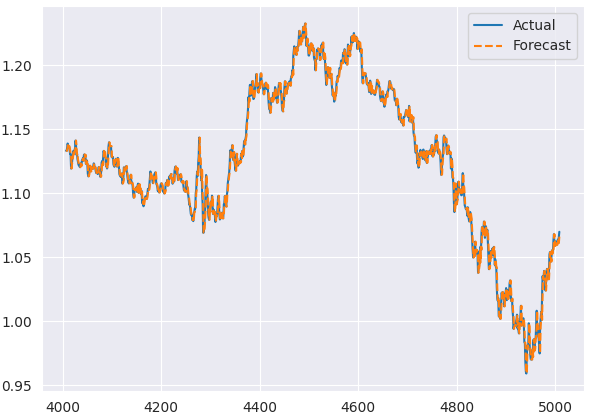
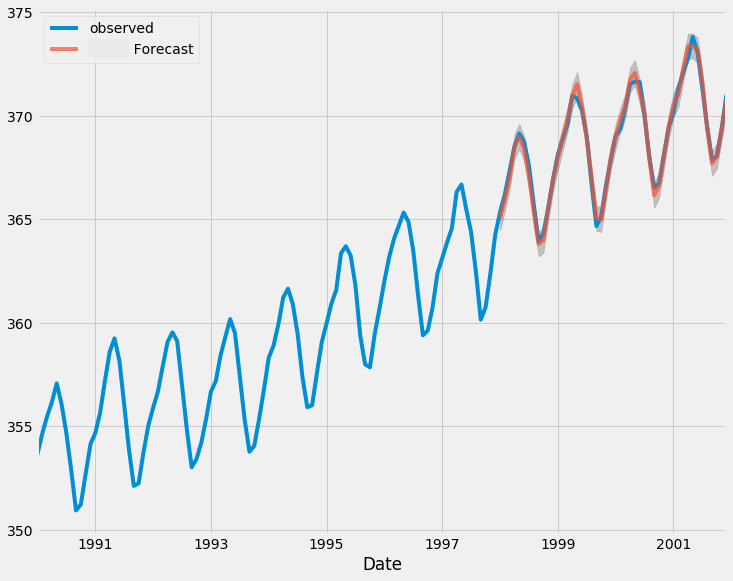
Unten sehen Sie das Diagramm, in dem die tatsächlichen und die vorhergesagten Ergebnisse der Teststichprobe verglichen werden.
Residuendiagramme des ARIMA-Modells
ARIMA verfügt über Methoden zur Visualisierung der Residuen, die ein besseres Verständnis des Modells ermöglichen.
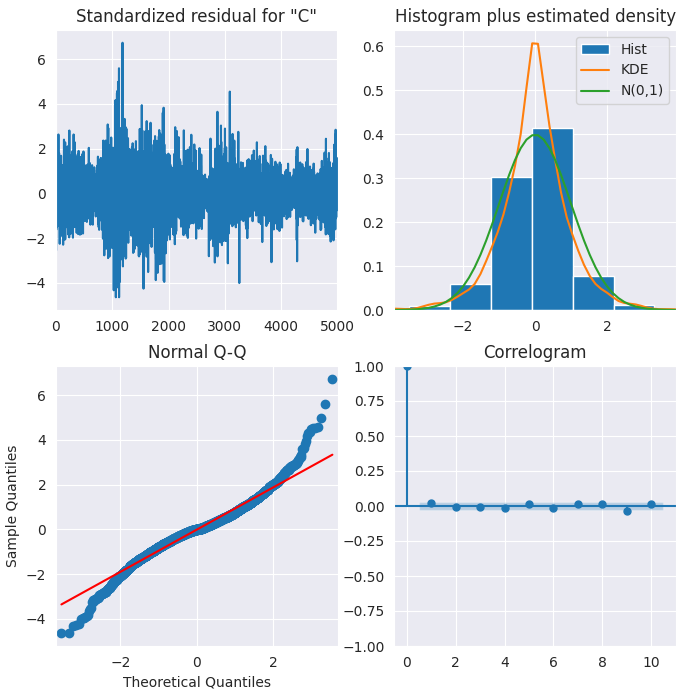
results.plot_diagnostics(figsize=(8,8)) plt.show()
Ausgabe:
Standardisierte Residuen
Die Residuen scheinen um einen Mittelwert von Null zu schwanken und eine einheitliche Varianz zu haben.
Histogramme
Die Dichtekurve deutet auf eine Normalverteilung hin, wobei der Mittelwert leicht nach rechts verschoben ist.
Theoretische Quantile
Die meisten der Punkte liegen genau auf der roten Linie. Jede signifikante Abweichung würde bedeuten, dass die Verteilung schief ist.
Korrelationsdiagramm
Das Korrelationsdiagramm (oder ACF-Diagramm) zeigt, dass die Residuen nicht autokorreliert sind. Das ACF-Diagramm deutet darauf hin, dass es ein Muster in den Residuen gibt, das nicht durch das Modell erklärt wird.
Insgesamt scheint das Modell gut geeignet zu sein.
SARIMA-Modell
Das einfache ARIMA-Modell hat ein Problem. Es unterstützt keine Saisonalität.
Saisonalität bezieht sich auf wiederkehrende Muster in Finanzdaten, die sich in festen Intervallen wiederholen, z. B. stündlich, täglich, wöchentlich, monatlich, vierteljährlich und jährlich.
Wir sehen oft, dass Instrumente bestimmte sich wiederholende Muster aufweisen. Beispielsweise steigen Einzelhandelsaktien häufig im vierten Quartal (Weihnachtseinkaufssaison), während einige Energietitel saisonalen Wettermustern folgen, bei Deviseninstrumenten können wir eine erhöhte Marktvolatilität während bestimmter Handelssitzungen feststellen usw.
Wenn die Zeitreihendaten eine beobachtbare oder definierte Saisonalität aufweisen, sollten wir uns für das saisonale ARIMA-Modell (kurz SARIMA) entscheiden, da es eine saisonale Differenzierung verwendet.
SARIMAX(p, d, q)x(P, D, Q, S) Modellkomponenten
- Autoregression (AR)
Wie bereits beschrieben, werden bei der Autoregression vergangene Werte der Zeitreihe untersucht, um aktuelle Werte vorherzusagen. - Gleitender Durchschnitt (MA)
Der gleitende Durchschnitt modelliert weiterhin die Fehler der Vergangenheit in den Vorhersagen. - Integration (I)
Die Integration ist immer vorhanden, um die Zeitreihe stationär zu machen. - Saisonale Komponente (S)
Die saisonale Komponente erfasst Schwankungen, die in regelmäßigen Abständen wiederkehren.
Die saisonale Differenzierung ähnelt der regulären Differenzierung, aber anstatt aufeinanderfolgende Terme zu subtrahieren, wird der Wert der vorherigen Saison abgezogen.
Bevor wir das SARIMAX-Modell aufrufen, sollten wir die richtigen Parameter für das Modell unter Verwendung von auto_arima bestimmen.
from pmdarima.arima import auto_arima # Auto-fit SARIMA (automatically detects P, D, Q, S) auto_model = auto_arima( series, seasonal=True, # Enable seasonality m=5, # Weeky cycle (5 days) for daily data trace=True, # Show search progress stepwise=True, # Faster optimization suppress_warnings=True, error_action="ignore" ) print(auto_model.summary())
Ausgabe:
Performing stepwise search to minimize aic ARIMA(2,1,2)(1,0,1)[5] intercept : AIC=-35529.092, Time=3.81 sec ARIMA(0,1,0)(0,0,0)[5] intercept : AIC=-35537.068, Time=0.29 sec ARIMA(1,1,0)(1,0,0)[5] intercept : AIC=-35536.573, Time=0.97 sec ARIMA(0,1,1)(0,0,1)[5] intercept : AIC=-35536.570, Time=4.38 sec ARIMA(0,1,0)(0,0,0)[5] : AIC=-35538.731, Time=0.21 sec ARIMA(0,1,0)(1,0,0)[5] intercept : AIC=-35536.048, Time=0.67 sec ARIMA(0,1,0)(0,0,1)[5] intercept : AIC=-35536.024, Time=0.87 sec ARIMA(0,1,0)(1,0,1)[5] intercept : AIC=-35534.248, Time=0.92 sec ARIMA(1,1,0)(0,0,0)[5] intercept : AIC=-35537.492, Time=0.37 sec ARIMA(0,1,1)(0,0,0)[5] intercept : AIC=-35537.511, Time=0.55 sec ARIMA(1,1,1)(0,0,0)[5] intercept : AIC=-35535.683, Time=0.57 sec Best model: ARIMA(0,1,0)(0,0,0)[5] Total fit time: 13.656 seconds SARIMAX Results ============================================================================== Dep. Variable: y No. Observations: 5009 Model: SARIMAX(0, 1, 0) Log Likelihood 17770.365 Date: Tue, 27 May 2025 AIC -35538.731 Time: 11:16:40 BIC -35532.212 Sample: 0 HQIC -35536.446 - 5009 Covariance Type: opg ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ sigma2 4.846e-05 6.06e-07 80.005 0.000 4.73e-05 4.96e-05 =================================================================================== Ljung-Box (L1) (Q): 2.42 Jarque-Bera (JB): 2028.68 Prob(Q): 0.12 Prob(JB): 0.00 Heteroskedasticity (H): 0.34 Skew: 0.08 Prob(H) (two-sided): 0.00 Kurtosis: 6.11 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step).
Obwohl es nicht notwendig ist, das Modell noch einmal manuell anzupassen, weil auto_arima einen SARIMAX zurückgibt, gibt uns die manuelle Neuanpassung eines SARIMAX-Modells mehr Kontrolle über die Ergebnisse, also lassen Sie es uns noch einmal tun.
from statsmodels.tsa.statespace.sarimax import SARIMAX model = SARIMAX( train, order=auto_model.order, # Non-seasonal (p,d,q) seasonal_order=auto_model.order+(5,), # Seasonal (P,D,Q,S) enforce_stationarity=False ) results = model.fit() print(results.summary())
Ausgabe:
SARIMAX Results ========================================================================================= Dep. Variable: Close No. Observations: 4007 Model: SARIMAX(0, 1, 0)x(0, 1, 0, 5) Log Likelihood 12613.829 Date: Tue, 27 May 2025 AIC -25225.658 Time: 11:16:41 BIC -25219.364 Sample: 0 HQIC -25223.427 - 4007 Covariance Type: opg ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ sigma2 0.0001 1.68e-06 63.423 0.000 0.000 0.000 =================================================================================== Ljung-Box (L1) (Q): 3.42 Jarque-Bera (JB): 676.61 Prob(Q): 0.06 Prob(JB): 0.00 Heteroskedasticity (H): 0.48 Skew: -0.01 Prob(H) (two-sided): 0.00 Kurtosis: 5.01 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step).
Da die von auto_model zurückgegebene Reihenfolge für ARIMA(p,d,q) gilt, obwohl der saisonale Wert auf true gesetzt wurde. Wir müssen bei der Deklaration des SARIMAX-Modells den Wert 5 an ein Tupel anhängen, um sicherzustellen, dass das Modell nun (p,d,q,s) ist.
Bevor wir die tatsächlichen und vorhergesagten Ergebnisse visualisieren und analysieren, müssen wir die ersten Elemente, die dem saisonalen Fenster entsprechen, aus unserem Array entfernen. Werte vor diesem Wert sind unvollständig.
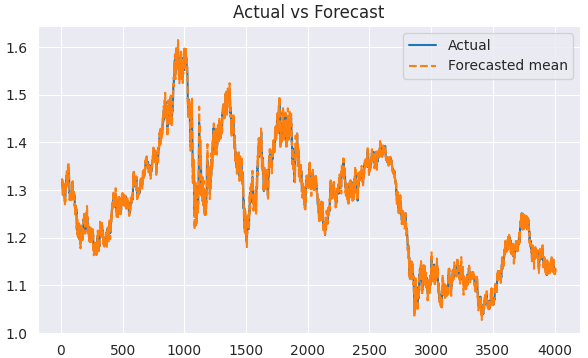
predicted = results.predict(start=1, end=len(train)) clean_train = train[5:] clean_predicted = predicted[5:] plt.figure(figsize=(7,4)) plt.plot(clean_train.index[5:], clean_train[5:], label='Actual') plt.plot(clean_train.index[5:], clean_predicted[5:], label='Forecasted mean', linestyle='--') plt.title('Actual vs Forecast') plt.legend() plt.savefig("sarimax train actual&forecast plot.png") plt.show()
Ausgabe:
Wir können dieses Modell in ähnlicher Weise bewerten, wie wir das ARIMA-Modell bewertet haben.
# Initialize forecasts forecasts = [results.forecast(steps=1).iloc[0]] # First forecast # Update with test data iteratively for i in range(len(test)): # Append new observation without refitting results = results.append(test.iloc[i:i+1], refit=False) # Forecast next step forecasts.append(results.forecast(steps=1).iloc[0]) clean_test = test[5:] forecasts = forecasts[5:-1] # remove the last element which is the predicted next value and the first 5 items
forecast_accuracy(forecasts, clean_test)
Ausgabe:
{'mape': 0.004900183060803821,
'me': -6.94082142749275e-06,
'mae': 0.005432456867698095,
'mpe': -7.226495372320155e-06,
'rmse': 0.007127465498996785,
'corr': 0.9931778828074744,
'minmax': 0.004880027322298863,
'acf1': 0.10724254539104018,
'r2_score': 0.9864021833085908} Eine Genauigkeit von 98,6 % gemäß dem r2_score. Ein anständiger Wert.
Schließlich können wir das ARIMA-Modell verwenden, um Echtzeit-Vorhersagen anhand der vom MetaTrader5 erhaltenen Daten zu treffen.
Zunächst müssen wir die Zeitplanbibliothek importieren, um Vorhersagen nach einem Tag treffen zu können, da wir dieses Modell auf einen täglichen Zeitrahmen trainiert haben.
import schedule # Make realtime predictions based on the recent data from MetaTrader5 def predict_close(): rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, 1) if not rates: print(f"Failed to get recent OHLC values, error = {mt5.last_error}") time.sleep(60) rates_df = pd.DataFrame(rates) global results # Get the variable globally, outside the function global forecasts # Append new observation to the model without refitting new_obs_value = rates_df["close"].iloc[-1] new_obs_index = results.data.endog.shape[0] # continue integer index new_obs = pd.Series([new_obs_value], index=[new_obs_index]) # Its very important to continue making predictions where we ended on the training data results = results.append(new_obs, refit=False) # Forecast next step forecasts.append(results.forecast(steps=1).iloc[0]) print(f"Current Close Price: {new_obs_value} Forecasted next day Close Price: {forecasts[-1]}")
Terminplanung mit Vorhersagen.
schedule.every(1).days.do(predict_close) # call the predict function after a given time while True: schedule.run_pending() time.sleep(60) mt5.shutdown()
Ausgabe:
Current Close Price: 1.1374900000000001 Forecasted next day Close Price: 1.1337899981049262 Current Close Price: 1.1372200000000001 Forecasted next day Close Price: 1.1447100065656721
Ausgehend von diesen vorhergesagten Schlusskursen können Sie dies zu einer Handelsstrategie ausbauen und Handelsoperationen mit MetaTrader5-Python durchführen.
Abschließende Überlegungen
Sowohl ARIMA als auch SARIMA sind gute traditionelle Zeitreihenmodelle, die in vielen Bereichen und Industrien verwendet werden; Sie müssen jedoch ihre Grenzen und Nachteile kennen, einschließlich:
- Sie gehen von Stationarität aus (nach Differenzierung)
Wir arbeiten aber nicht immer mit stationären Daten und wollen die Daten oft so verwenden, wie sie sind. Die Differenzierung der Daten kann die natürliche Struktur und die von uns erwarteten Trends verzerren. - Linearitätsannahme
ARIMA ist von Natur aus ein lineares Modell; es geht davon aus, dass zukünftige Werte linear von vergangenen Verzögerungen und Fehlern abhängen. Dies ist falsch in Finanz-und Forex-Märkte Muster, wie komplexe Muster beobachtet werden können mehr als oft nicht, bedeutet dies, dass diese Modelle flach irgendwo fallen könnte. - Univariate Modelle
Beide Modelle gehen von einem Merkmal zum anderen. Wir wissen beide, dass die Finanzmärkte kompliziert sind und dass wir mehrere Merkmale und Perspektiven brauchen, um die Märkte zu betrachten. Diese Modelle betrachten den Markt nur aus einem Blickwinkel (eindimensional), wodurch uns andere Merkmale entgehen, die hilfreich sein könnten.
Sie können zwar exogene Merkmale zum SARIMAX-Modell hinzufügen, aber das reicht oft nicht aus.
Trotz ihrer Einschränkungen, wenn sie mit den richtigen Parametern, der richtigen Problemart und den richtigen Informationen eingesetzt werden. Ein einfaches ARIMA-Modell kann komplexe Modelle wie RNNs für Zeitreihenprognosen übertreffen.
Mit freundlichen Grüßen.
Quellen und Referenzen
- https://www.geeksforgeeks.org/python-arima-model-for-time-series-forecasting/
- https://www.machinelearningplus.com/time-series/arima-model-time-series-forecasting-python/
- https://datascientest.com/en/sarimax-model-what-is-it-how-can-it-be-applied-to-time-series
- https://www.kaggle.com/code/prashant111/arima-model-for-time-series-forecasting
Tabelle der Anhänge
| Dateiname | Beschreibung und Verwendung |
|---|---|
| forex_ts_forecasting_using_arima.py | Python-Skript mit allen besprochenen Beispielen in der Sprache Python. |
| requirements.txt | Eine Textdatei mit Python-Abhängigkeiten und deren Versionsnummer |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/18247
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
Meistern der Log-Einträge (Teil 7): Protokolle auf dem Chart anzeigen
Einführung in MQL5 (Teil 17): Aufbau von Expert Advisors für eine Trendumkehr
MetaTrader 5 Machine Learning Blueprint (Teil 1): Datenlecks und Zeitstempelfehler
Erstellen von selbstoptimierenden Expertenberatern in MQL5 (Teil 7): Handel mit mehreren Periodenlängen gleichzeitig
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.