数据科学与机器学习（第 15 部分）：SVM，每个交易员工具箱中的必备工具

MetaTrader 5 — 交易系统 | 8 四月 2025, 07:37

262

Omega J Msigwa

目录：

概述

支持向量机（SVM）是一种强大的监督机器学习算法，用于线性或非线性分类和回归任务，有时也用于异常检测任务。

与使用简单数学模型对信息进行分类的贝叶斯分类技术和逻辑回归不同，SVM 具有一些复杂的数学学习功能，旨在找到在 N 维空间中分离数据的最佳超平面。

支持向量机通常用于分类任务，我们在本文中也会这样做。

什么是超平面？

超平面是用于分离不同类别的数据点的线。

svm hperplane：图片来源：wikipedia.com

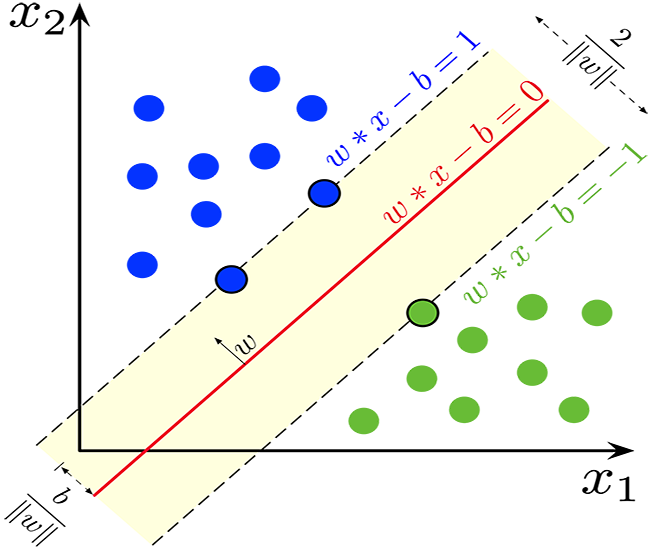
超平面具有以下属性：

维度：在二元分类问题中，超平面是(d-1) 维子空间，其中“d”是特征空间的维数。例如，在二维特征空间中，超平面是一维线。

方程式：从数学上来说，超平面可以用以下形式的线性方程式来表示：

是与超平面正交并确定其方向的向量。

是特征向量。

b 是标量偏差项，它将超平面移离原点。

分离：超平面将特征空间分为两个半空间：

区域对应一个类。

区域对应于另一个类。

间隔：在 SVM 中，目标是找到最大化间隔的超平面，间隔是超平面与任一类别的最近数据点之间的距离。这些最近的数据点被称为“支持向量”。SVM 的目标是找到实现最大间隔同时最小化分类误差的超平面。

分类：一旦找到最优超平面，就可以用它来对新的数据点进行分类。通过估算，你可以确定数据点落在超平面的哪一侧，从而将其归为两类之一。

超平面的概念是 SVM 中的关键元素，因为它构成了最大间隔分类器的基础。SVM 的目的是找到最佳分离数据的超平面，同时保持类别之间的最大间隔，从而增强模型的泛化和对看不见的数据的鲁棒性。

double CLinearSVM::hyperplane(vector &x)
 {
   return x.MatMul(W) - B;   
 }

方程

和方程

是等效的，并且描述相同的超平面。选择使用哪种形式是惯例和个人偏好的问题，但这两种形式在代数上是等价的。在我的代码中，我没有转置 x 矩阵，因为我选择使用 W 作为向量，所以没有必要。

如前所述，表示为 b 的偏差项是一个标量项，因此必须为其声明一个双精度变量。

class CLinearSVM
  {
   protected:
   
      CMatrixutils      matrix_utils;
      CMetrics          metrics;
      
      CPreprocessing<vector, matrix> *normalize_x;
      
      vector            W; //Weights vector 
      double            B; //bias term
      
      bool is_fitted_already;
      
      struct svm_config 
        {
          uint batch_size;
          double alpha;
          double lambda;
          uint epochs;
        };

   private:
      svm_config config;

我们已经看到了类名 CLinearSVM ，它本身就解释了这是一个线性支持向量机，这将我们带到了 SVM 的各个方面，其中我们有线性和对偶支持向量机。

线性 SVM

线性 SVM 是一种采用线性核的 SVM，这意味着它使用线性决策边界来分离数据点。在线性 SVM 中，你直接使用特征空间，优化问题通常以原始形式表示。线性 SVM 的主要目标是找到一个最佳分离数据的线性超平面。

这最适用于线性可分离数据。

对偶 SVM

对偶 SVM 并不是 SVM 的一种独特类型，而是 SVM 优化问题的一种表示。SVM 的对偶形式是对原始优化问题的数学重新表述，它允许更有效的求解方法。它引入拉格朗日乘子来最大化对偶目标函数，这相当于原始问题。解决对偶问题可以确定支持向量，这对于分类至关重要。

这最适合非线性可分的数据

线性与非线性问题

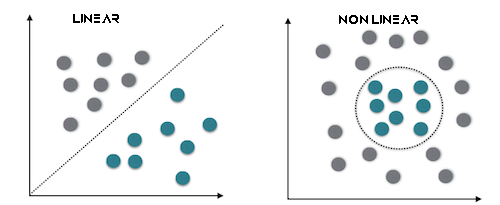
还需要知道的是，我们可以使用硬间隔或软间隔来使用超平面做出 SVM 分类器决策。

硬间隔

如果训练数据是线性可分的，我们可以选择两个平行的超平面来分隔这两类数据，使它们之间的距离尽可能大。这两个超平面所围成的区域称为“间隔”，最大间隔超平面是位于它们中间的超平面。对于标准化或归一化的数据集，这些超平面可以用以下方程来描述

（此边界上或之上的任何东西都属于同一类，标签为 1）

和

（此边界上或以下的任何东西都属于另一个类，标签为 -1）。

它们之间的距离是 2/||w||，并且为了最大化距离，||w||应该最小。为了防止任何数据点落入间隔内，我们添加了限制，yi(wTXi -b) >= 1，其中 yi = 目标中的第 i 行，Xi = X 中的第 i 行

软间隔

为了将 SVM 扩展到数据不可线性分离的情况，铰链损失函数是有帮助的

。

请注意，是第 i 个目标（即，在本例中为 1 或 −1），并且是第 i 个输出。

如果数据点的类别为 1，则损失为 0，否则损失为间隔与数据点之间的距离。我们的目标是最小化

其中 λ 是边距大小和 xi 在边距正确侧之间的权衡。如果 λ 太低，方程将变成硬间隔。

对于线性 SVM 类，我们将使用硬间隔，这可以通过 sign 函数实现，该函数以数学符号形式返回实数的符号。表达为：

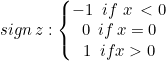
int CLinearSVM::sign(double var)
 {   
   if (var == 0)
    return (0);
   else if (var < 0)
    return -1;
   else 
    return 1; 
 }

训练线性支持向量机模型

支持向量机（SVM）的训练过程涉及寻找分离数据同时最大化间隔的最佳超平面。间隔是超平面与任一类别的最近数据点之间的距离。目标是找到最大化间隔同时最小化分类错误的超平面。

更新权重（w）：

a.第一项：损失函数中的第一项对应于铰链损失，它测量分类误差。对于每个训练示例 i ，我们计算损失关于权重 w 的导数，如下所示：

如果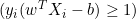，这意味着数据点被正确分类并且在间隔之外，导数为 0。
如果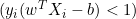，这意味着数据点在间隔内或被错误分类，导数是。

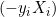b.第二项：

第二项表示正则化项。它鼓励较小的裕度并有助于防止过度拟合。该项关于权重 w 的导数是 2λw ，其中 λ 是正则化参数。

c.结合第一项和第二项的导数，

权重 w 的更新如下：

-如果，我们按如下方式更新权重：如果，我们按如下方式更新权重：这里， α 是学习率。

更新截距（b）：

a.第一项：

铰链损失关于截距 b 的导数的计算方法与权重类似：

如果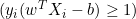，导数为 0。
如果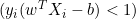，导数为。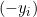

b.第二项：

第二项不依赖于截距，因此它对 b 的导数为 0。c。截距 b 的更新如下：

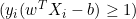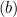如果，我们更新如下：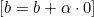
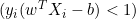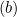如果，我们更新如下：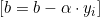

松弛变量（ξ）：

松弛变量（ξ）允许一些数据点位于间隔内，这意味着它们被错误分类或在间隔内。条件表示决策边界至少应为距离数据点 i 的 单位。

总之，SVM 的训练过程涉及根据铰链损失和正则化项更新权重和截距。目标是找到最大化间隔的最佳超平面，同时考虑松弛变量允许的边际内的潜在错误分类。该过程通常使用优化技术来解决，并在训练过程中识别支持向量来定义决策边界。

void CLinearSVM::fit(matrix &x, vector &y)
 {
   matrix X = x;
   vector Y = y;
  
   ulong rows = X.Rows(),
         cols = X.Cols();
   
   if (X.Rows() != Y.Size())
      {
         Print("Support vector machine Failed | FATAL | X m_rows not same as yvector size");
         return;
      }
   
   W.Resize(cols);
   B = 0;
    
   normalize_x = new CPreprocessing<vector, matrix>(X, NORM_STANDARDIZATION); //Normalizing independent variables
     
//---

  if (rows < config.batch_size)
    {
      Print("The number of samples/rows in the dataset should be less than the batch size");
      return;
    }
   
    matrix temp_x;
    vector temp_y;
    matrix w, b;
    
    vector preds = {};
    vector loss(config.epochs);
    during_training = true;

    for (uint epoch=0; epoch<config.epochs; epoch++)
      {
        
         for (uint batch=0; batch<=(uint)MathFloor(rows/config.batch_size); batch+=config.batch_size)
           {              
              temp_x = matrix_utils.Get(X, batch, (config.batch_size+batch)-1);
              temp_y = matrix_utils.Get(Y, batch, (config.batch_size+batch)-1);
              
              #ifdef DEBUG_MODE:
                  Print("X\n",temp_x,"\ny\n",temp_y);
              #endif 
              
               for (uint sample=0; sample<temp_x.Rows(); sample++)
                  {                                        
                     // yixiw-b≥1
                     
                      if (temp_y[sample] * hyperplane(temp_x.Row(sample))  >= 1) 
                        {
                          this.W -= config.alpha * (2 * config.lambda * this.W); // w = w + α* (2λw - yixi)
                        }
                      else
                         {
                           this.W -= config.alpha * (2 * config.lambda * this.W - ( temp_x.Row(sample) * temp_y[sample] )); // w = w + α* (2λw - yixi)
                           
                           this.B -= config.alpha * temp_y[sample]; // b = b - α* (yi)
                         }  
                  }
           }
        
        //--- Print the loss at the end of an epoch
       
         is_fitted_already = true;  
         
         preds = this.predict(X);
         
         loss[epoch] = preds.Loss(Y, LOSS_BCE);
        
         printf("---> epoch [%d/%d] Loss = %f Accuracy = %f",epoch+1,config.epochs,loss[epoch],metrics.confusion_matrix(Y, preds, false));
         
        #ifdef DEBUG_MODE:  
          Print("W\n",W," B = ",B);  
        #endif   
      }
    
    during_training = false;
    
    return;
 }

从线性支持向量模型获取预测

为了从模型中获取预测结果，必须在超平面给出输出后将数据传递给 sign 函数。

int CLinearSVM::predict(vector &x)
 { 
   if (!is_fitted_already)
     {
       Print("Err | The model is not trained, call the fit method to train the model before you can use it");
       return 1000;
     }
   
   vector temp_x = x;
   if (!during_training)
     normalize_x.Normalization(temp_x); //Normalize a new input data when we are not running the model in training 
     
   return sign(hyperplane(temp_x));
 }

训练测试线性 SVM 模型

作为一种常见的做法，在部署模型对市场数据做出任何重大预测之前，最好先对其进行测试，让我们首先初始化线性 SVM 类实例。

#include <MALE5\Support Vector Machine(SVM)\svm.mqh>
CLinearSVM *svm;

input uint bars = 1000;
input uint epochs_ = 1000;
input uint batch_size_ = 64;
input double alpha__ =0.1;
input double lambda_ = 0.01;

bool train_once;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---          
    svm = new CLinearSVM(batch_size_, alpha__, epochs_, lambda_);
    train_once = false;
//---

   return(INIT_SUCCEEDED);
  }

我们将继续收集数据，我们将使用 4 个独立变量，即 RSI、布林带的高点、低点和中点。

vec_.CopyIndicatorBuffer(rsi_handle, 0, 0, bars);
dataset.Col(vec_, 0);
vec_.CopyIndicatorBuffer(bb_handle, 0, 0, bars);
dataset.Col(vec_, 1);
vec_.CopyIndicatorBuffer(bb_handle, 1, 0, bars);
dataset.Col(vec_, 2);
vec_.CopyIndicatorBuffer(bb_handle, 2, 0, bars);
dataset.Col(vec_, 3);

open.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OPEN, 0, bars);
close.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 0, bars);
      
for (ulong i=0; i<vec_.Size(); i++) //preparing the independent variable
   dataset[i][4] = close[i] > open[i] ? 1 : -1; // if price closed above its opening thats bullish else bearish

我们通过将数据分成训练和测试样本来完成数据收集过程。

matrix_utils.TrainTestSplitMatrices(dataset,train_x,train_y,test_x,test_y,0.7,42); //split the data into training and testing samples

训练/拟合模型

svm.fit(train_x, train_y);

输出：

        0       15:15:42.394    svm test (EURUSD,H1)    ---> epoch [1/1000] Loss = 7.539322 Accuracy = 0.489000
IK      0       15:15:42.395    svm test (EURUSD,H1)    ---> epoch [2/1000] Loss = 7.499849 Accuracy = 0.491000
EG      0       15:15:42.395    svm test (EURUSD,H1)    ---> epoch [3/1000] Loss = 7.499849 Accuracy = 0.494000
....
....
GG      0       15:15:42.537    svm test (EURUSD,H1)    ---> epoch [998/1000] Loss = 6.907756 Accuracy = 0.523000
DS      0       15:15:42.537    svm test (EURUSD,H1)    ---> epoch [999/1000] Loss = 7.006438 Accuracy = 0.521000
IM      0       15:15:42.537    svm test (EURUSD,H1)    ---> epoch [1000/1000] Loss = 6.769601 Accuracy = 0.516000

观察模型在训练和测试中的准确性。

vector train_pred = svm.predict(train_x), 
    test_pred = svm.predict(test_x);

printf("Train accuracy = %f",metrics.confusion_matrix(train_y, train_pred, true));
printf("Test accuracy = %f ",metrics.confusion_matrix(test_y, test_pred, true));

输出：

CH      0       15:15:42.538    svm test (EURUSD,H1)    Confusion Matrix
IQ      0       15:15:42.538    svm test (EURUSD,H1)    [[171,175]
HE      0       15:15:42.538    svm test (EURUSD,H1)     [164,190]]
DQ      0       15:15:42.538    svm test (EURUSD,H1)    
NO      0       15:15:42.538    svm test (EURUSD,H1)    Classification Report
JD      0       15:15:42.538    svm test (EURUSD,H1)    
LO      0       15:15:42.538    svm test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
JQ      0       15:15:42.538    svm test (EURUSD,H1)    -1.0    0.51     0.49     0.54       0.50     346.0
DH      0       15:15:42.538    svm test (EURUSD,H1)    1.0    0.52     0.54     0.49       0.53     354.0
HL      0       15:15:42.538    svm test (EURUSD,H1)    
FG      0       15:15:42.538    svm test (EURUSD,H1)    Accuracy                                   0.52
PP      0       15:15:42.538    svm test (EURUSD,H1)    Average   0.52    0.52    0.52      0.52    700.0
PS      0       15:15:42.538    svm test (EURUSD,H1)    W Avg     0.52    0.52    0.52      0.52    700.0
FK      0       15:15:42.538    svm test (EURUSD,H1)    Train accuracy = 0.516000

MS      0       15:15:42.538    svm test (EURUSD,H1)    Confusion Matrix
LI      0       15:15:42.538    svm test (EURUSD,H1)    [[79,74]
CM      0       15:15:42.538    svm test (EURUSD,H1)     [68,79]]
FJ      0       15:15:42.538    svm test (EURUSD,H1)    
HF      0       15:15:42.538    svm test (EURUSD,H1)    Classification Report
DM      0       15:15:42.538    svm test (EURUSD,H1)    
NH      0       15:15:42.538    svm test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
NN      0       15:15:42.538    svm test (EURUSD,H1)    -1.0    0.54     0.52     0.54       0.53     153.0
PQ      0       15:15:42.538    svm test (EURUSD,H1)    1.0    0.52     0.54     0.52       0.53     147.0
JE      0       15:15:42.538    svm test (EURUSD,H1)    
GP      0       15:15:42.538    svm test (EURUSD,H1)    Accuracy                                   0.53
RI      0       15:15:42.538    svm test (EURUSD,H1)    Average   0.53    0.53    0.53      0.53    300.0
JH      0       15:15:42.538    svm test (EURUSD,H1)    W Avg     0.53    0.53    0.53      0.53    300.0
DO      0       15:15:42.538    svm test (EURUSD,H1)    Test accuracy = 0.527000

我们的模型在样本外预测中的准确率为 53%，有些人会说这是一个糟糕的模型，但我认为这是一个平均水平的模型。导致这种情况的因素可能有很多，包括模型中的错误、规范化不佳、收敛标准等等，你可以尝试调整参数，看看是什么导致了更好的结果。然而，也可能是数据对于线性模型来说太复杂了，对此我很有信心，所以让我们尝试对偶 SVM，看看它是否有帮助。

对于我们将要以 ONXX python 格式探索的对偶 SVM，我无法使 mql5 编码模型在性能和准确性方面接近 python sklearn 对偶 SVM 模型，因此我认为现在值得在 python 中探索对偶 SVM，MQL5 中的对偶 SVM 库仍然可以在本文提供的主要 svm.mqh 文件和本文末尾链接的 GitHub 上找到。

为了在 Python 中启动对偶 SVM，我们需要收集数据并使用 mql5 进行规范化，我们可能需要在 svm.mqh 文件中创建一个名为 CDualSVMONNX 的新类，此类将负责处理从 Python 代码获得的 ONNX 模型。

class CDualSVMONNX
  {
private:
      CPreprocessing<vectorf, matrixf> *normalize_x;
      CMatrixutils matrix_utils;
      
      struct data_struct
       {
         ulong rows,
               cols;
       } df;
      
public:  
                     CDualSVMONNX(void);
                    ~CDualSVMONNX(void);
      
                     long onnx_handle;              
                     
                     void SendDataToONNX(matrixf &data, string csv_name = "DualSVMONNX-data.csv", string csv_header="");
                     bool LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags=ONNX_NO_CONVERSION);
                     int Predict(vectorf &inputs);
                     vector Predict(matrixf &inputs);
  };

乍一看，这个类是这样的，

收集和规范化数据

我们需要数据供模型学习，我们还需要对数据进行净化，使其适合我们的 SVM 模型，也就是说：

void CDualSVMONNX::SendDataToONNX(matrixf &data, string csv_name = "DualSVMONNX-data.csv", string csv_header="")
 {
    df.cols = data.Cols();
    df.rows = data.Rows();
    
    if (df.cols == 0 || df.rows == 0)
      {
         Print(__FUNCTION__," data matrix invalid size ");
         return;
      }
    
    matrixf split_x;
    vectorf  split_y;
    
    matrix_utils.XandYSplitMatrices(data, split_x, split_y); //since we are going to be normalizing the independent variable only we need to split the data into two
    
    normalize_x = new CPreprocessing<vectorf,matrixf>(split_x, NORM_MIN_MAX_SCALER); //Normalizing Independent variable only
    
    
    matrixf new_data = split_x;
    new_data.Resize(data.Rows(), data.Cols());
    new_data.Col(split_y, data.Cols()-1);
    
    if (csv_header == "")
      {
         for (ulong i=0; i<df.cols; i++)
           csv_header += "COLUMN "+string(i+1) + (i==df.cols-1 ? "" : ","); //do not put delimiter on the last column
      }
    
//--- Save the Normalization parameters also
    
   matrixf params = {};
    
   string sep=",";
   ushort u_sep;
   string result[];
   
   u_sep=StringGetCharacter(sep,0); 
   int k=StringSplit(csv_header,u_sep,result); 
   
   ArrayRemove(result, k-1, 1); //remove the last column header since we do not have normalization parameters for the target variable  as it is not normalized
    
    normalize_x.min_max_scaler.min.Swap(params);
    matrix_utils.WriteCsv("min_max_scaler.min.csv",params,result,false,8);
    normalize_x.min_max_scaler.max.Swap(params);
    matrix_utils.WriteCsv("min_max_scaler.max.csv",params,result,false,8); 
    
//--- 
    
    matrix_utils.WriteCsv(csv_name, new_data, csv_header, false, 8); //Save dataset to a csv file 
 }

由于训练的数据收集需要一次性完成一次，因此没有比在脚本中收集数据更好的地方了。

GetDataforONNX.mq5 脚本内部

#include <MALE5\Support Vector Machine(SVM)\svm.mqh>

CDualSVMONNX dual_svm;

input uint bars = 1000;
input uint epochs_ = 1000;
input uint batch_size_ = 64;
input double alpha__ =0.1;
input double lambda_ = 0.01;

input int rsi_period = 13;
input int bb_period = 20;
input double bb_deviation = 2.0;

int rsi_handle, 
    bb_handle;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
  
    rsi_handle = iRSI(Symbol(),PERIOD_CURRENT,rsi_period, PRICE_CLOSE);
    bb_handle = iBands(Symbol(), PERIOD_CURRENT, bb_period,0, bb_deviation, PRICE_CLOSE);
    
//---

    matrixf data = GetTrainTestData<float>();
    dual_svm.SendDataToONNX(data,"DualSVMONNX-data.csv","rsi,bb-high,bb-low,bb-mid,target");
  }
//+------------------------------------------------------------------+
//|   Getting data for Training and Testing the model                |
//+------------------------------------------------------------------+
template <typename T>
matrix<T> GetTrainTestData()
 {
   matrix<T> data(bars, 5);
   vector<T> v; //Temporary vector for storing Inidcator buffers
    
   v.CopyIndicatorBuffer(rsi_handle, 0, 0, bars);
   data.Col(v, 0);
   v.CopyIndicatorBuffer(bb_handle, 0, 0, bars);
   data.Col(v, 1);
   v.CopyIndicatorBuffer(bb_handle, 1, 0, bars);
   data.Col(v, 2);
   v.CopyIndicatorBuffer(bb_handle, 2, 0, bars);
   data.Col(v, 3);
   
   vector open, close;
   open.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OPEN, 0, bars);
   close.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 0, bars);
   
   for (ulong i=0; i<v.Size(); i++) //preparing the independent variable
     data[i][4] = close[i] > open[i] ? 1 : -1; // if price closed above its opening thats bullish else bearish
     
   return data;  
 }

输出：

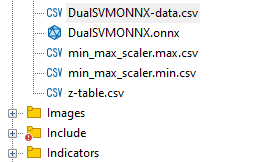
在 MQL5 目录文件下创建了一个名为 DualSVMONNX-data.csv 的 csv 文件。

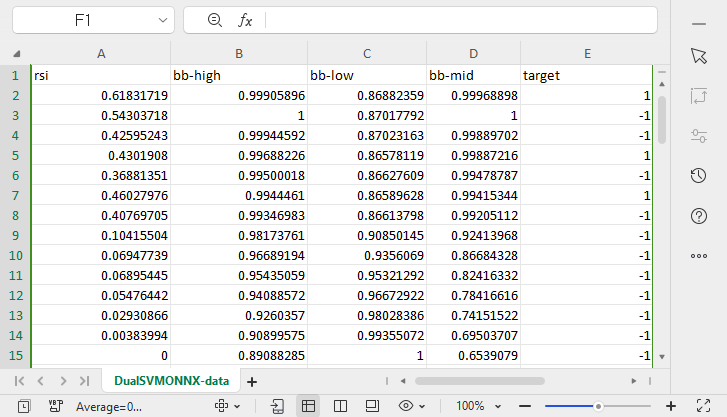
注意函数 SendDataToONNX 的末尾！！

我还保存了规范化参数，

normalize_x.min_max_scaler.min.Swap(params);
matrix_utils.WriteCsv("min_max_scaler.min.csv",params,result,false,8);
normalize_x.min_max_scaler.max.Swap(params);
matrix_utils.WriteCsv("min_max_scaler.max.csv",params,result,false,8);

这是因为曾经使用过的规范化参数需要重新使用，以从模型中获得最佳预测，保存它们将有助于我们跟踪数据规范化参数值。CSV 文件将与数据集位于同一文件夹中，我们还将把 ONNX 模型保存在那里。

DualSVMONNX 类实例 | 初始化类：

class DualSVMONNX:
    def __init__(self, dataset, c=1.0, kernel='rbf'):
        
        data = pd.read_csv(dataset) # reading a csv file 
        np.random.seed(42)
        
        self.X = data.drop(columns=['target']).astype(np.float32) # dropping the target column from independent variable 
        self.y = data["target"].astype(int) # storing the target variable in its own vector 
        
        self.X = self.X.to_numpy()
        self.y = self.y.to_numpy()            

        # Split the data into training and testing sets
        self.X_train, self.X_test, self.y_train, self.y_test = train_test_split(self.X, self.y, test_size=0.2, random_state=42) 

        self.onnx_model_name = "DualSVMONNX" #our final onnx model file name for saving purposes really
        
        # Create a dual SVM model with a kernel
        
        self.svm_model = SVC(kernel=kernel, C=c)

在 Python 中训练对偶 SVM 模型

    def fit(self):
        
        self.svm_model.fit(self.X_train, self.y_train) # fitting/training the model
        
        y_preds = self.svm_model.predict(self.X_train)
        
        print("accuracy = ",accuracy_score(self.y_train, y_preds))

模型训练完成后，让我们看看运行此代码片段后的准确度如何。

输出：

我们得到了 63% 的准确率，这告诉我们用于对这个特定问题进行分类的 SVM 模型充其量只是平均水平，但是，我感到怀疑，让我进行交叉验证以证明准确率是否达到了应有的水平：

        scores = cross_val_score(self.svm_model, self.X_train, self.y_train, cv=5)
        mean_cv_accuracy = np.mean(scores)

        print(f"\nscores {scores} mean_cv_accuracy {mean_cv_accuracy}")

输出：

这个交叉验证结果意味着什么？

当模型以不同的参数运行时，结果并没有太大的差异，这说明我们的模型正走在正确的轨道上，我们得到的平均准确率是 59.875，与我们得到的 63.3 相差不远。

将 SVC 模型从 sklearn 转换为 ONNX 并保存。

    def saveONNX(self):                 
        
        initial_type = [('float_input', FloatTensorType(shape=[None, 4]))]  # None means we don't know the rows but we know the columns for sure, Remember !! we have 4 independent variables
        onnx_model = convert_sklearn(self.svm_model, initial_types=initial_type) # Convert the scikit-learn model to ONNX format

        onnx.save_model(onnx_model, dataset_path + f"\\{self.onnx_model_name}.onnx") #saving the onnx model

输出：注意：该模型保存在 MQL5/Files 目录下

下面是 ONNX 文件在 MetaEditor 中打开时的样子。重要的是你要注意我将要解释的内容；

内有 Onnx 文件

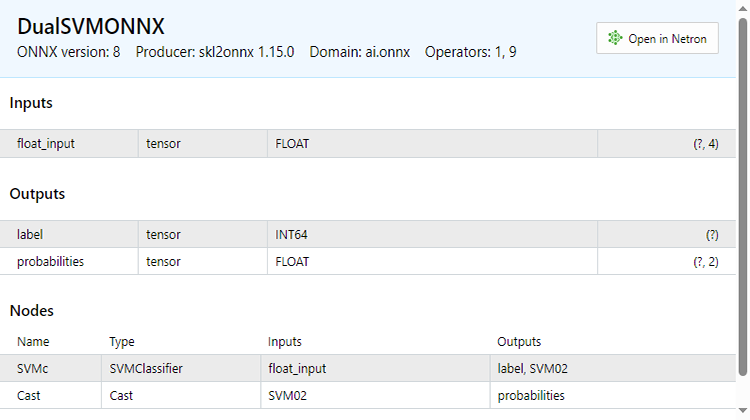
查看输入参数部分； float_input 说明这是一个浮点类型的输入，旁边是张量，这告诉我们可能需要为 OnnxRun 函数提供矩阵或向量，因为它们都是张量，最后您会看到 (?, 4)，这是输入大小，问号代表行数未知，列数为 4。这适用于其余部分，但您会看到输出部分。

它有两个节点，一个节点给我们预测标签 -1 或 1，在这种情况下，它们是 INT64 类型或仅仅是 mql5 中的 INT 。

另一个节点为我们提供概率，这是一个浮点类型的张量，它有未知的行但有 2 列，因此可以使用 nx2 矩阵来提取此处的值，或者只是一个大小 >= 2 的向量

由于输出中有两个节点，我们可以提取输出两次：

   long outputs_0[] = {1};
   if (!OnnxSetOutputShape(onnx_handle, 0, outputs_0)) //giving the onnx handle first node output shape
     {
       Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError());
       return false;
     }
     
   long outputs_1[] = {1,2};
   if (!OnnxSetOutputShape(onnx_handle, 1, outputs_1)) //giving the onnx handle second node output shape
     {
       Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError());
       return false;
     }

另一方面，我们可以提取我们拥有的单个输入节点。

   const long inputs[] = {1,4};
   
   if (!OnnxSetInputShape(onnx_handle, 0, inputs)) //Giving the Onnx handle the input shape
     {
       Print(__FUNCTION__," Failed to set the input shape Err=",GetLastError());
       return false;
     }

此 ONNX 代码是从下面给出的 LoadONNX 函数中提取的：

bool CDualSVMONNX::LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags=ONNX_NO_CONVERSION)
 {
   onnx_handle =  OnnxCreateFromBuffer(onnx_buff, flags); //creating onnx handle buffer 
   
   if (onnx_handle == INVALID_HANDLE)
    {
       Print(__FUNCTION__," OnnxCreateFromBuffer Error = ",GetLastError());
       return false;
    }
   
//---
   
   const long inputs[] = {1,4};
   
   if (!OnnxSetInputShape(onnx_handle, 0, inputs)) //Giving the Onnx handle the input shape
     {
       Print(__FUNCTION__," Failed to set the input shape Err=",GetLastError());
       return false;
     }
   
   long outputs_0[] = {1};
   if (!OnnxSetOutputShape(onnx_handle, 0, outputs_0)) //giving the onnx handle first node output shape
     {
       Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError());
       return false;
     }
     
   long outputs_1[] = {1,2};
   if (!OnnxSetOutputShape(onnx_handle, 1, outputs_1)) //giving the onnx handle second node output shape
     {
       Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError());
       return false;
     }

   return true;
 }

仔细观察该函数，您可能会注意到我们在加载规范化参数时缺少这些参数，这些参数对于规范化新输入数据至关重要，以便它与模型已经熟悉的训练数据的维度相匹配。

我们可以从 CSV 文件中加载参数，这将在实时交易中顺利运行，然而，这种方法可能会变得复杂，并且对于策略测试器来说并不总是有效，让我们至少现在手动将规范化参数复制到我们的 EA 代码中，以便我们最终得到 EA 内部的规范化参数。首先让我们修改 LoadONNX 函数，使其采用输入向量 max 和 min，这在 Min Max Scaler 中起着重要作用。

bool CDualSVMONNX::LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags, vectorf &norm_max, vectorf &norm_min)

在我介绍的函数结束时。

normalize_x = new CPreprocessing<vectorf,matrixf>(norm_max, norm_min); //Load min max scaler with parameters

将规范化参数从 CSV 文件复制并粘贴到 EA。

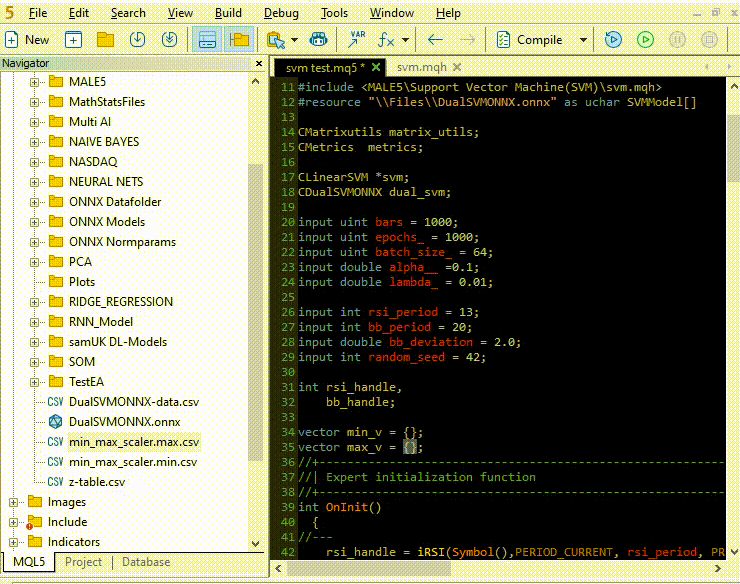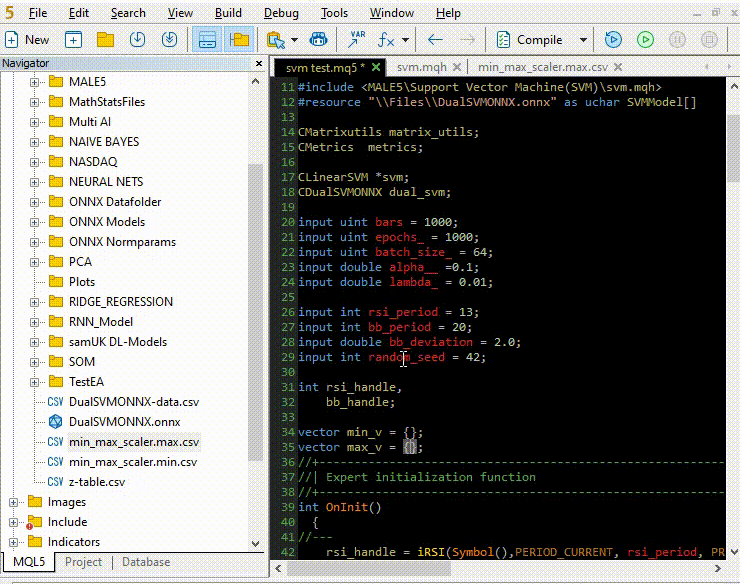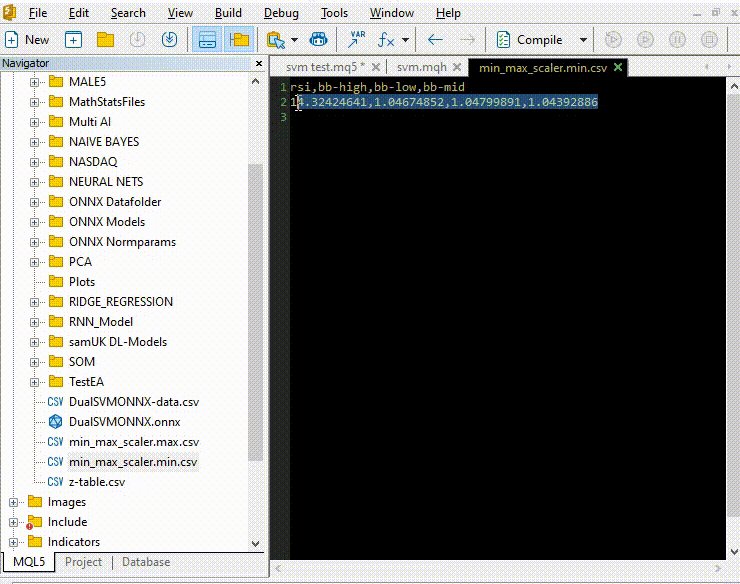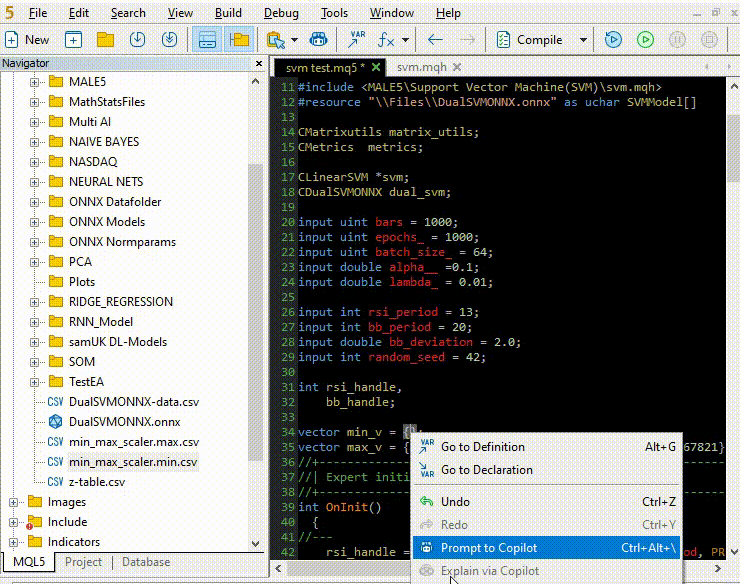
让我们像使用 Python 一样的方式训练和测试模型，目的是确保我们在两种语言中走在同一条道路上。

svm test.mq5 的 OnInit 函数内部

vector min_v = {14.32424641,1.04674852,1.04799891,1.04392886};
vector max_v = {86.28263092,1.07385755,1.07907069,1.07267821};
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---    
    rsi_handle = iRSI(Symbol(),PERIOD_CURRENT, rsi_period, PRICE_CLOSE);
    bb_handle = iBands(Symbol(), PERIOD_CURRENT, bb_period, 0 , bb_deviation, PRICE_CLOSE);

    
      vector y_train,
             y_test;
        
    // float values
      
      matrixf datasetf = GetTrainTestData<float>();
      matrixf x_trainf,
              x_testf;
      
      vectorf y_trainf,
              y_testf;
            
//---
      
      matrix_utils.TrainTestSplitMatrices(datasetf,x_trainf,y_trainf,x_testf,y_testf,0.8,42); //split the data into training and testing samples
      
      vectorf max_vf = {}, min_vf = {}; //convertin the parameters into float type
      max_vf.Assign(max_v); 
      min_vf.Assign(min_v);
      
      dual_svm.LoadONNX(SVMModel, ONNX_DEFAULT, max_vf, min_vf);
            
      y_train.Assign(y_trainf);
      y_test.Assign(y_testf);
      
      vector train_preds = dual_svm.Predict(x_trainf);
      vector test_preds = dual_svm.Predict(x_testf);
      
      Print("\n<<<<< Train Classification Report >>>>\n");
      metrics.confusion_matrix(y_train, train_preds);
      
      Print("\n<<<<< Test  Classification Report >>>>\n");
      metrics.confusion_matrix(y_test, test_preds);


   return(INIT_SUCCEEDED);
  }

输出：

RP      0       17:08:53.068    svm test (EURUSD,H1)    <<<<< Train Classification Report >>>>
HE      0       17:08:53.068    svm test (EURUSD,H1)    
MR      0       17:08:53.068    svm test (EURUSD,H1)    Confusion Matrix
IG      0       17:08:53.068    svm test (EURUSD,H1)    [[245,148]
CO      0       17:08:53.068    svm test (EURUSD,H1)     [150,257]]
NK      0       17:08:53.068    svm test (EURUSD,H1)    
DE      0       17:08:53.068    svm test (EURUSD,H1)    Classification Report
HO      0       17:08:53.068    svm test (EURUSD,H1)    
FI      0       17:08:53.068    svm test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
ON      0       17:08:53.068    svm test (EURUSD,H1)    1.0    0.62     0.62     0.63       0.62     393.0
DP      0       17:08:53.068    svm test (EURUSD,H1)    -1.0    0.63     0.63     0.62       0.63     407.0
JG      0       17:08:53.068    svm test (EURUSD,H1)    
FR      0       17:08:53.068    svm test (EURUSD,H1)    Accuracy                                   0.63
CK      0       17:08:53.068    svm test (EURUSD,H1)    Average   0.63    0.63    0.63      0.63    800.0
KI      0       17:08:53.068    svm test (EURUSD,H1)    W Avg     0.63    0.63    0.63      0.63    800.0
PP      0       17:08:53.068    svm test (EURUSD,H1)    
DH      0       17:08:53.068    svm test (EURUSD,H1)    <<<<< Test  Classification Report >>>>
PQ      0       17:08:53.068    svm test (EURUSD,H1)    
EQ      0       17:08:53.068    svm test (EURUSD,H1)    Confusion Matrix
HJ      0       17:08:53.068    svm test (EURUSD,H1)    [[61,31]
MR      0       17:08:53.068    svm test (EURUSD,H1)     [40,68]]
NH      0       17:08:53.068    svm test (EURUSD,H1)    
DP      0       17:08:53.068    svm test (EURUSD,H1)    Classification Report
HL      0       17:08:53.068    svm test (EURUSD,H1)    
FF      0       17:08:53.068    svm test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
GJ      0       17:08:53.068    svm test (EURUSD,H1)    -1.0    0.60     0.66     0.63       0.63     92.0
PO      0       17:08:53.068    svm test (EURUSD,H1)    1.0    0.69     0.63     0.66       0.66     108.0
DD      0       17:08:53.068    svm test (EURUSD,H1)    
JO      0       17:08:53.068    svm test (EURUSD,H1)    Accuracy                                   0.65
LH      0       17:08:53.068    svm test (EURUSD,H1)    Average   0.65    0.65    0.65      0.64    200.0
CJ      0       17:08:53.068    svm test (EURUSD,H1)    W Avg     0.65    0.65    0.65      0.65    200.0

我们获得的准确度值与 Python 脚本获得的准确度值相同，为 63%。这不是很棒吗！

预测函数的内部结构如下：

int CDualSVMONNX::Predict(vectorf &inputs)
 {
    vectorf outputs(1); //label outputs
    vectorf x_output(2); //probabilities
    
    vectorf temp_inputs = inputs;
    
    normalize_x.Normalization(temp_inputs); //Normalize the input features
    
    if (!OnnxRun(onnx_handle, ONNX_DEFAULT, temp_inputs, outputs, x_output))
      {
         Print("Failed to get predictions from onnx Err=",GetLastError());
         return (int)outputs[0];
      }
      
   return (int)outputs[0];
 }

它运行 ONNX 文件来获取预测并返回预测标签的整数。

最后，我必须实施一个简单的策略，以便我们在策略测试器中测试两个支持向量机模型。该策略很简单，如果 SVM 预测的类别 == 1，则开启买入交易，否则，如果预测的类别 == -1，则开启卖出交易。

策略测试器中的结果：

对于线性支持向量机：

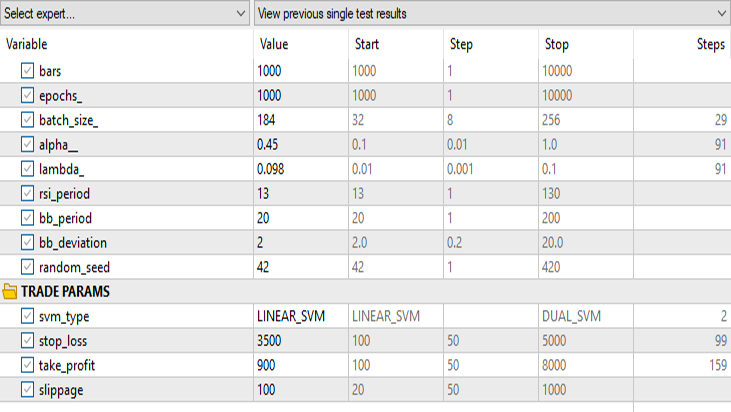
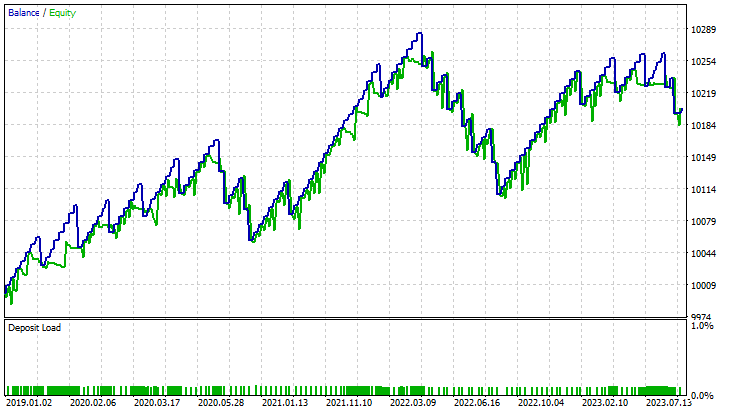
对于对偶支持向量机：

除 svm_type 之外，所有输入保持相同。

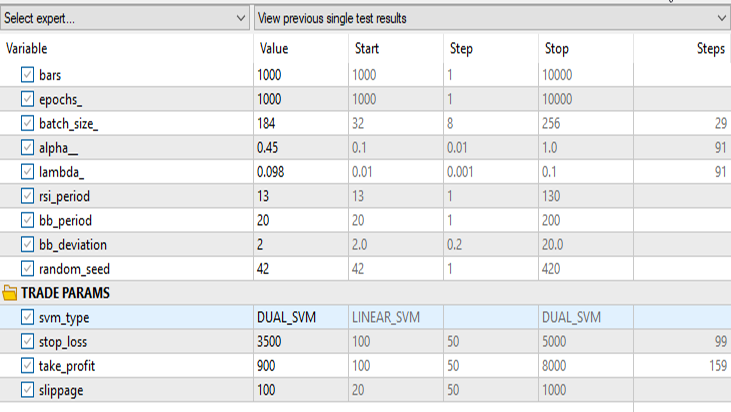
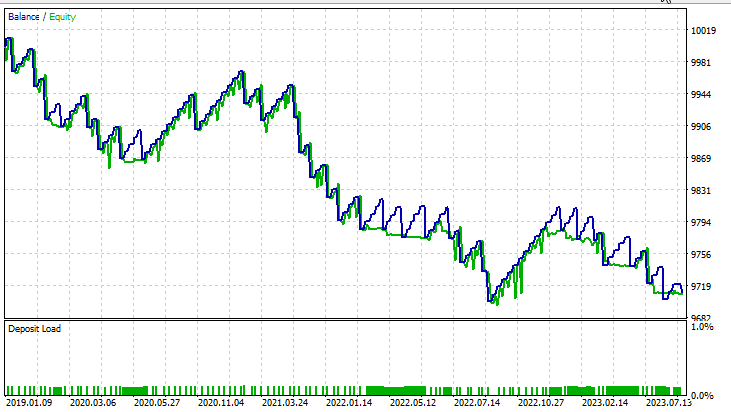
对于线性 SVM 的输入，对偶 SVM 的表现并不好，可能需要进一步优化并探究 ONNX 模型无法收敛的原因，但这是另一篇文章的主题。

最后的想法

SVM 模型的优点：

在高维空间中有效：SVM 在高维空间中表现良好，使其适用于具有众多特征（例如交易指标和市场变量）的金融数据集。
抗过度拟合：SVM 不太容易过拟合，提供了一种更通用的解决方案，可以更好地适应看不见的市场条件。
内核的多功能性：SVM 通过不同的内核函数提供多功能性，允许交易者尝试各种策略，并使模型适应特定的市场模式。
非线性场景中的出色表现：SVM 擅长捕捉数据中的非线性关系，这是处理复杂金融市场时的一个关键方面。

缺点：

噪声敏感性：SVM 可能对噪声数据敏感，影响其性能，使其更容易受到不稳定市场行为的影响。
计算复杂性：训练 SVM 模型的计算成本很高，特别是对于大型数据集，这限制了它们在某些实时交易场景中的可扩展性。
需要质量特征工程：SVM 严重依赖于特征工程，需要领域专业知识来选择相关指标并有效地预处理数据。
平均表现：如我们所见，SVM 模型对于双重 SVM 实现了 63% 的平均准确率，对于线性 SVM 实现了 59% 的平均准确率。虽然这些模型可能无法超越一些先进的机器学习技术，但它们仍然为MQL5交易者提供了一个合理的起点。

人气下降：

尽管 SVM 历史上取得了成功，但近年来其受欢迎程度有所下降。这归因于：

深度学习的出现：深度学习技术，特别是神经网络的兴起，由于其自动提取层次特征的能力，已经使 SVM 等传统机器学习算法黯然失色。
更多可用的数据：随着海量金融数据集的日益普及，以海量数据为基础的深度学习模型变得越来越有吸引力。
计算的进展：强大的硬件和分布式计算资源的可用性使得训练和部署复杂的深度学习模型变得更加可行。

总之，虽然 SVM 模型可能不是最先进的解决方案，但它们在 MQL5 交易环境中的使用是合理的。它们的简单性、稳健性和适应性使其成为一种有价值的工具，特别是对于数据或计算资源有限的交易者。交易员必须将 SVM 视为更广泛工具包的一部分，随着市场动态的发展，可能会用更新的机器学习方法对其进行补充。

致以最诚挚的问候，愿您平安。

文件	描述 \| 用法
dual_svm.py \| python 脚本	它有 Python 中的对偶 SVM 实现
GetDataforONNX.mq5 \| mql5 脚本	可用于收集、规范化并将数据存储在位于 MQL5/Files 下的 csv 文件中
preprocessing.mqh \| mql5 包含文件	包含用于规范化和标准化输入数据的类和函数
matrix_utils.mqh \| mql5 包含文件	具有附加矩阵运算的库
metrics.mqh \| mql5 包含文件	包含用于分析 ML 模型性能的附加函数的库
svm test.mq5 \| EA	用于测试本文中所有代码的 EA 交易