Algorithmen zur Optimierung mit Populationen: Widerstand gegen das Steckenbleiben in lokalen Extremen (Teil II)

Inhalt

1. Algorithmen
2. Verbesserter Agent für BGA
3. Schlussfolgerungen

Im Rahmen unserer Forschung untersuchen wir die Robustheit der Optimierungsalgorithmen von Populationen und ihre Fähigkeit, lokale Fallen zu überwinden und globale Maxima für eine Vielzahl von Testfunktionen zu erreichen. Im vorigen Artikel haben wir uns mit Algorithmen befasst, die bescheidene Ergebnisse in der Rangliste aufweisen. Jetzt ist es an der Zeit, den Spitzenreitern Aufmerksamkeit zu schenken.

Wir bemühen uns um eine gründliche Analyse jedes dieser Algorithmen, wobei wir ihre Vorteile und einzigartigen Merkmale herausarbeiten. Unser Ziel ist es, zu verstehen, welche Strategien und Ansätze diese Algorithmen erfolgreich machen, um die Komplexität zu überwinden und globale Optimierungsziele zu erreichen.

Diese Forschungsphase wird es uns nicht nur ermöglichen, die Widerstandsfähigkeit von Populationsalgorithmen gegen das Hängenbleiben in lokalen Fallen besser zu verstehen, sondern auch die Schlüsselfaktoren zu ermitteln, die zu ihrem Erfolg angesichts der vielfältigen und komplexen Testfunktionen beitragen. Meine Bemühungen zielen darauf ab, das Verständnis dafür zu verbessern, wie diese Algorithmen optimiert und verbessert werden können, und Möglichkeiten für ihre gemeinsame Nutzung und Hybridisierung zu identifizieren, um verschiedene Optimierungsprobleme in der Zukunft effektiv zu lösen.

1. Algorithmen

Betrachten wir nun die Algorithmen, die in unserer Vergleichstabelle die ersten Plätze belegen. Sie verdienen definitiv eine genauere Betrachtung und Aufmerksamkeit. Lassen Sie uns in eine detaillierte Analyse ihrer Eigenschaften eintauchen, um alle Aspekte aufzudecken, die sie so wertvoll und effektiv für die Lösung komplexer Optimierungsprobleme machen.

Nachstehend finden Sie Berichte über die Algorithmen, die wie folgt zu lesen sind:

• C_AO_FSS:50;0.01;0.8             - Name des Algorithmus und externe Parameter.
  
• 5 Hilly's                                   - Name der Testfunktion und ihrer Nummer im Test.
  
•  Func runs: 10000                   - Anzahl der Durchläufe.
  
• result: 0.32457068874346456  - erzieltes Ergebnis, wobei 0,0 das Minimum der Testfunktion und 1,0 das Maximum ist. Je höher der Wert, desto besser
  
• All score: 1.33084                   - Gesamtwert der erzielten Punkte. Je höher der Wert, desto besser.

Evolutionäre Strategien, (P+O)ES

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
5 Hilly's; Func runs: 10000; result: 0.45574011563217454
25 Hilly's; Func runs: 10000; result: 0.5979154724556998
500 Hilly's; Func runs: 10000; result: 0.3415203622112476
=============================
5 Forest's; Func runs: 10000; result: 0.18929181937830403
25 Forest's; Func runs: 10000; result: 0.1837517532554242
500 Forest's; Func runs: 10000; result: 0.15411134176683486
=============================
5 Megacity's; Func runs: 10000; result: 0.10153846153846155
25 Megacity's; Func runs: 10000; result: 0.12030769230769231
500 Megacity's; Func runs: 10000; result: 0.08793846153846216
=============================
All score: 2.23212

Im Gegensatz zu seinem jüngeren Bruder (PO)ES ist (P+O)ES im Suchraum sehr aktiv, insbesondere auf der glatten Hilly-Funktion, bei der die Population in mehrere Gruppen aufgeteilt ist, die jeweils verschiedene Bereiche erkunden. Aus irgendeinem Grund nimmt jedoch seine Effizienz bei der glatten Forest-Funktion ab, während er bei der diskreten Funktion schlecht abschneidet (nur der nächstgelegene Hügel (hill) wird erreicht). Im Allgemeinen ist der Algorithmus für glatte differenzierbare Funktionen sehr interessant, aber es gibt eine klare Tendenz, stecken zu bleiben. Außerdem fehlt es ihm an Möglichkeiten, das Ergebnis zu verfeinern.

Grauer-Wolf-Optimierer (GWO)

C_AO_GWO:50;10
=============================
5 Hilly's; Func runs: 10000; result: 0.5385541648909985
25 Hilly's; Func runs: 10000; result: 0.33060651191769963
500 Hilly's; Func runs: 10000; result: 0.25796885816873344
=============================
5 Forest's; Func runs: 10000; result: 0.33256641908450685
25 Forest's; Func runs: 10000; result: 0.2040563379483599
500 Forest's; Func runs: 10000; result: 0.15278428644972566
=============================
5 Megacity's; Func runs: 10000; result: 0.2784615384615384
25 Megacity's; Func runs: 10000; result: 0.1587692307692308
500 Megacity's; Func runs: 10000; result: 0.133153846153847
=============================
All score: 2.38692

Ein Rudel Wölfe des GWO-Algorithmus stürmt durch die Weiten der virtuellen Welt und verteilt sich schnell in alle Richtungen auf verschiedene Testfunktionen. Diese Eigenschaft kann in den ersten Iterationen effektiv genutzt werden, insbesondere wenn der Algorithmus mit einer anderen Methode gepaart wird, die die gefundenen Lösungen verbessern und ergänzen kann. Die hervorragenden Forschungsfähigkeiten der Gruppe sprechen für ihr Potenzial, aber leider bleibt die Genauigkeit bei der Identifizierung von Gebieten ihr Schwachpunkt. Interessanterweise zeigte der Algorithmus sogar bessere Ergebnisse als im konventionellen Test mit einer gleichmäßigen Verteilung der Agenten.

Der Algorithmus eines schlurfenden Froschsprungs (SFL)

C_AO_SFL:50;25;15;5;0.7
=============================
5 Hilly's; Func runs: 10000; result: 0.5009251084703008
25 Hilly's; Func runs: 10000; result: 0.3175649450809088
500 Hilly's; Func runs: 10000; result: 0.25514153268631673
=============================
5 Forest's; Func runs: 10000; result: 0.4165336325557746
25 Forest's; Func runs: 10000; result: 0.21617658684174407
500 Forest's; Func runs: 10000; result: 0.15782134182434096
=============================
5 Megacity's; Func runs: 10000; result: 0.2892307692307692
25 Megacity's; Func runs: 10000; result: 0.14892307692307696
500 Megacity's; Func runs: 10000; result: 0.10636923076923148
=============================
All score: 2.40869

Der SFL-Algorithmus zeigte eine noch größere Bandbreite an Ausbreitungsmöglichkeiten in verschiedenen Richtungen des Suchraums, selbst bei einer diskreten Megacity-Funktion, als der vorherige Algorithmus in der Liste. SFL ist in der Lage, selbst globale Maximalregionen innerhalb einer bestimmten Anzahl von Iterationen zu erreichen. Die Genauigkeit bei der Verfeinerung der gefundenen Lösungen ist jedoch nicht die Stärke von SFL. Ähnlich wie bei GWO zeigte der Algorithmus Ergebnisse, die denen der konventionellen Tests überlegen waren.

Algorithmus einer zufälligen (random) Suche (RND)

C_AO_RND:50
=============================
5 Hilly's; Func runs: 10000; result: 0.5024853724464499
25 Hilly's; Func runs: 10000; result: 0.3284469438564529
500 Hilly's; Func runs: 10000; result: 0.2600678718550755
=============================
5 Forest's; Func runs: 10000; result: 0.3989291459162246
25 Forest's; Func runs: 10000; result: 0.22913381881119183
500 Forest's; Func runs: 10000; result: 0.16727444696703453
=============================
5 Megacity's; Func runs: 10000; result: 0.2753846153846154
25 Megacity's; Func runs: 10000; result: 0.14861538461538465
500 Megacity's; Func runs: 10000; result: 0.09890769230769311
=============================
All score: 2.40925

Diese einfachste Optimierungsmethode setzte sich bei diesem einzigartigen Wettbewerb gegen viele angesehene und bekannte Teilnehmer durch. Wie Sie sich vielleicht erinnern, besteht die Strategie des RND-Algorithmus aus einer 50%igen Wahrscheinlichkeit: Entweder wird die Koordinate eines zufällig ausgewählten Individuums aus der Population ausgewählt oder es wird eine Zufallskoordinate mit einer Gleichverteilung erzeugt. Dadurch konnte der Algorithmus jedoch in die Mitte der Teilnehmerliste aufsteigen. Möglich wurde dies durch die weitreichenden Möglichkeiten zur Erkundung des Weltraums, wobei es in diesem Fall nicht notwendig ist, über die Genauigkeit zu sprechen.

Evolution sozialer Gruppen (ESG)

C_AO_ESG:200:100:0.1:2.0:10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.3695915822772909
25 Hilly's; Func runs: 10000; result: 0.3396716009249312
500 Hilly's; Func runs: 10000; result: 0.2727013729189837
=============================
5 Forest's; Func runs: 10000; result: 0.2956316169252261
25 Forest's; Func runs: 10000; result: 0.2875217303660672
500 Forest's; Func runs: 10000; result: 0.16124201361354124
=============================
5 Megacity's; Func runs: 10000; result: 0.30769230769230765
25 Megacity's; Func runs: 10000; result: 0.306153846153846
500 Megacity's; Func runs: 10000; result: 0.13183076923077003
=============================
All score: 2.47204

Der ESG-Algorithmus zeigt gute Fähigkeiten bei der Erkundung des Suchraums, indem er in charakteristische Gruppen unterteilt wird. Dabei werden jedoch weit entfernte Regionen des Raums ausgelassen, was zu Problemen führen kann, wenn das gesamte Ausmaß des Problems untersucht werden soll. Es gibt auch Anzeichen dafür, dass man sich in erheblichen lokalen Extremen festfährt, was das Erreichen eines globalen Optimums erschweren könnte. Trotzdem zeigt der Algorithmus bei der Behandlung der diskreten Megacity-Funktion beachtliche Erfolge, was sein Potenzial bei bestimmten Bedingungen und Aufgaben unterstreicht.

Algorithmus intelligenter Wassertropfen (IWDm)

C_AO_IWDm:50;10;3.0
=============================
5 Hilly's; Func runs: 10000; result: 0.4883273901756646
25 Hilly's; Func runs: 10000; result: 0.34290016593207995
500 Hilly's; Func runs: 10000; result: 0.2581256124908963
=============================
5 Forest's; Func runs: 10000; result: 0.5119191969436073
25 Forest's; Func runs: 10000; result: 0.2564038040639046
500 Forest's; Func runs: 10000; result: 0.1675925588605327
=============================
5 Megacity's; Func runs: 10000; result: 0.34153846153846157
25 Megacity's; Func runs: 10000; result: 0.15784615384615389
500 Megacity's; Func runs: 10000; result: 0.09889230769230851
=============================
All score: 2.62355

Wie die Strömungen eines reißenden Flusses gleitet der IWDm-Algorithmus schnell durch den Suchraum, erreicht schnell die Region des globalen Maximums und beweist hervorragende Suchfähigkeiten. Es ist jedoch anzumerken, dass dieser Algorithmus nicht über ausreichend klärende Eigenschaften verfügt, was die genaue Bestimmung der optimalen Lösung erschweren kann.

In der konventionellen Rangliste gehört dieser Algorithmus nicht zu den Besten, aber in diesem speziellen Test hat er im Vergleich zu anderen Algorithmen eindrucksvoll abgeschnitten. IWDm kann für den Einsatz in der Anfangsphase der Optimierung empfohlen werden, um dann zu genaueren Algorithmen überzugehen, die den Optimierungsprozess als Ganzes bereichern und verbessern.

Partikelschwarm (PSO)

C_AO_PSO:50;0.8;0.4;0.4
=============================
5 Hilly's; Func runs: 10000; result: 0.5548169875802522
25 Hilly's; Func runs: 10000; result: 0.3407594364160912
500 Hilly's; Func runs: 10000; result: 0.2525297014321252
=============================
5 Forest's; Func runs: 10000; result: 0.4573903259815636
25 Forest's; Func runs: 10000; result: 0.27561812346057046
500 Forest's; Func runs: 10000; result: 0.19079124396445962
=============================
5 Megacity's; Func runs: 10000; result: 0.3092307692307693
25 Megacity's; Func runs: 10000; result: 0.14923076923076928
500 Megacity's; Func runs: 10000; result: 0.09553846153846236
=============================
All score: 2.62591

Der PSO-Algorithmus überraschte in diesem Experiment mit unerwartet guten Ergebnissen und zeigte im Vergleich zum früheren IWDm-Algorithmus eine noch höhere Geschwindigkeit bei der Bewegung in unerforschtes Gebiet. Dieser plötzliche Erfolg lässt sich dadurch erklären, dass die Partikel in PSO in der ersten Iteration eine zufällig gewählte Anfangsgeschwindigkeit haben, die es ihnen ermöglicht, ihre ursprüngliche Position schnell zu verlassen. Die ersten Schritte des Algorithmus ähneln dem Tanz der Teilchen im Raum, bis sie ihre besondere Harmonie finden. Leider führt diese Harmonie nicht immer zu einem globalen Optimum. Der Mangel an klärenden Eigenschaften verlangsamt das Erreichen einer idealen Lösung.

Wie IWDm kann PSO für den Einsatz in den Anfangsphasen der Optimierung empfohlen werden, wo seine Fähigkeit, den Suchraum schnell zu erkunden, der Schlüssel zur Entdeckung vielversprechender Lösungen sein kann.

Algorithmus der Fledermaus (bat, BA)

C_AO_BA:50;0.0;1.0;0.0;1.5;0.0;1.0;0.3;0.3
=============================
5 Hilly's; Func runs: 10000; result: 0.5127608047854995
25 Hilly's; Func runs: 10000; result: 0.4239882910506281
500 Hilly's; Func runs: 10000; result: 0.3127353914885268
=============================
5 Forest's; Func runs: 10000; result: 0.4355521825589907
25 Forest's; Func runs: 10000; result: 0.29303187383086005
500 Forest's; Func runs: 10000; result: 0.19433130092541523
=============================
5 Megacity's; Func runs: 10000; result: 0.28769230769230764
25 Megacity's; Func runs: 10000; result: 0.16030769230769232
500 Megacity's; Func runs: 10000; result: 0.10907692307692407
=============================
All score: 2.72948

Die Fledermäuse im BA-Algorithmus haben die erstaunliche Eigenschaft, die Region des globalen Extremums schnell zu finden und sich gleich in den ersten Iterationen zu bewegen. Die Gleichsetzung von Schallimpulsen bei dieser Suchmethode führt jedoch dazu, dass die Bewegungen der Fledermäuse trotz der offensichtlichen Notwendigkeit, die Suche fortzusetzen, schnell verblassen. BA rangiert in der regulären Rangliste weit unten, steht aber in dieser Challenge ganz oben in der Tabelle.

 Optimierung der invasiven Unkräuter (IWO)

C_AO_IWO:50;12;5;2;0.2;0.01
=============================
5 Hilly's; Func runs: 10000; result: 0.4570149872637351
25 Hilly's; Func runs: 10000; result: 0.4252105325836707
500 Hilly's; Func runs: 10000; result: 0.28299287471456525
=============================
5 Forest's; Func runs: 10000; result: 0.43322917175445896
25 Forest's; Func runs: 10000; result: 0.33438950288190694
500 Forest's; Func runs: 10000; result: 0.18632383795879612
=============================
5 Megacity's; Func runs: 10000; result: 0.3061538461538461
25 Megacity's; Func runs: 10000; result: 0.24369230769230765
500 Megacity's; Func runs: 10000; result: 0.12887692307692397
=============================
All score: 2.79788

Der Algorithmus für invasives Unkraut folgt ebenfalls der Ausbreitungsrate als Funktion der aktuellen Iteration, genau wie der Fledermaus-Algorithmus (BA). In diesem Fall sind die Agenten jedoch in der Lage, den Raum effizienter und vollständiger zu erforschen, was es ihnen ermöglicht, im Vergleich zu BA schnell und genau optimale Lösungen zu finden, wobei die wichtigsten Merkmale der Funktion und der Bereich des globalen Maximums berücksichtigt werden. Ist die Entfernung vom Startpunkt zum Ziel jedoch groß, erreicht das Unkraut nicht die maximale Fläche. Dies macht sich besonders bei der Funktion Megacity bemerkbar - die Agenten bleiben im nächstgelegenen signifikanten Extremum stecken.

Künstliches Bienenvolk (ABC)

C_AO_ABC:50;45;10;0.1;0.4
=============================
5 Hilly's; Func runs: 10000; result: 0.5969246550857782
25 Hilly's; Func runs: 10000; result: 0.3899058056869557
500 Hilly's; Func runs: 10000; result: 0.26574506946962373
=============================
5 Forest's; Func runs: 10000; result: 0.536535405336652
25 Forest's; Func runs: 10000; result: 0.29048311417293887
500 Forest's; Func runs: 10000; result: 0.17322987568991322
=============================
5 Megacity's; Func runs: 10000; result: 0.3307692307692308
25 Megacity's; Func runs: 10000; result: 0.18492307692307694
500 Megacity's; Func runs: 10000; result: 0.11512307692307773
=============================
All score: 2.88364

Das interessante Verhalten des ABC-Algorithmus ist seine Fähigkeit, eine Population in separate Schwärme aufzuteilen, die aktiv lokale Extreme erkunden. Es ist jedoch möglich, dass der Algorithmus nicht genügend klärende Eigenschaften hat, was sich in seiner Position in der Standardbewertungstabelle widerspiegelt. Es gibt jedoch ein Potenzial zur Verbesserung und Nutzung seiner Suchfunktionen in hybriden Algorithmen. Die Fähigkeit des Algorithmus, globale Optima zu finden, sowie seine Gesamteffizienz bei verschiedenen Optimierungsproblemen kann durch die Integration mit anderen Optimierungsmethoden erheblich verbessert werden.

Rechnen einer Evolution des Geistes (mind, MEC)

C_AO_MEC:50;10;0.4
=============================
5 Hilly's; Func runs: 10000; result: 0.5566946043237988
25 Hilly's; Func runs: 10000; result: 0.430203412538813
500 Hilly's; Func runs: 10000; result: 0.2724348221662864
=============================
5 Forest's; Func runs: 10000; result: 0.4548936450507163
25 Forest's; Func runs: 10000; result: 0.3156014530351309
500 Forest's; Func runs: 10000; result: 0.17625852850331755
=============================
5 Megacity's; Func runs: 10000; result: 0.3415384615384615
25 Megacity's; Func runs: 10000; result: 0.23107692307692304
500 Megacity's; Func runs: 10000; result: 0.1186615384615393
=============================
All score: 2.89736

Der MEC-Algorithmus ist erstaunlich schnell, da er fast alle signifikanten lokalen Extremwerte sofort erkennt und den Bereich des globalen Maximums erfolgreich identifiziert. Trotz des leichten Rückstands gegenüber dem konventionellen Test zeigt der MEC weiterhin eine hohe Stabilität und Effizienz bei der Suche nach optimalen Lösungen.

Kuckucks-Optimierungsalgorithmus (COAm)

C_AO_COAm:100;40;0.6;0.6;0.63
=============================
5 Hilly's; Func runs: 10000; result: 0.600998666320958
25 Hilly's; Func runs: 10000; result: 0.42709404776275245
500 Hilly's; Func runs: 10000; result: 0.26571090745735276
=============================
5 Forest's; Func runs: 10000; result: 0.5533129896276743
25 Forest's; Func runs: 10000; result: 0.30413063297063025
500 Forest's; Func runs: 10000; result: 0.1703031415266755
=============================
5 Megacity's; Func runs: 10000; result: 0.3261538461538461
25 Megacity's; Func runs: 10000; result: 0.2046153846153847
500 Megacity's; Func runs: 10000; result: 0.1112615384615393
=============================
All score: 2.96358

Unser Durchschnittskandidat in der konventionellen COAm-Bewertungstabelle bewegt sich erstaunlich schnell im Suchraum und kommt leicht aus dem globalen Minimum heraus. Sie hat jedoch gewisse Schwierigkeiten, an signifikanten lokalen Extremen hängen zu bleiben, was sie daran hindert, das globale Maximum zu erreichen.

Künstliches Mikro-Immunsystem (Mikro-AIS)

C_AO_Micro_AIS:50:1:2:0.3
=============================
5 Hilly's; Func runs: 10000; result: 0.6193671060348247
25 Hilly's; Func runs: 10000; result: 0.4656896752001433
500 Hilly's; Func runs: 10000; result: 0.24995620778886124
=============================
5 Forest's; Func runs: 10000; result: 0.7121901446084455
25 Forest's; Func runs: 10000; result: 0.4254191301238518
500 Forest's; Func runs: 10000; result: 0.211517515004865
=============================
5 Megacity's; Func runs: 10000; result: 0.2676923076923077
25 Megacity's; Func runs: 10000; result: 0.16461538461538466
500 Megacity's; Func runs: 10000; result: 0.10927692307692398
=============================
All score: 3.22572

Der Micro-AIS-Algorithmus kann eine sehr gleichmäßige Wolke erkennen, die von den Antigenen erzeugt wird, was dem Prozess eine gewisse Ordnung verleiht, die eher an Harmonie als an Chaos erinnert. Trotzdem sind seine Aufklärungseigenschaften verbesserungswürdig, obwohl der Algorithmus über gute Suchfunktionen verfügt. Es ist jedoch auch anfällig für lokale Fallen.

Harmonie-Suche (HS)

C_AO_HS:50;0.9;0.1;0.2
=============================
5 Hilly's; Func runs: 10000; result: 0.602082991833691
25 Hilly's; Func runs: 10000; result: 0.5533985889779909
500 Hilly's; Func runs: 10000; result: 0.2820448101527182
=============================
5 Forest's; Func runs: 10000; result: 0.6503798132320532
25 Forest's; Func runs: 10000; result: 0.5104503170911219
500 Forest's; Func runs: 10000; result: 0.19337757947865844
=============================
5 Megacity's; Func runs: 10000; result: 0.30769230769230765
25 Megacity's; Func runs: 10000; result: 0.29538461538461525
500 Megacity's; Func runs: 10000; result: 0.12826153846153937
=============================
All score: 3.52307

Bei diesem speziellen Problem zeigt HS beeindruckende Suchfähigkeiten und eine hohe Geschwindigkeit der Bewegung durch den Raum bei der Suche nach einem globalen Maximum. Wenn er jedoch auf das erste signifikante lokale Extremum trifft, verlangsamt er sich aufgrund seiner Abhängigkeit von der aktuellen Epochenzahl. Dieses Manko tritt jedoch nur bei der diskreten Funktion Megacity auf, während die Suchmöglichkeiten bei den glatten Funktionen Hilly und Forest beeindruckend bleiben. In der Bewertungstabelle belegt Harmonic Search die vorderen Plätze und beweist damit auch im aktuellen Test seine Effizienz.

Spiraldynamische Optimierung (SDOm)

C_AO_SDOm:100;0.5;4.0;10000.0
=============================
5 Hilly's; Func runs: 10000; result: 0.7132463872323508
25 Hilly's; Func runs: 10000; result: 0.43264564401427485
500 Hilly's; Func runs: 10000; result: 0.25506574720969816
=============================
5 Forest's; Func runs: 10000; result: 0.804287574819851
25 Forest's; Func runs: 10000; result: 0.4249161540200845
500 Forest's; Func runs: 10000; result: 0.2193817986301354
=============================
5 Megacity's; Func runs: 10000; result: 0.4938461538461539
25 Megacity's; Func runs: 10000; result: 0.22030769230769232
500 Megacity's; Func runs: 10000; result: 0.11410769230769328
=============================
All score: 3.67780

Der SDOm-Algorithmus erscheint plötzlich an der Spitze der Rangliste. Dieser Algorithmus, der auf harmonischen Schwingungen beruht, zeigt sich im Rahmen dieses Experiments auf sehr ungewöhnliche und einzigartige Weise und hinterlässt ein schwer zu enträtselndes Geheimnis. Eine an einem Seil aufgehängte Pendelkugel kann sich plötzlich lösen und in den freien Flug übergehen. Das Verhalten des Algorithmus hat viele Aspekte, die ihn besonders machen, und es ist fast unmöglich, die Bedingungen vorherzusagen, die zu einem solchen unerwarteten Verhalten führen. Aus diesem Grund ist es schwierig, ihn in seiner jetzigen Form für eine breite Palette von Aufgaben zu empfehlen. In Kombination mit anderen Algorithmen (z. B. Übergabe einiger Agenten aus der allgemeinen Population an die SDOm-Kontrolle) können jedoch zyklische Muster in der Aufgabe erkannt werden.

Optimierung einer bakteriellen Nahrungssuche - Genetischer Algorithmus (BFO-GA)

C_AO_BFO_GA:50;0.01;0.8;50;10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.8233662999080027
25 Hilly's; Func runs: 10000; result: 0.5031148772790799
500 Hilly's; Func runs: 10000; result: 0.27434497581097494
=============================
5 Forest's; Func runs: 10000; result: 0.8611314745481611
25 Forest's; Func runs: 10000; result: 0.45038118646429437
500 Forest's; Func runs: 10000; result: 0.1806538222176609
=============================
5 Megacity's; Func runs: 10000; result: 0.3907692307692308
25 Megacity's; Func runs: 10000; result: 0.272
500 Megacity's; Func runs: 10000; result: 0.11061538461538559
=============================
All score: 3.86638

Der BFO_GA-Algorithmus zeigt eine erstaunliche Fähigkeit, die Region des globalen Maximums schnell zu erkennen - mehrere Agenten nähern sich den Zielkoordinaten bereits während der ersten Iterationen. Die Ergebnisse bei der diskreten Funktion sind jedoch weniger beeindruckend. Offensichtlich reicht die begrenzte Anzahl von Iterationen im Rahmen der Tests nicht aus, um das globale Optimum vollständig zu finden. Es ist jedoch wichtig zu beachten, dass unser Test innerhalb eines strengen Rahmens stattfindet, innerhalb dessen wir die Fähigkeit des Algorithmus bewerten, seine beabsichtigten Ziele zu erreichen.

Stochastische Diffusionssuche (SDSm)

C_AO_SDSm:100;100;0.05
=============================
5 Hilly's; Func runs: 10000; result: 0.6838494804548411
25 Hilly's; Func runs: 10000; result: 0.6796828568841194
500 Hilly's; Func runs: 10000; result: 0.32584905164208583
=============================
5 Forest's; Func runs: 10000; result: 0.6703019775594297
25 Forest's; Func runs: 10000; result: 0.6398441335988195
500 Forest's; Func runs: 10000; result: 0.24899123954861618
=============================
5 Megacity's; Func runs: 10000; result: 0.5307692307692308
25 Megacity's; Func runs: 10000; result: 0.49446153846153845
500 Megacity's; Func runs: 10000; result: 0.14973846153846293
=============================
All score: 4.42349

Bei der Erörterung des SDSm-Algorithmus ist es nicht ganz angemessen, sich auf die Geschwindigkeit zu konzentrieren, mit der sich die Agenten im Suchraum ausbreiten, da ihre Koordinaten innerhalb zufällig ausgewählter Sektoren der Umgebung festgelegt werden. Im Wesentlichen werden diese Agenten nach der ersten Iteration sofort auf das gesamte Suchfeld verteilt. Dieser einzigartige Ansatz führt zu bemerkenswerten Ergebnissen, die die Effizienz der Algorithmusstrategie belegen.

Was SDSm auszeichnet, ist die Fähigkeit, die Macht des Zufalls zu nutzen, was die Wahrscheinlichkeit erhöht, dass keine Ecke des Suchraums unerforscht bleibt. Durch die Berücksichtigung dieser stochastischen Natur kann der Algorithmus große Bereiche effizient abdecken und wertvolle Informationen über die Funktionsoberfläche aufdecken, was ihn zu einem wirklich leistungsstarken Werkzeug für die Problemlösung macht.

Binärer genetischer Algorithmus (BGA)

C_AO_BGA:50:50:1.0:3:0.001:0.7:3
=============================
5 Hilly's; Func runs: 10000; result: 1.0
25 Hilly's; Func runs: 10000; result: 1.0
500 Hilly's; Func runs: 10000; result: 0.8703352617259978
=============================
5 Forest's; Func runs: 10000; result: 0.8872607468925364
25 Forest's; Func runs: 10000; result: 0.8177419261242314
500 Forest's; Func runs: 10000; result: 0.2603521654104144
=============================
5 Megacity's; Func runs: 10000; result: 0.7492307692307694
25 Megacity's; Func runs: 10000; result: 0.5833846153846155
500 Megacity's; Func runs: 10000; result: 0.24415384615384667
=============================
All score: 6.41246

Der binäre genetische Algorithmus (BGA) profitiert von der Mutation der Gene, die es ihm ermöglicht, jede Region des Suchraums ohne zusätzliche Iterationen sofort zu erreichen. In diesem speziellen Testszenario hat die BGA jedoch die Nase vorn, obwohl sie manchmal in einem lokalen Optimum gefangen ist. In dieser Hinsicht scheint die SDSm vorzuziehen zu sein, da sie besser in der Lage ist, solche Situationen zu vermeiden.

Allerdings muss man der BGA zugute halten, dass sie insgesamt die besten Ergebnisse erzielt hat, selbst wenn man ihre Unzulänglichkeiten in Betracht zieht. Diese Leistung unterstreicht das Potenzial des Algorithmus und zeigt, wie wichtig es ist, im Suchprozess ein Gleichgewicht zwischen Forschung und Nutzung herzustellen. Wenn wir uns näher mit dem Vergleich befassen, wird deutlich, dass jeder Algorithmus seine eigenen Stärken und Schwächen hat.

Zusammenfassend lässt sich sagen, dass BGA in diesem Test beeindruckende Ergebnisse vorweisen kann und sich damit die Spitzenposition sichert.

2. Verbesserter Agent für BGA

Zur Durchführung dieser Forschung war es notwendig, den Code des BGA-Algorithmus für diese spezielle Prüfaufgabe zu ändern. Die Möglichkeit, Agenten an einer beliebigen Stelle im Suchraum zu platzieren, kann sehr nützlich sein, wenn Sie die Optimierung mit nutzerdefinierten Mengen beginnen müssen.

In der BGA werden die Lösungen des Problems in Form eines Binärcodes präsentiert. Um die Agenten der Population in den gegebenen Koordinaten zu platzieren, ist es daher notwendig, die Koordinatenwerte von einer realen Darstellung in eine binäre Darstellung umzuwandeln, in diesem Fall in einen binären Gray-Code.

Fügen wir die Methode „DoubleToGene“ zu den Agentenbeschreibungen hinzu, die einen Wert vom Typ „double“ in eine genetische Darstellung im Array „genes“ umwandelt. Die wichtigsten Schritte bei dieser Methode sind:

• Ist die eingegebene Zahl kleiner als der minimale gültige Wert, erstellt die Funktion eine Reihe von Nullen (die reelle Zahl „0.0“ in Gray-Code-Notation), um sicherzustellen, dass der Wert innerhalb des gültigen Bereichs bleibt.

• Wenn die eingegebene Zahl den maximal zulässigen Wert überschreitet, erstellt die Funktion ein Array, das die Werte aus dem ursprünglichen Array kopiert, das die maximal zulässige Zahl in Gray-Kodierung enthält (diese Zahl wird für Fälle wie diesen gespeichert, wenn wir zu dem Bereich zurückkehren müssen, wenn es einen Anstieg außerhalb des Bereichs gibt).
  

• Liegt die Zahl innerhalb des zulässigen Bereichs, wird sie skaliert und in einen Gray-Code umgewandelt. Dieser Wert wird dann in einem Array zur Verwendung in der genetischen Darstellung gespeichert.

So wandelt die Methode „DoubleToGene“ einen reellen Wert in eine genetische Darstellung um und schreibt ihn in das entsprechende Array „genes“. Die Funktion behandelt Fälle, in denen ein Eingabewert außerhalb des Bereichs liegt, indem sie bestimmte Arrays initialisiert oder kopiert und die Ausführung frühzeitig beendet. Andernfalls skaliert die Funktion den Wert, wandelt die ganzzahligen und gebrochenen Teile in Gray-Code um und kombiniert sie zur endgültigen genetischen Darstellung.

Angepasster BGA-Agentencode:

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords, const double &min [], const double &max [], int doubleDigitsInChromo)
  {
    ArrayResize(c, coords);
    f = -DBL_MAX;

    ArrayResize(genes, coords);
    ArrayResize(chromosome, 0, 1000);

    for(int i = 0; i < coords; i++)
    {
      genes [i].Init(min [i], max [i], doubleDigitsInChromo);
      ArrayCopy(chromosome, genes [i].gene, ArraySize(chromosome), 0, WHOLE_ARRAY);
    }
  }

  void ExtractGenes ()
  {
    uint pos = 0;

    for (int i = 0; i < ArraySize (genes); i++)
    {
      c [i] = genes [i].ToDouble (chromosome, pos);
      pos  += genes [i].length;

    }
  }

  void DoubleToGene (const double val, const int genePos)
  {
    double value = val;

    //--------------------------------------------------------------------------
    if (value < genes [genePos].rangeMin)
    {
      ArrayInitialize(genes [genePos].gene, 0);
      ArrayCopy (chromosome, genes [genePos].gene, genePos * genes [genePos].length, 0, WHOLE_ARRAY);
      return;
    }

    //--------------------------------------------------------------------------
    else
    {
      if (value > genes [genePos].rangeMax)
      {
        ArrayCopy (chromosome, genes [genePos].geneMax, genePos * genes [genePos].length, 0, WHOLE_ARRAY);
        return;
      }
    }

    //--------------------------------------------------------------------------
    value = Scale(value, genes [genePos].rangeMin, genes [genePos].rangeMax, 0.0, genes [genePos].maxCodedDistance);

    DecimalToGray ((ulong)value, genes [genePos].integPart);

    value = value - (int)value;

    value *= genes [genePos].digitsPowered;

    DecimalToGray ((ulong)value, genes [genePos].fractPart);

    ArrayInitialize(genes [genePos].gene, 0);

    uint   integGrayDigits = genes [genePos].integGrayDigits;
    uint   fractGrayDigits = genes [genePos].fractGrayDigits;
    uint   digits = ArraySize (genes [genePos].integPart);

    if (digits > 0) ArrayCopy (genes [genePos].gene, genes [genePos].integPart, integGrayDigits - digits, 0, WHOLE_ARRAY);

    digits = ArraySize (genes [genePos].fractPart);

    if (digits > 0) ArrayCopy (genes [genePos].gene, genes [genePos].fractPart, genes [genePos].length - digits, 0, WHOLE_ARRAY);

    ArrayCopy (chromosome, genes [genePos].gene, genePos * genes [genePos].length, 0, WHOLE_ARRAY);
  }

  void InjectGeneToChromosome ()
  {

  }

  //----------------------------------------------------------------------------
  double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
    else
    {
      if (In < InMIN) return OutMIN;
      if (In > InMAX) return OutMAX;

      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }

  double c [];           //coordinates
  double f;              //fitness

  S_BinaryGene genes []; //there are as many genes as there are coordinates
  char chromosome    [];
};
//——————————————————————————————————————————————————————————————————————————————

3. Zusammenfassung

Fassen wir die Ergebnisse einer groß angelegten vergleichenden Studie von Populationsalgorithmen zusammen, was bedeutet, dass das globale Minimum verlassen und alle Hindernisse überwunden werden müssen, um das globale Maximum zu erreichen.
Wir beginnen mit der Visualisierung des interessantesten Verhaltens der Algorithmen während der Tests.

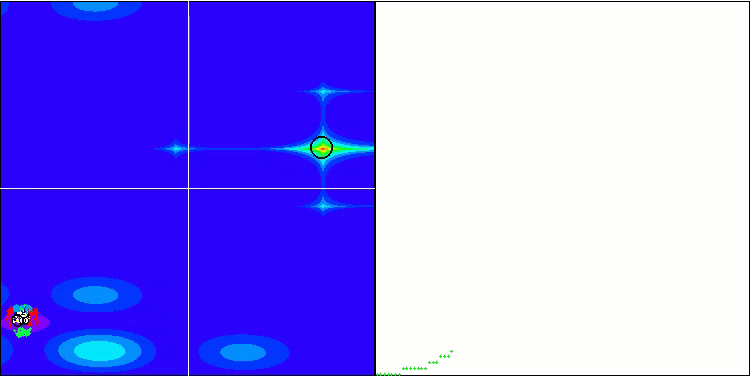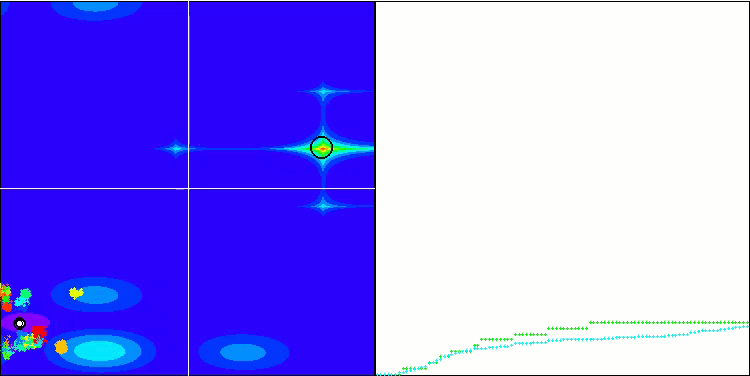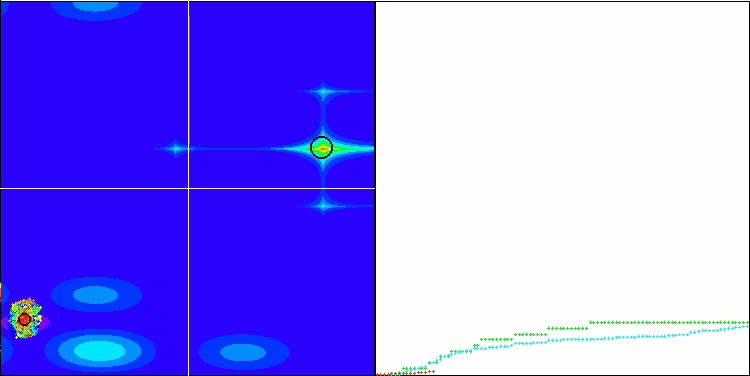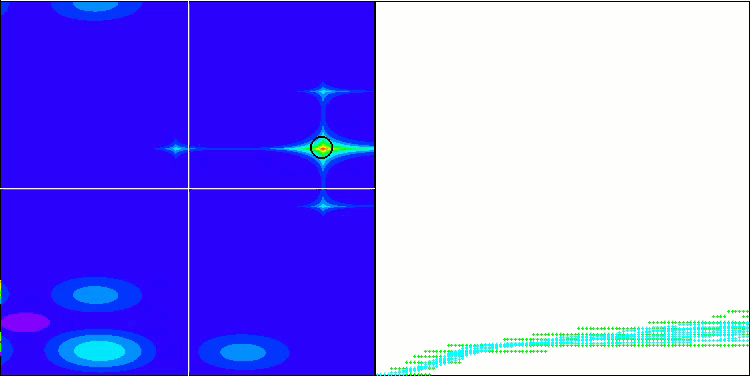
(PO)ES mit Megacity

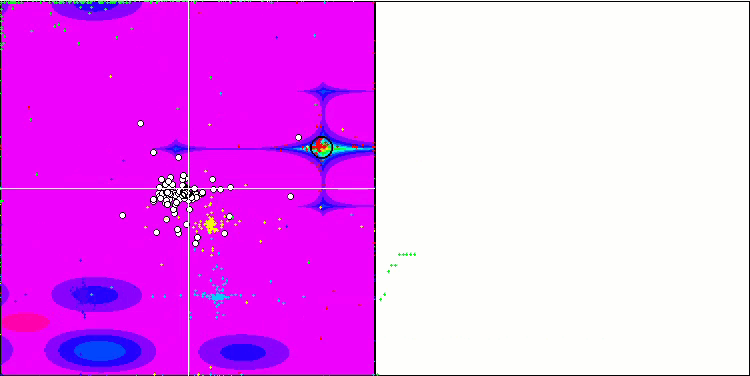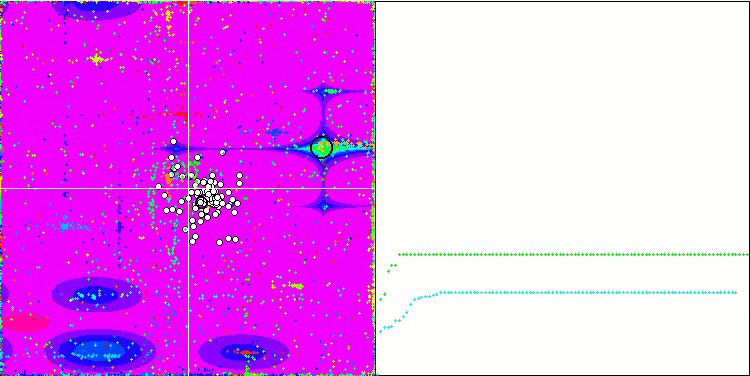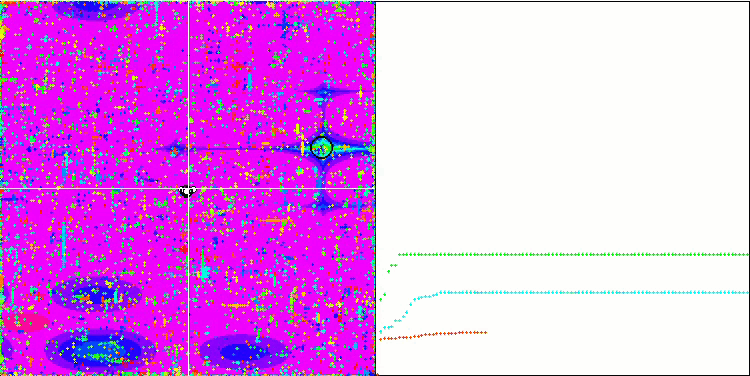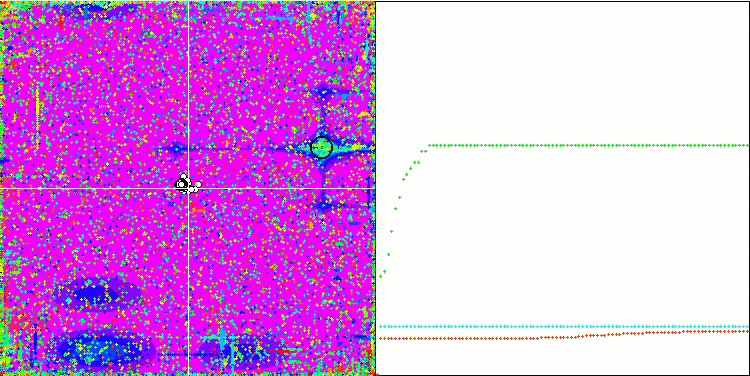
SDOm mit Megacity

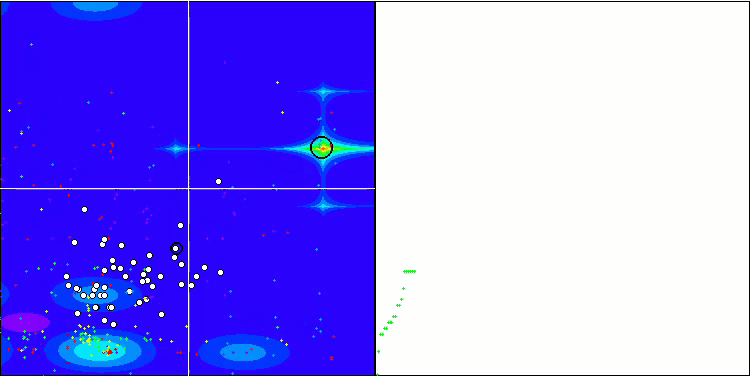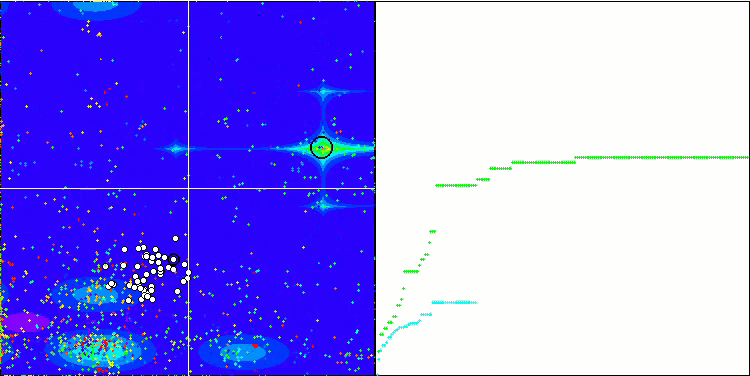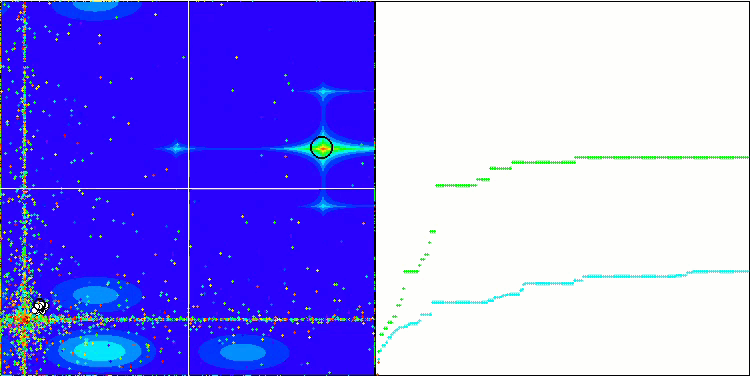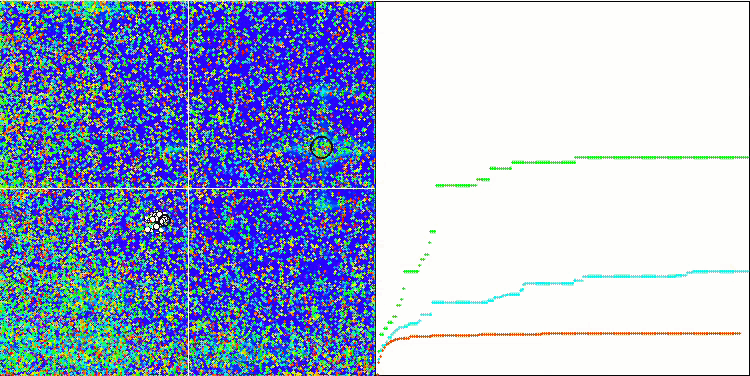
BFO_GA mit Megacity

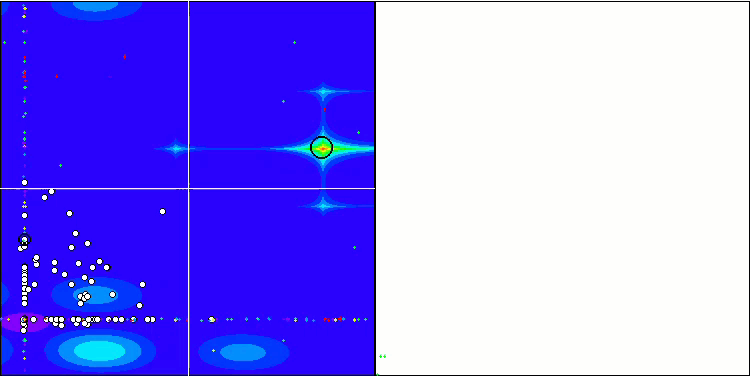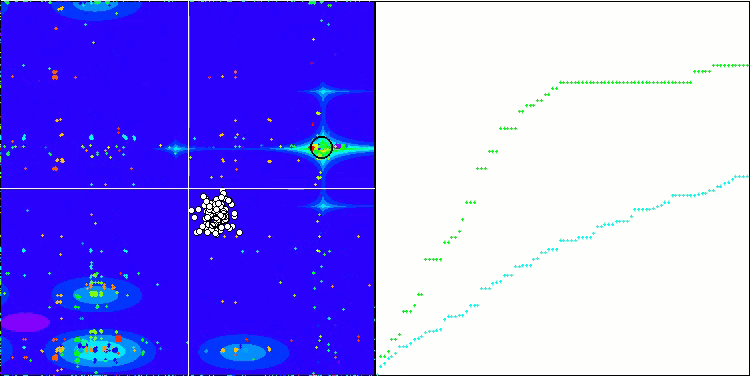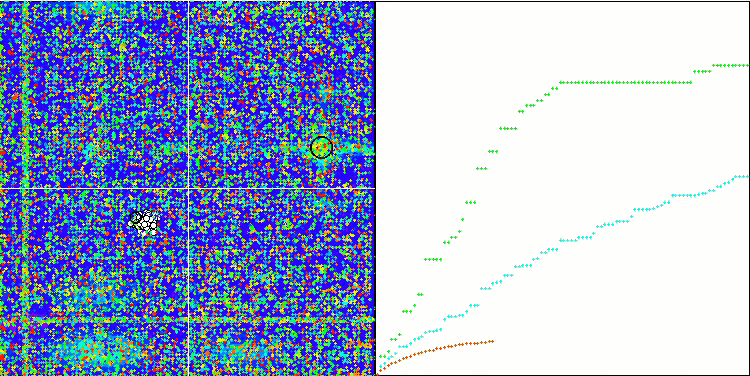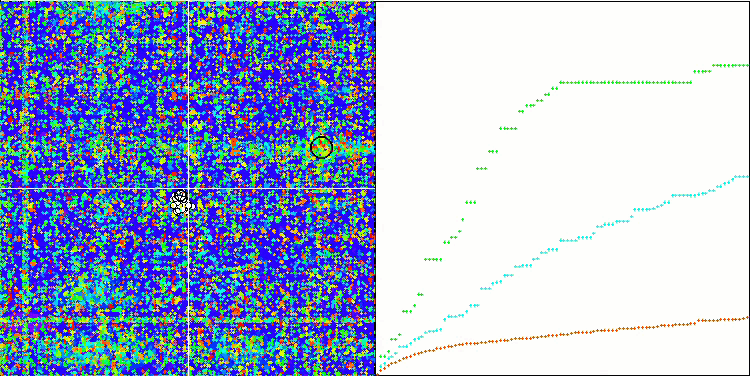
SDSm mit Megacity

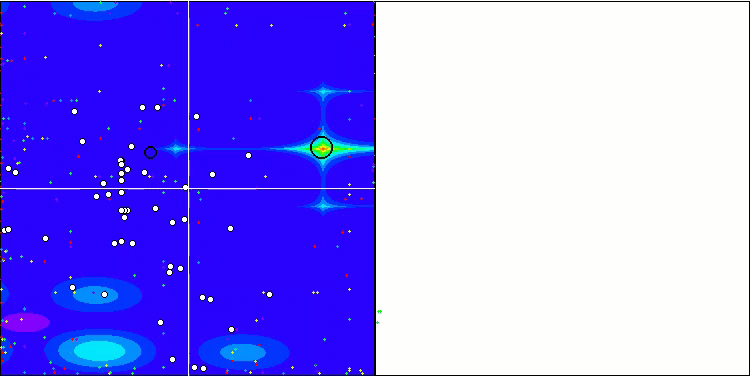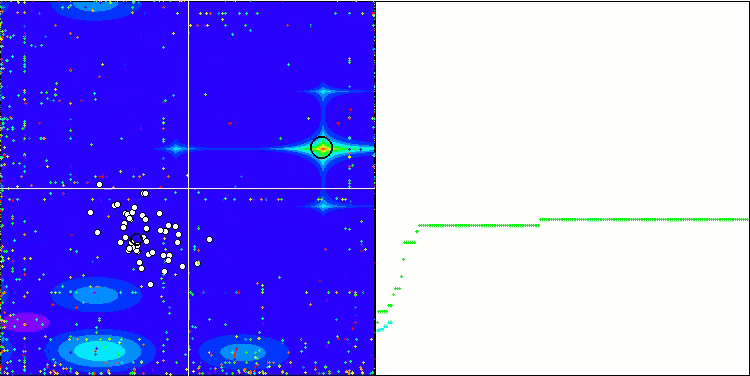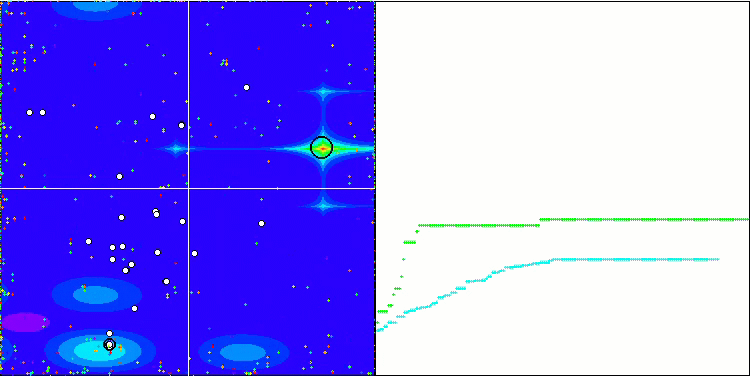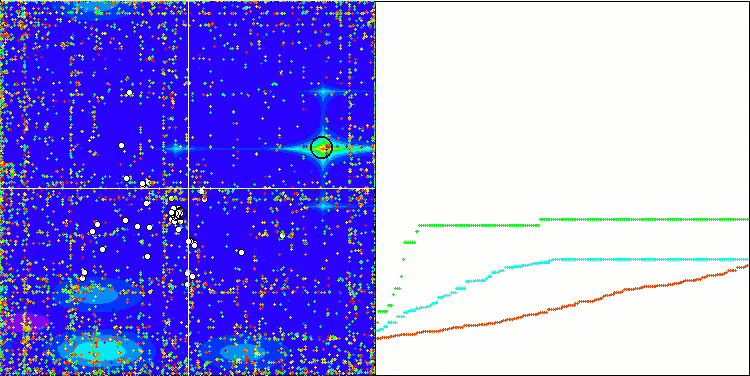
BGA mit Megacity

Nachfolgend finden Sie die abschließende Vergleichstabelle, in der die Arbeit der einzelnen Algorithmen mit den Testfunktionen im Detail dargestellt ist.

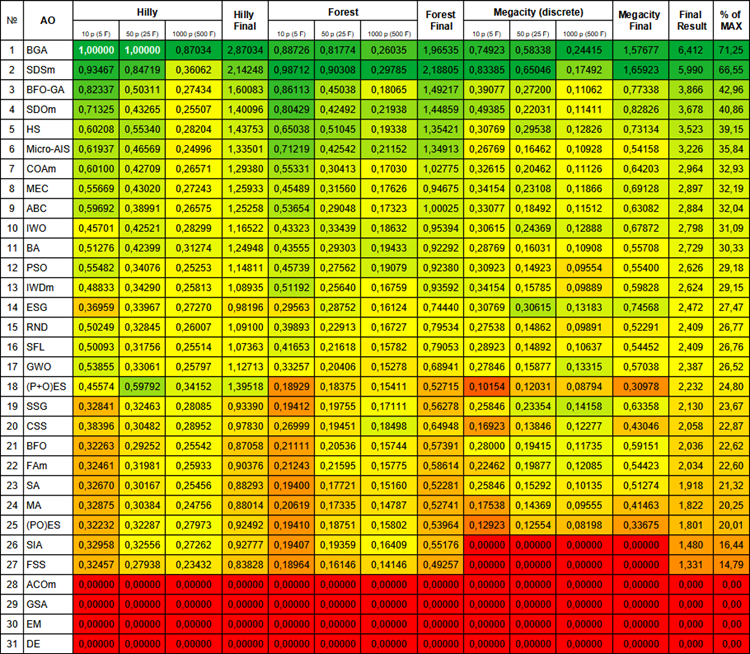
Abbildung 1. Farbliche Abstufung der Algorithmen nach relevanten Tests Ergebnisse größer oder gleich 0,99 sind weiß hervorgehoben

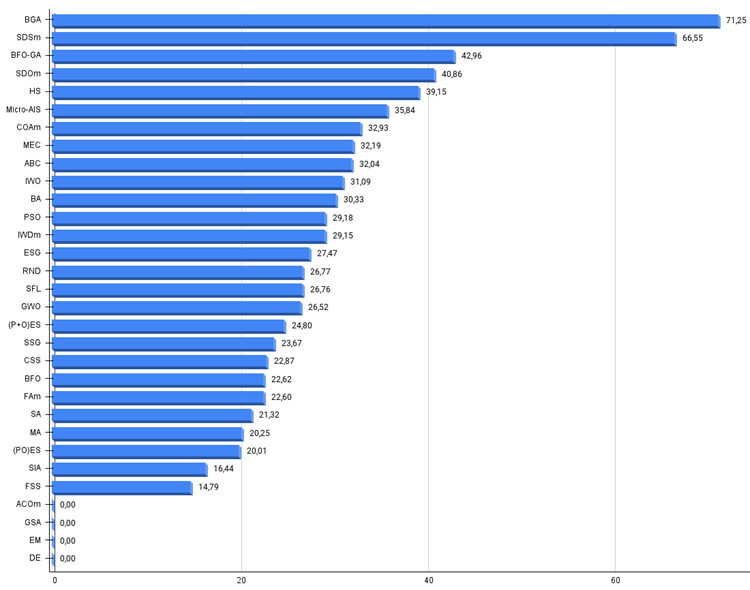
Bild 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, größer ist besser,

wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)

Abschließend möchte ich ausdrücklich betonen, dass alle Schlussfolgerungen und Beurteilungen für jeden Algorithmus ausschließlich im Rahmen des Experiments getroffen wurden.

Die gesamte Diskussion und Analyse des Verhaltens der Populationsoptimierungsalgorithmen legt nahe, dass der Erfolg der Algorithmen stark von den Ausgangsbedingungen ihrer Anwendung abhängt. Bei einigen Methoden, wie DE, EM, GSA, ACOm, können Tests mit einem Ausstieg aus dem Minimalpunkt der Testfunktion so komplex sein, dass sie schon am Anfang zu Schwierigkeiten führen. Gleichzeitig ist die Effizienz bei anderen Unternehmen wie (P+O)ES und ESG (die ursprünglich die Spitzenplätze in der Rangliste belegten, dann aber zu Außenseitern wurden) stark zurückgegangen. Im Gegenteil, durch bewusst gewählte Anfangskoordinaten können die Ergebnisse für Algorithmen wie PSO, GWO, SFL, BA und ABC erheblich verbessert werden. Einige Algorithmen (BFO-GA und SDOm) haben mit diesem Ansatz sogar eine herausragende Leistung gezeigt und übertreffen die zufällige gleichmäßige Initialisierung von Agenten.

Andere Algorithmen wie IWO, HS, SDSm und BGA haben unabhängig von der Ausgangsposition der Agenten universelle Stabilität gezeigt. Bei diesem speziellen Experiment wurde deutlich, dass einige Algorithmen, obwohl sie während des Tests schlecht abschnitten, an bestimmten Punkten des Experiments dennoch beeindruckende Fähigkeiten zeigten. Einige von ihnen haben den Raum schon früh im Prozess erfolgreich erkundet, während andere die Ergebnisse in späteren Phasen deutlich verbessern konnten. Diese einzigartigen Eigenschaften der einzelnen Algorithmen können erfolgreich kombiniert und hybridisiert werden, wodurch ihre positiven Aspekte verstärkt und ihre Nachteile verringert werden, was letztendlich zu effizienteren Optimierungsmethoden führen kann.