Cоздание стратегии возврата к среднему на основе машинного обучения

Введение

В данной статье предлагается очередной оригинальный подход к созданию торговых систем на основе машинного обучения. В предыдущей статье уже были рассмотрены способы применения кластеризации в задаче причинно-следственного вывода. В этой статье кластеризация будет использоваться для разделения финансовых временных рядов на несколько режимов с уникальными свойствами, а потом будет производиться построение и проверка торговых систем на каждом из них.

Кроме этого, мы рассмотрим несколько способов маркировки примеров для стратегий возврата к среднему и протестируем их на валютной паре EURGBP, которая считается флэтовой, а значит, эти стратегии должны быть применимы к ней в полной мере.

По итогу статьи можно будет обучать разные модели машинного обучения на языке Python и конвертировать их в торговые системы для торгового терминала МetaТrader 5.

Подготовка необходимых пакетов

Обучение моделей будет происходить на языке Python, поэтому следует убедиться в наличии следующих установленных пакетов:

import math
import pandas as pd
import pickle
from datetime import datetime
from catboost import CatBoostClassifier

from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans

from bots.botlibs.labeling_lib import *
from bots.botlibs.tester_lib import tester
from bots.botlibs.export_lib import export_model_to_ONNX

Последние 3 модуля написаны мной и будут приложены в конце статьи. В каждом из них могут быть импортированы другие пакеты, такие как Scipy, Numpy, Sklearn, Numba, которые тоже следует установить. Они широко известны и общедоступны, поэтому с их установкой не должно возникнуть никаких проблем.

Если у вас чистая версия Python, то ниже представлен список пакетов, который необходимо будет установить:

pip install numpy
pip install pandas
pip install scipy
pip install scikit-learn
pip install catboost
pip install numba

Также вам может потребоваться использовать абсолютные пути импорта приложенных в конце статьи библиотек, в зависимости от среды разработки и их локации.

Код спроектирован таким образом, что не сильно зависит от версии интерпретатора Python или конкретного пакета, но лучше использовать актуальные стабильные версии.

Как можно делать разметку примеров для стратегий возврата к среднему

Давайте вспомним, как мы размечали метки в предыдущих статьях. Создавался цикл, в котором случайным образом задавалась длительность каждой отдельной сделки, например, от 1 до 15 баров. Затем, в зависимости от того, вырос рынок или упал за это количество баров, прошедших с момента открытия виртуальной сделки, ставилась метка на покупку или продажу. Функция возвращала датафрейм с признаками и размеченными метками, и датасет был уже полностью подготовлен для последующего обучения на нем модели машинного обучения.

def get_labels(dataset, markup, min = 1, max = 15) -> pd.DataFrame:
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'].iloc[i]
        future_pr = dataset['close'].iloc[i + rand]

        if (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
        
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2.0].index)
    return dataset

Но у такой разметки есть один существенный недостаток: она случайная. Размечая данные таким образом, мы не закладываем никакую идею относительно того, какие закономерности должна аппроксимировать модель машинного обучения. Поэтому результат такой разметки и обучения будет тоже, в большей степени, случайным. Мы пытались исправить это за счет множественных обучений методом брутфорс и усложнения самих архитектур алгоритмов, однако сама разметка была все еще бессмысленной. Из-за случайного сэмплинга, только некоторые модели могли пройти OOS (тест на новых данных).

В этой статье я предлагаю новый подход для разметки сделок, основанный на фильтрации исходного временного ряда. Давайте сразу рассмотрим такую разметку на примере.

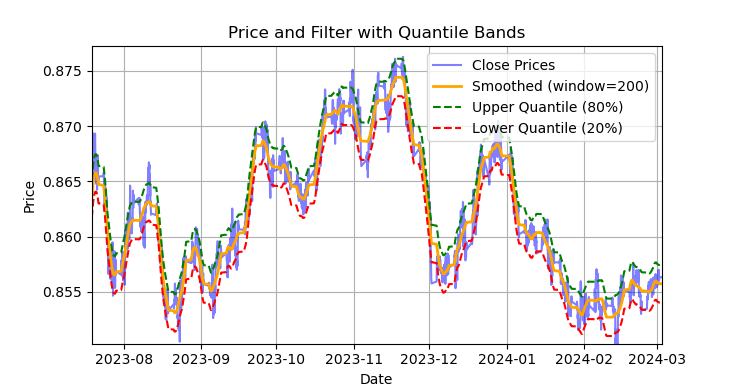
рис. 1  отображение фильтра Савицкого-Голея и лент (квантилей)

На риc. 1 изображена сглаживающая линия фильтра Савицкого-Голея и ленты 20 и 80 квантилей, чем-то напоминающие ленты Боллинджера. Основным отличием фильтра Савицкого-Голея от обычной скользящей средней является то, что он не запаздывает относительно цен. Благодаря такому свойству, фильтр хорошо сглаживает цены, а остаточный "шум" является отклонениями от средних значений (значений самого фильтра), что можно использовать для разработки стратегии возврата к среднему. При пересечении верхней и нижней лент, формируется сигнал на продажу или покупку. Если цена пересекает верхнюю линию, то это сигнал на продажу. Если цена пересекает нижнюю линию, то это сигнал на покупку.

Фильтр Савицкого-Голея — это цифровой фильтр, используемый для сглаживания данных и подавления шума, сохраняя при этом важные особенности сигнала, такие как пики и тренды. Он был предложен Абрахамом Савицким и Марселем Дж. Е. Голеем в 1964 году. Этот фильтр широко применяется в обработке сигналов и анализе данных.

Фильтр Савицкого-Голея работает на основе локальной аппроксимации данных полиномом низкой степени (обычно 2-4 степени) методом наименьших квадратов.  Для каждой точки данных выбирается окрестность (окно), и в пределах этого окна данные аппроксимируются полиномом. После аппроксимации, значение в центральной точке окна заменяется на значение, вычисленное по полиному. Это позволяет сгладить шум, сохраняя при этом форму сигнала.

Ниже представлен код для построения и визуальной оценки фильтра.

def plot_close_filter_quantiles(dataset, rolling=200, quantiles=[0.2, 0.8], polyorder=3):
    # Calculate smoothed prices
    smoothed = savgol_filter(dataset['close'], 
                            window_length=rolling, 
                            polyorder=polyorder)
    
    # Calculate difference between prices and filter
    lvl = dataset['close'] - smoothed
    
    # Get quantile values
    q_low, q_high = lvl.quantile(quantiles).tolist()
    
    # Calculate bands based on quantiles
    upper_band = smoothed + q_high  # Upper band
    lower_band = smoothed + q_low   # Lower band
    
    # Create plot
    plt.figure(figsize=(14, 7))
    plt.plot(dataset.index, dataset['close'], label='Close Prices', color='blue', alpha=0.5)
    plt.plot(dataset.index, smoothed, label=f'Smoothed (window={rolling})', color='orange', linewidth=2)
    plt.plot(dataset.index, upper_band, label=f'Upper Quantile ({quantiles[1]*100:.0f}%)', 
             color='green', linestyle='--')
    plt.plot(dataset.index, lower_band, label=f'Lower Quantile ({quantiles[0]*100:.0f}%)', 
             color='red', linestyle='--')
    
    # Configure display
    plt.title('Price and Filter with Quantile Bands')
    plt.xlabel('Date')
    plt.ylabel('Price')
    plt.legend()
    plt.grid(True)
    plt.show()

Таким образом, ошибочным является применение этого фильтра в режиме онлайн на нестационарных временных рядах, поскольку последние значения могут перерисовываться, но для разметки сделок на уже существующих данных он вполне подходит.

Давайте напишем код, который будет реализовывать разметку обучающих примеров посредством фильтра Савицкого-Голея. Функция разметки, наряду с другими аналогичными функциями, находится в питон-модуле labeling_lib.py, который затем будет импортирован в наш проект.

@njit
def calculate_labels_filter(close, lvl, q):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        curr_lvl = lvl[i]

        if curr_lvl > q[1]:
            labels[i] = 1.0
        elif curr_lvl < q[0]:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:
    """
    Generates labels for a financial dataset based on price deviation from a Savitzky-Golay filter.

    This function applies a Savitzky-Golay filter to the closing prices to generate a smoothed
    price trend. It then calculates trading signals (buy/sell) based on the deviation of the 
    actual price from this smoothed trend. Buy signals are generated when the price is 
    significantly below the smoothed trend, anticipating a potential price reversal. 

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling (int, optional): Window size for the Savitzky-Golay filter. Defaults to 200.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        polyorder (int, optional): Polynomial order for the Savitzky-Golay filter. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - The temporary 'lvl' column is removed. 
    """

    # Calculate smoothed prices using the Savitzky-Golay filter
    smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=polyorder)
    
    # Calculate the difference between the actual closing prices and the smoothed prices
    diff = dataset['close'] - smoothed_prices
    dataset['lvl'] = diff  # Add the difference as a new column 'lvl' to the DataFrame
    
    # Remove any rows with NaN values 
    dataset = dataset.dropna()
    
    # Calculate the quantiles of the 'lvl' column (price deviation)
    q = dataset['lvl'].quantile(quantiles).to_list() 

    # Extract the closing prices and the calculated 'lvl' values as NumPy arrays
    close = dataset['close'].values
    lvl = dataset['lvl'].values
    
    # Calculate buy/sell labels using the 'calculate_labels_filter' function 
    labels = calculate_labels_filter(close, lvl, q) 

    # Trim the dataset to match the length of the calculated labels
    dataset = dataset.iloc[:len(labels)].copy()
    
    # Add the calculated labels as a new 'labels' column to the DataFrame
    dataset['labels'] = labels
    
    # Remove any rows with NaN values
    dataset = dataset.dropna()
    
    # Remove rows where the 'labels' column has a value of 2.0 (no signals)
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)
    
    # Return the modified DataFrame with the 'lvl' column removed
    return dataset.drop(columns=['lvl']) 

Для ускорения процесса разметки используется пакет Numba, который был рассмотрен в предыдущей статье.

Функция get_labels_filter() принимает исходный датасет с ценами и построенными по ним признаками, длину окна аппроксиммации для фильтра, границы нижнего и верхнего квантилей и степень полинома. На выходе эта функция добавляет метки на покупку или продажу к исходному датасету, который затем можно использовать в качестве обучающего.

Цикл прохода по истории реализован в отдельной функции calc_labels_filter, которая выполняет тяжелые расчеты посредством пакета Numba.

У такой разметки есть свои особенности:

• не все размеченные сделки приносят прибыль, поскольку дальнейшее изменение цен, после пересечения с лентами, не всегда идут в противоположном напрвлении. Поэтом могут возникнуть примеры, ложно помеченные как покупка или продажа.
• этот недостаток, в теории, компенсируется тем, что разметка является однородной и неслучайной, а поэтому ложно помеченные примеры можно рассматривать как ошибки обучения или торговой системы в целом, что может давать меньшее переобучение на выходе.

Полное описание логики разметки сделок представлено ниже:

Функция calculate_labels_filter

Входные данные:

• close: массив цен закрытия
• lvl: массив отклонений цены от сглаженного тренда
• q: массив квантилей, определяющих зоны сигналов

Логика:

1. Инициализация: Создаем пустой массив labels той же длины, что и close, для хранения сигналов.

2. Цикл по ценам: Для каждой цены close[i] и соответствующего отклонения lvl[i]:

• Сигнал "Sell": Если отклонение lvl[i] больше верхнего квантиля q[1], то цена находится значительно выше сглаженного тренда, что указывает на сигнал "Sell" (labels[i] = 1.0).
• Сигнал "Buy": Если отклонение lvl[i] меньше нижнего квантиля q[0], то цена находится значительно ниже сглаженного тренда, что указывает на сигнал "Buy" (labels[i] = 0.0).
• Нет сигнала: В остальных случаях (отклонение находится между квантилями), сигнал не генерируется (labels[i] = 2.0).

3. Возврат результата: Возвращаем массив labels с сигналами.

Функция get_labels_filter

Входные данные:

• dataset: DataFrame с финансовыми данными, содержащий столбец 'close' (цены закрытия)
• rolling: размер окна для сглаживания фильтра Savitzky-Golay
• quantiles: квантили для определения зон сигналов
• polyorder: порядок полинома для сглаживания Savitzky-Golay

Логика:

1. Сглаживание цены:

• Вычисляем сглаженные цены smoothed_prices с помощью фильтра Savitzky-Golay, применяемого к ценам закрытия (dataset['close']).

2. Расчет отклонения:

• Вычисляем разницу (diff) между фактическими ценами закрытия и сглаженными ценами.
• Добавляем разницу как новый столбец 'lvl' в DataFrame.

3. Удаление пропусков:

• Удаляем строки с пропущенными значениями (NaN) из DataFrame.

4. Расчет квантилей:

• Вычисляем квантили для столбца 'lvl', которые будут использоваться для определения зон сигналов.

5. Расчет сигналов:

• Вызываем функцию calculate_labels_filter, передавая ей цены закрытия, отклонения и квантили. 
• Получаем массив labels с сигналами.

6. Обработка DataFrame:

• Обрезаем DataFrame до длины массива labels.
• Добавляем массив labels как новый столбец 'labels' в DataFrame.
• Удаляем строки, где 'labels' равно 2.0 (нет сигнала).
• Удаляем временный столбец 'lvl'.

7. Возврат результата: Возвращаем модифицированный DataFrame с сигналами "Buy" и "Sell" в столбце 'labels'.

Вышеприведенный способ разметки будем считать эталоном, посредством которого продемонстрированы основные принципы разметки для стратегии возврата к среднему. Это рабочий метод, который можно использовать. Мы можем обобщить и модифицировать его на случай использования множественных фильтров, а также для учета переменной дисперсии отклонений от среднего значения. Ниже приведена функция get_labels_multiple_filters, которая реализует такие изменения.

@njit
def calc_labels_multiple_filters(close, lvls, qs):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        label_found = False
        
        for j in range(len(lvls)):
            curr_lvl = lvls[j][i]
            curr_q_low = qs[j][0][i]
            curr_q_high = qs[j][1][i]
            
            if curr_lvl > curr_q_high:
                labels[i] = 1.0
                label_found = True
                break
            elif curr_lvl < curr_q_low:
                labels[i] = 0.0
                label_found = True
                break
                
        if not label_found:
            labels[i] = 2.0
            
    return labels

def get_labels_multiple_filters(dataset, 
                              rolling_periods=[200, 400, 600], 
                              quantiles=[.45, .55], 
                              window=100,
                              polyorder=3) -> pd.DataFrame:
    """
    Generates trading signals (buy/sell) based on price deviation from multiple 
    smoothed price trends calculated using a Savitzky-Golay filter with different
    rolling periods and rolling quantiles. 

    This function applies a Savitzky-Golay filter to the closing prices for each 
    specified 'rolling_period'. It then calculates the price deviation from these
    smoothed trends and determines dynamic "reversion zones" using rolling quantiles.
    Buy signals are generated when the price is within these reversion zones 
    across multiple timeframes.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling_periods (list, optional): List of rolling window sizes for the Savitzky-Golay filter. 
                                           Defaults to [200, 400, 600].
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.05, .95].
        window (int, optional): Window size for calculating rolling quantiles. Defaults to 100.
        polyorder (int, optional): Polynomial order for the Savitzky-Golay filter. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed. 
    """
    
    # Create a copy of the dataset to avoid modifying the original
    dataset = dataset.copy()
    
    # Lists to store price deviation levels and quantiles for each rolling period
    all_levels = []
    all_quantiles = []
    
    # Calculate smoothed price trends and rolling quantiles for each rolling period
    for rolling in rolling_periods:
        # Calculate smoothed prices using the Savitzky-Golay filter
        smoothed_prices = savgol_filter(dataset['close'].values, 
                                      window_length=rolling, 
                                      polyorder=polyorder)
        # Calculate the price deviation from the smoothed prices
        diff = dataset['close'] - smoothed_prices
        
        # Create a temporary DataFrame to calculate rolling quantiles
        temp_df = pd.DataFrame({'diff': diff})
        
        # Calculate rolling quantiles for the price deviation
        q_low = temp_df['diff'].rolling(window=window).quantile(quantiles[0])
        q_high = temp_df['diff'].rolling(window=window).quantile(quantiles[1])
        
        # Store the price deviation and quantiles for the current rolling period
        all_levels.append(diff)
        all_quantiles.append([q_low.values, q_high.values])
    
    # Convert lists to NumPy arrays for faster calculations (potentially using Numba)
    lvls_array = np.array(all_levels)
    qs_array = np.array(all_quantiles)
    
    # Calculate buy/sell labels using the 'calc_labels_multiple_filters' function 
    labels = calc_labels_multiple_filters(dataset['close'].values, lvls_array, qs_array)
    
    # Add the calculated labels to the DataFrame
    dataset['labels'] = labels
    
    # Remove rows with NaN values and no signals (labels == 2.0)
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)
    
    # Return the DataFrame with the new 'labels' column
    return dataset

Данная функция способна принимать неограниченное количество параметров сглаживания для фильтра Савицкого-Голея. Это может дать дополнительное преимущество, поскольку в разметке будут участвовать сразу несколько фильтров с разными периодами. Для формирования сигнала достаточно, чтобы отклонения от среднего, на расстояние границ квантилей, сработали хотя бы для одного из фильтров.

Это позволит выстроить иерархическую структуру разметки сделок. Например, сначала проверяется условие для высокочастотного фильтра, затем — для среднечастотного фильтра, а затем — для низкочастотного. Сигналы по низкочастотному фильтру могут считаться более надежными, поэтому предыдущие сигналы будут перезаписаны на сигнал по низкочастотному фильтру, если он возник. Но если низкочастотный фильтр не сгенерировал сигнал, то сделки все равно окажутся размеченными, на основе сигналов предыдущих фильтров. Это способствует увеличению размеченных примеров и позволяет увеличить пороги входов (квантилей), потому что увеличивается шанс на появление хотя бы одного сигнала по набору фильтров.

Расчет квантилей теперь производится в скользящем окне с настраиваемым периодом, что позволяет учитывать переменную дисперсию отклонений от среднего, для более аккуратных сигналов.

Наконец, можно рассмотреть случай для несимметричных сделок, исходя из предположения, что для разметки на покупку и продажу, ввиду скоса среднего котировок, могут потребоваться фильтры с разными периодами сглаживания. Такой подход реализован в функции get_labels_filter_bidirectional.

@njit
def calc_labels_bidirectional(close, lvl1, lvl2, q1, q2):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        curr_lvl1 = lvl1[i]
        curr_lvl2 = lvl2[i]

        if curr_lvl1 > q1[1]:
            labels[i] = 1.0
        elif curr_lvl2 < q2[0]:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_filter_bidirectional(dataset, rolling1=200, rolling2=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:
    """
    Generates trading labels based on price deviation from two Savitzky-Golay filters applied
    in opposite directions (forward and reversed) to the closing price data.

    This function calculates trading signals (buy/sell) based on the price's 
    position relative to smoothed price trends generated by two Savitzky-Golay filters 
    with potentially different window sizes (`rolling1`, `rolling2`). 

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling1 (int, optional): Window size for the first Savitzky-Golay filter. Defaults to 200.
        rolling2 (int, optional): Window size for the second Savitzky-Golay filter. Defaults to 200.
        quantiles (list, optional): Quantiles to define the "reversion zones". Defaults to [.45, .55].
        polyorder (int, optional): Polynomial order for both Savitzky-Golay filters. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - Temporary 'lvl1' and 'lvl2' columns are removed.
    """

    # Apply the first Savitzky-Golay filter (forward direction)
    smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling1, polyorder=polyorder)
    
    # Apply the second Savitzky-Golay filter (could be in reverse direction if rolling2 is negative)
    smoothed_prices2 = savgol_filter(dataset['close'].values, window_length=rolling2, polyorder=polyorder)

    # Calculate price deviations from both smoothed price series
    diff1 = dataset['close'] - smoothed_prices
    diff2 = dataset['close'] - smoothed_prices2

    # Add price deviations as new columns to the DataFrame
    dataset['lvl1'] = diff1
    dataset['lvl2'] = diff2
    
    # Remove rows with NaN values 
    dataset = dataset.dropna()

    # Calculate quantiles for the "reversion zones" for both price deviation series
    q1 = dataset['lvl1'].quantile(quantiles).to_list()
    q2 = dataset['lvl2'].quantile(quantiles).to_list()

    # Extract relevant data for label calculation
    close = dataset['close'].values
    lvl1 = dataset['lvl1'].values
    lvl2 = dataset['lvl2'].values
    
    # Calculate buy/sell labels using the 'calc_labels_bidirectional' function
    labels = calc_labels_bidirectional(close, lvl1, lvl2, q1, q2)

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove bad signals (if any)
    
    # Return the DataFrame with temporary columns removed
    return dataset.drop(columns=['lvl1', 'lvl2']) 

Данная функция принимает периоды сглаживания rolling1 и rolling2, которые соответствуют сделкам на продажу и на покупку. Варьируя эти параметры, можно попытаться добиться более качественной разметки и обобщающей способности на новых данных. Например, если валютная пара имеет восходящий тренд и более предпочтительно открывать сделки на покупку, то можно увеличить длину окна roling1 для разметки сделок на продажу, и их станет меньше, либо они будут возникать только в моменты действительно сильных разворотов тренда. А для сделок на покупку можно уменьшить длину окна roling2, тогда сделок на покупку станет больше, чем сделок на продажу.

Разметка с ограничением на строго прибыльные сделки и с выбором фильтра

Выше было упомянуто, что предложенные разметчики сделок допускают наличие размеченных, заведомо убыточных сделок. Это не является багом, скорее особенностью.

Можно добавить проверки, благодаря которым будут размечаться только прибыльные сделки. Это может быть полезно в том случае, если есть необходимость приблизить график баланса к идеальной прямой, без значительных просадок.

Также использовался всего один фильтр Савицкого-Голея, но хотелось бы увеличить их разнообразие, добавив в качестве фильтров простое скользящее среднее и сплайн.

Давайте рассмотрим варианты таких сэмплеров сделок. За базис возьмем функцию get_labels_mean_reversion, которая предусматривает ограничения на прибыльность и выбор фильтра.

@njit
def calculate_labels_mean_reversion(close, lvl, markup, min_l, max_l, q):
    labels = np.empty(len(close) - max_l, dtype=np.float64)
    for i in range(len(close) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close[i]
        curr_lvl = lvl[i]
        future_pr = close[i + rand]

        if curr_lvl > q[1] and (future_pr + markup) < curr_pr:
            labels[i] = 1.0
        elif curr_lvl < q[0] and (future_pr - markup) > curr_pr:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0) -> pd.DataFrame:
    """
    Generates labels for a financial dataset based on mean reversion principles.

    This function calculates trading signals (buy/sell) based on the deviation of
    the price from a chosen moving average or smoothing method. It identifies
    potential buy opportunities when the price deviates significantly below its 
    smoothed trend, anticipating a reversion to the mean.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        rolling (float, optional): Rolling window size for smoothing/averaging. 
                                     If method='spline', this controls the spline smoothing factor.
                                     Defaults to 0.5.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        method (str, optional): Method for calculating the price deviation:
                                 - 'mean': Deviation from the rolling mean.
                                 - 'spline': Deviation from a smoothed spline.
                                 - 'savgol': Deviation from a Savitzky-Golay filter.
                                 Defaults to 'spline'.
        shift (int, optional): Shift the smoothed price data forward (positive) or backward (negative).
                                 Useful for creating a lag/lead effect. Defaults to 0.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - The temporary 'lvl' column is removed. 
    """

    # Calculate the price deviation ('lvl') based on the chosen method
    if method == 'mean':
        dataset['lvl'] = (dataset['close'] - dataset['close'].rolling(rolling).mean())
    elif method == 'spline':
        x = np.array(range(dataset.shape[0]))
        y = dataset['close'].values
        spl = UnivariateSpline(x, y, k=3, s=rolling) 
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))
        yHat_shifted = np.roll(yHat, shift=shift) # Apply the shift
        dataset['lvl'] = dataset['close'] - yHat_shifted
        dataset = dataset.dropna()  # Remove NaN values potentially introduced by spline/shift
    elif method == 'savgol':
        smoothed_prices = savgol_filter(dataset['close'].values, window_length=int(rolling), polyorder=3)
        dataset['lvl'] = dataset['close'] - smoothed_prices

    dataset = dataset.dropna()  # Remove NaN values before proceeding
    q = dataset['lvl'].quantile(quantiles).to_list()  # Calculate quantiles for the 'reversion zone'

    # Prepare data for label calculation
    close = dataset['close'].values
    lvl = dataset['lvl'].values
    
    # Calculate buy/sell labels 
    labels = calculate_labels_mean_reversion(close, lvl, markup, min_l, max_l, q) 

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)  # Remove sell signals (if any)
    return dataset.drop(columns=['lvl'])  # Remove the temporary 'lvl' column 

В качестве проверки прибыльности сделок и за ее основу, взят код из функции get_labels, которая была рассмотрена в начале раздела и использовалась в прошлых статьях. По этому принципу отбираются сделки, которые прошли через разметку с помощью фильтра. Выбираются только те сделки, которые, на заданное количество шагов вперед, приносят прибыль, иначе — размечаются как 2.0 и затем удаляются из датасета. Также добавлены два новых фильтра: скользящее среднее и сплайн.

Если простое скользящее широко известно в кругах трейдеров, то способ построения сплайна знаком не всем, и его следует раскрыть.

Сплайны — это гибкий инструмент для аппроксимации (приближения) функций. Вместо того, чтобы строить один сложный полином для всей функции, сплайны разбивают область определения на интервалы и строят отдельные полиномы на каждом интервале. Эти полиномы гладко соединяются на границах интервалов, создавая непрерывную и гладкую кривую.

Существуют разные типы сплайнов, но все они строятся по похожему принципу:

1. Разбиение области определения: исходный интервал, на котором определена функция, разбивается на подынтервалы точками, называемыми узлами.
2. Выбор степени полинома: определяется степень полинома, который будет использоваться на каждом подынтервале. 
3. Построение полиномов: на каждом подынтервале строится полином выбранной степени, который проходит через точки данных на этом интервале.
4. Обеспечение гладкости: коэффициенты полиномов подбираются таким образом, чтобы обеспечить гладкость сплайна на границах интервалов. Обычно это означает, что значения соседних полиномов и их производных должны совпадать в узлах.

Сплайны могут быть полезны при анализе финансовых временных рядов для:

• Интерполяции и сглаживания данных: сплайны позволяют сгладить шум в данных и оценить значения временного ряда в точках, где измерения отсутствуют. 
• Моделирования трендов: сплайны могут использоваться для моделирования долгосрочных тенденций в данных, отделяя их от краткосрочных колебаний.
• Прогнозирования: некоторые типы сплайнов могут быть использованы для прогнозирования будущих значений временного ряда.
• Оценки производных: сплайны позволяют оценить производные временного ряда, что может быть полезно для анализа скорости изменения цен.

В нашем случае, мы будем сглаживать временной ряд сплайном и скользящем средним точно так же, как это делалось с помощью фильтра Савицкого-Голея. Можно произвести разметку с использованием каждого фильтра по отдельности, а затем сравнить результаты и выбрать лучший, для данной конкретной ситуации.

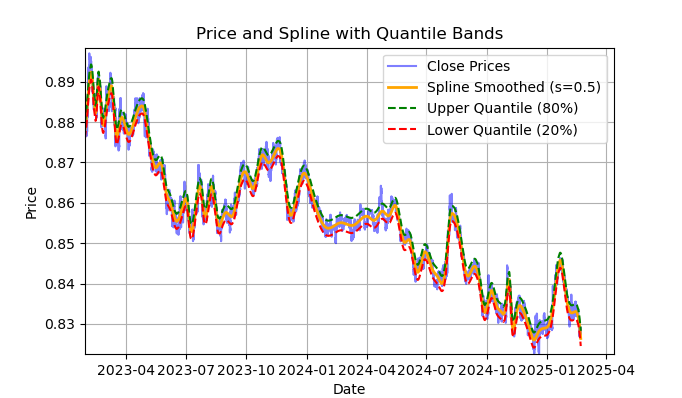
рис. 2  отображение фильтра spline и лент (квантилей)

На риc. 2 изображена сглаживающая линия фильтра spline и ленты 20 и 80 квантилей. Основным отличием фильтра spline от фильтра Савицкого-Голея является то, что он сглаживает ряд посредством кусочно-линейных или нелинейных функций, в зависимости от сглаживающего фактора s, который лучше задавать в пределах 0.1;1 и от степени полинома, которая обычно задается в пределах от 1 до 3. Варьируя эти параметры, вы можете визуально оценить отличия полученного сглаживания. В коде степень полинома k=3 фиксирована, ее тоже можно изменять.

Код для построения и визуальной оценки сплайна выглядит следующим образом:

import pandas as pd
from scipy.interpolate import UnivariateSpline
import matplotlib.pyplot as plt

def plot_close_filter_quantiles(dataset, rolling=200, quantiles=[0.2, 0.8]):
    """
    Plots close prices with spline smoothing and quantile bands.

    Args:
        dataset (pd.DataFrame): DataFrame with 'close' column and datetime index.
        rolling (int, optional): Rolling window size for spline smoothing. 
                                  Defaults to 200.
        quantiles (list, optional): Quantiles for band calculation. 
                                     Defaults to [0.2, 0.8].
        s (float, optional): Smoothing factor for UnivariateSpline. 
                             Adjusts the spline stiffness. Defaults to 1000.
    """
    
    # Create spline smoothing
    # Convert datetime index to numerical values (Unix timestamps)
    numerical_index = pd.to_numeric(dataset.index)
    
    # Create spline smoothing using the numerical index
    spline = UnivariateSpline(numerical_index, dataset['close'], k=3, s=rolling)  
    smoothed = spline(numerical_index)
    
    # Calculate difference between prices and filter
    lvl = dataset['close'] - smoothed
    
    # Get quantile values
    q_low, q_high = lvl.quantile(quantiles).tolist()
    
    # Calculate bands based on quantiles
    upper_band = smoothed + q_high
    lower_band = smoothed + q_low
    
    # Create plot
    plt.figure(figsize=(14, 7))
    plt.plot(dataset.index, dataset['close'], label='Close Prices', color='blue', alpha=0.5)
    plt.plot(dataset.index, smoothed, label=f'Spline Smoothed (s={rolling})', color='orange', linewidth=2)
    plt.plot(dataset.index, upper_band, label=f'Upper Quantile ({quantiles[1]*100:.0f}%)', 
             color='green', linestyle='--')
    plt.plot(dataset.index, lower_band, label=f'Lower Quantile ({quantiles[0]*100:.0f}%)', 
             color='red', linestyle='--')
    
    # Configure display
    plt.title('Price and Spline with Quantile Bands')
    plt.xlabel('Date')
    plt.ylabel('Price')
    plt.legend()
    plt.grid(True)
    plt.show()

Подробное описание всей функции calculate_labels_mean_reversion, для полного понимания кода разметки сделок, представлено ниже.

Функция calculate_labels_mean_reversion:

Входные данные:

• close: массив цен закрытия
• lvl: массив отклонений цен от сглаженного ряда
• markup: наценка (в процентах)
• min_l: минимальное количество свечей для проверки условия
• max_l: максимальное количество свечей для проверки условия
• массив квантилей, определяющих зоны сигналов

Логика:

1. Инициализация: Создаем пустой массив labels длиной len(close) — max_l для хранения сигналов. Длина сокращена, чтобы учесть будущие значения цен. 

2. Цикл по ценам: Для каждой цены close[i] с индексом i от 0 до len(close) — max_l - 1:

• Определяем случайное число rand между min_l и max_l.
• Получаем текущую цену curr_pr, текущее отклонение curr_lvl и будущую цену future_pr на rand свечей вперед. 
• Сигнал "Sell": Если curr_lvl больше верхнего квантиля (q[1]) и будущая цена future_pr с учетом наценки markup меньше текущей цены, устанавливаем labels[i] = 1.0.
• Сигнал "Buy": Если curr_lvl меньше нижнего квантиля (q[0]) и будущая цена future_pr с учетом вычета наценки markup больше текущей цены, устанавливаем labels[i] = 0.0.
• Нет сигнала: В остальных случаях устанавливаем labels[i] = 2.0.

3. Возврат результата: Возвращаем массив labels с сигналами.

Функция get_labels_mean_reversion:

Входные данные:

• dataset: DataFrame с финансовыми данными, содержащий столбец 'close'
• markup: наценка (в процентах)
• min_l: минимальное количество свечей для проверки условия
• max_l: максимальное количество свечей для проверки условия
• rolling: параметр сглаживания (размер окна или коэффициент)
• quantiles: квантили для определения зон сигналов
• method: метод сглаживания ('mean', 'spline', 'savgol')
• shift: сдвиг сглаженного ряда

Логика:

1. Расчет отклонений: Вычисляем отклонения lvl от сглаженного ряда цен (close) в зависимости от выбранного метода method:

• mean: отклонение от скользящего среднего 
• spline: отклонение от сглаженной сплайном кривой
• savgol: отклонение от сглаженного фильтра Савицкого-Голея

2. Удаление пропусков: удаляем строки с пропусками (NaN) из dataset.

3. Расчет квантилей: вычисляем квантили q для отклонений lvl.

4. Подготовка данных: извлекаем массивы цен close и отклонений lvl из dataset.

5. Расчет сигналов:

• Вызываем функцию calculate_labels_mean_reversion с подготовленными данными, чтобы получить массив labels с сигналами.

6. Обработка DataFrame:

• Обрезаем dataset до длины labels.
• Добавляем labels как новый столбец 'labels' в dataset.
• Удаляем строки с пропусками (NaN) из dataset.
• Удаляем строки, где labels равно 2.0 (нет сигнала).
• Удаляем столбец lvl.

7. Возврат результата: Возвращаем модифицированный dataset с сигналами "Buy" и "Sell" в столбце 'labels'

Для разнообразия, давайте реализуем вариант такого же сэмплера, который проверяет условия по нескольким фильтрам с разными периодами, а не только по одному. Если все условия по всем фильтрам выполнены и они имеют одинаковое направление (покупка или продажа), а также сделка является прибыльной на промежутке n баров в будущее, то она удовлетворяет условиям разметки, иначе — игнорируется и удаляется из обучающей выборки.

@njit
def calculate_labels_mean_reversion_multi(close_data, lvl_data, q, markup, min_l, max_l, windows):
    labels = []
    for i in range(len(close_data) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close_data[i]
        future_pr = close_data[i + rand]

        buy_condition = True
        sell_condition = True
        qq = 0
        for rolling in windows:
            curr_lvl = lvl_data[i, qq]            
            if not (curr_lvl >= q[qq][1]):
                sell_condition = False
            if not (curr_lvl <= q[qq][0]):
                buy_condition = False
            qq+=1
    
        if sell_condition and (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif buy_condition and (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
    return labels

def get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55]):
    """
    Generates labels for a financial dataset based on mean reversion 
    principles using multiple smoothing windows.

    This function calculates trading signals (buy/sell) based on the deviation 
    of the price from smoothed price trends calculated using multiple spline 
    smoothing factors (windows). It identifies potential buy opportunities when 
    the price deviates significantly below its smoothed trends across multiple
    timeframes.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        windows (list, optional): List of smoothing factors (rolling window equivalents) 
                                   for spline calculations. Defaults to [0.2, 0.3, 0.5].
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (sell signal) are removed.
                       - Rows with missing values (NaN) are removed. 
    """

    q = []  # Initialize an empty list to store quantiles for each window
    lvl_data = np.empty((dataset.shape[0], len(windows)))  # Initialize a 2D array to store price deviation data

    # Calculate price deviation from smoothed trends for each window
    for i, rolling in enumerate(windows):
        x = np.array(range(dataset.shape[0]))  # Create an array of x-values (time index)
        y = dataset['close'].values  # Extract closing prices
        spl = UnivariateSpline(x, y, k=3, s=rolling)  # Create a spline smoothing function
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))  # Generate smoothed price data
        lvl_data[:, i] = dataset['close'] - yHat  # Calculate price deviation from smoothed prices
        q.append(np.quantile(lvl_data[:, i], quantiles).tolist())  # Calculate and store quantiles

    dataset = dataset.dropna()  # Remove NaN values before proceeding

    close_data = dataset['close'].values  # Extract closing prices 

    # Calculate buy/hold labels using multiple price deviation series
    labels = calculate_labels_mean_reversion_multi(close_data, lvl_data, q, markup, min_l, max_l, windows)

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()  # Trim the dataset to match label length
    dataset['labels'] = labels  # Add the calculated labels as a new column
    dataset = dataset.dropna()  # Remove rows with NaN values
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)  # Remove sell signals (if any)
    
    return dataset

Наконец, давайте напишем еще одну функцию разметки сделок для возврата к среднему, которая вычисляет квантили в скользящем окне с заданным периодом, а не за всю историю наблюдений. Это поможет сгладить влияние переменной волатильности в отклонении цен от среднего значения.

@njit
def calculate_labels_mean_reversion_v(close_data, lvl_data, volatility_group, quantile_groups, markup, min_l, max_l):
    labels = []
    for i in range(len(close_data) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close_data[i]
        curr_lvl = lvl_data[i]
        curr_vol_group = volatility_group[i]
        future_pr = close_data[i + rand]

        q = quantile_groups[curr_vol_group]

        if curr_lvl > q[1] and (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif curr_lvl < q[0] and (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
    return labels

def get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=1, volatility_window=20) -> pd.DataFrame:
    """
    Generates trading labels based on mean reversion principles, incorporating
    volatility-based adjustments to identify buy opportunities.

    This function calculates trading signals (buy/sell), taking into account the 
    volatility of the asset. It groups the data into volatility bands and calculates 
    quantiles for each band. This allows for more dynamic "reversion zones" that 
    adjust to changing market conditions.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        rolling (float, optional): Rolling window size or spline smoothing factor (see 'method'). 
                                     Defaults to 0.5.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        method (str, optional): Method for calculating the price deviation:
                                 - 'mean': Deviation from the rolling mean.
                                 - 'spline': Deviation from a smoothed spline.
                                 - 'savgol': Deviation from a Savitzky-Golay filter.
                                 Defaults to 'spline'.
        shift (int, optional): Shift the smoothed price data (lag/lead effect). Defaults to 1.
        volatility_window (int, optional): Window size for calculating volatility. Defaults to 20.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - Temporary 'lvl', 'volatility', 'volatility_group' columns are removed.
    """

    # Calculate Volatility
    dataset['volatility'] = dataset['close'].pct_change().rolling(window=volatility_window).std()
    
    # Divide into 20 groups by volatility 
    dataset['volatility_group'] = pd.qcut(dataset['volatility'], q=20, labels=False)
    
    # Calculate price deviation ('lvl') based on the chosen method
    if method == 'mean':
        dataset['lvl'] = (dataset['close'] - dataset['close'].rolling(rolling).mean())
    elif method == 'spline':
        x = np.array(range(dataset.shape[0]))
        y = dataset['close'].values
        spl = UnivariateSpline(x, y, k=3, s=rolling)
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))
        yHat_shifted = np.roll(yHat, shift=shift) # Apply the shift 
        dataset['lvl'] = dataset['close'] - yHat_shifted
        dataset = dataset.dropna() 
    elif method == 'savgol':
        smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=5)
        dataset['lvl'] = dataset['close'] - smoothed_prices

    dataset = dataset.dropna()
    
    # Calculate quantiles for each volatility group
    quantile_groups = {}
    for group in range(20):
        group_data = dataset[dataset['volatility_group'] == group]['lvl']
        quantile_groups[group] = group_data.quantile(quantiles).to_list()
    
    # Prepare data for label calculation (potentially using Numba)
    close_data = dataset['close'].values
    lvl_data = dataset['lvl'].values
    volatility_group = dataset['volatility_group'].values

    # Calculate buy/sell labels 
    labels = calculate_labels_mean_reversion_v(close_data, lvl_data, volatility_group, quantile_groups, markup, min_l, max_l)
    
    # Process dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove sell signals
    
    # Remove temporary columns and return
    return dataset.drop(columns=['lvl', 'volatility', 'volatility_group'])

Таким образом, у нас уже есть некоторое количество разметчиков сделок, с которыми можно экспериментировать. Подходы можно комбинировать и создавать новые.

Полный список описанных выше сэмплеров сделок из библиотеки labeling_lib.py представлен ниже. На их базе можно модифицировать старые и создавать новые, в зависимости от того, насколько хорошо вы понимаете рыночные закономерности и какую стратегию хотите иметь на выходе. Модуль содержит и другие кастомные сэмплеры сделок, но они не относятся к стратегиям возврата к среднему, поэтому не описаны в данной статье.

# FILTERING BASED LABELING W/O RESTRICTIONS
def get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame
def get_labels_multiple_filters(dataset, rolling_periods=[200, 400, 600], quantiles=[.45, .55], window=100, polyorder=3) -> pd.DataFrame
def get_labels_filter_bidirectional(dataset, rolling1=200, rolling2=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:

# MEAN REVERSION WITH RESTRICTIONS BASED LABELING
def get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0) -> pd.DataFrame
def get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55]) -> pd.DataFrame
def get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=1, volatility_window=20) -> pd.DataFrame:

Настало время перейти ко второй части статьи, а именно к кластеризации рыночных режимов, а затем объединить оба подхода для создания торговых систем, торгующих по принципу возврата к среднему.

Что кластеризовать и зачем это нужно

Прежде чем что-то кластеризовать, необходимо определиться, зачем это вообще нужно. Представим себе график котировок, на котором есть тренд, флэт, периоды высокой и низкой волатильности, различные паттерны и другие особенности. То есть график котировок не является чем-то однородным, где присутствуют одни и те же закономерности. Можно даже сказать, что в разные периоды времени существуют или могут существовать разные закономерности, которые пропадают на других временных промежутках.

Кластеризация позволяет разделить исходный временной ряд на несколько состояний по определенным признакам, чтобы каждое из этих состояний описывало похожие наблюдения. Это может облегчить задачу построения торговой системы, ведь обучение будет происходить на более однородных, похожих данных. По крайней мере, так это можно себе представлять. Естественно, что торговая система будет работать уже не на всем историческом периоде, а на какой-то выбранной его части, составленной из разных моментов времени, значения признаков которых попадают в данный конкретный кластер.

После кластеризации, можно сделать разметку только выбранных примеров, то есть, присвоить им уникальные метки классов, для построения финальной модели. Если кластер содержит однородные данные с похожими наблюдениями, то и их разметка должна стать более однородной и, впоследствии, более предсказуемой. Можно взять несколько кластеров данных, разметить каждый из них отдельно, затем обучить модели машинного обучения на данных каждого кластера и проверить их на обучающих и тестовых данных. Если будет найден кластер, который позволяет модели хорошо обучаться, то есть, обобщать и предсказывать на новых данных, задачу построения торговой системы можно считать практически выполненной.

Кластеризация финансовых временных рядов для определения рыночных режимов

Перед началом прочтения данного раздела, полезно ознакомиться с различными видами алгоритмов кластеризации, которые были описаны в предыдущей статье. Также там приведена сравнительная таблица различных алгоритмов кластеризации и результаты их тестирования. Для этой статьи выбран классический алгоритм кластеризации k-means, как наиболее быстрый и достаточно эффективный.

На этапе создания признаков посредством функции get_features, нам необходимо предусмотреть возможность наличия в датасете именно тех признаков, по которым будет проводиться кластеризация. Я предлагаю рассмотреть три базовых варианта, от которых можно отталкиваться. Если у вас есть какие-то другие признаки, которые, как вы считаете, хорошо описывают рыночные режимы, вы можете смело их использовать. Для этого необходимо добавить их расчет в функцию формирования признаков, и они должны содержать символы "meta_feature" в своем названии, для их дальнейшего отделения от основных признаков.

def get_features(data: pd.DataFrame) -> pd.DataFrame:
    pFixed = data.copy()
    pFixedC = data.copy()
    count = 0

    for i in hyper_params['periods']:
        pFixed[str(count)] = pFixedC.rolling(i).mean()
        count += 1
    
    for i in hyper_params['periods_meta']:
        pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).skew()
        count += 1

    # for i in hyper_params['periods_meta']:
    #     pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).std()
    #     count += 1

    # for i in hyper_params['periods_meta']:
    #     pFixed[str(count)+'meta_feature'] = pFixedC - pFixedC.rolling(i).mean()
    #     count += 1

    return pFixed.dropna()

В первом цикле идет расчет всех признаков, заданных в списке 'periods'. Это основные признаки, которые будут использоваться для обучения основной модели машинного обучения, которая предсказывает сделки на покупку или продажу. В данном случае, это простые скользящие средние с разными периодами.

Во втором цикле рассчитываются признаки, которые заданы в списке 'periods_meta'. Это именно те признаки, которые будут участвовать в процессе кластеризации рыночных режимов. По умолчанию кластеризация будет рассчитана по скосу котировок в скользящем окне. Закомментированные поля соответствуют расчету признаков по стандартному отклонению в скользящем окне, либо по ценовым приращениям. Выбор признаков осуществляется эмпирическим образом, через перебор различных вариантов. Эксперименты показали, что кластеризация по скосу (асимметрии) хорошо разделяет данные, поэтому в статье будет использована именно она.

Скос (или асимметрия) в распределениях — это характеристика, которая описывает степень несимметричности распределения данных относительно его среднего значения. Скос показывает, насколько распределение отклоняется от симметричного (например, от нормального распределения).  Скос измеряется с помощью коэффициента асимметрии (skewness). Кластеризация по скосу позволяет выделить группы данных с похожими характеристиками распределения, что помогает идентифицировать эти режимы. Например, положительный скос может указывать на периоды с редкими, но сильными скачками цен (например, во время кризисов), а отрицательный — на периоды с более плавными изменениями.

После формирования признаков, итоговый датасет передается в функцию, которая выполняет кластеризацию. И добавляет к нему новый столбец "clusters", который содержит номера кластеров.

def clustering(dataset, n_clusters: int) -> pd.DataFrame:
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    meta_X = data.loc[:, data.columns.str.contains('meta_feature')]
    data['clusters'] = KMeans(n_clusters=n_clusters).fit(meta_X).labels_
    return data

Чтобы исключить подглядывание, данные обрезаются до и после установленных в настройках алгоритма дат, чтобы кластеризация проводилась только на тех данных, которые будут участвовать в процессе обучения модели. В коде также присутствует выбор признаков для кластеризации, которые отбираются по ключевому слову 'meta_feature' в названии столбца признака.

Все гиперпараметры алгоритма вынесены в словарь, данные из которого будут использоваться при составлении признаков, выборе периода обучения и прочего.

hyper_params = {
    'symbol': 'EURGBP_H1',
    'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files/MetaTrader 5/MQL5/Include/Mean reversion/',
    # 'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files (x86)/RoboForex MT4 Terminal/MQL4/Include/',
    'model_number': 0,
    'markup': 0.00010,
    'stop_loss':  0.02000,
    'take_profit': 0.00200,
    'periods': [i for i in range(5, 300, 30)],
    'periods_meta': [10],
    'backward': datetime(2000, 1, 1),
    'forward': datetime(2021, 1, 1),
    'n_clusters': 10,
    'rolling': 200,
}

• Название файла на диске, который содержит котировки символа
• Путь экспорта для экспорта обученных моделей в каталог #include терминала MetaTrader5
• Идентификационный номер модели, чтобы отличать их после экспорта, когда есть необходимость экспортировать множество моделей
• Маркап, который должен учитывать средний спред и комиссию, в пунктах. Для более правильной разметки сделок и последующего тестирования на истории.
• Стоп-лосс, который поддерживается быстрым кастомным тестером
• Тэйк-профит
• Список периодов для расчета основных признаков. Каждый отдельный элемент списка представляет собой период для отдельного признака. Чем больше элементов, тем больше признаков.
• Список периодов для признаков, которые участвуют в кластеризации.
• Начальная дата обучения модели
• Конечная дата обучения модели
• Количество кластеров (режимов), на которые будут разделяться данные
• Параметр скользящего окна для сглаживания фильтром

Теперь давайте соберем все вместе, посмотрим на основной цикл обучения моделей и разберем все этапы как препроцессинга, так и непосредственно обучения.

# LEARNING LOOP
dataset = get_features(get_prices())
models = []
for i in range(1):
    data = clustering(dataset, n_clusters=hyper_params['n_clusters'])
    sorted_clusters = data['clusters'].unique()
    sorted_clusters.sort()
    for clust in sorted_clusters:
        clustered_data = data[data['clusters'] == clust].copy()
        if len(clustered_data) < 500:
            print('too few samples: {}'.format(len(clustered_data)))
            continue
    
        clustered_data = get_labels_filter(clustered_data, 
                                           rolling=hyper_params['rolling'],
                                           quantiles=[0.45, 0.55],
                                           polyorder=3
                                            )

        print(f'Iteration: {i}, Cluster: {clust}')
        clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)

        meta_data = data.copy()
        meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))

Сначала создается датасет, который содержит цены и признаки. Процесс создания признаков был описан выше. Затем создается список models, который будет хранить уже обученные модели. Далее у нас есть выбор: сколько итераций обучений будет произведено в цикле. По умолчанию — одна итерация. Если необходимо обучение множества моделей, то задать их количество в итераторе range(). 

После этого происходит кластеризация исходного датасета, и каждому примеру назначается номер кластера. Если в гиперпараметрах задано 10 n_clusters, то этот параметр передается в функцию, и происходит кластеризация на 10 кластеров. Эксперименты показали, что 10 кластеров — это оптимальное количество рыночных режимов, но, конечно, можно эксперементировать с этим параметром. 

Далее определяется итоговое количество кластеров, их порядковые номера сортируются по возрастанию, и затем, для каждого номера кластера, выбираются только те строки из датасета, которые ему соответствуют. Нас не интересуют кластеры, в которых оказалось слишком мало наблюдений, поэтому делаем проверку, чтобы примеров было не меньше 500.

На следующем этапе происходит вызов функции разметки сделок для текущего выбранного кластера. В данном случае я взял самую первую функцию разметки get_labels_filter, с рассмотрения которой началась эта статья. После разметки сделок данные разделяются на два датасета. Первый датасет будет содержать основные признаки и метки, а второй будет содержать мета-признаки, по которым делалась кластеризация, а также метки 0 и 1. Единица означает, что данные соответствуют выбранному кластеру, а нули означают, что это любой другой кластер, кроме выбранного. Ведь мы хотим, чтобы торговая система торговала только в конкретном рыночном режиме.

Таким образом, первая модель будет учиться предсказывать направление сделки, а вторая модель будет предсказывать, когда их можно открывать, а когда не стоит.

Давайте теперь расcмотрим саму функцию fit_final_models, которая принимает два датасета для двух финальных моделей и производит на них обучение алгоритма CatBoost.

def fit_final_models(clustered, meta) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = clustered[clustered.columns[:-1]], meta[meta.columns[:-1]]
    X = X.loc[:, ~X.columns.str.contains('meta_feature')]
    X_meta = X_meta.loc[:, X_meta.columns.str.contains('meta_feature')]
    
    # labels for model\meta models
    y = clustered['labels']
    y_meta = meta['clusters']
    
    y = y.astype('int16')
    y_meta = y_meta.astype('int16')

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.7, test_size=0.3, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.7, test_size=0.3, shuffle=True)


    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=1000,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=False,
                               task_type='CPU',
                               thread_count=-1)
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=30, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=500,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU',
                                    thread_count=-1)
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=25, plot=False)

    
    R2 = test_model([model, meta_model], hyper_params['stop_loss'], hyper_params['take_profit'])
    if math.isnan(R2):
        R2 = -1.0
        print('R2 is fixed to -1.0')
    print('R2: ' + str(R2))

    return [R2, model, meta_model]

Описание этапов обучения:

1. Подготовка данных:

• Из входных датафреймов clustered и meta выделяются признаки (X, X_meta) и метки (y, y_meta).
• Типы данных меток преобразуются в int16. Это необходимо для бесшовной конвертации модели в ONNX формат.
• Данные разделяются на обучающие и тестовые наборы с помощью train_test_split.

2. Обучение основной модели:

• Создаётся объект CatBoostClassifier с заданными гиперпараметрами.
• Модель обучается на обучающих данных (train_X, train_y) с использованием проверочного набора (test_X, test_y) для ранней остановки.

3. Обучение мета-модели:

• Создаётся объект CatBoostClassifier для мета-модели с заданными гиперпараметрами.
• Мета-модель обучается аналогично основной модели, используя соответствующие обучающие и проверочные данные.

4. Оценка моделей:

• Обученные модели (model, meta_model) передаются в функцию test_model вместе с параметрами stop_loss и take_profit для оценки их производительности.
• Возвращаемое значение R2 представляет собой метрику производительности модели.

5. Обработка R2 и возврат результата:

• Если R2 равно NaN, оно заменяется на -1.0.
• Значение R2 выводится на экран.
• Функция возвращает список, содержащий R2 и обученные модели (model, meta_model). 

Для каждого кластера на выходе получаются две обученные модели-классификатора, готовые к финальному визуальному тестированию и экспорту в терминал MetaTrader 5. Следует помнить, что для каждой итерации обучения создается столько пар моделей, сколько кластеров было задано в гиперпараметрах. Это количество следует умножить на количество итераций, чтобы иметь представление, сколько всего пар моделей получится. Например, задано 10 кластеров и 10 итераций, значит, на выходе будет 100 пар моделей, исключая те, которые не прошли фильтрацию на минимальное количество примеров.

Обучение и тестирование моделей. Проводим тесты нашего алгоритма

Для более удобного использования алгоритма, желательно запускать его в интерактивной среде Python построчно. Тогда можно менять гиперпараметры и экспериментировать с разными сэмплерами. Либо перенести весь код в формат .ipynb для запуска в IPython через ноутбук. Если вы собираетесь запускать скрипт целиком, то вам все равно придется его править для настройки параметров.

Предлагаю протестировать каждую из функций разметки, запустив для каждой 10 итераций. Остальные параметры будут такими же, которые заданы в приложенном скрипте.

После запуска цикла обучения, будут отображаться результаты обучения на каждой итерации для каждого кластера данных.

R2: 0.9815970951474068
Iteration: 9, Cluster: 5
R2: 0.9914890771969395
Iteration: 9, Cluster: 6
R2: 0.9450681335265942
Iteration: 9, Cluster: 7
R2: 0.9631330369697314
Iteration: 9, Cluster: 8
R2: 0.9680380185183347
Iteration: 9, Cluster: 9
R2: 0.8203651933893291

Затем можно отсортировать все результаты по возрастанию R^2, для выбора лучшего из них. И визуально оценить кривую баланса в тестере.

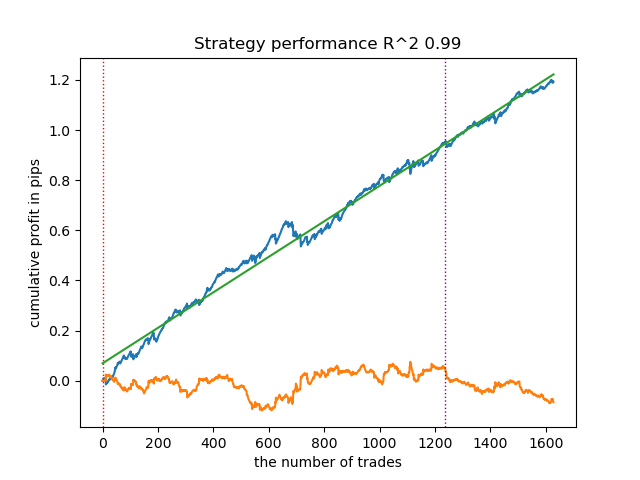
models.sort(key=lambda x: x[0])
test_model(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], plt=True)

Выделенное означает, что будет тестироваться первая модель с конца. То есть, с самым высоким R^2. Чтобы протестировать вторую с конца модель, нужно задать -2 и так далее. Тестер отобразит график баланса (синий) и график валютной пары (оранжевый), а также вертикальную линию, которая разделяет тренировочный период и новые данные. Все модели обучаются с начала 2010 года по начало 2021 года, это задано в гиперпараметрах. Вы можете изменять интервалы обучения и тестирования на свое усмотрение. Тестовый период для всех моделей из этой статьи с начала 2021 года по начало 2025.

Тестируем разные сэмплеры сделок

• get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3)

Ниже представлен лучший результат для разметчика get_labels_filter.

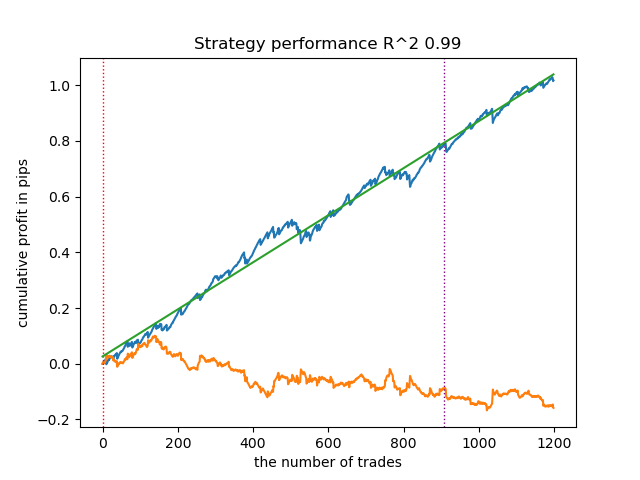
Базовый разметчик неплохо разметил сделки, и все модели оказались прибыльными на новых данных. Проделаем все то же самое для остальных разметчиков и посмотрим на результаты.

• get_labels_multiple_filters(dataset,rolling_periods=[50,100,200],quantiles=[.45,.55],window=100,polyorder=3)

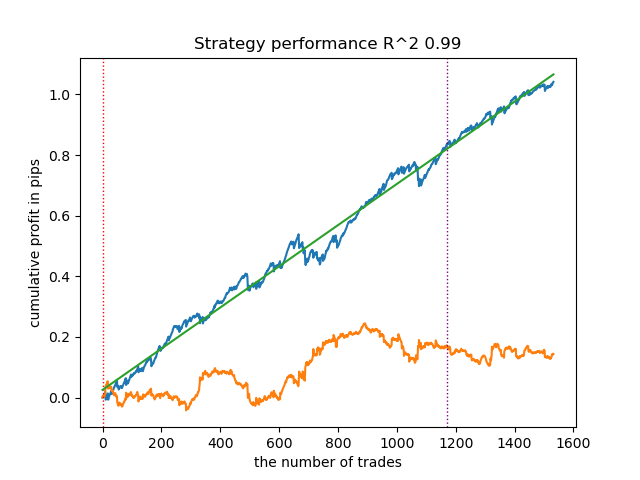
Модели, обученные на данных этого разметчика, часто демонстрируют увеличение количества сделок по отношению к базовому. Здесь я не эксперементировал с настройками, потому что статья оказалась бы слишком длинной.

• get_labels_filter_bidirectional(dataset, rolling1=50, rolling2=200, quantiles=[.45, .55], polyorder=3)

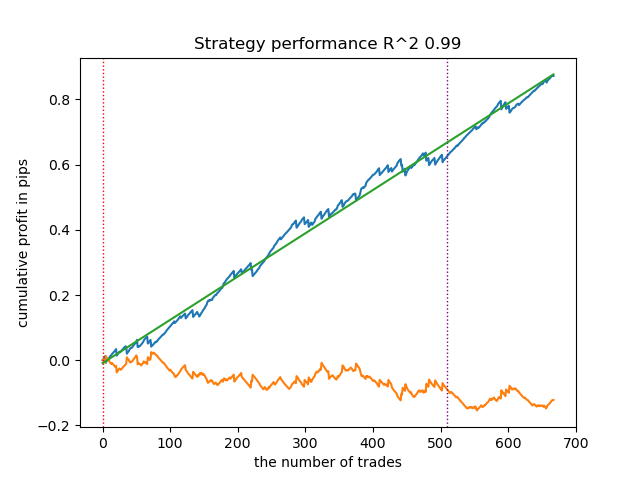
Данный асимметричный разметчик тоже продемонстрировал свою эффективность на новых данных. Подбирая различные параметры сглаживания отдельно для сделок на покупку и продажу, можно достичь оптимального результата.

Теперь перейдем к разметчикам с ограничением на строго прибыльные сделки. Хорошо видно, что предыдущие разметчики не дают ровную кривую баланса даже на обучающем периоде, зато хорошо улавливают общие закономерности. Посмотрим, что изменится, если удалять из обучающего датасета убыточные сделки.

• get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0)

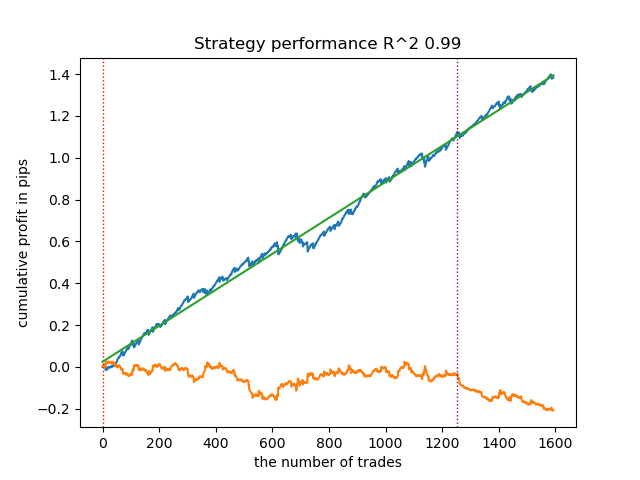
Я протестировал этот разметчик, использовав сплайн в качестве фильтра и с фиксированным сглаживающим фактором 0.5. В статье не приведены тесты для фильтра Савицкого-Голея и простого скользящего среднего. Однако видно, что можно добиться более гладких кривых, используя ограничение на прибыльность сделок.

• get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55])

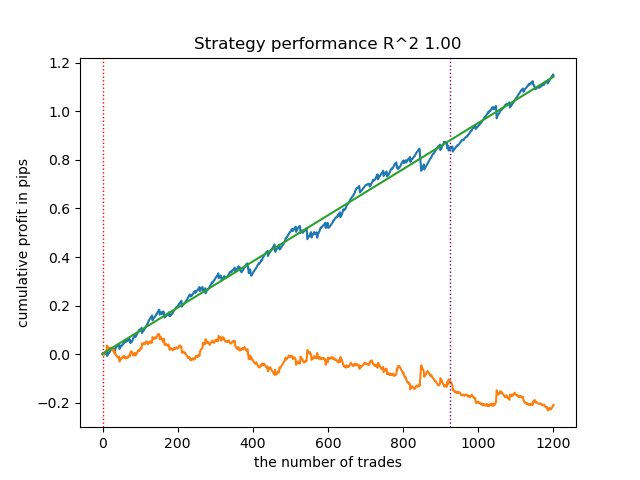
Данный сэмплер тоже способен предоставить качественные выборки, благодаря которым, модель продолжает прибыльно торговать на новых данных.

• get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.2, quantiles=[.45, .55], method='spline', shift=0, volatility_window=20)

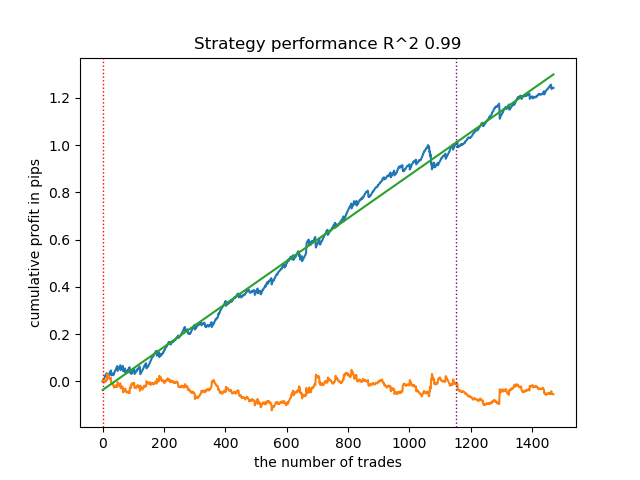
Данный алгоритм тоже способен продемонстрировать приемлемую разметку и хорошие модели на выходе.

Выводы по разметчикам сделок:

• Когда вы не знаете с чего начать, и для вас все это кажется слишком сложным, используйте самый базовый сэмплер, который может дать приемлемый результат.
• Если не получаются красивые картинки сразу, то не забывайте, что в разметке сделок и обучении моделей есть случайные компоненты. Просто перезапустите алгоритм несколько раз.
• Все сэмплеры с базовыми настройками могут выдавать приемлемый результат. Для более тонкой настройки нужно сосредоточиться на одном из них и заняться подбором параметров.

Выводы по кластеризации:

• За кадром были проведены множественные тесты сэмплеров без использования кластеризации, а также кластеризации без использования сэмплеров. Я на практике убедился, что по отдельности эти алгоритмы работают не так хорошо, как в тандеме.
• Не стоит создавать слишком много признаков, по которым будет осуществляться кластеризация. Это усложнит модель и сделает ее менее устойчивой на новых данных.
• Оптимальное количество кластеров находится в диапазоне 5-10. Меньшее количество кластеров приводит к плохой обобщающей способности и плохим результатам на новых данных, тогда как слишком большое количество влечет за собой резкое сокращение количества сделок.

Для удобства использования, в коде раскомментируйте нужный разметчик сделок.

# LEARNING LOOP
dataset = get_features(get_prices())
models = []
for i in range(10):
    data = clustering(dataset, n_clusters=hyper_params['n_clusters'])
    sorted_clusters = data['clusters'].unique()
    sorted_clusters.sort()
    for clust in sorted_clusters:
        clustered_data = data[data['clusters'] == clust].copy()
        if len(clustered_data) < 500:
            print('too few samples: {}'.format(len(clustered_data)))
            continue
    
        clustered_data = get_labels_filter(clustered_data, 
                                           rolling=hyper_params['rolling'],
                                           quantiles=[0.45, 0.55],
                                           polyorder=3
                                            )
        # clustered_data = get_labels_multiple_filters(clustered_data, 
        #                                              rolling_periods=[50, 100, 200], 
        #                                              quantiles=[.45, .55], 
        #                                              window=100, 
        #                                              polyorder=3)
        # clustered_data = get_labels_filter_bidirectional(clustered_data, 
        #                                                  rolling1=50, 
        #                                                  rolling2=200, 
        #                                                  quantiles=[.45, .55], 
        #                                                  polyorder=3)
        # clustered_data = get_labels_mean_reversion(clustered_data,
        #                                             markup = hyper_params['markup'],
        #                                             min_l=1, max_l=15, 
        #                                             rolling=0.5, 
        #                                             quantiles=[.45, .55], 
        #                                             method='spline', shift=0)
        # clustered_data = get_labels_mean_reversion_multi(clustered_data, 
        #                                                  markup = hyper_params['markup'], 
        #                                                  min_l=1, max_l=15, 
        #                                                  windows=[0.2, 0.3, 0.5], 
        #                                                  quantiles=[.45, .55])
        # clustered_data = get_labels_mean_reversion_v(clustered_data,
        #                                             markup = hyper_params['markup'],
        #                                             min_l=1, max_l=15, 
        #                                             rolling=0.2, 
        #                                             quantiles=[.45, .55], 
        #                                             method='spline', 
        #                                             shift=0, 
        #                                             volatility_window=100)

        print(f'Iteration: {i}, Cluster: {clust}')
        clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)

        meta_data = data.copy()
        meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))

# TESTING & EXPORT
models.sort(key=lambda x: x[0])
test_model(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], plt=True)

Экспорт обученных моделей в MetaTrader 5 

Остался предпоследний этап — экспорт обученных моделей и заголовочного файла в ONNX формат. Модуль export_lib.py, прикрепленный в конце статьи, содержит функцию export_model_to_ONNX(**kwargs). Давайте подробно ее рассмотрим.

def export_model_to_ONNX(**kwargs):
    model = kwargs.get('model')
    symbol = kwargs.get('symbol')
    periods = kwargs.get('periods')
    periods_meta = kwargs.get('periods_meta')
    model_number = kwargs.get('model_number')
    export_path = kwargs.get('export_path')

    model[1].save_model(
    export_path +'catmodel ' + symbol + ' ' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'main model',
        'onnx_graph_name': 'CatBoostModel_main'
    },
    pool=None)

    model[2].save_model(
    export_path + 'catmodel_m ' + symbol + ' ' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'meta model',
        'onnx_graph_name': 'CatBoostModel_meta'
    },
    pool=None)
    
    code = '#include <Math\Stat\Math.mqh>'
    code += '\n'
    code += '#resource "catmodel '+ symbol + ' '+str(model_number)+'.onnx" as uchar ExtModel_' + symbol + '_' + str(model_number) + '[]'
    code += '\n'
    code += '#resource "catmodel_m '+ symbol + ' '+str(model_number)+'.onnx" as uchar ExtModel2_' + symbol + '_' + str(model_number) + '[]'
    code += '\n\n'
    code += 'int Periods' + symbol + '_' + str(model_number) + '[' + str(len(periods)) + \
        '] = {' + ','.join(map(str, periods)) + '};'
    code += '\n'
    code += 'int Periods_m' + symbol + '_' + str(model_number) + '[' + str(len(periods_meta)) + \
        '] = {' + ','.join(map(str, periods_meta)) + '};'
    code += '\n\n'

    # get features
    code += 'void fill_arays' + symbol + '_' + str(model_number) + '( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(Periods'+ symbol + '_' + str(model_number) + ')-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_H1,1,Periods' + symbol + '_' + str(model_number) + '[i],pr);\n'
    code += '       ret[0] = MathMean(pr);\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    # get features
    code += 'void fill_arays_m' + symbol + '_' + str(model_number) + '( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(Periods_m' + symbol + '_' + str(model_number) + ')-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_H1,1,Periods_m' + symbol + '_' + str(model_number) + '[i],pr);\n'
    code += '       ret[0] = MathSkewness(pr);\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    file = open(export_path + str(symbol) + ' ONNX include' + ' ' + str(model_number) + '.mqh', "w")
    file.write(code)

    file.close()
    print('The file ' + 'ONNX include' + '.mqh ' + 'has been written to disk')

В функцию нужно передать список аргументов, таких как:

• model = models[-1]— список из двух обученных моделей, который был предварительно заполнен моделями с разных итераций обучения. По аналогии с тестером, -1 индекс будет соответствовать модели с самым высоким R^2, под индексом -2 будет вторая по скору модель и так далее. Если вам понравилась какая-то определенная модель при визуальном тестировании, то при экспорте используйте тот же самый индекс.
• symbol = hyper_params['symbol'] — название символа, например "EURGBP_H1", которое задано в гиперпараметрах. Это название будет добавлено при экспорте моделей, чтобы можно было отличать модели для разных символов.
• periods = hyper_params['periods']— список периодов признаков основной модели.
• periods_meta = hyper_params['periods_meta']  — список периодов признаков дополнительной модели, которая определяет текущий режим рынка.
• model_number = hyper_params['model_number']— номер модели, если вы экспортируете много моделей и не хотите чтобы они перезаписывались. Добавляется к именам моделей.

• export_path = hyper_params['export_path']— путь до include папки терминала или ее подкаталога для сохранения файлов на диск.

Функция сохраняет обе модели в формат .onnx и формирует заголовочный файл, через который происходит вызов этих моделей и расчет признаков для них. Следует учесть, что расчет признаков осуществляется непосредственно в терминале, поэтому необходимо убедиться, что он идентичен их расчету в Python-скрипте. По коду видно, что функция fill_arrays рассчитывает скользящие средние для первой модели, а функция fill_arrays_m рассчитывает скос цен для второй модели. Если вы меняете признаки в Pyhon-скрипте, то измените их расчет в этой функции, либо уже в самом заголовочном файле.

Пример вызова самой функции, для сохранения моделей на диск, показан ниже.

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods_meta'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

Создание торгового бота, который использует ONNX-модели для совершения торговых операций

Предположим, что мы обучили и выбрали визуально понравившуюся модель посредством кастомного тестера, например, следующую:

Теперь необходимо вызвать функцию экспорта в терминал.

После экспорта модели, в папке include/mean reversion/терминала MetaTrader 5 (в моем случае используется подкаталог, чтобы не было путаницы среди прочих моделей) появятся 3 файла:

• catmodel EURGBP_H1 0.onnx  — основная модель, которая дает сигналы на покупку и продажу
• catmodel_m EURGBP_H1 0.onnx  — дополнительная модель, которая разрешает или запрещает торговлю
• EURGBP_H1 ONNX include 0.mqh  — заголовочный файл, в котором осуществляется импорт этих моделей и расчет признаков.

Имена ONNX-моделей всегда начинаются со слова "catmodel", что расшифровывается как catboost model, дальше идет название символа и тфйм-фрейм. Дополнительная модель помечается суффиксом _m от слов meta model. Имя заголовочного файла всегда начинается с торгового символа и заканчивается номером модели, который задается при экспорте, чтобы новые экспортируемые модели не перезаписывали друг друга, если это не требуется.

Рассмотрим содержимое .mqh файла.

#include <Math\Stat\Math.mqh>
#resource "catmodel EURGBP_H1 0.onnx" as uchar ExtModel_EURGBP_H1_0[]
#resource "catmodel_m EURGBP_H1 0.onnx" as uchar ExtModel2_EURGBP_H1_0[]

int PeriodsEURGBP_H1_0[10] = {5,35,65,95,125,155,185,215,245,275};
int Periods_mEURGBP_H1_0[1] = {10};

void fill_araysEURGBP_H1_0( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(PeriodsEURGBP_H1_0)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_H1,1,PeriodsEURGBP_H1_0[i],pr);
       ret[0] = MathMean(pr);
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

void fill_arays_mEURGBP_H1_0( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(Periods_mEURGBP_H1_0)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_H1,1,Periods_mEURGBP_H1_0[i],pr);
       ret[0] = MathSkewness(pr);
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

Сначала подключается библиотека математических вычислений, которая понадобится для расчета среднего и скоса, а также потенциально — для других моментов распределений и прочих математических вычислений, если понадобится изменить расчет признаков. Дальше загружаются наши две ONNX-модели в качестве ресурсов, которые будут использоваться для получения торговых сигналов. После этого объявляются массивы с периодами для расчета признаков, которые будут являться входными данными для основной и мета моделей.

Оставшиеся две функции заполняют массивы значениями признаков. Напомню, что эти файлы создаются при экспорте моделей из Python-скрипта и их не нужно писать каждый раз с нуля. Достаточно просто подключить к торговому эксперту. Это очень удобно в тех случаях, когда вы хотите переобучить модель через какое-то время, то затем просто делаете экспорт в терминал, модель перезаписывается на более свежую, и вы заново компилируете бота, не внося никаких изменений в код. Обилие кода может сначала отпугнуть, но на практике обучение сводится к запуску скрипта и затем компиляции бота, что может занять всего несколько минут времени.

Теперь необходимо создать торгового эксперта, к которому будет подключаться этот заголовочный файл и инициализировать ONNX-модели.

#include <Mean reversion/EURGBP_H1 ONNX include 0.mqh>
#include <Trade\Trade.mqh>
#include <Trade\AccountInfo.mqh>
#property strict
#property copyright "Copyright 2025, Dmitrievsky max."
#property link      "https://www.mql5.com/ru/users/dmitrievsky"
#property version   "1.0"

CTrade mytrade;
CPositionInfo myposition;

input bool Allow_Buy = true;           //Allow BUY
input bool Allow_Sell = true;          //Allow SELL
double main_threshold = 0.5;
double meta_threshold = 0.5;
sinput double   MaximumRisk=0.001;     //Progressive lot coefficient
sinput double   ManualLot=0.01;        //Fixed lot, set 0 if progressive
sinput ulong    OrderMagic = 57633493; //Orders magic
input int max_orders = 3;              //Max positions number
input int orders_time_delay = 5;       //Time delay between positions
input int max_spread = 20;             //Max spread
input int stoploss = 2000;             //Stop loss
input int takeprofit = 200;            //Take profit
input string comment = "mean reversion bot";

static datetime last_time = 0;
#define Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK)
#define Bid SymbolInfoDouble(_Symbol, SYMBOL_BID)


const long  ExtInputShape [] = {1, ArraySize(PeriodsEURGBP_H1_0)};
const long  ExtInputShape2 [] = {1, ArraySize(Periods_mEURGBP_H1_0)};
long     ExtHandle = INVALID_HANDLE, ExtHandle2 = INVALID_HANDLE;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   mytrade.SetExpertMagicNumber(OrderMagic);

   ExtHandle = OnnxCreateFromBuffer(ExtModel_EURGBP_H1_0, ONNX_DEFAULT);
   ExtHandle2 = OnnxCreateFromBuffer(ExtModel2_EURGBP_H1_0, ONNX_DEFAULT);

   if(ExtHandle == INVALID_HANDLE || ExtHandle2 == INVALID_HANDLE)
     {
      Print("OnnxCreateFromBuffer error ", GetLastError());
      return(INIT_FAILED);
     }

   if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape))
     {
      Print("OnnxSetInputShape 1 failed, error ", GetLastError());
      OnnxRelease(ExtHandle);
      return(-1);
     }

   if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape2))
     {
      Print("OnnxSetInputShape 2 failed, error ", GetLastError());
      OnnxRelease(ExtHandle2);
      return(-1);
     }

   const long output_shape[] = {1};
   if(!OnnxSetOutputShape(ExtHandle, 0, output_shape))
     {
      Print("OnnxSetOutputShape 1 error ", GetLastError());
      return(INIT_FAILED);
     }
   if(!OnnxSetOutputShape(ExtHandle2, 0, output_shape))
     {
      Print("OnnxSetOutputShape 2 error ", GetLastError());
      return(INIT_FAILED);
     }

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   OnnxRelease(ExtHandle);
   OnnxRelease(ExtHandle2);
  }

Самое главное — правильно инициализировать размерность входных массивов для каждой модели. Он равняется размеру массива в заголовочном файле, который содержит значения периодов для расчета признаков. Сколько значений периодов, столько и признаков.

Размерность выхода для обеих моделей равна единице.

const long  ExtInputShape [] = {1, ArraySize(PeriodsEURGBP_H1_0)};
const long  ExtInputShape2 [] = {1, ArraySize(Periods_mEURGBP_H1_0)};

Затем присваиваем моделям хэндлы.

ExtHandle = OnnxCreateFromBuffer(ExtModel_EURGBP_H1_0, ONNX_DEFAULT);
ExtHandle2 = OnnxCreateFromBuffer(ExtModel2_EURGBP_H1_0, ONNX_DEFAULT);

И устанавливаем правильную размерность входов и выходов в теле функции инициализации бота.

if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape))
     {
      Print("OnnxSetInputShape 1 failed, error ", GetLastError());
      OnnxRelease(ExtHandle);
      return(-1);
     }

if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape2))
     {
      Print("OnnxSetInputShape 2 failed, error ", GetLastError());
      OnnxRelease(ExtHandle2);
      return(-1);
     }

После удаления бота с графика, модели тоже удаляются.

Бот торгует при открытии каждой новой свечи, для ускорения расчетов. Теперь необходимо рассмотреть способ получения сигналов от наших моделей.

void OnTick()
  {
   if(!isNewBar())
      return;

   double features[], features_m[];
   fill_araysEURGBP_H1_0(features);
   fill_arays_mEURGBP_H1_0(features_m);

   double f[ArraySize(PeriodsEURGBP_H1_0)], f_m[ArraySize(Periods_mEURGBP_H1_0)];

   for(int i = 0; i < ArraySize(PeriodsEURGBP_H1_0); i++)
     {
      f[i] = features[i];
     }

   for(int i = 0; i < ArraySize(Periods_mEURGBP_H1_0); i++)
     {
      f_m[i] = features_m[i];
     }

   static vector out(1), out_meta(1);

   struct output
     {
      long           label[];
      float          proba[];
     };

   output out2[], out2_meta[];
   
   OnnxRun(ExtHandle, ONNX_DEBUG_LOGS, f, out, out2);
   OnnxRun(ExtHandle2, ONNX_DEBUG_LOGS, f_m, out_meta, out2_meta);

   double sig = out2[0].proba[1];
   double meta_sig = out2_meta[0].proba[1];

Очередность получения сигналов от ONNX моделей:

• Создаются два массива features и features_m
• Они заполняются значениями признаков через соответствующие функции fill_arrays.
• Порядок элементов в этих массивах инвертирован относительно того, в каком их должна принимать модель. Поэтому создаются массивы f и f_m и данные перезаписываются в нужном порядке.
• Создаются два вектора out и out_meta, которые сообщают моделям размерности выходных векторов.
• Создается структура output, которая принимает предсказанные метки 0;1 и вероятности. В расчете сигналов используются вероятности. 
• Создаются два экземпляра структуры output out2 и out2_meta для получения сигналов.
• Запускаются модели, в которые передаются признаки и размерности выходных значений, они возвращают предсказания.
• Из экземпляров структур извлекаются предсказания (вероятности).

В заключение осталось рассмотреть логику открытия позиций на основе полученных сигналов. Сигналы на закрытие работают по обратной логике.

// OPEN POSITIONS BY SIGNALS
   if((Ask-Bid < max_spread*_Point) && meta_sig > meta_threshold &&
      AllowTrade(OrderMagic))
      if(countOrders(OrderMagic) < max_orders &&
         CheckMoneyForTrade(_Symbol, LotsOptimized(), ORDER_TYPE_BUY))
        {
         double l = LotsOptimized();
         if(sig < 1-main_threshold && Allow_Buy)
           {
            int res = -1;
            do
              {
               double stop = Bid - stoploss * _Point;
               double take = Ask + takeprofit * _Point;
               res = mytrade.PositionOpen(_Symbol, ORDER_TYPE_BUY, l, Ask, stop, take, comment);
               Sleep(50);
              }
            while(res == -1);
           }
         else
           {
            if(sig > main_threshold && Allow_Sell)
              {
               int res = -1;
               do
                 {
                  double stop = Ask + stoploss * _Point;
                  double take = Bid - takeprofit * _Point;
                  res = mytrade.PositionOpen(_Symbol, ORDER_TYPE_SELL, l, Bid, stop, take, comment);
                  Sleep(50);
                 }
               while(res == -1);
              }
           }
        }

Сначала производится проверка сигнала второй модели. Если вероятность больше 0.5, значит разрешено открытие сделок (рынок находится в нужном режиме). Дальше проверяются условия по основной модели, которая предсказывает вероятность покупки или продажи. Вероятность < 0.5 указывает на покупку, вероятность > 0.5 указывает на продажу. В зависимости от условия, открываются сделки.

Теперь можно скомпилировать бота и проверить его в тестере стратегий.

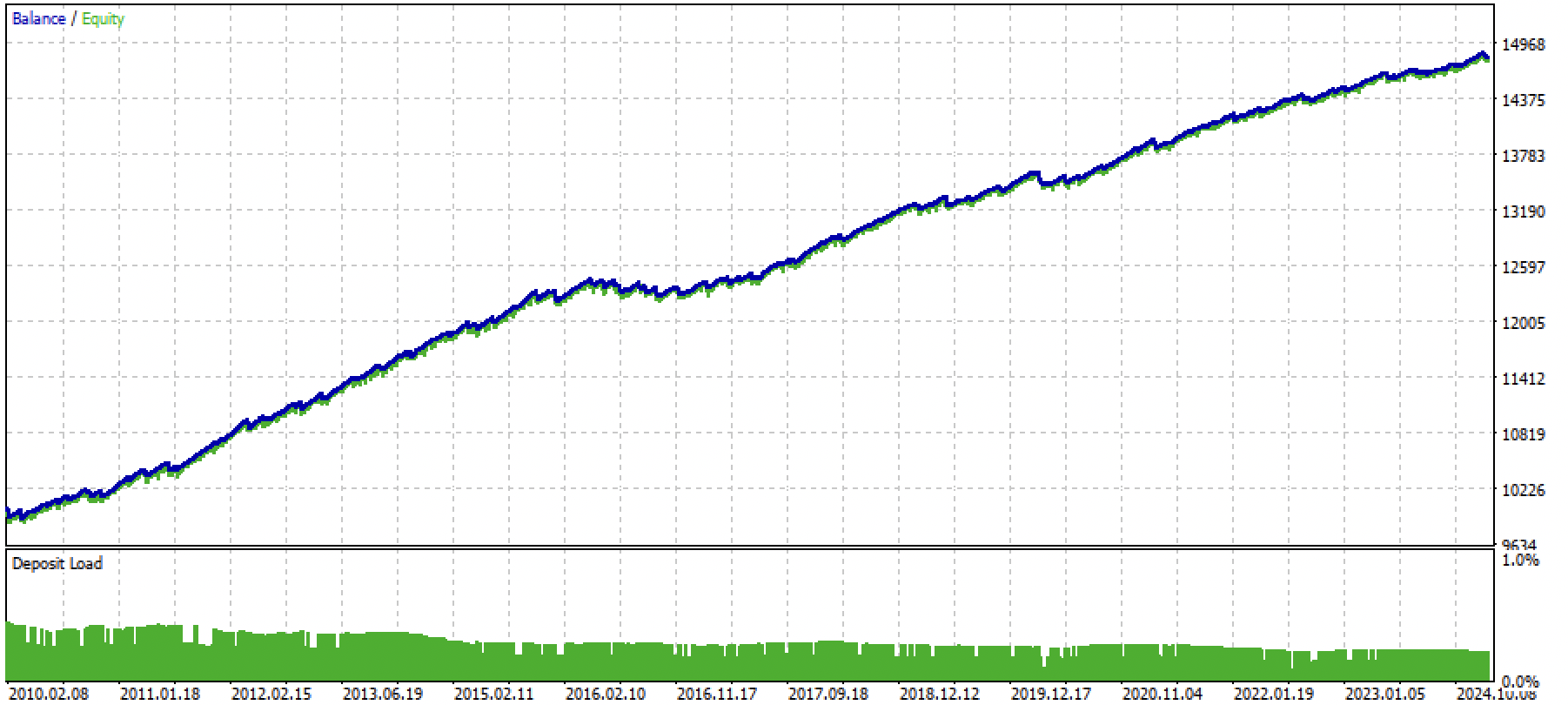
Рис. 3 тестирование обученной модели по стратегии возврата к среднему

Заключение

В данной статье продемонстрированы все этапы разработки стратегии возврата к среднему с применением машинного обучения. В ней изложен комплексный подход: начиная от разметки сделок и определения рыночных режимов, заканчивая обучением моделей и созданием полноценного торгующего бота.

К статье приложены все необходимые коды для самостоятельных экспериментов.

Архив Python files.zip содержит следующие файлы для разработки в среде Python:

Имя файла	Описание
mean reversion.py	Основной скрипт для обучения моделей
labeling_lib.py	Модуль с разметчиками сделок
tester_lib.py	Кастомный тестер стратегий, основанных на машинном обучении
export_lib.py	Библиотека для экспорта моделей в терминал MetaTrader 5 в формате ONNX
EURGBP_H1.csv	Файл с котировками, экспортированный из терминала MetaTrader 5

Архив MQL5 files.zip cодержит файлы для терминала MetaTrader 5:

Имя файла	Описание
mean reversion.ex5	Скомпилированный бот из данной статьи
mean reversion.mq5	Исходник бота из статьи
папка Include//Mean reversion	Расположены модели ONNX и заголовочный файл для подключения к боту