Отбор признаков и снижение размерности с помощью анализа главных компонент (PCA)

Введение

Прогнозирование финансовых временных рядов часто включает в себя анализ многочисленных характеристик, многие из которых могут быть сильно коррелированы. Методы уменьшения размерности, такие как Анализ главных компонент (Principal Component Analysis, PCA), могут помочь создать более компактное представление этих объектов. Однако PCA имеет свои ограничения, особенно при наличии сильно коррелированных переменных. В таких случаях PCA, как правило, демонстрирует группирующий эффект, при котором набор сильно коррелированных переменных в совокупности вносит свой вклад в данный главный компонент. Вместо выделения какой-либо отдельной переменной, PCA распределяет влияние относительно равномерно по всем переменным в коррелированной группе.

Такое равномерное распределение может быть полезным для подавления шума, поскольку главные компоненты подчеркивают общие паттерны, а не случайные колебания, характерные только для отдельных переменных. Однако такое подавление шума обходится дорого: оно часто снижает вклад отдельных переменных в каждый главный компонент. Переменные, которые могли бы быть значимыми сами по себе, могут казаться менее важными в преобразованном пространстве, поскольку их влияние поглощается более широкой структурой, охватываемой группой. Это может быть существенным недостатком в таких задачах, как выбор переменных, где целью является выявление наиболее важных характеристик, или в анализе первопричин, где решающее значение имеет понимание прямого влияния конкретных переменных.

Кроме того, эта характеристика усложняет интерпретацию модели. Поскольку каждый главный компонент представляет собой комбинацию всех исходных переменных, преобразование вклада этих компонентов обратно в контекст исходных переменных может оказаться сложной задачей. Практикующим специалистам может быть трудно получить четкое представление об основных компонентах, поскольку становится трудно определить, какие исходные переменные определяют наблюдаемые паттерны. Чтобы решить эту проблему, мы представляем реализацию Анализа компонентов прямого отбора (FSCA), метода, вдохновленного работой Луки Пуггини и Шона Маклуна, который направлен на то, чтобы избежать ошибок PCA при работе с сильно коррелированными признаками.

Анализ компонентов прямого отбора

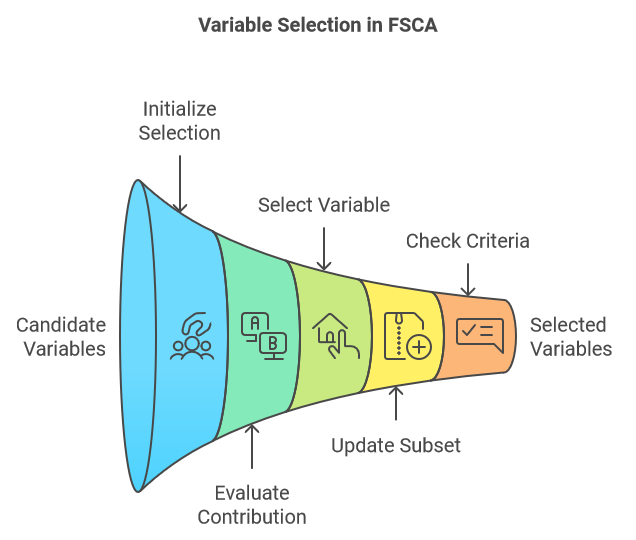
Анализ компонентов прямого отбора (FSCA) это метод уменьшения размерности, сочетающий в себе уменьшение размерности и выбор признаков путем определения наиболее информативных переменных для объяснения исходных данных. FSCA использует жадный подход, выбирая переменные по одной за раз на основе их способности фиксировать оставшуюся дисперсию в данных. Ниже приводится краткое описание основных этапов процедуры FSCA:

1. Инициализация:
   
   • Начнем с пустого набора выбранных переменных и полного набора переменных-кандидатов.
   • Вычислим общую дисперсию набора данных.
   • Начнём итеративный процесс путем выбора переменной, которая наилучшим образом предсказывает значения всех остальных переменных, гарантируя, что этот выбор отражает максимальную величину объясняемой дисперсии.
     
2. Итеративный отбор:
   
   • На каждом шаге оцениваем вклад каждой оставшейся переменной-кандидата в объясняемую дисперсию при добавлении к текущему набору выбранных переменных.
   • Выберем переменную, которая приводит к наибольшему увеличению объясняемой дисперсии при добавлении в подмножество.
     
3. Обновление:
   
   • Добавим отобранную переменную в подмножество выбранных переменных.
   • Удалим отобранную переменную из набора переменных-кандидатов.
   • Повторно вычислим остаточную дисперсию или оставшуюся необъясненную дисперсию после учета вклада отобранных переменных.
     
4. Критерии остановки:
   
   • Продолжаем процесс до тех пор, пока не будет достигнут заданный критерий остановки. Это может быть заданное количество отобранных переменных, целевая доля от общей объясняемой дисперсии или пороговое значение для дополнительной дисперсии, объясняемой добавлением новой переменной.

     
     

Получив набор необработанных переменных, мы упорядочиваем их в виде матрицы, где каждый столбец представляет отдельный признак, а каждая строка - отдельный образец. Исходные значения сначала преобразуются с помощью стандартизации. С этого момента любая ссылка на исходные переменные относится к набору стандартизированных переменных, который мы будем называть матрицей X. Эта матрица X имеет v столбцов (переменных). Алгоритм FSCA генерирует по меньшей мере три новых набора переменных:

• Матрица Z: Эта матрица состоит из подмножества k (где k<v) столбцов X, ранжированных в соответствии с тем, насколько хорошо они влияют на реконструкцию X. Эти столбцы известны как Переменные прямого отбора (FSV).
• Матрица М: Столбцы этой матрицы называются Компоненты прямого отбора (FSC). Каждый компонент является функцией соответствующего столбца в Z, а также тех, которые ему предшествуют, если таковые имеются.
• Матрица U: Эта матрица содержит коэффициенты или нагрузки, которые в сочетании с FSV дают FSC.
  

Цель алгоритма - получить оптимальное подмножество переменных, которые наилучшим образом отражают уникальную вариацию X. Однако это сложная задача оптимизации. FSCA не всегда гарантированно найдет оптимальное подмножество переменных в соответствии с определенными критериями оптимизации. При работе с большими наборами данных поиск по всем возможным подмножествам может оказаться непрактичным, поэтому FSCA предлагает более прагматичный подход. Тем не менее, иногда не удается найти оптимальное подмножество, поскольку переменные, выбранные на ранних итерациях, могут стать избыточными при добавлении дополнительных переменных. Чтобы устранить это ограничение, авторы исследовательской работы, на которую ссылаются в начале этой статьи, предлагают ввести шаг обратного уточнения в процедуре FSCA.

FSCA с обратным уточнением

Обратное уточнение - это процедура, позволяющая удалять и заменять ранее отобранные переменные. Этот процесс включает в себя повторную оценку вклада каждой выбранной переменной в общую объясняемую дисперсию и рассмотрение альтернативных переменных, которые могли бы обеспечить лучшее соответствие. Несмотря на то, что это может улучшить качество конечного набора переменных, при этом нарушается строгий порядок значимости, поддерживаемый чисто прямым отбором.

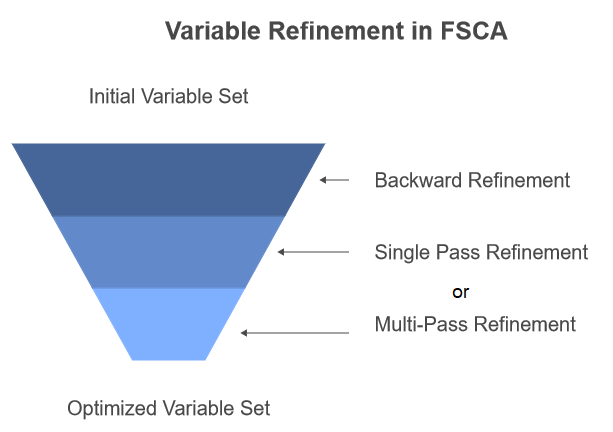
В исследовательской работе описываются два подхода к включению обратного уточнения. При первом подходе применяется обратное уточнение после завершения всех этапов FSCA в качестве этапа последующей обработки. Второй подход, называемый рекурсивным обратным уточнением, предполагает проведение обратного уточнения каждый раз, когда к Z добавляется новая переменная в конце шага 3 алгоритма FSCA. Этот подход реализован в коде, который будет представлен в следующем разделе этого текста.

Существует также два варианта самого этапа уточнения. Первый, называемый Одиночным обратным уточнением (SPBR), последовательно оценивает релевантность каждой переменной, переходя от самой старой к самой новой. Во втором, Многоходовом обратном уточнении (MPBR), признается, что переменные, первоначально считавшиеся релевантными, могут стать нерелевантными по мере внесения корректив в переменные на более поздних этапах последовательности. В MPBR процесс повторяется до тех пор, пока не будет выполнен полный проход без каких-либо дальнейших уточнений. Обратите внимание, что представленный далее в этой статье код реализует только SPBR.

В последующих разделах мы опишем этапы алгоритма FSCA более подробно, используя некоторую математику и код. Все фрагменты кода, на которые даны ссылки, взяты из файла fsca.mqh, который можно найти в приложении в конце этой статьи.

Главные компоненты

Алгоритм FSCA основан на использовании главных компонентов для первоначального определения уникальных источников вариации в наборе данных X. На этом этапе также указывается максимальное количество переменных компонентов для матрицы Z, определяющее значение k (как определено ранее). В исследовательской работе алгоритм использует заданное пользователем значение k. Однако в нашей реализации k всегда устанавливается равным количеству главных компонентов. Главные компоненты получены путем разложения характеристических значений корреляционной матрицы X. В следующем списке показана процедура, которая вычисляет факторную структуру с использованием функции compute_factor_structure().

//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix            compute_factor_structure(matrix &covar,matrix &eigenvectors,vector &eigenvalues,vector &cumeigenvalues)
  {
   if(!covar.EigenSymmetricDC(EIGVALUES_V,eigenvalues,eigenvectors))
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return matrix::Zeros(1,1);
     }
   double sum = 0.0;


   if(!np::reverseVector(eigenvalues) ||  !np::reverseMatrixCols(eigenvectors))
     {
      Print(__FUNCTION__, " reverse operation error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   double cumulate[];
   for(ulong i=0 ; i<eigenvalues.Size() ; i++)
     {
      if(eigenvalues[i]>1.e-8)
        {
         sum += eigenvalues[i] ;
         if(!cumulate.Push(sum))
           {
            Print(__FUNCTION__," error adding element ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }
     }

   if(!cumeigenvalues.Assign(cumulate))
     {
      Print(__FUNCTION__," vector assignment error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   cumeigenvalues/=cumeigenvalues[cumeigenvalues.Size()-1];

   cumeigenvalues*=100.0;

   matrix structmat=eigenvectors;

   for(ulong i = 0; i<structmat.Cols(); i++)
      if(!structmat.Col(eigenvectors.Col(i)*sqrt(eigenvalues[i]>=0.0?eigenvalues[i]:0.0),i))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return matrix::Zeros(1,1);
        }

   if(!structmat.Clip(-1.0,1.0))
     {
      Print(__FUNCTION__, "error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   return structmat;
  }

//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix compute_factor_structure(matrix &covar, matrix &eigenvectors, vector &eigenvalues, vector &cumeigenvalues) {
    if (!covar.EigenSymmetricDC(EIGVALUES_V, eigenvalues, eigenvectors)) {
        Print(__FUNCTION__, " error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double sum = 0.0;

    if (!np::reverseVector(eigenvalues) || !np::reverseMatrixCols(eigenvectors)) {
        Print(__FUNCTION__, " reverse operation error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double cumulate[];
    for (ulong i = 0; i < eigenvalues.Size(); i++) {
        if (eigenvalues[i] > 1.e-8) {
            sum += eigenvalues[i];
            if (!cumulate.Push(sum)) {
                Print(__FUNCTION__, " error adding element ", GetLastError());
                return matrix::Zeros(1, 1);
            }
        }
    }

    if (!cumeigenvalues.Assign(cumulate)) {
        Print(__FUNCTION__, " vector assignment error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    cumeigenvalues /= cumeigenvalues[cumeigenvalues.Size() - 1];
    cumeigenvalues *= 100.0;

    matrix structmat = eigenvectors;

    for (ulong i = 0; i < structmat.Cols(); i++) {
        if (!structmat.Col(eigenvectors.Col(i) * sqrt(eigenvalues[i] >= 0.0 ? eigenvalues[i] : 0.0), i)) {
            Print(__FUNCTION__, "error ", GetLastError());
            return matrix::Zeros(1, 1);
        }
    }

    if (!structmat.Clip(-1.0, 1.0)) {
        Print(__FUNCTION__, "error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    return structmat;
}

Эта функция принимает корреляционную матрицу covar в качестве входных данных и возвращает матрицу, содержащую факторные нагрузки. Она выполняет разложение по характеристическим значениям в отношении корреляционной матрицы с использованием функции EigenSymmetricDC. Результирующие характеристические значения сохраняются в векторе характеристических значений, в то время как собственные векторы сохраняются в матрице собственных векторов. Затем функция изменяет порядок характеристических значений и векторов на противоположный, чтобы обеспечить их сортировку в порядке убывания. Она вычисляет кумулятивные характеристические значения путем их итеративного суммирования и сохраняет их в векторе cumeigenvalues. Совокупные характеристические значения нормализуются, чтобы представлять процент от общей дисперсии.

Далее функция вычисляет коэффициентные нагрузки путем умножения каждого собственного вектора на квадратный корень из соответствующего характеристического значения, сохраняя результат в матрице structmat. Чтобы гарантировать, что коэффициентные нагрузки остаются в разумных пределах, они находятся в диапазоне от -1 до 1. Наконец, функция возвращает структурную матрицу, содержащую рассчитанные факторные нагрузки.

Факторная структура, полученная из корреляционной матрицы, состоит из факторных нагрузок, которые представляют взаимосвязи между переменными и лежащими в их основе скрытыми факторами. Эти нагрузки помогают интерпретировать значение скрытых факторов и оценить важность каждой переменной для объяснения разброса в данных.

Выходные данные функции compute_factor_structure() используются в функции compute_principal_components() для вычисления главных компонентов.

//+------------------------------------------------------------------+
//|   calculates the principal components                            |
//+------------------------------------------------------------------+
matrix compute_principal_components(void) {
    matrix out(m_data.Rows(), ulong(m_num_comps));
    vector drow, eigcol, nv;
    double sum;

    for (ulong i = 0; i < m_data.Rows(); i++) {
        drow = m_data.Row(i);
        for (ulong j = 0; j < m_num_comps; j++) {
            sum = 0.0;
            for (ulong k = 0; k < m_data.Cols(); k++) {
                sum += drow[k] * m_eigvectors[k][j] / sqrt(m_eigvalues[j]);
            }
            out[i][j] = sum;
        }
    }

    return out;
}

Функция compute_principal_components() не принимает входных параметров и возвращает матрицу, содержащую главные компоненты. Для хранения главных компонентов инициализируется выходная матрица out, размеры которой равны количеству рядов во входных данных и количеству желаемых главных компонентов. Функция выполняет итерацию по каждому ряду матрицы входных данных, вычисляя каждый главный компонент путем вычисления скалярного произведения ряда на соответствующий собственный вектор ковариационной матрицы, деленного на квадратный корень из соответствующего характеристического значения. Результирующий главный компонент сохраняется в матрице out. Эта функция вычисляет главные компоненты, используя стандартную формулу для проецирования точек данных на подпространство главных компонентов.

Фундаментальной концепцией, лежащей в основе главных компонентов, является аппроксимация исходной матрицы данных X, которая содержит множество переменных, с использованием сокращенного набора составляющих переменных. Эта аппроксимация достигается с помощью линейного преобразования.

Мы можем оценить погрешность в этой аппроксимации, вычислив сумму квадратов разностей между X и её аппроксимацией.

В качестве альтернативы мы можем оценить качество аппроксимации, вычислив долю общей дисперсии X, которая объясняется переменными компонентов.

Для достижения оптимальной аппроксимации необходимо стратегически выбрать подмножество столбцов от X до Z, которые будут использоваться для вычисления составляющих переменных. Важно отметить, что главные компоненты и конечные переменные компонентов, представленные матрицей M, различны.

Максимизация объясненной дисперсии

Одним из ключевых этапов алгоритма FSCA является отбор оптимальной переменной для добавления к существующему подмножеству. Для этого мы присваиваем показатель каждой потенциальной переменной и выбираем ту, которая наберет наибольший показатель. Расчет этого критерия (показателя), как описано в исследовательской работе, является относительно сложным. Однако авторы приводят математическое доказательство того, что порядок рангов этого критерия для конкурирующих переменных соответствует порядку рангов их объясняемой дисперсии. Это означает, что переменная с наивысшим показателем также максимизирует объясняемую дисперсию.

Более простой способ описать расчет показателя для каждой потенциальной переменной - это использовать приведенное ниже уравнение. Читатели, интересующиеся математическим выводом этой формулы, могут обратиться к исследовательской работе.

Z(i) - это матрица Z с добавленным к ней столбцом i из X.
Переменная x(j) - это столбец j из X.
Член v - это количество переменных (столбцов) в X.
Промежуточный член q - это вектор-столбец длиной в k элементов. Н

иже приведен код, реализующий вычисление критерия.

//+------------------------------------------------------------------+
//|  calculates the criterion for assessing a component              |
//+------------------------------------------------------------------+
double compute_criterion(matrix &covar, ulong &keptcols[], ulong nkept, ulong trial_col) {
    ulong i, j, k, irow, new_kept;
    double sum, crit, dtemp;
    new_kept = nkept + 1;
    matrix mt(new_kept, new_kept);

    for (i = 0; i < new_kept; i++) {
        if (i < nkept)
            irow = keptcols[i];
        else
            irow = trial_col;

        for (j = 0; j < nkept; j++)
            mt[i][j] = covar[irow][keptcols[j]];

        mt[i][nkept] = covar[irow][trial_col];
    }

    matrix mtinv = mt.Inv();
    vector vec(new_kept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {
        for (i = 0; i < nkept; i++)
            vec[i] = covar[j][keptcols[i]];

        vec[nkept] = covar[j][trial_col];

        sum = 0.0;
        for (i = 0; i < new_kept; i++)
            sum += vec[i] * vec[i] * mtinv[i][i];

        crit += sum;

        sum = 0.0;
        for (i = 1; i < new_kept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++)
                sum += dtemp * vec[k] * mtinv[i][k];
        }

        crit += 2.0 * sum;
    }

    return crit;
}

Функция compute_criterion() вычисляет критерий для оценки компонента в процессе отбора прзнака. В качестве входных данных она принимает корреляционную матрицу, covar, массив выбранных переменных, keptcols, количество выбранных переменных, nkept, а также индекс оцениваемой тестовой переменной.

Функция начинается с создания новой матрицы mt, которая дополняет существующий набор выбранных переменных тестовой переменной. Затем вычисляет значение, обратное этой расширенной матрице, mt. Функция выполняет итерацию по всем переменным в исходном наборе данных, вычисляя критерий для каждой переменной на основе ковариации между этой переменной и выбранными переменными, взвешенными с помощью обратного значения матрицы mt. Вычисленный критерий накапливается в переменной crit.

Цель этой функции - оценить влияние добавления новой переменной к набору выбранных переменных. Более высокое значение критерия указывает на то, что новая переменная, вероятно, улучшит эффективность модели, в то время как более низкое значение критерия предполагает, что она может оказаться бесполезной. Эта функция может быть использована в алгоритме отбора признаков для определения наиболее информативных переменных для данной модели.

Рекурсивное обратное уточнение

Обратное уточнение - это разновидность прямого отбора, как показано в приведенном ниже списке кода backward_refinement().

//+------------------------------------------------------------------+
//| backward refinement routine                                      |
//+------------------------------------------------------------------+
ulong backward_refinement(matrix &covar, ulong &kept_columns[], ulong nkept, double &best_crit) {
    ulong i, old_col, new_col, best_col, refined;
    double crit;

    best_crit = substvar(covar, kept_columns, nkept, 0, kept_columns[0]);
    refined = 0;

    for (old_col = 0; old_col < nkept; old_col++) {

        if (old_col == nkept - 1 && !refined)
            break;

        best_col = ULONG_MAX;
        for (new_col = 0; new_col < m_preds; new_col++) {

            for (i = 0; i < nkept; i++) {
                if (new_col == kept_columns[i])
                    break;
            }

            if (i < nkept)
                continue;

            crit = substvar(covar, kept_columns, nkept, old_col, new_col);

            if (crit > best_crit) {
                best_crit = crit;
                best_col = new_col;
            }
        }

        if (best_col != ULONG_MAX && best_col >= 0) {
            // Print(__FUNCTION__,"  Replaced predictor at column ",kept_columns[old_col], " with ",best_col," to get criterion = ", best_crit);
            kept_columns[old_col] = best_col;
            refined = 1;
        }
    }
    return refined;
}

Этот код на MQL5 реализует алгоритм обратного уточнения для выбора признаков. Он итеративно оценивает влияние удаления каждой выбранной переменной на конкретный критерий. Вычисляя критерий для каждой удаляемой переменной, функция определяет, удаление какой переменной приводит к наименее существенному изменению критерия. Если изменение ниже заданного порогового значения, переменная удаляется из выбранного набора, а процесс повторяется до тех пор, пока не будет возможности внести дополнительные уточнения. Функция возвращает 1, если было произведено уточнение, и 0 в противном случае.

Процедура substvar(), вызываемая в рамках функции backward_refinement(), реализует механизм подстановки переменных, который вычисляет критерий на основе корреляционной матрицы и набора выбранных переменных. Эта процедура используется в алгоритме выбора признаков для оценки влияния замены одной переменной на другую.

//+------------------------------------------------------------------+
//| variable substitution routine                                    |
//+------------------------------------------------------------------+
double substvar(matrix &covar, ulong &keptcols[], ulong nkept, ulong old_col, ulong new_col) {
    ulong i, j, k, irow, saved_col;
    double sum, crit, dtemp;
    matrix mt(nkept, nkept);

    saved_col = keptcols[old_col];
    keptcols[old_col] = new_col;

    for (i = 0; i < nkept; i++) {
        irow = keptcols[i];
        for (j = 0; j < nkept; j++) {
            mt[i][j] = covar[irow][keptcols[j]];
        }
    }

    matrix mtinv = mt.Inv();
    vector vec(nkept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {

        for (i = 0; i < nkept; i++) {
            vec[i] = covar[j][keptcols[i]];
        }

        sum = 0.0;
        for (i = 0; i < nkept; i++) {
            sum += vec[i] * vec[i] * mtinv[i][i];
        }
        crit += sum;

        sum = 0.0;
        for (i = 1; i < nkept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++) {
                sum += dtemp * vec[k] * mtinv[i][k];
            }
        }
        crit += 2.0 * sum;
    }

    keptcols[old_col] = saved_col;

    return crit;
}

Функция принимает в качестве входных данных корреляционную матрицу covar, массив выбранных переменных keptcols, количество выбранных переменных nkept, а также индексы старых и новых переменных, подлежащих замене. Она создает временную матрицу mt для хранения подматрицы covar, соответствующей выбранным переменным. Затем функция вычисляет значение, обратное матрице mt, используя функцию Inv(). Она выполняет итерацию по всем переменным в исходном наборе данных, вычисляя критерий для каждой переменной на основе ковариации между этой переменной и выбранными переменными, взвешенными с помощью обратного значения матрицы mt. Вычисленный критерий накапливается в переменной crit. После вычисления критерия функция восстанавливает исходную переменную в массиве keptcols и возвращает вычисленный критерий.

Цель этой функции - оценить влияние замены одной переменной другой на общей модели. Более высокое значение критерия указывает на то, что замена, вероятно, улучшит эффективность модели, в то время как более низкое значение критерия предполагает, что она может оказаться бесполезной. Эта функция может быть интегрирована в алгоритм выбора признаков для определения оптимальной комбинации переменных для данной модели.

Ортогонализация компонентов

Отбор переменных с помощью строго прямого уточнения, без учета обратного уточнения, устанавливает иерархический порядок, основанный на их значимости, начиная с наиболее влиятельных и прогрессивно снижаясь с точки зрения значимости. Такое упорядочение часто имеет неоценимое значение в практическом применении. В то время как исходные значения можно использовать напрямую, переменные с ортогональными компонентами, построенные в виде линейных комбинаций исходных переменных, обладают неоспоримыми преимуществами. Эти компоненты не связаны между собой, что облегчает обучение модели и сводит к минимуму избыточность. Кроме того, отсутствие избыточности в этих переменных может упростить интерпретацию их вкладов.

Для достижения переменных с ортогональными компонентами при сохранении исходного порядка подходит метод ортогонализации Грама-Шмидта (Gram-Schmidt orthogonalization method). Эта процедура начинается с определения исходного компонента в качестве масштабируемой первой выбранной переменной. Для последующих компонентов вычитаются проекции на существующие компоненты. Систематически вычитая эти проекции и нормализуя их к единице длины, обеспечивается ортогональность компонентов. Наконец, изменение масштаба до единицы стандартного отклонения обеспечивает согласованность. По сути, ортогонализация Грама-Шмидта преобразует выбранные переменные в набор ортогональных компонентов, сохраняющих первоначальный порядок значимости, что предполагает потенциальные преимущества в интерпретируемости и эффективности модели.

Ниже приведена реализация преобразования Грама-Шмидта. Результатом работы функции является новая матрица, в которой каждый столбец представляет собой ортогонализированный вектор.

//+------------------------------------------------------------------+
//|   Gram Schmidt routine                                           |
//+------------------------------------------------------------------+
matrix gram_schmidt(matrix &input_) {
    ulong irow, icol, inner;
    double dtemp, sum;
    ulong nrows = input_.Rows();
    ulong ncols = input_.Cols();
    matrix output = input_;

    sum = 0.0;

    vector colsum = output.Col(0);
    colsum = MathPow(colsum, 2.0);
    sum = colsum.Sum();
    sum = sqrt(sum);

    if (sum == 0.0) {
        Print(__FUNCTION__, " sum == 0.0 ");
        return matrix::Zeros(0, 0);
    }

    if (!output.Col(output.Col(0) / sum, 0)) {
        Print(__FUNCTION__, " failed column insertion ", GetLastError());
        return matrix::Zeros(0, 0);
    }

    for (icol = 1; icol < ncols; icol++) {
        for (inner = 0; inner < icol; inner++) {
            sum = 0.0;
            for (irow = 0; irow < nrows; irow++)
                sum += (output[irow][icol] * output[irow][inner]);

            for (irow = 0; irow < nrows; irow++)
                output[irow][icol] -= (sum * output[irow][inner]);
        }

        sum = 0.0;
        for (irow = 0; irow < nrows; irow++) {
            dtemp = output[irow][icol];
            sum += dtemp * dtemp;
        }

        sum = sqrt(sum);

        if (sum == 0.0) {
            Print(__FUNCTION__, " sum == 0.0 ");
            return matrix::Zeros(0, 0);
        }

        if (!output.Col(output.Col(icol) / sum, icol)) {
            Print(__FUNCTION__, " failed column insertion ", GetLastError());
            return matrix::Zeros(0, 0);
        }
    }

    return output;
}

Алгоритм работает путем итеративной ортогонализации каждого столбца входной матрицы относительно ранее ортогонализированных столбцов. Это достигается путем проецирования текущего столбца на подпространство, охватываемое предыдущими столбцами, и вычитания этой проекции из текущего столбца. Затем результирующий вектор нормализуется, чтобы иметь единичную длину. Код включает в себя несколько оптимизаций для повышения эффективности, таких как использование векторных операций для вычислений и отказ от ненужных вычислений. Кроме того, функция включает обработку ошибок для проверки потенциальных проблем, таких как векторы нулевой длины или сбой при вставке столбцов.

После рассмотрения всех основных процедур для выполнения прямого уточнения с возможностью обратного уточнения, в следующем разделе будет продемонстрировано, как эти процедуры используются при полной реализации алгоритма FSCA.

Класс CFsca

Класс CFsca инкапсулирует функциональность для выполнения анализа компонентов прямого отбора на наборе данных. Полный класс определен в fsca.mqh, наряду с простой процедурой стандартизации преобразования, называемой stdmat(). Эта функция принимает матрицу в качестве входных данных и возвращает стандартизированную матрицу.

//+------------------------------------------------------------------+
//| standardize a matrix                                             |
//+------------------------------------------------------------------+
matrix stdmat(matrix &in) {
    vector mean = in.Mean(0);
    vector std = in.Std(0);
    std += 1e-10;
    matrix out = in;

    for (ulong row = 0; row < out.Rows(); row++) {
        if (!out.Row((in.Row(row) - mean) / std, row)) {
            Print(__FUNCTION__, " error ", GetLastError());
            return matrix::Zeros(in.Rows(), in.Cols());
        }
    }

    return out;
}

Функция stdmat() вычисляет среднее значение и стандартное отклонение для каждого столбца матрицы входных данных, используя функции Mean и Std. Затем создает матрицу выходных данных с теми же размерами, что и у матрицы входных данных. Функция выполняет итерацию по каждому ряду матрицы входных данных, стандартизируя ее путем вычитания среднего значения соответствующего столбца и деления на стандартное отклонение столбца. Стандартизированный ряд сохраняется в матрице выходных данных out, которая возвращается в конце выполнения функции. Эта функция вынесена за пределы класса CFsca, чтобы обеспечить возможность независимого использования.

Класс CFsca начинается с определения его закрытых членов, используемых для хранения промежуточных результатов и структур данных, необходимых для FSCA.

//+------------------------------------------------------------------+
//| fsca class implementation                                        |
//+------------------------------------------------------------------+
class CFsca
  {
private:
   bool              m_fitted;              //flag showing if principal factors were extracted
   matrix m_corrmat,             //correlation matrix
          m_covar,               //altered correlation matrix
          m_data,                //standardized data is here
          m_eigvectors,          //matrix of eigen vectors of m_corrmat matrix
          m_structmat,           //factor loading matrix of m_corrmat matrix
          m_principal_components,             //principal components
          m_fscv_struct,        //fsca factor structure
          m_fscv_eigvects,      //fsca eigen structure
          m_Fsca,        //ordered fsca variables
          m_coeffs,      //fsca component coefficients
          m_Fscv;        //refined fsca variables
   vector m_eigvalues,           //vector of eigen values of m_corrmat matrix
          m_sqcorr,              //mean squared correlation matrix
          m_fscv_eigvals,        //fsca eigen values
          m_fscv_cumeigvals,     //fsca cumulative variance contribution
          m_cumeigvalues;        //cumulative variance contributions of m_corrmat matrix
   ulong             m_num_comps;           //unique instances of redundent variation in m_data
   ulong             m_preds;               //number of variables (columns) in dataset (m_data)
   ulong  m_keptorderedcolumns[],//indices of columns upon which components are calculated for ordered fsca
          m_keptrefinedcolumns[],//indices of columns upon which components are calculated for backward refined fsca
          m_keptcolumns[],
          m_bestcolumn;          //index of first selected column in analysis
   double            m_best_crit;           //best criterion value

Далее приведены приватные методы класса CFsca, некоторые из которых мы рассмотрели в предыдущих разделах этого текста. Другие методы будут кратко упомянуты при обсуждении публичных методов класса.

Публичные методы определены в конце класса CFsca. Метод fit() должен быть вызван первым после инициализации экземпляра класса. Этот метод выполняет анализ компонентов прямого отбора в исходном наборе данных. Он принимает в качестве входных данных матрицу, содержащую исходные необработанные данные, и возвращает логическое значение, указывающее, был ли процесс обучения успешным.

//+------------------------------------------------------------------+
//| perform forward selection component analysis on a raw dataset    |
//+------------------------------------------------------------------+
bool fit(matrix &data) {
    m_preds = data.Cols();
    m_fitted = false;
    m_sqcorr = vector::Zeros(m_preds);

    m_data = stdmat(data);
    m_corrmat = m_data.CorrCoef(false);

    m_structmat = compute_factor_structure(m_corrmat, m_eigvectors, m_eigvalues, m_cumeigvalues);

    if (m_structmat.Rows() == 1)
        return false;

    m_num_comps = m_cumeigvalues.Size();

    if (ArrayResize(m_keptorderedcolumns, int(m_num_comps)) < 0 || 
        ArrayResize(m_keptrefinedcolumns, int(m_num_comps)) < 0 ||
        ArrayResize(m_keptcolumns, int(m_num_comps)) < 0 || 
        ArrayInitialize(m_keptcolumns, ULONG_MAX) < 0) {
        Print(__FUNCTION__, " array error ", GetLastError());
        return false;
    }

    m_principal_components = compute_principal_components();

    for (ulong i = 0; i < m_preds; i++)
        m_sqcorr[i] = (compute_criterion(m_corrmat, m_keptcolumns, 0, i) - 1.0) / double(m_preds - 1);

    vector evd_vals = m_eigvalues;
    while (evd_vals[m_preds - 1] <= 0.0) {
        for (ulong j = 1; j < m_preds; j++) {
            for (ulong k = 0; k < j; k++) {
                m_corrmat[j][k] *= 0.99999;
                m_corrmat[k][j] = m_corrmat[j][k];
            }
        }

        matrix empty;
        if (!m_corrmat.EigenSymmetricDC(EIGVALUES_N, evd_vals, empty)) {
            Print(__FUNCTION__, " failed eig decomp ", GetLastError());
            return false;
        }
    }

    m_Fsca = compute_fsca_components(m_data);
    m_Fscv = compute_fscv_components(m_data);

    m_fitted = (m_Fsca.Rows() > 1 && m_Fscv.Rows() > 1);

    return m_fitted;
}

Функция fit() инициализирует различные переменные и матрицы, используемые в процессе FSCA. Сначала она стандартизирует матрицу входных данных, гарантируя, что она имеет нулевое среднее значение и единичную дисперсию. Затем функция вычисляет корреляционную матрицу стандартизированных данных, сохраняя ее в m_corrmat. Затем вычисляет факторную структуру корреляционной матрицы, используя функцию compute_factor_structure. Эта факторная структура включает в себя собственные векторы (m_eigvectors), собственные значения (m_eigvalues) и совокупные собственные значения (m_cumeigvalues) корреляционной матрицы. Функция проверяет, содержит ли матрица факторной структуры (m_struct mat) только один ряд; если да, то это указывает на ошибку при вычислении факторной структуры, и функция возвращает значение false.

Количество компонентов (m_num_comps) устанавливается равным количеству ненулевых собственных значений. Затем функция инициализирует различные массивы, используемые в процессе FSCA. Она вычисляет главные компоненты стандартизированных данных с помощью функции compute_principal_components и вычисляет квадратные корреляции между каждой переменной и первым главным компонентом. Кроме того, функция проверяет наличие любых отрицательных собственных значений. Если таковые обнаруживаются, она вносит небольшие коррективы в корреляционную матрицу и пересчитывает собственные значения до тех пор, пока все они не станут положительными. Наконец, функция вычисляет компоненты FSCA с помощью функции compute_fsca_components, а компоненты FSCV - с помощью функции compute_fscv_components. Если оба компонента FSCA и FSCV вычислены успешно, функция устанавливает для флага m_fitted значение true.

Завершая определение класса CFsca, мы приводим функции получения, которые предоставляют доступ к различным аспектам аналитических вычислений, выполняемых в процессе FSCA.

//+------------------------------------------------------------------+
//| get the principal components                                     |
//+------------------------------------------------------------------+
matrix get_principal_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_principal_components;
}

//+------------------------------------------------------------------+
//| get the ordered fsca components                                  |
//+------------------------------------------------------------------+
matrix get_fsca_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fsca;
}

//+------------------------------------------------------------------+
//| get the backward refined fsca components                         |
//+------------------------------------------------------------------+
matrix get_fscv_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fscv;
}

//+------------------------------------------------------------------+
//| get indices of variables defining the ordered fsca components    |
//+------------------------------------------------------------------+
bool get_fsca_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptorderedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+---------------------------------------------------------------------------+
//| get indices of variables defining the backward refined fsca components    |
//+---------------------------------------------------------------------------+
bool get_fscv_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptrefinedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on principal components|
//+-------------------------------------------------------------------+
vector get_principal_components_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_cumeigvalues;
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on fscv components     |
//+-------------------------------------------------------------------+
vector get_fscv_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_fscv_cumeigvals;
}

//+-------------------------------------------------------------------+
//| get eigen structure of principal components                       |
//+-------------------------------------------------------------------+
bool get_principal_components_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_eigvectors;
    values = m_eigvalues;

    return true;
}

//+-------------------------------------------------------------------+
//| get eigen structure of backward refined FSCs                      |
//+-------------------------------------------------------------------+
bool get_fscv_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_fscv_eigvects;
    values = m_fscv_eigvals;

    return true;
}

//+-------------------------------------------------------------------+
//| get principal components factor structure                         |
//+-------------------------------------------------------------------+
matrix get_principal_components_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_structmat;
}

//+-------------------------------------------------------------------+
//| get the factor structure of FSC with backward refinement          |
//+-------------------------------------------------------------------+
matrix get_fscv_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_fscv_struct;
}

//+------------------------------------------------------------------+
//| get mean squared correlations                                    |
//+------------------------------------------------------------------+
vector get_avg_correlations(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_sqcorr;
}

//+-------------------------------------------------------------------+
//| get forward selection component coefficients matrix               |
//+-------------------------------------------------------------------+
matrix get_fsca_component_coeffs(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_coeffs;
}

Эти функции позволяют пользователям получать важные результаты, такие как стандартизированные данные, корреляционная матрица, факторная структура, главные компоненты и переменные компонентов, облегчая дальнейший анализ и интерпретацию результатов. Мы завершаем это изложение демонстрацией того, как применять класс CFsca.

Пример

Приведенный ниже список кода определяет скрипт на MQL5 с именем FSCA_Demo.mq5, выполняющий Анализ компонентов прямого отбора (FSCA) для случайно сгенерированного набора данных. Сценарий включает в себя заголовочный файл fsca.mqh, содержащий определение класса CFsca, используемого для анализа FSCA.

//+------------------------------------------------------------------+
//|                                                    FSCA_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<fsca.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   MathSrand(120);
//---
   matrix mat(100,9);
//---
   mat.Random(0.0,1.0);
//---
   vector var1 = mat.Col(0) + mat.Col(1);
// ---
   vector var2 = mat.Col(2) + mat.Col(3);
//---
   vector var3 = var1 + var2;
//---
   if(!mat.Col(var1,6) || !mat.Col(var2,7) || !mat.Col(var3,8))
     {
      Print("failed column assignment ", GetLastError());
      return;
     }
//---
   CFsca fsca;
//---
   if(!fsca.fit(mat))
      return;
//---
   ulong index[];
   Print("Principal components cumulative variance conributions \n", fsca.get_principal_components_cumulative_variance_contribution());
   Print(" Principal components factor structure \n", fsca.get_principal_components_factorstructure());
   Print("Mean squared correlation of each variable with all others \n", fsca.get_avg_correlations());
//---
   if(fsca.get_fsca_var_indices(index))
     {
      Print(" Ordered FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   Print(" Ordered FSCA component coefficients matrix \n", fsca.get_fsca_component_coeffs());
//---
   if(fsca.get_fscv_var_indices(index))
     {
      Print(" Backward refined FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   matrix vects;
   vector vals;
//---
   if(fsca.get_fscv_eigstructure(vects,vals))
     Print("Backward refined fsca component eigenvalues \n", vals);
//---
   Print(" Backward refined cumulative variance contributions \n", fsca.get_fscv_cumulative_variance_contribution());
//---
   Print(" Backward refined fsca components factor structure \n", fsca.get_fscv_factorstructure());
  }
//+------------------------------------------------------------------+

Все начинается с установки случайного начального значения и создания матрицы случайных значений. Три новых вектора создаются путем суммирования существующих столбцов в матрице. Затем скрипт пытается обучить матричным данным модель FSCA и извлекает различные результаты FSCA, включая вклад в совокупную вариантность, факторную структуру и среднеквадратичные корреляции. Он также выполняет как стандартную FSCA, так и обратно-уточненную FSCA, выводя на печать упорядоченные переменные индексы и коэффициенты компонентов. А также факторная структура обратно-уточненных компонентов FSCA. Скрипт просто генерирует набор данных рандомных переменных со 100 выборками и 9 признаками. Последние 3 переменные набора данных настроены так, чтобы они зависели от других переменных, в то время как остальные являются независимыми. 

При запуске скрипта и проведении анализа характеристик основных компонентов, мы обнаруживаем, что существует только шесть уникальных источников вариации из девяти.

DG      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Principal components cumulative variance conributions 
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [31.72121326219056,54.98374706330443,70.21399790786099,82.34742379766755,91.9067775629936,100]
CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Principal components factor structure 
MH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[-0.5430877600903072,0.4698851388299595,-0.02139789374204959,0.5468988095320395,-0.4254498037566715,-0.06082703269184352,-1.3842452210817e-09,-7.527559895073524e-10,0]
RH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5283294988376427,0.4246506210338227,-0.1190026606589024,-0.6285471675075863,0.3351428244532062,0.1377893424956133,-1.351333204556555e-09,-7.34858353171856e-10,0]
ES      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5563230307728618,-0.3632156082945803,0.4770295070287525,0.3051596297191441,0.4575827252246154,-0.1688715686919785,-1.694159101189325e-09,2.164855665400724e-10,0]
NF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.2379617600470182,-0.6943076552356867,-0.4580766878219635,-0.2737307249578351,-0.4112051990027778,0.08636320534609224,-1.769139142521297e-09,2.260667780777343e-10,0]
DO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [0.02487447101754412,-0.08203927651647476,-0.6079889924620585,0.4701685445643955,0.3604839483405348,0.5215295442601863,1.313244252124911e-25,1.228203109452781e-25,0]
IP      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.07016546285360215,-0.110242984252018,0.7306990214221818,-0.07491798042552207,-0.2276538908363994,0.6257501374625694,4.158606798395552e-25,-7.369218656716687e-26,0]
NE      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.7598477338270035,0.6346843827822741,-0.09872272409405579,-0.04786755450396145,-0.0705236166963274,0.05287812507625003,-1.359967783374346e-10,1.333715775589249e-09,0]
NO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5934182368659159,-0.8024046895986707,-0.000973814713973191,0.01424096330384607,0.02077689502375221,-0.05801790712583575,2.667167815186452e-10,-1.355042254629964e-11,0]
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.9897757278036692,-0.1138316306178367,-0.07343616940955985,-0.02494592427830717,-0.03690113231990194,-0.0030829919659495,2.802923111601039e-09,-3.865027968054199e-10,0]]

Это ожидаемо, поскольку три из переменных являются комбинациями других. Рассматривая совокупный вклад каждой переменной в дисперсию, мы видим, что на первый компонент приходится около трети общего варьирования. Факторная структура указывает на умеренную или сильную обратную корреляцию между первым главным компонентом и переменными в столбцах с 0 по 3 и с 6 по 8 включительно, в то время как переменные в столбцах 4 и 5 демонстрируют противоположную тенденцию. Второй компонент отображает различия между переменными 0 и 1 по сравнению со 2 и 3. Вместе взятые, первые два компонента объясняют более 55 процентов общего варьирования.

QK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Mean squared correlation of each variable with all others 
GK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [0.09874555673359317,0.09196664871445229,0.09678803260182336,0.08640965168371836,0.009232616218980055,0.01341075732654295,0.1892345119240549,0.1695472310064176,0.2291509382521983]

Переходя к вектору среднеквадратичных корреляций каждой переменной с объединенной коллекцией всех переменных, этот вектор отображает корреляции в том порядке, в котором переменные отображаются в исходном наборе данных. Последние три переменные имеют наибольшие средние корреляции, в то время как переменные в столбцах 4 и 5 имеют наименьшие значения.

LR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA components based on variables located in column indices 
QQ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   8 6 2 4 1 5

Далее мы рассмотрим прямо выбранные значения, которые получаются при вызове функции get_fscv_var_indices(). В ней показаны индексы переменных, которые наилучшим образом отражают большую часть вариаций в наборе данных, расположенные в порядке убывания того, какая переменная вносит наибольший вклад в общий разброс данных. Здесь мы видим, что последняя переменная отражает наибольшие различия в данных, поскольку она появляется первой.

QJ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA component coefficients matrix 
DM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[0.9999999989356357,-0.9551778313323678,-1.196676438579672,-0.163265209103464,-0.1301792726137802,0.0741114239785734]
IR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [7.62883988565579e-10,1.382882745177175,0.7080052470472653,0.1327136589445282,-0.8962870520067646,-0.01038862969019799]
LF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.044914586250671e-10,-1.162965671680505e-09,1.327736785211269,0.1291890234653878,0.1244453203448803,-0.2315140872599129]
EM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [5.84342504938995e-11,-9.115276242144255e-11,-1.685031073006549e-10,1.005785752630206,0.08917398176616295,0.2288955899392838]
JM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.626278020206711e-11,8.05911615654048e-10,2.135397240976555e-10,-3.939133914887538e-11,1.404086244047662,0.03569800251260542]
KK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-2.859616016204214e-11,3.48387846349496e-11,2.600743786995707e-10,-1.479500966183878e-10,-3.333024481411151e-11,1.048952273510343]]

Далее мы изучаем таблицу коэффициентов, необходимых для вычисления шести компонентов. Переменные представлены в том же порядке важности, представленном индексами массива, который мы только что рассмотрели. Здесь мы видим, что поскольку последняя переменная является наиболее важной, соответствующий коэффициент очень близок к 1. Двигаясь вниз по этой матрице, обратите внимание, как коэффициенты становятся настолько малыми, что практически равны нулю.

CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Backward refined FSCA components based on variables located in column indices 
ND      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   3 0 2 4 1 5

Наконец, мы исследуем индексы переменных, отобранных с помощью комбинации прямого отбора и обратного уточнения. Важно отметить, что в этом варианте FSCA порядок выбранных переменных не имеет значения. Однако результирующий набор выбранных переменных более значим, чем подход со строгим упорядочением, поскольку он сохраняет только независимые случайные величины, отбрасывая величины, демонстрирующие некоторую зависимость. Это наглядно видно из сравнения результатов как стандартного прямого отбора, так и обратного уточненного прямого отбора.

Заключение

В заключение мы представили реализацию анализа компонентов прямого отбора в MQL5, продемонстрировав его эффективность как инструмента уменьшения размерности и отбора признаков. Этот инструмент также может быть использован для предварительного анализа данных. Одним из побочных продуктов алгоритма является факторная структура набора данных, которая может быть полезна при попытке понять действующие эффекты. Весь код, на который мы ссылаемся в настоящей статье, прилагается ниже.

Название файла	Описание
MQL5/include/np.mqh	заголовочный файл универсальных векторных и матричных служебных функций
MQL5/include/fsca.mqh	заголовочный файл, содержащий определение класса CFsca, реализующего Анализ компонентов прямого отбора
MQL5/scripts/FSCA_Demo.mq5	скрипт MetaTrader 5, демонстрирующий использование класса CFsca