
Универсальная регрессионная модель для прогнозирования рыночной цены
к. т. н., доцент кафедры Экономики и предпринимательства Института Экономики и Торговли Таджикского государственного университета коммерции ( ИЭиТ ТГУК ) УДК 330.115
Введение
Рыночная цена складывается в результате устойчивого равновесия между спросом и предложением, которые, в свою очередь, зависят от множества экономических, политических и психологических факторов, непосредственный учет которых осложнен как различием природы, так и причиной воздействия этих факторов.
Тем не менее, чтобы иметь способность принимать правильные решения о покупке или продаже товаров, включая валюту или акции, в текущий момент времени необходимо уметь предвидеть и прогнозировать с достаточной степенью точности поведение рыночной цены в будущем. Для решения этой задачи используется значительное количество информации различного характера, добытой из всевозможных источников, обрабатываемой тем или иным способом.
Для разработки эффективной стратегии и тактики поведения на рынке используются 4 вида анализа /1/ в зависимости от целей, квалификации или предрасположенности исследователя:
- Технический анализ, основанный на утверждении, что рыночная цена учитывает в себе всё, что может на него повлиять. Использует развитый математический аппарат /2/;
- Фундаментальный анализ, изучающий влияние на рыночную цену различных экономических факторов. В основном использует макроэкономические модели /3-5/;
- Интуитивный анализ, подкрепленный знанием основных рыночных показателей и индикаторов, способ прогнозирования их дальнейшего поведения, результаты которого не могут быть доказаны непосредственным путем применением правил логики и математических соотношений к исходным посылкам, и которые, тем не менее, необъяснимым образом очень часто оказываются верны;
- Психоанализ, основанный на собственном психологическом анализе состояния рынка каждым покупателем в отдельности и их совокупности в целом, приводящий к переменному успеху.
Состояние изученности проблемы
Любой, в том числе новый, вновь предлагаемый способ прогнозирования рыночной цены, на наш взгляд, должен учесть, а при удачном стечении обстоятельств и объяснить, объективно существующие закономерности, базирующие на трех аксиомах, известные как теория Доу /6,7/, которые кратко можно сформулировать так:
- Рыночная цена учитывает все факторы, влияющие на него в соответствии с законом спроса и предложения, и для ее прогнозирования необходимо и достаточно располагать данными об ее изменении во времени;
- Зависимость рыночной цены от времени подвержена тенденциям (трендам), имеющим, чаще всего, S-образные формы, соединенными на восходящих или нисходящих участках горизонтальными («флэт») линиями, называемыми боковым трендом или без таковых;
- Объективно существуют закономерности изменения рыночной цены, остающиеся неизменными во времени, известные как принципы: «история повторяется» или «они работали в прошлом, работают в настоящем и будут работать в будущем».
Однако, стадии динамического покоя временных рядов рыночных цен, например валютных курсов, сменяются стадиями настолько сложными, что производит впечатление полного и непредсказуемого хаоса, а из беспорядка, в процессе самоорганизации, снова рождается порядок.
Но в определенный момент ослабленная стабильностью динамическая система вновь рождает хаос, что дает основание считать смешанной природу временных рядов экономических показателей, заключающейся в том, что на одних участках временной ряд рыночных цен является детерминированным и поддающимся анализу, на других – не поддается достоверным прогнозам, а на третьих – подчиняется нормальному закону распределения /8/ и ведет себя как случайная величина.
Следовательно, пока в научном мире нет единого мнения на счёт природы изменения рыночных цен, что не позволяет выйти на зависимости, адекватно их описывающих и пригодных для практического применения.
Функции переходных процессов для одноячеечной модели "черного ящика"
В связи с неопределенностью процесса предлагаю рассмотреть сначала одноячеечную модель «черного ящика», к которой иногда относят рассматриваемую проблему /1/, и применить к ней уравнения материального баланса.
Развивая описанные выше аксиомы, предположим, что находящаяся в равновесии рыночная цена может изменяться только под действием некоторой внешней силы D(t), величину и значение которой будем измерять в той же размерности, что и цену.
Также предположим, что изменение рыночной цены P(t) с течением времени t от начала воздействия указанной силы, непрерывно увеличиваясь от нулевого значения по некоторой, неизвестной пока нам закономерностью, стремится достичь значения P(∞) = D0 в бесконечности. То есть под D0 будем подразумевать конечное приращение или снижение рыночной цены, в зависимости от природы и знака этой воздействующей силы.
Причем, подразумевается, что D(t=0) = D0. Предположим далее, что в течении бесконечно малого отрезка времени dt воздействующая сила уменьшится на величину dD(t) пропорционально оставшейся к моменту времени t силе D(t):
![]()
откуда получим экспоненциальную зависимость D(t) от времени t в виде:
![]() (1)
(1)
где: ![]()
t – время от начала воздействия дестабилизирующей силы в единицах временного ряда, сек.(мин, часы, дни, недели, декады, месяцы, годы);
τ (тау) – коэффициент пропорциональности, численно равный постоянной времени процесса, сек.(мин, часы, дни, недели, декады, месяцы, годы).
Теперь допустим, что скорость V(t) изменения рыночной цены P(t) пропорциональна как величине D(t), так и времени t:
![]()
где: ![]() (2)
(2)
k - коэффициент пропорциональности, имеющий размерность 1/(время)^2;
β = k*τ*D0 - коэффициент пропорциональности, имеющая размерность скорости изменения рыночной цены.
Абсолютное приращение или снижение цены за единицу времени к данному моменту времени t, которое выразим как H(t), численно равна V(t):
H(t) = V(t) = β*m
Несомненно, интегрируя H(t) во всем диапазоне изменения времени t, мы должны получить общую величину изменения рыночной цены P(t) к моменту времени t от начала ее дестабилизации:
![]()
где: ![]() (3)
(3)
Поскольку из (3) следует, что при t = ∞ s = 1, то заключаем:
P(∞) = β*τ = D0;
или: β = D0/τ;
Сравнивая предыдущее обозначение β с полученным результатом, заключаем, что:
k = 1/τ^2;
Теперь справедливы соотношения:
H(t) = D0*m;
P(t) = D0*s.
Следовательно, если определить коэффициенты τ и β , то можно оценить и прогнозировать предельное значение изменения цены D0 на любой, в том числе на ранней, стадии изменения цены. Тем не менее, указанные утверждения будут справедливы только тогда, когда будет выполняться условие материального баланса:
D(t) + H(t) + P(t) = D0 (4)
или: ![]()
Следовательно, должно выполняться условие нормировки:
ℓ + m + s = 1; (5)
Проверим это обстоятельство, используя соотношения (1-3):
![]()
Однозначное выполнение условия материального баланса (4) и условия нормировки (5) указывают на справедливость принятых допущений и предлагаемых соотношений.
Функции переходных процессов для многоячеечной модели
Рассуждая аналогичным образом, получим следующие соотношения для функций D(t), H(t) и P(t) в случае многоячеечной модели черного ящика, состоящей из n ячеек:
D(t) = D0 * L;
H(t) = D0 * M;
P(t) = D0 * S;
где:
![]() - названная мною пока "двухпараметрическая интегральная экспоненциальная функция распределения" (6)
- названная мною пока "двухпараметрическая интегральная экспоненциальная функция распределения" (6)
![]() - разновидность плотности функции Гамма-распределения, или плотность функции распределения Эрланга; (7)
- разновидность плотности функции Гамма-распределения, или плотность функции распределения Эрланга; (7)
![]() - разновидность интегральной функции Гамма-распределения, или интегральная функция распределения Эрланга, (8)
- разновидность интегральной функции Гамма-распределения, или интегральная функция распределения Эрланга, (8)
t/τ, n – параметры распределений;
1 – логическое выражение, имеющее значение – «истина»;
0 - логическое выражение, имеющее значение – «ложь»;
Интегрированием (8) можно убедиться, что:
или:
![]()
Следовательно, и в этом случае, согласно (6-8), условие нормировки выполняется однозначно:
L+M+S = 1; (9)
Функцию L я назвал «функцией будущих периодов», поскольку от ее величины зависит значения рыночной цены в будущем, функцию M - «функцией настоящего времени», поскольку она определяет изменение рыночной цены за единицу рассматриваемого периода времени, а функцию S – «функцией прошлого», поскольку от ее значения зависит достигнутая уровень рыночной цены за весь период времени, прошедшей с момента ее дестабилизации, что не противоречит понятию переходного процесса и значительно расширяет наше прдставление о происходящем в смысле философии проблемы.
Подстановкой n = 1 в (6-8) можно убедиться, что при этом функции L, M и S превращаются соответственно, в функции ℓ, m и s, поэтому в дальнейшем для целей прогнозирования будем рассматривать именно функции L, M и S, как наиболее общие случаи функций этого класса.
Разработка универсальной регрессионной модели для прогнозирования рыночной цены на основе выявленных функций переходных процессов
Уровень рыночной цены P(h) от времени t от начала наблюдений выразим следующим образом:
Для одноячеечной модели:
Для многоячеечной модели:
![]() (10b)
(10b)
где: P0 - уровень рыночной цены непосредственно перед ее дестабилизацией, т.е., к моменту времени t = 0.
Параметры n, τ и коэффициент β определяются по фактическим значениям рыночной цены от начала ее дестабилизации на рынке, причем при этом анализируется изменение рыночной цены f за единицу времени t, которое можно принять как величину производной от (10b). Можно убедиться, что ошибка от принятия данного допущения ничтожно мала и составляет сотые доли процента от величины изменения цены. Принятие этого допущения значительно упрощает процесс нахождения вышеуказанных параметров и коэффициента β.
Действительно, теперь можно от анализа функции S перейти к анализу функции M:
![]() (11)
(11)
Разделив обе части (11) на t^n и логарифмируя найденное соотношение, получим уравнение прямой линии в полулогарифмических координатах:
![]()
Теперь, если известны значения функции f к соответствующим моментам времени t, то из этого уравнения параметры n, τ и коэффициент β определяются следующим образом:
![]() (12)
(12)
![]() (13)
(13)
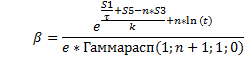 (14)
(14)
где:
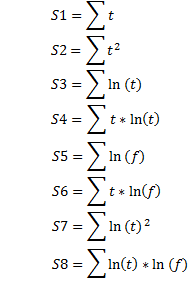
Значения функции f к соответствующим моментам времени t и время t определяются по фактическим значениям рыночной цены Р0, Р1,…, Рк к моментам времени һ0, һ1,…, һк от начала ее дестабилизации путем численного дифференцирования, отнесенным к середине интервала:
f1 = (P1 - P0)/(һ1 – һ0); f2 = (P2 – P1)/( һ2– һ1); f3 = (P3 – P2)/( һ3– һ2); и так далее;
t1 = (һ0 + һ1)/2; t2 = (һ1 + һ2)/2; t3 = (һ3 + һ2)/2; и так далее.
Корректировка и приспособление модели
Практическая апробация уравнений (10a) и (10b) в качестве регрессионной модели на фактических данных показала, что необходимо произвести коррекцию значений Р(0) и D0, которая была осуществлена следующим образом:
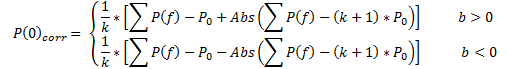 (15)
(15)
![]() (16)
(16)
где: Sf и Sr – площади, соответственно, фактических и расчетных кривых;
∑Pf = P0+ P1 + P2 + …+ Pk – сумма фактических значений цены;
![]() (17)
(17)
i = 0, 1,2,......k;
k>2 – количество временных интервалов, для которых определены разность цен;
b – коэффициент линейного уравнения регрессии ![]() , определяющий направление тренда фактических данных.
, определяющий направление тренда фактических данных.
Теперь регрессионное уравнение (10b), для прогнозирования рыночной цены P(t), принимает следующий окончательный вид:
![]() (18)
(18)
Опробация модели
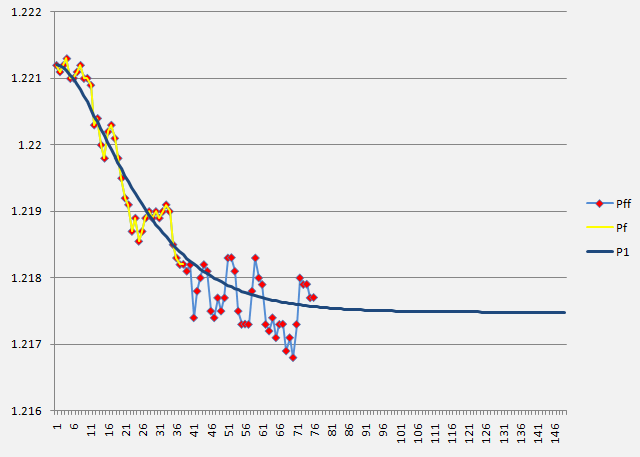
Обнаружилось, что рассчитанные таким образом значения рыночной цены P(t) и фактические ее значения Pf, осуществленные на примере рынка Форекс, всегда полностью и однозначно удовлетворяют условию материального баланса:
∑ P(t) = ∑ Pf. (19)
Абсолютно точное совпадение сумм фактических и расчетных значений исследуемого параметра, в частности рыночной цены, при всех значениях аргумента, в частности, времени, свидететельствует о справедливости принятых, при выводе функций, выкладок, преобразований, допущений и об универсальности предлагаемой регрессионной модели.
На рисунке показаны результаты обработки фактических данных рынка Форекс (минутные таймфреймы) предложенным способом по уравнению (18), откуда видно удовлетворительное соответствие фактических (Pf) - (желтая линия с красными точками), расчетных и прогнозных (P1) - (синяя линия) и будущих фактических, но не участвовавших в расчетах (Pff ) - (синяя линия с красными точками), значений курса валюты EUR/USD.
Выводы
Выявлены и предложены три функции описывающих, соответственно, три стадии динамических переходных процессов, которые определены в виде различных модификаций функции Гамма-распределения, определяющих поведение изучаемого параметра, в частности рыночной цены, в зависимости от времени в будущем, настоящем и прошедшем периодах времени от начала ее дестабилизации.
В результате анализа указанных процессов предложена универсальная регрессионная модель для прогнозирования рыночной цены, на основе которой могут быть разработаны, в частности, различные по назначению индикаторы рынка, торговые советники для оптимизации деятельности трейдеров, автоматических торговых систем (АТС) и, возможно, создана реальная основа для разработки торгового робота - РОБОТРЕЙДЕРА, осуществляющего выгодные торговые операции без участия и во благо человека.
P.S. - Все пронумерованные соотношения и формулы, а также основные положения и выводы настоящей статьи разработаны, выявлены, предложены и выставлены мною на обозрение в открытой печати впервые.
Литература
- Котенко А. Е., О методах технического и фундаментального анализа при исследовании рынка Forex, Электронный журнал «ИССЛЕДОВАНО В РОССИИ», http://zhurnal.ape.relarn.ru/articles/2003/151.pdf
- Якимкин В. Н., Рынок Форекс – Ваш путь к успеху, М., «Акмос- Медиа», 2001.
- Лиховидов В. Н., Фундаментальный анализ валютных рынков: методы прогнозирования и принятия решений, Владивосток, 1999.
- Бункина М.К., Семенов А. М., Основы валютных отношений, М., Юрайт, 2000.
- Сакс Джеффри Д., Ларрен Б. Филипс, Макроэкономика: глобальный подход., М., Дело, 1996.
- Rhea, Robert. Dow Theory,- New York; Barrons, 1932.
- Greiner, P. and H. C. Whitcomb: Dow Theory, New York: Investor’s Intelligence, 1969.
- Гуляева О. С., Управление валютными рисками на основе предпрогнозного анализа валютных курсов фрактальными методами, Автореферат диссертации на соискание ученой степени кандидата экономических наук, Москва-Тверь, ТвГУ, 2008.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Торговый эксперт по книге Б. Вильямса "Новые измерения в биржевой торговле"
Торговый эксперт по книге Б. Вильямса "Новые измерения в биржевой торговле"
 Реализация индикаторов в виде классов на примере Zigzag и ATR
Реализация индикаторов в виде классов на примере Zigzag и ATR
 Как открыть мир C# из MQL5 путем экспорта неуправляемого кода
Как открыть мир C# из MQL5 путем экспорта неуправляемого кода
 Курс Монетки и основанный на нем Индикатор Трендовости
Курс Монетки и основанный на нем Индикатор Трендовости
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Индикаторы платные что ли? Опубликован в кодбазе, пользуйтесь на здоровье!
Опубликована новая статья Универсальная регрессионная модель для прогнозирования рыночных цен:
Автор: Юсуфходжа
хорошая статья.
очень впечатляет
Жаль, но ошибки в самом начале статьи.
Во первых, приращение цены в некоторый момент времени t, конечно же будет иметь некоторое значение и обозначили его D0. Допустим.
Далее... Теперь при t=0, я так понимаю, что воздействия на цену пока нет и приращения цены от внешнего воздействия по видимому тоже нет. Однако мы снова обозвали дельту D0.
Далее в формулу подсунули dt/тау, это по любому размерность 1/C^2, т.е. воздействию придали ускорение, которое по любому уже двинет по геометрической регрессии. С какой стати? Ведь мы пока не определились - что это за воздействие такое...
ну, в общем...
Жаль, но ошибки в самом начале статьи.
Во первых, приращение цены в некоторый момент времени t, конечно же будет иметь некоторое значение и обозначили его D0. Допустим.
Далее... Теперь при t=0, я так понимаю, что воздействия на цену пока нет и приращения цены от внешнего воздействия по видимому тоже нет. Однако мы снова обозвали дельту D0.
Далее в формулу подсунули dt/тау, это по любому размерность 1/C^2, т.е. воздействию придали ускорение, которое по любому уже двинет по геометрической регрессии. С какой стати? Ведь мы пока не определились - что это за воздействие такое...
ну, в общем...
1. Do - это не приращение цены, а первоначальный потенциал силы, воздействующая на цену в момент времени t=0.
2. из статьи: ".... предположим, что находящаяся в равновесии рыночная цена может изменяться только под действием некоторой внешней силы D(t), величину и значение которой будем измерять в той же размерности, что и цену.
Также предположим, что изменение рыночной цены P(t) с течением времени t от начала воздействия указанной силы, непрерывно увеличиваясь от нулевого значения по некоторой, неизвестной пока нам закономерностью, стремится достичь значения P(∞) = D0 в бесконечности. То есть под D0 будем подразумевать конечное приращение или снижение рыночной цены, в зависимости от природы и знака этой воздействующей силы.
Причем, подразумевается, что D(t=0) = D0. Предположим далее, что в течении бесконечно малого отрезка времени dt воздействующая сила уменьшится на величину dD(t) пропорционально оставшейся к моменту времени t силе D(t):
откуда получим экспоненциальную зависимость D(t) от времени t в виде:
где: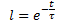
t – время от начала воздействия дестабилизирующей силы в единицах временного ряда, сек.(мин, часы, дни, недели, декады, месяцы, годы);
τ (тау) – коэффициент пропорциональности, численно равный постоянной времени процесса, сек.(мин, часы, дни, недели, декады, месяцы, годы)."
Откуда Вы нашли размерность 1/с^2? Это отношение не имеет размерность. Это я не подсунул, а предположил, что, скорость изменения (убыли) силы, воздействующая на процесс, пропорциональна самой силе, что не противоречит логике, а затем, эта гипотезе полностью подтвердилась. В качестве коэффициента пропорциональности и введено отношение а (альфа) = 1/тау, имеющее обратная времени, размерность. Под а (альфа) я понимаю импеданс системы, означающий сопротивление системы течению процесса, а тау - это изображение времени в преобразованиях Лапласа, как позже выяснилось, и позволяет увести анализ процесса из дифференциальной области в обычную. Это означает, что, у любого процесса есть свое время, отличное от нашего и тау выступает в роли "переводчика" времен, если так можно выразиться. В недрах статьи я дал способ оценки тау:
Теперь, если известны значения функции f к соответствующим моментам времени t, то из этого уравнения параметры n, τ и коэффициент β определяются следующим образом:
где:
Значения функции f к соответствующим моментам времени t и время t определяются по фактическим значениям рыночной цены Р0, Р1,…, Рк к моментам времени һ0, һ1,…, һк от начала ее дестабилизации путем численного дифференцирования, отнесенным к середине интервала:
f1 = (P1 - P0)/(һ1 – һ0); f2 = (P2 – P1)/( һ2– һ1); f3 = (P3 – P2)/( һ3– һ2); и так далее;
t1 = (һ0 + һ1)/2; t2 = (һ1 + һ2)/2; t3 = (һ3 + һ2)/2; и так далее.