
Universal Regression Model for Market Price Prediction
Introduction
The market price is formed out of a stable balance between demand and supply which, in turn, depend on a variety of economic, political and psychological factors that are difficult to be directly considered due to differences in nature as well as causes of their influence.
It is however necessary to be able to foresee and predict the future market price behavior with a certain degree of accuracy in order to be capable of making right decisions regarding the purchase or sale of goods, including currency or shares, in the current situation. This problem can be solved using a considerable amount of information of different nature from all sorts of sources that is processed in one way or another.
There are 4 types of analysis /1/ that are used for development of an effective strategy and tactics of the market behavior depending on purpose, qualification or predisposition of the researcher:
- Technical analysis based on the assertion that the market price takes into account everything that can affect it. It employs advanced mathematical techniques /2/;
- Fundamental analysis dealing with the effect of different economic factors on the market price. It substantially employs macroeconomic models /3-5/;
- Intuitive analysis substantiated by the knowledge of the major market indices and indicators, method of predicting their future behavior the results of which cannot be proved by directly applying logical rules and mathematics to the initial premises, but which nevertheless inexplicably very often turn out to be true;
- Psychoanalysis based on a psychological analysis of the market conditions by each customer individually and together as a whole resulting in varied success.
State of Knowledge Regarding the Problem
Any technique, including a new newly proposed method for market price prediction, should in our opinion consider and, in a lucky combination of circumstances, explain the objectively existing laws based on three axioms known as the Dow Theory /6,7/ which can be briefly formulated, as follows:
- Market price takes into account all affecting factors in accordance with the law of supply and demand and it is sufficient to have data on changes in the market price in the course of time in order to predict it;
- Dependence of the market price on time is subject to tendencies (trends) which are mainly S-shaped, the highs and lows of which are connected by horizontal (flat) lines called a sideways trend, or without any;
- There are objectively existing market price change patterns that remain unchanged in the course of time known as principles "history repeats itself" or "they worked in the past, work now and will work in the future."
However dynamical rest stages of the market price time series, e.g. currency rates, are followed by stages which are so complex that one gets an impression of complete unpredictable chaos which in the process of self-organization gives rise to the order again.
But at a certain point, the dynamical system weakened by stability again produces chaos which gives us grounds to believe that the nature of economic indicator time series is mixed. This means that the market price time series are deterministic and analyzable at one point but cannot be reliably predicted at another point and follow the normal distribution law /8/ and act as a random variable at yet another point.
Thus the scientific world as yet lacks a common opinion regarding the nature of changes in the market price which prevents us from finding the dependencies that would adequately define them and be applicable in practice.
Transient Functions for a Black Box Single-Cell Model
Due to fuzziness of the process I suggest that we first take a look at a black box single-cell model which is sometimes attributed to the problem in question /1/ and apply the material balance equation.
Elaborating on the above axioms, let us assume that the equilibrium market price can only change when affected by an external force D(t) the amount and value of which will be measured in the same dimension as the price.
We also assume that the change in the market price P(t) in the course of time t from the beginning of impact of the specified force is continuously increasing from zero value in accordance with some law which is as yet unknown trying to reach a value of P(∞) = D0 at infinity. In other words, D0 will mean a finite increment or decrement of the market price depending on the nature and sign of the affecting force.
It is also implied that D(t=0) = D0. We further assume that in the course of infinitesimal period of time dt, the affecting force will decrease by the value of dD(t) in proportion to the force D(t) remaining by the time t:
![]()
whence we get the exponential dependence D(t) on time t, as follows:
![]() (1)
(1)
where: ![]()
t is the time from the beginning of impact of the destabilizing force in units of the time series, sec. (min, hrs, days, weeks, decades, months, years);
τ (tau) is the factor of proportionality numerically equal to the process time constant, sec. (min, hrs, days, weeks, decades, months, years).
Let us now assume that the market price P(t) change velocity V(t) is proportional to both the value of D(t) and time t:
![]()
where: ![]() (2)
(2)
k is the factor of proportionality that has dimension 1/(time)^2;
β = k*τ*D0 is the factor of proportionality that has the dimension of the market price change velocity.
The absolute increment or decrement of the price per unit of time by the given time t which is expressed as H(t) is numerically equal to V(t):
H(t) = V(t) = β*m
Undoubtedly, by integrating H(t) throughout the whole range of the time t change, we shall get a total value of the change in the market price P(t) by the time t from the beginning of its destabilization:
![]()
where: ![]() (3)
(3)
Since based on (3) it appears that when t = ∞ s = 1, we draw a conclusion that:
P(∞) = β*τ = D0;
or: β = D0/τ;
When comparing the previous notation of β with the result we have received, we conclude that:
k = 1/τ^2;
Now the following relations are true:
H(t) = D0*m;
P(t) = D0*s.
Consequently, if τ and β coefficients are determined, it is possible to estimate and predict the price change limit value D0 at any stage of the price change, including the early stage. However these statements will only be true when the material balance condition is fulfilled:
D(t) + H(t) + P(t) = D0 (4)
or: ![]()
Therefore the normalization requirement shall be met:
ℓ + m + s = 1; (5)
Let us check this fact using relations (1-3):
![]()
Precise fulfillment of the material balance condition (4) and satisfaction of the normalization requirement (5) indicate that the assumptions we made and the proposed relations are true.
Transient Functions for a Multiple-Cell Model
Reasoning in a similar manner regarding a black box multiple-cell model consisting of n cells, we get the following relations for D(t), H(t) and P(t) functions:
- D(t) = D0 * L;
- H(t) = D0 * M;
- P(t) = D0 * S;
where:
![]() (6)
(6)
which I have called a "two-parameter cumulative exponential distribution function" for now
![]() (7)
(7)
is a kind of the probability density function of the Gamma distribution or probability density function of the Erlang distribution;
![]() (8)
(8)
is a kind of the cumulative distribution function of the Gamma distribution or cumulative distribution function of the Erlang distribution,
- t/τ, n are distribution parameters;
- 1 is a Boolean expression evaluated to "true";
- 0 is a Boolean expression evaluated to "false";
The integration (8) can prove that:
or:
![]()
Consequently, according to (6-8) the normalization requirement is met precisely in this case, too:
L+M+S = 1; (9)
I have called L function a "function of future periods" since the future market price depends on its value, M function a "function of the present" since it determines the change in the market price per unit of the given period of time, and S function a "function of the past" as the market price level achieved over the entire period of time since the price destabilization occurred depends on the value of this function which doesn't contradict the notion of the transient and greatly expands our idea of what is going on in terms of philosophy of the problem.
By substituting n = 1 into (6-8) we can see that L, M and S functions become ℓ, m and s functions, respectively, therefore we will consider just L, M and S functions as the most general cases of the functions of this class for prediction purposes.
Development of Universal Regression Model for Market Price Prediction on the Basis of the Transient Functions Revealed
Dependence of the market price level P(h) on time t from the beginning of observations will be expressed, as follows:
In a single-cell model:
In a multiple-cell model:
![]() (10b)
(10b)
where: P0 is the price level right before its destabilization, i.e. by the time t = 0.
Parameters n and τ as well as β coefficient are determined using the actual market price values from the beginning of its destabilization in the market, whereby one analyzes changes in the market price f per unit of time t which can be taken as the value of the derivative of (10b). It can be seen that the error of accepting this assumption is negligibly small being a few hundredth of a percent of the price change value. Acceptance of this assumption greatly facilitates the process of determining the above parameters and β coefficient.
From analyzing S function we can now actually proceed to the analysis of M function:
![]() (11)
(11)
Dividing both parts of (11) by t^n and taking the logarithm of the obtained relation, we get an equation of a straight line in semi-logarithmic coordinates:
![]()
Now, if values of the function f to the corresponding points of time t are known, the parameters n and τ as well as β coefficient can be determined, as follows:
![]() (12)
(12)
![]() (13)
(13)
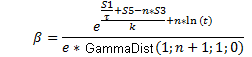 (14)
(14)
where:
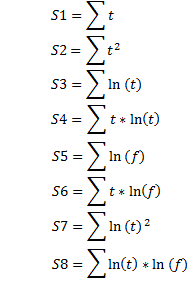
The values of the function f to the corresponding points of time t as well as the time t are determined based on the actual market price values Р0, Р1,…, Рк by the points of time һ0, һ1,…, һк from the beginning of the market price destabilization by means of numerical differentiation and integration at the middle of the interval:
f1 = (P1 - P0)/(һ1 – һ0);
f2 = (P2 – P1)/( һ2– һ1);
f3 = (P3 – P2)/( һ3– һ2); and so forth;
t1 = (һ0 + һ1)/2;
t2 = (һ1 + һ2)/2;
t3 = (һ3 + һ2)/2; and so forth.
Model Correction and Adjustment
Practical testing of (10a) and (10b) equations as a regression model when using the actual data has shown that Р(0) and D0 values should be corrected, as follows:
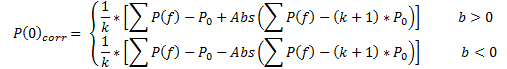 (15)
(15)
![]() (16)
(16)
where: Sf and Sr are areas of actual and theoretical curves, respectively;
∑Pf = P0+ P1 + P2 + …+ Pk is the sum of actual price values;
![]() (17)
(17)
i = 0, 1,2,......k;
k>2 is the number of time intervals for which the price variance is determined;
b is the coefficient of linear regression equation ![]() that determines the trend direction of the actual data.
that determines the trend direction of the actual data.
Now, the regression equation (10b) for prediction of the market price P(t) takes the final form, as follows:
![]() (18)
(18)
Model testing
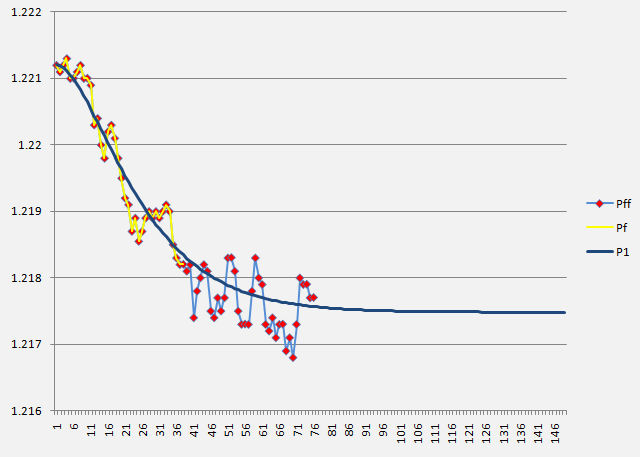
It has turned out that the market price values P(t) calculated in this manner and the actual price values Pf as provided in the Forex market example below, always entirely and precisely fulfill the material balance condition:
∑ P(t) = ∑ Pf. (19)
The fact that the sums of actual and theoretical values of the parameter under study, particularly the market price, are absolute, exact matches at any argument value, in particular the time, proves that the calculations, transformations and assumptions accepted at the function output are correct, and is indicative of universality of the proposed regression model.
The picture below shows the results of the Forex market actual data processing (1-minute time frame) in a specified way using equation (18) where one can note a satisfactory correspondence between the actual values (Pf) (yellow line with red dots), theoretical and prediction values (P1) (blue line) and actual future values that were not taken into account for calculation purposes (Pff) (blue line with red dots) of the EUR/USD quotes.
Conclusions
We have identified and proposed three functions that describe three dynamic transients, respectively, which are defined as various modifications of the Gamma distribution function determining the behavior of the parameter under study, particularly the market price, depending on the time in the future, present and past from the beginning of its destabilization.
Following the analysis of the specified processes, the universal regression model for the market price prediction was brought forward; it can serve as the basis for development of, e.g. market indicators for various purposes, Expert Advisors optimizing the traders' activity, automated trading systems and may even give rise to development of a trading robot - ROBOTRADER trading on its own for the benefit of a person.
P.S. All relations and formulas as well as the main assumptions and conclusions in this article have been ascertained, elaborated, introduced and made public in the open press for the first time.
References
- A. E. Kotenko. On Methods of Technical and Fundamental Analysis in the Forex Market Study. Electronic Magazine "INVESTIGATED IN RUSSIA", http://zhurnal.ape.relarn.ru/articles/2003/151.pdf
- V. N. Yakimkin. Forex Market – Your Way to Success, М., "Akmos-Media", 2001.
- V. N. Likhovidov. Fundamental Analysis of the Currency Markets: Methods for Prediction and Decision-Making. Vladivostok, 1999.
- M. K. Bunkina. A. M. Semenov. Principles of Currency Relations, М., Urait, 2000.
- Jeffrey D. Sachs, Felipe B. Larrain. Macroeconomics in the Global Economy. М., Delo, 1996.
- Rhea, Robert. Dow Theory,- New York; Barrons, 1932.
- Greiner, P. and H. C. Whitcomb: Dow Theory, New York: Investor’s Intelligence, 1969.
- O. S. Gulyaeva. Foreign Exchange Risk Management on the Basis of Currency Rate Pre-Prediction Analysis Using Fractal Methods. Ph.D. thesis, Moscow-Tver, TvGU, 2008.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/250
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Creating Expert Advisors Using Expert Advisor Visual Wizard
Creating Expert Advisors Using Expert Advisor Visual Wizard
 The Role of Statistical Distributions in Trader's Work
The Role of Statistical Distributions in Trader's Work
 Analysis of the Main Characteristics of Time Series
Analysis of the Main Characteristics of Time Series
 Custom Graphical Controls. Part 3. Forms
Custom Graphical Controls. Part 3. Forms
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Are the indicators paid or something? Published in the codebase, use it to your heart's content!
New article Universal Regression Model for Market Price Prediction is published:
Author: Юсуфходжа
good article.
very impressive
It is a pity, but there are mistakes at the very beginning of the article.
Firstly, the price increment at some time t will of course have some value and we denote it by D0. Let's assume.
Next... Now at t=0, I understand that there is no impact on the price and apparently there is no price increment from the external impact either. However, we again called the delta D0.
Then we put dt/tau into the formula, which is 1/C^2 anyway, i.e. we gave acceleration to the impact, which will move the geometric regression anyway. Why should we? After all, we have not yet defined - what this impact is such...
well, in general.
It is a pity, but there are mistakes at the very beginning of the article.
Firstly, the price increment at some time t will of course have some value and we denote it by D0. Let's assume.
Next... Now at t=0, I understand that there is no impact on the price and apparently there is no price increment from the external impact either. However, we again called the delta D0.
Then we put dt/tau into the formula, which is 1/C^2 anyway, i.e. we gave acceleration to the impact, which will move the geometric regression anyway. Why should we? After all, we have not yet defined - what this impact is such...
well, in general...
1. Do is not the price increment, but the initial potential of the force affecting the price at time t=0.
2. from the article: ".... assume that the market price, which is in equilibrium, can change only under the action of some external force D(t), the magnitude and value of which we will measure in the same dimension as the price.
Let us also assume that the change in the market price P(t) with the passage of time t from the beginning of the influence of this force, continuously increasing from zero value by some regularity unknown to us yet, tends to reach the value P(∞) = D0 in infinity. That is, by D0 we mean a finite increment or decrease of the market price, depending on the nature and sign of this influencing force.
Moreover, we assume that D(t=0) = D0. Let us further assume that during the infinitesimal period of time dt the influencing force will decrease by the value dD(t) in proportion to the remaining force D(t) by the moment of time t:
whence we obtain the exponential dependence of D(t) on time t in the form:
Where: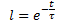
t - time from the beginning of the impact of destabilising force in time series units, sec. (min, hours, days, weeks, decades, months, years);
τ (tau) - the proportionality coefficient, numerically equal to the time constant of the process, sec.(min, hours, days, weeks, decades, months, years)."
Where did you find the dimensionality of 1/s^2 from? That ratio has no dimensionality. I didn't slip it in, I hypothesised that, the rate of change (decrease) of a force acting on a process is proportional to the force itself, which doesn't contradict logic, and then, this hypothesis was fully confirmed. As a coefficient of proportionality and introduced the ratio a (alpha) = 1/tau, which has the inverse of time, dimension. By a (alpha) I understand the impedance of the system, meaning the resistance of the system to the flow of the process, and tau is the image of time in Laplace transformations, as it turned out later, and allows to take the analysis of the process from the differential domain to the ordinary one. This means that any process has its own time, different from ours, and tau acts as a "translator" of times, if I may put it this way. In the bowels of the article I gave a way to estimate tau:
Now, if the values of the function f to the corresponding moments of time t are known, then from this equation the parameters n, τ and the coefficient β are determined as follows:
where:
The values of the function f to the corresponding moments of time t and time t are determined by the actual values of the market price P0, P1,..., Pk to the moments of time h0, h1,..., һk from the beginning of its destabilisation by numerical differentiation, referred to the middle of the interval:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); and so on;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; and so on.