
Modelo de Regresión Universal para la Predicción de Precio de Mercado
Introducción
El precio de mercado se forma mediante un equilibrio estable entre oferta y demanda, que a su vez depende de una variedad de factores económicos , políticos y psicológicos que son difíciles de considerar directamente a causa de las diferencias en su naturaleza, así como las causas de su influencia.
No obstante, es necesario ser capaz de prever y predecir el comportamiento futuro del precio del mercado con una cierta precisión para ser capaz de tomar las decisiones correctas respecto a la compra o venta de bienes, incluyendo divisas o acciones, en la situación actual. Este problema se puede solucionar usando una cantidad considerable de información de diferente naturaleza de todo tipo de fuentes que se procesa de una forma u otra.
Hay 4 tipos de análisis /1/ que se usan para el desarrollo de una estrategia efectiva y tácticas del comportamiento del mercado dependiendo del propósito, cualificación o predisposición del investigador:
- Análisis técnico basado en la afirmación de que el precio de mercado tiene en consideración todo lo que lo puede afectar. Utiliza técnicas matemáticas avanzadas /2/;
- Análisis fundamental que trata el efecto de diversos factores económicos en el precio de mercado. Substancialmente usa modelos macroeconómicos /3-5/;
- Análisis intuitivo basado en el conocimiento de los mayores índices e indicadores de mercado, método de predicción de sus comportamientos futuros, cuyos resultados no se pueden probar aplicando directamente reglas lógicas y matemáticas a las premisas iniciales, pero que, inexplicablemente, suelen acabar siendo ciertos;
- Psicoanálisis basado en un análisis psicológico de las condiciones de mercado para cada cliente individualmente, y juntos como un grupo, resultado en éxitos variados.
Estado de Conocimiento con Respecto al Problema
En nuestra opinión, cualquier técnica, incluyendo un nuevo método propuesto para la predicción de precio de mercado, debería considerar y, en una afortunada combinación de circunstancias, explicar las leyes basadas en tres axiomas conocidos como la Teoría Dow /6,7/ que se puede formular brevemente de la siguiente manera:
- El precio de mercado tiene en cuenta todos los factores que lo afectan, de acuerdo con la ley de oferta y demanda, y basta con tener información sobre los cambios en el precio de mercado a través del tiempo para poder predecirlo;
- La dependencia del precio de mercado en el tiempo es sujeto de tendencias que generalmente tienen forma de S, y los altos y bajos suelen estar conectados por líneas horizontales (planas) que se llaman tendencias laterales;
- Existen patrones de cambio de precio de mercado que ya existen objetivamente y que permanecen inalterables a través del tiempo, conocidos como los principios de que "la historia se repite", o "funcionaron bien en el pasado, y seguirán funcionando bien en el futuro".
No obstante, a las fases de reposo dinámicas de las series de precio de mercado, por ejemplo los tipos de cambio, le siguen fases que son tan complejas que dan la impresión de un caos completamente impredecible, que en el proceso de la auto-organización dan lugar al orden de nuevo.
Pero llegados a un determinado punto, el sistema dinámico debilitado por la estabilidad produce de nuevo un caos que nos da motivos para creer que la naturaleza de las series cronológicas de indicadores económicos es diversa. Esto significa que las series de precio de mercado son deterministas y analizables en algunos momentos, pero no se pueden predecir de forma segura en otros momentos; siguen la ley de distribución normal /8/ y actúan como una variable aleatoria en otros momentos.
Por tanto, el mundo científico actual no tiene todavía una opinión común respecto a la naturaleza de los cambios en el precio de mercado, lo que nos impide encontrar las dependencias que los definirían adecuadamente y serían aplicables en la práctica.
Funciones Transitorias para un Modelo de Celda Única de Caja Negra
A causa de la confusión que supone el proceso, yo sugiero echar primero un vistazo a un modelo de celda única de caja negra, que se atribuye a veces al problema en cuestión /1/, y aplicar la ecuación de equilibrio material.
Yendo más a fondo con los axiomas mencionados, imaginemos que el precio de mercado de equilibrio solo puede cambiar cuando resulta afectado por una fuerza externa D(t), cuya cantidad y valor se pueden medir en la misma dimensión que el precio.
Imaginemos también que el cambio en el precio de mercado P(t) a través del tiempo t desde el principio del impacto de la fuerza especificada se incrementa continuamente desde el valor cero de acuerdo con alguna ley que hasta ahora desconocemos, tratando de llegar a un valor de P(∞) = D0 en el infinito. En otras palabras, D0 implica un incremento o decremento finito del precio de mercado dependiendo de la naturaleza y signo de la fuerza que lo afecta.
También se implica que D(t=0) = D0. Podemos asumir también que, en el curso del período infinitesimal del período de tiempo dt, la fuerza que lo afecta disminuirá por el valor de dD(t) en proporción a la fuerza D(t) restante para el tiempo t:
![]()
de donde obtenemos la dependencia exponencial D(t) en el tiempo t, tal y como se muestra aquí:
![]() (1)
(1)
donde: ![]()
t es el período desde el principio del impacto de la fuerza desestabilizadora en unidades de series cronológicas, sec. (min, hrs, días, semanas, décadas, meses, años);
τ (tau) es el factor de proporcionalidad numérica igual a la constante de proceso de tiempo, sec. (min, hrs, días, semanas, décadas, meses, años).
Ahora, imaginemos que el cambio de velocidad V(t) del precio de mercado es proporcional tanto al valor de D(t) como al tiempo t:
![]()
donde: ![]() (2)
(2)
k es el factor de proporcionalidad que tiene la dimensión 1/(tiempo)^2;
β = k*τ*D0 es el factor de proporcionalidad que tiene la dimensión de la velocidad de cambio de precio de mercado.
El incremento o decremento absoluto del precio por unidad de tiempo para el tiempo t que se expresa como H(t) es numéricamente igual a V(t):
H(t) = V(t) = β*m
Sin duda, integrando H(t) a través de toda la extensión del cambio de tiempo t obtendremos un valor total del cambio en el precio de mercado P(t) para el tiempo t desde el comienzo de su desestabilización:
![]()
donde: ![]() (3)
(3)
Puesto que está basado en (3), parece que el momento en que t = ∞ s = 1, llegamos a la conclusión que:
P(∞) = β*τ = D0;
or: β = D0/τ;
Al comparar la nota anterior de β con el resultado recibido, concluimos que:
k = 1/τ^2;
Ahora, las siguientes relaciones son ciertas:
H(t) = D0*m;
P(t) = D0*s.
Por tanto, si los coeficientes de τ y β están determinados, es posible estimar y predecir el cambio de precio D0 en cualquier fase del cambio de precio, incluyendo la fase temprana. No obstante, estas declaraciones solo serán ciertas cuando la condición de equilibrio material se cumpla:
D(t) + H(t) + P(t) = D0 (4)
o: ![]()
Por tanto, se cumplirá el requisito de normalización:
ℓ + m + s = 1; (5)
Comprobemos este hecho usando las relaciones (1-3):
![]()
El cumplimiento preciso de la condición de equilibrio material (4) y satisfacción del requisito de normalización (5) indican que las suposiciones que hicimos y las relaciones propuestas son ciertas.
Funciones Transitorias para un Modelo de Celda Múltiple
Siguiendo un razonamiento similar respecto a un modelo de caja negra de celda múltiple consistente en n celdas, obtenemos las siguientes relaciones para las funciones D(t), H(t) y P(t):
- D(t) = D0 * L;
- H(t) = D0 * M;
- P(t) = D0 * S;
donde:
![]() (6)
(6)
que yo he llamado una "función de distribución exponencial acumulativa de dos parámetros" por ahora
![]() (7)
(7)
es un tipo de función de densidad de probabilidad de la distribución Gamma, o función de densidad de probabilidad de la distribución Erlang;
![]() (8)
(8)
es un tipo de función de distribución acumulativa de la distribución Gamma o función de distribución acumulativa de la distribución Erlang,
- t/τ, n son parámetros de distribución;
- 1 es una expresión booleana evaluada a "true";
- 0 es una expresión booleana evaluada a "false";
La integración (8) puede probar que:
o:
![]()
Consecuentemente, de acuerdo con (6-8), el requisito de normalización se cumple precisamente en este caso, también:
L+M+S = 1; (9)
He llamado a la función L una "función de períodos futuros", puesto que el precio de mercado futuro depende de su valor; la función M, "función del presente", puesto que determina el cambio en el precio de mercado por unidad del período de tiempo especificado; y la función S, "función del pasado", puesto que el nivel de precio de mercado conseguido durante el período de tiempo entero desde que se dio la desestabilización depende del valor de esta función, que no contradice la noción de transitoriedad, y expande en gran medida nuestra idea de qué está pasando en términos de filosofía del problema.
Sustituyendo n = 1 en (6-8) podemos ver que las funciones L, M y S se convierten en funciones ℓ, m y s respectivamente, y por tanto consideraremos solo las funciones L, M y S como los casos más generales de las funciones de esta clase para propósitos de predicción.
Desarrollo de Modelo de Regresión Universal de Predicción de Precio de Mercado en la Base de Funciones Transitorias Revelado
La dependencia del nivel de precio de mercado (P(h) en el tiempo t desde el principio de las observaciones se expresará de la siguiente manera:
En un modelo de celda única:
En un modelo de celda múltiple:
![]() (10b)
(10b)
donde: P0 es el nivel de precio justo antes de su desestabilización, por ejemplo para el tiempo t = 0.
Los parámetros n y τ, así como el coeficiente de β, se determinan usando los valores de precio de mercado reales del principio de su desestabilización en el mercado, donde se analizan cambios en el precio de mercado f por unidad de tiempo t que se pueden tomar como el valor de la derivativa de (10b). Se puede ver que el error de aceptar esta suposición es prácticamente insignificante, puesto que se trata de varios cientos de un porcentaje del valor de cambio de precio. La aceptación de esta suposición facilita mucho el proceso de determinar los parámetros anteriores y el coeficiente de β.
Tras analizar la función S, ahora podemos continuar con el análisis de la función M:
![]() (11)
(11)
Dividiendo ambas partes de (11) por t^n y tomando el logaritmo de la relación obtenida, conseguiremos una ecuación de línea recta en coordinadas semi-logarítmicas:
![]()
Ahora, si se conocen los valores de la función f con los puntos de tiempo t correspondientes, los parámetros n y τ, así como el coeficiente β, se pueden determinar de la siguiente manera:
![]() (12)
(12)
![]() (13)
(13)
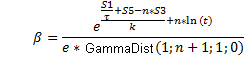 (14)
(14)
donde:
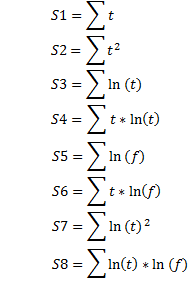
Los valores de la función f con los puntos de tiempo t correspondientes se determinan con base en los valores de precio de mercado reales Р0, Р1,…, Рк por los puntos de tiempo һ0, һ1,…, һк del principio de la desestabilización del precio de mercado por medio de diferenciación e integración numérica en mitad del intervalo:
f1 = (P1 - P0)/(һ1 – һ0);
f2 = (P2 – P1)/( һ2– һ1);
f3 = (P3 – P2)/( һ3– һ2); and so forth;
t1 = (һ0 + һ1)/2;
t2 = (һ1 + һ2)/2;
t3 = (һ3 + һ2)/2; and so forth.
Corrección y Ajuste del Modelo
La comprobación práctica de las ecuaciones (10a) y (10b) como modelo de regresión al usar los datos reales muestra que los valores Р(0) y D0 deberían corregirse de la siguiente manera:
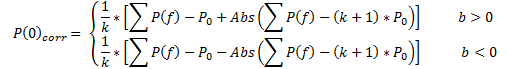 (15)
(15)
![]() (16)
(16)
donde: Sf y Sr son áreas de curvas reales y teóricas, respectivamente;
∑Pf = P0+ P1 + P2 + …+ Pk es la suma de valores de precio reales;
![]() (17)
(17)
i = 0, 1,2,......k;
k>2 es el número de intervalos de tiempo por los cuales se determina la diferencia de precio;
b es el coeficiente de la ecuación de regresión lineal ![]() que determina la dirección de la tendencia de la información real.
que determina la dirección de la tendencia de la información real.
Ahora la ecuación de regresión (10b) para predecir el precio de mercado P(t) toma la forma final, como se muestra a continuación:
![]() (18)
(18)
Comprobación de modelo
Al parecer, los valores de precio de mercado P(t) calculados de esta forma y los valores de precio reales Pf facilitados por el ejemplo del mercado Forex de abajo siempre cumplen la condición de equilibrio material de forma completa y precisa:
∑ P(t) = ∑ Pf. (19)
El hecho de que las sumas de valores reales y teóricos del parámetro que se estudia, en particular el precio de mercado, son exactamente iguales que cualquier valor de argumento, en particular el del tiempo, prueba que los cálculos, transformaciones y suposiciones aceptadas en la salida de función son correctas, y es una señal de la universalidad del modelo de regresión propuesto.
La imagen de abajo muestra los resultados del procesamiento de datos reales del mercado Forex (marco temporal de 1 minuto) de forma específica usando la ecuación (18), en la que se puede notar una correspondencia satisfactoria entre los valores reales (Pf) (línea amarilla con puntos rojos), los valores teóricos y de predicción (P1) (línea azul) y los valores futuros reales que no se tomaron en cuenta en los cálculos (Pff) (línea azul con puntos rojos) de las cuotas EUR/USD.
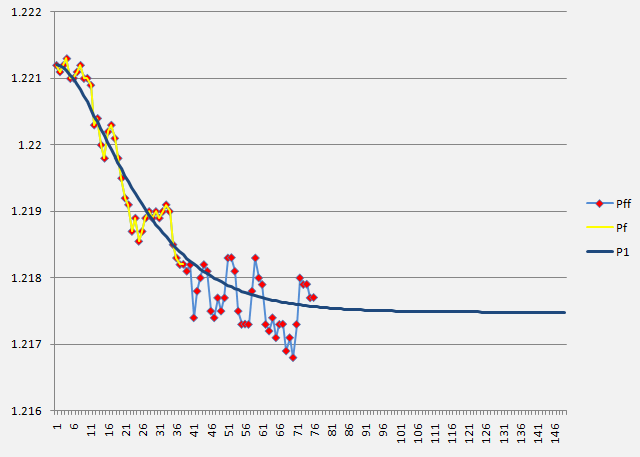
Conclusiones
Hemos identificado y propuesto tres funciones que describen tres elementos transitorios dinámicos, respectivamente, que se definen como varias modificaciones de la distribución Gamma que determinan el comportamiento del parámetro estudiado, particularmente el precio de mercado, dependiendo del tiempo en el futuro, presente y pasado desde el comienzo de la desestabilización.
Siguiendo el análisis de los procesos especificados, se mostró el modelo de regresión universal para la predicción de precio de mercado; puede servir como base para el desarrollo, por ejemplo, de indicadores de mercado para varios propósitos, Asesores Expertos que optimicen la actividad del trader, sistemas de trading automatizados, y podría incluso llevar al desarrollo de un robot de trading - ROBOTRADER, que podría llevar a cabo trading por sí mismo en beneficio de una persona.
P.S. Todas las relaciones y fórmulas, así como las suposiciones y conclusiones principales en este artículo, se han hecho, elaborado, introducido y publicado en la prensa pública por primera vez.
Referencias
- A. E. Kotenko. On Methods of Technical and Fundamental Analysis in the Forex Market Study (Sobre Métodos de Análisis Técnico y Fundamental en el Estudio del Mercado Forex). Revista electrónica "INVESTIGATED IN RUSSIA" ("INVESTIGADO EN RUSIA"), http://zhurnal.ape.relarn.ru/articles/2003/151.pdf
- V. N. Yakimkin. Forex Market – Your Way to Success (Mercado Forex - Su Camino hacia el Éxito), М., "Akmos-Media", 2001.
- V. N. Likhovidov. Fundamental Analysis of the Currency Markets: Methods for Prediction and Decision-Making (Análisis Fundamental de los Mercados de Divisas: Métodos de Predicción y Toma de Decisiones). Vladivostok, 1999.
- M. K. Bunkina. A. M. Semenov. Principles of Currency Relations (Principios de Relaciones de Divisas), М., Urait, 2000.
- Jeffrey D. Sachs, Felipe B. Larrain. Macroeconomics in the Global Economy (Macroeconomía en la Economía Global). М., Delo, 1996.
- Rhea, Robert. Dow Theory (Teoría Dow),- New York; Barrons, 1932.
- Greiner, P. and H. C. Whitcomb: Dow Theory, New York: Investor’s Intelligence (Teoría Dow, Nueva York: la Inteligencia del Inversor), 1969.
- O. S. Gulyaeva. Foreign Exchange Risk Management on the Basis of Currency Rate Pre-Prediction Analysis Using Fractal Methods (Gestión de Riesgos de Intercambio Extranjero en Base al Análisis Predicción de Tipos de Cambio Usando Métodos de Fractales). Ph.D. thesis, Moscow-Tver, TvGU, 2008.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/250
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Usar Indicadores de MetaTrader 5 con la Estructura de Aprendizaje Automático ENCOG para Predicción de Series Cronológicas
Usar Indicadores de MetaTrader 5 con la Estructura de Aprendizaje Automático ENCOG para Predicción de Series Cronológicas
 Exponer código C# a MQL5 usando exportaciones no gestionadas
Exponer código C# a MQL5 usando exportaciones no gestionadas
 La implementación del análisis automático de las Ondas de Elliott en MQL5
La implementación del análisis automático de las Ondas de Elliott en MQL5
 Random Walk y el Indicador de Tendencias
Random Walk y el Indicador de Tendencias
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
¿Los indicadores son de pago o algo así? Publicado en la base de código, ¡úsalo a tu antojo!
Se publica un nuevo artículo Modelo de regresión universal para la predicción de precios de mercado:
Autor: Юсуфходжа
buen artículo.
muy impresionante
Es una pena, pero hay errores al principio del artículo.
En primer lugar, el incremento del precio en algún momento t tendrá, por supuesto, algún valor y lo denotamos por D0. Supongamos.
A continuación... Ahora en t=0, entiendo que no hay impacto en el precio y aparentemente tampoco hay incremento de precio por el impacto externo. Sin embargo, volvemos a llamar al delta D0.
Entonces ponemos dt/tau en la fórmula, que de todas formas es 1/C^2, es decir, le damos aceleración al impacto, que de todas formas moverá la regresión geométrica ¿Por qué deberíamos hacerlo? Después de todo, todavía no hemos definido - lo que este impacto es tal ...
bueno, en general.
Es una pena, pero hay errores al principio del artículo.
En primer lugar, el incremento del precio en algún momento t tendrá, por supuesto, algún valor y lo denotamos por D0. Supongamos.
A continuación... Ahora en t=0, entiendo que no hay impacto en el precio y aparentemente tampoco hay incremento de precio por el impacto externo. Sin embargo, volvemos a llamar al delta D0.
Entonces ponemos dt/tau en la fórmula, que de todas formas es 1/C^2, es decir, le damos aceleración al impacto, que de todas formas moverá la regresión geométrica ¿Por qué deberíamos hacerlo? Después de todo, todavía no hemos definido - lo que este impacto es tal ...
bueno, en general...
1. Do no es el incremento del precio, sino el potencial inicial de la fuerza que afecta al precio en el momento t=0.
2. del artículo: ".... supongamos que el precio de mercado, que está en equilibrio, sólo puede cambiar bajo la acción de alguna fuerza externa D(t), cuya magnitud y valor mediremos en la misma dimensión que el precio.
Supongamos también que el cambio en el precio de mercado P(t) con el paso del tiempo t desde el comienzo de la influencia de esta fuerza, aumentando continuamente desde el valor cero por alguna regularidad que aún desconocemos, tiende a alcanzar el valor P(∞) = D0 en el infinito. Es decir, por D0 entendemos un incremento o decremento finito del precio de mercado, dependiendo de la naturaleza y signo de esta fuerza influyente.
Además, suponemos que D(t=0) = D0. Supongamos además que durante el período infinitesimal de tiempo dt la fuerza influyente disminuirá en el valor dD(t) en proporción a la fuerza restante D(t) en el momento del tiempo t:
de donde obtenemos la dependencia exponencial de D(t) con el tiempo t en la forma:
Donde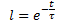
t - tiempo transcurrido desde el inicio del impacto de la fuerza desestabilizadora en unidades de la serie temporal, seg. (min, horas, días, semanas, décadas, meses, años);
τ (tau) - el coeficiente de proporcionalidad, numéricamente igual a la constante de tiempo del proceso, seg.(min, horas, días, semanas, décadas, meses, años)."
¿De dónde has sacado la dimensionalidad de 1/s^2? Ese cociente no tiene dimensionalidad. No lo colé, hipoteticé que, la tasa de cambio (disminución ) de una fuerza que actúa sobre un proceso es proporcional a la propia fuerza, lo cual no contradice la lógica, y luego, esta hipótesis se confirmó plenamente. Como coeficiente de proporcionalidad e introdujo la relación a (alfa) = 1/tau, que tiene la inversa del tiempo, dimensión. Por a (alfa) entiendo la impedancia del sistema, es decir, la resistencia del sistema al flujo del proceso, y tau es la imagen del tiempo en las transformaciones de Laplace, como se vio después, y permite llevar el análisis del proceso desde el dominio diferencial al ordinario. Esto significa que cualquier proceso tiene su propio tiempo, distinto del nuestro, y tau actúa como un "traductor" de tiempos, si se me permite la expresión. En las entrañas del artículo di una forma de estimar tau:
Ahora bien, si se conocen los valores de la función f a los correspondientes instantes de tiempo t, entonces a partir de esta ecuación se determinan los parámetros n, τ y el coeficiente β de la siguiente manera:
donde:
Los valores de la función f a los correspondientes instantes de tiempo t y tiempo t vienen determinados por los valores reales del precio de mercado P0, P1,..., Pk a los instantes de tiempo h0, h1,..., һk desde el inicio de su desestabilización por diferenciación numérica, referida a la mitad del intervalo:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); y así sucesivamente;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; etc.