
Universelles Regressionsmodell für die Prognostizierung von Marktpreisen
Einleitung
Der Marktpreis wird aus einer stabilen Balance zwischen Angebot und Nachfrage geformt, die ihrerseits von diversen wirtschaftlichen, politischen und psychologischen Faktoren abhängen, deren direkte Betrachtung aufgrund der Unterschiede in der Natur und den Ursachen ihrer Auswirkungen schwierig ist.
Allerdings ist es notwendig, das zukünftige Verhalten des Marktes mit einer gewissen Genauigkeit vorhersehen und prognostizieren zu können, um die richtigen Entscheidungen in Bezug auf den Kauf oder Verkauf von Gütern, einschließlich Währungen oder Aktien, unter den aktuellen Umständen zu treffen. Dieses Problem lässt sich mithilfe einer beträchtlichen Menge an Informationen verschiedenster Art aus allen möglichen Quellen, die auf die eine oder andere Weise verarbeitet werden, lösen.
Es gibt 4 Typen der Analyse /1/, die für die Entwicklung einer effektiven Strategie und Taktik für das Marktverhalten verwendet werden, je nach Ziel, Qualifizierung oder Veranlagung des Forschers:
- Technische Analyse auf Basis der Annahme, dass der Marktpreis alle Faktoren berücksichtigt, die sich auf ihn auswirken können. Sie nutzt fortschrittliche mathematische Techniken /2/;
- Fundamentalanalyse, die sich mit den Auswirkungen verschiedener wirtschaftlicher Faktoren auf den Marktpreis beschäftigt. Sie nutzt im Wesentlichen makroökonomische Modelle /3-5/;
- Intuitive Analyse, gestützt durch die Kenntnis der wichtigen Marktindizes und -indikatoren, eine Methode zur Prognostizierung ihres zukünftigen Verhaltens, deren Ergebnisse sich nicht durch die direkte Anwendung logischer und mathematischer Regeln auf die Grundvoraussetzungen beweisen lassen, die sich aber dennoch häufig unerklärlicherweise als richtig erweist;
- Psychoanalyse auf Basis einer psychologischen Analyse der Marktbedingungen durch jeden einzelnen Kunden sowie als Gruppe mit unterschiedlichen Erfolgen.
Wissensstand zum Problem
Jede Technik, einschließlich einer neu vorgeschlagenen Methode zur Prognostizierung des Marktpreises, sollte unserer Meinung nach die objektiv bestehenden Gesetzmäßigkeiten auf Basis von drei als Dow-Theorie /6, 7/ bekannten Axiomen berücksichtigen und, in einer glücklichen Kombination von Gegebenheiten, erklären können. Diese lassen sich kurz gefasst wie folgt formulieren:
- Der Marktpreis berücksichtigt alle Einflussfaktoren in Übereinstimmung mit dem Gesetz von Angebot und Nachfrage und es genügt, über Daten über Änderungen des Marktpreises im Verlauf der Zeit zu verfügen, um ihn prognostizieren zu können;
- Die Abhängigkeit des Marktpreises von der Zeit unterliegt Tendenzen (Trends), die überwiegend S-förmig sind und deren Hoch- und Tiefpunkte durch horizontale (flache) Linien, die als Seitwärtstrend bezeichnet werden, verbunden sind oder keine solchen Linien aufweisen;
- Es existieren objektiv vorhandene Änderungsmuster des Marktpreises, die im Verlauf der Zeit unverändert bleiben. Diese sind als Prinzipien "die Geschichte wiederholt sich" oder "sie haben in der Vergangenheit funktioniert, funktionieren jetzt und werden in Zukunft funktionieren" bekannt.
Allerdings folgen auf dynamische Ruhephasen der Zeitreihe von Marktpreisen, beispielsweise Währungskurse, Phasen, die so komplex sind, dass man den Eindruck bekommt, es handle sich um unvorhersehbares Chaos, das im Prozess der Selbstorganisation wieder zu Ordnung führt.
Doch an einem gewissen Punkt produziert das durch Stabilität geschwächte dynamische System erneut Chaos, was uns Grund zur Annahme gibt, dass wirtschaftliche Indikatoren von Zeitreihen gemischter Natur sind. Das bedeutet, dass Zeitreihen von Marktpreisen an einem Punkt deterministisch und analysierbar sind, an einem anderen Punkt aber nicht zuverlässig prognostiziert werden können und dem normalen Verteilungsgesetz /8/ folgen und an noch einem weiteren Punkt als zufällige Variablen fungieren.
Somit fehlt der Forschung zur Zeit eine einheitliche Meinung über die Natur von Änderungen des Marktpreises, was uns daran hindert, die Abhängigkeiten zu finden, die sie angemessen definieren würden und praktisch umsetzbar wären.
Übergangsfunktionen für das einzellige Black-Box-Modell
Aufgrund der Unbestimmtheit des Prozesses schlage ich vor, dass wir uns zuerst ein einzelliges Black-Box-Modell ansehen, das manchmal dem Problem in Frage /1/ zugeschrieben wird, und die Gleichung der Materialbilanz anwenden.
Nehmen wir auf den oben aufgeführten Axiomen aufbauend an, dass sich der Gleichgewichtspreis nur ändern kann, wenn er durch eine externe Kraft D(t) betroffen ist, deren Höhe und Wert in der gleichen Dimension wie der Preis gemessen werden.
Wir nehmen auch an, dass die Änderung des Marktpreises P(t) im Verlauf der Zeit t ab dem Anfang der Wirkung der angegebenen Kraft kontinuierlich ab dem Nullwert in Übereinstimmung mit einem derzeit noch unbekannten Gesetz steigt und versucht, im Unendlichen einen Wert von P(∞) = D0 zu erreichen. In anderen Worten: D0 bedeutet eine endliche Zu- oder Abnahme des Marktpreises abhängig von der Natur und dem Zeichen der auf ihn einwirkenden Kraft.
Es wird auch impliziert, dass D(t=0) = D0. Wir nehmen weiter an, dass im Verlauf des infinitesimalen Zeitraums dt die einwirkende Kraft um den Wert dD(t) proportional zur zum Zeitpunkt t verbleibenden Kraft D(t) abnimmt:
![]()
woraus wir die exponentielle Abhängigkeit D(t) von der Zeit t erhalten, wie folgt:
![]() (1)
(1)
wobei: ![]()
t ist die Zeit ab dem Beginn der Wirkung der destabilisierenden Kraft in Einheiten der Zeitreihe, Sek. (Min., Std., Tage, Wochen, Jahrzehnte, Monate, Jahre);
τ (Tau) ist der Proportionalitätsfaktor, der der Konstante der Prozesszeit, Sek. (Min., Std., Tage, Wochen, Jahrzehnte, Monate, Jahre) numerisch gleich ist.
Nehmen wir nun an, dass die Änderungsgeschwindigkeit V(t) des Marktpreises P(t) sowohl zum Wert D(t) als auch zur Zeit t proportional ist:
![]()
wobei: ![]() (2)
(2)
k ist der Proportionalitätsfaktor mit der Abmessung 1/(Zeit)^2;
β = k*τ*D0 ist der Proportionalitätsfaktor, der die Abmessung der Änderungsgeschwindigkeit des Marktpreises hat.
Die absolute Zu- oder Abnahme des Preises pro Zeiteinheit zur gegebenen Zeit t, die als H(t) ausgedrückt wird, ist numerisch gleich V(t):
H(t) = V(t) = β*m
Zweifelsohne erhalten wir durch die Integration von H(t) im gesamten Bereich der Änderung der Zeit t einen Gesamtwert der Änderung des Marktpreises P(t) zum Zeitpunkt t ab dem Beginn der Destabilisierung:
![]()
wobei: ![]() (3)
(3)
Da es anhand von (3) scheint, dass t = ∞ s = 1, schlussfolgern wir:
P(∞) = β*τ = D0;
oder: β = D0/τ;
Beim Vergleich der vorherigen Darstellung von β mit unserem Ergebnis schlussfolgern wir:
k = 1/τ^2;
Nun sind die folgenden Verhältnisse wahr:
H(t) = D0*m;
P(t) = D0*s.
Anschließend kann der Grenzwert D0 der Preisänderung bei der Bestimmung der Koeffizienten τ und β in jeder Phase der Preisänderung prognostiziert werden, einschließlich der frühen Phase. Allerdings sind diese Aussagen nur dann wahr, wenn die Bedingung der Materialbilanz erfüllt ist:
D(t) + H(t) + P(t) = D0 (4)
oder: ![]()
Folglich muss die Normalisierungsanforderung erfüllt werden:
ℓ + m + s = 1; (5)
Prüfen wir dies mithilfe der Verhältnisse (1-3):
![]()
Die genaue Erfüllung der Bedingung der Materialbilanz (4) und die Erfüllung der Normalisierungsanforderung (5) deuten darauf hin, dass unsere Annahmen und vorgeschlagenen Verhältnisse wahr sind.
Übergangsfunktionen für ein mehrzelliges Modell
Mit ähnlichen Überlegungen bezüglich eines mehrzelligen Black-Box-Modells aus n Zellen erhalten wir die folgenden Verhältnisse für die Funktionen D(t), H(t) und P(t):
- D(t) = D0 * L;
- H(t) = D0 * M;
- P(t) = D0 * S;
wobei:
![]() (6)
(6)
die ich im Moment "kumulative exponentielle Verteilungsfunktion mit zwei Parametern" nenne
![]() (7)
(7)
Ist eine Art der Wahrscheinlichkeitsdichtefunktion der Gamma-Verteilung oder Wahrscheinlichkeitsdichtefunktion der Erlang-Verteilung;
![]() (8)
(8)
Ist eine Art der kumulativen Verteilungsfunktion der Gamma-Verteilung oder kumulativen Verteilungsfunktion der Erlang-Verteilung;
- t/τ, n sind Parameter der Verteilung;
- 1 ist ein boolescher Ausdruck mit dem Wert "true";
- 0 ist ein boolescher Ausdruck mit dem Wert "false";
Die Integration (8) kann beweisen, dass:
oder:
![]()
Somit ist die Normalisierungsanforderung gemäß (6-8) auch in diesem Fall genau erfüllt:
L+M+S = 1; (9)
Die Funktion L bezeichne ich als "Funktion zukünftiger Zeiträume", weil der zukünftige Marktpreis von ihrem Wert abhängt, die Funktion M als "Funktion der Gegenwart", weil sie die Änderung des Marktpreises pro Einheit des gegebenen Zeitraums bestimmt, und die Funktion S eine "Funktion der Vergangenheit", da das Marktpreisniveau, das über den gesamten Zeitraum seit dem Auftreten der Destabilisierung erreicht wurde, vom Wert dieser Funktion abhängig ist, was dem Verständnis des Übergangsprozesses nicht widerspricht und unsere Vorstellung dessen, was in Bezug auf die Philosophie des Problems passiert, deutlich erweitert.
Durch die Ersetzung von n = 1 durch (6-8) erkennen wir, dass aus den Funktionen L, M und S jeweils die Funktionen ℓ, m und s werden. Deshalb betrachten wir für Prognosezwecke nur die Funktionen L, M und S als allgemeingültigste Fälle der Funktionen dieser Klasse.
Entwicklung eines universellen Regressionsmodells für die Prognostizierung des Marktpreises auf Basis der gezeigten Übergangsfunktionen
Die Abhängigkeit des Marktpreisniveaus P(h) von der Zeit t ab dem Beginn der Beobachtungen wird ausgedrückt wie folgt:
In einem einzelligen Modell:
In einem mehrzelligen Modell:
![]() (10b)
(10b)
wobei: P0 ist das Preisniveau unmittelbar vor seiner Destabilisierung, d. h. zum Zeitpunkt t = 0.
Die Parameter n und τ sowie der Koeffizient β werden mithilfe der tatsächlichen Marktpreiswerte ab dem Beginn seiner Destabilisierung auf dem Markt bestimmt, wobei Änderungen des Marktpreises f pro Zeiteinheit t, was als Wert der Ableitung von (10b) angenommen werden kann, analysiert werden. Es zeigt sich, dass der Fehler aus der Übernahme dieser Annahme vernachlässigbar klein ist – nur einige Hundertstel Prozent des Wertes der Preisänderung. Die Übernahme dieser Annahme erleichtert den Prozess zur Bestimmung der oben aufgeführten Parameter und des Koeffizienten β deutlich.
Von der Analyse der Funktion S können wir nun zur Analyse der Funktion M übergehen:
![]() (11)
(11)
Durch die Teilung beider Teile von (11) durch t^n und Anwendung des Logarithmus des erhaltenen Verhältnisses erhalten wir die Gleichung einer geraden Linie in semi-logarithmischen Koordinaten:
![]()
Wenn nun die Werte der Funktion f zu den entsprechenden Zeitpunkten t bekannt sind, können die Parameter n und τ sowie der Koeffizient β auf die folgende Art bestimmt werden:
![]() (12)
(12)
![]() (13)
(13)
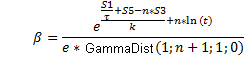 (14)
(14)
wobei:
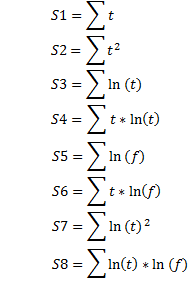
Die Werte der Funktion f zu den entsprechenden Zeitpunkten t sowie die Zeit t werden basierend auf den tatsächlichen Marktpreiswerten P0, P1,..., Pк zu den Zeitpunkten h0, h1,...,hк ab dem Beginn der Destabilisierung des Marktpreises durch eine numerische Differentiation und Integration in der Mitte des Intervalls bestimmt:
f1 = (P1 - P0)/(һ1 – һ0);
f2 = (P2 – P1)/(һ2– һ1);
f3 = (P3 – P2)/(һ3– һ2); und so weiter;
t1 = (һ0 + һ1)/2;
t2 = (һ1 + һ2)/2;
t3 = (һ3 + һ2)/2; und so weiter.
Korrektur und Einstellung des Modells
Praktische Erprobungen der Gleichungen (10a) und (10b) als Regressionsmodell bei der Verwendung der tatsächlichen Daten haben gezeigt, dass die Werte P(0) und D0 korrigiert werden sollten, wie folgt:
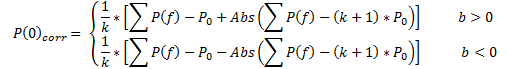 (15)
(15)
![]() (16)
(16)
wobei: Sf und Sr sind jeweils Bereiche tatsächlicher bzw. theoretischer Kurven;
∑Pf = P0+ P1 + P2 + …+ Pk ist die Summe der tatsächlichen Preiswerte;
![]() (17)
(17)
i = 0, 1,2,......k;
k>2 ist die Menge der Zeitintervalle, für die die Preisvarianz bestimmt wird;
b ist der Koeffizient der linearen Regressionsgleichung ![]() , die die Trendrichtung der tatsächlichen Daten bestimmt.
, die die Trendrichtung der tatsächlichen Daten bestimmt.
Nun nimmt die Regressionsgleichung (10b) für die Prognostizierung des Marktpreises P(t) ihre endgültige Form an:
![]() (18)
(18)
Modellerprobung
Es hat sich erwiesen, dass die auf diese Weise errechneten Marktpreiswerte P(t) und die tatsächlichen Preiswerte Pf, wie im unten aufgeführten Forex-Marktbeispiel dargestellt, die Bedingung der Materialbilanz vollständig und genau erfüllen:
∑ P(t) = ∑ Pf. (19)
Die Tatsache, dass die Summen tatsächlicher und theoretischer Werte des untersuchten Parameters, insbesondere des Marktpreises, bei jedem Argumentwert, insbesondere der Zeit, absolut und genau übereinstimmen, beweist, dass die Berechnungen, Umwandlungen und übernommenen Annahmen bei der Ausgabe der Funktionen korrekt sind, und unterstreicht die universelle Einsatzfähigkeit des vorgeschlagenen Regressionsmodells.
Die unten aufgeführte Abbildung zeigt die Ergebnisse der Verarbeitung tatsächlicher Daten des Forex-Marktes (1-minütiger Timeframe) auf eine festgelegte Art, die Gleichung (18) nutzt, bei der man eine zufriedenstellende Entsprechung zwischen den tatsächlichen Werten (Pf) (gelbe Linie mit roten Punkten), theoretischen und prognostizierten Werten (P1) (blaue Linie) und tatsächlichen zukünftigen Werten, die für Berechnungszwecke nicht berücksichtigt wurden (Pff) (blaue Linie mit roten Punkten), der EUR/USD-Gebote erkennt.
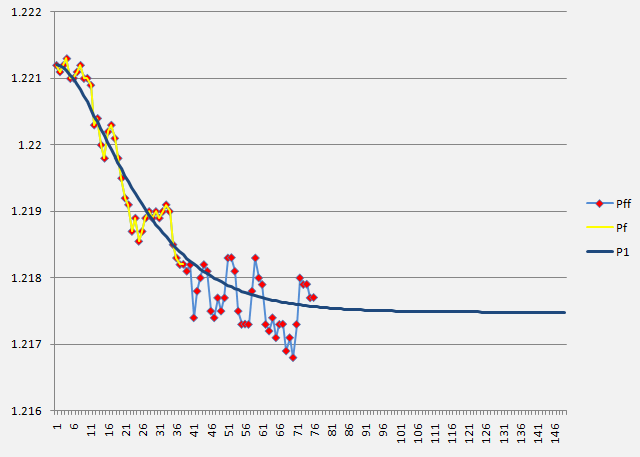
Fazit
Wir haben drei Funktionen identifiziert und vorgeschlagen, die drei entsprechende dynamische Übergangsprozesse beschreiben, die als unterschiedliche Modifikationen der Gamma-Verteilungsfunktion definiert sind und das Verhalten des untersuchten Parameters bestimmen, insbesondere des Marktpreises, in Abhängigkeit von der Zeit in der Zukunft, Gegenwart und Vergangenheit ab dem Beginn seiner Destabilisierung.
Anhand der Analyse der festgelegten Prozesse wurde das universelle Regressionsmodell für die Prognostizierung des Marktpreises vorgestellt. Es kann als Entwicklungsbasis dienen, z. B. für Marktindikatoren für verschiedene Zwecke, Expert Advisors, die die Aktivitäten der Händler optimieren, automatische Handelssysteme und kann sogar die Entwicklung des Handelsroboters ROBOTRADER ermöglichen, der selbstständig zugunsten einer Person handelt.
P.S. Alle Verhältnisse und Formeln sowie die grundlegenden Annahmen und Schlussfolgerungen in diesem Beitrag wurden zum ersten Mal ermittelt, ausgearbeitet, vorgestellt und in der freien Presse veröffentlicht.
Literatur
- A. E. Kotenko. Über Methoden der technischen und Fundamentalanalyse in der Studie des Forex-Marktes (russisch). Elektronisches Magazin "INVESTIGATED IN RUSSIA", http://zhurnal.ape.relarn.ru/articles/2003/151.pdf
- V. N. Yakimkin. Forex-Markt – Ihr Weg zum Erfolg, M., "Akmos-Media", 2001.
- V. N. Lichowidow. Fundamentalanalyse der Währungsmärkte: Methoden für Prognostizierung und Entscheidungsfindung. Wladiwostok, 1999.
- M. K. Bunkina. A. M. Semenow. Prinzipien der Währungsverhältnisse, M., Urait, 2000.
- Jeffrey D. Sachs, Felipe B. Larrain. Makroökonomik: in globaler Sicht. М., Delo, 1996.
- Rhea, Robert. Dow Theory,- New York; Barrons, 1932.
- Greiner, P. und H. C. Whitcomb: Dow Theory, New York: Investor’s Intelligence, 1969.
- O. S. Gulyaeva. Management von Währungsrisiken auf Basis der Analyse von Vorabprognosen von Währungskursen mithilfe von Fraktalmethoden. Doktorarbeit, Moskau-Tver, TvGU, 2008.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/250
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Hedging-System zur Verrechnung von Positionen in MetaTrader 5 verfügbar
Hedging-System zur Verrechnung von Positionen in MetaTrader 5 verfügbar
 Offenlegen von C#-Code in MQL5 mithilfe nicht gemanagter Exporte
Offenlegen von C#-Code in MQL5 mithilfe nicht gemanagter Exporte
 Ändern Externer Parameter von MQL4 Programmen ohne Neustart
Ändern Externer Parameter von MQL4 Programmen ohne Neustart
 Random Walk und der Trendindikator
Random Walk und der Trendindikator
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Werden die Indikatoren bezahlt oder so? Veröffentlicht in der Codebase, verwenden Sie es nach Herzenslust!
Neuer Artikel Universal Regression Model for Market Price Prediction ist veröffentlicht:
Autor: Юсуфходжа
guter Artikel.
sehr beeindruckend
Es ist schade, aber gleich zu Beginn des Artikels gibt es Fehler.
Erstens: Der Preisanstieg zu einem bestimmten Zeitpunkt t hat natürlich einen bestimmten Wert, den wir mit D0 bezeichnen. Nehmen wir an.
Weiter... Zum Zeitpunkt t=0 gibt es also keine Auswirkung auf den Preis, und offensichtlich gibt es auch keinen Preisanstieg durch die externe Auswirkung. Dennoch haben wir das Delta wieder D0 genannt.
Dann setzen wir dt/tau in die Formel ein, die ohnehin 1/C^2 ist, d.h. wir haben dem Einfluss eine Beschleunigung gegeben, die die geometrische Regression ohnehin verschieben wird. Warum sollten wir? Schließlich haben wir noch nicht definiert - was dieser Stoß so ist...
naja, ganz allgemein.
Es ist schade, aber gleich zu Beginn des Artikels gibt es Fehler.
Erstens hat der Preisanstieg zu einem bestimmten Zeitpunkt t natürlich einen bestimmten Wert, den wir mit D0 bezeichnen. Nehmen wir an.
Weiter... Zum Zeitpunkt t=0 gibt es also keine Auswirkung auf den Preis, und offensichtlich gibt es auch keinen Preisanstieg durch die externe Auswirkung. Dennoch haben wir das Delta wieder D0 genannt.
Dann setzen wir dt/tau in die Formel ein, die ohnehin 1/C^2 ist, d.h. wir haben dem Einfluss eine Beschleunigung gegeben, die die geometrische Regression ohnehin verschieben wird. Warum sollten wir? Wir haben doch noch gar nicht definiert - was dieser Stoß so ist...
Nun, ganz allgemein...
1. Do ist nicht der Preisanstieg, sondern das anfängliche Potenzial der Kraft, die zum Zeitpunkt t=0 auf den Preis wirkt.
2. aus dem Artikel: ".... nehmen wir an, dass sich der Marktpreis, der sich im Gleichgewicht befindet, nur unter der Einwirkung einer externen Kraft D(t) ändern kann, deren Größe und Wert wir in derselben Dimension wie den Preis messen werden.
Nehmen wir weiter an, dass die Veränderung des Marktpreises P(t) im Laufe der Zeit t seit Beginn des Einflusses dieser Kraft, die von Null an durch eine uns noch unbekannte Regelmäßigkeit kontinuierlich ansteigt, dazu neigt, im Unendlichen den Wert P(∞) = D0 zu erreichen. Das heißt, mit D0 meinen wir eine endliche Zunahme oder Abnahme des Marktpreises, je nach Art und Vorzeichen dieser Einflusskraft.
Außerdem nehmen wir an, dass D(t=0) = D0 ist. Nehmen wir weiter an, dass während der infinitesimalen Zeitspanne dt die Einflusskraft um den Wert dD(t) im Verhältnis zur verbleibenden Kraft D(t) zum Zeitpunkt t abnimmt:
Daraus ergibt sich die exponentielle Abhängigkeit von D(t) von der Zeit t in der Form:
Wobei: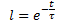
t - Zeit vom Beginn der Einwirkung der destabilisierenden Kraft in Zeitreiheneinheiten, sec. (min, Stunden, Tage, Wochen, Jahrzehnte, Monate, Jahre);
τ (tau) - der Proportionalitätskoeffizient, numerisch gleich der Zeitkonstante des Prozesses, sec.(min, Stunden, Tage, Wochen, Dekaden, Monate, Jahre)".
Woher haben Sie die Dimensionalität von 1/s^2? Dieses Verhältnis hat keine Dimensionalität. Ich habe es nicht hineingeschmuggelt, sondern die Hypothese aufgestellt, dass die Änderungsrate (Abnahme) einer Kraft, die auf einen Prozess wirkt, proportional zur Kraft selbst ist, was der Logik nicht widerspricht, und dann wurde diese Hypothese vollständig bestätigt. Als Proportionalitätskoeffizient führte er das Verhältnis a (alpha) = 1/tau ein, das den Kehrwert der Zeit, die Dimension, hat. Unter a (alpha) verstehe ich die Impedanz des Systems, d.h. den Widerstand des Systems gegen den Fluss des Prozesses, und tau ist das Bild der Zeit in der Laplace-Transformation, wie sich später herausstellte, und erlaubt es, die Analyse des Prozesses aus dem Differentialbereich in den gewöhnlichen Bereich zu übertragen. Das bedeutet, dass jeder Prozess seine eigene Zeit hat, die sich von der unseren unterscheidet, und tau fungiert als "Übersetzer" der Zeiten, wenn ich es so ausdrücken darf. In den Eingeweiden des Artikels habe ich eine Methode zur Schätzung von tau angegeben:
Wenn nun die Werte der Funktion f zu den entsprechenden Zeitpunkten t bekannt sind, dann werden aus dieser Gleichung die Parameter n, τ und der Koeffizient β wie folgt bestimmt:
wobei:
Die Werte der Funktion f zu den entsprechenden Zeitpunkten t und t werden durch die tatsächlichen Werte des Marktpreises P0, P1,..., Pk zu den Zeitpunkten h0, h1,..., һk ab dem Beginn seiner Destabilisierung durch numerische Differenzierung bestimmt, bezogen auf die Mitte des Intervalls:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); und so weiter;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; und so weiter.