Нейросети в трейдинге: Адаптивное обнаружение рыночных аномалий (DADA)

Введение

С развитием технологий и автоматизацией процессов временные ряды стали неотъемлемой частью анализа финансовых рынков. Эффективное обнаружение аномалий в рыночных данных позволяет вовремя выявлять потенциальные угрозы, такие как резкие ценовые колебания, манипуляции с активами и изменения в ликвидности. Это особенно важно для алгоритмической торговли, управления рисками и оценки устойчивости финансовых систем. Внезапные всплески волатильности, отклонения в объемах торгов или необычные корреляции между активами могут сигнализировать о сбоях, спекулятивной активности или даже рыночных кризисах.

Современные методы обнаружения аномалий, основанные на глубоком обучении, достигли значительных успехов, но они имеют ограничения. Чаще всего такие подходы требуют отдельного обучения для каждого нового набора данных, что мешает их применению в реальных условиях. Финансовые данные постоянно меняются, а их исторические паттерны не всегда повторяются.

Одна из главных проблем — разная структура данных на различных рынках. Современные алгоритмы обычно используют автоэнкодеры, чтобы "запомнить" нормальное поведение рынка, так как аномалии встречаются редко. Однако если модель сохраняет слишком много информации, она начинает учитывать рыночный шум и снижается точность обнаружения аномалий. Слишком сильное сжатие данных, наоборот, может привести к потере важных закономерностей. В большинстве подходов используется фиксированная степень сжатия, что ограничивает адаптацию моделей к различным рыночным условиям.

Еще одна сложность — разнообразие аномалий. Многие модели обучаются только на нормальных данных, но без понимания самих аномалий их сложно обнаруживать. Например, резкий скачок цен может быть аномалией на одном рынке, но нормальным явлением на другом. В одних активах аномалии связаны с резкими всплесками ликвидности, а в других — с неожиданными корреляциями. Из-за этого модель может либо не замечать важные сигналы, либо слишком часто генерировать ложные.

Для решения этих проблем авторы работы "Towards a General Time Series Anomaly Detector with Adaptive Bottlenecks and Dual Adversarial Decoders" предложили новый фреймворк DADA, который использует адаптивное сжатие информации и два независимых декодера. В отличие от традиционных методов, DADA гибко подстраивается под разные данные. Вместо фиксированного уровня сжатия, он использует несколько вариантов и выбирает наиболее подходящий для каждого случая. Это помогает лучше учитывать особенности рыночных данных и сохранять важные закономерности.

На выходе модели используются два декодера. Один отвечает за нормальные данные, а второй — за аномальные. Первый декодер учится восстанавливать временной ряд, а второй изучает примеры аномалий. Это помогает четко разделять норму и аномалии, а также снижает вероятность ложных сигналов.

Алгоритм DADA

Временные ряды представляют собой последовательности данных, изменяющихся во времени. Любые отклонения от нормального поведения данных могут сигнализировать о кризисах, сбоях или мошеннических действиях. Для эффективного выявления таких аномалий в фреймворке DADA (Detector with Adaptive Bottlenecks and Dual Adversarial Decoders) используются методы глубинного обучения адаптивного анализа временных рядов и детекции аномальных паттернов. Ключевой особенностью DADA является его универсальность. Он не требует предварительной адаптации под конкретную предметную область и может работать с широким спектром исходных данных.

Фреймворк DADA основан на идее реконструкции данных с применением маскирования, что делает его эффективным инструментом для анализа временных зависимостей и выявления отклонений от нормы. Этот метод позволяет модели не просто запоминать закономерности в данных, а учиться понимать их структуру, восстанавливая недостающие или искаженные участки.

Процесс обучения включает работу с двумя типами последовательностей: нормальными и аномальными. В отличие от традиционных подходов, где требуется предварительная разметка аномальных данных вручную, авторы фреймворка DADA использовали генеративный подход — добавление искусственного шума к исходным временным рядам. Такой подход не только упрощает подготовку данных, исключая ручной труд, но и делает модель более универсальной. Ведь она обучается выявлять отклонения разного характера: скачки, выбросы, сдвиги тренда, изменение волатильности и другие паттерны.

На первом этапе исходные данные разделяются на сегменты (патчи), к которым применяется случайное маскирование. Это необходимо для того, чтобы модель обучалась восстанавливать недостающие части данных. Это усиливает ее способность выявлять аномалии и скрытые закономерности.

Затем сегменты поступают в энкодер, где преобразуются в компактное скрытое представление. Энкодер обучается находить ключевые признаки временного ряда, игнорируя шум и несущественные детали. Такой подход позволяет модели лучше обобщать информацию и работать с данными различной природы, будь то ценовые графики на финансовых рынках, временные ряды объемов торгов или другие индикаторы.

Одним из ключевых компонентов модели является механизм адаптивных "бутылочных горлышек", регулирующий степень сжатия информации в зависимости от структуры и качества данных. Когда данные содержат значимый сигнал, модель сохраняет больше деталей, а если информация избыточна или сильно зашумлена, сжатие усиливается, что помогает минимизировать влияние помех и улучшает детекцию аномалий.

Модуль адаптивных узких мест (AdaBN) динамически изменяет степень сжатия данных. Этот механизм состоит из пула небольших моделей, напоминающих автоэнкодеры. Каждая из них имеет латентное представление разного размера:

где DownNeti(•) выполняет сжатие анализируемых данных, а UpNeti(•) — восстановление.

Адаптивный маршрутизатор выбирает оптимальный маршрут на основе анализа исходных данных:

где Wrouter, Wnoise — обучаемые матрицы.

Для сжатия каждого сегмента используется k наиболее подходящих маршрутов с максимальным значением R(z).

После кодирования скрытые представления поступают в два параллельных декодера. Один из них предназначен для восстановления нормальных данных и обучается минимизировать ошибку реконструкции. А второй — для выявления аномалий, создавая максимальное расхождение между восстановленными и исходными значениями. Такой состязательный процесс позволяет модели эффективно различать стандартные паттерны и неожиданные отклонения.

В процессе тестирования и промышленной эксплуатации аномальный декодер отключается, и оценка осуществляется исключительно по нормальному декодеру. Если модель восстанавливает данные с высокой точностью, значит, временной ряд соответствует нормальному поведению. Если же реконструкция сопровождается значительными ошибками, это указывает на возможную аномалию.

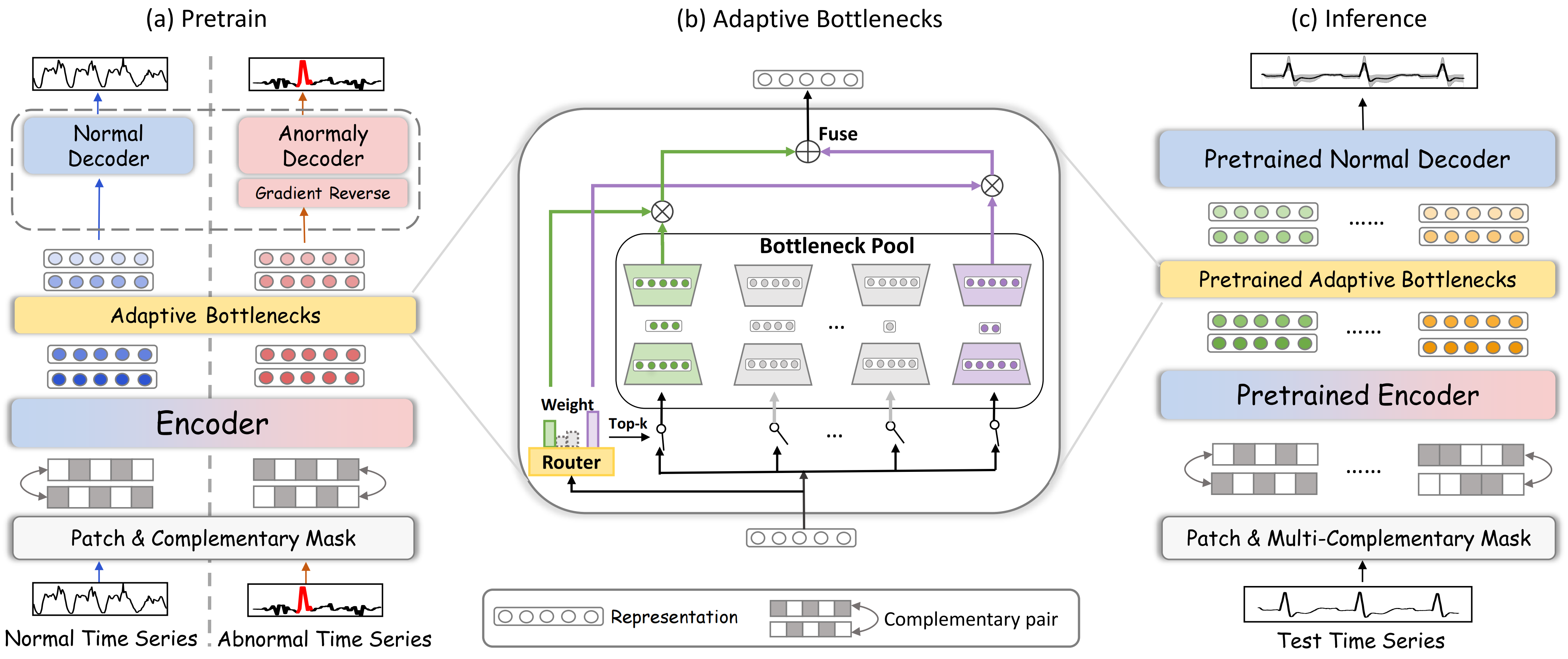
Авторская визуализация фреймворка DADA представлена ниже.

Реализация средствами MQL5

После рассмотрения теоретических аспектов фреймворка DADA мы переходим к практической части нашей работы, в которой рассмотрим вариант реализации собственного видения предложенных подходов средствами MQL5. Ключевым элементом данного фреймворка является модуля адаптивных узких мест. Именно с его построения мы и начнем работу.

Думаю, не только я заметил его сходство с реализованным нами ранее модулем Mixture of Experts. Но есть одно важное отличие. В построенном нами объекте CNeuronMoE предполагается использование мини-моделей одинаковой архитектуры. Однако, в данном случае нам необходимо варьировать размер слоя латентного состояния для каждой модели, адаптируя их под различные характеристики данных. Такой вариант мы уже не сможем реализовать с помощью объектов сверточных слоев, как это было сделано ранее. Конечно, можно создать каждую модель отдельно и пропускать данные через них последовательно. Но это приводит к снижению эффективности использования оборудования и увеличению затрат на обучение и эксплуатацию модели.

С целью исключения указанных проблем было принято решение разработать новый объект мультиоконного сверточного слоя. В его основе лежит идея одновременного использования нескольких вариантов размерности окна свертки. Это позволяет модели анализировать данные с разной степенью детализации в параллельных вычислительных потоках. Такой подход делает архитектуру более гибкой, улучшает качество обработки исходных данных и позволяет эффективнее использовать вычислительные мощности. В результате модель способна лучше адаптироваться к различным временным структурам исходных данных, обеспечивая высокую точность и скорость работы.

Построение алгоритмов на стороне OpenCL-программы

Как всегда, основной объем математических операций мы вынесем в OpenCL-контекст. Здесь создаем кернел FeedForwardMultWinConv, в рамках которого организуем процесс прямого прохода нашего нового слоя.

__kernel void FeedForwardMultWinConv(__global const float *matrix_w,
                                     __global const float *matrix_i,
                                     __global float *matrix_o,
                                     __global const int *windows_in,
                                     const int inputs,
                                     const int windows_total,
                                     const int window_out,
                                     const int activation
                                    )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t outputs = get_global_size(0);

В параметрах кернела получаем указатели на 4 буфера данных и 4 константы, определяющих структуру исходных данных и результатов.

Обратите внимание, что один из глобальных буферов (windows_in) содержит целочисленные значения. В нем передаются размеры окон свертки. Предполагается, что в буфере исходных данных (matrix_i) находится последовательность сегментов. В рамках каждого сегмента последовательны расположены данные для каждого окна свертки.

Данный кернел мы планируем вызывать в двухмерном пространстве задач. Размерность первого измерения указывает на количество значений в буфере результатов для каждой унитарной последовательности, а второе измерение укажет на количество таких унитарных последовательностей.

Здесь следует уточнить, что первое измерение указывает именно на количество значений в буфере результатов, а не число элементов в унитарной последовательности. Иными словами, размер первого измерения равен произведению количества анализируемых сегментов в унитарной последовательности на число используемых фильтров и окон свертки. При этом каждый элемент использует одинаковое количество фильтров, независимо от размера окна свертки. Это связано с необходимостью получения единства форматов данных, восстановленных из сжатого представления.

В теле кернела мы сначала идентифицируем текущий поток в двухмерном пространстве задач по каждому измерению.

Далее необходимо определить смещение в глобальных буферах данных до нужных элементов. Очевидно, что идентификатор потока по первому измерению укажет на элемент буфера результатов в рамках анализируемой унитарной последовательности. А вот для определения смещения в остальных буферов данных нам потребуется немого поработать.

Сначала определим позицию элемента в рамках анализируемого сегмента. Для этого возьмем остаток от деления идентификатора первого измерения на общее число элементов в буфере результатов для одного сегмента.

   const int id = i % (window_out * windows_total);

Подготовим несколько локальных переменных для временного хранения промежуточных значений.

   int step = 0;
   int shift_in = 0;
   int shift_weight = 0;
   int window_in = 0;
   int window = 0;

И организуем цикл перебора всех значений буфера окон свертки.

#pragma unroll
   for(int w = 0; w < windows_total; w++)
     {
      int win = windows_in[w];
      step += win;

В теле цикла мы посчитаем сумму всех окон свертки, что даст нам размер одного сегмента в буфере исходных данных. Кроме того, в рамках данного цикла мы определим смещение в рамках текущего сегмента до нужного окна свертки (shift_in), размер анализируемого окна свертки (window_in) и смещение в буфере обучаемых параметров до начала элементов матрицы нужного окна свертки (shift_weight).

      if((w * window_out) < id)
        {
         shift_in = step;
         window_in = win;
         shift_weight += (win + 1) * window_out;
        }
     }

Далее определим количество полных сегментов до текущего элемента в буфере результатов (steps) и добавим соответствующее смещение в буфере исходных данных до нужного сегмента.

   int steps = (int)(i / (window_out * windows_total));
   shift_in += steps * step + v * inputs;

К смещению в буфере обучаемых параметров добавим поправку на корректный фильтр. Для этого мы возьмем остаток от деления позиции анализируемого элемента в текущем сегменте буфера результатов, что даст нам номер элемента в рамках результатов текущего окна свертки. По существу, полученное значение указывает на нужный нам фильтр. Количество обучаемых параметров в каждом фильтре равно размеру окна свертки плюс bias-элемент. Таким образом, умножив номер фильтра на количества обучаемых параметров получаем нужное нам смещение.   

shift_weight += (id % window_out) * (window_in+1);

После завершения подготовительной работы мы организуем цикл вычисления значения текущего элемента в локальную переменную.

   float sum = matrix_w[shift_weight + window_in];
#pragma unroll
   for(int w = 0; w < window_in; w++)
      if((shift_in + w) < inputs)
         sum += IsNaNOrInf(matrix_i[shift_in + w], 0) * matrix_w[shift_weight + w];

Полученное значение корректируем на функцию активации и сохраняем в соответствующем элементе глобального буфера результатов.

 matrix_o[v * outputs + i] = Activation(sum, activation);
}

После построения алгоритма прямого прохода, мы переходим к организации процессов обратного прохода. Здесь сначала создадим кернел распределения градиентов ошибки до уровня исходных данных CalcHiddenGradientMultWinConv. Структура параметров данного кернела во многом заимствована от кернела прямого прохода. Мы лишь добавляем указатели на буферы соответствующих градиентов ошибки.

__kernel void CalcHiddenGradientMultWinConv(__global const float *matrix_w,
                                            __global const float *matrix_i,
                                            __global float *matrix_ig,
                                            __global const float *matrix_og,
                                            __global const int *windows_in,
                                            const int outputs,
                                            const int windows_total,
                                            const int window_out,
                                            const int activation
                                           )
  {
   const size_t i = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t inputs = get_global_size(0);

Работа данного кернела построена так же в двухмерном пространстве. Только на этот раз, первое измерение указывает на смещение в буфере исходных данных. Ведь именно на уровне исходных данных нам предстоит собрать значения градиентов ошибки от всех фильтров.

В теле кернела, как всегда, сначала осуществляем идентификацию потока во всех измерениях пространства задач. А затем, организуем цикл суммирования всех окно свертки, с целью определения размера одного сегмента в буфере исходных данных.

   int step = 0;
#pragma unroll
   for(int w = 0; w < windows_total; w++)
      step += windows_in[w];

Это позволит нам определить порядковый номер сегмента анализируемого элемента и смещение в рамках данного сегмента.

int steps = (int)(i / step);
int id = i % step;

Далее, объявим несколько локальных переменных временного хранения данных и организуем еще один цикл, в рамках которого определим размер анализируемого окна свертки (window_in), порядковый номер окна свертки (window) и смещение в рамках текущего сегмента до начала текущего окна свертки (before).

   int window = 0;
   int before = 0;
   int window_in = 0;
#pragma unroll
   for(int w = 0; w < windows_total; w++)
     {
      window_in = windows_in[w];
      if((before + window_in) >= id)
         break;
      window = w + 1;
      before += window_in;
     }

Полученные значения позволят нам определить смещение в буфере результатов (shift_out) и тензоре параметров (shift_weight).

int shift_weight = (before + window) * window_out + id - before;
int shift_out = (steps * windows_total + window) * window_out + v * outputs;

На этом завершается подготовительная работа, и у нас достаточно информации, чтобы суммировать градиенты ошибки. Организуем еще один цикл, в котором соберем значения градиентов ошибки от всех фильтров с учетом соответствующих весовых коэффициентов.

   float sum = 0;
#pragma unroll
   for(int w = 0; w < window_out; w++)
      sum += IsNaNOrInf(matrix_og[shift_out + w], 0) * matrix_w[shift_weight + w * (window_in + 1)];

Полученное значение скорректируем на производную функции активации слоя исходных данных, а результат сохраним в соответствующем элементе глобального буфера градиентов ошибки.

 matrix_ig[v * inputs + i] = Deactivation(sum, matrix_i[v * inputs + i], activation);
}

Третьим этапом нашей работы является построение процесса распределения градиента ошибки до уровня весовых коэффициентов и их корректировка в сторону минимизации общей ошибки работы модели. В рамках данной работы мы реализуем алгоритм оптимизации параметров Adam в кернеле UpdateWeightsMultWinConvAdam.

Для целей корректного построения указанного алгоритма мы расширим количество параметров кернела, добавим специфические константы и 2 глобальных буфера моментов.

__kernel void UpdateWeightsMultWinConvAdam(__global float *matrix_w,
                                           __global const float *matrix_og,
                                           __global const float *matrix_i,
                                           __global float *matrix_m,
                                           __global float *matrix_v,
                                           __global const int *windows_in,
                                           const int windows_total,
                                           const int window_out,
                                           const int inputs,
                                           const int outputs,
                                           const float l,
                                           const float b1,
                                           const float b2
                                          )
  {
   const size_t i = get_global_id(0);  // weight shift
   const size_t v = get_local_id(1);   // variable
   const size_t variables = get_local_size(1);

Данный кернел мы также планируем использовать в двухмерном пространстве задач. И на этот раз первое измерение укажет на оптимизируемый элемент в глобальном буфере обучаемых параметров. Однако, в данном случае есть нюанс. При работе с многомерными временными рядами каждая унитарная последовательность анализируется с использованием общих обучаемых параметров. Следовательно, на данном этапе нам предстоит собрать градиенты ошибки от всех унитарных последовательностей. С целью организации параллельной работы отдельных унитарных последовательностей, мы распределили их по второму измерению пространства задач. Но объединили их в рабочие группы, что позволит нам организовать процесс обмена данными. Именно для целей обмена данными в рамках рабочей группы, мы создаем массив в локальной памяти OpenCL-контекста.

__local float temp[LOCAL_ARRAY_SIZE];

Далее переходим к подготовительной работе, в рамках которой нам предстоит определить смещения в буферах данных. Наверное, самое простое, что мы можем сделать,— это определить шаг в буфере результатов (step_out). Он равен произведению числа окон свертки для одного сегмента на количество фильтров.

int step_out = window_out * windows_total;

Для получения остальных параметров придется поработать. Сначала объявим локальные переменные, в которые будем сохранять промежуточные результаты.

int step_in = 0;
int shift_in = 0;
int shift_out = 0;
int window = 0;
int number_w = 0;

И организуем цикл перебора значений в глобальном буфере размеров окон свертки.

#pragma unroll
   for(int w = 0; w < windows_total; w++)
     {
      int win = windows_in[w];
      if((step_in + w)*window_out <= i &&
         (step_in + win + w + 1)*window_out > i)
        {
         shift_in = step_in;
         shift_out = (step_in + w + 1) * window_out;
         window = win;
         number_w = w;
        }
      step_in += win;
     }

В теле цикла мы определяем смещение до нужного окна свертки в буферах исходных данных (shift_in) и результатов (shift_out), размер окна свертки (window) и его порядковый номер в буфере (number_w). Кроме того, посчитаем сумму всех окон свертки (step_in), что укажет нам на размер сегмента. Это же значение мы будем использовать в качестве шага по буферу исходных данных.

Здесь стоит обратить внимание, что не каждый обучаемый параметр связан с буфером исходных данных. Ведь существует bias-элемент. И мы введем флаг обнаружения подобного элемента.

bool bias = ((i - (shift_in + number_w) * window_out) % (window + 1) == window);

Далее скорректируем смещение до нужного элемента в буфере результатов.

int t = (i - (shift_in + number_w) * window_out) / (window + 1);
shift_out += t + v * outputs;

И аналогичную операцию выполним для смещения в глобальном буфере исходных данных.

   shift_in += (i - (shift_in + number_w) * window_out) % (window + 1) + v * inputs;

На этом мы завершаем этап подготовительной работы и переходим непосредственно к определению градиента ошибки анализируемого параметра. С этой целью, мы организуем цикл сбора градиента ошибки со всех элементов буфера результатов, при расчете значений которых, использовался оптимизируемый в данном потоке параметр.

   float grad = 0;
   int total = (inputs + step_in - 1) / step_in;
#pragma unroll
   for(int t = 0; t < total; t++)
     {
      int sh_out = t * step_out + shift_out;
      if(bias && sh_out < outputs)
        {
         grad += IsNaNOrInf(matrix_og[sh_out], 0);
         continue;
        }

Для bias-элементов мы просто суммируем значения градиентов ошибки, а остальные корректируем с учетом соответствующего элемента исходных данных.

 int sh_in = t * step_in + shift_in;
 if(sh_in >= inputs)
    break;
 grad += IsNaNOrInf(matrix_og[sh_out] * matrix_i[sh_in], 0);
}

Здесь следует обратить внимание, что в рамках данного цикла мы собрали значения ошибки только в рамках одной унитарной последовательности. Но, как уже упоминалось ранее, оптимизируемый параметр использовался всеми последовательностями многомерного временного ряда. Поэтому, перед началом работ по оптимизации параметра, нам предстоит собрать значения со всех унитарных последовательностей, которые были вычислены в рамках рабочей группы. Для этого, на первом этапе, суммируем отдельные значения в элементах локального массива.

//--- sum
   const uint ls = min((uint)variables, (uint)LOCAL_ARRAY_SIZE);
#pragma unroll
   for(int s = 0; s < (int)variables; s += ls)
     {
      if(v >= s && v < (s + ls))
         temp[v % ls] = (i == 0 ? 0 : temp[v % ls]) + grad;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

А затем суммируем значения, накопленные в элементах локального массива.

   uint count = ls;
#pragma unroll
   do
     {
      count = (count + 1) / 2;
      if(v < ls)
         temp[v] += (v < count && (v + count) < ls ? temp[v + count] : 0);
      if(v + count < ls)
         temp[v + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

После получения суммарного градиента ошибки от всех потоков рабочей группы, мы можем обновить значение анализируемого параметра. И для этого нам достаточного одного потока.

   if(v == 0)
     {
      grad = temp[0];
      float mt = IsNaNOrInf(clamp(b1 * matrix_m[i] + (1 - b1) * grad, -1.0e5f, 1.0e5f), 0);
      float vt = IsNaNOrInf(clamp(b2 * matrix_v[i] + (1 - b2) * pow(grad, 2), 1.0e-6f, 1.0e6f), 1.0e-6f);
      float weight = clamp(matrix_w[i] + IsNaNOrInf(l * mt / sqrt(vt), 0), -MAX_WEIGHT, MAX_WEIGHT);
      matrix_w[i] = weight;
      matrix_m[i] = mt;
      matrix_v[i] = vt;
     }
  }

По результатам операций, корректируем в глобальных буферах данных значение анализируемого параметра и соответствующих моментов.

На этом мы завершаем построение алгоритмов мультиоконного сверточного слоя в нашей OpenCL-программе. С полным её кодом вы можете ознакомиться во сложении.

Объект мультиоконного сверточного слоя

Следующим этапом нашей работы является интеграция построенных выше алгоритмов мультиоконного сверточного слоя в основную программу. С этой целью, мы создаем новый объект CNeuronMultiWindowsConvOCL, в котором организуем процессы обслуживания, созданных на стороне OpenCL-контекста, кернелов. Структура нового объекта представлена ниже.

class CNeuronMultiWindowsConvOCL    :  public CNeuronConvOCL
  {
protected:
   int               aiWindows[];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronMultiWindowsConvOCL(void) {  activation = SoftPlus;  iWindow = -1; }
                    ~CNeuronMultiWindowsConvOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint &windows[], uint window_out, uint units_count, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMultiWindowsConvOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

По сути, наш новый объект CNeuronMultiWindowsConvOCL представляет собой модифицированный вариант стандартного сверточного слоя. Поэтому логично использовать его в качестве родительского класса. Это позволяет унаследовать базовую логику работы со свертками и избежать дублирования кода.

В представленной структуре мы видим привычный набор переопределяемых виртуальных методов. Однако, основное отличие нового объекта заключается в работе сразу с несколькими вариантами размерности окон свертки. Это требует создание дополнительных элементов хранения данных и интерфейсов передачи их в OpenCL-контекст. С этой целью мы объявляем дополнительный массив aiWindows и вносим изменения в параметры метода инициализации объекта Init.

bool CNeuronMultiWindowsConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                      uint &windows[], uint window_out, uint units_count,
                                      uint variables, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(windows.Size() <= 0 || ArrayCopy(aiWindows, windows) < int(windows.Size()))
      return false;

Здесь важно подчеркнуть, что, несмотря на все внесенные изменения в алгоритм работы CNeuronMultiWindowsConvOCL, мы постарались максимально сохранить логику и возможности родительского класса. Это не просто упрощает интеграцию нового объекта в существующую архитектуру, но и позволяет повторно использовать уже отлаженные механизмы.

Алгоритм работы метода инициализации объекта начинается с проверки размера массива окон свертки, полученного в параметрах и копирования его значений в специально созданный внутренний массив.

Затем определим сумму всех окон свертки, добавив в каждому bias-элемент.

int window = 0;
for(uint i = 0; i < aiWindows.Size(); i++)
   window += aiWindows[i] + 1;

Немного не очевидная, но нужная операция. Дело в том, что для каждого окна свертки нам предстоит сгенерировать матрицу весов размером (Windowi + 1) * Filters. Таким образом, общий размер буфера параметров составит:

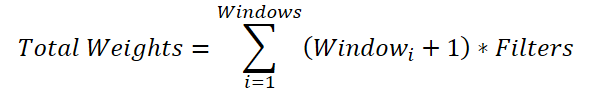
Общую переменную количества фильтров мы можем вынести за знак суммирования:

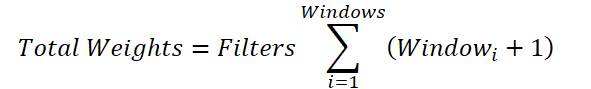
Если заменить сумму окон общим значением, мы придем к формуле определения количества обучаемых параметров для одного сверточного окна. Только в нашем родительском классе предусмотрено добавление одного bias-элемента, а не по числу нужного нам окон свертки. Поэтому в общую сумму мы добавили элемент смещения для каждого окна. А затем, уменьшим полученное значение на 1 и передадим в качестве окна и шага свертки в метод инициализации родительского класса.

window--;
if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, window, window_out,
                         units_count * aiWindows.Size()*variables, 1, ADAM, batch))
   return false;

Так как мы планируем использовать одинаковые параметры для всех унитарных последовательностей, то количество таковых укажем равным "1". В то же время, увеличим количество элементов в последовательности путем умножения на число окон свертки и унитарных последовательностей.

Такой подход позволил нам инициализировать все унаследованные буфера данных в нужном размере. В том числе инициализировать буфер обучаемых параметров случайными значениями.

Теперь нам остается создать глобальный буфер данных для передачи массива окон свертки в OpenCL-контекст. Как вы понимаете, значения данного буфера мы заполняем при инициализации объекта и не изменяем в процессе обучения и эксплуатации модели. Поэтому буфер данных создаем только в OpenCL-контексте, а в нашем объекте сохраняем лишь указатель на него.

   iVariables = variables;
   iWindow = OpenCL.AddBufferFromArray(aiWindows, 0, aiWindows.Size(), CL_MEM_READ_ONLY);
   if(iWindow < 0)
      return false;
//---
   return true;
  }

Проверяем корректность создания глобального буфера данных по возвращаемому хендлу и завершаем работу метода инициализации нового объекта, предварительно вернув логический результат выполнения операций вызывающей программе.

После инициализации нового объекта, мы переходим к переопределению метода прямого прохода CNeuronMultiWindowsConvOCL::feedForward. Как вы уже наверное догадались, здесь осуществляется постановка в очередь выполнения ранее созданного кернела FeedForwardMultWinConv. Однако, несмотря на использование общего для таких случаев алгоритма, есть пара нюансов, на которые хотелось бы обратить внимание.

bool CNeuronMultiWindowsConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL)
      return false;

В параметрах метода получаем указатель на объект исходный данных, актуальность которого сразу проверяем.

После успешного прохождения блока контролей инициализируем массивы пространства задач.

uint global_work_offset[2] = {0, 0};
uint global_work_size[2] = {Neurons() / iVariables, iVariables};

Как было сказано выше, при описании алгоритма указанного кернела, второе измерение указывает на количество унитарных последовательностей в исходных данных. А вот количество потоков в первом измерении определяется отношением общего числа элементов в буфере результатов нашего объекта к числу унитарных последовательностей.

Далее идет передача данных в параметры кернела.

   ResetLastError();
   int kernel = def_k_FeedForwardMultWinConv;
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_ffmwc_matrix_i, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_ffmwc_matrix_o, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_ffmwc_matrix_w, WeightsConv.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(kernel, def_k_ffmwc_windows_in, iWindow))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Здесь стоит обратить внимание, что в качестве буфера размерности окон свертки, мы передаем ранее сохраненный хендл. А размерность последовательности исходных данных определяем путем деления размера буфера исходных данных на число унитарных последовательностей.

   if(!OpenCL.SetArgument(kernel, def_k_ffmwc_inputs, NeuronOCL.Neurons() / iVariables))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(kernel, def_k_ffmwc_window_out, iWindowOut))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(kernel, def_k_ffmwc_windows_total, (int)aiWindows.Size()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(kernel, def_k_ffmwc_activation, (int)activation))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.Execute(kernel, 2, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

После успешной передачи всех параметров, осуществляем постановку кернела в очередь выполнения и завершаем работу метода, вернув логический результат выполнения операций вызывающей программе.

Аналогичным образом осуществляется постановка в очередь выполнения кернелов организации процессов обратного прохода. Только при распределении градиентов ошибки, мы указываем функцию активации слоя исходных данных. А для операций оптимизации параметров модели, не забываем создать рабочие группы в рамках второго измерения пространства задач.

bool CNeuronMultiWindowsConvOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL)
      return false;
//---
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2] = {WeightsConv.Total(), iVariables};
   uint local_work_size[2] = {1, iVariables};
//---
.........
.........
.........
//---
   if(!OpenCL.Execute(kernel, 2, global_work_offset, global_work_size, local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

На этом мы завершаем рассмотрение алгоритмов построения мультиоконного сверточного слоя. Полный код объекта CNeuronMultiWindowsConvOCL и всех его методов представлен во вложении.

Объем статьи практически исчерпан, а мы еще не завершили свою работу. Сделаем небольшой перерыв и продолжим реализацию собственного видения подходов, предложенных авторами фреймворка DADA, в следующей статье.…

Заключение

Современные финансовые рынки характеризуются не только огромными объемами данных, но и высокой изменчивостью. Это делает задачу обнаружения аномалий особенно сложной. Фреймворк DADA предлагает принципиально новый подход, который сочетает адаптивные узкие места и два параллельных декодера для более точного анализа временных рядов. Его ключевым преимуществом является способность динамически подстраиваться под различные структуры данных без необходимости предварительной адаптации, что делает его универсальным инструментом.

В практической части статьи мы начали реализацию собственного видения предложенных авторами фреймворка подходов средствами MQL5. Однако наша работа ещё не завершена и мы продолжим её в следующей статье.

Ссылки

• Towards a General Time Series Anomaly Detector with Adaptive Bottlenecks and Dual Adversarial Decoders
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы