Redes neurais em trading: Detecção adaptativa de anomalias de mercado (Conclusão)

Introdução

No artigo anterior, exploramos os aspectos teóricos do DADA (Adaptive Bottlenecks and Dual Adversarial Decoders), um framework projetado para identificar anomalias em séries temporais por meio de métodos de aprendizado profundo. Essa ferramenta auxilia na análise de dados e na detecção de estados de mercado anômalos, o que é especialmente importante em condições de alta volatilidade. O uso de métodos adaptativos de processamento de informação permite que o modelo se ajuste de maneira flexível ao ambiente de mercado em constante mudança, o que o torna um instrumento versátil para a análise de diferentes séries temporais.

A arquitetura do framework DADA é construída sobre três componentes principais, cada um responsável por uma tarefa específica. O primeiro componente é o módulo de gargalos adaptativos (Adaptive Bottlenecks), que é capaz de alterar dinamicamente o grau de compressão dos dados analisados. Essa abordagem ajuda a preservar as características mais relevantes dos dados de mercado e a minimizar a perda de informação, o que poderia afetar a qualidade da análise. Ao contrário dos modelos tradicionais, nos quais os parâmetros de compressão são fixos, aqui tudo é ajustado em tempo real, de acordo com a situação do mercado.

O segundo elemento importante é o sistema de dois decodificadores adversários. O primeiro decodificador reconstrói os estados normais do mercado, permitindo que o modelo compreenda melhor os padrões típicos de comportamento. O segundo decodificador foca nos dados anômalos, ajudando a distinguir claramente entre situações padrão e desvios. Essa abordagem reduz a probabilidade de falsos positivos, tornando o modelo mais confiável.

O terceiro componente-chave é o mecanismo de patching e mascaramento, que desempenha um papel essencial no processamento de séries temporais. Esse mecanismo permite destacar dinamicamente as áreas críticas dos dados, ocultar componentes ruidosos e aprimorar a qualidade da representação da informação. O patching divide os dados em pequenos segmentos, possibilitando ao modelo analisar as características locais da série temporal. O mascaramento aleatório contribui para um melhor treinamento do modelo. Ao reconstruir as partes mascaradas, o modelo é forçado a considerar dependências ocultas nos dados, o que aprimora sua capacidade de identificar padrões e relações complexas. Em conjunto, esses métodos aumentam a precisão na detecção de anomalias e tornam o modelo mais resistente às oscilações do mercado. O mascaramento também melhora a capacidade de generalização do modelo, evitando o sobreajuste a trechos específicos dos dados de mercado.

Uma das principais vantagens do DADA é sua adaptabilidade. Ao contrário dos algoritmos tradicionais, que exigem retreinamento sempre que as condições de mercado mudam, o DADA ajusta automaticamente seus parâmetros. Isso é especialmente importante no trading de alta frequência, em que as decisões precisam ser tomadas em frações de segundo. A capacidade de ajuste dinâmico permite que o modelo opere de maneira eficiente nos mais variados cenários de mercado, desde tendências estáveis até bruscos picos de volatilidade.

A visualização original do framework DADA é apresentada a seguir.

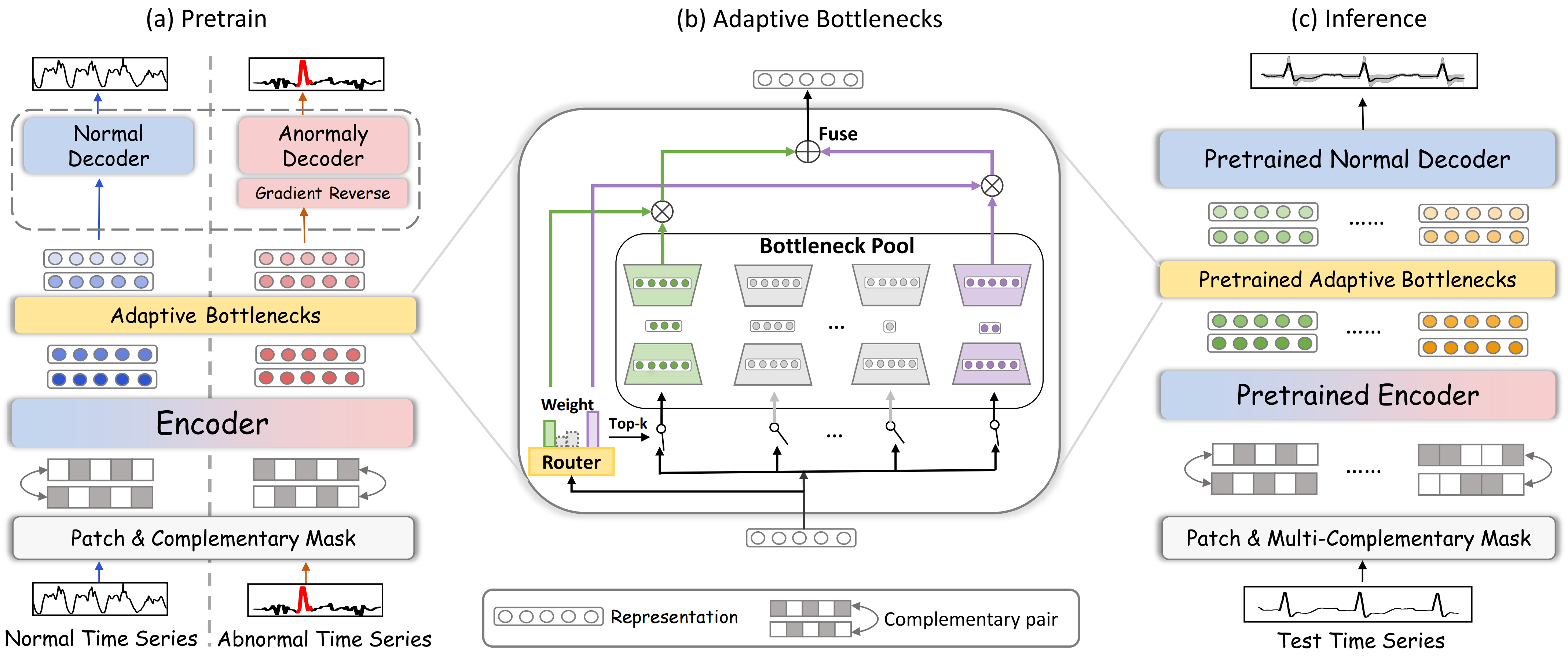
Na parte prática do artigo anterior, foi construído o objeto de camada convolucional multi-janela CNeuronMultiWindowsConvOCL. É importante ressaltar que a criação desse objeto não decorre diretamente da descrição original da arquitetura do DADA. No entanto, em nossa implementação, ele desempenhará um dos papéis centrais dentro do módulo Adaptive Bottlenecks. É justamente o uso desse componente que nos permitirá alterar dinamicamente o grau de compressão dos dados analisados.

Módulo Adaptive Bottlenecks

A próxima etapa importante do nosso trabalho é a construção direta do módulo de gargalos adaptativos (Adaptive Bottlenecks). Esse módulo representa uma poderosa ferramenta para o processamento dinâmico de dados brutos, pois permite analisar de maneira eficiente séries temporais complexas e identificar anomalias em seu comportamento.

Já mencionamos a semelhança conceitual desse módulo com o Mixture of Experts (MoE), anteriormente implementado no objeto CNeuronMoE. Ambos exploram a abordagem de processamento paralelo por meio de múltiplos submodelos, responsáveis pela análise dos dados brutos. O módulo seleciona dinamicamente as k minimodelos mais adequadas para processar o segmento analisado, com base na avaliação de seu contexto. Essa estratégia aumenta a adaptabilidade e a precisão do modelo como um todo, permitindo que ele se concentre nos padrões mais relevantes.

A principal característica do Adaptive Bottlenecks está no uso de um conjunto de autocodificadores como minimodelos, cada um com um grau diferente de compressão das informações analisadas no espaço latente. Isso permite que o modelo se adapte de maneira mais flexível às condições em constante mudança, ajustando o nível de detalhamento da representação dos dados brutos de acordo com as particularidades identificadas na série temporal. Com essa arquitetura, o Adaptive Bottlenecks reduz eficazmente a redundância dos dados, minimiza o impacto do ruído e melhora a detecção de padrões anômalos.

Nossa versão do módulo Adaptive Bottlenecks será construída dentro do objeto CNeuronAdaBN. Como se pode deduzir, a classe base utilizada será o CNeuronMoE. Essa escolha se deve à intenção de reaproveitar os principais mecanismos do Mixture of Experts, como a distribuição dinâmica de carga entre os minimodelos e a seleção adaptativa dos especialistas mais relevantes. Pois eles se encaixam perfeitamente na lógica do Adaptive Bottlenecks. Isso também se reflete na estrutura do novo objeto, apresentada a seguir.

class CNeuronAdaBN   :  public CNeuronMoE
  {
public:
                     CNeuronAdaBN(void) {};
                    ~CNeuronAdaBN(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint &bottlenecks[], uint top_k, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronAdaBN; }
  };

Como se pode notar, planejamos apenas redefinir o método de inicialização do objeto, sem criar componentes internos adicionais.

É importante ressaltar que a classe base CNeuronMoE inclui o objeto responsável pela seleção dos k especialistas mais relevantes (cGates) e um array dinâmico (cExperts), que contém ponteiros para os objetos consecutivos do modelo interno. À primeira vista, a ideia de especialistas paralelos pode parecer pouco compatível com o conceito tradicional de modelos sequenciais. No entanto, utilizamos uma sequência de camadas convolucionais, que são capazes de analisar sequências unitárias de maneira independente. Isso possibilitou a criação de mini-MLPs especializados que funcionam em paralelo. Cada minimodelo possui seus próprios parâmetros treináveis.

Essa solução arquitetônica aumenta consideravelmente a adaptabilidade do sistema, pois cada especialista é treinado em uma subtarefa específica, o que melhora a capacidade de identificar padrões complexos em séries temporais. Além disso, o sistema dinâmico de seleção dos especialistas mais adequados garante que apenas os minimodelos mais relevantes sejam utilizados durante o processo de análise, aumentando a precisão das previsões.

class CNeuronMoE  :  public CNeuronBaseOCL
  {
protected:
   CNeuronTopKGates     cGates;
   CLayer               cExperts;
   //---
   ..........
   ..........
   ..........
  };

O mecanismo herdado da classe base, responsável por selecionar as k especialistas mais relevantes, atende plenamente aos requisitos do módulo CNeuronAdaBN. Por esse motivo, aproveitaremos o funcional herdado. Além disso, basta preencher o array dinâmico herdado com uma nova sequência de objetos conforme a tarefa a ser resolvida, e sua manutenção pode ser realizada pelos recursos já existentes na classe base. O mesmo se aplica à execução dos processos de propagação para frente e reversa.

A sequência dos objetos internos é definida no método Init, que iremos redefinir.

bool CNeuronAdaBN::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                        uint window, uint window_out, uint units_count,
                        uint &bottlenecks[], uint top_k, uint variables,
                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables,
                                                                 optimization_type, batch))
      return false;

Como de costume, os parâmetros do método recebem um conjunto de constantes que permitem interpretar de forma precisa a arquitetura da classe. Entre os diversos parâmetros herdados da classe base, destaca-se o array bottlenecks, que contém os tamanhos dos estados latentes dos autocodificadores a serem criados.

No corpo do método, chamamos imediatamente o método de mesmo nome pertencente à classe base da camada neural totalmente conectada. É importante ressaltar que esse objeto é o ancestral comum de todas as camadas neurais da nossa biblioteca. Neste caso, optamos deliberadamente por não utilizar o método de inicialização da classe-pai direta, pois não queremos inicializar o pool de especialistas do objeto herdado. No entanto, essa decisão nos leva à necessidade de construir manualmente o processo de inicialização de todos os objetos herdados.

Após a inicialização bem-sucedida das interfaces básicas, passamos à inicialização dos objetos herdados da classe-pai. O primeiro a ser inicializado é o módulo responsável pela seleção adaptativa das k especialistas mais relevantes. Aqui, o número total de especialistas é determinado pelo tamanho do array bottlenecks. Como parâmetros adicionais, utilizamos as constantes recebidas do programa externo.

   int index = 0;
   if(!cGates.Init(0, index, OpenCL, window, units_count * variables, bottlenecks.Size(), top_k, optimization, iBatch))
      return false;

Em seguida, preparamos o array dinâmico e as variáveis locais necessárias para armazenar temporariamente os ponteiros dos objetos internos que comporão o módulo Adaptive Bottlenecks.

   cExperts.Clear();
   cExperts.SetOpenCL(OpenCL);
   CNeuronConvOCL *conv = NULL;
   CNeuronMultiWindowsConvOCL *mwconv = NULL;
   CNeuronTransposeRCDOCL *transp = NULL;

Logo depois, organizamos um laço e calculamos o tamanho total de todos os estados latentes dos autocodificadores que serão criados.

   uint bn_size = 0;
   for(uint i = 0; i < bottlenecks.Size(); i++)
      bn_size += bottlenecks[i];

Concluída essa etapa de preparação, passamos à criação da sequência de objetos dos nossos autocodificadores.

Curiosamente, o primeiro componente criado é uma camada convolucional padrão. À primeira vista, essa pode não parecer uma escolha muito óbvia, especialmente considerando a complexidade da arquitetura do módulo Adaptive Bottlenecks. No entanto, esse passo desempenha um papel importante nas etapas seguintes do processamento de dados.

O ponto central é que, ao criarmos a camada convolucional, definimos o número de filtros igual à soma de todos os tamanhos dos estados latentes dos autocodificadores. Isso se justifica porque cada autocodificador trabalha com o mesmo conjunto de dados brutos. E o nível de detalhamento dos dados comprimidos depende do tamanho do estado latente. Cada filtro da camada convolucional opera de maneira independente dos demais, gerando o valor correspondente ao seu próprio elemento no buffer de resultados. Na prática, isso pode ser comparado a um grande conjunto de minimodelos que comprimem os dados analisados até um único elemento. Agora, podemos agrupá-los no número desejado de grupos, cada um com a quantidade de elementos necessária. Ao mesmo tempo, o número de elementos em cada grupo pode variar. Desde que o total geral seja preservado.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window, window, bn_size, units_count, variables, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(SoftPlus);

É exatamente essa propriedade que vamos aproveitar. Em seguida, declaramos a camada convolucional multi-janela. Cada janela de convolução processará seu próprio grupo de elementos, que formarão o estado latente de um autocodificador individual. E depois restaurará os dados até o tamanho definido.

   index++;
   mwconv = new CNeuronMultiWindowsConvOCL();
   if(!mwconv ||
      !mwconv.Init(0, index, OpenCL, bottlenecks, window_out, units_count, variables, optimization, iBatch) ||
      !cExperts.Add(mwconv))
     {
      delete conv;
      return false;
     }
   mwconv.SetActivationFunction(SoftPlus);

Depois disso, planejamos adicionar mais uma camada ao decodificador dos autocodificadores criados. Cada autocodificador deve receber sua própria camada com parâmetros de treinamento exclusivos. É importante observar que o resultado da camada convolucional multi-janela, inicializada por último, pode ser representado como um tensor 4D [Variável, Unidades, Autoencoder, Dimensão]. Se utilizarmos uma camada convolucional comum, não conseguiremos garantir a exclusividade dos parâmetros de cada autocodificador. No entanto, isso pode ser facilmente implementado se colocarmos a dimensão do autocodificador na primeira posição. Portanto, a próxima etapa é declarar uma camada de transposição de dados.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_count * variables, bottlenecks.Size(), window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

Logo após, adicionamos uma camada convolucional, especificando no parâmetro de variáveis o número de autocodificadores, o que indicará ao objeto inicializado a necessidade de criar matrizes de pesos exclusivas.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_out, window_out, window, units_count * variables, bottlenecks.Size(),
                                                                                       optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Em seguida, adicionamos outro objeto de transposição de dados, que devolverá os resultados das operações à sua forma original.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, bottlenecks.Size(), units_count * variables, window, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

Com isso, encerramos o método, retornando previamente o resultado lógico da execução das operações ao programa que o chamou.

Ao mesmo tempo, concluímos a análise dos algoritmos de construção dos métodos que compõem nossa visão sobre a organização do módulo Adaptive Bottlenecks. Como já mencionado anteriormente, as operações de propagação para frente e reversa são realizadas pelos recursos herdados da classe base. O código completo desse objeto e de todos os seus métodos pode ser consultado no anexo.

Arquitetura das modelos

Hoje decidimos não unificar todo o framework DADA em um único objeto. Em vez disso, utilizaremos as soluções já testadas da nossa biblioteca, adicionaremos o módulo Adaptive Bottlenecks desenvolvido anteriormente e construiremos a partir disso uma arquitetura linear e flexível para o modelo treinável.

Essa abordagem nos oferece muito mais liberdade. Primeiro, torna o sistema mais flexível, pois é possível substituir ou otimizar módulos individuais sem a necessidade de reescrever todo o código. Segundo, "nos dá liberdade" na escolha da arquitetura do codificador e do decodificador. Agora não há mais limitações rígidas, o que nos permite experimentar, adaptar o modelo a tarefas específicas e buscar configurações ideais.

Sim, essa modularidade torna o processo de descrição do modelo um pouco mais complexo, mas é um preço razoável a se pagar pela flexibilidade e adaptabilidade que ela proporciona.

Neste experimento, treinaremos três modelos simultaneamente, cada um desempenhando um papel essencial dentro do sistema geral de análise e tomada de decisão. Essa abordagem permite construir um sistema inteligente em múltiplos níveis, capaz de analisar dados, adaptar-se às mudanças na dinâmica do mercado, prever o movimento futuro dos preços e ajustar a estratégia com base em uma análise abrangente das informações.

O primeiro modelo é o Codificador do estado do ambiente, desenvolvido sobre a arquitetura do framework DADA com um decodificador de estado normal. Seu treinamento será baseado nos princípios clássicos de um autocodificador, cuja principal função é reconstruir os dados originais a partir do espaço latente com perdas mínimas. Isso nos permite treinar o sistema para encontrar a forma mais informativa de compressão dos dados, preservando todas as características relevantes do ambiente. Esse mecanismo não apenas reduz o volume de informação, mas também revela dependências ocultas nos dados analisados, o que é extremamente importante para a construção de um modelo analítico de alta precisão.

O segundo componente-chave do sistema é o Ator, que substitui o decodificador de elementos anômalos presente na arquitetura original do framework DADA. Esse módulo desempenha o papel de agente ativo na interação com o ambiente de mercado, já que sua principal função é identificar tendências sustentáveis, reconhecer possíveis pontos de reversão e tomar decisões voltadas à otimização da estratégia de trading.

O Ator analisa os dados multidimensionais de entrada, reconhece padrões recorrentes e a dinâmica das mudanças nos estados de mercado e, com base nas relações identificadas, gera sinais de trading. Isso torna o sistema não apenas analítico, mas também adaptativo, capaz de interpretar as informações, ajustar-se às condições em mudança e determinar os momentos ideais para entrar ou sair do mercado.

Entretanto, mesmo com um mecanismo robusto de análise e geração de sinais, a precisão das previsões continua sendo um fator crítico. É nesse ponto que entra o terceiro modelo, cuja principal função é avaliar a direção mais provável do movimento futuro dos preços. Esse componente complementa o trabalho do Ator e atua como um filtro adicional para a validação das decisões de trading.

A arquitetura de todos os modelos é descrita no método CreateDescriptions. Nos parâmetros desse método, são passados três ponteiros para buffers dinâmicos de dados, nos quais será formada a descrição da arquitetura das modelos que serão treinadas.

bool CreateDescriptions(CArrayObj *&encoder, CArrayObj *&actor, CArrayObj *&probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

No corpo do método, verificamos imediatamente a validade dos ponteiros recebidos e, se necessário, criamos novas instâncias dos objetos.

Na primeira etapa, formamos a descrição da arquitetura do Codificador do estado do ambiente. Como é fácil deduzir, esse modelo recebe como entrada um tensor que representa o estado do ambiente a ser analisado. Para registrar os dados brutos, criamos uma camada totalmente conectada de tamanho adequado.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Os dados de entrada do modelo serão os "dados brutos" provenientes do terminal. É evidente que as diversas variáveis do conjunto multimodal que descreve o estado do ambiente pertencem a diferentes distribuições. E isso torna sua análise significativamente mais complexa. Por esse motivo, a próxima etapa consiste em adicionar uma camada de normalização em lote (batch normalization), que ajusta essas variáveis para uma escala comparável.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, os autores do framework DADA recomendam o uso do módulo de patching e mascaramento. Para aplicar o mascaramento aleatório em 20% dos dados analisados, utilizaremos uma camada Dropout.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDropoutOCL;
   descr.count = prev_count;
   descr.probability = 0.2f;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

O patching dos dados, segundo os autores do DADA, é realizado dentro de sequências unitárias. No nosso caso, para criar as condições ideais de processamento dessas sequências unitárias, é necessário transpor os dados.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.window = BarDescr;
   prev_count = descr.count = HistoryBars;
   descr.activation = SoftPlus;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Agora, basta utilizarmos uma camada convolucional para realizar o processamento independente dos segmentos de tamanho definido. Neste caso, usamos duas camadas convolucionais sequenciais, que executam o codificação paralela de segmentos não sobrepostos e, ao mesmo tempo, desempenham o papel do codificador do nosso modelo de codificação do estado do ambiente.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.window = HistoryBars / Segments;
   prev_count = descr.count = (HistoryBars + descr.window - 1) / descr.window;
   descr.step = descr.window;
   descr.layers = BarDescr;
   descr.activation = SoftPlus;
   int prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize;
   descr.layers = BarDescr;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, entra em ação o módulo Adaptive Bottlenecks, dentro do qual criamos 15 pequenos autocodificadores, cada um com um estado latente múltiplo de 8. Para codificar os dados de cada segmento, utilizaremos os três autocodificadores mais adequados.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronAdaBN;
   descr.window = prev_wout;
   descr.count = prev_count;
   descr.window_out = 256;
   descr.step = 3; // Top K
   descr.layers = BarDescr; // Variables
     {
      int temp[15];
      for(uint i = 0; i < temp.Size(); i++)
         temp[i] = int(i + 1) * 8;
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Para restaurar os dados dos segmentos analisados, empregamos um decodificador composto por duas camadas convolucionais sequenciais, de forma análoga ao codificador do modelo.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count * BarDescr;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize / 2;
   descr.activation = SoftPlus;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count * BarDescr;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = HistoryBars / Segments;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Vale destacar que, na saída do decodificador, utilizamos a tangente hiperbólica como função de ativação. E isso não é por acaso. Após a camada de normalização em lote, o modelo trabalha com dados normalizados cuja dispersão é próxima de "1" e com média zero. Pela regra das "3 sigmas", pouco mais de 68% dos dados normalmente distribuídos se situam dentro do intervalo de ± um desvio padrão em relação à média. Com um desvio padrão igual a "1", o intervalo resultante é [-1, 1]. É exatamente nesse intervalo que se encontra o domínio principal da tangente hiperbólica. Dessa forma, na saída do decodificador, obtemos valores dentro da faixa mais provável, eliminando valores atípicos.

Em seguida, para verificar a qualidade da restauração dos dados analisados, é necessário comparar os resultados obtidos pelo decodificador com os próprios dados analisados. No entanto, vale lembrar que, para facilitar o processamento das sequências unitárias, realizamos a transposição dos dados. Agora, precisamos revertê-los ao formato original por meio da transposição inversa.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Depois disso, retornamos os valores obtidos à distribuição dos dados originais.

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = HistoryBars * BarDescr;
   descr.layers = 1;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

O funcionamento das outras duas modelos baseia-se na análise do estado latente do nosso Codificador do estado do ambiente, gerado na saída do módulo Adaptive Bottlenecks. Portanto, armazenamos os parâmetros desse módulo em uma variável local.

//--- Latent
   CLayerDescription *latent = encoder.At(LatentLayer);
   if(!latent)
      return false;

Na etapa seguinte, criamos a descrição da arquitetura do Ator. Supõe-se que o Ator analisa o estado do ambiente no contexto do saldo atual e das posições abertas, gerando a operação de trading mais adequada. Para estruturar esse processo, planejamos fornecer ao modelo, na entrada, um vetor que descreve o estado da conta. Para registrar esses dados, criamos uma camada totalmente conectada de tamanho apropriado.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Os dados recebidos também passam por normalização.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, aplicamos uma camada de concatenação, que combina dois grupos de informações: os dados sobre o estado da conta e a representação comprimida do ambiente, obtida a partir do estado latente do Codificador. Essa combinação permite que o modelo leve em consideração tanto os indicadores financeiros quanto as características generalizadas do ambiente ao tomar decisões.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = latent.count * latent.window * latent.layers;
   descr.batch = 1e4;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Logo depois, vem o módulo de tomada de decisão, composto por três camadas totalmente conectadas. Esse módulo processa os dados combinados, extraindo as principais relações e formando a decisão final do modelo.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.batch = 1e4;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = SIGMOID;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

O último modelo, responsável por prever as probabilidades do movimento futuro dos preços, possui a arquitetura mais simples. Nessa configuração, pretende-se analisar apenas a representação comprimida do estado do ambiente. Para obter os dados de entrada, criamos uma camada totalmente conectada baseada nas informações do estado latente do Codificador.

   probability.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = latent.count * latent.window * latent.layers;
   descr.activation = latent.activation;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, o módulo de tomada de decisão, composto por três camadas totalmente conectadas, realiza o processamento.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions / 3;
   descr.activation = SoftPlus;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

Os resultados da análise são convertidos em valores probabilísticos por meio da função SoftMax.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   prev_count = descr.count = prev_count;
   descr.step = 1;
   descr.activation = None;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

A descrição completa da arquitetura dos modelos está disponível no anexo deste artigo.

Treinamento dos modelos

Após descrevermos a arquitetura dos modelos, passamos à próxima etapa, nomeadamente o treinamento, cujo algoritmo está implementado no EA "...\DADA\Study.mq5". Nossa tarefa é realizar o treinamento paralelo de três modelos simultaneamente, o que exigiu algumas modificações no algoritmo desse EA. Nesta parte do artigo, não entraremos em detalhes sobre o código completo do EA. Concentrando-nos apenas no método de treinamento direto das modelos, o método Train.

Dentro do método, começamos com uma breve preparação, declarando algumas variáveis locais.

void Train(void)
  {
//---
   vector<float> probability = vector<float>::Full(Buffer.Size(), 1.0f / Buffer.Size());
//---
   vector<float> result, target, state;
   matrix<float> fstate = matrix<float>::Zeros(1, NForecast * BarDescr);
   bool Stop = false;
//---
   uint ticks = GetTickCount();

O treinamento propriamente dito ocorre dentro de um sistema de laços. O laço externo percorre os pacotes de treinamento. Para cada pacote, é amostrada aleatoriamente uma trajetória do buffer de replay de experiência, junto com o estado inicial de treinamento dessa trajetória selecionada.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch)
     {
      int tr = SampleTrajectory(probability);
      int start = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast - Batch));
      if(start <= 0)
        {
         iter -= Batch;
         continue;
        }
      if(!Encoder.Clear() ||
         !Actor.Clear())
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }
      result = vector<float>::Zeros(NActions);

Dentro do laço interno, ocorre o treinamento dos modelos nos estados sequenciais de um mesmo pacote.

Vale destacar que os modelos desenvolvidos neste artigo não contêm blocos recorrentes. Normalmente, modelos desse tipo são treinados em estados totalmente aleatórios extraídos do buffer de replay. No entanto, neste caso, o treinamento é realizado em trajetórias "quase ideais", cujas ações são geradas diretamente pelo algoritmo do EA, com base nas informações disponíveis sobre os estados futuros do ambiente. Diferentemente do treinamento em tempo real, ao trabalhar com o buffer de replay, temos acesso aos dados dos estados seguintes do ambiente para todos os registros salvos, exceto o último. Isso permite direcionar o processo de aprendizado de maneira mais precisa.

Contudo, há um outro lado da questão. Nessa configuração, não temos informações sobre as posições abertas. E é importante que o modelo aprenda não apenas a abrir posições, mas também a gerenciá-las, buscando o ponto de saída mais favorável. Por esse motivo, durante o treinamento, formaremos pequenos lotes de aprendizado que incluirão posições "ótimas".

      for(int i = start; i < MathMin(Buffer[tr].Total, start + Batch); i++)
        {
         if(!state.Assign(Buffer[tr].States[i].state) ||
            MathAbs(state).Sum() == 0 ||
            !bState.AssignArray(state))
           {
            iter -= Batch + start - i;
            break;
           }
         //---
         bTime.Clear();
         double time = (double)Buffer[tr].States[i].account[7];
         double x = time / (double)(D'2024.01.01' - D'2023.01.01');
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_MN1);
         bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_W1);
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_D1);
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(bTime.GetIndex() >= 0)
            bTime.BufferWrite();
         //--- Account
         float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
         float profit = float(bState[0] / _Point * (result[0] - result[3]));
         bAccount.Clear();
         bAccount.Add(1);
         bAccount.Add((PrevEquity + profit) / PrevEquity);
         bAccount.Add(profit / PrevEquity);
         bAccount.Add(MathMax(result[0] - result[3], 0));
         bAccount.Add(MathMax(result[3] - result[0], 0));
         bAccount.Add((bAccount[3] > 0 ? profit / PrevEquity : 0));
         bAccount.Add((bAccount[4] > 0 ? profit / PrevEquity : 0));
         bAccount.Add(0);
         bAccount.AddArray(GetPointer(bTime));
         if(bAccount.GetIndex() >= 0)
            bAccount.BufferWrite();

Dentro do laço, extraímos primeiro as informações do buffer de replay e formamos os objetos de dados de entrada para os modelos em treinamento. Em seguida, chamamos os métodos de propagação para frente do Codificador do estado do ambiente.

         //--- Feed Forward
         if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Depois, executamos os métodos correspondentes para os outros dois modelos, passando como dado de entrada o ponteiro para o objeto do Codificador do estado do ambiente.

         if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder), LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }
         if(!Probability.feedForward(GetPointer(Encoder), LatentLayer, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Em seguida, ocorre o processo de formação da "operação de trading ideal". Esse processo foi completamente transferido do artigo dedicado ao aprendizado multitarefa. A explicação detalhada desse procedimento pode ser consultada nesse material; aqui, optamos por omiti-lo.

Após preparar os valores-alvo, passamos à otimização dos parâmetros dos modelos, com o objetivo de minimizar os desvios em relação a esses valores. O primeiro modelo a ser treinado é o Codificador do estado do ambiente. Como tensor de valores-alvo, fornecemos a ele o vetor que descreve o estado analisado do ambiente, o mesmo utilizado durante a propagação para frente.

         //--- State Encoder
         if(!Encoder.backProp(GetPointer(bState), (CBufferFloat*)NULL, NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Em seguida, treinamos o Ator, minimizando o desvio em relação à "operação de trading ideal".

         //--- Actor Policy
         if(!Actor.backProp(GetPointer(bActions), (CNet*)GetPointer(Encoder), LatentLayer)
            || !Encoder.backPropGradient((CBufferFloat*)NULL, (CBufferFloat*)NULL, LatentLayer, true)
            )
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Para o treinamento do terceiro modelo, determinamos a direção do movimento futuro do preço com base na cor da próxima barra.

         target = vector<float>::Zeros(NActions / 3);
         if(fstate[0, 0] > 0)
            target[0] = 1;
         else
            if(fstate[0, 0] < 0)
               target[1] = 1;
         if(!Result.AssignArray(target) ||
            !Probability.backProp(Result, (CBufferFloat*)NULL)
            || !Encoder.backPropGradient((CBufferFloat*)NULL, (CBufferFloat*)NULL, LatentLayer)
           )
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Depois disso, resta apenas informar o usuário sobre o andamento do processo de treinamento e avançar para a próxima iteração do sistema de laços.

         //---
         if(GetTickCount() - ticks > 500)
           {
            double percent = double(iter + i - start) * 100.0 / (Iterations);
            string str = StringFormat("%-13s %6.2f%% -> Error %15.8f\n", "Encoder",
                                         percent, Encoder.getRecentAverageError());
            str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent,
                                                     Actor.getRecentAverageError());
            str += StringFormat("%-13s %6.2f%% -> Error %15.8f\n", "Probability", 
                                      percent, Probability.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

Após a execução bem-sucedida de todas as iterações de treinamento dos modelos, os resultados obtidos são exibidos no log, e iniciamos o processo de finalização do EA.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Probability", Probability.getRecentAverageError());
   ExpertRemove();
//---
  }

O código completo desse EA está disponível no anexo, juntamente com os programas responsáveis pela interação com o ambiente e pelos testes dos modelos treinados.

Testes

Após o extenso trabalho de implementação das abordagens propostas pelos autores do framework DADA, utilizando os recursos do MQL5 e sua integração aos modelos treináveis, chega o estágio mais importante, que consiste em verificar a eficácia das soluções desenvolvidas em dados históricos reais. Isso nos permitirá avaliar o potencial de aplicação prática dessas técnicas em condições reais de mercado.

Para o treinamento do modelo, foi gerado um conjunto de passagens aleatórias no testador de estratégias do MetaTrader 5, com base em dados históricos do par de moedas EURUSD no timeframe M1, abrangendo todo o ano de 2024. Os dados históricos foram coletados utilizando os parâmetros padrão dos indicadores, garantindo a pureza do experimento e eliminando a influência de fatores externos.

O teste dos modelos treinados foi realizado em dados históricos de janeiro e fevereiro de 2025. Todos os parâmetros do experimento foram mantidos inalterados, permitindo obter uma avaliação objetiva da política de comportamento do Ator treinado. Avaliar a eficiência do modelo em dados que não foram utilizados durante o treinamento é uma etapa essencial de sua validação. Pois demonstra sua capacidade de operar em condições próximas às reais.

Os resultados dos testes são apresentados a seguir.

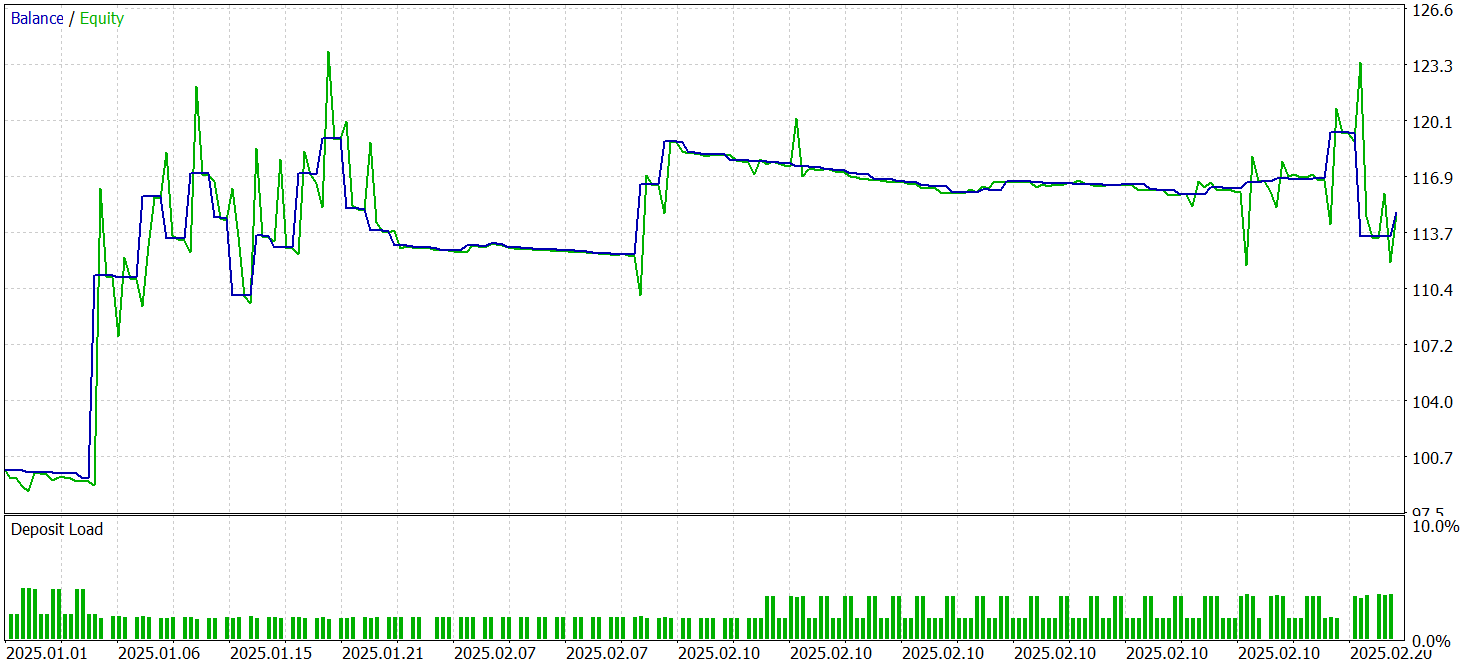
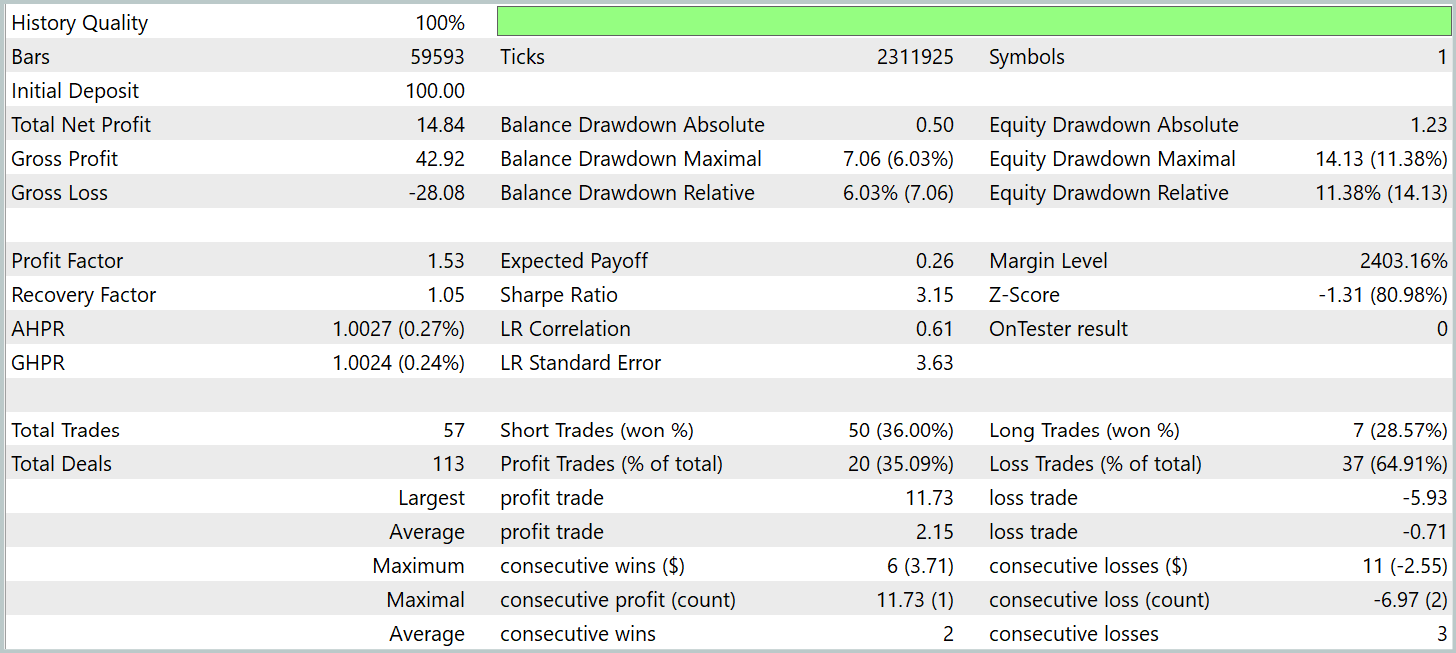
Durante o período de teste, o modelo executou 57 operações de trading, das quais mais de 35% foram encerradas com lucro. No entanto, o triplo da média das posições lucrativas em relação às perdas médias permitiu ao modelo obter lucro no período de teste, registrando um profit factor de 1,53.

No entanto, é importante observar que o lucro foi obtido na primeira metade de janeiro. Durante o restante do período, o gráfico de saldo oscilou dentro de uma faixa estreita. Isso pode indicar a necessidade de estudar opções para otimizar o desempenho do modelo.

Também vale destacar que, durante a implementação, fizemos uma série de alterações estruturais na arquitetura do framework DADA. Portanto, os resultados obtidos são relevantes apenas para esta versão específica da implementação.

Considerações finais

Neste trabalho, estudamos o framework DADA, que propõe uma abordagem inovadora combinando o mecanismo de gargalos adaptativos e dois decodificadores paralelos para uma análise mais precisa de séries temporais. A principal vantagem desse método está em sua capacidade de se ajustar dinamicamente a diferentes estruturas de dados sem a necessidade de adaptação prévia.

Foi realizado um trabalho extenso de implementação, utilizando os recursos do MQL5, de uma versão própria baseada nos conceitos propostos pelos autores do framework. As soluções desenvolvidas foram integradas aos modelos, que em seguida foram treinados com dados históricos reais. Durante os testes, os modelos treinados conseguiram apresentar rentabilidade. No entanto, o gráfico de saldo não mostrou uma tendência consistente de crescimento, o que indica a necessidade de uma otimização adicional da estratégia.

Referências

• Towards a General Time Series Anomaly Detector with Adaptive Bottlenecks and Dual Adversarial Decoders
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL