Нейросети в трейдинге: Двойная кластеризация временных рядов (DUET)

MetaTrader 5 — Торговые системы | 12 марта 2025, 12:16

448

Dmitriy Gizlyk

Введение

Многомерные временные ряды — это последовательность данных, в которой каждая временная отметка содержит несколько взаимосвязанных переменных, характеризующих сложные процессы. Они широко используются в экономическом анализе, управлении рисками, а также в других сферах, требующих прогнозирования многомерных данных. В отличие от одномерных временных рядов, многомерные позволяют учитывать корреляции между переменными, что дает возможность строить более точные прогнозы.

На финансовых рынках анализ многомерных временных рядов применяется для прогнозирования цен активов, оценки волатильности, выявления трендов и разработки торговых стратегий. Например, при прогнозировании стоимости акций учитываются такие факторы, как объем торгов, процентные ставки, макроэкономические индикаторы и новости. Все эти параметры взаимосвязаны, и их совместный анализ позволяет выявлять закономерности, недоступные при рассмотрении каждой переменной в отдельности.

Ключевой задачей в обработке многомерных временных рядов является построение методов, способных выявлять временные и межканальные зависимости. Однако, на практике возникают сложности, связанные с изменчивостью данных. В периоды экономических кризисов корреляционные структуры между активами меняются, что затрудняет использование традиционных моделей.

Существующие методы обработки данных можно разделить на три категории. Первый подход — независимый анализ каждого канала, но он игнорирует взаимосвязи между переменными. Второй — объединение всех каналов, однако, это может привести к включению лишней информации и снижению точности. Третий — кластеризация переменных, но она ограничивает гибкость модели.

Для решения указанных проблем авторы работы "DUET: Dual Clustering Enhanced Multivariate Time Series Forecasting" предложили метод DUET, который сочетает два типа кластеризации: временную и канальную. Временная кластеризация (TCM) группирует данные на основе схожих характеристик и позволяет адаптировать модели к изменениям во времени. При анализе финансовых рынков, это позволяет учитывать различные фазы экономических циклов. Канальная кластеризация (CCM) определяет ключевые переменные, устраняя шум и повышая точность прогнозирования. Она выявляет устойчивые взаимосвязи между активами, что особенно важно для построения диверсифицированных инвестиционных портфелей.

После этого, результаты объединяются модулем Fusion Module (FM), который синхронизирует информацию о временных закономерностях и межканальных зависимостях. Такой подход позволяет более точно прогнозировать поведение сложных систем, таких как финансовые рынки. Эксперименты, проведенные авторами фреймворка, показали, что DUET превосходит существующие методы, обеспечивая более точные прогнозы. Он учитывает гетерогенные временные паттерны и динамику межканальных связей, адаптируясь к изменчивости данных.

Алгоритм DUET

Архитектура фреймворка DUET представляет собой инновационный подход к прогнозированию многомерных временных рядов, который использует двойную кластеризацию исходных данных по временным и канальным измерениям. Это повышает качество работы модели и делает её результаты более интерпретируемыми. Подход можно сравнить с работой опытного аналитика, который разделяет сложную систему данных на отдельные блоки, анализируя их сначала по отдельности, а затем в совокупности для получения более детального представления. Фреймворк DUET включает несколько ключевых модулей, каждый из которых выполняет специализированную роль в процессе анализа данных:

Нормализация исходных данных (Instance Normalization).
Модуль временной кластеризации (Temporal Clustering Module — TCM).
Модуль кластеризации каналов (Channel Clustering Module — CCM).
Модуль объединения информации (Fusion Module — FM).
Модуль прогнозирования (Prediction Module).

Нормализация исходных данных позволяет устранить выбросы и сгладить резкие колебания, что делает модель более устойчивой к различиям между обучающей и тестовой выборками. Это особенно важно в анализе финансовых данных, где высокочастотный шум может скрывать значимые тенденции. Нормализация также помогает выровнять статистические характеристики унитарных временных последовательностей, поступающих из разных источников, снижая влияние аномальных значений.

Temporal Clustering Module (TCM) анализирует временные зависимости и группирует последовательности в кластеры, подобно тому, как финансовые аналитики классифицируют активы по их волатильности, ликвидности и историческим характеристикам. В основе работы TCM лежит архитектура из нескольких параллельных энкодеров (Mixture of Experts — MoE), позволяющая динамически выбирать наиболее подходящие из них для каждого анализируемого сегмента в зависимости от ранее проведенной кластеризации временного ряда. Это обеспечивает точное представление временных последовательностей, так как разные группы данных могут требовать уникальных методов обработки. MoE адаптивно переключается между энкодерами, позволяя модели эффективно работать с временными рядами разной природы, включая высокочастотные биржевые данные.

Энкодеры анализируют временные ряды, представленные в виде скрытых признаков, которые затем разлагаются на долгосрочные и краткосрочные тенденции. Это позволяет выявить скрытые закономерности, улучшающие прогнозирование будущих изменений цен на финансовых рынках.

Channel Clustering Module (CCM) выполняет кластеризацию каналов, используя частотные характеристики сигналов. Этот модуль оценивает корреляции между каналами, выявляя ключевые зависимости и исключая избыточные или незначимые компоненты. Аналогично финансовому аналитику, который отбирает значимые макроэкономические и технические индикаторы, исключая случайные рыночные колебания, CCM помогает выделить наиболее информативные сигналы.

Анализ расстояний между векторами амплитуд частотных характеристик каналов позволяет определить коррелирующие сигналы и исключить шумовые явления. Это особенно полезно на финансовых рынках, где скрытые зависимости между активами могут использоваться для построения арбитражных стратегий или выявления систематических рисков.

Fusion Module (FM) объединяет временные и канальные представления, используя механизм маскированного внимания. Этот процесс схож с анализом сложных взаимосвязей между различными рыночными факторами, когда аналитик синтезирует информацию из разных источников для получения целостной картины. FM выявляет наиболее значимые кластеры и фильтрует несущественные сигналы, повышая точность прогнозирования. Использование механизма маскированного внимания позволяет динамически изменять значимость различных компонентов данных, делая обработку более адаптивной. Это критически важно в финансовых приложениях, где структура зависимостей между активами может изменяться под влиянием макроэкономических событий.

На финальном этапе Prediction Module использует агрегированные признаки для прогнозирования будущих значений временных рядов. Этот процесс можно сравнить с работой профессионального инвестора, который на основе исторических рыночных данных делает обоснованные прогнозы о будущих изменениях цен. Prediction Module использует нейросетевые методы, позволяющие учитывать сложные нелинейные зависимости и адаптироваться к потенциальным структурным изменениям в данных. Итоговые прогнозы проходят обратную нормализацию, что позволяет интерпретировать их в масштабе исходных данных.

Благодаря применению передовых методов машинного обучения, таких как маскированный механизм внимания, анализ частотных характеристик и кластеризация скрытых признаков, DUET обеспечивает высокую точность и интерпретируемость прогнозов. Он помогает находить скрытые закономерности в сложных временных последовательностях и применять полученные знания для оптимизации торговых стратегий, где традиционные подходы оказываются недостаточно эффективными. По сравнению с традиционными методами, требующими значительной ручной настройки и экспертного вмешательства, DUET автоматически выявляет структурные особенности данных и адаптируется к ним в реальном времени. Это делает его особенно полезным для анализа высокочастотных временных рядов и работы в условиях быстро меняющейся рыночной среды.

Авторская визуализация фреймворка DUET представлена ниже.

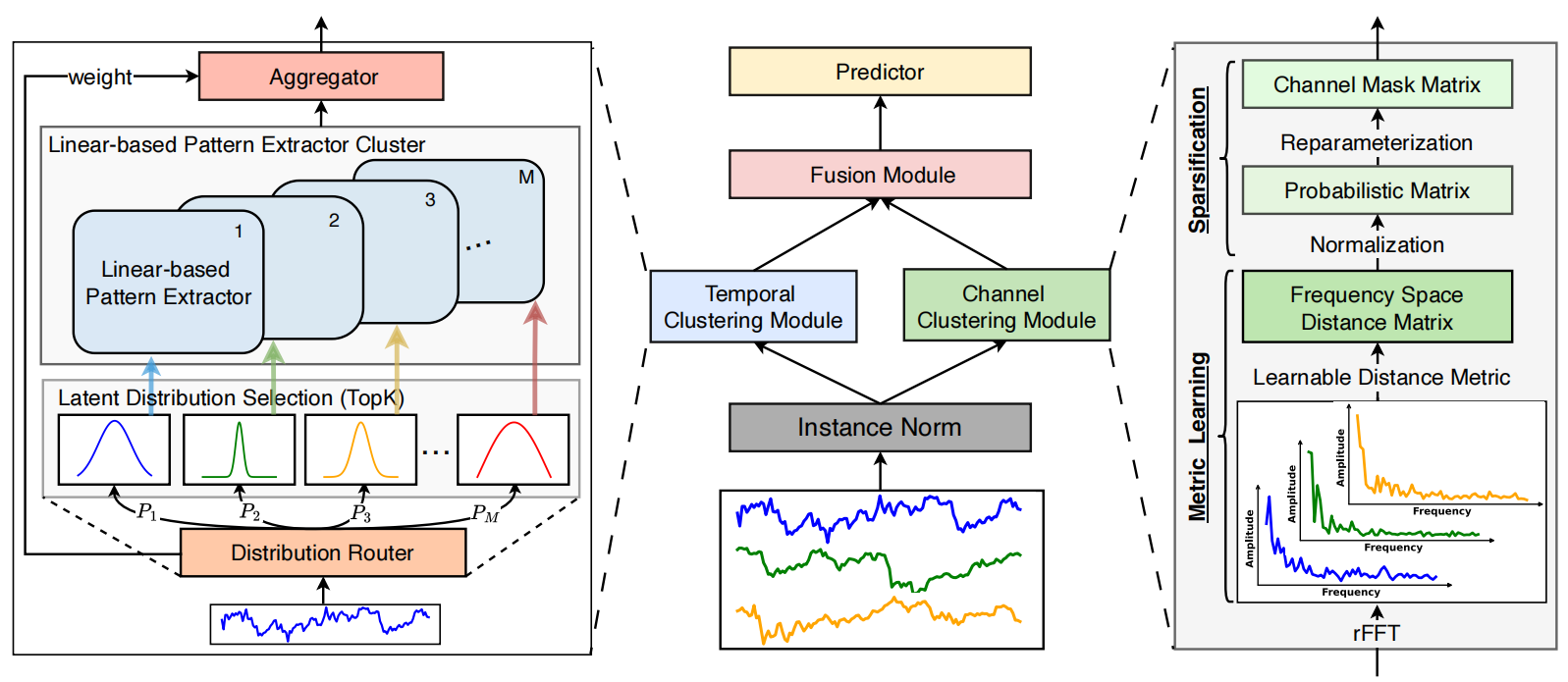
Авторская визуализация фреймворка DUET

Реализация свойствами MQL5

После детального рассмотрения теоретических аспектов фреймворка DUET мы переходим к практической части нашей работы, в которой реализуем собственное видение предложенных подходов средствами MQL5.

Модульная архитектура DUET делает его удобным для пошаговой разработки: каждый функциональный блок можно рассматривать как независимый элемент системы. Разделение на автономные модули упрощает отладку, тестирование и последующую оптимизацию. А начнем мы работу с построения модуля временной кластеризации.

Temporal Clustering Module

Как уже было сказано выше, модуль временной кластеризации включает несколько параллельно работающих энкодеров. В рамках данной работы, мы создадим максимально простую архитектуру энкодера из двух последовательных полносвязных слоев с созданием нелинейности между ними с помощью функции активации. Однако следует учесть, что каждый энкодер обрабатывает отдельные независимые сегменты с использованием собственных обучаемых параметров. И для организации подобной работы мы воспользуемся сверточными слоями. Подавая ему на вход полную последовательность исходных данных, мы установим размер анализируемого окна и его шаг равный размеру сегмента. В результате, параметры сверточного слоя будут выполнять роль полносвязного слоя энкодера, обеспечивая параллельную обработку всех сегментов последовательности. А чтобы увеличить число параллельно работающих энкодеров, нам достаточно кратно увеличить число фильтров сверточного слоя.

С организацией параллельной работы энкодеров определились. Однако следует обратить внимание, что авторы фреймворка DUET предлагают использовать только наиболее релевантные энкодеры. Предполагается, что временные ряды следуют латентному нормальному распределению. Как вы знаете, нормальное распределение характеризуется средним значением и дисперсией. Для выбора k наиболее вероятных латентных распределений авторы фреймворка используют метод "Noisy Gating", который можно представить в виде:

Добавление шума с нормальным распределением (ε) стабилизирует обучение, а Softplus сохраняет дисперсию положительной.

Затем выбираем k наиболее вероятных латентных распределений и вычисляем их веса с помощью функции SoftMax. Таким образом, временные ряды, принадлежащие одним и тем же k наиболее вероятным латентным распределениям, обрабатываются общей группой энкодеров. Умножение полученной маски на результаты работы энкодеров позволит получить взвешенный результат и исключить влияние нерелевантных фильтров.

Определившись с архитектурным решением, мы приступаем к работе. И сначала реализуем алгоритм выбора k наиболее релевантных энкодеров. Параметризацию параметров распределения отдельных сегментов мы организуем с помощью сверточного слоя. А вот алгоритм выбора k наиболее релевантных энкодеров реализуем на стороне OpenCL-контекста. Для этого создадим кернел TopKgates.

__kernel void TopKgates(__global const float *inputs,
                        __global const float *noises,
                        __global float *gates,
                        const uint k)
  {
   size_t idx = get_local_id(0);
   size_t var = get_global_id(1);
   size_t window = get_local_size(0);
   size_t vars = get_global_size(1);

В параметрах кернела получаем указатели на 3 буфера данных (исходные данные, шум, результаты) и количество отбираемых элементов.

В теле кернела мы, как обычно, сначала идентифицируем текущий поток в пространстве задач. В данном случае используется двухмерное пространство задач с объединением в локальные группы по первому измерению, которое объединяет потоки относящиеся к одному сегменту и соответствует количеству используемых моделью энкодеров.

Далее определяем смещение в локальных буферах данных.

   const int shift_logit = var * 2 * window + idx;
   const int shift_std = shift_logit + window;
   const int shift_gate = var * window + idx;

И загружаем соответствующие исходные данные.

   float logit = IsNaNOrInf(inputs[shift_logit], MIN_VALUE);
   float noise = IsNaNOrInf(noises[shift_gate], 0);
   if(noise != 0)
     {
      noise *= Activation(inputs[shift_std], 3);
      logit += IsNaNOrInf(noise, 0);
     }

Если шум не равен "0", то корректируем значение переменной logit с учетом дисперсии и шума.

Далее нам предстоит определить k максимальных значений logit в рамках одной рабочей группы. С этой целью создаем массив в локальной памяти, как средство для обмена данными между потоками рабочей группы и объявим вспомогательные локальные переменные.

   __local float temp[LOCAL_ARRAY_SIZE];
//---
   const uint ls = min((uint)window, (uint)LOCAL_ARRAY_SIZE);
   uint bigger = 0;
   float max_logit = logit;

Далее объявим цикл перебора элементов рабочей группы с шагом, равным размеру локального массива.

//--- Top K
#pragma unroll
   for(int i = 0; i < window; i += ls)
     {
      if(idx >= i && idx < (i + ls))
         temp[idx % ls] = logit;
      barrier(CLK_LOCAL_MEM_FENCE);

В теле цикла элементы текущего окна сохраняют свои значения в локальный массив с обязательной последующей синхронизацией работы потоков рабочей группы.

Затем создадим вложенный цикл, в рамках итераций которого каждый поток посчитает сколько элементов в локальном массиве больше logit текущего потока.

      for(int i1 = 0; (i1 < min((int)ls,(int)(window-i)) && bigger <= k); i1++)
        {
         if(temp[i1] > logit)
            bigger++;
         if(temp[i1] > max_logit)
            max_logit = temp[i1];
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Параллельно мы ищем максимальное значение в рамках локальной группы.

После выполнения всех итераций вложенного цикла, мы снова синхронизируем работу потоков рабочей группы и только после этого переходим к следующей итерации внешнего цикла.

Думаю очевидно, что только k потоков с максимальными значениями logit не набрали порогового значения превышающих элементов. Их значения мы и сохраним в буфер результатов.

   if(bigger <= k)
      gates[shift_gate] = logit - max_logit;
   else
      gates[shift_gate] = MIN_VALUE;
  }

В остальных случаях в буфер результатов записываем константу минимального значения, которая в процессе применения функции SoftMax даст нулевой коэффициент влияния.

Представленный выше кернел организовывает прямой проход процесса выбора k наиболее релевантных энкодеров в каждом конкретном случае. Однако, для построения по-настоящему адаптивной модели нам необходимо организовать процесс обучения отбора энкодеров. Конечно, в рамках представленного выше кернела мы не использовали обучаемых параметров. Тем не менее, они применяются для генерации используемых нами исходных данных. Поэтому мы просто обязаны передать градиент ошибки на уровень исходных данных. Данный процесс организуем в кернеле TopKgatesGrad. В структуре параметров которого добавляем указатели на буферы соответствующих градиентов ошибки.

__kernel void TopKgatesGrad(__global const float *inputs,
                            __global float *grad_inputs,
                            __global const float *noises,
                            __global const float *gates,
                            __global float *grad_gates)
  {
   size_t idx = get_global_id(0);
   size_t var = get_global_id(1);
   size_t window = get_global_size(0);
   size_t vars = get_global_size(1);

В теле кернела осуществляем идентификацию текущего потока операций в двухмерном пространстве задач. Структура пространства задач заимствована из кернела прямого прохода, только теперь мы не объединяем потоки в рабочие группы.

Далее определяем смещение в глобальных буферах данных, аналогично алгоритму прямого прохода.

   const int shift_logit = var * 2 * window + idx;
   const int shift_std = shift_logit + window;
   const int shift_gate = var * window + idx;

И первым делом загружаем результат прямого прохода соответствующего потока.

   const float gate = IsNaNOrInf(gates[shift_gate], MIN_VALUE);
   if(gate <= MIN_VALUE)
     {
      grad_inputs[shift_logit] = 0;
      grad_inputs[shift_std] = 0;
      return;
     }

Как не сложно догадаться, если полученное значение равно минимальной константе, то можно сразу сохранить нулевые значения в буфере градиентов исходных данных. Ведь такое значение соответствует исключению энкодера из дальнейших операций.

В противном случае, загружаем значение градиента ошибки на уровне результатов и сразу передаем его в соответствующий элемент буфера градиентов исходных данных (погрешность logit).

   float grad = IsNaNOrInf(grad_gates[shift_gate], 0);
   grad_inputs[shift_logit] = grad;

На уровень шума мы, конечно, не распределяем градиент ошибки. Однако, нам осталось определить значение погрешности на уровне дисперсии. Как вы знаете, в процессе прямого прохода дисперсия умножалась на шум, поэтому следующим этапом мы извлекаем значение шума.

   float noise = IsNaNOrInf(noises[shift_gate], 0);
   if(noise == 0)
     {
      grad_inputs[shift_std] = 0;
      return;
     }

Очевидно, что при шуме равном "0", дисперсия не принимает участие в операциях прямого прохода. Следовательно, в подобном случае, мы просто сохраняем нулевой градиент без выполнения дальнейших операций.

Ну и в последнем случае, мы корректируем значение градиента ошибки на коэффициент шума и производную функции активации.

   grad *= noise;
   grad_inputs[shift_std] = Deactivation(grad, Activation(inputs[shift_std], 3), 3);
  }

Полученный результат сохраняем в глобальном буфере данных и завершаем работу кернела.

Полный код обоих выше представленных кернелов вы можете найти во вложении к статье.

Следующим этапом нашей работы будет организация данного процесса на стороне основной программы. Прежде всего создадим объект CNeuronTopKGates в котором построим алгоритм выбора k наиболее релевантных энкодеров. Структура нового объекта представлена ниже.

class CNeuronTopKGates  :  public CNeuronSoftMaxOCL
  {
protected:
   int               iK;
   CBufferFloat      cbNoise;
   CNeuronConvOCL    cProjection;
   CNeuronBaseOCL    cGates;
   //---
   virtual bool      TopKgates(void);
   virtual bool      TopKgatesGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTopKGates(void) {};
                    ~CNeuronTopKGates(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint gates, uint top_k,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronTopKGates; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual uint      GetGates(void) const { return cProjection.GetFilters() / 2; }
   virtual uint      GetUnits(void) const { return cProjection.GetUnits(); }
  };

В представленной структуре мы видим, что к привычному набору переопределяемых виртуальных методов добавляются TopKgates и TopKgatesGradient. Это методы-обертки выше описанных кернелов, созданных на стороне OpenCL-программы. Для их создания использовался знакомый вам алгоритм, и мы не будем сегодня на нем детально останавливаться.

Немногочисленные внутренние объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. А инициализация всех объявленных и унаследованных объектов осуществляется в методе Init, в параметрах которого получаем константы, позволяющие однозначно интерпретировать архитектуру создаваемого объекта.

bool CNeuronTopKGates::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint units_count, uint gates, uint top_k, 
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, gates * units_count,
                                                        optimization_type, batch))
      return false;
   SetHeads(units_count);

Операции метода инициализации начинаются с вызова одноименного метода родительского класса, в котором уже организованы минимально необходимые контроли и инициализация унаследованных объектов.

Обратите внимание, что в данном случае мы используем объект функции SoftMax в качестве родительского класса. Это позволяет нам переводить результаты отбора k наиболее релевантных энкодеров в вероятностное представление без создания дополнительного внутреннего объекта. Для этого достаточно просто воспользоваться функционалом родительского класса.

После успешного выполнения операций метода родительского класса, переходим к построению алгоритма инициализации вновь объявленных объектов. Здесь первым инициализируем сверточный слой проекции параметров распределения данных анализируемых сегментов.

   if(!cProjection.Init(0, 0, OpenCL, window, window, 2 * gates, units_count, 1, optimization, iBatch))
      return false;
   cProjection.SetActivationFunction(None);

На выходе данного слоя мы ожидаем получить средние значения и дисперсии для каждого из энкодера нашей модели. Следовательно, количество фильтров сверточного слоя в 2 раза превышает заданное количество энкодеров.

Тут же мы добавим буфер данных, в который будем генерировать шум.

   if(!cbNoise.BufferInit(Neurons(), 0) ||
      !cbNoise.BufferCreate(OpenCL))
      return false;

И в завершении операций метода инициализируем полносвязный слой для записи результатов работы выше созданного кернела прямого прохода TopKgates.

   if(!cGates.Init(0, 1, OpenCL, Neurons(), optimization, iBatch))
      return false;
   cGates.SetActivationFunction(None);
//---
   return true;
  }

После чего, вернем логический результат выполнения операций вызывающей программе и завершим работу метода.

Обратите внимание, что в данном случае мы не создаем объекты записи вероятностного распределения Top K энкодеров. Абсолютные значения logit в вероятностное пространство мы планируем переводить средствами родительского класса. Следовательно, все объекты по обслуживанию данного процесса уже созданы и инициализированы в родительском классе.

Следующим этапом нашей работы является построение метода прямого прохода объекта отбора k наиболее релевантных энкодеров CNeuronTopKGates::feedForward. В параметрах данного метода мы, как обычно, получаем указатель на объект исходных данных, который сразу передаем в одноименный метод объекта генерации статистических показателей распределения анализируемых сегментов.

bool CNeuronTopKGates::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cProjection.FeedForward(NeuronOCL))
      return false;

Далее следует обратить внимание, что шум к значениям logit авторы фреймворка DUET предлагают добавлять только в процессе обучения. Поэтому мы проверяем режим работы модели и, при необходимости, генерируем шум.

   if(bTrain)
     {
      double random[];
      if(!Math::MathRandomNormal(0, 1, Neurons(), random))
         return false;
      if(!cbNoise.AssignArray(random))
         return false;
      if(!cbNoise.BufferWrite())
         return false;
     }
   else
      if(!cbNoise.Fill(0))
         return false;

В противном случае буфер шума заполняем нулевыми значениями.

А затем вызываем метод-обернтку отбора k наиболее релевантных энкодеров.

   if(!TopKgates())
      return false;
//---
   return CNeuronSoftMaxOCL::feedForward(cGates.AsObject());
  }

Полученные результаты передаем в одноименный метод родительского класса, что позволит перевести абсолютные значения в вероятностное пространство.

Логический результат выполнения операций возвращаем вызывающей программе и завершаем работу метода.

Как вы могли заметить, метод прямого прохода имеет линейный алгоритм. Соответственно, такой же линейный алгоритм получили и методы обратного прохода. Поэтому я предлагаю оставить их для самостоятельного изучения. Полный код данного объекта и всех его методов вы можете найти во вложении к статье.

На данном этапе мы построили алгоритмы отбора k наиболее релевантных энкодеров как на стороне основной программы, так и в OpenCL-контексте. И можем перейти к построению архитектуры Mixture of Experts, которую реализуем в рамках объекта CNeuronMoE. Структура нового объекта представлена ниже.

class CNeuronMoE  :  public CNeuronBaseOCL
  {
protected:
   CNeuronTopKGates     cGates;
   CLayer               cExperts;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMoE(void) {};
                    ~CNeuronMoE(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint experts, uint top_k,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMoE; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual void      TrainMode(bool flag)
     {  bTrain = flag;  cGates.TrainMode(bTrain); }
  };

В представленной структуре мы видим лишь 2 внутренних объекта. Один из них — выше созданный объект выбора k наиболее релевантных энкодеров. А второй — динамический массив для записи указателей на объекты наших энкодеров. Оба объекта объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Вся работа по инициализации указанных объектов организована в методе Init.

В параметрах метода инициализации передаются константы, дающие однозначное представление об архитектуре создаваемого объекта. При этом допускается возможность изменение размерности данных на выходе объекта.

bool CNeuronMoE::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                      uint window, uint window_out, uint units_count,
                      uint experts, uint top_k,
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_count, optimization_type, batch))
      return false;

Алгоритм начинается с вызова одноименного метода родительского класса, в котором уже организован процесс инициализации унаследованных объектов и точки контроля исходных данных.

Затем инициализируем объект выбора наиболее релевантных энкодеров.

   int index = 0;
   if(!cGates.Init(0, index, OpenCL, window, units_count, experts, top_k, optimization, iBatch))
      return false;

И переходим к непосредственной инициализации объектов энкодеров. Вначале мы подготовим динамический массив и локальные переменные для временного хранения указателей на объекты.

   cExperts.Clear();
   cExperts.SetOpenCL(OpenCL);
   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeRCDOCL *transp = NULL;

Первым создаем сверточный слой, который выполняет роль первого слоя энкодеров. На вход данного объекта мы планируем подавать тензор исходных данных, актуальный для всех энкодеров. Количество фильтров данного слоя равно произведению размера тензора результатов одного энкодера на их количество в моделе. Такой подход позволяет нам осуществить параллельное вычисление значений сразу для всех энкодеров.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window, window, window_out * experts, units_count, 1, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(SoftPlus);

С целью создания нелинейности между слоями энкодера, мы используем SoftPlus в качестве функции активации.

Далее нам необходимо добавить второй слой энкодеров. И, как вы понимаете, каждый энкодер должен получить свой набор параметров. Такая возможность у нас есть. Мы так же можем воспользоваться свертончым слоем. Достаточно лишь указать количество энкодеров в параметре числа независимых анализируемых последовательностей. Однако здесь следует обратить внимание, что на выходе первого слоя получаем трехмерный тензор размерностей { Units, Encoders, Dimension }. Это не соответствует алгоритму работы созданного нами ранее сверточного слоя.

Для организации корректного процесса нам необходимо поменять местами первых 2 измерения. Эту работу выполняет слой транспонирования данных.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_count, experts, window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

Теперь мы можем инициализировать сверточный слой, который будет выполнять роль второго слоя наших независимых энкодеров.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_out, window_out, window_out, units_count, experts, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

И добавим слой обратного транспонирования данных.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, experts, units_count, window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

На этом завершается алгоритм инициализации внутренних объектов. Возвращаем логический результат выполнения операций вызывающей программе и завершаем работу метода.

После завершения работы по инициализации объекта переходим к построению алгоритма прямого прохода в рамках метода CNeuronMoE::feedForward.

bool CNeuronMoE::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cGates.FeedForward(NeuronOCL))
      return false;

В параметрах метода получаем указатель на объект исходных данных, который сразу передаем в одноименный метод объекта отбора наиболее релевантных энкодеров.

Затем переходим к работе с энкодерами. Обратите внимание, что в качестве исходных данных они используют тот же объект, полученный нами в параметрах метода. Мы предварительно сохраним полученный указатель в локальной переменной.

   CNeuronBaseOCL *prev = NeuronOCL;
   int total = cExperts.Total();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *neuron = cExperts[i];
      if(!neuron ||
         !neuron.FeedForward(prev))
         return false;
      prev = neuron;
     }

И организуем цикл последовательного перебора слоев энкодеров с вызовом их методов прямого прохода.

После выполнения всех итераций цикла мы получаем полный комплект результатов работы всех энкодеров. Напомню, что ранее мы уже получили вероятностную маску наиболее релевантных энкодеров для каждого сегмента исходных данных. И теперь для получения взвешенной суммы по каждому сегменту анализируемых исходных данных нам достаточно умножить вектор-строку вероятностного распределения релевантности энкодеров для сегмента на матрицу результатов работы энкодеров с ним.

   if(!MatMul(cGates.getOutput(), prev.getOutput(), getOutput(),
              1, cGates.GetGates(), Neurons() / cGates.GetUnits(), cGates.GetUnits()))
      return false;
//---
   return true;
  }

Полученные значения сохраняем в буфере результатов нашего объекта. После чего завершаем работу метода, предварительно вернув логический результат выполнения операций вызывающей программе.

На этом мы завершаем рассмотрение алгоритмов, используемых при построении методов объекта набора энкодеров. Методы обратного прохода данного объекта я предлагаю оставить для самостоятельного изучения. Полный код данного объекта и всех его методов, как всегда, доступен во вложении к статье.

Сегодня мы славно потрудились и практически исчерпали объем статьи. Однако наша работа ещё не завершена. Сделаем небольшой перерыв и продолжим реализацию собственного видения подходов, предложенных авторами фреймворка DUET, в следующей статье.

Заключение

Сегодня мы познакомились с фреймворком DUET, который объединяет временную (TCM) и канальную (CCM) кластеризацию многомерных временных рядов для более точного их анализа и прогнозирования. TCM адаптирует модели к изменениям во времени, а CCM выделяет ключевые переменные, снижая уровень шума.

В практической части статьи представлена реализация модуля временной кластеризации (TCM). В следующей статье мы продолжим начатую реализацию. Представим собственное видение предложенных авторами фреймворка подходов и доведем работу до логического завершения, осуществив тестирование модели на реальных исторических данных.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (2538.92 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Алгоритм успешного ресторатора — Successful Restaurateur Algorithm (SRA)

Алгоритм успешного ресторатора (SRA) — инновационный метод оптимизации, вдохновленный принципами управления ресторанным бизнесом. В отличие от традиционных подходов, SRA не отбрасывает слабые решения, а улучшает их, комбинируя с элементами успешных. Алгоритм показывает конкурентоспособные результаты и предлагает свежий взгляд на балансирование между исследованием и эксплуатацией в задачах оптимизации.

Возможности Мастера MQL5, которые вам нужно знать (Часть 34): Эмбеддинг цены с нетрадиционной RBM

Ограниченные машины Больцмана (Restricted Boltzmann Machines, RBM) — форма нейронной сети, разработанная в середине 1980-х годов, когда вычислительные ресурсы были непомерно дорогими. Вначале она опиралась на выборку Гиббса (Gibbs Sampling) и контрастивную дивергенцию (Contrastive Divergence) с целью уменьшения размерности или выявления скрытых вероятностей/свойств во входных обучающих наборах данных. Мы рассмотрим, как обратное распространение ошибки (backpropagation) может работать аналогичным образом, когда RBM "встраивает" (embeds) цены в прогнозирующий многослойный перцептрон.

Удаленный профессиональный риск-менеджер Forex на Python

Делаем удаленный профессиональный риск-менеджер Для Forex на Python, разворачиваем его на сервере по шагам. В процессе статьи поймем, как программно управлять рисками на Форекс, и как больше не слить депозит на Форекс.

Автоматизация торговли с помощью трендовой стратегии Parabolic SAR на MQL5: Создаем эффективный советник

В этой статье мы автоматизируем торговлю с помощью стратегии Parabolic SAR на MQL5, создав эффективный советник. Советник будет совершать сделки по трендам, определяемым индикатором Parabolic SAR.