Распознавание паттернов с использованием динамической трансформации временной шкалы в MQL5

Введение

Распознавание паттернов всегда было ценным инструментом для трейдеров. Будь то определение уникальных комбинаций свечей или рисование воображаемых линий на графике, эти закономерности стали неотъемлемой частью технического анализа. Люди всегда преуспевали в поиске и распознавании закономерностей — настолько, что часто говорят, что иногда мы видим закономерности там, где их нет. Поэтому нам было бы полезно применять более объективные методы при выявлении потенциально прибыльных паттернов в финансовых временных рядах. В этой статье мы обсудим применениеДинамическую трансформацию временной шкалы (Dynamic Time Warping, DTW) как объективного метода поиска уникальных закономерностей в ценовых данных. Мы рассмотрим ее происхождение, принципы работы и применение в финансовом анализе временных рядов. Кроме того, мы представим реализацию алгоритма на чистом MQL5 и продемонстрируем его использование на практическом примере.

Динамическая трансформация временной шкалы

Динамическая трансформация временной шкалы — это сложный алгоритм, предназначенный для измерения сходства между двумя последовательностями данных, которые изменяются с течением времени, даже если их скорости или ритмы различаются. В отличие от традиционных методов, требующих строгого соответствия между точками данных, DTW предлагает более гибкий подход, позволяя деформировать или растягивать время для поиска оптимального соответствия между последовательностями. Представьте себе двух людей, идущих по лесу по разным тропам. Они оба отправляются из одной точки и встречаются в другой, но один из них может идти быстрее другого и делать произвольные остановки. DTW помогает найти наилучший способ сопоставить шаги обоих, даже если они пошли разными путями. DTW может эффективно учитывать различия в скорости ходьбы, ускорении или замедлении, предоставляя меру сходства. Такая универсальность позволяет применять его к широкому спектру типов данных, включая аудио, видео и графику. Любые данные, которые можно преобразовать в последовательный формат, являются потенциальным кандидатом для анализа DTW.

DTW изначально был разработан Винцюком для распознавания речи в 1968 году и позднее улучшен Сако и Чибой в 1978 году. Метод получил распространение в различных областях благодаря своей способности сравнивать последовательности разной длины, деформируя временное измерение для выравнивания схожих закономерностей. С тех пор DTW нашел применение в различных областях, таких как биоинформатика и анализ походки. Финансовые рынки характеризуются нелинейными и нестационарными временными рядами данных. Традиционные меры измерения расстояния, такие как евклидово расстояние, могут не отражать всю сложность и искажения таких данных. Однако DTW отлично подходит для выявления сходств между временными рядами с временными искажениями, что делает его подходящим инструментом для анализа финансовых рынков. Выравнивая последовательности на основе их формы, а не временного выравнивания, DTW может выявлять уникальные закономерности в финансовых данных.

Принцип работы

При применении алгоритма DTW цель состоит в том, чтобы определить, похожа ли потенциальная последовательность на предопределенную эталонную последовательность. Окончательная метрика, выдаваемая алгоритмом, указывает на сходство между кандидатом и эталонной последовательностью — чем ниже это значение, тем более похожи последовательности. Если последовательности одинаковы, это значение будет равно 0. Чтобы найти оптимальное выравнивание между потенциальной последовательностью и эталонным набором данных, алгоритм DTW придерживается определенных принципов. Каждая точка в потенциальной последовательности должна соответствовать по крайней мере одной точке данных в референтной последовательности, и наоборот. Начало одной последовательности должно совпадать с началом другой, а конец одной должен совпадать с концом другой. Кроме того, при прохождении последовательностей соответствующие точки должны продвигаться только вперед. Это гарантирует, что ни одна точка в одной последовательности не может совпасть с точкой, которая находится перед ней в другой последовательности, что исключает любую возможность выравнивания с предыдущими точками.

Процесс начинается с построения матрицы расстояний, которая фиксирует попарные расстояния между элементами двух последовательностей. Каждый элемент этой матрицы представляет собой расстояние между точкой в первой последовательности и соответствующей точкой во второй последовательности. На этом этапе можно использовать любые традиционные меры пространственного расстояния. Меры пространственного расстояния — это математические методы, используемые для количественной оценки расстояния или различия между точками данных в заданном пространстве. Выбор меры расстояния зависит от конкретных характеристик данных и поставленной задачи. В таблице ниже перечислены наиболее распространенные меры пространственного расстояния и краткие описания каждой из них.

Метрика расстояния	Описание
Евклидово расстояние	Евклидово расстояние — это расстояние по прямой между двумя точками в евклидовом пространстве. Это наиболее интуитивная и широко используемая мера расстояния.
Манхэттенское расстояние	Манхэттенское расстояние, также известное как метрика такси или расстояние городских кварталов, измеряет расстояние между двумя точками путем суммирования абсолютных разностей их координат.
Расстояние Минковского	Расстояние Минковского является обобщенной формой евклидова и манхэттенского расстояний. Он включает в себя параметр, который можно настраивать для переключения между различными измерениями расстояния.
Расстояние Чебышева	Расстояние Чебышева, также известное как метрика шахматной доски, измеряет наиболее существенную разницу между координатами пары точек.
Косинусный коэффициент	Косинусный коэффициент измеряет косинус угла между двумя ненулевыми векторами, представляя их направленное сходство, а не величину.

Выбор меры пространственного расстояния зависит от характера данных и конкретных требований задачи. Понимание различий и областей применения этих мер помогает выбрать наиболее подходящую для содержательного анализа.

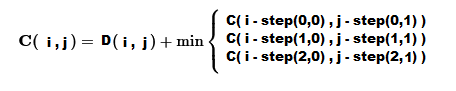
На следующем этапе матрица расстояний используется для расчета матрицы кумулятивных затрат, где каждый элемент представляет собой минимальную стоимость выравнивания последовательностей. Этот процесс выравнивания включает в себя преобразование потенциальной последовательности таким образом, чтобы она максимально напоминала референтную последовательность. Матрица кумулятивных затрат количественно определяет, насколько необходимо изменить отдельные точки в потенциальной последовательности, чтобы они наилучшим образом соответствовали эталонным значениям. Более высокая стоимость указывает на более значительную трансформацию, что означает большее различие между последовательностями. Эти кумулятивные значения матрицы затрат используются для определения оптимального пути трансформации (warping), которая представляет собой последовательность выравниваний, сопоставляющих один временной ряд с другим, минимизируя при этом расстояние между ними. По сути, путь трансформации иллюстрирует, как части последовательности растягиваются или сжимаются, чтобы максимально точно выровняться с другой последовательностью.

Чтобы найти путь трансформации, мы представляем последовательности, размещенные на сетке, при этом одна последовательность расположена вдоль оси x, а другая — вдоль оси y. Каждая точка на этой сетке представляет собой возможное соответствие между элементом из первой последовательности и элементом из второй последовательности. Путь трансформации — это маршрут через эту сетку, который обеспечивает наилучшее выравнивание между двумя последовательностями. Путь начинается в нижнем левом углу сетки, соответствуя первым элементам обеих последовательностей, и заканчивается в верхнем правом углу, соответствуя последним элементам обеих последовательностей. По мере продвижения по пути он может двигаться в трех направлениях: по диагонали, при этом сопоставляются элементы из обеих последовательностей; по горизонтали, при этом повторяется элемент из первой последовательности; или по вертикали, при этом повторяется элемент из второй последовательности. Это движение гарантирует, что процесс выравнивания всегда движется вперед во времени и не пропускает ни одного элемента в последовательностях.

Путь трансформации выбирается таким образом, чтобы минимизировать совокупное расстояние или стоимость между выровненными элементами двух последовательностей. Для этого значения матрицы расстояний накладываются на сетку, которая будет использоваться для выравнивания точек. Стоимость в каждой точке сетки рассчитывается путем добавления соответствующей метрики расстояния к минимальному значению смежных кумулятивных расстояний от предыдущих точек по трем возможным направлениям (диагонали, горизонтали или вертикали), которые можно выбрать при движении вперед во времени. Поскольку каждая точка сетки связана с метрикой расстояния соответствующих значений последовательности, минимальное значение представляет собой операцию, необходимую для преобразования потенциальной последовательности в соответствии с эталонной. Если минимальное кумулятивное расстояние лежит по диагонали к текущей точке, то это представляет собой операцию сопоставления. Если наименьшее совокупное расстояние от предыдущих точек горизонтально относительно текущей точки, это указывает на операцию вставки, при которой значение из эталонной последовательности фактически вставляется в потенциальную. И наоборот, если минимальное кумулятивное расстояние вертикально к текущей точке, это означает операцию удаления, при которой значение из последовательности кандидатов удаляется. Выбор предшествующих значений кумулятивного расстояния, учитываемых для нахождения минимума, регулируется определенным шаблоном шага.

Шаблоны шагов определяют допустимые перемещения или переходы между точками в последовательностях во время выравнивания. Они определяют количество точек в любом из допустимых направлений (диагонали, горизонтали, вертикали), учитываемых при расчете минимального совокупного расстояния. Выбор схемы шага существенно влияет на процесс выравнивания и общий расчет расстояния. Существуют различные схемы шагов, каждая из которых предназначена для определенных областей применения. Пользователи также могут создавать индивидуальные схемы шагов, при условии соблюдения принципов поступательного движения и непрерывности. В этой статье мы сосредоточимся на наиболее распространенных и универсальных схемах шагов, которые доказали свою эффективность в различных областях. Те, кто заинтересован в изучении других моделей шагов могут ознакомиться с работами Сако и Чибы, Рабинера и Джуанга а также Рабинера и Майерса.

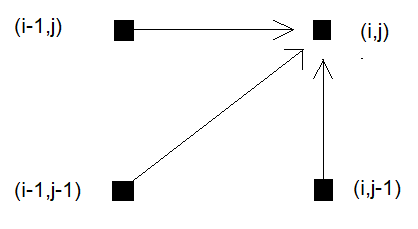
Наиболее часто применяется стандартный паттерн шага, также известный как симметричный или классический. Его главное преимущество заключается в том, что он обеспечивает полный охват обоих временных рядов. Он учитывает только непосредственные значения выше, справа и по диагонали к текущей точке, допуская диагональные, горизонтальные и вертикальные одношаговые перемещения по сетке.

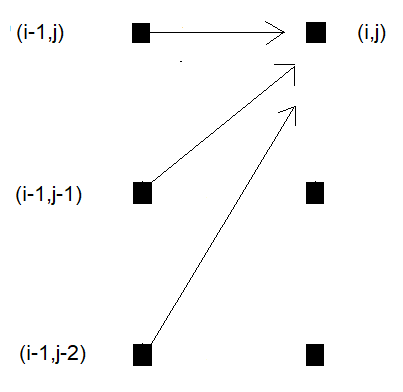
Еще один популярный паттерн. Подобно стандартному, он определяет переходы в трех направлениях, но вносит смещение в сторону одной последовательности. Этот паттерн позволяет алгоритму двигаться по диагонали, но если точка пропущена, он отдает предпочтение продвижению вперед в одной последовательности больше, чем в другой. Его часто используют вместе с дополнительными ограничениями, которые ограничивают перемещения алгоритма по сетке. В случае асимметричного паттерна шага применяется дополнительное ограничение по уклону, ограничивающее крутизну или плоскостность пути трансформации. Это ограничение полезно, когда ожидается, что последовательности будут схожими по длине и сдвигу, поскольку оно предотвращает чрезмерное растяжение или сжатие одной последовательности относительно другой.

Дополнительные ограничения могут быть применены для предотвращения технически идеальных, но бессмысленных выравниваний, которые могут привести к переобучению данных. Эти ограничения гарантируют, что выравнивание имеет логический смысл в контексте анализируемых данных, предотвращая чрезмерное растяжение или сжатие последовательностей. Такие ограничения известны как глобальные ограничения и повышают эффективность и интерпретируемость алгоритма DTW в практических приложениях. Двумя общими глобальными ограничениями являются полоса Сако-Чиба и параллелограмм Итакуры.

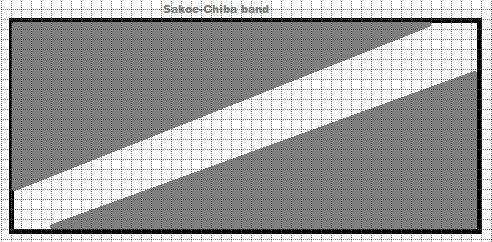
Полоса Сако-Чиба ограничивает путь трансформации, чтобы он оставался в пределах фиксированной полосы вокруг диагонали матрицы выравнивания. Это предотвращает слишком большое отклонение выравнивания от исходного времени или сдвига, что полезно в задачах, где ожидаются небольшие различия во времени, но не ожидаются большие отклонения.

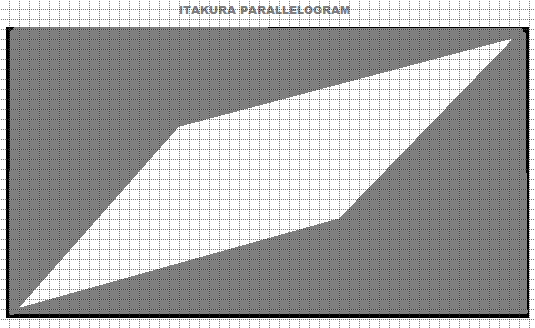
Ограничение параллелограмма Итакуры определяет область в форме параллелограмма, внутри которой должен оставаться путь трансформации. Он уже на концах и шире в середине, что особенно полезно, когда ожидается, что последовательности будут более тесно выровнены в начале и конце, но при этом будет обеспечена некоторая гибкость в середине. Глобальные ограничения необходимы DTW для управления процессом трансформации и обеспечения соответствия полученного выравнивания конкретной задаче. Важно выбрать наиболее подходящие ограничения, исходя из характеристик наборов данных и целей анализа.

После того, как матрица кумулятивных затрат заполнена, она используется для определения оптимального пути трансформации. Алгоритм отслеживает расстояние от последнего элемента матрицы кумулятивных затрат до первого, определяя путь, который минимизирует общую стоимость выравнивания. Этот путь представляет собой наилучшее выравнивание между последовательностями. Окончательное значение в матрице кумулятивных затрат дает общую оценку расстояния, которая также используется для расчета нормализованной оценки расстояния. Путь трансформации будет содержать список парных индексов, представляющих выровненные точки в обеих последовательностях. Для оценки процедуры выравнивания обычно строят оптимальный путь трансформации. Удовлетворительный результат должен дать приблизительно диагональный график. Этот диагональный график показывает, что последовательности хорошо выровнены, при этом идеально прямая диагональная линия соответствует двум идентичным последовательностям. Теперь рассмотрим нативную реализацию динамической трансформации временной шкалы в MQL5.

Реализация в MQL5

Реализация DTW в MQL5 представлена во включаемом файле dtw.mqh. Он не предлагает полного или всестороннего охвата всех аспектов динамической трансформации временной шкалы. Позже мы рассмотрим реализацию DTW на Python, которая предлагает гораздо больше возможностей. Целью создания этой библиотеки было предоставление базового функционала для расчета оценки расстояния. Библиотека представляет собой частичное ответвление модуля dtw-python.

Код начинается с определения перечислений для паттернов шага, различных мер расстояния и глобальных ограничений.

//+------------------------------------------------------------------+
//|  step patterns                                                   |
//+------------------------------------------------------------------+
enum ENUM_STEP_PATTERN
  {
   STEP_SYMM1=0,//symmetric1
   STEP_SYMM2,//symmetric2
   STEP_ASYMM//asymmetric
  };

ENUM_STEP_PATTERN - определяет набор перечислений, которые ограничивают допустимые шаблоны перехода на этапе поиска пути алгоритма DTW. Эти закономерности направляют процесс трансформации и влияют на допустимые выравнивания между временными рядами.

//+------------------------------------------------------------------+
//|  distance metric                                                 |
//+------------------------------------------------------------------+
enum ENUM_DIST_METRIC
  {
   DIST_EUCLIDEAN=0,//euclidean
   DIST_CITYBLOCK,//city block
   DIST_COSINE,//cosine
   DIST_CORRELATION,//correlation
   DIST_CHEBYSHEV,//chebyshev
   DIST_SQEUCLIDEAN//squared euclidean
  };

ENUM_DIST_METRIC - коллекция перечислений, соответствующих поддерживаемым метрикам расстояния. Эти метрики количественно определяют различия между точками данных во временном ряду, используя такие параметры, как евклидово расстояние, манхэттенское расстояние и другие.

//+------------------------------------------------------------------+
//|   window function                                                |
//+------------------------------------------------------------------+
enum ENUM_GLOBAL_CONSTRAINT
  {
   CONSTRAINT_NONE=0,// no constrains applied
   CONSTRAINT_SAKOECHIBA,// sakoe chiba
   CONSTRAINT_SLATEDBAND,// slated band
   CONSTRAINT_ITAKURA// itakura
  };

ENUM_GLOBAL_CONSTRAINT охватывает различные глобальные ограничения во время поиска пути. Они могут влиять на гибкость трансформации и потенциально повышать точность выравнивания.

//+------------------------------------------------------------------+
//| lists the transitions allowed while searching                    |
//|for the minimum-distance path                                     |
//+------------------------------------------------------------------+
class CStepPattern
  {
private:
   matrix            m_mx,m_stepsMatrix;
   ENUM_HINT         m_stephint;
public:
                     CStepPattern(matrix &mx, matrix &stepmatrix, ENUM_HINT hint=HINT_NA)
     {
      m_mx = mx;
      m_stepsMatrix = stepmatrix;
      m_stephint = hint;
     }
                    ~CStepPattern(void)
     {

     }
   matrix            getStepMatrix(void)
     {
      return m_stepsMatrix;
     }
   ulong             getNRows(void)
     {
      return m_mx.Rows();
     }
   int               getNPatterns(void)
     {
      vector vec = m_mx.Col(0);
      return (int(vec.Max()));
     }

   CStepPattern*     T(void)
     {
      ulong cols[] = {0, 2, 1, 3};

      matrix cpy = np::selectMatrixCols(m_mx,cols);
      ENUM_HINT hint = m_stephint;

      if(m_stephint == HINT_N)
         hint = HINT_M;
      else
         if(m_stephint == HINT_M)
            hint = HINT_N;

      CStepPattern* out = new CStepPattern(cpy,m_stepsMatrix,hint);

      return out;
     }

   matrix            extractPattern(vector &sn)
     {
      vector col  =  m_mx.Col(0);
      matrix out = matrix::Ones(1,1);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == sn[j])
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols()-1,100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               vector vv = np::sliceVector(v,1);
               if(!out.Row(vv,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      if(!np::reverseMatrixRows(out))
        {
         Print(__FUNCTION__, " Reverse Matrix failure ");
         return matrix::Zeros(1,1);
        }
      return out;
     }

   matrix            mkDIrDeltas(void)
     {
      matrix out = matrix::Zeros(1,1);
      vector col = m_mx.Col(3);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == -1.0)
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols(),100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               if(!out.Row(v,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      return np::sliceMatrixCols(out,1,3);
     }

   matrix             getP(void)
     {
      ulong sel[] = {0, 2, 1, 3};
      matrix s = np::selectMatrixCols(m_mx,sel);
      return s;
     }

   matrix            getMx(void)
     {
      return m_mx;
     }
  };

CStepPattern — это класс, предназначенный для обработки различных паттернов шага путем управления матрицами, определяющими разрешенные переходы и операции. Он предоставляет методы для извлечения шаблонов на основе определенных последовательностей и для манипулирования матрицами для направленных дельт, необходимых для вычислений DTW.

//+------------------------------------------------------------------+
//| Global constraints                                               |
//+------------------------------------------------------------------+
class CConstraint
  {
public:
                     CConstraint(void)
     {

     }
                    ~CConstraint(void)
     {

     }

   static matrix       noConstraint(ulong iw,ulong jw)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      for(ulong i = 0; i<mats[0].Rows(); i++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            long value = long(mats[0][i][j]);
            mats[0][i][j] = (double)(value|1);
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       sakoeChibaConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize, ulong winsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      matrix abs = MathAbs(mats[1]-mats[0]);

      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;
     }

   static matrix       itakuraConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      long a,b,c,d;

      for(ulong i = 0, k = 0; i<mats[0].Rows() && k<mats[1].Rows(); i++,k++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            a = long(mats[1][k][j]) < (2*long(mats[0][i][j]))?1:0;
            b = long(mats[0][i][j]) <=(2*long(mats[1][k][j]))?1:0;
            c = long(mats[0][i][j]) >=(long(qsize)-1-2*(long(refsize)-long(mats[1][k][j])))?1:0;
            d = long(mats[1][k][j]) > (long(refsize)-1-2*(long(qsize)-long(mats[0][i][j])))?1:0;
            mats[0][i][j] = double(ulong(a&b&c&d));
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       slantedBandConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize,ulong winsize)
     {

      matrix mats[];

      np::indices(iw,jw,mats);

      matrix  diagj = (mats[0]*refsize/qsize);

      matrix abs = MathAbs(mats[1]-diagj);


      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;

     }

  };

Класс CConstraint включает статические методы для реализации различных типов ограничений, таких как Сако-Чиба, Итакура и наклонная полоса (Slanted Band). Это позволяет ограничить выравнивание DTW для повышения вычислительной эффективности и релевантности за счет ограничения пространства поиска на основе предопределенных критериев.

• Метод noConstraint() создает матрицу, заполненную единицами, что означает отсутствие каких-либо ограничений.

• Метод sakoeChibaConstraint() накладывает ограничение Сако-Чиба на основе указанного размера окна и длины временного ряда.

• Метод itakuraWindow() обеспечивает ограничение Итакуры, используя длину временного ряда.

• Метод slantedBandConstraint() реализует ограничение наклонной полосы на основе размера окна и длины временного ряда.
  

Класс Cdtw является основным классом, отвечающим за расчеты DTW.

   //+------------------------------------------------------------------+
   //|     main interface method for dtw                                |
   //+------------------------------------------------------------------+

   bool              dtw(matrix&x, matrix&y, ENUM_DIST_METRIC dist_method,ENUM_STEP_PATTERN step_pattern=STEP_SYMM2, ENUM_GLOBAL_CONSTRAINT win_type=CONSTRAINT_NONE,ulong winsize=0)
     {
      if(y.Cols()!=x.Cols())
        {
         Print(__FUNCTION__, " invalid input parameters, size containers donot match. ");
         return false;
        }

      if(CheckPointer(m_stepPattern)==POINTER_DYNAMIC)
         delete m_stepPattern;

      switch(step_pattern)
        {
         case STEP_SYMM1:
            m_stepPattern = new CStepPattern(_symmetric1,Symmetric);
            m_stephint = HINT_NA;
            break;

         case STEP_SYMM2:
            m_stepPattern = new CStepPattern(_symmetric2,Symmetric,HINT_NM);
            m_stephint = HINT_NM;
            break;

         case STEP_ASYMM:
            m_stepPattern = new CStepPattern(_asymmetric,Asymmetric,HINT_N);
            m_stephint = HINT_N;
            break;
        }

      if(CheckPointer(m_stepPattern)==POINTER_INVALID)
        {
         Print(__FUNCTION__," failed step pointer initialization ", GetLastError());
         return false;
        }

      matrix stepsMatrix = m_stepPattern.getStepMatrix();
      m_query = x;
      m_qlen = x.Rows();
      m_ref = y;
      m_reflen = y.Rows();
      m_distMetric = dist_method;
      m_winMethod = win_type;
      m_winsize = winsize;

      if(y.Rows())
        {
         if(!m_distance.Resize(m_qlen,m_reflen))
           {
            Print(__FUNCTION__," resize error ", GetLastError());
            return false;
           }
         for(ulong i = 0; i<m_qlen; i++)
            for(ulong j =0; j<m_reflen; j++)
               m_distance[i][j]=dist(m_query.Row(i),m_ref.Row(j));
        }
      else
         m_distance = m_query;

      ulong n,m;
      n=m_distance.Rows();
      m=m_distance.Cols();
      matrix wm;
      if(m_winMethod == CONSTRAINT_NONE)
         wm = matrix::Ones(m_distance.Rows(), m_distance.Cols());
      else
        {
         switch(m_winMethod)
           {
            case CONSTRAINT_ITAKURA:
               wm = CConstraint::itakuraConstraint(n,m,m_qlen,m_reflen);
               break;
            case CONSTRAINT_SAKOECHIBA:
               wm = CConstraint::sakoeChibaConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            case CONSTRAINT_SLATEDBAND:
               wm = CConstraint::slantedBandConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            default:
               wm = CConstraint::noConstraint(n,m);
               break;
           }
        }

      if(m_winMethod!=CONSTRAINT_NONE)
        {
         for(ulong i = 0; i<wm.Rows(); i++)
            for(ulong j = 0; j<wm.Cols(); j++)
               if((i+j)>0 && wm[i][j] != 1.0)
                  m_distance[i][j] = wm[i][j];
        }


      m_costMatrix = matrix::Zeros(m_distance.Rows()+ulong(stepsMatrix.Col(0).Max()),m_distance.Cols()+ulong(stepsMatrix.Col(1).Max()));
      m_costMatrix.Fill(double("inf"));
      m_costMatrix[ulong(stepsMatrix.Col(0).Max())][ulong(stepsMatrix.Col(1).Max())] = m_distance[0][0];

      m_dirMatrix = matrix::Zeros(m_costMatrix.Rows(),m_costMatrix.Cols());
      m_dirMatrix.Fill(double(INT_MIN));
      for(ulong i = 0; i<m_dirMatrix.Cols(); i++)
         m_dirMatrix[0][i] = double(1);
      for(ulong i = 0; i<m_dirMatrix.Rows(); i++)
         m_dirMatrix[i][0] = double(2);

      if(!calCM(m_distance,stepsMatrix,m_costMatrix,m_dirMatrix))
        {
         Print(__FUNCTION__, " computeCM() failed ");
         return false;
        }

      m_jmin = m_costMatrix.Cols() - 1;

      return true;
     }

Он предоставляет метод dtw() в качестве основной функции для выполнения DTW. Обратите внимание, что метод перегружен для обработки одномерных (векторов) и многомерных (матриц) временных рядов. В качестве входных аргументов он принимает два временных ряда (представленных в виде матриц или векторов), метрику расстояния, шаблон шага, глобальное ограничение и размер окна. При вызове метод начинает с выполнения различных проверок правильности входных данных и выбранного шаблона шага. Затем следует расчет матрицы расстояний на основе выбранной метрики расстояния. Если указано глобальное ограничение, то матрицы стоимости и направления, используемые в алгоритме DTW, подготавливаются соответствующим образом. Затем вызывается функция calCM() для вычисления матрицы накопленных затрат. Наконец, функция dtw() возвращает логическое значение, указывающее на успех или неудачу. 

   //+------------------------------------------------------------------+
   //|    Get the optimal path: corresponding points from both series   |
   //+------------------------------------------------------------------+

   matrix            warpPath(bool openEnd=false)
     {
      matrix stmatrix = m_stepPattern.getStepMatrix();
      return backtrack(m_dirMatrix,stmatrix,openEnd,openEnd?long(m_costMatrix.Row(m_costMatrix.Rows()-1).ArgMin()):-1);
     }

Метод warpPath() извлекает оптимальный путь (соответствующие точки), определенный из обоих временных рядов, на основе необязательного аргумента openEnd, который управляет окончанием пути (открыт или закрыт).

   //+------------------------------------------------------------------+
   //|     Get the accumulated cost matrix                              |
   //+------------------------------------------------------------------+

   matrix            costMatrix(void)
     {
      return m_costMatrix;
     }

Метод costMatrix() обеспечивает доступ к накопленной матрице затрат, ключевому результату алгоритма DTW.

   //+------------------------------------------------------------------+
   //|       Get the cost matrix                                        |
   //+------------------------------------------------------------------+

   matrix            localCostMatrix(void)
     {
      return m_distance;
     }

Метод localCostMatrix() возвращает матрицу локальных расстояний, представляющую попарные расстояния между точками данных во временном ряду.

   //+------------------------------------------------------------------+
   //|        Get the direction matrix                                  |
   //+------------------------------------------------------------------+

   matrix            directionMatrix(void)
     {
      return m_dirMatrix;
     }

Метод directionMatrix() предоставляет доступ к матрице направления, которая играет роль в управлении процессом поиска пути во время DTW.

   //+------------------------------------------------------------------+
   //|  private method implementing accumulated cost calculation        |
   //+------------------------------------------------------------------+

   bool              calCM(matrix &distMatrix,matrix &stepMatrix,matrix &costMatrix,matrix &dirMatrix)
     {
      ulong max0,max1;
      max0 = ulong(stepMatrix.Col(0).Max());
      max1 = ulong(stepMatrix.Col(1).Max());
      double curCost,curd;

      for(ulong i = max0; i<costMatrix.Rows(); i++)
        {
         for(ulong j = max1; j<costMatrix.Cols(); j++)
           {
            for(ulong k = 0; k<stepMatrix.Rows(); k++)
              {
               curd = costMatrix[i-ulong(stepMatrix[k][0])][j-ulong(stepMatrix[k][1])];
               curCost = curd + distMatrix[i-max0][j-max1];
               if(curCost<costMatrix[i][j])
                 {
                  costMatrix[i][j] = curCost;
                  dirMatrix[i][j] = double(k);
                 }
              }
           }
        }
      costMatrix = np::sliceMatrix(costMatrix,max0,END,1,max1);
      dirMatrix  = np::sliceMatrix(dirMatrix,max0,END,1,max1);
      return true;

     }

Закрытый метод calCM() вычисляет накопленную матрицу затрат, основной компонент алгоритма DTW. В качестве входных данных он использует матрицу расстояний, паттерн шага, матрицу затрат и матрицу направлений.

   //+------------------------------------------------------------------+
   //|  distance metric calculation                                     |
   //+------------------------------------------------------------------+


   double            dist(vector &u,vector &v)
     {
      switch(m_distMetric)
        {
         case DIST_EUCLIDEAN:
            return euclidean(u,v);
         case DIST_CITYBLOCK:
            return cityblock(u,v);
         case DIST_CHEBYSHEV:
            return chebyshev(u,v);
         case DIST_CORRELATION:
            return correlation(u,v);
         case DIST_COSINE:
            return cosine(u,v);
         case DIST_SQEUCLIDEAN:
            return sqeuclidean(u,v);
         default:
            Print(__FUNCTION__, " invalid parameter ");
            return EMPTY_VALUE;
        }
     }

Частная функция dist() вычисляет расстояние между двумя точками данных на основе выбранной метрики расстояния.

Тестирование класса Cdtw

В этом разделе мы продемонстрируем возможности класса Cdtw, сравнив его выходные данные с данными, полученными с помощью реализации DTW на основе Python. Модуль dtw-python является одной из многих реализаций DTW на Python. Мы запустим простой скрипт на Python и посмотрим, можно ли воспроизвести результаты с помощью нашей реализации на MQL5. Начнем с листинга скрипта Python.

import numpy as np
import matplotlib.pyplot as plt
import dtw

len = 10
add_noise = True
noise = np.random.uniform(size=len)if add_noise else np.zeros((len,))
arx = np.linspace(start = 1, stop = 6.28,num = len)
query = np.sin(arx) + noise
ref = np.cos(arx)

alignment =  dtw.dtw(query,ref,dist_method='cosine',step_pattern='symmetric2', window_type=None,keep_internals=True)
print( f'Accumulated Cost Matrix is {alignment.costMatrix}')
print(f'Distance is {alignment.distance}, \n normalize distance is {alignment.normalizedDistance}')
print(f'Warp Path is {alignment.index1[:]}:{alignment.index2[:]}')
plt.plot(alignment.index1,alignment.index2)
plt.show()

Скрипт демонстрирует, как выровнять два временных ряда с помощью алгоритма DTW и визуализировать выравнивание. Код начинается с импорта необходимых библиотек: numpy - для числовых операций, matplotlib.pyplot - для построения графиков и dtw - для реализации алгоритма DTW. Длина временного ряда установлена равной 10, также создается массив arx из 10 равномерно распределенных значений от 1 до 6,28. Временной ряд query генерируется путем взятия синуса arx и добавления некоторого случайного шума, в то время как опорный временной ряд ref генерируется путем взятия косинуса arx. Затем выполняется выравнивание DTW между сериями query и ref. Расстояние между временными рядами измеряется с помощью метода косинусного расстояния, а к траектории трансформации применяется симметричный паттерн шага. Ограничения на оконную обработку не используются, а внутренние данные, такие как матрица затрат и путь трансформации, сохраняются.

Затем код выводит накопленную матрицу стоимости, общее расстояние выравнивания, нормализованное расстояние и индексы пути трансформации между двумя сериями. Наконец, путь деформации визуализируется путем построения графика индексов выравнивания, показывающего, как выравниваются индексы двух временных рядов, и выводится график. Такой подход позволяет проводить детальное сравнение двух временных рядов, которые могут не совпадать по фазе или иметь разную длину, что позволяет наблюдать, как один ряд трансформируется, чтобы согласоваться с другим.

Ниже приведен эквивалент только что описанного кода Python на языке MQL5.

//+------------------------------------------------------------------+
//|                                                      dtwTest.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Uniform.mqh>
#include<dtw.mqh>
//---
input ulong series_len = 10;
input bool  AddRandomNoise = false;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input bool WarpPathConstraint = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(series_len<10)
     {
      Alert(" Invalid input for series_len parameter. Should be >=10 ");
      return;
     }
//---
   vector arg = np::linspace(1.0,6.28,series_len);
   vector noise = vector::Zeros(series_len);

   if(AddRandomNoise)
     {
      double array[];
      if(!MathRandomUniform(0.0,1.0,int(series_len),array))
        {
         Print(__LINE__, " MathRandomUniform() failed ", GetLastError());
         return;
        }

      if(!noise.Assign(array))
        {
         Print(__LINE__, " vector assignment failure ", GetLastError());
         return;
        }
     }

   vector q = sin(arg) + noise; // candidate sequence
   vector rf =  cos(arg);       // reference sequence

   Cdtw cdtw;

   cdtw.dtw(q,rf,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize);

   Print(" local cm ", cdtw.localCostMatrix());
   Print(" final cm ", cdtw.costMatrix());
   Print(" direction matrix \n", cdtw.directionMatrix());
   matrix path = cdtw.warpPath();
   Print(" Warp path \n", cdtw.warpPath());
   Print(" Distance metric ", cdtw.distance());
   Print(" Normalized Distance metric ", cdtw.normalizedDistance());

   vector xx = path.Col(0);
   vector yy = path.Col(1);

   CGraphic *g = np::plotXY(xx,yy,"Warp Plot", " Query ", " Reference ");

   Sleep(20000);
   g.Destroy();
   ChartRedraw();
   delete g;
  }
//+------------------------------------------------------------------+

Вывод скрипта Python:

KQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Accumulated Cost Matrix is [[ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
RD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
FH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
JL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
NQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
GD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 2.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
QH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 4.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
KL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
GS      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  2.  2.  2.  2.  2.  2.  0.  0.  0.]
PJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  4.  4.  4.  4.  4.  4.  0.  0.  0.]]
LJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Distance is 0.0, 
MM      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  normalize distance is 0.0
CH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Warp Path is [0 1 2 3 4 5 5 5 5 6 7 8 8 9]:[0 0 0 0 0 1 2 3 4 5 6 7 8 9]

Вывод скрипта MQL5:

NE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         local cm [[0,2,2,2,2,2,2,0,0,0]
LH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
HE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
RL      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
DF      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,0,0,2.220446049250313e-16,0,0,2,2,2]
ND      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,2,2,2]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,2.220446049250313e-16,2,2,2]
RS      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
OH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]]
ML      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         final cm [[0,2,4,6,8,10,12,12,12,12]
JR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
EI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16,2,4,6]
CP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2,4,6]
EH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,2,4,6]
IN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2,2,2,2,2,2,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4,4,4,4,4,4,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]]
MO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         direction matrix 
QK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[-2147483648,1,1,1,1,1,1,1,1,1]
GN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
QQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
CK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
MR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
OE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,1,1,1,1,1,1,1,1]
HO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,1,1,1,0,0]
MF      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,0,0]
CH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,1,1]
LN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,2,0,0]]
PK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Warp path 
HM      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[9,9]
GJ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,8]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,7]
DK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [7,6]
HP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,5]
QI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4]
GQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,3]
RN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,2]
MG      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,1]
CO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,0]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [3,0]
EL      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0]
JE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [1,0]
DO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,0]]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Distance metric 4.440892098500626e-16
NR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Normalized Distance metric 2.2204460492503132e-17

Сравнение результатов обоих скриптов подтверждает, что код работает достаточно хорошо. Поэтому мы можем использовать его для чего-то более практического. Посмотрим, как DTW можно использовать при разработке стратегии.

Применение динамической трансформации временной шкалы

DTW можно использовать для автоматизированной разработки стратегии, обеспечивая гибкие методы распознавания образов и сравнения финансовых временных рядов. Например, DTW позволяет выявлять повторяющиеся ценовые закономерности, даже если они происходят в разных масштабах или с различной временной динамикой. Сопоставляя эти закономерности с историческими данными, становится возможным обнаружить едва заметные сдвиги и аномалии, которые могут предшествовать значительным движениям рынка.

При тестировании на истории DTW можно применять для сравнения эффективности различных стратегий в различных рыночных условиях путем сопоставления их соответствующих результатов временных рядов. Такой подход помогает оценить, насколько хорошо стратегия адаптируется к изменениям поведения рынка, обеспечивая более глубокое понимание ее надежности. Кроме того, DTW можно использовать для кластеризации схожих торговых сигналов или состояний рынка, которые затем можно анализировать для выявления высоковероятностных торговых возможностей. Распознавая эти кластеры, можно скорректировать стратегию для более эффективного использования повторяющегося поведения рынка.

Кроме того, при оптимизации алгоритмических стратегий DTW может помочь в сопоставлении наиболее перспективных наборов параметров с историческими рыночными условиями, которые максимально соответствуют текущей динамике рынка. Это позволяет стратегии более динамично адаптироваться к меняющимся рыночным условиям. При использовании DTW автоматизированные стратегии могут стать более адаптивными, контекстно-зависимыми и способными распознавать сложные временные взаимосвязи в финансовых данных. Хотя DTW может быть полезным инструментом, это не волшебная палочка. С ним может быть сложно работать, особенно неопытным пользователям.

Одна из самых больших проблем с DTW связана с настройкой его рабочих параметров. Правильное сочетание глобальных и локальных ограничений имеет решающее значение для получения максимальной отдачи от метода. DTW склонен выдавать ложные совпадения, а достижение наилучших результатов часто требует множества проб и ошибок. Это продемонстрировано в скрипте MQL5 ниже.

//+------------------------------------------------------------------+
//|                                             dtwPatternSearch.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\LogReturns.ex5"
#property script_show_inputs
#include<dtw.mqh>
#include<ErrorDescription.mqh>
enum ENUM_PRICE
  {
   CLOSE=0,//close price
   MEDIAN,//median price
   TYPICAL//typical price
  };

enum ENUM_TRANSFORM_TYPE
  {
   PERCENT_DIFF=0,//percent difference
   LOG_DIFF//log difference
  };
//--- input parameters
input string   Pattern = "0.0469,0.0093,0.0697,-0.0699";
input string   SymbolName="BTCUSD";
input datetime SearchStartDate=D'2024.06.01';
input datetime SearchStopDate=D'2018.04.22';
input double   NormalizedDistanceThreshold=0.01;
input ENUM_TIMEFRAMES      TimeFrame=PERIOD_D1;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input ENUM_PRICE AppliedPrice=CLOSE;
input ENUM_TRANSFORM_TYPE AppliedTransform=LOG_DIFF;
input int Lag = 1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   string pattern_values[];
//---
   int len = StringSplit(Pattern,StringGetCharacter(",",0),pattern_values);
   if(pattern_values[len-1]=="")
      len--;
//---
   if(len<3)
     {
      Alert("Pattern sequence is inadequately defined");
      return;
     }
//---
   vector pattern(len);
   for(ulong i = 0; i<pattern.Size(); i++)
      pattern[i]=StringToDouble(pattern_values[i]);
//---set prices handle
   int handle = INVALID_HANDLE;
   handle=iCustom(SymbolName!=""?SymbolName:NULL,TimeFrame,"::Indicators\\LogReturns.ex5",AppliedPrice,AppliedTransform,1);
   if(handle==INVALID_HANDLE)
     {
      Print("invalid handle ",ErrorDescription(GetLastError()));
      return;
     }
//---
   vector searchBuffer;
   if(!searchBuffer.CopyIndicatorBuffer(handle,0,SearchStartDate,SearchStopDate))
     {
      Print("History loading error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   ulong stop = searchBuffer.Size()-pattern.Size();
   vector subv;
   Cdtw cdtw;
   ulong counter=0;
   for(ulong i = 0; i<stop; i++)
     {
      subv = np::sliceVector(searchBuffer,i,i+pattern.Size());

      if(!cdtw.dtw(subv,pattern,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize))
        {
         Print(" dtw failed ");
         return;
        }

      if(cdtw.normalizedDistance()<NormalizedDistanceThreshold)
        {
         counter++;
         Print(" pattern found  ", datetime(SearchStopDate+(PeriodSeconds(TimeFrame)*(i+pattern.Size()-1))));
        }
     }
//---
   Print(" SearchBuffer size ", searchBuffer.Size());
   Print(" Reference pattern found ", counter, " times.");
  }
//+------------------------------------------------------------------+

Скрипт позволяет пользователю определить произвольный паттерн, составленный из последовательности логарифмических возвратов, рассчитанных индикатором LogReturns.ex5. Скрипт предназначен для поиска определенной закономерности в данных о ценах финансового инструмента, используя для сравнения динамическую трансформацию временной шкалы (DTW). Он включает в себя необходимые библиотеки, такие как dtw.mqh для алгоритма DTW и ErrorDescription.mqh для обработки описаний ошибок. Скрипт определяет два перечисления: ENUM_PRICE, которое указывает тип используемой цены (близкая, медианная или типичная), и ENUM_TRANSFORM_TYPE, которое определяет, как будут преобразованы ценовые данные (процентная или логарифмическая разница).

Входные параметры позволяют пользователю указать детали поиска, включая шаблон для сопоставления, имя символа (например, "BTCUSD"), диапазон дат для поиска, пороговое значение для нормализованного расстояния, временные рамки данных, метрику расстояния, паттерн шага, глобальное ограничение, размер окна для ограничения, тип используемой цены, тип применяемого преобразования и значение задержки. При запуске скрипта он сначала разбивает входную строку паттерна на массив значений, гарантируя, что паттерн адекватно определен как минимум тремя значениями. Если паттерн действителен, он преобразуется в векторный формат для дальнейшей обработки. Затем скрипт пытается загрузить данные о ценах, используя функцию iCustom для вызова пользовательского индикатора (LogReturns.ex5), который применяет выбранный тип цены и преобразование к данным. Если хэндл, возвращаемый iCustom, недействителен, выводится сообщение об ошибке и скрипт завершает работу.

Если данные о ценах загружены успешно, они сохраняются в векторе searchBuffer. Затем скрипт проходит по searchBuffer, разбивая его на более мелкие подвекторы того же размера, что и паттерн, и сравнивая каждый подвектор с паттерном с помощью алгоритма DTW. Сравнение DTW использует указанную метрику расстояния, паттерн шага и глобальное ограничение. Для каждого сравнения, если нормализованное расстояние между подвектором и паттерном меньше указанного порогового значения, скрипт считает, что паттерн найден в этой точке ценовых данных. Он выводит сообщение с указанием временной метки, где был обнаружен паттерн, и увеличивает счетчик. Наконец, скрипт выводит размер searchBuffer и общее количество раз, когда паттерн был найден в указанном диапазоне дат. Скрипт позволяет автоматически обнаруживать определенные закономерности в исторических ценовых данных, что может быть полезно при разработке торговых стратегий, основанных на распознавании паттернов.

Последовательность по умолчанию описывает шаблон, показанный ниже.

Запуск скрипта с различными ограничениями приводит к разному количеству совпадений. Ниже представлен вывод с использованием настроек по умолчанию.

RN      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Chosen Parameters
IJ      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Distance Threshold 0.01
CS      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    DIST_EUCLIDEAN
ND      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    STEP_SYMM2
CN      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    CONSTRAINT_NONE
HG      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     WinSize 0
OO      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     pattern found  2018.04.25 00:00:00
NJ      0       22:00:09.221    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.04.28 00:00:00
KD      0       22:00:09.222    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.07.01 00:00:00
QO      0       22:00:09.230    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.04.27 00:00:00
II      0       22:00:09.234    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.10.26 00:00:00
PD      0       22:00:09.237    dtwPatternSearch (BTCUSD,D1)     pattern found  2021.02.06 00:00:00
RN      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     pattern found  2024.01.29 00:00:00
DH      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     SearchBuffer size 2197
PQ      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     Reference pattern found 7 times.

Параметр NormalizedDistanceThreshold, очевидно, играет важную роль в определении наличия соответствия. Тем не менее, различные ограничения могут привести к совершенно разным результатам. Дело не только в ограничениях. Пользователям также приходится выбирать подходящую метрику расстояния. Очевидно, что при использовании алгоритма DTW необходимы глубокие знания предметной области.

Заключение

Динамическая трансформация временной шкалы предлагает сложный подход к распознаванию закономерностей в финансовом анализе временных рядов, но при этом имеет ряд недостатков, которые следует учитывать. Во-первых, DTW требует больших вычислительных ресурсов, особенно при работе с длинными временными рядами или большими наборами данных. Алгоритм заключается в сравнении каждой точки одного временного ряда с каждой точкой другого, что может привести к значительному времени обработки и использованию памяти. Это становится особенно проблематичным при попытке анализа высокочастотных финансовых данных или проведении анализа в реальном времени. Во-вторых, DTW чувствителен к шуму и выбросам в финансовых данных.

Финансовые временные ряды часто бывают зашумленными из-за волатильности рынка, а небольшие колебания или аномалии могут привести к тому, что алгоритм DTW будет выдавать вводящие в заблуждение выравнивания. Такая чувствительность может приводить к ложным срабатываниям при распознавании образов, когда выявляются образы, не обладающие значительной предсказательной силой. Наконец, DTW может испытывать трудности с интерпретируемостью. Путь трансформации и полученную метрику расстояния может быть сложно интерпретировать осмысленно, особенно в контексте финансового анализа, где четкие и применимые на практике идеи имеют решающее значение. Эти проблемы свидетельствуют о том, что, хотя DTW может быть полезным инструментом для распознавания закономерностей в финансовых временных рядах, его следует применять осторожно и в сочетании с другими аналитическими методами, которые могут устранить его ограничения.

Файл	Описание
Mql5\include\np.mqh	Заголовочный файл различных векторных и матричных служебных функций
Mql5\include\dtw.mqh	Включаемый файл, содержащий реализацию алгоритма динамической трансформации временной шкалы на MQL5
Mql5\indicators\LogReturns.mq5	Индикатор логарифмической доходности ценового ряда
Mql5\scripts\dwTest.mq5	Скрипт для тестирования и демонстрации использования реализации DTW на MQL5
Mql5\scripts\dtwPatternSearch.mq5	Скрипт для поиска произвольного паттерна в выборке данных
Mql5\scripts\DTW.py	Скрипт Python, который применяет модуль dtw-python для выравнивания двух рядов с использованием алгоритма DTW