Возможности Мастера MQL5, которые вам нужно знать (Часть 47): Обучение с подкреплением (алгоритм временных различий)

Введение

Рассмотрим, чем TD отличается от других алгоритмов, таких как Монте-Карло, Q-обучение и SARSA. Целью статьи является разрешение сложностей, связанных с обучением TD, путем подчеркивания его уникальной способности постепенно обновлять оценки значений на основе частичной информации из эпизодов, а не ждать завершения эпизодов, как это происходит в методах Монте-Карло. Это различие делает обучение TD мощным инструментом, особенно в тех случаях, когда среда динамична и требует оперативного обновления политики обучения.

В предыдущей статье об обучении с учителем мы рассмотрели алгоритм Монте-Карло, который собирал информацию о вознаграждениях в течение нескольких циклов, прежде чем выполнить одно обновление для каждого эпизода. TD подразумевает обучение на основе частичных и неполных эпизодов, что очень похоже на алгоритмы Q-обучения и SARSA, которые мы рассматривали ранее здесь и здесь.

Ниже приведена сводная таблица основных различий между TD, Q-обучением и SARSA.

Подводя итог, можно сказать, что формула для пар "состояние-действие" с обновлением в рамках политики, например, SARSA, выглядит следующим образом:

	Обучение TD	Q-обучение	SARSA
Типы значений	Значения состояния V(s)	Значения действия Q(s,a)	Значения действия Q(s,a)
Подход к обучению	Оценки будущих значений состояния	Вне политики	В рамках политики
Тип политики	Не зависит от конкретной политики	Изучает оптимальную политику	Изучает текущую политику поведения
Обновление цели	Следующее значение состояния V(s′)	Макс Q(s′,a′)	Фактическое Q(s′,a′)
Исследование	Часто требуется отдельная политика	Предполагается, что агент ищет оптимальную политику	Более консервативная
Поведение	Двигается к значению следующего состояния	Жадный; предпочитает оптимальный путь	Следует фактическому пути исследования

Подводя итог, можно сказать, что обновления политики означают, что обновляемые пары "состояние-действие" являются текущими и не обязательно оптимальными или имеющими самые высокие значения Q. Если мы хотим обновить пары "состояние-действие" с наивысшими значениями Q, то это будет несоответствующий политике подход. Эти обновления в MQL5 мы выполняем следующим образом:

//+------------------------------------------------------------------+
// Update using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q_SA-action from Q_SA-Map
   double _sa = Q_SA[transition_act][e_row[1]][e_col[1]];
   double _v = Q_V[e_row[1]][e_col[1]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[1]][e_col[1]]);
   }
   Q_V[e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[1]][e_col[1]]);
}

//+------------------------------------------------------------------+
// Update using Off-policy
//+------------------------------------------------------------------+
void Cql::SetOffPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 0 represents highest valued Q_SA-action from Q_SA-Map
//as determined from Action() function above.
   double _sa = Q_SA[transition_act][e_row[0]][e_col[0]];
   double _v = Q_V[e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[0]][e_col[0]]);
   }
   Q_V[e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[0]][e_col[0]]);
}

В наши измененные и пересмотренные функции включены обновления с добавлением нового объекта Q_V, который мы представили в виде матрицы для ясности сопоставления с соответствующими состояниями среды, но мы могли бы легко представить его в виде вектора, поскольку координаты состояния среды можно сопоставить с одним целым числом индекса. Старая Q-карта переименована в Q_SA. Это новое наименование соответствует новому отслеживанию объектов значений Q-карты независимо от действий, на чем и фокусируется TD, в то время как переименование старой Q-карты в Q_SA подчеркивает его парные значения "состояние-действие", которые обновляются при каждом вызове функции. Наши реализации MQL5, представленные выше, получены из следующей формулы для TD (которая может быть включена или выключена):

где:

• V (s) - текущее состояние s
• V (s′) - следующее состояние s′
• α - скорость обучения (насколько мы корректируем текущее значение)
• r - награда за выполнение действия
• γ - коэффициент дисконтирования (важность будущих вознаграждений)
• Формула обновляет оценку стоимости состояния V (s) на основе полученного вознаграждения и оценки стоимости следующего состояния V (s′)

Подводя итог, можно сказать, что формула для пар "состояние-действие" с обновлением в рамках политики, например, SARSA, выглядит следующим образом:

где:

• Q (s, a) - Q-значение текущей пары состояние-действие (s, a)
• Q (s′, a′) - Q-значение следующей пары состояние-действие (s′, a′), где a′ - действие, выбранное текущей политикой в следующем состоянии s′
• α - скорость обучения
• r - награда за выполнение действия a
• γ - коэффициент дисконтирования

Аналогично, формула для обновлений, не соответствующих политике, выглядит следующим образом:

где:

• Q (s, a) - Q-значение текущей пары состояние-действие (s, a)
• max a′ ​Q (s′, a′) - максимальное значение Q следующего состояния s′ среди всех возможных действий a′ (предполагается, что будет выполнено наилучшее действие в s′)
• α - скорость обучения
• r - награда за выполнение действия a
• γ - коэффициент дисконтирования

Из последних двух формул становится ясно, что обновления, относящиеся к конкретным действиям, вносят определенный вклад в выбор следующего действия. Однако для обновления TD, поскольку оно агрегирует значения по всем действиям и просто присваивает их соответствующему состоянию среды, влияние этого процесса на выбираемое действие не является четко определенным.

Вот почему при использовании TD необходимо использовать дополнительную модель, которая в нашем случае является нейронной сетью политики для управления выбором следующего действия для актера. Эта модель может принимать различные формы, но для наших целей это просто трехслойный перцептрон (MLP) размером 3-9-3, где выходной слой обеспечивает распределение вероятностей для каждого из трех возможных действий, которые в нашем случае по-прежнему представляют собой покупку, продажу и удержание. Таким образом, этот MLP будет классификатором, а не регрессором. Укажем код объявления этого класса в интерфейсе пользовательского класса сигнала, как показано ниже:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalTD   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   
public:
   void                          CSignalTD(void);
   void                          ~CSignalTD(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   int               GetOutput(Cql *QL, CNeuralNetwork &PN);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   CNeuralNetwork    POLICY_NETWORK_BUY,POLICY_NETWORK_SELL;
};

Полный исходный код нашего пользовательского класса сигналов приложен внизу и предназначен для создания советника с помощью Мастера MQL5. Руководства для новичков можно найти здесь и здесь. С помощью нашего исходного кода читатель может легко вносить изменения в конструкцию MLP, изменяя не только количество слоев, но и их размер. Однако в нашей конструкции входной слой с номером 3 предназначен для приема в качестве входных данных координаты среды по оси X, значения перехода или текущего показания матрицы Q_V и показания среды по оси Y. Значение перехода берется из матрицы Q_V, которую мы обновляем в параметрах политики включения и выключения, как уже указано в исходном коде выше. Этот выбор значения перехода обрабатывается в пересмотренной функции действия, как указано ниже:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   transition_value = Q_V[_next_row][_next_col];
   policy_history[1][0] = policy_history[0][0];
   policy_history[1][1] = policy_history[0][1];
   policy_history[1][2] = policy_history[0][2];
   policy_history[0][0] = _next_row;
   policy_history[0][1] = transition_value;
   policy_history[0][2] = _next_col;
   transition_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
   //if(transition_act!=1)printf(__FUNCSIG__+ " act is : %i ",transition_act);
}

Таким образом, основополагающий тезис нашей сети политики, вышеупомянутый MLP, заключается в том, что подходящее действие, которое должно быть выбрано следующим, является функцией только текущего состояния среды и ее Q-значения. Это отличается от того, что мы использовали до сих пор, когда для выбора подходящего действия из Q-карты использовался марковский процесс принятия решений (Markov Decision Process, MDP), который мы переименовали в этой статье (прикрепленный код) в Q_SA. Во всех случаях мы использовали MDP без памяти, вычисляя буфер последних последовательностей состояний среды. Эти последовательности сред, благодаря функции Маркова, которая рассматривается ниже, дают нам проекцию следующего состояния среды.

//+------------------------------------------------------------------+
// Function to update markov matrix
//+------------------------------------------------------------------+
void Cql::LetMarkov(int OldRow, int OldCol, vector &E)  //
{  matrix _transitions;  // Count the transitions
   _transitions.Init(markov.Rows(), markov.Cols());
   _transitions.Fill(0.0);
   vector _states;  // Count the occurrences of each state
   _states.Init(markov.Rows());
   _states.Fill(0.0);
// Count transitions from state i to state ii
   for (int i = 0; i < int(E.Size()) - 1; i++)
   {  int _old_state = int(E[i]);
      int _new_state = int(E[i + 1]);
      _transitions[_old_state][_new_state]++;
      _states[_old_state]++;
   }
// Reset prior values to zero.
   markov.Fill(0.0);
// Compute probabilities by normalizing transition counts
   for (int i = 0; i < int(markov.Rows()); i++)
   {  for (int ii = 0; ii < int(markov.Cols()); ii++)
      {  if (_states[i] > 0)
         {  markov[i][ii] = double(_transitions[i][ii] / _states[i]);
         }
         else
         {  markov[i][ii] = 0.0;  // No transitions from this state
         }
      }
   }
}

Этот процесс определения следующих состояний благодаря MDP по-прежнему выполняется с помощью TD, однако разница здесь в том, что мы не можем использовать эти спроецированные координаты следующего состояния сами по себе для определения следующего действия. Раньше, когда мы использовали Q_SA, речь шла о считывании действия с наивысшей вероятностью, взвешивая координаты следующего состояния, чтобы узнать, что должен был сделать субъект. Однако теперь наша эквивалентная матрица Q_V дает нам только значения для любых предоставленных координат состояния, и тем не менее определение следующего действия актера имеет решающее значение в цикле обучения с подкреплением.

Вот почему мы вводим сеть политики, MLP, которую для наших целей мы просто спроектировали как 3-9-3, имеющую один скрытый слой из 9, принимающую 3 вышеупомянутых входных параметра двух координат среды и их Q-значение, и выводящую вектор из 3, который предназначен для захвата распределения вероятностей по 3 возможным действиям: купить, продать и удерживать, при этом значение, набравшее наибольшее количество баллов в векторе, является рекомендуемым действием.

Преимущества и цель TD

TD обновляет свои Q-значения чаще, чем в Монте-Карло, что дает очевидные преимущества на быстро меняющихся и изменчивых финансовых рынках. Однако что отличает его, скажем, от SARSA или Q-обучения с точки зрения преимуществ? Мы попытаемся ответить на этот вопрос, рассмотрев несколько повседневных примеров.

По определению, основное различие между TD и SARSA/Q-обучением заключается в том, что TD больше фокусируется на обучении на основе ценностей, где изучаются и обновляются только значения состояний, в то время как два других алгоритма фокусируются на сопряжении состояния и действия для выполнения аналогичных обновлений.

Сценарий А

Предположим, что на складе имеется система управления запасами, которая отслеживает уровень запасов множества товаров. Целью этой системы будет исключительно управление уровнями запасов и предотвращение нехватки продукции и затоваривания.

В этой ситуации TD будет иметь преимущество перед SARSA или Q-обучением просто из-за его фокуса на парах состояние-значение, а не состояние-действие. В этом случае системе может потребоваться только предсказать "значение" каждого состояния (например, общие уровни запасов) без оценки каждого конкретного действия (например, заказ для каждого номера SKU). Таким образом, в этой ситуации, без необходимости в сетевой политике MLP, обучение TD может обновить функцию стоимости для состояния (уровни запасов) без расчета каждого возможного решения о заказе для каждого продукта.

Кроме того, управление запасами может характеризоваться постепенными изменениями вместо резких пар "состояние-действие", которые имеют четкую обратную связь в виде вознаграждения. Поскольку обучение TD имеет дело с постепенным получением обратной связи, это делает его пригодным для сред с плавными переходами, где знание общего состояния важнее, чем знание каждого результата состояния-действия. Наконец, среды, в которых есть несколько действий и большие пространства состояний и действий, такие как управление запасами, которое является более сложным (где нам нужно будет сопоставить курс действий с каждым состоянием уровня запасов), Q-обучение и SARSA, хотя и применимы, неизбежно потребуют вычислительных затрат, с которыми TD никогда не сталкивается из-за своего более простого целостного применения.

 

Сценарий B

Рассмотрим интеллектуальную систему здания, которая регулирует параметры отопления, вентиляции и кондиционирования воздуха (HVAC) таким образом, чтобы минимизировать потребление энергии и при этом обеспечить комфорт для жильцов. Таким образом, ее цели, заключающиеся в достижении баланса между краткосрочными выгодами и долгосрочными целями, совпадают с сокращением счетов за электроэнергию и поддержанием оптимальной температуры и качества воздуха в здании соответственно.

В этом случае TD подойдет лучше, чем SARSA или Q-обучение, поскольку уровни энергопотребления или комфорт пользователя являются абсолютными показателями, к которым не привязаны никакие действия в зависимости от их значений. В этом конкретном случае для того, чтобы сбалансировать краткосрочные и долгосрочные вознаграждения, можно обучить два цикла обучения с подкреплением прогнозировать оба результата параллельно. Постепенные обновления TD за цикл (а не за эпизод, как мы видели в случае с Монте-Карло) также делают его идеальным для этой интеллектуальной системы здания, поскольку условия окружающей среды, такие как температура, размещение и качество воздуха, изменяются постепенно. Это позволяет TD обеспечить плавный механизм регулировки.

Наконец, как упоминалось выше, эквивалент SARSA или Q-обучение будет иметь дополнительные требования к вычислениям и памяти, поскольку потребуются определенные действия для "исправления" любых недостатков или излишков значений состояния среды.  

 

Сценарий С

Система прогнозирования и управления транспортным потоком, целью которой является минимизация заторов на нескольких перекрестках посредством прогнозирования транспортного потока и соответствующей корректировки сигналов светофора. TD также выгоден в этой ситуации по сравнению с SARSA или Q-обучением, поскольку основная задача заключается в понимании и прогнозировании общего состояния дорожного движения (например, уровней загруженности), а не в оптимизации каждого отдельного действия светофора. Обучение TD позволяет системе изучать общую "ценность" состояния дорожного движения, а не влияние каждого конкретного изменения сигнала.

Кроме того, поскольку трафик по своей природе динамичен и постоянно меняется в течение дня, он также вносит свой вклад в пошаговое обновление TD. Это очень гибкий алгоритм, в отличие от Монте-Карло, который ждет завершения эпизода перед выполнением обновлений. В этом случае также актуально снижение вычислительных нагрузок и перегрузок памяти для TD, особенно если учесть, насколько переплетенными и взаимосвязанными могут быть транспортные развязки даже в относительно небольшом городе. Затраты на вычисления и память, безусловно, станут важнейшим фактором при внедрении системы прогнозирования транспортных потоков, и TD внесет большой вклад в решение этой проблемы.

Сценарий D

Предиктивное обслуживание в производстве представляет наш последний вариант использования TD как предпочтительного алгоритма по сравнению с другими алгоритмами в обучении с подкреплением, которые мы рассмотрели до сих пор. Рассмотрим случай, когда производственное предприятие стремится предсказать, когда машинам потребуется обслуживание, чтобы избежать простоя. Как и в случае с системой "умного здания", эта система должна будет сбалансировать краткосрочные выгоды (экономию затрат на техническое обслуживание за счет отсрочки проверок) с долгосрочными выгодами (предотвращение поломок). Обучение TD здесь было бы уместно, поскольку оно может обновлять общее значение работоспособности машины с течением времени на основе частичной обратной связи, а не отслеживать конкретные действия (ремонт или замена), как это делают SARSA или Q-обучение.

Алгоритм TD также будет лучшим, поскольку ухудшение состояния машины происходит постепенно, и TD может легко обновлять значение работоспособности непрерывно на основе дополнительных данных датчика, а не ждать в течение более длительных периодов времени, что может повлечь за собой дополнительные риски. Кроме того, на заводе, где имеется несколько машин, обучение TD может хорошо масштабироваться по мере уменьшения или увеличения количества машин, поскольку оно фокусируется только на отслеживании состояния/работоспособности каждой машины и не требует хранения и обновления определенных пар "состояние-действие" для каждой машины на заводе.

Это лишь несколько случаев, выходящих за рамки финансовой торговли и рынков, поэтому давайте теперь рассмотрим, как мы можем конкретно применить алгоритм в качестве класса пользовательских сигналов.

Структурирование пользовательского класса сигналов с использованием алгоритма TD

Пользовательский класс сигнала, который мы создаем для реализации TD, опирается на два дополнительных класса. Поскольку это алгоритм обучения с подкреплением, одним из таких классов является класс CQL. Мы уже использовали или ссылались на этот класс во всех предыдущих статьях. Его интерфейс снова представлен ниже:

//+------------------------------------------------------------------+
//| Q_SA-Learning Class Interface.                                      |
//+------------------------------------------------------------------+
class Cql
{
protected:
   matrix            markov;
   void              LetMarkov(int OldRow, int OldCol, vector &E);

   vector            acts;
   matrix            environment;
   matrix            Q_SA[];
   matrix            Q_V;

public:
   void              Action(vector &E);
   void              Environment(vector &E_Row, vector &E_Col, vector &E);

   void              SetOffPolicy(double Reward, vector &E);
   void              SetOnPolicy(double Reward, vector &E);

   double            GetReward(double MaxProfit, double MaxLoss, double Float);
   vector            SetTarget(vector &Rewards, vector &TargetOutput);

   void              SetMarkov(int Index, int &Row, int &Col);
   int               GetMarkov(int Row, int Col);


   Sql               THIS;

   int               act[2];

   int               e_row[2];
   int               e_col[2];

   int               transition_act;
   double            transition_value;
   
   matrix            policy_history;

   vector            Q_Loss()
   {  vector _loss;
      _loss.Init(THIS.actions);
      _loss.Fill(0.0);
      for(int i = 0; i < THIS.actions; i++)
      {  _loss[i] = Q_SA[e_row[0]][e_col[0]][i];
      }
      return(_loss);
   }


   void              Cql(Sql &RL)
   {  //
      if(RL.actions > 0 && RL.environments > 0)
      {  policy_history.Init(2,2+1);
         policy_history.Fill(0.0);
         acts.Init(RL.actions);
         ArrayResize(Q_SA, RL.actions);
         for(int i = 0; i < RL.actions; i++)
         {  acts[i] = i + 1;
            Q_SA[i].Init(RL.environments, RL.environments);
         }
         Q_V.Init(RL.environments, RL.environments);
         environment.Init(RL.environments, RL.environments);
         for(int i = 0; i < RL.environments; i++)
         {  for(int ii = 0; ii < RL.environments; ii++)
            {  environment[i][ii] = ii + (i * RL.environments) + 1;
            }
         }
         markov.Init(RL.environments * RL.environments, RL.environments * RL.environments);
         markov.Fill(0.0);
         THIS = RL;
         ArrayFill(e_row, 0, 2, 0);
         ArrayFill(e_col, 0, 2, 0);
         ArrayFill(act, 0, 2, 1);
         transition_act = 1;
      }
   };
   void              ~Cql(void) {};
};

Это основной класс обучения с подкреплением, и некоторые из его классов, определяющих обновления в рамках и вне политики, уже были представлены выше. Кроме того, этого класса часто достаточно для реализации обучения с подкреплением для пользовательского класса сигналов, однако для TD, поскольку мы не используем и не полагаемся исключительно на значения окружающей среды для принятия торговых решений, а решаем продолжить прогнозирование подходящих действий, как мы делали это раньше, нам нужна модель для создания таких прогнозов.

Вот почему для определения этой модели как нейронной сети или MLP используется дополнительный класс — CNeuralNetwork. Аналогично его интерфейс класса представлен ниже:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CNeuralNetwork
{
protected:
   
   matrix               TransposeToCol(vector &V);
   matrix               TransposeToRow(vector &V);
   
public:
   CLayer               *layers[];
   double               m_learning_rate;
   ENUM_LOSS_FUNCTION   m_loss;
   void                 AddDenseLayer(ulong Neurons, ENUM_ACTIVATION_FUNCTION AF = AF_RELU, ulong LastNeurons = 0)
   {  ArrayResize(layers, layers.Size() + 1);
      layers[layers.Size() - 1] = new CLayer(Neurons, AF);
      if(LastNeurons  != 0)
      {  layers[layers.Size() - 1].AddWeights(LastNeurons);
      }
      else if(layers.Size() - 1 > 0)
      {  layers[layers.Size() - 1].AddWeights(layers[layers.Size() - 2].activations.Size());
      }
   };
   void                 Init(double LearningRate, ENUM_LOSS_FUNCTION LF)
   {  m_loss = LF;
      m_learning_rate = LearningRate;
   };
   
   vector               Forward(vector& Data);
   void                 Backward(vector& LabelAnswer);
   
   void                 CNeuralNetwork(){};
   void                 ~CNeuralNetwork()
   {  if(layers.Size() > 0)
      {  for(int i = 0; i < int(layers.Size()); i++)
         {  delete layers[i];
         }
      }
   };
};

Мы внесли некоторые заметные изменения по сравнению с последним классом CMLP, который выполнял аналогичную функцию. Основной упор делался на эффективность, однако это все еще бета-версия, хотя для наших целей она и смогла дать некоторые результаты. Помимо изменений эффективности, которые в основном коснулись функции обратного распространения (Backward) и находятся в стадии разработки, мы ввели класс слоев, а также изменили способ построения сети. Инициализация пользовательского класса сигналов теперь выглядит так: 

//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CSignalTD::CSignalTD(void) :    m_scale(5),
   m_use_markov(true),
   m_policy(true)

{
//--- initialization of protected data
   m_used_series = USE_SERIES_OPEN + USE_SERIES_HIGH + USE_SERIES_LOW + USE_SERIES_CLOSE + USE_SERIES_SPREAD + USE_SERIES_TIME;
   //
   RL.actions  = 3;//buy, sell, do nothing
   RL.environments = 3;//bullish, bearish, flat
   RL.use_markov = m_use_markov;
   RL.epsilon = m_epsilon;
   QL_BUY = new Cql(RL);
   QL_SELL = new Cql(RL);
   //
   POLICY_NETWORK_BUY.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_BUY.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_BUY.Init(0.0004,LOSS_BCE);
   //
   POLICY_NETWORK_SELL.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_SELL.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_SELL.Init(0.0004,LOSS_BCE);
}

Помимо двух классов CQL для обработки обучения с подкреплением на стороне покупки и продажи соответственно, теперь у нас есть две сети политик, которые также могут делать прогнозы действий на стороне покупки и продажи соответственно. Функция get output по-прежнему работает так же, как и в предыдущих статьях, главное изменение заключается в том, что экземпляр класса нейронной сети является одним из ее входов в качестве сети политики. Новый листинг выглядит так:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CSignalTD::GetOutput(Cql *QL, CNeuralNetwork &PN)
{  int _td_act = 1;
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_row.Size() == m_scale+1
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale+1) &&
      _in_row_old.Size() == m_scale+1
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_col.Size() == m_scale+1
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale+1) &&
      _in_col_old.Size() == m_scale+1
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      _in_row.Resize(m_scale);
      _in_col.Resize(m_scale);
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
      PN.Forward(QL.policy_history.Row(1));
      vector _label;
      _label.Init(3);
      _label.Fill(0.0);
      if(_in_row[m_scale-1] > 0.0)
      {  _label[0] = 1.0;
      }
      else if(_in_row[m_scale-1] < 0.0)
      {  _label[2] = 1.0;
      }
      else if(_in_row[m_scale-1] == 0.0)
      {  _label[1] = 1.0;
      }
      PN.Backward(_label);
      vector _td_output = PN.Forward(QL.policy_history.Row(0));
      if(_td_output[0] >= _td_output[1] && _td_output[0] >= _td_output[2])
      {  _td_act = 0;
      }
      else if(_td_output[2] >= _td_output[0] && _td_output[2] >= _td_output[1])
      {  _td_act = 2;
      }
   }
   return(_td_act);
}

Используя в качестве одного из входных данных сеть политики, теперь можно выполнять онлайн-обучение или пошаговое обучение, поскольку перед прогнозированием мы обучаемся не на пакете данных, а только на последних данных по одному столбцу. Должен быть только запуск обратного распространения и один запуск прямого распространения, но, поскольку нам необходимо загрузить информацию о текущем ценовом баре в нашу нейронную сеть перед выполнением обратного распространения, мы делаем один запуск прямой подачи с информацией о предыдущем баре перед ним, чтобы загрузить эту информацию. Наша функция Forward также изменена для возврата выходного вектора классификации из прохода прямого распространения. Она имеет размер три, где каждое значение соответствующего индекса обеспечивает "вероятность" или пороговое значение вероятности продажи, удержания или покупки, если мы следуем порядку индексации 0, 1, 2 соответственно.

Итак, если подвести итог вышесказанному, мы придерживаемся той же простой среды обучения с подкреплением и настройки действий из 3 состояний и 3 действий. Выбор обновления политики можно оптимизировать, как в последней статье об обучении с подкреплением, в которой рассматривался метод Монте-Карло. Однако при выполнении здесь обновлений обновляются только Q-значения новой введенной матрицы Q_V. Это контрастирует с тем, что мы делали в прошлом, обновляя Q-значения по всей карте среды для каждого действия. Обновление значений для каждого действия было конструктивным при выборе следующего действия, поскольку после использования марковского процесса принятия решений для определения координат следующего состояния среды остается лишь считать действие с наивысшим значением Q и выбрать его в качестве следующего действия.

При использовании TD наша матрица среды Q_V не имеет действий с Q-значениями, а имеет только значения, назначенные конкретной среде. Это означает, что для выбора или определения следующего курса действий используется сеть политики (в нашем случае MLP) для составления этих прогнозов, а ее входными данными будет значение для текущей среды (которое по сути является суммой всех Q-значений применимых действий в этом состоянии), а также координаты состояния среды. Как уже упоминалось, результатом является "распределение вероятностей" по трем возможным действиям, указывающее, какое из них будет наилучшим с учетом текущей обстановки и ее ценности.

Таким образом, этот пользовательский класс сигналов собирается с помощью мастера MQL5 в советника, и после непродолжительной оптимизации для 2022 года на часовом таймфрейме и символе GBPUSD, одна из благоприятных настроек этого периода предоставляет нам следующий отчет:

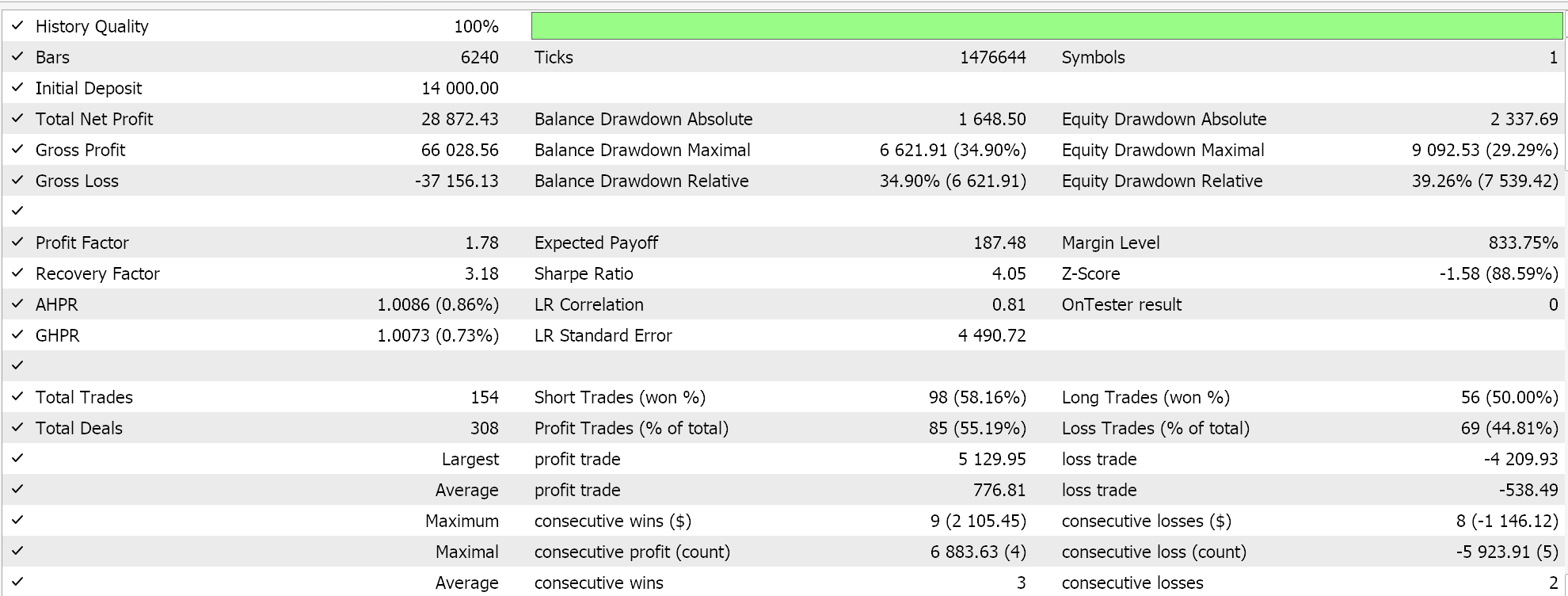
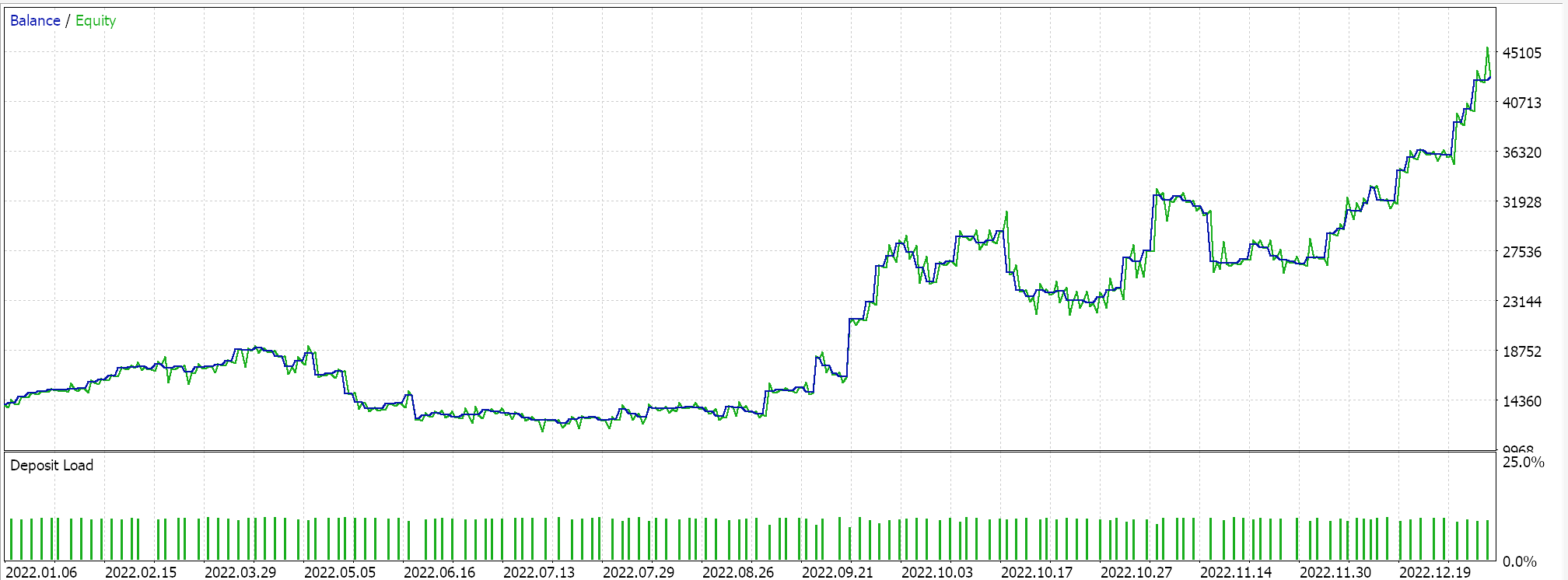
Эти результаты, возможно, говорят о потенциале нашего класса пользовательских сигналов, но, не принижая их значение, следует отметить, что всегда рекомендуется проводить перекрестную проверку настроек любогопертного советника, прежде чем решать, развернуть ли его в реальной среде. Перекрестная проверка и дополнительное тестирование в течение более длительного периода времени, чем то, что мы сделали здесь, оставлены на усмотрение читателя.

Оптимизация и настройка класса сигнала с помощью обучения TD

В наших тестовых запусках, описанных выше, мы оптимизировали исключительно значение epsilon, необходимость использования весовых коэффициентов Маркова в процессе обновления и необходимость выполнения обновлений в рамках или вне политики. Конечно, были и дополнительные типичные параметры, не связанные с TD, такие как пороги открытия и закрытия для длинных и коротких позиций, уровень тейк-профита, а также порог цены входа в пунктах.

Однако в TD и обучении с подкреплением, есть довольно много параметров, которые мы упустили из виду и использовали их с предустановленными значениями. Это alpha и gamma, которым присвоены значения 0,1 и 0,5 соответственно. Эти два параметра являются ключевыми в обновлениях политики и, возможно, могут быть очень чувствительны к общей производительности класса сигнала. Другие ключевые параметры, которые мы упустили из виду при реализации нашего класса сигналов, фактически присвоив им постоянные значения, — это настройки сетей политики. Мы остановились на сети 3-9-3, в которой все функции активации на каждом слое были заданы заранее, как и скорость обучения. Каждая из них, а возможно, и все они при одновременной настройке могут оказать большое влияние на результаты и производительность класса пользовательских сигналов.

Заключение

Мы рассмотрели алгоритм временных различий обучения с подкреплением и попытались выделить варианты его использования, которые отличают его от других рассмотренных алгоритмов. Один из аспектов, который мы не рассматривали и который представляет интерес для обучения с подкреплением в целом, — это затухание исследования с течением времени. Возможная причина заключается в том, что по мере того, как модель обучения с подкреплением со временем учится, необходимость исследовать новую территорию или продолжать обучение значительно уменьшается; более важной становится эксплуатация. Это то, на что читатели могут обратить внимание, когда захотят настроить прикрепленный код для дальнейшего использования.

Другим аспектом может быть превращение epsilon в переменную величину, а не просто ее уменьшение, что и подразумевает приведенное выше затухание. Суть этого подхода заключается в том, что обучение с подкреплением должно быть очень динамичным и адаптивным, в отличие от моделей контролируемого обучения, которые опираются на статические данные. Таким образом, структура обучения с подкреплением TD может активно взаимодействовать с изменяющейся средой. Мы рассмотрели методы динамической скорости обучения в прошлой статье, и можно утверждать, что то же самое можно рассмотреть и для эпсилона, так что предположение об угасании само по себе не будет единственным способом удержания обучения с подкреплением в его исконном виде.