MQL5 Wizard Techniques you should know (Part 23): CNNs

MetaTrader 5 — Tester | 20 June 2024, 09:41

1 091

Stephen Njuki

Introduction

We continue this series where we look at machine learning and statistics ideas that could be of benefit to traders given the rapid testing & prototyping environment provided by the MQL5 wizard. The goal remains to look at a single idea within one article and for this piece, I had initially thought this would take at least 2 articles, however it appears we are able to squeeze it into one. Convolutional Neural Networks (CNNs) as their name suggests, process multi-dimensioned data in convolutions thanks to kernels.

These kernels bear the network weights and, like the multi-dimensioned input data, are typically in matrix format. They have smaller overall dimensions when compared to the input data, and by iterating over the input data matrix during a feed forward as we’ll see below, each iteration essentially cycles across the input data. It is this ‘cycle’ that lends the name ‘convolutional’.

So for this article we are going to have an introduction to the key steps involved in a CNN, build a simple MQL5 class that implements these steps, integrate this class into a custom MQL5 wizard signal class, and finally perform test runs with an Expert Advisor that is assembled from this signal class.

CNNs are typically complex neural networks whose main applications are in video and image processing, like we saw with GANs in the previous article. However, unlike GANs that are trained in identifying real images and or subjects in the images from fakes, CNNs tend to work more like a classifier in that they split the input data (which is often image pixels) into various subgroups of data whereby each subgroup is meant to capture a key or very important property of the input data. These produced subgroups are often referred to as feature maps.

The steps involved in arriving at these feature maps are: Padding, feeding forward, Activation, Pooling, and finally if the network is trained, back propagation. We take a peek at each of these steps below with a very simple single layer CNN. By single layer we mean the input data is processed through a single layer of kernels. This is not always the case with CNNs as they can span many layers such that each of the 4 steps mentioned above of padding, forward feed, activation, and pooling gets repeated for each layer. In multi-layer set-ups, the implication is that for each feature map produced from a higher up layer, there are other key component properties in it that get split up into new feature maps down the line.

Padding

This marks the start of a CNN and, whether or not this particular step is included, can be optional. So, what is padding? Well, like the name suggests, it is simply the addition of a border of data along the edges of the input data. Essentially, the input data gets padded. Recall input data is usually more than one dimension, in fact it is often 2-dimensional which is why a matrix representation is often appropriate. Images are made of pixels in an XY plane, so their classification with a CNN is straight forward.

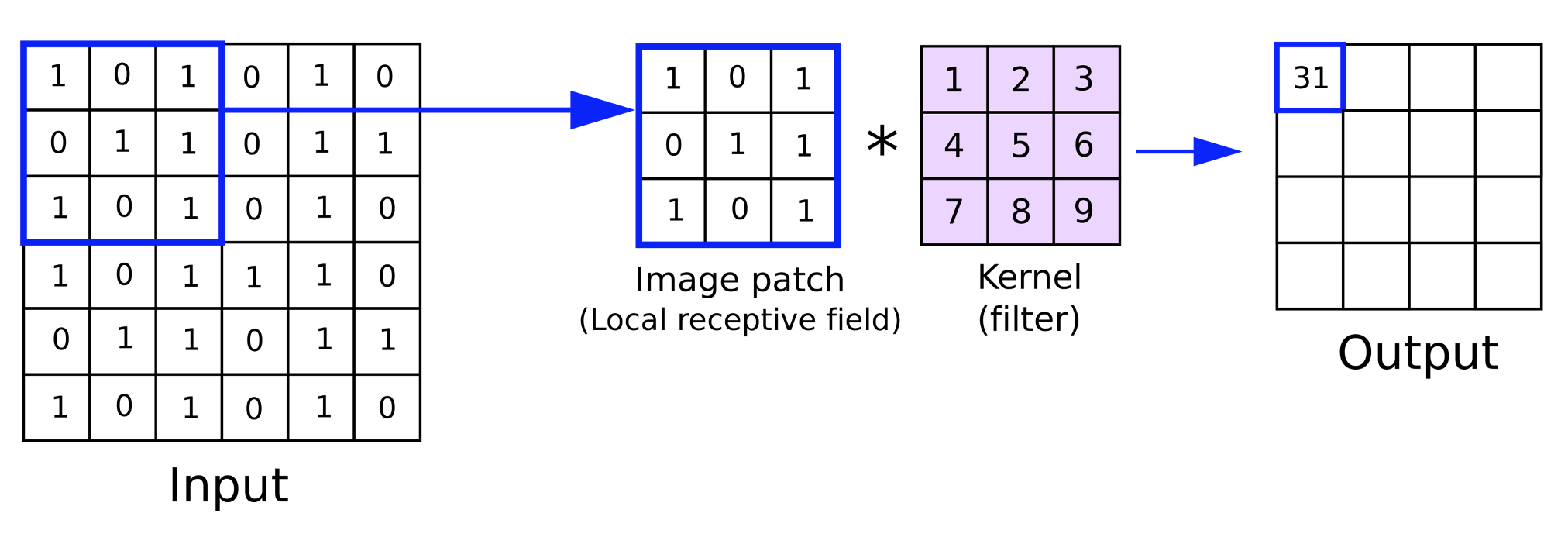
So why do we need to do padding? The need arises from the nature of the convolution with the kernels during the feed forward step. The kernels like the input data are also in matrix format. They bear the network’s weights. Typically, a layer will have more than one kernel, since each kernel is responsible for outputting a specific feature map.

The process of multiplying the weights in the kernel with the input data happens over an iteration or cycle, or what is synonymous as a convolution. The end product of this multiplication is a feature map matrix whose dimensions are always less than the input data. So, the point of padding is in the event that the user would like the feature map to have the same dimensions as the raw input data then extra data borders will need to be added to the input data.

source

To understand this, if we consider an input data matrix of size 6 x 6 and a kernel of weights sized 3 x 3 then a direct weights multiplication will yield a 4 x 4 matrix as indicated above. The formula for the output matrix size given input data size and kernel matrix size is:

eq_1

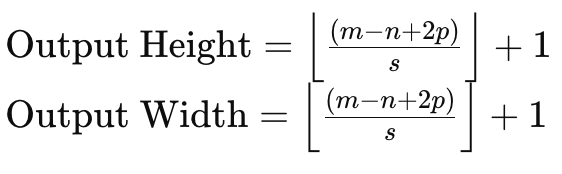
Where:

m is the dimension of the input data matrix,
n is the dimension of the weights kernel,
p is the padding size,
and s is the striding size.

Therefore, if we need to maintain the size of an input data matrix in the feature maps, we would need to pad the input data matrix by an amount that does not only consider the size of the input matrix and the kernel matrices but also the amount of stride to be used.

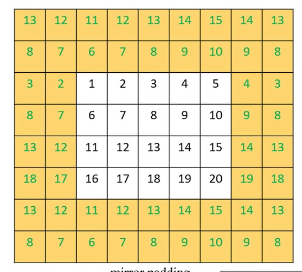
There are primarily 3 methods of padding. The first is zero padding, where 0s are added along the border of the input matrix to match the required width. The second form of padding is edge padding, where the numbers on the edge of the matrix are repeated along the new border also to match the new target size. And finally, there is reflected padding where the numbers on the new enlarged border are got from within the input data matrix, with the numbers along its edge acting as a mirror line.

< reflect_1

source

Once the padding is complete, then the feed forward step can be carried out. This padding, though, as mentioned, is optional in that if the user does not require matching sized feature maps then it can be skipped all together. For instance, consider a situation where a CNN is meant to comb through many images and extract photos of human faces within those images.

Inevitably the feature map or output images from each iteration will have fewer pixels and therefore dimensions than the input image, so in this case there might be no point in doing an initial pad or enlargement of the input image. We do implement padding via this listing:

//+------------------------------------------------------------------+
//| Pad                                                              |
//+------------------------------------------------------------------+
void Ccnn::Pad()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   if(padding != PADDING_NONE)
   {  matrix _padded;
      _padded.Init(inputs.Rows() + 2, inputs.Cols() + 2);
      _padded.Fill(0.0);
      for(int i = 0; i < int(_padded.Cols()); i++)
      {  for(int j = 0; j < int(_padded.Rows()); j++)
         {  if(i == 0 || i == int(_padded.Cols()) - 1 || j == 0 || j == int(_padded.Rows()) - 1)
            {  if(padding == PADDING_ZERO)
               {  _padded[j][i] = 0.0;
               }
               else if(padding == PADDING_EDGE)
               {  if(i == 0 && j == 0)
                  {  _padded[j][i] = inputs[0][0];
                  }
                  else if(i == 0 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][0];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == 0)
                  {  _padded[j][i] = inputs[0][inputs.Cols() - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][inputs.Cols() - 1];
                  }
                  else if(i == 0)
                  {  _padded[j][i] = inputs[j - 1][i];
                  }
                  else if(j == 0)
                  {  _padded[j][i] = inputs[j][i - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1)
                  {  _padded[j][i] = inputs[j - 1][inputs.Cols() - 1];
                  }
                  else if(j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][i - 1];
                  }
               }
               else if(padding == PADDING_REFLECT)
               {  if(i == 0 && j == 0)
                  {  _padded[j][i] = inputs[1][1];
                  }
                  else if(i == 0 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][1];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == 0)
                  {  _padded[j][i] = inputs[1][inputs.Cols() - 2];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][inputs.Cols() - 2];
                  }
                  else if(i == 0)
                  {  _padded[j][i] = inputs[j - 1][1];
                  }
                  else if(j == 0)
                  {  _padded[j][i] = inputs[1][i - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1)
                  {  _padded[j][i] = inputs[j - 1][inputs.Cols() - 2];
                  }
                  else if(j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][i - 1];
                  }
               }
            }
            else
            {  _padded[j][i] = inputs[j - 1][i - 1];
            }
         }
      }
      //
      Set(_padded, false);
   }
}

For our purposes as traders and not image scientists, we’ll be having an input data matrix of indicator values. These indicator values can be customized to a wide variety of options, however we have selected close price gaps from various moving average indicators.

Feed forward (Convolve)

Once the input data is prepared, then a weight's multiplication is performed across the input data for each kernel in the layer to produce a feature map. Besides the weight's multiplication which produces a smaller sized matrix, a bias gets added to each matrix value and this bias, like the respective weights, is unique for each kernel.

Each kernel has the weights and bias that specialize in extracting a key feature or property of the input data. So, the more features one is interested in harvesting, the more kernels he would employ within the network. Feeding forward is performed by the ‘Convolve’ function, and this listing is given here:

//+------------------------------------------------------------------+
//| Convolve through all kernels                                     |
//+------------------------------------------------------------------+
void Ccnn::Convolve()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
// Loop through kernel at set padding_stride
   for (int f = 0; f < kernels; f++)
   {  bool _stop = false;
      int _stride_row = 0, _stride_col = 0;
      output[f].Fill(0.0);
      for (int g = 0; g < int(output[f].Cols()); g++)
      {  for (int h = 0; h < int(output[f].Rows()); h++)
         {  for (int i = 0; i < int(kernel[f].weights.Cols()); i++)
            {  for (int j = 0; j < int(kernel[f].weights.Rows()); j++)
               {  output[f][h][g] += (kernel[f].weights[j][i] * inputs[_stride_row + j][_stride_col + i]);
               }
            }
            output[f][h][g] += kernel[f].bias;
            _stride_col += padding_stride;
            if(_stride_col + int(kernel[f].weights.Cols()) > int(inputs.Cols()))
            {  _stride_col = 0;
               _stride_row += padding_stride;
               if(_stride_row + int(kernel[f].weights.Rows()) > int(inputs.Rows()))
               {  _stride_col = 0;
                  _stride_row = 0;
               }
            }
         }
      }
   }
}

Activation

After convolving, the produced matrices would be activated much like the activation in typical multi-layer perceptions. In image processing though the most common purpose of activation is to introduce within a model, the ability to map non-linear data such that more complex relationships (e.g. quadratic equations) can be captured as well. Common activation algorithms are ReLU, leaky ReLU, Sigmoid, and Tanh.

ReLU is arguably the more popular activation algorithm typically used since it handles vanishing gradient problems much better, however it does face a dead neuron problem which is remedied by the leaky ReLU. A dead neuron refers to situations where network outputs get updated to constant values regardless of changes in inputs. This can be a big deal in networks that are initialized with weights and negative inputs are provided, then static outputs will be got regardless of the variability of the negative inputs. This would even happen through training, which inevitably would lead to warped weights. This would be a loss in representational capacity, which makes the model unable to represent more complex patterns. In back propagation, the flow of gradients through the network would happen with slower convergence or even a complete stagnation.

The leaky ReLU therefore partly mitigates this by allowing a small, optimizable, positive value labelled ‘alpha’ to be assigned as a small slope for negative inputs such that neurons with negatives do not die but still contribute to the learning process. A smoother gradient flow in back propagation also leads to a more stable and efficient training process than the typical ReLU.

Pooling

After the feature images, which are the outputs of the convolution, are activated they are screened for noise in a process referred to as pooling. Pooling is the process of reducing the dimensions of the feature maps, in height and width. The point of pooling is to reduce computational load and by lessening the amount of parameters the network has to grapple with. Pooling also helps with translation invariance by being able to detect key properties of each feature map with minimal data.

There are predominantly 3 types of pooling namely: max pooling, average pooling, and global pooling. Max-pooling chooses the maximum value in each feature matrix patch at a convolution point. And each of the chosen points is brought together in a new matrix, which will be the pooled matrix. Its proponents argue it preserves most of the critical properties of the pooled feature map while reducing the likelihood of overfitting.

Average pooling computes the average value of each patch during convolution and, like with the max pooling, returns it to the pooled matrix. The size of the pooled matrix is influenced not just by the pooling window size and its difference in size from the feature map but also by the pooling stride. Pooling strides are often used with a value more than 1 which inevitably makes the pooled matrix significantly smaller than the feature map. For this article since we want to keep things simple as we are assuming this article is introductory to CNN, we are using a pooling stride of one. Proponents of average pooling claim it is more nuanced and less aggressive than max pooling and is therefore less likely to overlook critical features when pooling.

The 3^rdtype of pooling often used in CNNs is global pooling. In this type of pooling no convolutions are performed, instead the entire feature map is reduced to a single value by taking either the average of the feature map or by selecting its maximum. It is a type of pooling that could be applied in the final layer of multi layered CNNs, where a single value is targeted for each kernel.

The pooling window size and pooling stride size are major determinants of the pooled data size.Larger strides tend to result in smaller pooled data, while on the other hand the feature map size and pooling window size are inversely related. Smaller pooled data sizes significantly reduce network activations and memory requirements. Our pooling is implemented in MQL5 as follows:

//+------------------------------------------------------------------+
//| Pool                                                             |
//+------------------------------------------------------------------+
void Ccnn::Pool()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   if(pooling != POOLING_NONE)
   {  for(int f = 0; f < int(output.Size()); f++)
      {  matrix _pooled;
         if(output[f].Cols() > 2 && output[f].Rows() > 2)
         {  _pooled.Init(output[f].Rows() - 2, output[f].Cols() - 2);
            _pooled.Fill(0.0);
            for (int g = 0; g < int(_pooled.Cols()); g++)
            {  for (int h = 0; h < int(_pooled.Rows()); h++)
               {  if(pooling == POOLING_MAX)
                  {  _pooled[h][g] = DBL_MIN;
                  }
                  for (int i = 0; i < int(output[f].Cols()); i++)
                  {  for (int j = 0; j < int(output[f].Rows()); j++)
                     {  if(pooling == POOLING_MAX)
                        {  _pooled[h][g] = fmax(output[f][j][i], _pooled[h][g]);
                        }
                        else if(pooling == POOLING_AVERAGE)
                        {  _pooled[h][g] += output[f][j][i];
                        }
                     }
                  }
                  if(pooling == POOLING_AVERAGE)
                  {  _pooled[h][g] /= double(output[f].Cols()) * double(output[f].Rows());
                  }
               }
            }
            output[f].Copy(_pooled);
         }
      }
   }
}

Backpropagate (Evolve)

Back propagation like in any neural network is the stage where the network weights and biases get ‘to learn’ by getting adjusted. It is performed during the training process, and the frequency of this training is bound to be determined by the model employed. For financial models used by traders, some models can be programmed to train their networks once a quarter, say to adjust for the latest bout of company earnings news, while others could do their training once a month on dates after key economic calendar news releases. The point here being that yes having the right network weights and biases is important, but perhaps more so is having a clear preset regime for training and updating these weights and biases.

Are there networks that could use a single training and be used after that without any worry on training needs? Yes, this is possible, though not probable in many scenarios. So, the prudent thing is to always have a network training calendar in place if one intends to trade with a neural network.

So, the typical steps involved in any back propagation are always 3 namely: computing the error, and using this error delta to work out the gradients, and then using these gradients to update the weights and biases. We perform all three of these steps in our ‘Evolve’ function, whose code is shared below:

//+------------------------------------------------------------------+
//| Evolve pass through the neural network to update kernel          |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Ccnn::Evolve(double LearningRate = 0.05)
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   
   for(int f = 0; f < kernels; f++)
   {  matrix _output_error = target[f] - output[f];
      // Calculate output layer gradients
      matrix _output_gradients;
      _output_gradients.Init(output[f].Rows(),output[f].Cols());
      for (int g = 0; g < int(output[f].Rows()); g++)
      {  for (int h = 0; h < int(output[f].Cols()); h++)
         {  _output_gradients[g][h] =  LeakyReLUDerivative(output[f][g][h]) * _output_error[g][h];
         }
      }
      
      // Update output layer kernel weights and biases
      int _stride_row = 0, _stride_col = 0;
      for (int g = 0; g < int(output[f].Cols()); g++)
      {  for (int h = 0; h < int(output[f].Rows()); h++)
         {  double _bias_sum = 0.0;
            for (int i = 0; i < int(kernel[f].weights.Cols()); i++)
            {  for (int j = 0; j < int(kernel[f].weights.Rows()); j++)
               {  kernel[f].weights[j][i] += (LearningRate * _output_gradients[_stride_row + j][_stride_col + i]); // output[f][_stride_row + j][_stride_col + i]);
                  _bias_sum += _output_gradients[_stride_row + j][_stride_col + i];
               }
            }
            kernel[f].bias += LearningRate * _bias_sum;
            _stride_col += padding_stride;
            if(_stride_col + int(kernel[f].weights.Cols()) > int(_output_gradients.Cols()))
            {  _stride_col = 0;
               _stride_row += padding_stride;
               if(_stride_row + int(kernel[f].weights.Rows()) > int(_output_gradients.Rows()))
               {  _stride_col = 0;
                  _stride_row = 0;
               }
            }
         }
      }
   }
}

Our outputs at the end are matrices and because of this the error deltas are bound to be captured in matrix format as well. Once we have these error deltas we then need to get them adjusted for their activation product because prior to getting to this final layer they were activated. And how this adjustment for activation is performed is by multiplying the error deltas with the derivative of the activation function.

Also keep in mind that even though the output errors and output gradients are in matrix form, this process needs to be repeated for each kernel. That’s why we have enveloped each of these operations in another overarching for-loop whose indexer is integer ‘f’ and maximum size never exceeds the kernel count. Our output matrices, for the test CNN class we are showcasing for this article, are three in number. They provide maps of bullishness, bearishness, and whipsaw for the security whose price gaps with the various moving averages were provided as inputs in the CNN. These price gaps are also in matrix form.

Because the output error and output gradient values are in matrix form and have been pooled in a previous step already highlighted above, their sizes do not match the kernel matrix weigh sizes. This then does initially present a challenge in determining how to use the gradients to adjust the kernel weights. The solution though is quite simple because it follows the convolutions approach we applied in the feed forward where kernel weight matrices of sizes different from the input data matrix (and its padding) were multiplied in cycles such that at each point a single value was summed up from all the kernel products on the window in focus and they were placed in the output matrix.

This is performed with strides and our stride for this testing is only one as it should match the stride used in the feed forward. Updating the biases though is a bit tricky because they are just a single value, nonetheless the solution is always to sum up the gradients in the matrix and multiply this sum with the old bias (after adjusting with a learning rate).

Integrating into a Signal Class

To use our CNN class within a custom signal, we’d essentially have to define 2 things. Firstly, what form of input data are we going to use and secondly the target type of data we expect in the output matrices. The answers to both these questions have already been hinted at above, as the input data is price gaps between the current close price and many (25 by default) moving average price values. The many moving averages are distinguished by their unique moving average period, and we populate these into the input matrix via the ‘GetOutput’ function as highlighted below:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  int _index = 5;
   matrix _inputs;
   vector _ma, _h, _l, _c;
   _inputs.Init(m_input_size, m_input_size);
   for(int g = 0; g < m_epochs; g++)
   {  for(int h = m_train_set - 1; h >= 0; h--)
      {  _inputs.Fill(0.0);
         _index = 0;
         for(int i = 0; i < m_input_size; i++)
         {  for(int j = 0; j < m_input_size; j++)
            {  if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, h, __KERNEL + 1))
               {  _inputs[i][j] = _c[0] - _ma[0];
                  _index++;
               }
            }
         }
         //
         
        ...

      }
   }

        ...
   
        ...

}

What is not as straight forward is the target data in our output matrices. As mentioned above, we want to get maps of bullishness or bearishness. And for simplicity they should have been just these two (and not include a measure for whether markets are flat), but the reader can modify the source code to address this. How we are measuring this though is by looking at the post price action for each input data point. Again, our data point takes indicator readings for which we have chosen to close price gaps to an array of moving average prices, but this can easily be customized to your preference.

Now our chosen measure of bullishness which we want to capture in a matrix as opposed to a single value will be changes in the high price over different spans. Likewise, to capture eventual bearishness after logging a data point we record changes in low prices over different spans into a matrix. This is coded as shown below:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  
   ...

   for(int g = 0; g < m_epochs; g++)
   {  for(int h = m_train_set - 1; h >= 0; h--)
      {  _inputs.Fill(0.0);
         _index = 0;
         
        ...

         //
         _h.CopyRates(m_symbol.Name(), m_period, 2, h, __KERNEL + 1);
         _l.CopyRates(m_symbol.Name(), m_period, 4, h, __KERNEL + 1);
         _c.CopyRates(m_symbol.Name(), m_period, 8, h, __KERNEL + 1);
         //Print(" inputs are: \n", _inputs);
         CNN.Set(_inputs);
         CNN.Pad();
         //Print(" padded inputs are: \n", CNN.inputs);
         CNN.Convolve();
         CNN.Activate();
         CNN.Pool();
         // targets as eventual price changes with each matrix a proxy for bullishness, bearishness, or whipsaw action
         // implying matrices for eventual:
         // high price changes
         // low price changes
         // close price changes,
         // respectively
         //
         // price changes in each column are over 1 bar, 2 bar and 3 bars respectively
         // & price changes in each row are over different weightings of the applied price with other applied prices
         // so high is: highs only(H); (Highs + Highs + Close)/3 (HHC); and (Highs + Close)/3 (HC)
         // while low is: lows only(L); (Lows + Lows + Close)/3 (LLC); and (Lows + Close)/3 (LC)
         // and close is: closes only(C); (Highs + Lows + Close + Close)/3 (HLCC); and (Highs + Lows + Close)/3 (HLC)
         //
         // assumptions here are:
         // large values in highs mean bullishness
         // large values in lows mean bearishness
         // and small magnitude in close imply a whipsaw market
         matrix _targets[];
         ArrayResize(_targets, __KERNEL_SIZES.Size());
         for(int i = 0; i < int(__KERNEL_SIZES.Size()); i++)
         {  _targets[i].Init(__KERNEL_SIZES[i], __KERNEL_SIZES[i]);
            //
            for(int j = 0; j < __KERNEL_SIZES[i]; j++)
            {  if(i == 0)// highs for 'bullishness'
               {  _targets[i][j][0] = _h[j] - _h[j + 1];
                  _targets[i][j][1] = ((_h[j] + _h[j] + _c[j]) / 3.0) - ((_h[j + 1] + _h[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_h[j] + _c[j]) / 2.0) - ((_h[j + 1] + _c[j + 1]) / 2.0);
               }
               else if(i == 1)// lows for 'bearishness'
               {  _targets[i][j][0] = _l[j] - _l[j + 1];
                  _targets[i][j][1] = ((_l[j] + _l[j] + _c[j]) / 3.0) - ((_l[j + 1] + _l[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_l[j] + _c[j]) / 2.0) - ((_l[j + 1] + _c[j + 1]) / 2.0);
               }
               else if(i == 2)// close for 'whipsaw'
               {  _targets[i][j][0] = _c[j] - _c[j + 1];
                  _targets[i][j][1] = ((_h[j] + _l[j] + _c[j] + _c[j]) / 3.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_h[j] + _l[j] + _c[j]) / 2.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1]) / 2.0);
               }
            }
            //
            //Print(" targets for: "+IntegerToString(i)+" are: \n", _targets[i]);
         }
         CNN.Get(_targets);
         CNN.Evolve(m_learning_rate);
      }
   }
   
        ...

}

Our 3^rdoutput matrix which also logs how flat the markets get after each data point is represented by focusing on the magnitude of close price changes again over different spans and the various lengths of these spans match the sizes used in measuring both the bullishness and bearishness mentioned above. The capturing of this target data on each new bar means our model is training on each new bar, and again this is just one approach since one can choose to have this training done less frequently such as monthly or quarterly as mentioned above.

After each training session though we need to make a forecast on what the bullishness and bearishness outlook will be given the current data point and the part of our code that handles this is shared below:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  
        ...

        ...

   _index = 0;
   _h.CopyRates(m_symbol.Name(), m_period, 2, 0, __KERNEL + 1);
   _l.CopyRates(m_symbol.Name(), m_period, 4, 0, __KERNEL + 1);
   _c.CopyRates(m_symbol.Name(), m_period, 8, 0, __KERNEL + 1);
   for(int i = 0; i < m_input_size; i++)
   {  for(int j = 0; j < m_input_size; j++)
      {  if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, 0, __KERNEL + 1))
         {  _inputs[i][j] = _c[__KERNEL] - _ma[__KERNEL];
            _index++;
         }
      }
   }
   CNN.Set(_inputs);
   CNN.Pad();
   CNN.Convolve();
   CNN.Activate();
   CNN.Pool();
   double _long = 0.0, _short = 0.0;
   if(CNN.output[0].Median() > 0.0)
   {  _long = fabs(CNN.output[0].Median());
   }
   if(CNN.output[1].Median() < 0.0)
   {  _short = fabs(CNN.output[1].Median());
   }
   double _neutral = fabs(CNN.output[2].Median());
   if(_long+_short+_neutral == 0.0)
   {  return(0.0);
   }
   return((_long-_short)/(_long+_short+_neutral));
}

A matrix has a lot of data points, so the best approach that is chosen in getting a sense of bearishness or bullishness from the output matrices is by reading the respective median values of each matrix. So, for the bullish matrix we would like to get a large positive value, while for the bearish matrix we would like a very negative value. For our flat market matrix, we want the magnitude of this median and the smaller it is, the flatter the markets are projected to be.

So, the result of the ‘GetOutput’ function will be a floating-point value that if below 0.5 points to more bearishness ahead or if above 0.5 means we have a bullish outlook. From test runs performed with a single layer CNN of 5 x 5 input matrix with 3 3 x 3 kernels that also uses padding to have output matrices at the size of 3 x 3 for the symbol EURJPY on the daily time frame, we had outputs that were very close to 0.5 value plus or minus. This meant that in this implementation, anything above 0.5 was assigned the 100 value in the long condition function and anything below 0.5 was assigned 100 in the short condition function.

Strategy Tester Reports

The assembled signal class is put together into an Expert Advisor via the MQL5 wizard while following guidelines here and here and on testing on EURJPY for the year 2023 on the daily timeframe we get the following results:

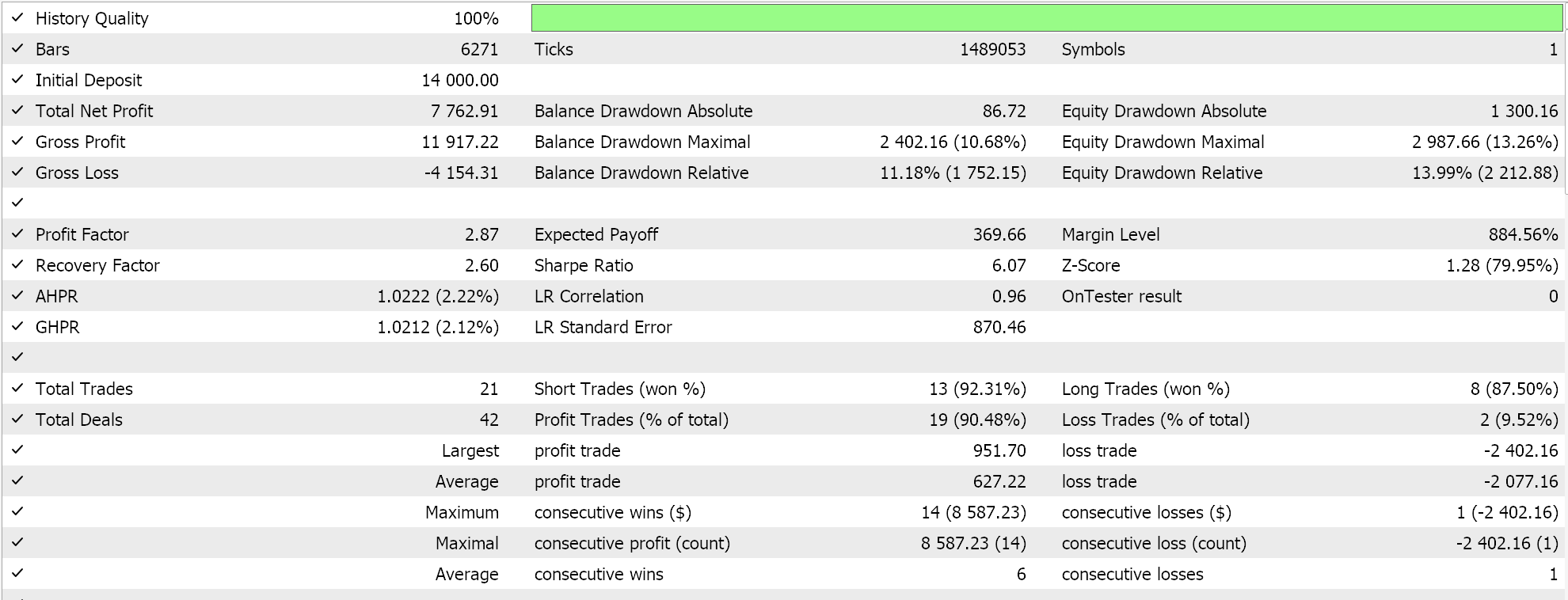
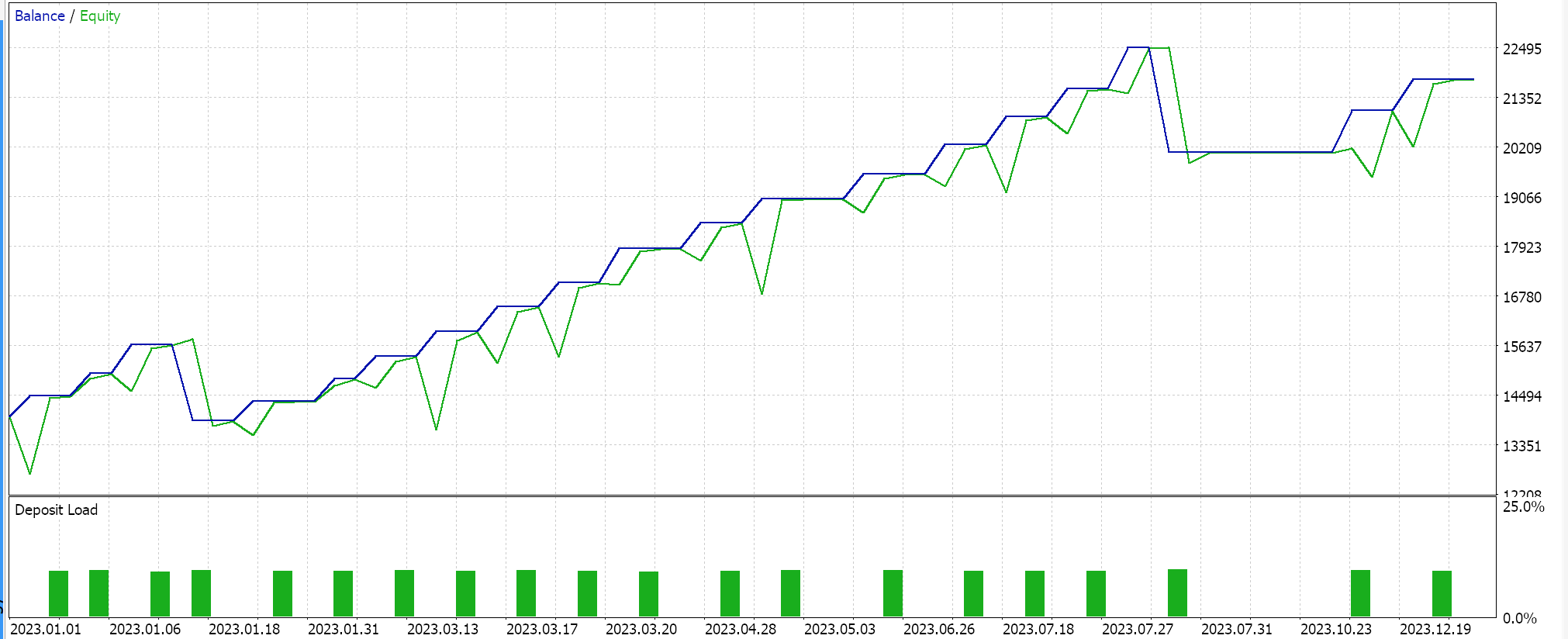
These results are from long and short condition results that are either 0 or 100 since the network output value is not normalized. Trying to normalize the network results should provide a more ‘sensitive’ result, since the open and close thresholds will be open for fine-tuning.

Conclusion

To sum up, we have looked at CNNs, a machine learning algorithm that is often used in image processing, through the lens of a trader. We have examined and coded its key steps of padding, feeding forward, activation, and pooling in an independent MQL5 class file. We have also looked at the training process by delving into CNN back propagation while highlighting the role convolutions play in pairing unequal sized matrices. This article showcased a single layer CNN, so there is a lot of uncovered ground here that the reader can explore not just by stacking this single layer class in a transformer(s) but even by looking at different input data types and target output data sets.

Attached files |

Download ZIP

cnn.mq5 (6.75 KB)

SignalWZ_23_.mqh (12.12 KB)

Ccnn__.mqh (14.55 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.