Características del Wizard MQL5 que debe conocer (Parte 23): Redes neuronales convolucionales (CNNs, Convolutional Neural Networks)

Introducción

Continuamos con esta serie en la que analizamos ideas de aprendizaje automático y estadística que podrían ser beneficiosas para los traders dado el rápido entorno de pruebas y creación de prototipos que ofrece el asistente MQL5. El objetivo sigue siendo ver una sola idea dentro de un artículo y para esta pieza, inicialmente había pensado que esto tomaría al menos 2 artículos, sin embargo parece que somos capaces de exprimirlo en uno. Las redes neuronales convolucionales (CNNs, Convolutional Neural Networks), como su nombre indica, procesan datos multidimensionados en convoluciones gracias a los núcleos.

Estos núcleos contienen los pesos de la red y, al igual que los datos de entrada multidimensionales, suelen estar en formato de matriz. Tienen dimensiones totales más pequeñas en comparación con los datos de entrada y, al iterar sobre la matriz de datos de entrada durante un avance, como veremos más adelante, cada iteración recorre esencialmente los datos de entrada. Es este «ciclo» el que le da el nombre de «convolucional».

Así que para este artículo vamos a tener una introducción a los pasos clave que intervienen en una CNN, construir una simple clase MQL5 que implementa estos pasos, integrar esta clase en una clase de señal personalizada MQL5 asistente, y, finalmente, realizar ejecuciones de prueba con un Asesor Experto que se ensambla a partir de esta clase de señal.

Las CNN suelen ser redes neuronales complejas cuyas principales aplicaciones son el procesamiento de vídeo e imágenes, como vimos con las GAN en el artículo anterior. Sin embargo, a diferencia de las GAN, que se entrenan para distinguir las imágenes reales y los sujetos de las imágenes de las falsificaciones, las CNN tienden a funcionar más como un clasificador en el sentido de que dividen los datos de entrada (que suelen ser píxeles de imágenes) en varios subgrupos de datos en los que cada subgrupo pretende captar una propiedad clave o muy importante de los datos de entrada. Estos subgrupos producidos suelen denominarse mapas de características.

Los pasos necesarios para llegar a estos mapas de características son: relleno, realimentación, activación, agrupación y, finalmente, si la red está entrenada, propagación hacia atrás. A continuación, echamos un vistazo a cada uno de estos pasos con una CNN de una sola capa muy simple. Por capa única queremos decir que los datos de entrada se procesan a través de una sola capa de núcleos. Este no siempre es el caso con las CNN, ya que pueden abarcar muchas capas, de modo que cada uno de los cuatro pasos mencionados anteriormente (relleno, alimentación hacia adelante, activación y agrupamiento) se repite para cada capa. En configuraciones de múltiples capas, la implicación es que para cada mapa de características producido a partir de una capa superior, hay otras propiedades componentes clave que se dividen en nuevos mapas de características más adelante.

Relleno

Esto marca el inicio de una CNN y, independientemente de si este paso en particular está incluido o no, puede ser opcional. Entonces, ¿qué es el relleno? Bueno, como sugiere el nombre, es simplemente la adición de un borde de datos a lo largo de los bordes de los datos de entrada. Básicamente, los datos de entrada se rellenan. Los datos de entrada de recuperación suelen tener más de una dimensión; de hecho, suelen ser bidimensionales, por lo que una representación matricial suele ser apropiada. Las imágenes están formadas por píxeles en un plano XY, por lo que su clasificación con una CNN es sencilla.

Entonces, ¿por qué necesitamos hacer relleno? La necesidad surge de la naturaleza de la convolución con los núcleos durante el paso de avance. Los núcleos, al igual que los datos de entrada, también están en formato matricial. Ellos soportan el peso de la red. Normalmente, una capa tendrá más de un núcleo, ya que cada núcleo es responsable de generar un mapa de características específico.

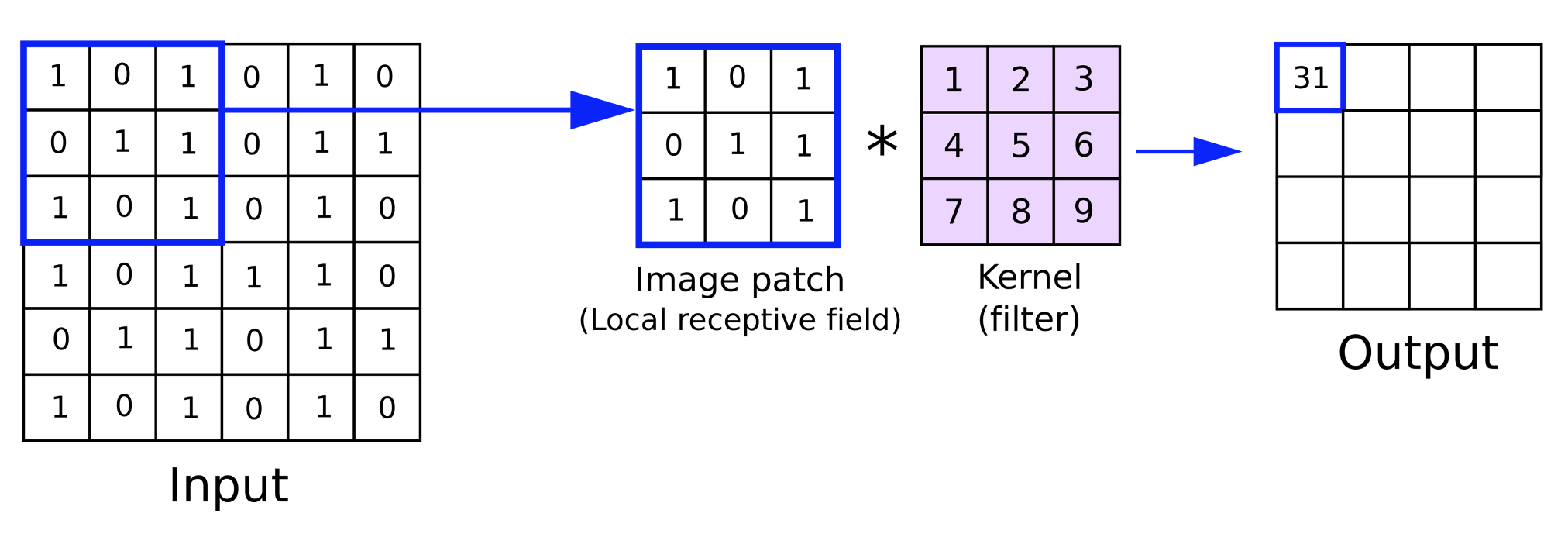
El proceso de multiplicar los pesos en el kernel con los datos de entrada ocurre a lo largo de una iteración o ciclo, o lo que es sinónimo de una convolución. El producto final de esta multiplicación es una matriz de mapas de características cuyas dimensiones son siempre menores que los datos de entrada. Entonces, el objetivo del relleno es que, en el caso de que el usuario quiera que el mapa de características tenga las mismas dimensiones que los datos de entrada sin procesar, se deberán agregar bordes de datos adicionales a los datos de entrada.

Fuente

Para entender esto, si consideramos una matriz de datos de entrada de tamaño 6 x 6 y un núcleo de pesos de tamaño 3 x 3, entonces una multiplicación directa de pesos producirá una matriz de 4 x 4 como se indicó anteriormente. La fórmula para el tamaño de la matriz de salida dado el tamaño de los datos de entrada y el tamaño de la matriz del kernel es:

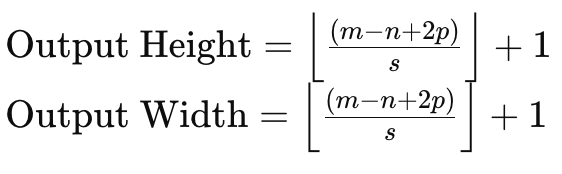
Donde:

• m - Es la dimensión de la matriz de datos de entrada.
• n - Es la dimensión del núcleo de pesos.
• p - Es el tamaño del relleno.
• s - Es el tamaño del paso.

Por lo tanto, si necesitamos mantener el tamaño de una matriz de datos de entrada en los mapas de características, tendríamos que rellenar la matriz de datos de entrada con una cantidad que no sólo tenga en cuenta el tamaño de la matriz de entrada y las matrices del núcleo, sino también la cantidad de stride que se va a utilizar.

Existen principalmente tres métodos de relleno. El primero es el relleno de ceros, donde se agregan 0 a lo largo del borde de la matriz de entrada para que coincida con el ancho requerido. La segunda forma de relleno es el relleno de borde, donde los números en el borde de la matriz se repiten a lo largo del nuevo borde también para que coincidan con el nuevo tamaño objetivo. Y, por último, está el relleno reflejado, donde los números en el nuevo borde ampliado se obtienen desde dentro de la matriz de datos de entrada, con los números a lo largo de su borde actuando como una línea de espejo.

<

Fuente

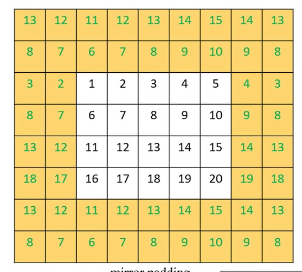
Una vez completado el relleno, se puede llevar a cabo el paso de avance. Sin embargo, este relleno, como se mencionó, es opcional, ya que si el usuario no requiere mapas de características de tamaño coincidente, se puede omitir por completo. Por ejemplo, consideremos una situación en la que una CNN debe examinar muchas imágenes y extraer fotografías de rostros humanos dentro de esas imágenes.

Inevitablemente, el mapa de características o las imágenes de salida de cada iteración tendrán menos píxeles y, por lo tanto, dimensiones que la imagen de entrada, por lo que en este caso podría no tener sentido realizar un relleno o ampliación inicial de la imagen de entrada. Implementamos el relleno a través de este listado:

//+------------------------------------------------------------------+
//| Pad                                                              |
//+------------------------------------------------------------------+
void Ccnn::Pad()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   if(padding != PADDING_NONE)
   {  matrix _padded;
      _padded.Init(inputs.Rows() + 2, inputs.Cols() + 2);
      _padded.Fill(0.0);
      for(int i = 0; i < int(_padded.Cols()); i++)
      {  for(int j = 0; j < int(_padded.Rows()); j++)
         {  if(i == 0 || i == int(_padded.Cols()) - 1 || j == 0 || j == int(_padded.Rows()) - 1)
            {  if(padding == PADDING_ZERO)
               {  _padded[j][i] = 0.0;
               }
               else if(padding == PADDING_EDGE)
               {  if(i == 0 && j == 0)
                  {  _padded[j][i] = inputs[0][0];
                  }
                  else if(i == 0 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][0];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == 0)
                  {  _padded[j][i] = inputs[0][inputs.Cols() - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][inputs.Cols() - 1];
                  }
                  else if(i == 0)
                  {  _padded[j][i] = inputs[j - 1][i];
                  }
                  else if(j == 0)
                  {  _padded[j][i] = inputs[j][i - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1)
                  {  _padded[j][i] = inputs[j - 1][inputs.Cols() - 1];
                  }
                  else if(j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][i - 1];
                  }
               }
               else if(padding == PADDING_REFLECT)
               {  if(i == 0 && j == 0)
                  {  _padded[j][i] = inputs[1][1];
                  }
                  else if(i == 0 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][1];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == 0)
                  {  _padded[j][i] = inputs[1][inputs.Cols() - 2];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][inputs.Cols() - 2];
                  }
                  else if(i == 0)
                  {  _padded[j][i] = inputs[j - 1][1];
                  }
                  else if(j == 0)
                  {  _padded[j][i] = inputs[1][i - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1)
                  {  _padded[j][i] = inputs[j - 1][inputs.Cols() - 2];
                  }
                  else if(j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][i - 1];
                  }
               }
            }
            else
            {  _padded[j][i] = inputs[j - 1][i - 1];
            }
         }
      }
      //
      Set(_padded, false);
   }
}

Para nuestros propósitos como comerciantes y no como científicos de imágenes, tendremos una matriz de datos de entrada de valores de indicadores. Estos valores de indicador se pueden personalizar con una amplia variedad de opciones, sin embargo, hemos seleccionado brechas de precios cerradas de varios indicadores de promedio móvil.

Realimentación hacia adelante (Convoluciónar)

Una vez preparados los datos de entrada, se realiza una multiplicación de pesos en los datos de entrada de cada núcleo de la capa para producir un mapa de características. Además de la multiplicación de los pesos, que produce una matriz de menor tamaño, se agrega un sesgo a cada valor de la matriz y este sesgo, al igual que los pesos respectivos, es único para cada kernel.

Cada núcleo tiene pesos y sesgos que se especializan en extraer una característica o propiedad clave de los datos de entrada. Por lo tanto, cuantas más características le interese a uno recolectar, más núcleos empleará dentro de la red. La realimentación hacia adelante se realiza mediante la función 'Convolve', y este listado se proporciona aquí:

//+------------------------------------------------------------------+
//| Convolve through all kernels                                     |
//+------------------------------------------------------------------+
void Ccnn::Convolve()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
// Loop through kernel at set padding_stride
   for (int f = 0; f < kernels; f++)
   {  bool _stop = false;
      int _stride_row = 0, _stride_col = 0;
      output[f].Fill(0.0);
      for (int g = 0; g < int(output[f].Cols()); g++)
      {  for (int h = 0; h < int(output[f].Rows()); h++)
         {  for (int i = 0; i < int(kernel[f].weights.Cols()); i++)
            {  for (int j = 0; j < int(kernel[f].weights.Rows()); j++)
               {  output[f][h][g] += (kernel[f].weights[j][i] * inputs[_stride_row + j][_stride_col + i]);
               }
            }
            output[f][h][g] += kernel[f].bias;
            _stride_col += padding_stride;
            if(_stride_col + int(kernel[f].weights.Cols()) > int(inputs.Cols()))
            {  _stride_col = 0;
               _stride_row += padding_stride;
               if(_stride_row + int(kernel[f].weights.Rows()) > int(inputs.Rows()))
               {  _stride_col = 0;
                  _stride_row = 0;
               }
            }
         }
      }
   }
}

Activación

Después de la convolución, las matrices producidas se activarían de forma muy similar a la activación en las percepciones multicapa típicas. Sin embargo, en el procesamiento de imágenes el propósito más común de la activación es introducir dentro de un modelo la capacidad de mapear datos no lineales de modo que también se puedan capturar relaciones más complejas (por ejemplo, ecuaciones cuadráticas). Los algoritmos de activación comunes son ReLU, ReLU con fugas, Sigmoid y Tanh.

Se podría decir que ReLU es el algoritmo de activación más popular que se usa habitualmente, ya que maneja mucho mejor los problemas de gradiente evanescente, sin embargo, enfrenta un problema de neuronas muertas que se soluciona con el ReLU con fugas. Una neurona muerta se refiere a situaciones en las que las salidas de la red se actualizan a valores constantes independientemente de los cambios en las entradas. Esto puede ser un gran problema en redes que se inicializan con pesos y se proporcionan entradas negativas, luego se obtendrán salidas estáticas independientemente de la variabilidad de las entradas negativas. Esto podría ocurrir incluso a través del entrenamiento, lo que inevitablemente conduciría a pesos deformados. Esto supondría una pérdida de capacidad de representación, lo que haría que el modelo no pudiera representar patrones más complejos. En la retropropagación, el flujo de gradientes a través de la red ocurriría con una convergencia más lenta o incluso un estancamiento completo.

Por lo tanto, el ReLU con fugas mitiga esto en parte al permitir que se asigne un valor positivo pequeño y optimizable denominado "alfa" como una pendiente pequeña para entradas negativas, de modo que las neuronas con valores negativos no mueran sino que sigan contribuyendo al proceso de aprendizaje. Un flujo de gradiente más suave en la propagación hacia atrás también conduce a un proceso de entrenamiento más estable y eficiente que el ReLU típico.

Agrupamiento

Después de que se activan las imágenes características, que son los resultados de la convolución, se examinan para detectar ruido en un proceso conocido como agrupamiento. La agrupación es el proceso de reducir las dimensiones de los mapas de características, en altura y ancho. El objetivo de la agrupación es reducir la carga computacional y disminuir la cantidad de parámetros con los que la red tiene que lidiar. La agrupación también ayuda con la invariancia de la traducción al poder detectar propiedades clave de cada mapa de características con datos mínimos.

Existen predominantemente tres tipos de agrupación, a saber: agrupación máxima, agrupación promedio y agrupación global. La agrupación máxima elige el valor máximo en cada parche de la matriz de características en un punto de convolución. Y cada uno de los puntos elegidos se reúne en una nueva matriz, que será la matriz agrupada. Sus defensores argumentan que preserva la mayoría de las propiedades críticas del mapa de características agrupadas y al mismo tiempo reduce la probabilidad de sobreajuste.

La agrupación promedio calcula el valor promedio de cada parche durante la convolución y, al igual que con la agrupación máxima, lo devuelve a la matriz agrupada. El tamaño de la matriz agrupada está influenciado no solo por el tamaño de la ventana de agrupación y su diferencia de tamaño con respecto al mapa de características, sino también por el paso de agrupación. Los pasos de agrupación se utilizan a menudo con un valor superior a 1, lo que inevitablemente hace que la matriz agrupada sea significativamente más pequeña que el mapa de características. Para este artículo, dado que queremos mantener las cosas simples ya que asumimos que este artículo es una introducción a CNN, estamos usando un paso agrupado de uno. Los defensores de la agrupación promedio afirman que es más matizada y menos agresiva que la agrupación máxima y, por lo tanto, es menos probable que pase por alto características críticas al realizar la agrupación.

El 3^tercer tipo de agrupación que se utiliza a menudo en las CNN es la agrupación global. En este tipo de agrupamiento no se realizan convoluciones, sino que todo el mapa de características se reduce a un único valor tomando el promedio del mapa de características o seleccionando su máximo. Es un tipo de agrupamiento que podría aplicarse en la capa final de CNN multicapa, donde se apunta a un único valor para cada núcleo.

El tamaño de la ventana de agrupación y el tamaño del paso de agrupación son determinantes principales del tamaño de los datos agrupados. Los pasos más grandes tienden a dar como resultado datos agrupados más pequeños, mientras que, por otro lado, el tamaño del mapa de características y el tamaño de la ventana de agrupación están inversamente relacionados. Los tamaños de datos agrupados más pequeños reducen significativamente las activaciones de red y los requisitos de memoria. Nuestra agrupación se implementa en MQL5 de la siguiente manera:

//+------------------------------------------------------------------+
//| Pool                                                             |
//+------------------------------------------------------------------+
void Ccnn::Pool()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   if(pooling != POOLING_NONE)
   {  for(int f = 0; f < int(output.Size()); f++)
      {  matrix _pooled;
         if(output[f].Cols() > 2 && output[f].Rows() > 2)
         {  _pooled.Init(output[f].Rows() - 2, output[f].Cols() - 2);
            _pooled.Fill(0.0);
            for (int g = 0; g < int(_pooled.Cols()); g++)
            {  for (int h = 0; h < int(_pooled.Rows()); h++)
               {  if(pooling == POOLING_MAX)
                  {  _pooled[h][g] = DBL_MIN;
                  }
                  for (int i = 0; i < int(output[f].Cols()); i++)
                  {  for (int j = 0; j < int(output[f].Rows()); j++)
                     {  if(pooling == POOLING_MAX)
                        {  _pooled[h][g] = fmax(output[f][j][i], _pooled[h][g]);
                        }
                        else if(pooling == POOLING_AVERAGE)
                        {  _pooled[h][g] += output[f][j][i];
                        }
                     }
                  }
                  if(pooling == POOLING_AVERAGE)
                  {  _pooled[h][g] /= double(output[f].Cols()) * double(output[f].Rows());
                  }
               }
            }
            output[f].Copy(_pooled);
         }
      }
   }
}

Retropropagación (Evolucionar)

La retropropagación, como en cualquier red neuronal, es la etapa en la que los pesos y sesgos de la red “aprenden” ajustándose. Se realiza durante el proceso de entrenamiento, y la frecuencia de este entrenamiento estará determinada por el modelo empleado. En el caso de los modelos financieros utilizados por los comerciantes, algunos modelos pueden programarse para entrenar sus redes una vez al trimestre, por ejemplo, para ajustarse a las últimas noticias sobre las ganancias de la empresa, mientras que otros podrían hacer su entrenamiento una vez al mes en fechas posteriores a los comunicados de noticias clave del calendario económico. El punto aquí es que sí, es importante tener los pesos y sesgos de red correctos, pero quizás lo sea más tener un régimen preestablecido claro para entrenar y actualizar estos pesos y sesgos.

¿Existen redes que podrían utilizar un solo entrenamiento y ser utilizadas posteriormente sin preocuparse por las necesidades de entrenamiento? Sí, esto es posible, aunque no probable en muchos escenarios. Por lo tanto, lo prudente es tener siempre un calendario de entrenamiento de red si uno pretende operar con una red neuronal.

Por lo tanto, los pasos típicos involucrados en cualquier propagación hacia atrás son siempre tres, a saber: calcular el error, usar este delta de error para calcular los gradientes y luego usar estos gradientes para actualizar los pesos y los sesgos. Realizamos estos tres pasos en nuestra función 'Evolve', cuyo código se comparte a continuación:

//+------------------------------------------------------------------+
//| Evolve pass through the neural network to update kernel          |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Ccnn::Evolve(double LearningRate = 0.05)
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   
   for(int f = 0; f < kernels; f++)
   {  matrix _output_error = target[f] - output[f];
      // Calculate output layer gradients
      matrix _output_gradients;
      _output_gradients.Init(output[f].Rows(),output[f].Cols());
      for (int g = 0; g < int(output[f].Rows()); g++)
      {  for (int h = 0; h < int(output[f].Cols()); h++)
         {  _output_gradients[g][h] =  LeakyReLUDerivative(output[f][g][h]) * _output_error[g][h];
         }
      }
      
      // Update output layer kernel weights and biases
      int _stride_row = 0, _stride_col = 0;
      for (int g = 0; g < int(output[f].Cols()); g++)
      {  for (int h = 0; h < int(output[f].Rows()); h++)
         {  double _bias_sum = 0.0;
            for (int i = 0; i < int(kernel[f].weights.Cols()); i++)
            {  for (int j = 0; j < int(kernel[f].weights.Rows()); j++)
               {  kernel[f].weights[j][i] += (LearningRate * _output_gradients[_stride_row + j][_stride_col + i]); // output[f][_stride_row + j][_stride_col + i]);
                  _bias_sum += _output_gradients[_stride_row + j][_stride_col + i];
               }
            }
            kernel[f].bias += LearningRate * _bias_sum;
            _stride_col += padding_stride;
            if(_stride_col + int(kernel[f].weights.Cols()) > int(_output_gradients.Cols()))
            {  _stride_col = 0;
               _stride_row += padding_stride;
               if(_stride_row + int(kernel[f].weights.Rows()) > int(_output_gradients.Rows()))
               {  _stride_col = 0;
                  _stride_row = 0;
               }
            }
         }
      }
   }
}

Nuestras salidas al final son matrices y debido a esto los deltas de error seguramente se capturarán también en formato de matriz. Una vez que tenemos estos deltas de error, debemos ajustarlos para su producto de activación porque antes de llegar a esta capa final estaban activados. Y la forma en que se realiza este ajuste por activación es multiplicando los deltas de error por la derivada de la función de activación.

También tenga en cuenta que, aunque los errores de salida y los gradientes de salida están en forma de matriz, este proceso debe repetirse para cada núcleo. Es por eso que hemos envuelto cada una de estas operaciones en otro bucle for global cuyo indexador es el entero 'f' y cuyo tamaño máximo nunca excede el número de núcleos. Nuestras matrices de salida, para la clase CNN de prueba que mostramos en este artículo, son tres. Proporcionan mapas de tendencia alcista, bajista y de fluctuaciones variables para el valor cuyas brechas de precios con los diversos promedios móviles se proporcionaron como entradas en la CNN. Estas diferencias de precios también están en forma de matriz.

Debido a que los valores de error de salida y de gradiente de salida están en forma de matriz y se han agrupado en un paso anterior ya destacado anteriormente, sus tamaños no coinciden con los tamaños de ponderación de la matriz del kernel. Esto presenta inicialmente un desafío a la hora de determinar cómo utilizar los gradientes para ajustar los pesos del kernel. Sin embargo, la solución es bastante simple porque sigue el enfoque de convoluciones que aplicamos en el avance, donde las matrices de peso del núcleo de tamaños diferentes de la matriz de datos de entrada (y su relleno) se multiplicaron en ciclos de modo que en cada punto se sumó un único valor de todos los productos del núcleo en la ventana en foco y se colocaron en la matriz de salida.

Esto se realiza con pasos y nuestro paso para esta prueba es solo uno, ya que debe coincidir con el paso utilizado en el avance. Sin embargo, actualizar los sesgos es un poco complicado porque son solo un valor único; no obstante, la solución siempre es sumar los gradientes en la matriz y multiplicar esta suma con el sesgo anterior (después de ajustarlo con una tasa de aprendizaje).

Integración en una clase de señal

Para utilizar nuestra clase CNN dentro de una señal personalizada, esencialmente tendríamos que definir dos cosas. En primer lugar, qué forma de datos de entrada vamos a utilizar y, en segundo lugar, el tipo de datos de destino que esperamos en las matrices de salida. Las respuestas a ambas preguntas ya se han insinuado anteriormente, ya que los datos de entrada son brechas de precios entre el precio de cierre actual y muchos valores de precios promedio móviles (25 por defecto). Los numerosos promedios móviles se distinguen por su período de promedio móvil único, y los completamos en la matriz de entrada a través de la función 'GetOutput' como se destaca a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  int _index = 5;
   matrix _inputs;
   vector _ma, _h, _l, _c;
   _inputs.Init(m_input_size, m_input_size);
   for(int g = 0; g < m_epochs; g++)
   {  for(int h = m_train_set - 1; h >= 0; h--)
      {  _inputs.Fill(0.0);
         _index = 0;
         for(int i = 0; i < m_input_size; i++)
         {  for(int j = 0; j < m_input_size; j++)
            {  if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, h, __KERNEL + 1))
               {  _inputs[i][j] = _c[0] - _ma[0];
                  _index++;
               }
            }
         }
         //
         
        ...

      }
   }

        ...
   
        ...

}

Lo que no es tan sencillo son los datos objetivo en nuestras matrices de salida. Como se mencionó anteriormente, queremos obtener mapas de tendencia alcista o bajista. Y para simplificar, deberían haber sido solo estos dos (y no incluir una medida para determinar si los mercados están estables), pero el lector puede modificar el código fuente para abordar esto. Sin embargo, la manera de medir esto es observando la acción del precio posterior a cada punto de datos de entrada. Nuevamente, nuestro punto de datos toma lecturas de indicadores para los cuales hemos elegido cerrar brechas de precios en una serie de precios promedio móviles, pero esto se puede personalizar fácilmente según sus preferencias.

Ahora, nuestra medida elegida de optimismo que queremos capturar en una matriz en lugar de un valor único serán los cambios en el precio alto en diferentes períodos. De la misma manera, para capturar un posible pesimismo después de registrar un punto de datos, registramos los cambios en los precios bajos durante diferentes períodos en una matriz. Esto está codificado como se muestra a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  
   ...

   for(int g = 0; g < m_epochs; g++)
   {  for(int h = m_train_set - 1; h >= 0; h--)
      {  _inputs.Fill(0.0);
         _index = 0;
         
        ...

         //
         _h.CopyRates(m_symbol.Name(), m_period, 2, h, __KERNEL + 1);
         _l.CopyRates(m_symbol.Name(), m_period, 4, h, __KERNEL + 1);
         _c.CopyRates(m_symbol.Name(), m_period, 8, h, __KERNEL + 1);
         //Print(" inputs are: \n", _inputs);
         CNN.Set(_inputs);
         CNN.Pad();
         //Print(" padded inputs are: \n", CNN.inputs);
         CNN.Convolve();
         CNN.Activate();
         CNN.Pool();
         // targets as eventual price changes with each matrix a proxy for bullishness, bearishness, or whipsaw action
         // implying matrices for eventual:
         // high price changes
         // low price changes
         // close price changes,
         // respectively
         //
         // price changes in each column are over 1 bar, 2 bar and 3 bars respectively
         // & price changes in each row are over different weightings of the applied price with other applied prices
         // so high is: highs only(H); (Highs + Highs + Close)/3 (HHC); and (Highs + Close)/3 (HC)
         // while low is: lows only(L); (Lows + Lows + Close)/3 (LLC); and (Lows + Close)/3 (LC)
         // and close is: closes only(C); (Highs + Lows + Close + Close)/3 (HLCC); and (Highs + Lows + Close)/3 (HLC)
         //
         // assumptions here are:
         // large values in highs mean bullishness
         // large values in lows mean bearishness
         // and small magnitude in close imply a whipsaw market
         matrix _targets[];
         ArrayResize(_targets, __KERNEL_SIZES.Size());
         for(int i = 0; i < int(__KERNEL_SIZES.Size()); i++)
         {  _targets[i].Init(__KERNEL_SIZES[i], __KERNEL_SIZES[i]);
            //
            for(int j = 0; j < __KERNEL_SIZES[i]; j++)
            {  if(i == 0)// highs for 'bullishness'
               {  _targets[i][j][0] = _h[j] - _h[j + 1];
                  _targets[i][j][1] = ((_h[j] + _h[j] + _c[j]) / 3.0) - ((_h[j + 1] + _h[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_h[j] + _c[j]) / 2.0) - ((_h[j + 1] + _c[j + 1]) / 2.0);
               }
               else if(i == 1)// lows for 'bearishness'
               {  _targets[i][j][0] = _l[j] - _l[j + 1];
                  _targets[i][j][1] = ((_l[j] + _l[j] + _c[j]) / 3.0) - ((_l[j + 1] + _l[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_l[j] + _c[j]) / 2.0) - ((_l[j + 1] + _c[j + 1]) / 2.0);
               }
               else if(i == 2)// close for 'whipsaw'
               {  _targets[i][j][0] = _c[j] - _c[j + 1];
                  _targets[i][j][1] = ((_h[j] + _l[j] + _c[j] + _c[j]) / 3.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_h[j] + _l[j] + _c[j]) / 2.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1]) / 2.0);
               }
            }
            //
            //Print(" targets for: "+IntegerToString(i)+" are: \n", _targets[i]);
         }
         CNN.Get(_targets);
         CNN.Evolve(m_learning_rate);
      }
   }
   
        ...

}

Nuestra 3^a matriz de salida que también registra qué tan planos se vuelven los mercados después de cada punto de datos, se representa centrándose en la magnitud de los cambios de precios de cierre nuevamente en diferentes períodos y las diversas longitudes de estos períodos coinciden con los tamaños utilizados para medir tanto el optimismo como el pesimismo mencionados anteriormente. La captura de estos datos objetivo en cada nueva barra significa que nuestro modelo se entrena en cada nueva barra y, nuevamente, este es solo un enfoque, ya que uno puede elegir que este entrenamiento se realice con menor frecuencia, como mensualmente o trimestralmente, como se mencionó anteriormente.

Sin embargo, después de cada sesión de entrenamiento debemos hacer un pronóstico sobre cuál será la perspectiva alcista o bajista dado el punto de datos actual y la parte de nuestro código que maneja esto se comparte a continuación:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  
        ...

        ...

   _index = 0;
   _h.CopyRates(m_symbol.Name(), m_period, 2, 0, __KERNEL + 1);
   _l.CopyRates(m_symbol.Name(), m_period, 4, 0, __KERNEL + 1);
   _c.CopyRates(m_symbol.Name(), m_period, 8, 0, __KERNEL + 1);
   for(int i = 0; i < m_input_size; i++)
   {  for(int j = 0; j < m_input_size; j++)
      {  if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, 0, __KERNEL + 1))
         {  _inputs[i][j] = _c[__KERNEL] - _ma[__KERNEL];
            _index++;
         }
      }
   }
   CNN.Set(_inputs);
   CNN.Pad();
   CNN.Convolve();
   CNN.Activate();
   CNN.Pool();
   double _long = 0.0, _short = 0.0;
   if(CNN.output[0].Median() > 0.0)
   {  _long = fabs(CNN.output[0].Median());
   }
   if(CNN.output[1].Median() < 0.0)
   {  _short = fabs(CNN.output[1].Median());
   }
   double _neutral = fabs(CNN.output[2].Median());
   if(_long+_short+_neutral == 0.0)
   {  return(0.0);
   }
   return((_long-_short)/(_long+_short+_neutral));
}

Una matriz tiene muchos puntos de datos, por lo que el mejor enfoque elegido para obtener una idea de tendencia bajista o alcista de las matrices de salida es leer los respectivos valores medianos de cada matriz. Entonces, para la matriz alcista nos gustaría obtener un valor positivo grande, mientras que para la matriz bajista nos gustaría un valor muy negativo. Para nuestra matriz de mercado plana, queremos la magnitud de esta mediana y cuanto más pequeña sea, más planos se proyecta que serán los mercados.

Entonces, el resultado de la función 'GetOutput' será un valor de punto flotante que, si es inferior a 0,5, indica que habrá más pesimismo en el futuro y, si es superior a 0,5, significa que tenemos una perspectiva alcista. A partir de ejecuciones de prueba realizadas con una CNN de una sola capa de matriz de entrada de 5 x 5 con 3 núcleos de 3 x 3 que también usa relleno para tener matrices de salida de tamaño 3 x 3 para el símbolo EURJPY en el marco de tiempo diario, obtuvimos salidas que estaban muy cerca del valor 0,5 más o menos. Esto significaba que en esta implementación, a cualquier valor superior a 0,5 se le asignaba el valor 100 en la función de condición larga y a cualquier valor inferior a 0,5 se le asignaba el valor 100 en la función de condición corta.

Informes del Probador de estrategias

La clase de señal ensamblada se junta en un Asesor Experto a través del asistente MQL5 mientras se siguen las directrices aquí y aquí y al probar en EURJPY para el año 2023 en el marco de tiempo diario obtenemos los siguientes resultados:

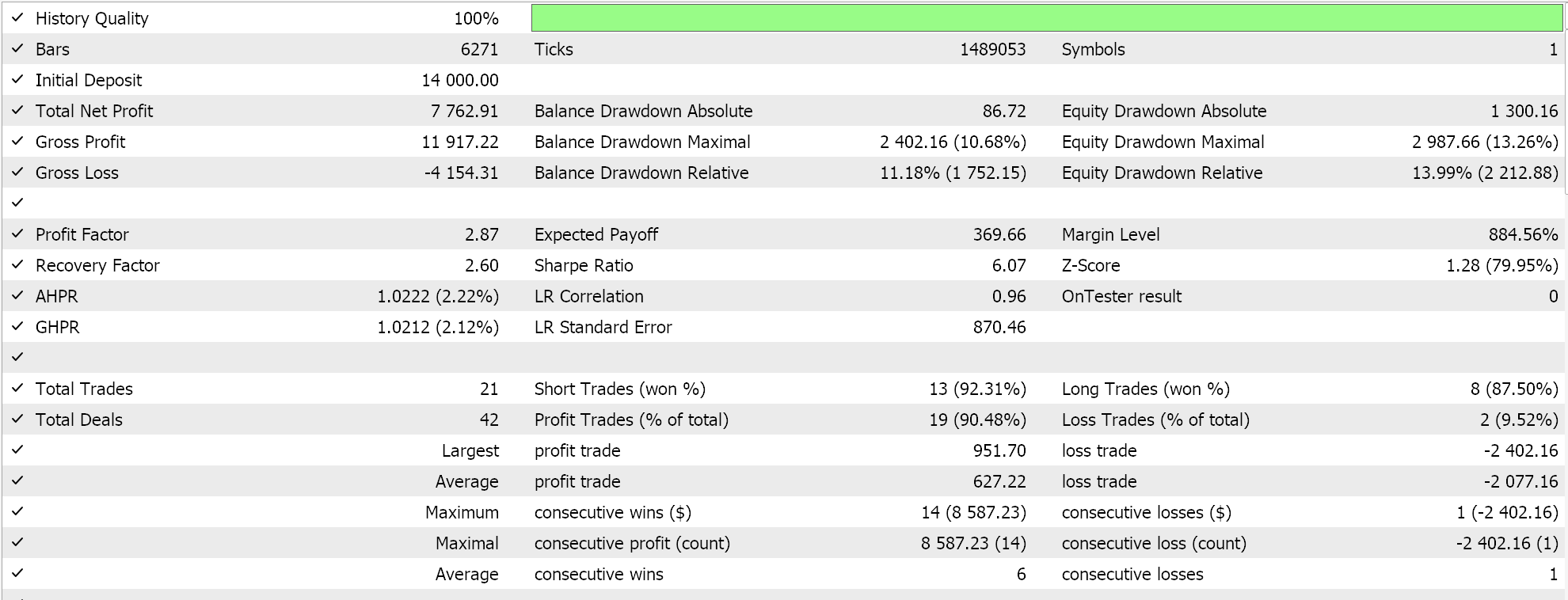
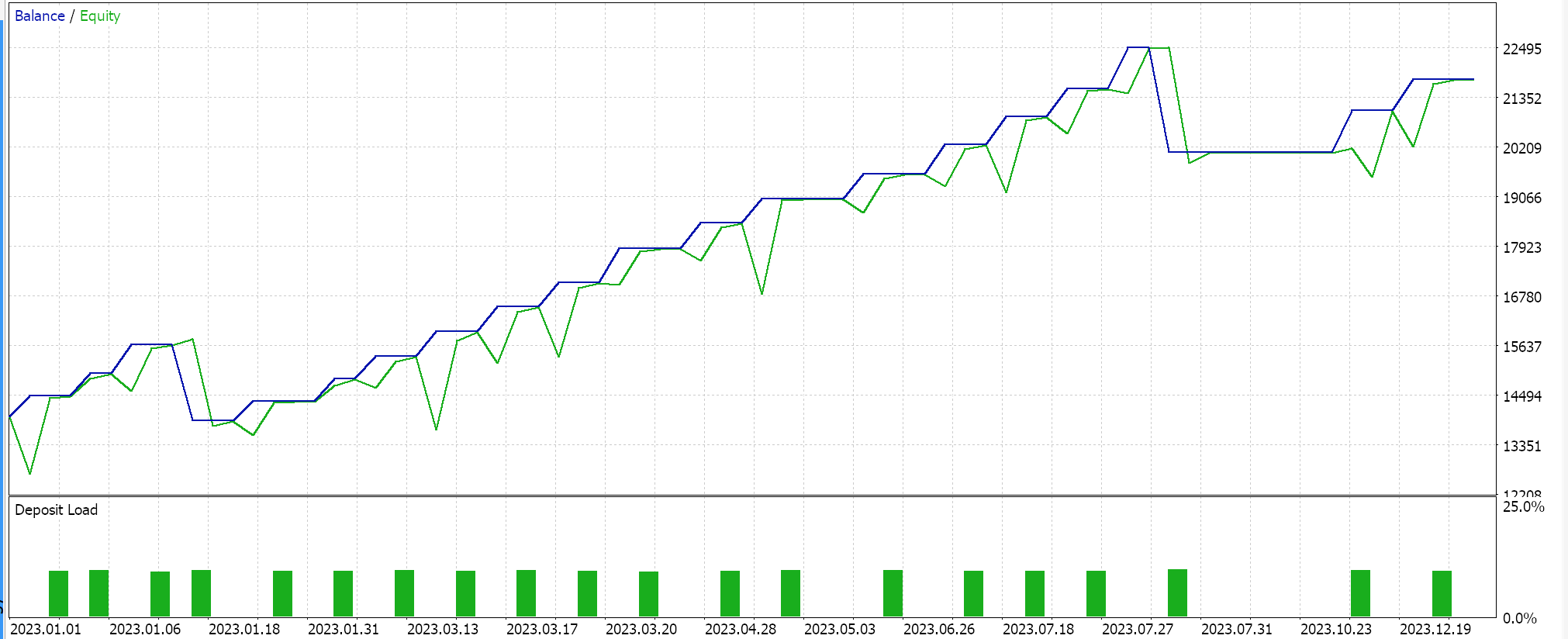
Estos resultados proceden de condiciones largas y cortas que son 0 ó 100, ya que el valor de salida de la red no está normalizado. Intentar normalizar los resultados de la red debería proporcionar un resultado más «sensible», ya que los umbrales de apertura y cierre podrán ajustarse con precisión.

Conclusión

En resumen, hemos analizado las CNN, un algoritmo de aprendizaje automático que se utiliza a menudo en el procesamiento de imágenes, a través de la lente de un comerciante. Hemos examinado y codificado sus pasos clave de relleno, avance, activación y agrupación en un archivo de clase MQL5 independiente. También hemos examinado el proceso de entrenamiento profundizando en la retropropagación de la CNN y destacando el papel que desempeñan las convoluciones a la hora de emparejar matrices de tamaño desigual. En este artículo se ha mostrado una CNN de una sola capa, por lo que hay mucho terreno sin cubrir aquí que el lector puede explorar no sólo apilando esta clase de una sola capa en un transformador(es), sino incluso examinando diferentes tipos de datos de entrada y conjuntos de datos de salida de destino.