您应当知道的 MQL5 向导技术（第 23 部分）：CNNs
227
3
概述
我们继续本系列，在其中看看机器学习和统计的思路，鉴于 MQL5 向导提供的快速测试和原型设计环境，令交易者能从中受益。目标仍然是在一篇文章内考察单一思路，至于这段节选，我最初认为这至少需要 2 个篇幅，不过看起来我们能够将其压缩到一个篇幅。卷积神经网络（CNN）顾名思义，借助内核，它可以在卷积中处理多维数据。
这些内核承载网络权重，且像多维输入数据一样，都采用典型的矩阵格式。与输入数据相比，它们的整体维度较小，并且在前馈期间遍历输入数据矩阵，正如我们将在下面看到，每次迭代本质上都是跨输入数据轮转。正是这个“轮转”赋予了“卷积”这个名字。
是故对于本文，我们将讲述 CNN 中涉及的关键步骤，构建一个简单的 MQL5 类来实现这些步骤，将该类集成到自定义的 MQL5 向导信号类当中，最后会配以由该信号类组装而成的智能系统执行测试。
CNN 典型情况下是复数神经网络，其主要应用是视频和图像处理，就像我们在上一篇文章中看到的 GAN 一样。然而，不同于经训练的 GAN，能从假造中识别真实图像和/或图像中的主题，CNN 的工作方式更倾向于是一个分类器，因为它们将输入数据（往往是图像像素）拆分为各种数据子集，其中每个子集旨在捕获输入数据的关键、或非常重要的属性。这些生成的子集往往称为特征映射。
通往这些特征映射所涉及的步骤是：填充、前馈、激活、池化，以及最后如果网络经过训练，则为反向传播。我们用一个非常简单的单层 CNN 来窥视下面的每个步骤。单层是指输入数据经由内核的单层进行处理。CNN 并非总是如此，因为它们可以跨越许多层，如此这般上述 4 个步骤（填充、前馈、激活、和池化）的每一步都会在每一层重复。在多层设定中，这意味着对于从较高层生成的每个特征映射，还有其它关键分量属性于内，在接下来的过程中会被拆分为新的特征映射。
填充
这标志着 CNN 的开始，且是否要包含该特定步骤，都可以是可选的。那么，什么是填充呢？嗯，顾名思义，它就是简单地沿着输入数据的边缘添加数据边界。实质上，输入数据得以填充。回调输入数据通常会有更多维度，实际上它往往是 2-维的，这就是为什么矩阵表示通常是合适的。图像由 XY 平面中的像素组成，故以 CNN 进行图像分类直截了当。
那么为什么我们需要做填充呢？需求源于前馈步骤期间，依据内核的卷积性质。内核，像是输入数据，也采用矩阵格式。它们承载网络的权重。典型情况，一个层会有多于一个的内核，因为每个内核负责输出特定的特征映射。
内核中的权重与输入数据相乘的过程发生在一次迭代、或轮次中，或与卷积同义。这种乘法的最终产物是一个特征映射矩阵，其维度始终小于输入数据。故此，填充的重点是如果用户希望特征映射与原始输入数据具有相同的维度，那么需要在输入数据中添加额外的数据边界。
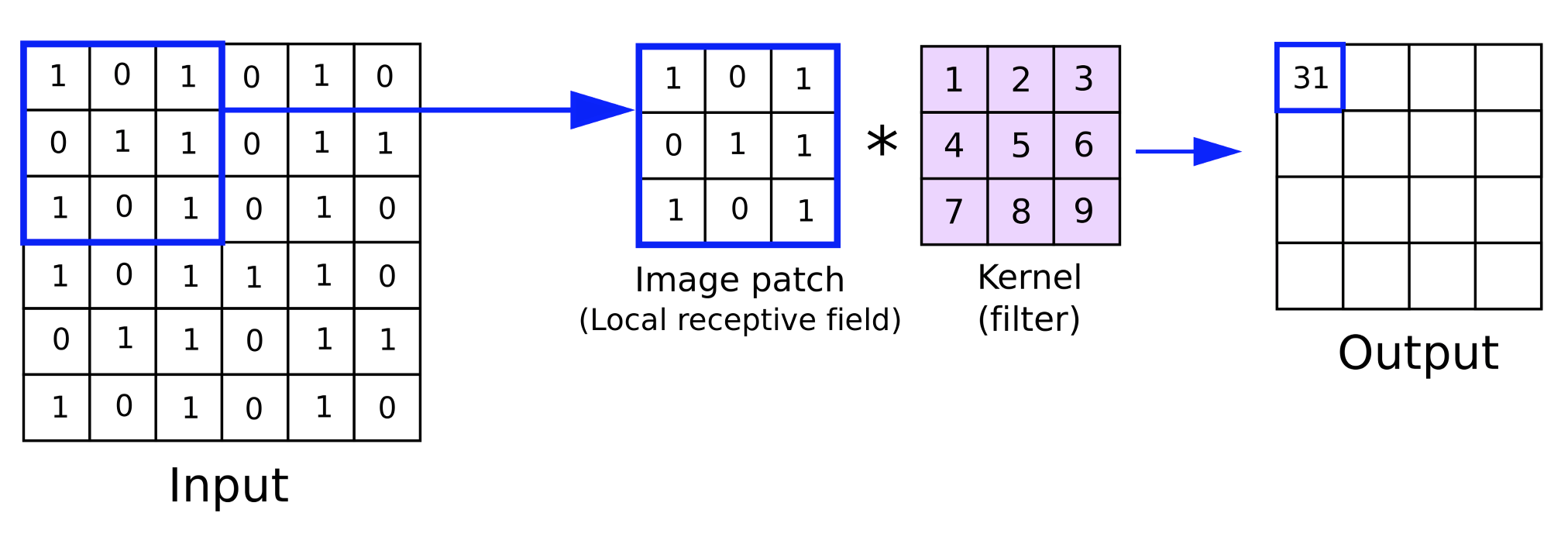
为了理解这一点，如果我们参照一个大小为 6 x 6 的输入数据矩阵，和一个大小为 3 x 3 的权重内核，那么直接权重乘法将产生一个 4 x 4 矩阵，如上所述。给定输入数据大小和内核矩阵大小的输出矩阵大小的公式为：
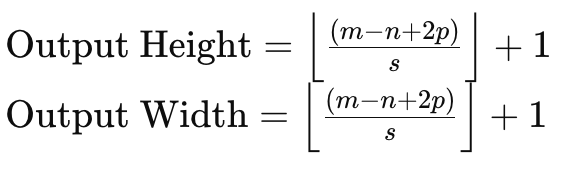
其中：
- m 是输入数据矩阵的维度，
- n 是权重内核的维度，
- p 是填充大小，
- 且 s 是步幅大小。
因此，如果我们需要在特征映射中维持输入数据矩阵的大小，我们需要往输入数据矩阵填充一定量，该量不仅要考虑输入矩阵和内核矩阵的大小，还要考虑所用的步幅量。
这主要有 3 种填充方法。第一种是填充零，其中沿输入矩阵的边界添加 0，以便匹配所需的宽度。第二种形式是边缘填充，其中矩阵边缘上的数字沿新边界重复，以便匹配新的目标尺度。最后，有反射填充，其中放大的新边界上的数字来自输入数据矩阵内部，沿其边界的数字充当镜像线。
< 
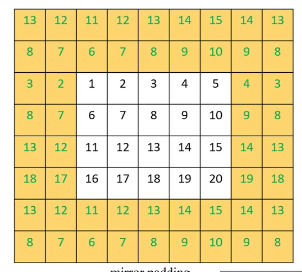
一旦填充完成，就可以运作前馈步骤。诚然，如前所述，该填充是可选的，因为如果用户不需要匹配特征映射的大小，则可统统跳过。举例，参照这样一种情形：CNN 旨在梳理许多图像，并从这些图像中提取人脸照片。
不可避免地，每次迭代的特征映射、或输出图像的像素和尺寸都比输入图像少，故在这种情况下，对输入图像进行初始填充、或放大可能没有意义。我们通过该清单实现了填充：
//+------------------------------------------------------------------+ //| Pad | //+------------------------------------------------------------------+ void Ccnn::Pad() { if(!validated) { printf(__FUNCSIG__ + " network invalid! "); return; } if(padding != PADDING_NONE) { matrix _padded; _padded.Init(inputs.Rows() + 2, inputs.Cols() + 2); _padded.Fill(0.0); for(int i = 0; i < int(_padded.Cols()); i++) { for(int j = 0; j < int(_padded.Rows()); j++) { if(i == 0 || i == int(_padded.Cols()) - 1 || j == 0 || j == int(_padded.Rows()) - 1) { if(padding == PADDING_ZERO) { _padded[j][i] = 0.0; } else if(padding == PADDING_EDGE) { if(i == 0 && j == 0) { _padded[j][i] = inputs[0][0]; } else if(i == 0 && j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 1][0]; } else if(i == int(_padded.Cols()) - 1 && j == 0) { _padded[j][i] = inputs[0][inputs.Cols() - 1]; } else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 1][inputs.Cols() - 1]; } else if(i == 0) { _padded[j][i] = inputs[j - 1][i]; } else if(j == 0) { _padded[j][i] = inputs[j][i - 1]; } else if(i == int(_padded.Cols()) - 1) { _padded[j][i] = inputs[j - 1][inputs.Cols() - 1]; } else if(j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 1][i - 1]; } } else if(padding == PADDING_REFLECT) { if(i == 0 && j == 0) { _padded[j][i] = inputs[1][1]; } else if(i == 0 && j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 2][1]; } else if(i == int(_padded.Cols()) - 1 && j == 0) { _padded[j][i] = inputs[1][inputs.Cols() - 2]; } else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 2][inputs.Cols() - 2]; } else if(i == 0) { _padded[j][i] = inputs[j - 1][1]; } else if(j == 0) { _padded[j][i] = inputs[1][i - 1]; } else if(i == int(_padded.Cols()) - 1) { _padded[j][i] = inputs[j - 1][inputs.Cols() - 2]; } else if(j == int(_padded.Rows()) - 1) { _padded[j][i] = inputs[inputs.Rows() - 2][i - 1]; } } } else { _padded[j][i] = inputs[j - 1][i - 1]; } } } // Set(_padded, false); } }
出于我们的目的，是当一名交易者，而非图像科学家，我们将得到一个指标值的输入数据矩阵。这些指标值可按宽泛的选项自定义，不过我们已从多种移动平均线指标中选择了收盘价缺口。
前馈（卷积）
一旦输入数据准备就绪，将跨层针对每个内核的输入数据执行权重乘法，从而生成特征映射。除了权重的乘法产生较小大小的矩阵外，还会向每个矩阵值添加一个偏差，就像各自的权重一样，对于每个内核都是唯一的。
每个内核都有权重和偏差，专门提取输入数据的关键特征、或属性。故此，收获中感兴趣的特征越多，他能在网络内使用的内核就越多。前馈由 'Convolve' 函数执行，此处给出了该清单：
//+------------------------------------------------------------------+ //| Convolve through all kernels | //+------------------------------------------------------------------+ void Ccnn::Convolve() { if(!validated) { printf(__FUNCSIG__ + " network invalid! "); return; } // Loop through kernel at set padding_stride for (int f = 0; f < kernels; f++) { bool _stop = false; int _stride_row = 0, _stride_col = 0; output[f].Fill(0.0); for (int g = 0; g < int(output[f].Cols()); g++) { for (int h = 0; h < int(output[f].Rows()); h++) { for (int i = 0; i < int(kernel[f].weights.Cols()); i++) { for (int j = 0; j < int(kernel[f].weights.Rows()); j++) { output[f][h][g] += (kernel[f].weights[j][i] * inputs[_stride_row + j][_stride_col + i]); } } output[f][h][g] += kernel[f].bias; _stride_col += padding_stride; if(_stride_col + int(kernel[f].weights.Cols()) > int(inputs.Cols())) { _stride_col = 0; _stride_row += padding_stride; if(_stride_row + int(kernel[f].weights.Rows()) > int(inputs.Rows())) { _stride_col = 0; _stride_row = 0; } } } } } }
激活
卷积之后，产生的矩阵将被激活，很像典型的多层感知中的激活一样。但在图像处理中，激活的最常见目的是在模型内引入映射非线性数据的能力，从而可以捕获更复杂的关系（例如二次方程）。常见的激活算法包括 ReLU、leaky ReLU、Sigmoid 和 Tanh。
ReLU 可以说是最流行的典型激活算法，因为它在处理梯度消失问题时更佳，但它也面临着一个死神经元问题，可由泄漏 ReLU 来补救。死神经元是指与输入变化无关，网络输出都会更新为常量值的情形。这在配以权重、及提供负值输入的网络中可能是件大事，然后无论负值输入如何变化，都将获得静态输出。甚至可经由训练来实现，而这不可避免地会导致权重翘曲。这将是表示能力的损失，这令模型无法表示更复杂的形态。在反向传播中，经由网络的梯度流，会发生较慢的收敛，甚至彻底停滞。
因此，泄漏 ReLU 能部分缓解这种情况，通过允许分配一个小型的、可优化的、标记为 'alpha' 的正值，作为负值输入的小斜率，如此这般具有负值的神经元就不会死亡，但对于学习过程仍有贡献。与典型的 ReLU 相比，反向传播中更平滑的梯度流也会导致更稳定、更高效的训练过程。
池化
激活特征图像之后，其是卷积的输出，它们会在称为池化的过程中筛选出噪声。池化是从高度和宽度降低特征映射维度的过程。池化的要点是降低计算负载，并减少网络必须与之纠缠的参数数量。池化还有助于传递不变性，因为它能够依据最少的数据来检测每个特征映射的关键属性。
主要有 3 种类型的池化，即：最大池化、平均池化、和全局池化。最大池化选择卷积点处每个特征矩阵补片中的最大值。每个选定的点都被汇集到一个新的矩阵当中，其将成为池化矩阵。其支持者认为，它保留了池化特征映射的大部分紧要属性，同时降低了过拟合的似然性。
平均池化计算卷积期间每个补片的平均值，且像最大池化一样，将其返回到池化的矩阵。池化矩阵的大小不仅受池化窗口大小、及其与特征映射的大小差异的影响，还受池化步幅的影响。池化步幅通常与大于 1 的值一起使用，这不可避免地会令池化矩阵明显小于特征映射。至于本文，由于我们想保持事情简单，是故我们假设这篇文章只是 CNN 的概论，所以我们选用的池化步幅为一。平均池化的支持者声称，它比最大池化更细致、更低的激进度，因此在池化时不太可能忽视紧要特征。
CNN 中经常使用的第三种池化类型是全局池化。在这种池化类型中，不执行卷积，取而代之的是通过取特征映射的平均值、或选择其最大值，将整个特征映射降低到单一值。这是一种池化，能被应用于多层 CNN 的最后一层，其中每个内核都对准一个单个值。
池化窗口大小和池化步幅大小是池化数据大小的主要决定因素。较大的步幅往往会导致较小的池化数据，而另一方面，特征映射大小和池化窗口大小成反比。较小的池化数据大小可显著降低网络激活和内存需求。我们的池化以 MQL5 实现如下：
//+------------------------------------------------------------------+ //| Pool | //+------------------------------------------------------------------+ void Ccnn::Pool() { if(!validated) { printf(__FUNCSIG__ + " network invalid! "); return; } if(pooling != POOLING_NONE) { for(int f = 0; f < int(output.Size()); f++) { matrix _pooled; if(output[f].Cols() > 2 && output[f].Rows() > 2) { _pooled.Init(output[f].Rows() - 2, output[f].Cols() - 2); _pooled.Fill(0.0); for (int g = 0; g < int(_pooled.Cols()); g++) { for (int h = 0; h < int(_pooled.Rows()); h++) { if(pooling == POOLING_MAX) { _pooled[h][g] = DBL_MIN; } for (int i = 0; i < int(output[f].Cols()); i++) { for (int j = 0; j < int(output[f].Rows()); j++) { if(pooling == POOLING_MAX) { _pooled[h][g] = fmax(output[f][j][i], _pooled[h][g]); } else if(pooling == POOLING_AVERAGE) { _pooled[h][g] += output[f][j][i]; } } } if(pooling == POOLING_AVERAGE) { _pooled[h][g] /= double(output[f].Cols()) * double(output[f].Rows()); } } } output[f].Copy(_pooled); } } } }
反向传播 （演化）
像在任何神经网络中一样，反向传播是网络权重和乖离边学习边调整的阶段。它是在训练过程期间执行的，这种训练的频率必然由所采用的模型决定。对于交易者所用的金融模型，一些模型的网络能由编程定为每季度训练一次，譬如说根据最新披露的公司收益公报进行调整，而其它的可能再每月关键财经日历新闻发布后的日子进行一次训练。此处的重点是，没错，拥有正确的网络权重和乖离很重要，但也许更重要的是有一个明确的预设机制来训练和更新这些权重和乖离。
是否有网络能只用单次训练，就能在以后反复实用，且无需担心训练需求？是的，这是可能的，尽管在许多场景下不太可能。故此，如果打算运用神经网络进行交易，谨慎的做法是始终准备一份网络训练日历。
故此，任何反向传播所涉及的典型步骤总是 3 步，即：计算误差，并用该误差增量求出梯度，然后使用这些梯度来更新权重和乖离。我们在 'Evolve' 函数中执行所有这三个步骤，其代码分享如下：
//+------------------------------------------------------------------+ //| Evolve pass through the neural network to update kernel | //| and biases using gradient descent | //+------------------------------------------------------------------+ void Ccnn::Evolve(double LearningRate = 0.05) { if(!validated) { printf(__FUNCSIG__ + " network invalid! "); return; } for(int f = 0; f < kernels; f++) { matrix _output_error = target[f] - output[f]; // Calculate output layer gradients matrix _output_gradients; _output_gradients.Init(output[f].Rows(),output[f].Cols()); for (int g = 0; g < int(output[f].Rows()); g++) { for (int h = 0; h < int(output[f].Cols()); h++) { _output_gradients[g][h] = LeakyReLUDerivative(output[f][g][h]) * _output_error[g][h]; } } // Update output layer kernel weights and biases int _stride_row = 0, _stride_col = 0; for (int g = 0; g < int(output[f].Cols()); g++) { for (int h = 0; h < int(output[f].Rows()); h++) { double _bias_sum = 0.0; for (int i = 0; i < int(kernel[f].weights.Cols()); i++) { for (int j = 0; j < int(kernel[f].weights.Rows()); j++) { kernel[f].weights[j][i] += (LearningRate * _output_gradients[_stride_row + j][_stride_col + i]); // output[f][_stride_row + j][_stride_col + i]); _bias_sum += _output_gradients[_stride_row + j][_stride_col + i]; } } kernel[f].bias += LearningRate * _bias_sum; _stride_col += padding_stride; if(_stride_col + int(kernel[f].weights.Cols()) > int(_output_gradients.Cols())) { _stride_col = 0; _stride_row += padding_stride; if(_stride_row + int(kernel[f].weights.Rows()) > int(_output_gradients.Rows())) { _stride_col = 0; _stride_row = 0; } } } } } }
在最后我们的输出是矩阵，这是因为误差增量也必然会以矩阵格式捕获。一旦我们得到这些误差增量，我们就需要针对它们的激活产物调整它们，因为在到达最后一层之前，它们已被激活了。这种针对激活的调整如何执行，这是将误差增量乘以激活函数的导数。
还要留意，即使输出误差和输出梯度都是矩阵形式，仍需要针对每个内核重复该过程。这就是为什么我们把这样的每个操作封装在另一个总体的 for-loop 循环之中，它的索引器是整数 'f'，并且最大尺度永远不会超过内核计数。对于我们在本文中展示的测试 CNN 类，我们的输出矩阵数量为 3。它们为证券提供了看涨、看跌、和窄幅震荡的映射，这些证券的价格与各种移动平均线的间隙作为 CNN 的输入提供。这些价格间隙也以矩阵形式存在。
由于输出误差和输出梯度值采用矩阵形式，并且已在上面高亮显示的上一步中池化，故它们的大小与内核矩阵权重大小并不匹配。这是判定如何使用梯度来调整内核权重时最先遇到的挑战。诚然，解决方案非常简单，因为它遵循我们在前馈中应用的卷积方式，其中内核权重矩阵大小不同于输入数据矩阵（及其填充）的会在循环中相乘，如此在每个点上从聚焦窗口上的所有内核产物中汇总出一个值，并将它们放置在输出矩阵之中。
这是按步幅执行的，至于该测试我们的步幅仅为一，在于它应当与前馈中所用的步幅相匹配。虽然更新乖离有点棘手，因为它们只是一个值，尽管如此，解决方案始终是将矩阵中的梯度相加，并将该总和乘以旧的乖离（按学习率进行调整后）。
集成到信号类中
为了在自定义信号中运用 CNN 类，我们实质上要定义 2 件事。首先，我们将采用什么形式的输入数据，其次是我们在输出矩阵中预期的目标数据类型。这两个问题的答案在上面已经暗示过，因为输入数据是当前收盘价、及许多（默认为 25）移动平均值之间的价格间隙。众多移动平均线按其独特的移动平均线周期来区分，我们调用 'GetOutput' 函数将它们填充到输入矩阵之中，如下所示：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalCNN::GetOutput() { int _index = 5; matrix _inputs; vector _ma, _h, _l, _c; _inputs.Init(m_input_size, m_input_size); for(int g = 0; g < m_epochs; g++) { for(int h = m_train_set - 1; h >= 0; h--) { _inputs.Fill(0.0); _index = 0; for(int i = 0; i < m_input_size; i++) { for(int j = 0; j < m_input_size; j++) { if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, h, __KERNEL + 1)) { _inputs[i][j] = _c[0] - _ma[0]; _index++; } } } // ... } } ... ... }
不那么直接了当的是输出矩阵中的目标数据。如上所述，我们想要获取看涨或看跌的映射。为简单起见，它们应当只是这两个（不包括衡量市场是否为横盘），但读者可以修改源代码来搞定它。不过，我们如何衡量这一点，是通过查看每个输入数据点的后期价格行为。再次，我们的数据点是取我们所选的指标读数、与收盘价格的间隙，放入一个移动平均价格的数组，但这可依您的喜好轻松定制。
现在我们选择衡量看涨，我们想要在矩阵中捕获，相较于单一值，这将是不同跨度内最高价的变化。同样，为了在记录数据点后捕捉最终的看跌情绪，我们把覆盖不同跨度的最低价变化记录到一个矩阵当中。其代码如下所示：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalCNN::GetOutput() { ... for(int g = 0; g < m_epochs; g++) { for(int h = m_train_set - 1; h >= 0; h--) { _inputs.Fill(0.0); _index = 0; ... // _h.CopyRates(m_symbol.Name(), m_period, 2, h, __KERNEL + 1); _l.CopyRates(m_symbol.Name(), m_period, 4, h, __KERNEL + 1); _c.CopyRates(m_symbol.Name(), m_period, 8, h, __KERNEL + 1); //Print(" inputs are: \n", _inputs); CNN.Set(_inputs); CNN.Pad(); //Print(" padded inputs are: \n", CNN.inputs); CNN.Convolve(); CNN.Activate(); CNN.Pool(); // targets as eventual price changes with each matrix a proxy for bullishness, bearishness, or whipsaw action // implying matrices for eventual: // high price changes // low price changes // close price changes, // respectively // // price changes in each column are over 1 bar, 2 bar and 3 bars respectively // & price changes in each row are over different weightings of the applied price with other applied prices // so high is: highs only(H); (Highs + Highs + Close)/3 (HHC); and (Highs + Close)/3 (HC) // while low is: lows only(L); (Lows + Lows + Close)/3 (LLC); and (Lows + Close)/3 (LC) // and close is: closes only(C); (Highs + Lows + Close + Close)/3 (HLCC); and (Highs + Lows + Close)/3 (HLC) // // assumptions here are: // large values in highs mean bullishness // large values in lows mean bearishness // and small magnitude in close imply a whipsaw market matrix _targets[]; ArrayResize(_targets, __KERNEL_SIZES.Size()); for(int i = 0; i < int(__KERNEL_SIZES.Size()); i++) { _targets[i].Init(__KERNEL_SIZES[i], __KERNEL_SIZES[i]); // for(int j = 0; j < __KERNEL_SIZES[i]; j++) { if(i == 0)// highs for 'bullishness' { _targets[i][j][0] = _h[j] - _h[j + 1]; _targets[i][j][1] = ((_h[j] + _h[j] + _c[j]) / 3.0) - ((_h[j + 1] + _h[j + 1] + _c[j + 1]) / 3.0); _targets[i][j][2] = ((_h[j] + _c[j]) / 2.0) - ((_h[j + 1] + _c[j + 1]) / 2.0); } else if(i == 1)// lows for 'bearishness' { _targets[i][j][0] = _l[j] - _l[j + 1]; _targets[i][j][1] = ((_l[j] + _l[j] + _c[j]) / 3.0) - ((_l[j + 1] + _l[j + 1] + _c[j + 1]) / 3.0); _targets[i][j][2] = ((_l[j] + _c[j]) / 2.0) - ((_l[j + 1] + _c[j + 1]) / 2.0); } else if(i == 2)// close for 'whipsaw' { _targets[i][j][0] = _c[j] - _c[j + 1]; _targets[i][j][1] = ((_h[j] + _l[j] + _c[j] + _c[j]) / 3.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1] + _c[j + 1]) / 3.0); _targets[i][j][2] = ((_h[j] + _l[j] + _c[j]) / 2.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1]) / 2.0); } } // //Print(" targets for: "+IntegerToString(i)+" are: \n", _targets[i]); } CNN.Get(_targets); CNN.Evolve(m_learning_rate); } } ... }
我们的第 3 个输出矩阵还记录了每个数据点之后市场达到的横盘程度，它通过再次关注不同跨度的收盘价变化幅度来表示，这些跨度的不同长度与上述衡量看涨和看跌的大小相匹配。在每根新柱线上捕获该目标数据，意味着我们的模型在每根新柱线上进行训练，再次，这只是一种方式，因为可选择不那么频繁地进行该训练，正如上述，每月或每季度进行一次。
在每次训练时段过后，我们需要做出预测，给出当前数据点看涨和看跌的前景，处理该问题的代码部分如下：
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CSignalCNN::GetOutput() { ... ... _index = 0; _h.CopyRates(m_symbol.Name(), m_period, 2, 0, __KERNEL + 1); _l.CopyRates(m_symbol.Name(), m_period, 4, 0, __KERNEL + 1); _c.CopyRates(m_symbol.Name(), m_period, 8, 0, __KERNEL + 1); for(int i = 0; i < m_input_size; i++) { for(int j = 0; j < m_input_size; j++) { if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, 0, __KERNEL + 1)) { _inputs[i][j] = _c[__KERNEL] - _ma[__KERNEL]; _index++; } } } CNN.Set(_inputs); CNN.Pad(); CNN.Convolve(); CNN.Activate(); CNN.Pool(); double _long = 0.0, _short = 0.0; if(CNN.output[0].Median() > 0.0) { _long = fabs(CNN.output[0].Median()); } if(CNN.output[1].Median() < 0.0) { _short = fabs(CNN.output[1].Median()); } double _neutral = fabs(CNN.output[2].Median()); if(_long+_short+_neutral == 0.0) { return(0.0); } return((_long-_short)/(_long+_short+_neutral)); }
矩阵有很多数据点，故此最佳方式选择是从输出矩阵中读取每个矩阵的相应中值，由此得到看跌或看涨的感觉。故此，对于看涨矩阵，我们希望获得一个较大的正值；而对于看跌矩阵，我们希望获得一个很大的负值。对于我们的横盘市场矩阵，我们希望这个中位数的量级越小，预计市场就越平坦。
故此，'GetOutput' 函数的结果将是一个浮点值，若低于 0.5 是指更多看跌，或者若高于 0.5 则意味着我们得到看涨前景。来自执行的测试运行，单层 CNN 配以 3 个 3 x 3 内核，5 x 5 输入矩阵，还用品种 EURJPY 的日线时间帧填充 3 x 3 大小的输出矩阵，我们的输出非常接近数值 ±0.5。这意味着在该实现中，在做多条件函数中，任何高于 0.5 的值都被赋值 100，而在做空条件函数中，任何低于 0.5 的值都被赋值 100。
策略测试器报告
组装好的信号类经由 MQL5 向导组合到智能交易系统中，同时遵循此处和此处的指南，并依据 EURJPY 的 2023 年日线时间帧数据进行测试，我们得到以下结果：
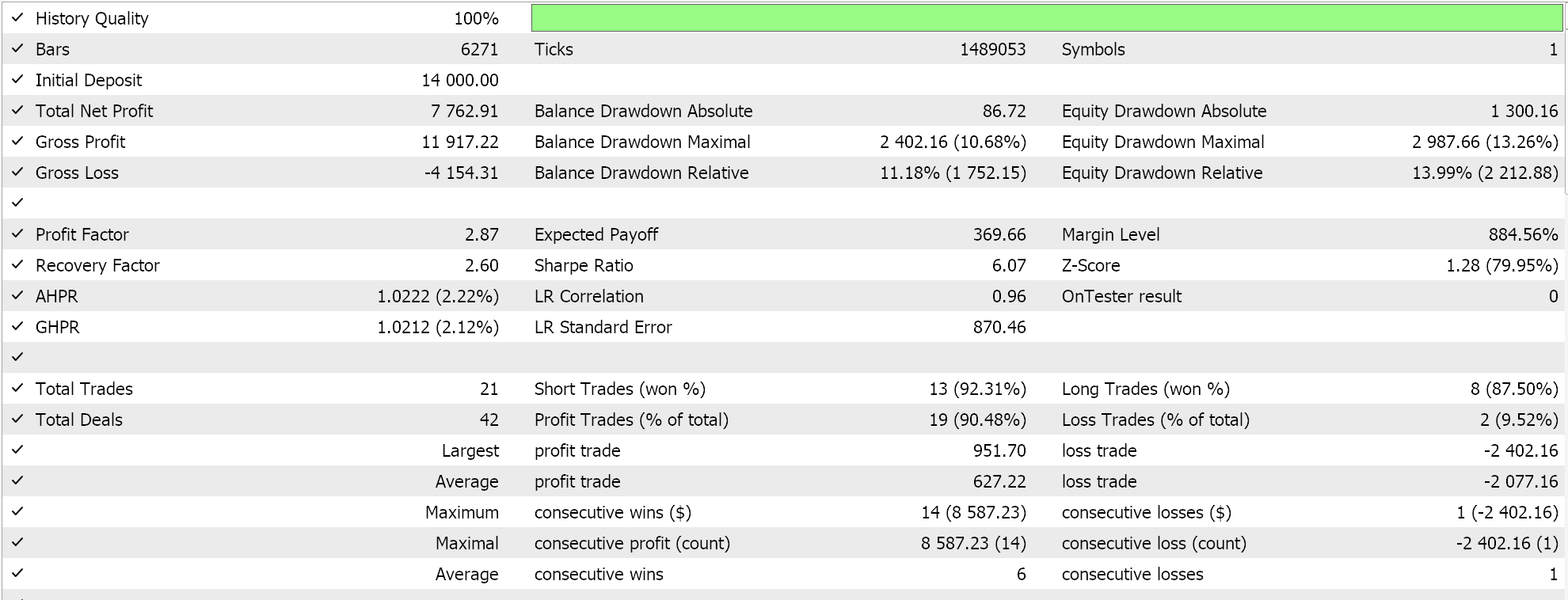
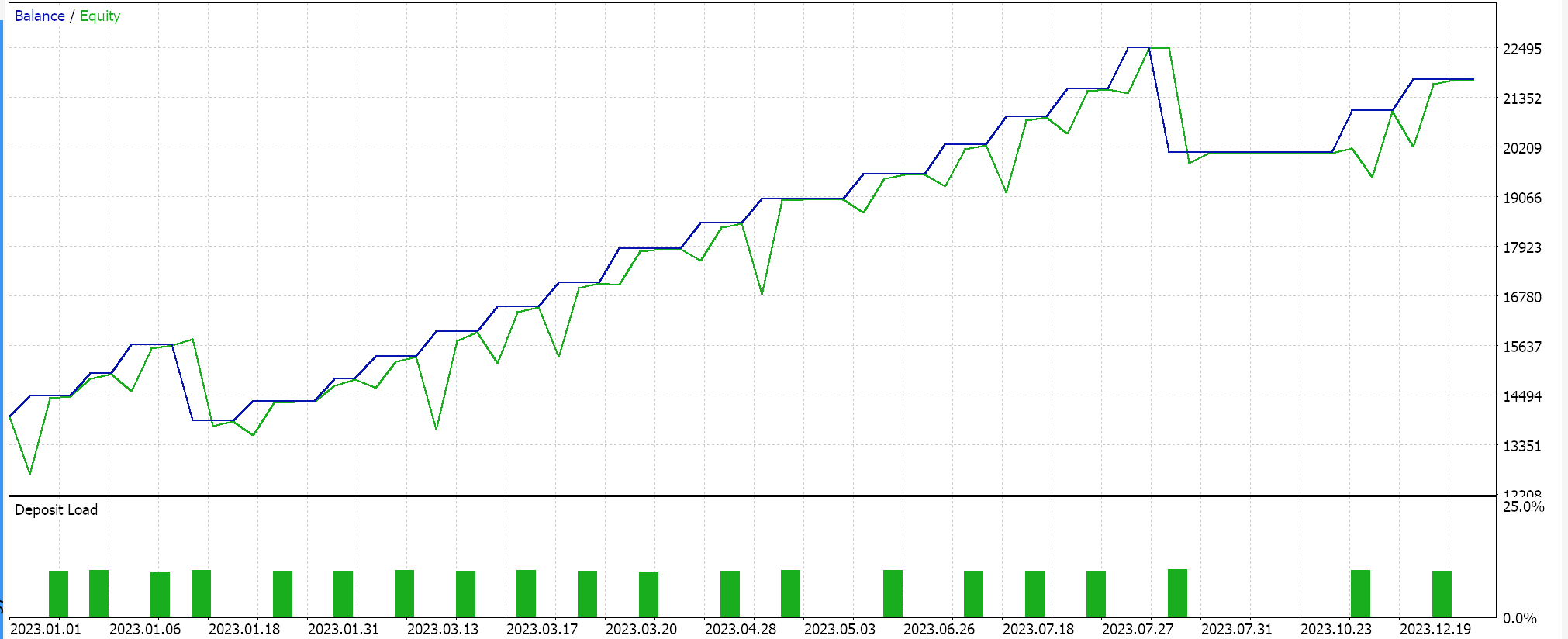
这些结果来自做多和做空条件结果，这些结果为 0 或 100，因为网络输出值未归一化。尝试归一化网络结果应当会提供更“敏感”的结果，因为开仓和平仓阈值都可开放进行优调。
结束语
总而言之，我们从交易员的角度研究了 CNN，这是一种经常用于图像处理的机器学习算法。我们已在一个独立的 MQL5 类文件中检查、并编码了它的关键步骤，即填充、前馈、激活、和池化。我们还通过深入研究 CNN 反向传播来研究训练过程，同时强调卷积在配对大小不等矩阵时的作用。本文展示了单层 CNN，如此这里有很多未发掘的领域，读者不仅可通过将这个单层类堆叠在一个转换器中来探索，甚至还可通过查看不同的输入数据类型、及目标输出数据集来探索。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/15101
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
开发回放系统（第 59 部分）：新的未来
交易中的神经网络：用于时间序列预测的轻量级模型
人工蜂巢算法（ABHA）：理论及方法
由于许多文件丢失而 无法编译，如
//--- 可用拖尾
您好
您提到的文件是 MQL5 IDE 附带的。这里 和这里 有如何使用向导的指南。
感谢您的阅读。