
Нейросети в трейдинге: Вероятностное прогнозирование временных рядов (Энкодер)
Введение
Продолжаем знакомство с фреймворком K²VAE — прогрессивной архитектурой, разработанной специально для моделирования временных рядов в условиях высокой неопределённости. Эта модель строится на синтезе трёх ключевых идей: линейной динамики в латентном пространстве (через операторы Купмана), адаптивной фильтрации ошибок (с помощью KalmanNet) и вероятностного моделирования (на основе вариационных автоэнкодера). Такой подход позволяет одновременно учитывать как закономерности в данных, так и степень доверия к этим закономерностям.
Главное достоинство K²VAE — не просто построение прогноза, а формирование вероятностного распределения будущих состояний системы. В отличие от традиционных моделей, которые ограничиваются одним наиболее вероятным вариантом развития событий, здесь результатом становится диапазон возможных исходов. Причём ширина этого диапазона зависит от степени уверенности модели в текущем состоянии. Это делает фреймворк особенно полезным в сферах, где важно учитывать риски и неопределённость — например, в финансовом прогнозировании, логистике или управлении техническими системами.
Чтобы понять, как достигается такая гибкость и адаптивность, рассмотрим общую архитектуру модели. Конструкцию K²VAE условно можно разделить на три крупных компоненты: Патчинг, Энкодер и Декодер, каждая из которых выполняет свою роль, но при этом тесно связана с другими.
- Патчинг осуществляет подготовку исходных данных и перевод их в латентное представление.
- Энкодер — отвечает за извлечение скрытого состояния Z из наблюдаемых временных рядов X. В отличие от стандартных VAE, здесь используется сложная структура, в которую входят:
- KoopmanNet, обучаемый аналог оператора Купмана, прогнозирующий эволюцию скрытых признаков как линейную систему;
- Модуль внимания, анализирующий различия между восстановленными и фактическими значениями, позволяющий выявлять моменты расхождения модели с реальностью;
- KalmanNet, гибридная нейросетевая реализация фильтра Калмана, формирующая ковариационную матрицу неопределённости на основе управляющих сигналов внимания;
- VAE-механизм, осуществляющий сэмплирование будущих токенов на основе параметров, заданных KalmanNet и KoopmanNet.
- Декодер — преобразует скрытые переменные обратно в наблюдаемые, восстанавливая прогнозируемые значения временного ряда. При этом, для соблюдения вероятностной природы модели, Декодер так же реализован как обучаемая нейросетевая структура с двумя выходами: среднее значение и дисперсия. Это позволяет в полной мере смоделировать распределение P(Y|Z) и учитывать неопределённость прогноза.
Авторская визуализация фреймворка K²VAE представлена ниже.
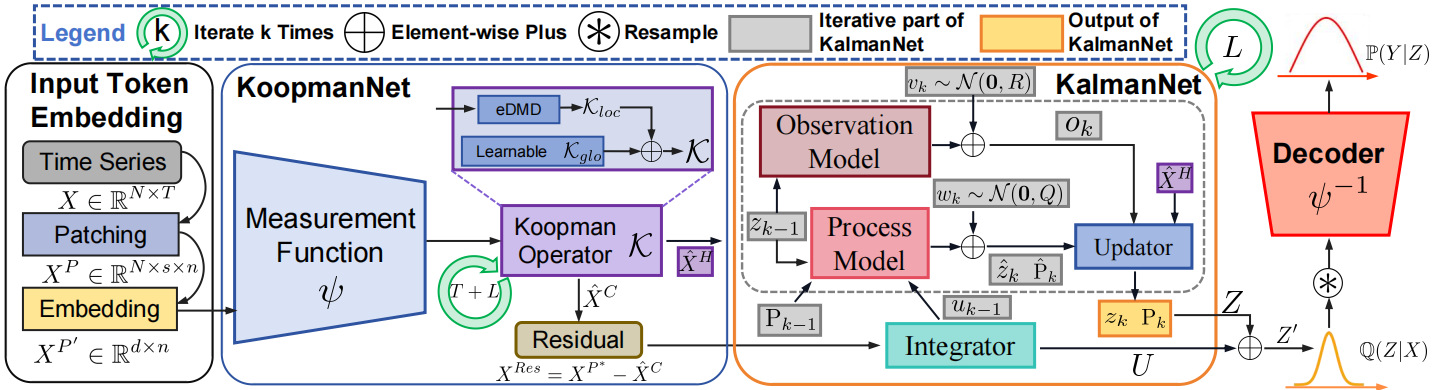
В предыдущей статье мы сосредоточились на подготовительной работе: реализовали базовую инфраструктуру, обеспечили поддержку многократного использования обучаемых матриц и заложили основу для корректной и масштабируемой архитектуры. Были созданы универсальные классы для генерации параметров, отлажен механизм их обновления через стандартные процедуры обратного распространения ошибки, и описана структура, пригодная для дальнейшего наращивания компонентов. Таким образом, мы заложили фундамент, на котором теперь можно строить более сложные модули.
Следующим логическим шагом становится разработка Энкодера, который выполняет критически важную функцию: он преобразует исходные временные ряды в скрытое латентное представление, пригодное для линейного анализа и вероятностного моделирования. Причём реализуется это не через простой набор слоёв, а через тщательно продуманную структуру.
Обсуждение подходов построения
Прежде чем приступить к практической реализации Энкодера средствами языка MQL5, давайте подробно разберёмся с его архитектурным устройством и логикой построения. Это поможет нам не только правильно сориентироваться в дальнейшей работе, но и понять, как каждый модуль вносит вклад в общее поведение модели.
Энкодер, используемый во фреймворке K²VAE, построен по модульному принципу и включает в себя четыре взаимосвязанных компонента, каждый из которых выполняет строго определённую функцию в процессе обработки временного ряда.
Первым элементом в цепочке обработки выступает KoopmanNet — нейросетевая интерпретация оператора Купмана, основная задача которого заключается в аппроксимации линейной динамики во временном ряду. Он принимает на вход скрытое состояние и возвращает прогноз следующего состояния, предполагая, что поведение системы может быть представлено как линейный сдвиг в некотором латентном пространстве. Однако, поскольку реальные временные ряды редко следуют строго линейной траектории, одной только проекции в латентное пространство KoopmanNet недостаточно для надёжного моделирования. Чтобы модель могла не просто воспроизводить тренд, но и оценивать собственную точность, авторы фреймворка предложили весьма оригинальный механизм.
KoopmanNet, помимо прогнозирования следующего состояния, обучается также восстанавливать уже совершённые переходы — по сути, ретроспективно реконструировать траекторию из предшествующих значений временного ряда. Таким образом, модель не ограничивается движением вперёд, но и оглядывается назад, проверяя, насколько её текущие параметры адекватны прошлым наблюдениям. Это двунаправленное мышление позволяет модели вычислить разницу между предполагаемой динамикой и фактическими состояниями системы.
Именно это отклонение (разница между расчетными KoopmanNet переходами и реальными историческими значениями) служит основой для оценки качества линейной аппроксимации. Таким образом, модель получает способность к самодиагностике и может динамически подстраиваться к изменениям или нестабильностям, не теряя связи с линейной структурой, лежащей в её основе.
В оригинальной реализации фреймворка K²VAE модуль KoopmanNet состоит из двух отдельных небольших полносвязных моделей (MLP), каждая из которых моделирует свой аспект переходов в скрытом пространстве: одна отвечает за глобальные зависимости, вторая — за локальные. Такой подход вполне логичен с теоретической точки зрения, но на практике может оказаться излишне жёстким и ограниченным — особенно в условиях нестабильных рыночных данных.
Мы предлагаем усилить KoopmanNet за счёт использования более универсального и гибкого блока разреженной смеси экспертов — CNeuronTimeMoESparseExperts. Это модуль из фреймворка TimeMoE, реализующий принцип Mixture of Experts (MoE) — механизма, при котором множество специализированных подмоделей (экспертов) работают параллельно, а управляющий механизм выбирает наиболее подходящего в зависимости от исходного контекста.
Блок разреженной смеси экспертов не просто техническая реализация — это логическая основа для разделения локальных и глобальных закономерностей, присутствующих в финансовых временных рядах. Внутри этого блока работают два типа экспертов. Первый — это группа специализированных, локальных экспертов, каждый из которых отвечает за распознавание короткосрочных переходов и контекстно-зависимых паттернов. Эти эксперты, по сути, анализируют поведение рынка в ограниченных временных интервалах, адаптируясь к текущей волатильности и микротрендам.
Второй — глобальный эксперт. Он встроен в структуру CNeuronTimeMoESparseExperts и выполняет роль обобщающего линейного оператора Купмана. Его задача — фиксировать устойчивую, долгосрочную динамику временного ряда, вычленяя те закономерности, которые сохраняются на протяжении всего обучающего окна. Таким образом, модель получает двойной взгляд на данные: детальный локальный анализ и широкую стратегическую перспективу.
Такая архитектура позволяет KoopmanNet не только прогнозировать следующее состояние, но и восстанавливать предшествующую траекторию, реконструируя серию переходов, которые привели к текущему положению. Сравнение восстановленных переходов с фактическими значениями даёт системе возможность оценить точность собственной аппроксимации.
После того как KoopmanNet завершает реконструкцию динамики и прогнозирует следующий шаг, в работу вступает модуль внимания, задача которого — не просто сравнить фактические и смоделированные значения, а проанализировать непосредственно отклонения между ними. В отличие от традиционного механизма кросс-внимания, где сравниваются два потока данных, здесь внимание сосредотачивается исключительно на тензоре ошибок, выявляя в нём повторяющиеся структуры и закономерности.
Авторы фреймворка K²VAE предлагают рассматривать эти отклонения не как побочный продукт, а в качестве полноценного источника информации. Идея заключается в том, что сами ошибки содержат сигнал: они указывают, где и насколько KoopmanNet справляется с описанием системы, и какие локальные особенности динамики остаются вне поля зрения линейной модели. Внимание позволяет извлечь из этих ошибок тензор управляющих сигналов, своего рода инструкцию для корректировки прогнозов на следующем этапе.
Таким образом, вместо простого сопоставления прогнозов с фактами, модель учится осмысленно интерпретировать свои слабости. И именно этот подход лежит в основе высокой адаптивности и интеллектуальности K²VAE, позволяя ему эффективно работать в условиях изменяющейся нестабильной среды.
В рамках предлагаемой реализации мы можем использовать один из уже проверенных на практике модулей Self-Attention, ранее успешно применявшихся для анализа временных рядов. Это не только значительно ускоряет процесс разработки, но и гарантирует совместимость с остальными компонентами фреймворка. Такой модуль способен выявлять внутренние закономерности в структуре ошибок, фиксируя повторяющиеся шаблоны и локальные зависимости между отклонениями на разных временных участках.
Важно отметить, что в данном контексте Self-Attention применяется не для обработки исходной последовательности входных данных, как это обычно делается в классических трансформерах, а для анализа ошибок реконструкции, возникающих при восстановлении динамики в KoopmanNet. Фактически, мы переносим фокус внимания модели с самих данных на результат её собственной работы, позволяя системе оценить себя со стороны и извлечь из ошибок полезную информацию.
Однако при реализации этого подхода возникает интересный нюанс. Глубина анализируемой истории и горизонт планирования, для которого формируются управляющие сигналы, могут различаться по размеру. В оригинальной версии фреймворка эта проблема решается с помощью линейной проекции — компактного преобразования, позволяющего адаптировать управляющий вектор под необходимый горизонт планирования.
В нашем случае ситуация несколько проще. Поскольку модель нацелена на генерацию лишь одного следующего токена, нам требуется не последовательность управляющих сигналов, а всего один вектор. Конечно, можно воспользоваться той же линейной проекцией. Но мы предлагаем пойти другим путём — и сфокусироваться на ошибке последнего токена в контексте всей предшествующей цепочки отклонений.
Такой подход открывает новые возможности. Вместо того, чтобы рассматривать ошибку как изолированную величину, мы анализируем её в связке с накопленной историей неточностей. Это позволяет механизму внимания определить, какие именно фрагменты прошлой динамики наиболее сильно повлияли на текущую ошибку. Результатом становится управляющий вектор, который не просто реагирует на текущую неточность, а отражает её причины, закодированные в предыдущих состояниях системы.
У этого метода есть ряд очевидных преимуществ:
- целевая концентрация внимания: модель сосредоточена на ошибке последнего шага, а не распределяет ресурсы по всей траектории;
- снижение вычислительной нагрузки: нет необходимости формировать длинные векторы для каждого будущего шага;
- лучшая интерпретируемость: управляющий сигнал становится осмысленным и пригодным для визуального анализа и диагностики.
В итоге мы получаем гибкий механизм внутреннего контроля, встроенный в Энкодер, который позволяет модели адаптироваться к собственным слабым местам и более уверенно формировать распределение для следующего шага через KalmanNet и VAE. Такой подход делает архитектуру не только более устойчивой, но и заметно более прозрачной в поведении, что особенно важно при работе в условиях рыночной неопределённости.
Следующим звеном в архитектуре Энкодера выступает KalmanNet — модуль, выполняющий роль адаптивного генератора ковариационной матрицы. Его задача — не просто пассивно передать информацию дальше, а активно оценить степень доверия к линейному прогнозу, полученному от KoopmanNet. Управляющий сигнал, поступающий из блока внимания, становится своего рода индикатором надёжности предыдущей модели. Если отклонения невелики и носят устойчивый характер, KalmanNet интерпретирует это как высокую уверенность, и, соответственно, сужает ковариационное распределение — предполагая, что последующее поведение временного ряда с большой вероятностью будет следовать прогнозируемому сценарию. Но если наблюдается значительная разбалансировка или структурные сдвиги в ошибках, модель, напротив, расширяет ковариационную матрицу, открывая пространство для более вариативных, вероятностных исходов.
Таким образом, KalmanNet фактически выступает в роли индикатора уверенности — своеобразного барометра, чувствительно реагирующего на турбулентность внутри данных. Он не просто передаёт сигналы, но интерпретирует их, трансформируя невидимые колебания в математическую форму, пригодную для дальнейшего использования.
Завершает работу Энкодераблок вариационного сэмплирования (VAE). Именно здесь формируется финальное латентное представление будущего состояния. При этом выборка не производится вслепую — она подчинена логике, заложенной в предыдущих этапах. Средние значения берутся из KoopmanNet — как основа предполагаемой динамики, а степень разброса задаётся ковариационной матрицей, сгенерированной KalmanNet. В результате мы получаем не точечный прогноз, а вероятностную модель, которая учитывает как линейную структуру временного ряда, так и стохастическую природу рынка.
Такой подход обладает очевидным стратегическим преимуществом. Он позволяет модели сохранять гибкость в условиях неопределённости, не зацикливаясь на единственном сценарии развития, а адаптируя свою уверенность в зависимости от контекста. Это делает фреймворк особенно подходящим для применения в условиях, где важно не столько прогнозирование последующих состояний, сколько способность к динамическому принятию решений на основе оценок риска и доверия.
Чтобы передать степень неопределённости и уровень возможных рисков, в нашей реализации мы не ограничиваемся единственным прогнозом. Вместо этого, сэмплируем заданное количество возможных сценариев развития временного ряда на следующем шаге. Каждый из этих сценариев — это отдельная траектория, сгенерированная на основе общего распределения, сформированного KoopmanNet и KalmanNet. Такой подход позволяет не просто получить усреднённую оценку, а охватить целый спектр вероятных исходов, тем самым выявив, насколько устойчиво модель чувствует будущее.
В совокупности, взаимодействие KoopmanNet, блока внимания, KalmanNet и VAE формирует сложную, но удивительно логичную структуру, где каждый компонент играет свою роль в построении достоверного и адаптивного представления будущего.
Структура объекта
После подробного обсуждения архитектурных принципов и логики взаимодействия компонентов внутри ЭнкодераK²VAE, самое время перейти к рассмотрению его практической реализации. С целью обеспечения модульности, гибкости и читаемости кода, мы объединили все ключевые элементы в рамках единого объекта класса CNeuronK2VAEEncoder, который наследует базовую функциональность от CNeuronBaseOCL.
Этот объект аккумулирует в себе всё, что необходимо для полного цикла работы Энкодера — от анализа динамики временных рядов с помощью KoopmanNet, до построения ковариационной структуры будущих состояний в KalmanNet и сэмплирования вероятностных прогнозов через механизм VAE. Внутри объекта представлены как специализированные компоненты Koopman-сети, блок внимания и фильтр Калмана, так и технические слои для трансформаций, линейных операций и матричных вычислений.
Ниже представлена структура класса CNeuronK2VAEEncoder, где каждый компонент реализует конкретную функцию внутри общего процесса кодирования наблюдаемой последовательности. Эта реализация делает возможным поэтапный анализ и отладку на любом уровне глубины модели, а также предоставляет расширенные возможности масштабирования при работе с различными архитектурными конфигурациями и глубиной анализа.
class CNeuronK2VAEEncoder : public CNeuronBaseOCL { protected: //--- Koopman CNeuronTimeMoESparseExperts cKoopman; CNeuronBaseOCL cKoopmanPred; CNeuronBaseOCL cKoopmanRest; //--- CNeuronTimeMoEAttention cAuxiliaryNet; //--- Kalman Filter CParams cB; // Control input matrix B CParams cF; // State transition matrix F CParams cH; // Observation matrix H CParams cQ; // Learnable covariance matrices Q CParams cR; // Learnable covariance matrices R CNeuronBaseOCL cP; // Covariance matrices P //--- CNeuronTransposeOCL cFT; CNeuronTransposeOCL cHT; CNeuronTransposeOCL cQT; CNeuronTransposeOCL cRT; CNeuronTransposeOCL cPT; //--- CNeuronBaseOCL cQ_QT; CNeuronBaseOCL cR_RT; CNeuronBaseOCL cXPred; CNeuronBaseOCL cF_P; CNeuronBaseOCL cPPred; //--- CNeuronBaseOCL cP_HT; CNeuronBaseOCL cH_P_HT; matrix<double> mS, mSGrad; CNeuronBaseOCL cSInv; CNeuronBaseOCL cK; CNeuronTransposeOCL cKT; CNeuronBaseOCL cYPred; CNeuronBaseOCL cDeltY; CNeuronBaseOCL cX; CNeuronBaseOCL cK_H; CNeuronBaseOCL cIdifK_H; CNeuronTransposeOCL cIdifK_HT; matrix<double> mP; matrix<double> mPGrad; matrix<double> mNoise; matrix<double> mGrad; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronK2VAEEncoder(void) {}; ~CNeuronK2VAEEncoder(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_cross, uint heads, uint layers, uint scenarios, uint experts, uint experts_dimension, uint topK, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(const int file_handle) override; virtual bool Load(const int file_handle) override; //--- virtual int Type(void) const { return defNeuronK2VAEEncoder; } virtual void TrainMode(bool flag) override; virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); };
В представленной структуре нового класса особое внимание следует уделить ключевым компонентам, отражающим логику всей архитектуры Энкодера. В качестве KoopmanNet используется мощный модуль CNeuronTimeMoESparseExperts, сочетающий в себе локальную гибкость разреженной смеси экспертов и устойчивость глобального предиктора. Это решение позволяет эффективно моделировать как краткосрочные, так и устойчивые динамики во временных рядах.
В роли модуля внимания используется CNeuronTimeMoEAttention, отвечающий за анализ структуры ошибок реконструкции. Он выявляет закономерности в отклонениях, формируя управляющие признаки для оценки доверия к прогнозам KoopmanNet.
Особое место в реализации занимает блок фильтра Калмана. Здесь мы видим обучаемые матрицы B, F, H, Q и R, каждая из которых представлена в виде отдельного экземпляра класса CParams. Такой подход позволяет не только централизованно управлять параметрами фильтра, но и обеспечить их полноценную адаптацию в процессе обучения.
Кроме этих компонентов, структура класса содержит и множество вспомогательных объектов, которые обеспечивают корректную реализацию пошаговой логики KalmanNet и позволяют эффективно управлять всеми тензорными операциями внутри Энкодера. Функционал вспомогательных объектов будет рассмотрен более подробно по мере реализации методов класса.
Внутренняя организация класса CNeuronK2VAEEncoder предполагает статичное объявление всех используемых компонентов. Это решение позволяет упростить жизненный цикл объекта: нам не требуется выполнять динамическое выделение и очистку памяти вручную. Соответственно, конструктор и деструктор класса могут оставаться пустыми, не перегружая код лишней логикой.
Вся настройка архитектуры, включая конфигурацию KoopmanNet, параметров внимания и фильтра Калмана, полностью сосредоточена в методе Init. Именно здесь объект получает конкретную форму: настраиваются параметры внимания, задаются размеры управляющих признаков, число экспертов, глубина входного окна и прочие критически важные характеристики модели.
bool CNeuronK2VAEEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy * open_cl, uint window, uint window_key, uint units_cross, uint heads, uint layers, uint scenarios, uint experts, uint experts_dimension, uint topK, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * scenarios, optimization_type, batch)) return false;
На первом этапе управление передаётся одноимённой функции базового класса. Это позволяет задействовать уже реализованные механизмы базовой валидации входных параметров, а также выполнить инициализацию унаследованных интерфейсов и общих компонентов. Такой подход обеспечивает единый стандарт инициализации для всех нейронных слоев, упрощая поддержку и расширение архитектуры.
Отдельного внимания заслуживает момент, связанный с организацией памяти. Поскольку в нашей реализации K²VAE-энкодер возвращает не одиночный вектор, а набор возможных будущих сценариев, сформированных путём сэмплирования, буфер результатов должен иметь соответствующий объём.
Далее переходим к инициализации блока KoopmanNet, который в нашей реализации представлен модулем CNeuronTimeMoESparseExperts. Инициализируем модуль разреженной смеси экспертов, задав количество моделей и их размерность. Этот компонент отвечает за извлечение как локальных, так и глобальных закономерностей временного ряда, имитируя работу операторов Купмана.
//--- Koopman int index = 0; if(!cKoopman.Init(0, index, OpenCL, window, 2 * window, units_cross, 1, experts, topK, optimization, iBatch)) return false; index++; if(!cKoopmanPred.Init(0, index, OpenCL, window, optimization, iBatch)) return false; index++; if(!cKoopmanRest.Init(0, index, OpenCL, window * (units_cross - 1), optimization, iBatch)) return false;
После этого инициализируем два вспомогательных объекта — cKoopmanPred и cKoopmanRest. Первый из них будет использоваться для хранения прогнозных значений, рассчитанных KoopmanNet, второй — для реконструкции уже наблюдавшихся состояний временного ряда.
Следующим шагом осуществляется инициализация модуля внимания, который в нашей реализации представлен объектом cAuxiliaryNet.
index++; if(!cAuxiliaryNet.Init(0, index, OpenCL, window, window_key, 1, window, units_cross - 1, heads, layers, optimization, iBatch)) return false;
Однако, ключевая часть внутренней архитектуры нового класса сосредоточена в организации работы фильтра Калмана — именно здесь основной массив вычислений и наибольший объём логики, реализуемой в методе Init.
На первом этапе мы последовательно инициализируем квадратные матрицы обучаемых параметров фильтра: это матрицы переходов состояния F, управляющих воздействий B, наблюдений H, а также ковариации ошибок модели Q и наблюдений R.
//--- Kalman Filter index++; if(!cB.Init(0, index, OpenCL, window * window, optimization, iBatch) || !cB.Identity(window, window)) return false; index++; if(!cF.Init(0, index, OpenCL, window * window, optimization, iBatch) || !cF.Identity(window, window)) return false; index++; if(!cH.Init(0, index, OpenCL, window * window, optimization, iBatch) || !cH.Identity(window, window)) return false; index++; if(!cQ.Init(0, index, OpenCL, window * window, optimization, iBatch) || !cQ.Identity(window, window)) return false; index++; if(!cR.Init(0, index, OpenCL, window * window, optimization, iBatch) || !cR.Identity(window, window)) return false; index++; if(!cP.Init(0, index, OpenCL, window * window, optimization, iBatch) || !cP.getOutput().Fill(matrix<float>::Identity(window, window))) return false;
В процессе инициализации каждой из этих матриц задаются их размерности. Затем, с целью обеспечения числовой устойчивости фильтра Калмана на начальных итерациях обучения, все эти матрицы заполняются диагональными значениями. Такая инициализация позволяет обеспечить положительную определённость ковариационных матриц и избежать нестабильности при вычислениях, связанных с инверсией матрицы S в процессе коррекции прогнозов.
Подход с диагональной инициализацией не только стабилизирует начальные шаги обучения, но и обеспечивает равномерную чувствительность модели к различным компонентам латентного состояния, что критически важно при работе с временными рядами, в которых доминирующие тенденции могут маскировать слабые, но значимые сигналы.
Следующим этапом становится подготовка объектов, отвечающих за транспонирование соответствующих матриц. Это важный и, на первый взгляд, технический момент, но он имеет прямое отношение к корректной работе всего алгоритма. Дело в том, что в ходе вычислений фильтра Калмана нам неоднократно приходится обращаться не только к самим матрицам F, H, Q, R и P, но и к их транспонированным версиям. Чтобы обеспечить это, мы заранее выделяем и инициализируем соответствующие объекты-транспозиции.
index++; if(!cFT.Init(0, index, OpenCL, window, window, optimization, iBatch)) return false; index++; if(!cHT.Init(0, index, OpenCL, window, window, optimization, iBatch)) return false; index++; if(!cQT.Init(0, index, OpenCL, window, window, optimization, iBatch)) return false; index++; if(!cRT.Init(0, index, OpenCL, window, window, optimization, iBatch)) return false; index++; if(!cPT.Init(0, index, OpenCL, window, window, optimization, iBatch)) return false;
Таким образом, реализуется своего рода буферизация транспонированных форм, что существенно ускоряет вычисления и упрощает структуру кода в основной части алгоритма фильтрации. Кроме того, это повышает модульность архитектуры, так как позволяет работать с каждым элементом фильтра независимо, не нарушая общей логики исполнения.
Стоит обратить особое внимание на ковариационные матрицы шума — Q (ковариация процесса) и R (ковариация наблюдений). Для корректной работы алгоритма фильтра Калмана эти матрицы должны обладать двумя ключевыми свойствами: быть диагонально симметричными и положительно определёнными. Нарушение этих условий может привести к неустойчивости фильтрации, появлению мнимых значений при обращении матриц, либо полной деградации оценки состояния.
Чтобы гарантировать выполнение этих свойств в рамках обучения, мы применяем проверенный временем и широко используемый приём: представляем матрицы Q и R в виде произведения самих матриц на их транспонированную копию. Такое представление автоматически делает полученные матрицы симметричными и положительно определёнными (если только исходная матрица не вырождена). Это избавляет нас от необходимости вручную контролировать значения на диагонали или вводить регуляризацию.
index++; if(!cQ_QT.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false; index++; if(!cR_RT.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false;
Следующим этапом настройки Энкодера становится инициализация объектов, предназначенных для хранения промежуточных результатов вычислений. Эти объекты играют ключевую роль в пошаговой реализации алгоритма фильтра Калмана, где каждое вычисление основывается на результатах предыдущих операций. Кроме того, данные значения мы будем использовать и в рамках обратного прохода с целью корректного распределения градиента ошибки.
Начинаем с инициализации объекта cXPred, который будет хранить прогнозное состояние системы до применения корректирующего шага.
index++; if(!cXPred.Init(0, index, OpenCL, window, optimization, iBatch)) return false; index++; if(!cF_P.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false; index++; if(!cPPred.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false;
Далее инициализируем объекты cF_P и cPPred, в которых, соответственно, сохраняются произведение матрицы переходов на ковариационную матрицу и прогнозируемая ковариация. Эти данные необходимы для дальнейших операций по оценке достоверности сделанного прогноза.
Затем последовательно настраиваются блоки cP_HT и cH_P_HT, отвечающие за вычисление промежуточных значений при расчёте матрицы S — ковариации ошибки прогноза наблюдений.
index++; if(!cP_HT.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false; index++; if(!cH_P_HT.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false; //--- mS = mSGrad = matrix<double>::Zeros(window, window);
Параллельно с этим создаются и инициализируются матрицы mS и mSGrad, которые будут использоваться для хранения самих значений ковариации и соответствующих градиентов при обучении.
Объект cSInv предназначен для хранения обратной матрицы от S, необходимой для вычисления матрицы КалманаcK, которая также сопровождается собственной транспонированной версией cKT.
index++; if(!cSInv.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false; index++; if(!cK.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false; index++; if(!cKT.Init(0, index, OpenCL, window, window, optimization, iBatch)) return false; //--- index++; if(!cYPred.Init(0, index, OpenCL, window, optimization, iBatch)) return false; //--- index++; if(!cDeltY.Init(0, index, OpenCL, window, optimization, iBatch)) return false;
Далее следует инициализация блока cYPred — предсказания наблюдаемых значений, и cDeltY — расхождения между предсказанием и фактическим наблюдением.
Особое внимание уделяется объекту cX, в котором сохраняется финальное скорректированное состояние после применения фильтра Калмана.
index++; if(!cX.Init(0, index, OpenCL, window, optimization, iBatch)) return false; //--- index++; if(!cK_H.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false; //--- index++; if(!cIdifK_H.Init(0, index, OpenCL, window * window, optimization, iBatch)) return false; //--- index++; if(!cIdifK_HT.Init(0, index, OpenCL, window, window, optimization, iBatch)) return false;
За ним следуют cK_H, cIdifK_H и cIdifK_HT, предназначенные для записи результатов математических преобразований, необходимых для корректной обратной передачи ошибок и обновления ковариационных оценок.
В завершении инициализируем матрицы mP и mPGrad, а также вспомогательные массивы mNoise и mGrad, которые будут использоваться при генерации шумов в фазе сэмплирования и в процессе расчёта градиентов при обучении модели.
mP = mPGrad = mS; mNoise = mGrad = matrix<double>::Zeros(scenarios, window); //--- return true; }
Таким образом, на данном этапе создаётся полноценная вычислительная инфраструктура, обеспечивающая стабильную и корректную работу фильтра Калмана в составе ЭнкодераK²VAE. После успешной инициализации всех внутренних компонентов, метод инициализации завершает работу, возвращая логический результат выполнения операций вызывающей программе.
Организация прямого прохода
Переходя от этапа инициализации объектов хранения к описанию метода прямого прохода feedForward, мы фактически опускаемся в глубины вычислительной логики ЭнкодераK²VAE. Именно здесь объединяются все подготовленные ранее компоненты в единую систему. Вся конструкция, словно слаженный механизм, начинает свою роботу, преобразуя исходные наблюдения во внутренние представления.
Прямой проход начинается с блока Koopman — ключевого компонента модели, изучающего линейную динамику системы в процессе обучения. На этапе инференса, в условиях прямого прохода, этот модуль генерирует целый ряд реконструкций и одно прогнозное состояние на основании анализируемой последовательности и ранее выученной линейной структуры изменений. Таким образом, его выход включает два важных компонента: во-первых, прогноз будущего состояния, который строится исключительно на основе последнего наблюдения и выученных линейных закономерностей, а во-вторых — реконструкцию всей последовательности предыдущих состояний, вплоть до глубины анализа исторических данных.
bool CNeuronK2VAEEncoder::feedForward(CNeuronBaseOCL * NeuronOCL) { //--- Koopman if(!cKoopman.FeedForward(NeuronOCL)) return false; //--- Pred / Rest if(!DeConcat(cKoopmanPred.getOutput(), cKoopmanRest.getPrevOutput(), cKoopman.getOutput(), cKoopman.GetWindow(), cKoopman.Neurons() - cKoopman.GetWindow(), 1)) return false; if(!Different(NeuronOCL.getOutput(), cKoopmanRest.getPrevOutput(), cKoopmanRest.getOutput(), cKoopman.GetWindow())) return false;
Это деление особенно важно: прогноз используется в блоке фильтра Калмана, а остаточная последовательность (разность между фактическими данными и их реконструкцией) передаётся в модуль внимания, обрабатывающий те аспекты динамики, которые не укладываются в линейную модель.
//--- Rest Attention if(!cAuxiliaryNet.FeedForward(cKoopmanRest.AsObject())) return false;
Затем, если модель работает в режиме обучения, происходит активация всех обучаемых компонентов фильтра Калмана. Это матрицы перехода состояния, управляющего воздействия, наблюдения, а также ковариационные матрицы ошибок модели и измерений.
//--- Kalman Filter if(bTrain) { if(!cB.FeedForward()) return false; if(!cF.FeedForward()) return false; if(!cH.FeedForward()) return false; if(!cQ.FeedForward()) return false; if(!cR.FeedForward()) return false; if(!cFT.FeedForward(cF.AsObject())) return false; if(!cHT.FeedForward(cH.AsObject())) return false; if(!cQT.FeedForward(cQ.AsObject())) return false; if(!cRT.FeedForward(cR.AsObject())) return false;
Поскольку для корректной работы фильтра требуется положительная определённость матриц Q и R, они предварительно стабилизируются с помощью умножения на собственные транспонированные копии.
if(!MatMul(cQ.getOutput(), cQT.getOutput(), cQ_QT.getOutput(), cQT.GetCount(), cQT.GetWindow(), cQT.GetCount(), 1, true)) return false; if(!MatMul(cR.getOutput(), cRT.getOutput(), cR_RT.getOutput(), cRT.GetCount(), cRT.GetWindow(), cRT.GetCount(), 1, true)) return false; }
После подготовки всех параметров, начинается этап прогнозирования. Сначала вычисляется прогноз состояния на следующем шаге, объединяя два потока информации — исходных данных и модуля внимания. Эти векторы проецируются с помощью матриц обучаемых параметров F и B, после чего, складываются. В результате формируется промежуточное состояние XPred.
//--- Prediction step if(!MatMul(NeuronOCL.getOutput(), cFT.getOutput(), cXPred.getGradient(), 1, cFT.GetWindow(), cFT.GetCount(), 1, true)) return false; if(!MatMul(cAuxiliaryNet.getOutput(), cB.getOutput(), cXPred.getPrevOutput(), 1, cFT.GetWindow(), cFT.GetCount(), 1, true)) return false; if(!SumAndNormilize(cXPred.getGradient(), cXPred.getPrevOutput(), cXPred.getOutput(), cFT.GetCount(), false, 0, 0, 0, 1)) return false;
Следом рассчитывается прогноз ковариации ошибки состояния. Для этого производится последовательное перемножение матрицы перехода и текущей ковариационной матрицы, а затем добавляется матрица шума модели Q, создавая тем самым прогнозную ковариацию P_pred.
if(!MatMul(cF.getOutput(), cP.getOutput(), cF_P.getOutput(), cFT.GetCount(), cFT.GetWindow(), cP.Neurons() / cFT.GetWindow(), 1, true)) return false; if(!MatMul(cF_P.getOutput(), cFT.getOutput(), cPPred.getOutput(), cFT.GetCount(), cFT.GetWindow(), cFT.GetCount(), 1, true)) return false; if(!SumAndNormilize(cPPred.getOutput(), cQ_QT.getOutput(), cPPred.getOutput(), cHT.GetWindow(), false, 0, 0, 0, 1)) return false;
На этом этапе начинается корректировка прогноза — то, за что фильтр Калмана так ценят. Сначала рассчитывается ковариация ошибки измерения, формируется матрица S, представляющая сумму наблюдаемой дисперсии и прогнозной.
//--- Update step if(!MatMul(cPPred.getOutput(), cHT.getOutput(), cP_HT.getOutput(), cPPred.Neurons() / cHT.GetWindow(), cHT.GetWindow(), cHT.GetCount(), 1, true)) return false; if(!MatMul(cH.getOutput(), cP_HT.getOutput(), cH_P_HT.getOutput(), cHT.GetCount(), cHT.GetWindow(), cHT.GetCount(), 1, true)) return false; if(!SumAndNormilize(cH_P_HT.getOutput(), cR_RT.getOutput(), cR_RT.getPrevOutput(), cRT.GetWindow(), false, 0, 0, 0, 1)) return false;
Для вычисления матрицы Калмана K, играющей роль весового коэффициента в коррекции состояния, используется обратная матрица S. Мы не стали строить с нуля алгоритм поиска обратной матрицы. Вместо этого, воспользовались существующим функционалом матричных операций MQL5. При необходимости матрица стабилизируется, диагонализируется и перестраивается, чтобы избежать вырождения.
if(cR_RT.getPrevOutput().GetData(mSGrad) <= 0) return false; mS = mSGrad.Inv(); if(mS.Rows() == 0) { mSGrad = mSGrad + mSGrad.Transpose(); vector<double> eigvals; matrix<double> eigvecs; if(!mSGrad.Eig(eigvecs, eigvals)) return false; if(eigvals.Size() > 0) { if(!eigvals.Clip(1e-6, DBL_MAX)) return false; mSGrad = matrix<double>::Zeros(eigvals.Size(), eigvals.Size()); mSGrad.Diag(eigvals); mSGrad = eigvecs.MatMul(mSGrad.MatMul(eigvecs.Transpose())); mSGrad = mSGrad + mSGrad.Transpose(); mS = mSGrad.Inv(); } if(mS.Rows() == 0) { mSGrad.Identity(); mS = mSGrad; } } cSInv.getOutput().Fill(mS); if(!MatMul(cP_HT.getOutput(), cSInv.getOutput(), cK.getOutput(), cHT.GetCount(), (int)mS.Rows(), (int)mS.Cols(), 1, true)) return false;
На этапе обновления измерения модель корректирует предварительно спрогнозированное состояние с опорой не на реальные наблюдения, а на альтернативный прогноз, полученный из KoopmanNet. Сначала вычисляется ожидаемое значение наблюдения — путём умножения прогнозного состояния XPred на транспонированную матрицу наблюдения H. Это значение (YPred) отражает то, каким должно быть наблюдение, если бы модель не ошибалась в прогнозе.
//--- Measurement update if(!MatMul(cXPred.getOutput(), cHT.getOutput(), cYPred.getOutput(), 1, cHT.GetWindow(), cHT.GetCount(), 1, true)) return false; if(!Different(cKoopmanPred.getOutput(), cYPred.getOutput(), cDeltY.getOutput(), 1, 0, 0, 0, 1)) return false; if(!MatMul(cDeltY.getOutput(), cK.getOutput(), cX.getPrevOutput(), 1, cDeltY.Neurons(), cX.Neurons(), 1, true)) return false; if(!SumAndNormilize(cX.getPrevOutput(), cXPred.getOutput(), cX.getOutput(), 1, false, 0, 0, 0, 1)) return false;
Разность между прогнозами двух моделей интерпретируется в качестве ошибки. Умножая эту ошибку на матрицу Калмана K, мы получаем вектор поправки, который добавляется к исходному прогнозу XPred, формируя скорректированное состояние X.
Параллельно выполняется обновление ковариационной матрицы состояния P в стабилизированной форме Джозефа, что позволяет избежать накопления численных ошибок и сохранить симметрию.
//--- Joseph stabilized form for P if(!MatMul(cK.getOutput(), cH.getOutput(), cK_H.getOutput(), cKT.GetCount(), cKT.GetWindow(), cHT.GetWindow(), 1, true)) return false; if(!IdentDifferent(cK_H.getOutput(), cIdifK_H.getOutput(), cHT.GetWindow(), 0, 0, 1)) return false; if(!cIdifK_HT.FeedForward(cIdifK_H.AsObject())) return false; if(!cKT.FeedForward(cK.AsObject())) return false; if(!MatMul(cIdifK_H.getOutput(), cPPred.getOutput(), cIdifK_H.getPrevOutput(), cIdifK_HT.GetCount(), cIdifK_HT.GetWindow(), cIdifK_HT.GetWindow(), 1, true)) return false; if(!MatMul(cIdifK_H.getPrevOutput(), cIdifK_HT.getOutput(), cP.getPrevOutput(), cIdifK_HT.GetCount(), cIdifK_HT.GetWindow(), cIdifK_HT.GetCount(), 1, true)) return false; if(!MatMul(cK.getOutput(), cR_RT.getOutput(), cK.getPrevOutput(), cKT.GetCount(), cRT.GetCount(), cRT.GetCount(), 1, true)) return false; if(!MatMul(cK.getPrevOutput(), cKT.getOutput(), cKT.getPrevOutput(), cKT.GetCount(), cKT.GetWindow(), cKT.GetCount(), 1, true)) return false; if(!SumAndNormilize(cP.getPrevOutput(), cKT.getPrevOutput(), cP.getOutput(), cPT.GetWindow(), false, 0, 0, 0, 1)) return false; if(!cPT.FeedForward(cP.AsObject())) return false; if(!SumAndNormilize(cP.getOutput(), cPT.getOutput(), cP.getOutput(), 1, false, 0, 0, 0, 0.5f)) return false;
По завершении всех вычислений производится финальный шаг — генерация выходного вектора. Для этого используется сэмплирование на основе полученной обратной ковариационной матрицы P⁻¹. Случайный шум масштабируется через P, и результат добавляется к вектору состояния X, формируя окончательное представление.
if(!SumAndNormilize(cX.getOutput(), cAuxiliaryNet.getOutput(), cX.getOutput(), 1, false, 0, 0, 0, 1)) return false; //--- Sample Output if(!cP.getOutput().GetData(mPGrad)) return false; if(mPGrad.HasNan() > 0) { mPGrad.Identity(); if(!cP.getOutput().Fill(mPGrad)) return false; } mP = mPGrad.Inv(); if(mP.Rows() == 0) { mPGrad = mPGrad + mPGrad.Transpose(); vector<double> eigvals; matrix<double> eigvecs; if(!mPGrad.Eig(eigvecs, eigvals)) return false; if(eigvals.Size() > 0) { if(!eigvals.Clip(1e-6, DBL_MAX)) return false; mPGrad = matrix<double>::Zeros(eigvals.Size(), eigvals.Size()); mPGrad.Diag(eigvals); mPGrad = eigvecs.MatMul(mPGrad.MatMul(eigvecs.Transpose())); mPGrad = mPGrad + mPGrad.Transpose(); mP = mPGrad.Inv(); } if(mP.Rows() == 0) { mPGrad.Identity(); if(!cP.getOutput().Fill(mPGrad)) return false; mP = mPGrad.Inv(); } } mNoise.Random(-1, 1); matrix<double> temp = mNoise.MatMul(mP); if(!PrevOutput.Fill(temp)) return false; if(!SumVecMatrix(cX.getOutput(), PrevOutput, Output, (int)mNoise.Cols(), 0, 0, 0, 1)) return false; //--- return true; }
Стоит особо подчеркнуть, что финальный этап генерации тензора результатов не ограничивается построением единственного сценария. Вместо этого модель формирует целый спектр возможных траекторий, каждая из которых является реализацией из многомерного распределения, описанного ковариационной матрицей P. Это не просто изящный математический трюк, а отражение степени уверенности модели в собственном прогнозе.
Именно благодаря этому подходу модель становится особенно ценной в условиях нестабильности рынка или отсутствия достоверной информации: она может не просто прогнозировать один вариант будущего развития событий, а нарисовать целый пучок возможных, подкреплённых обучением траекторий. Это превращает выход feedForward в вероятностное облако решений. И каждое из них отражает разные грани возможного развития событий.
Особенности распределения градиента ошибки
Как только модель сформировала спектр возможных траекторий, завершается фаза прямого прохода и начинается не менее важный этап — распространение градиента ошибки в обратном направлении. Его мы выстраиваем в методе calcInputGradients, главная задача которого передать градиенты от уровня результатов работы модели до исходных данных, корректно распространив ошибку через все связанные компоненты.
Алгоритм начинается с распределения градиента между средними прогнозными значениями линейной модели и матрицы ковариации P.
bool CNeuronK2VAEEncoder::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false; //--- From Output if(!SumVecMatrixGrad(cX.getGradient(), PrevOutput, Gradient, (int)mNoise.Cols(), 0, 0, 0, 1)) return false; if(!PrevOutput.GetData(mGrad)) return false; mPGrad = mNoise.Transpose().MatMul(mGrad); mP = mP.Transpose(); mP = (mP * (-1)).MatMul(mPGrad.MatMul(mP));
А так же проведем градиент ошибки через форму стабилизации Джозефа.
//--- Joseph stabilized form for P if(!cPT.getGradient().Fill(mP)) return false; if(!cP.CalcHiddenGradients(cPT.AsObject())) return false; if(!SumAndNormilize(cP.getGradient(), cPT.getGradient(), cP.getGradient(), 1, false, 0, 0, 0, 0.5f)) return false; //--- if(!MatMulGrad(cK.getPrevOutput(), cKT.getPrevOutput(), cKT.getOutput(), cKT.getGradient(), cP.getGradient(), cKT.GetCount(), cKT.GetWindow(), cKT.GetCount(), 1, true)) return false; if(!MatMulGrad(cK.getOutput(), cK.getPrevOutput(), cR_RT.getOutput(), cR_RT.getGradient(), cKT.getPrevOutput(), cKT.GetCount(), cRT.GetCount(), cRT.GetCount(), 1, true)) return false; if(!MatMulGrad(cIdifK_H.getPrevOutput(), cIdifK_HT.getPrevOutput(), cIdifK_HT.getOutput(), cIdifK_HT.getGradient(), cP.getGradient(), cIdifK_HT.GetCount(), cIdifK_HT.GetWindow(), cIdifK_HT.GetCount(), 1, true)) return false; if(!MatMulGrad(cIdifK_H.getOutput(), cIdifK_H.getPrevOutput(), cPPred.getOutput(), cPPred.getGradient(), cIdifK_HT.getPrevOutput(), cIdifK_HT.GetCount(), cIdifK_HT.GetWindow(), cIdifK_HT.GetWindow(), 1, true)) return false; //--- if(!cK.CalcHiddenGradients(cKT.AsObject())) return false; if(!SumAndNormilize(cK.getGradient(), cK.getPrevOutput(), cK.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Полученная матрица передаётся и инициализирует цепочку градиентных откликов в блоке фильтра Калмана. Сначала через модуль обновления измерений.
//--- Measurement update if(!cIdifK_H.CalcHiddenGradients(cIdifK_HT.AsObject())) return false; if(!SumAndNormilize(cIdifK_H.getGradient(), cIdifK_H.getPrevOutput(), cIdifK_H.getGradient(), 1, false, 0, 0, 0, 1)) return false; if(!IdentDifferentGrad(cK_H.getGradient(), cIdifK_H.getGradient(), cHT.GetWindow(), 0, 0, 1)) return false; if(!MatMulGrad(cK.getOutput(), cK.getPrevOutput(), cH.getOutput(), cH.getGradient(), cK_H.getGradient(), cKT.GetCount(), cKT.GetWindow(), cHT.GetWindow(), 1, true)) return false; //--- if(!MatMulGrad(cDeltY.getOutput(), cDeltY.getGradient(), cK.getOutput(), cK.getPrevOutput(), cX.getGradient(), 1, cDeltY.Neurons(), cX.Neurons(), 1, true)) return false; if(!SumAndNormilize(cK.getGradient(), cK.getPrevOutput(), cK.getGradient(), 1, false, 0, 0, 0, 1)) return false; if(!DifferentGrad(cKoopmanPred.getGradient(), cYPred.getGradient(), cDeltY.getGradient(), 1, 0, 0, 0, 1)) return false; if(!MatMulGrad(cXPred.getOutput(), cXPred.getGradient(), cHT.getOutput(), cHT.getGradient(), cYPred.getGradient(), 1, cHT.GetWindow(), cHT.GetCount(), 1, true)) return false; if(!SumAndNormilize(cXPred.getGradient(), cX.getGradient(), cXPred.getGradient(), 1, false, 0, 0, 0, 1)) return false;
Далее, в блоке коррекции, градиентное распространение проходит через матрицы прогнозов и ошибок. Все эти шаги аккуратно выстраивают поток градиента от выхода к скрытому пространству, и, что особенно важно, учитывают структурные связи между переменными.
//--- Update step if(!MatMulGrad(cP_HT.getOutput(), cP_HT.getGradient(), cSInv.getOutput(), cSInv.getGradient(), cK.getGradient(), cHT.GetCount(), (int)mS.Rows(), (int)mS.Cols(), 1, true)) return false; if(cSInv.getGradient().GetData(mSGrad) <= 0) return false; mS = mS.Transpose(); mS = (mS * (-1)).MatMul(mSGrad.MatMul(mS)); if(cH_P_HT.getGradient().Fill(mS) <= 0) return false; if(!MatMulGrad(cH.getOutput(), cH.getPrevOutput(), cP_HT.getOutput(), cP_HT.getPrevOutput(), cH_P_HT.getGradient(), cHT.GetCount(), cHT.GetWindow(), cHT.GetCount(), 1, true)) return false; if(!SumAndNormilize(cH_P_HT.getGradient(), cR_RT.getGradient(), cR_RT.getGradient(), int(mS.Cols()), false, 0, 0, 0, 1)) return false; if(!SumAndNormilize(cH.getGradient(), cH.getPrevOutput(), cH.getPrevOutput(), 1, false, 0, 0, 0, 1)) return false; if(!SumAndNormilize(cP_HT.getGradient(), cP_HT.getPrevOutput(), cP_HT.getGradient(), 1, false, 0, 0, 0, 1)) return false; if(!MatMulGrad(cPPred.getOutput(), cPPred.getPrevOutput(), cHT.getOutput(), cHT.getPrevOutput(), cP_HT.getGradient(), cPPred.Neurons() / cHT.GetWindow(), cHT.GetWindow(), cHT.GetCount(), 1, true)) return false; if(!SumAndNormilize(cPPred.getGradient(), cPPred.getPrevOutput(), cQ_QT.getGradient(), int(cQT.GetWindow()), false, 0, 0, 0, 1)) return false; if(!SumAndNormilize(cHT.getGradient(), cHT.getPrevOutput(), cHT.getGradient(), 1, false, 0, 0, 0, 1)) return false;
После этого следует блок прогнозирования — prediction step.
//--- Prediction step if(!MatMulGrad(cF_P.getOutput(), cF_P.getGradient(), cFT.getOutput(), cFT.getGradient(), cQ_QT.getGradient(), cFT.GetCount(), cFT.GetWindow(), cFT.GetCount(), 1, true)) return false; if(!MatMulGrad(cF.getOutput(), cF.getPrevOutput(), cP.getOutput(), cP.getGradient(), cF_P.getGradient(), cFT.GetCount(), cFT.GetWindow(), cP.Neurons() / cFT.GetWindow(), 1, true)) return false; if(!MatMulGrad(cAuxiliaryNet.getOutput(), cAuxiliaryNet.getGradient(), cB.getOutput(), cB.getGradient(), cXPred.getGradient(), 1, cFT.GetWindow(), cFT.GetCount(), 1, true)) return false; if(!MatMulGrad(NeuronOCL.getOutput(), NeuronOCL.getGradient(), cFT.getOutput(), cFT.getPrevOutput(), cXPred.getGradient(), 1, cFT.GetWindow(), cFT.GetCount(), 1, true)) return false; if(!SumAndNormilize(cFT.getGradient(), cFT.getPrevOutput(), cFT.getGradient(), 1, false, 0, 0, 0, 1)) return false; //--- if(!MatMulGrad(cR.getOutput(), cR.getPrevOutput(), cRT.getOutput(), cRT.getGradient(), cR_RT.getGradient(), cRT.GetCount(), cRT.GetWindow(), cRT.GetCount(), 1, false)) return false; if(!MatMulGrad(cQ.getOutput(), cQ.getPrevOutput(), cQT.getOutput(), cQT.getGradient(), cQ_QT.getGradient(), cQT.GetCount(), cQT.GetWindow(), cQT.GetCount(), 1, false)) return false; if(!cR.CalcHiddenGradients((CObject*)cRT.AsObject())) return false; if(!SumAndNormilize(cR.getGradient(), cR.getPrevOutput(), cR.getGradient(), cRT.GetWindow(), false, 0, 0, 0, 0.01f)) return false; if(!cQ.CalcHiddenGradients(cQT.AsObject())) return false; if(!SumAndNormilize(cQ.getGradient(), cQ.getPrevOutput(), cQ.getGradient(), cQT.GetWindow(), false, 0, 0, 0, 0.01f)) return false; if(!cH.CalcHiddenGradients(cHT.AsObject())) return false; if(!SumAndNormilize(cH.getGradient(), cH.getPrevOutput(), cH.getGradient(), cHT.GetWindow(), false, 0, 0, 0, 0.01f)) return false; if(!cF.CalcHiddenGradients(cFT.AsObject())) return false; if(!SumAndNormilize(cF.getGradient(), cF.getPrevOutput(), cF.getGradient(), cFT.GetWindow(), false, 0, 0, 0, 0.01f)) return false;
Завершающий блок касается представления в пространстве Купмана и модуле внимания. Здесь происходит передача градиента на прогнозную и реконструированную части (KoopmanPred, KoopmanRest).
//--- Rest Attention if(!cKoopmanRest.CalcHiddenGradients(cAuxiliaryNet.AsObject())) return false; //--- Pred / Rest if(!NeuronOCL.getPrevOutput().Fill(0)) return false; if(!DifferentGrad(NeuronOCL.getPrevOutput(), cKoopmanRest.getPrevOutput(), cKoopmanRest.getGradient(), cKoopman.GetWindow())) return false; if(!SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getPrevOutput(), NeuronOCL.getPrevOutput(), 1, false, 0, 0, 0, 1)) return false; if(NeuronOCL.Activation() != None) { if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getPrevOutput(), NeuronOCL.getPrevOutput(), NeuronOCL.Activation())) return false; } if(!Concat(cKoopmanPred.getGradient(), cKoopmanRest.getPrevOutput(), cKoopman.getGradient(), cKoopman.GetWindow(), cKoopman.Neurons() - cKoopman.GetWindow(), 1)) return false;
Для последней вычисляется градиент по разности, а затем, обе части объединяются через в единую структуру Koopman.
В финале градиент передается на уровень исходных данных.
//--- Koopman if(!NeuronOCL.CalcHiddenGradients(cKoopman.AsObject())) return false; if(!SumAndNormilize(NeuronOCL.getGradient(), NeuronOCL.getPrevOutput(), NeuronOCL.getGradient(), 1, false, 0, 0, 0, 1)) return false; //--- return true; }
Таким образом, метод шаг за шагом прокладывает полный путь обратного распространения ошибки, охватывая все ключевые компоненты модели: вероятностную латентную часть, фильтрацию состояний, прогнозирование, коррекцию и преобразование в пространстве Купмана. Всё это обеспечивает точную настройку параметров модели и позволяет ей эффективно обучаться на временных рядах.
Полный исходный код объекта CNeuronK2VAEEncoder и всех его методов представлен во вложении.
Сегодня мы проделали объёмную и детальную работу, и статья уже приобрела внушительный масштаб. Предлагаю сделать небольшой перерыв, чтобы дать возможность усвоить материал и взглянуть на него свежим взглядом. В следующей статье мы завершим начатое — подробно рассмотрим оставшиеся моменты и проведём тестирование реализованных подходов на реальных исторических данных. Это позволит не только закрепить теорию, но и оценить практическую эффективность.
Заключение
В этой статье мы подробно разобрали архитектуру и основные этапы реализации Энкодера в фреймворке K²VAE, который объединяет возможности KoopmanNet и фильтра Калмана в единой системе для анализа временных рядов. Такой подход позволяет эффективно моделировать сложную динамику финансовых данных, сочетая классическое линейное прогнозирование с гибкой адаптивной корректировкой на основе наблюдений. Рассмотренный фреймворк наглядно демонстрирует, как проверенные временем методы могут гармонично интегрироваться с современными нейросетевыми технологиями, открывая новые перспективы в анализе и прогнозировании финансовых рынков.
В следующей статье мы перейдём к практическому тестированию модели на реальных исторических данных, чтобы объективно оценить её эффективность и потенциал в условиях реальной торговли.
Ссылки
- K²VAE: A Koopman-Kalman Enhanced Variational AutoEncoder for Probabilistic Time Series Forecasting
- Другие статьи серии
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Study.mq5 | Советник | Советник офлайн обучения моделей |
| 2 | StudyOnline.mq5 | Советник | Советник онлайн обучения моделей |
| 3 | Test.mq5 | Советник | Советник для тестирования модели |
| 4 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 5 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 6 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Исследуем регрессионные модели для причинно-следственного вывода и трейдинга
Исследуем регрессионные модели для причинно-следственного вывода и трейдинга
 Связь торговых роботов MetaTrader 5 с внешними брокерами через API и Python
Связь торговых роботов MetaTrader 5 с внешними брокерами через API и Python
 Переосмысление индикаторов MQL5 и MetaTrader 5
Переосмысление индикаторов MQL5 и MetaTrader 5
 Алгоритм биржевого рынка — Exchange Market Algorithm (EMA)
Алгоритм биржевого рынка — Exchange Market Algorithm (EMA)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования