Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)

Содержание

• Введение
• 1. Понятие Q-функции
• 2. Глубокое Q-обучение
• 2.1. Воспроизведение опыта
• 2.2. Использование Target Net
• 3. Реализация средствами MQL5
• 4. Тестирование
• Заключение
• Ссылки
• Программы, используемые в статье

Введение

В предыдущей статье мы начали изучение методов обучения с подкрепление и построили первую модель, обучаемую методом кросс-энтропии. В данной статье мы продолжаем изучение методов обучения с подкреплением. И сегодня я предлагаю познакомиться с методом глубокого Q-обучения. Именно благодаря использованию метода глубокого Q-обучения команде DeepMind в 2013 году удалось создать модель, способную успешно играть в 7 компьютерных игр Atari. Примечательно, что на всех 7-ми играх обучалась одна и таже модель без изменения архитектуры и гиперпараметров. При этом, по результатам обучения модель смогла улучшить ранее достигнутые результаты в 6-ти из анализируемых игр. Кроме того, в 3-х играх модель показала результаты лучше человека. Можно сказать, что с выходом этой работы начался новый этап развития обучения с подкреплением. Давайте познакомимся с этим методом и попробуем его использовать для решения своих задач.

1. Понятие Q-функции

Вначале давайте немного повторим изученный в прошлой статье материал. В обучении с подкреплением мы строим процесс взаимодействия агента с окружающей средой. Агент анализирует текущее состояние окружающей среды и совершает действие, в результате которого изменяется состояние среды. В ответ на действие среда возвращает агенту вознаграждение. Агенту неизвестна природа формирования вознаграждения. Но его цель получить максимально возможное суммарное вознаграждение за анализируемую сессию.

Здесь надо обратить внимание, что вознаграждение агент получает не за действие. А за переход из одного состояние в другое. При этом совершение определенного действия в аналогичной ситуации не гарантирует перехода в то же состояние. Совершение действия дает лишь некоторую вероятность перехода в ожидаемое состояние. Вероятности и зависимости состояний, действий и переходов агенту неизвестны. И он должен их выучить из процесса взаимодействия со средой. 

По существу, обучение с подкреплением строится на предположении существования некой зависимости между текущим состоянием, совершенным действием и вознаграждением. Говоря математическим языком, существует некая функция Q, которая в зависимости от состояния s и действия a возвращает вознаграждение r. И обозначается Q(s|a). Данная функция называется функцией полезности действия.

Да, агенту неизвестна эта функция. Но если она существует, то в процессе взаимодействия со средой, повторяя действия бесконечное число раз, мы можем её аппроксимировать.

В реальных условиях мы, конечно, не можем повторять состояния и действия бесконечное число раз. Но повторив их достаточное количество, мы можем аппроксимировать функцию с приемлемой погрешностью. Форма выражения Q-функции может быть различная. В предыдущей статье определяя полезность каждого действия мы строили таблицу зависимостей состояния, действия и среднего вознаграждения. Но вполне приемлемы и могут давать даже лучшие результаты и другие формы выражения Q-функции. Это могут быть деревья решений, нейронные сети и т.д.

Здесь надо обратить внимание, что аппроксимированная агентом Q-функция не предсказывает полученное вознаграждение. Она лишь возвращает ожидаемое вознаграждение на основании прошлого опыта взаимодействия агента со средой.

2. Глубокое Q-обучение

Вероятно, Вы уже догадались, что глубокое Q-обучение подразумевает использование нейронной сети для аппроксимации Q-функции. В чем же преимущество такого подхода? Давайте вспомним реализацию табличного метода кросс-энтропии в прошлой статье. Помните, в ней я акцентировал внимание, что реализация табличного метода предполагает конечное количество возможных состояний и действий. Мы, конечно, ограничили число возможных состояний с помощью кластеризации исходных данных. Но так ли это хорошо? Всегда ли кластеризация нам даст лучшие результаты? В то же время, использование нейронной сети перед нами не ставит ограничения по числу возможных состояний. И мне кажется, что в случае решения задач трейдинга это большой плюс.

И тут кажется вполне очевидным подход взять и заменить таблицу из предыдущей статьи на нейронную сеть. Но, к сожалению, не все так просто. На практике оказалось, что такой подход не так хорош, как кажется вначале. Для реализации подхода нам потребуется добавить несколько эвристик.

Вначале давайте посмотрим на цель обучения нашего агента. В общем случае его цель максимизация совокупной награды. Посмотрите на рисунок ниже. Агенту предстоит перейти из клетки Start в клетку Finish. Награду агент получает одноразово при попадании в клетку Finish. Во всех остальных состояниях награда нулевая.

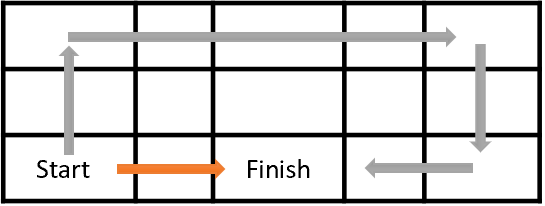
На рисунке представлено 2 пути. Для нас очевидно, что оранжевый путь короче и более предпочтителен. Но с точки зрения максимизации награды они равнозначны.

Точно также в трейдинге, для нас предпочтительно получить доход сразу. Чем инвестировать средства сейчас, а доход получить в отдаленном будущем. Конечно, здесь учитывается стоимость денег: учетная ставка, инфляция и ряд других признаков. Точно также мы поступаем и здесь. Для решения проблемы мы вводим фактор дисконтирования ɣ, который будет уменьшать ценность будущих наград.

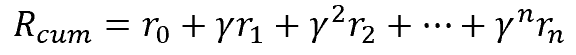
Фактор дисконтирования ɣ выбирается в диапазоне от 0 до 1. Если фактор дисконтирования равен 1, то дисконтирования не происходит. А при факторе дисконтирования равном 0, будущие награды не учитываются. На практике фактор дисконтирования берется близким к 1.

Но тут есть ещё одна проблема. То, что красиво выглядит на бумаге, не всегда можно реализовать на практике. Мы легко можем посчитать будущие награды, когда перед нами лежит полная карта переходов и вознаграждений. Среди них мы можем выбрать оптимальный путь с максимальной наградой в конце. Но при решении практических задач мы не знаем в какое следующее состояние мы попадем, совершив некое действие. И какую награду при этом получим. И это только на следующем шаге. А что говорить о полном пути до завершения сессии. Мы не можем заглянуть в будущее. Для получения очередной награды агенту необходимо совершить действие. И только после перехода в новое состояние среда вернет вознаграждение. И при этом у нас нет пути назад. Мы не можем вернуться к предыдущему состоянию и совершить другое действие, чтобы потом выбрать лучшее.

Поэтому мы обращаемся к методам динамического программирования. И, в частности, к методу оптимизации Беллмана. Который гласит, что для выбора оптимальной стратегии необходимо выбирать оптимальное действие на каждом шаге. То есть, выбирая на каждом шаге действие с максимальным вознаграждением мы получим максимальную кумулятивную награду за сессию. Математическая формула обновления функции полезности действия представлена ниже.

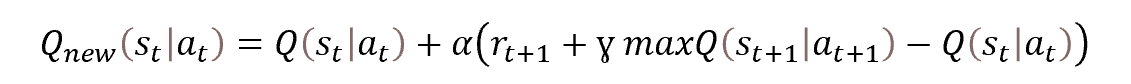
Посмотрите на представленную формулу. Не напоминает ли она Вам формулу обновления весов стохастического градиентного спуска? Действительно, мы здесь видим, что для обновления значения функции полезности действия нам необходимо предыдущее значение функции плюс некое отклонение, помноженное на коэффициент обучения.

Но также в представленной функции можно заметить, что для определения значения функции во временной точке t нам необходимо значение функции полезности действия на следующем временном шаге в точке t+1. Иными словами мы, находясь в состоянии st, совершаем действие at и после перехода в состояние st+1 получаем награду rt+1. Для обновления значения функции полезности действия нам необходимо к полученной награде прибавить ещё и максимум функции полезности действия на следующем шаге. То есть максимум ожидаемой награды, которую мы можем получить на следующем шаге. Наш агент, конечно, не может заглянуть в будущее и определить будущую награду. Но он может воспользоваться своей аппроксимируемой функцией и, находясь в состоянии st+1, посчитать значение функции для всех возможных действий из данного состояния и взять максимальное из полученных значений. Да, в процессе обучения её значения поначалу будут далеки от истинных. Но это лучше, чем ничего. А по мере обучения агента погрешность прогнозирования будет уменьшаться.

2.1. Воспроизведение опыта

Стохастический градиентный спуск хорош тем, что позволят осуществлять обновление значений функции на основании значений малой выборки из генеральной совокупности. По существу, он позволяет нашему агенту осуществлять актуализацию значений функции полезности действия на каждом шаге прохождения сессии. Но при обучении с учителем мы использовали обучающую выборку, состояния которой независимы между собой. Для усиления этого свойства мы перемешивали генеральную совокупность каждый раз перед выбором нового пакета обучающих данных.

В случае же обучения с учителем, двигаясь во времени по нашей среде агент каждый раз при совершении действия попадает в новое состояние, которое тесно связано с предыдущим. Просмотрите вокруг себя. Идете Вы или сидите за столом и совершаете какое-то действие, окружающая среда в поле Вашего видения не меняется кардинально. Изменяется лишь небольшая её составляющая, на воздействие которой направлено Ваше действие. Аналогично и состояния изучаемой среды не будут сильно меняться при совершении действий агента. А значит последовательные состояния будут иметь довольно большую взаимосвязь. Наш агент будет наблюдать автокорреляцию таких состояний.

Здесь сложность заключается в том, что даже использование малого обучающего коэффициента не спасает нашего агента от подстраивания функции полезности действия под текущее состояние в ущерб памяти прошлого опыта.

При обучении с учителем использование независимых состояний после довольно большого числа итераций позволяет усреднять значения весовых коэффициентов обучаемой модели. В случае же обучения с подкреплением, когда мы обучаем модель на связанных и, практически неизменных состояниях, модель переобучается под текущее состояние.

Как и в любом временном ряде взаимосвязь состояний падает с ростом времени между ними. Следовательно, для решения этой проблемы при обучении модели нашего агента нужно использовать состояния, разбросанные по временной шкале. Мы можем легко это сделать имея исторические данные. Но при прохождении по среде наш агент не обладает такой памятью. Он видит только текущее состояния и не может перепрыгивать из одного состояния в другое.

Но почему бы в таком случае нам не организовать память для агента. Посмотрите, для обновления значения функции полезности действия нам необходим следующий набор данных:

Состояние -> Действие -> Награда -> Состояние

Так давайте при прохождении по состояниям среды наш агент будет сохранять необходимый набор данных в некий буфер. Размер буфера является гиперпараметром и определяется архитектором модели. После заполнения буфера наиболее старые данные будут заменяться вновь поступившими. При этом для обучения модели мы будем использовать не текущее состояние, а случайно выбранные из буфера памяти агента. Таким образом мы минимизируем взаимосвязь между отдельными состояниями и повышаем способность модели к обобщению изучаемых данных.

2.2. Использование Target Net

Еще один момент, на который следует обратить внимание при обучении функции полезности действия это максимум значения данной функции на следующем шаге maxQ(st+1|at+1). Прежде всего, надо четко понимать, что это "значение из будущего". Да, мы берем прогнозное значение, основываясь на нашей аппроксимированной функции полезности действия. Но находясь в момент времени t мы не можем изменять значение из состояния времени t+1. Но каждый раз, когда мы актуализируем значение функции, мы обновляем весовые коэффициенты нашей модели и тем самым изменяем следующее прогнозное значение.

Более того, мы обучаем нашего агента на получение максимально награды. То есть на каждой итерации обновления модели мы максимизируем ожидаемое значение. А использование прогнозного значения рекуррентно максимизирует обновляемое значение. Таким образом осуществляется максимизация значений нашей функции полезности действия в прогрессии. Что ведет к завышению значений нашей функции и росту ошибки прогнозирования полезности действий. Как Вы понимаете, это не совсем хорошо. Поэтому нам необходим стационарный механизм оценки полезности будущего действия.

Мы могли бы решить этот вопрос путем создания дополнительной модели для прогнозирования полезности будущего действия. Но такой подход потребует дополнительные затраты на обучение второй модели. А нам бы этого не хотелось. С другой стороны, мы уже обучаем одну модель, которая выполняет этот функционал. Только нам необходимо, чтобы после изменения весовых коэффициентов модель возвращала значения функции как до обновления. Эта противоречивая задача решается путем копирования модели. Мы просто создаем 2 копии одной модели функции полезности действия. Одну копию обучаем, а вторую используем для прогнозирования полезности будущего действия.

Но зафиксировав однажды модель функции полезности действия, в процессе обучения она довольно скоро станет неактуальна. И это способно сделать продолжение обучения неэффективным. Для исключения влияния этого фактора, в процессе обучения нам необходимо будем актуализировать модель прогнозных значений. Мы не будем параллельно обучать вторую копию модели. Мы просто с определенной периодичностью будем копировать в неё весовые коэффициенты из обучаемой копии модели функции полезности действия. Таким образом, обучая только одну модель мы получаем довольно актуальные 2 копии модели функции полезности действия и избавляемся от рекуррентного завышения прогнозных значений. 

Итак, давайте обобщим вышесказанное:

1. Для обучения агента мы используем нейронную сеть.
2. Нейронная сеть обучается на прогнозирование ожидаемого значения Q-функции полезности действия.
3. Для минимизации корреляции между соседними состояниями в процессе обучения мы используем буфер памяти, из которого извлекаем состояния случайным образом.
4. Для прогнозирования будущего значения Q-функции в процессе обучения используется 2-я модель Target Net, которая является "замороженной" копией обучаемой модели.
5. Актуализация Target Net осуществляется путем периодического копирования матриц весовых коэффициентов обучаемой модели.

Далее я предлагаю посмотреть на реализацию описанного подхода средствами MQL5.

3. Реализация средствами MQL5

Реализацию глубокого Q-обучения средствами MQL5 мы будем осуществлять в файле советника "Q-learning.mq5". С полным кодом советника Вы можете познакомиться во вложении. Сейчас же мы остановимся только на моментах реализации метода глубокого Q-обучения.

И перед тек как приступить к реализации нам необходимо определиться с исходными данными и системой вознаграждения. И если исходные данные мы будем использовать те же, что и для всех предыдущих экспериментов. То над системой вознаграждения надо задуматься. Рассматриваемая нами ранее задача прогнозирования фракталов является довольно искусственной. Мы, конечно, можем подстроить модель под определения максимально возможного количества фракталов. Но наша основная цель получение максимальной прибыли от торговых операций.

В таком контексте вполне разумно использовать размер следующей свечи в качестве размера вознаграждения. Конечно, знак вознаграждения должен соответствовать совершенной операции. В упрощенной модели у нас есть 2 торговых операции: покупка и продажа. А также мы можем находиться вне позиции.

Мы не будем сейчас усложнять модель определяя объем позиции, доливки и частичное закрытие позиции. Считаем, что агент может находиться в позиции с фиксированным лотом. Или закрыть все позиции и находиться вне рынка.

Кроме того, прорабатывая политику вознаграждения мы должны понимать, что от правильно построенной системы вознаграждения во многом зависит результат обучения. Практика обучения с подкреплением довольно богата на примеры, когда неправильно выбранная политика вознаграждения приводила к неожиданным результатам. Модель может научиться делать неправильные выводы. А может зациклиться в получении максимального вознаграждения без достижения желаемого результата. К примеру, мы можем давать модели вознаграждение за открытие и закрытие позиции. Но если это вознаграждение будет превышать вознаграждение за накопленную от сделки прибыль, то модель может научиться просто открывать и закрывать позиции. Она будет максимизировать вознаграждения, а мы убытки.

С другой стороны, если мы будем наказывать модель за открытие и закрытие позиции по аналогии с комиссией за операцию, то модель может просто выучиться "сидеть вне рынка". Нет доходов, но нет и убытков.

Учитывая все вышеизложенное, было принято решение о создании модели с 3-мя возможными действиями: Покупка, Продажа, Вне рынка.

Прогнозировать направление ожидаемого движения агент будет на каждой новой свече и выбирать действие без учета совершенных ранее. То есть для упрощения модели мы не будем подавать на вход агенту информацию находится ли он в позиции и в каком направлении. Соответственно, агент не отслеживает открытие и закрытие позиции. Мы не начисляем вознаграждение за открытие и закрытие позиции.

С целью минимизации времени нахождения "вне рынка" мы вводим штраф за отсутствие позиции. Разумеется, данный штраф будет меньше штрафа за убыточную позицию.

Таким образом мы сформировали следующую политику вознаграждения агента:

1. Прибыльная позиция получает вознаграждения в размере тела свечи (мы анализируем состояние системы каждую свечу и находимся в позиции от открытия свечи до её закрытия).
2. Нахождение "вне рынка" штрафуется в размере тела свечи (размер тела свечи с отрицательным знаком — упущенная выгода).
3. Убыточная позиция штрафуется двойным размером тела свечи (убыток + упущенная выгода).

После определения системы вознаграждения мы переходим непосредственно к реализации метода.

Как уже было сказано выше, выстраиваемая модель будет использовать 2 нейронные сети. Для этого мы создадим 2 объекта работы с нейронными сетями. Обучать мы будем StudyNet, а TargetNet будет использоваться для прогнозирования будущих значений Q-функции.

CNet                StudyNet;
CNet                TargetNet;

Для организации работы метода глубокого Q-обучения нам также потребуются новые внешние переменные, которые будут определять гиперпараметры построения и обучения модели.

• Batch — размер пакета обновления весовых коэффициентов;
• UpdateTarget — количество обновлений матриц весовых коэффициентов обучаемой модели до копирования в "замороженную" модель прогнозирования будущих значений Q-функции;
• Iterations — общее количество итераций обновлений обучаемой модели в процессе обучения;
• DiscountFactor — фактор дисконтирования будущих наград.

input int                  Batch =  100;
input int                  UpdateTarget = 20;
input int                  Iterations = 1000;
input double               DiscountFactor =   0.9;

Непосредственное создание модели нейронной сети мы вынесем за рамки данного советника. Для её создания мы воспользуемся инструментом из статей о Transfer Learning. Такой подход позволит нам проводить эксперименты с использование моделей различных архитектур без внесения изменений в советник. Поэтому в методе инициализации советника мы организовываем лишь загрузку предварительно созданной модели.

//---
   float temp1, temp2;
   if(!StudyNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false) ||
      !TargetNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false))
      return INIT_FAILED;

Обратите внимание, что так как мы используем 2 копии одной модели, то и загружаем обе модели из одного файла.

Свобода использования различных архитектурных решений модели подразумевает не только возможность использования различных архитектур скрытых слоев и их размеров, но возможность регулирования глубины анализируемой истории. И если ранее мы создавали модель в коде советника, а глубину истории определяли внешним параметром. То сейчас мы можем определять глубину анализируемой истории размером слоя исходных данных. А советник будет определять её аналитическим путем, исходя из размера слоя исходных данных. Неизменным остается только количество нейронов на одну свечу анализируемой истории и размер слоя результатов. Так как эти параметры конструкционно связаны с используемыми индикаторами и количеством прогнозируемы действий.

   if(!StudyNet.GetLayerOutput(0, TempData))
      return INIT_FAILED;
   HistoryBars = TempData.Total() / 12;
   StudyNet.getResults(TempData);
   if(TempData.Total() != Actions)
      return INIT_PARAMETERS_INCORRECT;

Да, ранее мы не обсуждали размер исходного слоя в модели глубокого Q-обучения. Как было сказано выше Q-функция возвращает ожидаемую награду в зависимости от состояния и совершаемого действия. И для определения наиболее полезного действия нам необходимо вычислить значение функции для всех возможных действий в текущем состоянии. Использование нейронной сети нам позволяет создать слой результатов с количеством нейронов равным количеству всех возможных действий. В таком случае каждый нейрон слоя результатов будет отвечать за прогнозирование полезности конкретного действия. Что позволит получить нам значение полезности всех действий за один проход нейронной сети. И нам остаётся лишь выбрать максимальное значение.

В остальном функция инициализация советника остается без изменений. А с полным её кодом можно ознакомиться во вложении.

Процесс обучения модели мы выстаиваем в функции Train. В начале тела данной функции мы определяем размер обучающей сессии и загружаем исторические данные. Так же, как мы это делали ранее при обучении с учителем и без.

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);
//---
   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

Надо сказать, что благодаря использованию исторических данных для обучения модели мы можем не создавать буфер памяти. Ведь мы можем использовать все загруженные исторические данные как единый буфер памяти. В случае же организации обучения модели в реальном времени нам следует добавить буфер памяти и организовать процесс его обслуживания.

Далее мы подготовим вспомогательные переменные:

• total — размер обучающей выборки;
• use_target — флаг использования Target Net для прогнозирования будущих наград.

   int total = bars - (int)HistoryBars - 240;
   bool use_target = false;

Использование флага use_target обусловлено необходимостью отключения прогнозирования будущих наград до первой актуализации модели Target Net. На самом деле это довольно тонкий момент. Ведь на начальном этапе наша модель инициализирована случайными весовыми коэффициентами. А значит и прогнозируемые ей значения будут абсолютно случайными. И, скорее всего, очень далеки от истинных значений. Использование таких случайных значений может только исказить процесс обучения модели. В таком случае модель будет аппроксимировать не истинные значения наград, а случайные значения, заложенные в саму модель. Поэтому, до первой итерации актуализации модели Target Net нам больше пользы принесет исключение данного шума.

Далее мы организовываем систему циклов обучения агента. Внешний цикл будет отсчитывать общее число итераций обновления матрицы весов нашего агента.

   for(int iter = 0; (iter < Iterations && !IsStopped()); iter += UpdateTarget)
     {
      int i = 0;

Во вложенном цикле мы будем отсчитывать размер пакета обновления весовых коэффициентов и количество обновлений до актуализации Target Net. Здесь следует обратить внимание, что в нашей модели реализовано обновление весовых коэффициентов на каждой итерации обратного прохода. Поэтому использование пакета обновления, наверное, выглядит не совсем корректно. Так как для нашей модели он всегда задан равный "1". Тем не менее, для соблюдения баланса количества обработанных состояний между актуализациями Target Net, их периодичность будет равна произведению размера пакета на количество обновлений между актуализациями.

В теле цикла мы случайным образом определяем состояние системы для текущей итерации обучения модели. Здесь же мы очищаем буферы для записи 2-х последующих состояний. Первое состояния будет использоваться для прямого прохода обучаемой модели. А второе для прогнозных значений Q-функции в Target Net.

      for(int batch = 0; batch < Batch * UpdateTarget; batch++)
        {
         i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (total));
         State1.Clear();
         State2.Clear();
         int r = i + (int)HistoryBars;
         if(r > bars)
            continue;

Затем во вложенном цикле заполним подготовленные буферы историческими данными. С целью исключения излишних операций, перед заполнением буфера второго состояния мы проверяем флаг использования Target Net. Буфер заполняется только при необходимости.

         for(int b = 0; b < (int)HistoryBars; b++)
           {
            int bar_t = r - b;
            float open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            float rsi = (float)RSI.Main(bar_t);
            float cci = (float)CCI.Main(bar_t);
            float atr = (float)ATR.Main(bar_t);
            float macd = (float)MACD.Main(bar_t);
            float sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) ||
               !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) ||
               !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign))
               break;
            if(!use_target)
               continue;
            //---
            bar_t --;
            open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            rsi = (float)RSI.Main(bar_t);
            cci = (float)CCI.Main(bar_t);
            atr = (float)ATR.Main(bar_t);
            macd = (float)MACD.Main(bar_t);
            sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!State2.Add((float)Rates[bar_t].close - open) || !State2.Add((float)Rates[bar_t].high - open) ||
               !State2.Add((float)Rates[bar_t].low - open) || !State2.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State2.Add(sTime.hour) || !State2.Add(sTime.day_of_week) || !State2.Add(sTime.mon) ||
               !State2.Add(rsi) || !State2.Add(cci) || !State2.Add(atr) || !State2.Add(macd) || !State2.Add(sign))
               break;
           }

После успешного заполнения буферов историческими данными мы проверяем соответствие их размера и осуществляем прямой проход обоих моделей. При этом не забываем проверить результат выполнение операций.

         if(IsStopped())
           {
            ExpertRemove();
            return;
           }
         if(State1.Total() < (int)HistoryBars * 12 ||
            (use_target && State2.Total() < (int)HistoryBars * 12))
            continue;
         if(!StudyNet.feedForward(GetPointer(State1), 12, true))
            return;
         if(use_target)
           {
            if(!TargetNet.feedForward(GetPointer(State2), 12, true))
               return;
            TargetNet.getResults(TempData);
           }

За успешным прямым проходом мы получаем вознаграждение от среды и подготавливаем буфер целевых значений для обратного прохода в соответствии с определенной выше политикой вознаграждения.

Здесь следует обратить внимание на 2 момента. Первое, мы проверяем флаг использования Target Net. И добавляем прогнозное значение только при положительном результате. Если же флаг в положении false, то прогнозные значения Q-функции приравниваем к "0".

Второй момент заключается в отступлении от уравнения Беллмана. Как Вы помните, в уравнении Беллмана берется максимальное значение будущей награды. Тем самым модель обучается к получению максимальной доходности. Такой подход, конечно, ведет к получению максимальной доходности. Но в случае трейдинга, когда ценовые графики наполнены большим количеством шума это ведет к росту количества сделок. А наличие шума снижает качество прогнозов. Это можно сравнить с попыткой прогнозирования каждой новой свечи. Что потенциально ведет к открытию и закрытию позиции, практически, на каждой новой свече. Вместо того, чтобы определить тренд и открыть позицию в его направлении.

С целью исключения влияния вышеуказанного фактора я решил сделать отступления от уравнения Беллмана и для актуализации модели Q-функции я использовал однонаправленные значения. Максимум я использовал только для действия "Вне рынка".

         Rewards.Clear();
         double reward = Rates[i - 1 + 240].close - Rates[i - 1 + 240].open;
         if(reward >= 0)
           {
            if(!Rewards.Add((float)(reward + (use_target ? DiscountFactor * TempData.At(0) : 0))) ||
               !Rewards.Add((float)(-2 * (use_target ? reward + DiscountFactor * TempData.At(1) : 0)))
               ||
               !Rewards.Add((float)(-reward + (use_target ? DiscountFactor * TempData.At(TempData.Maximum(0, 3)) : 0))))
               return;
           }
         else
            if(!Rewards.Add((float)(2 * reward + (use_target ? DiscountFactor * TempData.At(0) : 0))) ||
               !Rewards.Add((float)(-reward + (use_target ? DiscountFactor * TempData.At(1) : 0))) ||
               !Rewards.Add((float)(reward + (use_target ? DiscountFactor * TempData.At(TempData.Maximum(0, 3)) : 0))))
               return;

После подготовки буфера вознаграждений осуществляем обратный проход обучаемой модели. И проверяем результат выполнения операции.

         if(!StudyNet.backProp(GetPointer(Rewards)))
            return;
        }

На этом завершаются операции вложенного цикла отсчета итераций обучения нашего агента. После его завершения мы осуществляем актуализацию модели Target Net. Наши модели не обладают методами обмена весовыми коэффициентами. И тут я не стал изобретать что-то новое и грандиозное. Вместо этого я решил воспользоваться существующим механизмом сохранения и загрузки модели. Ведь в таком случае мы получаем точную копию модели, со всем её содержимым.

Мы просто сохраняем обучаемую модель в файл. А затем загружаем сохраненную модель из файла в TargetNet. Конечно, не забываем проверить результат выполнения операций.

      if(!StudyNet.Save(FileName + ".nnw", StudyNet.getRecentAverageError(), 0, 0, Rates[i].time, false))
         return;
      float temp1, temp2;
      if(!TargetNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false))
         return;
      use_target = true;
      PrintFormat("Iteration %d, loss %.5f", iter, StudyNet.getRecentAverageError());
     }

После успешной актуализации модели TargetNet мы изменим флаг её использования, выведем информационное сообщение в журнал и перейдем к следующей итерации внешнего цикла.

По завершении процесса обучения мы очищаем комментарии и инициируем закрытие советника обучения модели.

   Comment("");
//---
   ExpertRemove();
  }

С полным кодом советника Вы можете ознакомиться во вложении.

4. Тестирование

Тестирование работы метода осуществлялось на инструменте EURUSD и таймфрейме H1 за последние 2 года. Впрочем, как и все предыдущие эксперименты. Параметры индикаторов использовались заданные в советнике по умолчанию.

Для тестирования была создана сверточная модель следующей архитектуры:

1. Слой исходных данных, 240 элементов (20 свечей, по 12 нейронов на описание одной свечи).
2. Сверточный слой, окно исходных данных 24 (2 свечи), шаг 12 (1 свеча), на выходе 6 фильтров.
3. Сверточный слой, окно исходных данных 2, шаг 1,  2 фильтра.
4. Сверточный слой, окно исходных данных 3, шаг 1,  2 фильтра.
5. Сверточный слой, окно исходных данных 3, шаг 1,  2 фильтра.
6. Полносвязный нейронный слой на 1000 элементов.
7. Полносвязный нейронный слой на 1000 элементов.
8. Полносвязный слой из 3 элементов (слой результатов на 3 действия).

Со 2-го по 7-й слой активировались сигмоидой. Для слоя результатов в качестве функции активации использовался гиперболический тангенс.

График динамики ошибки в процессе обучения модели представлен на графике ниже. Как можно заметить на графике, в процессе обучения ошибка прогнозирования ожидаемой награды довольно быстро стремилась вниз. И после 500 итераций стала близкой к "0". Процесс обучения модели из 1000 итераций завершился с ошибкой 0,00105.

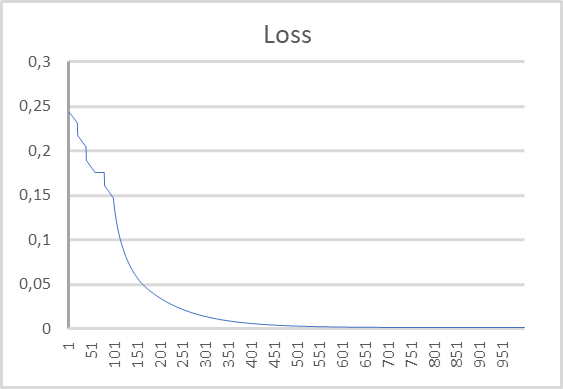
Заключение

В данной статье мы продолжили знакомство с методами обучения с подкреплением. Мы рассмотрели метод глубокого Q-обучения, который был представлен командой DeepMind в 2013 года. С появлением этого метода, можно сказать, начался новый этап в развитии алгоритмов обучения с подкреплением. Именно использование этого метода показало возможность обучения моделей построению стратегий. При этом использование одной модели позволяет обучить её решению различных задач без внесения конструктивных изменений в её архитектуру или гиперпараметры. И это были первые эксперименты, когда обученный алгоритм превзошел результаты эксперта.

Мы посмотрели на реализацию метода средствами MQL5. А результаты, полученные при тестировании модели, демонстрируют возможность использования метода для построения рабочих торговых моделей.

Ссылки

1. Playing Atari with Deep Reinforcement Learning
2. Нейросети — это просто (Часть 25): Практикум Transfer Learning
3. Нейросети — это просто (Часть 26): Обучение с подкреплением

Программы, используемые в статье

#	Имя	Тип	Описание
1	Q-learning.mq5	Советник	Советник для обучения модели
2	NeuroNet.mqh	Библиотека классов	Библиотека для организации моделей нейронных сетей
3	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL для организации моделей нейронных сетей